Introduction

Rapid advancements in industrial technology have posed significant challenges to the global climate. There has been a notable enhancement in people’s living standards and the degree of social modernization. However, this progress comes at the cost of continuous carbon dioxide emissions resulting from industrial development’s consumption of fossil energy (Chen et al. 2022). Consequently, greenhouse gas concentrations in the atmosphere continue to rise, causing a multitude of detrimental impacts on both the ecological environment and the global climate(Liu et al. 2022). To manage and control carbon dioxide emissions, the UNFCCC was initiated in 1992, serving as a cornerstone for international cooperation in tackling climate change. The Paris Agreement, reached in 2016, signified a pivotal achievement in the collective global push to address climate change (Nisbet et al. 2020). Its goal is to limit global warming to well below 2 degrees Celsius through aggressive mitigation of anthropogenic emissions. To achieve this goal, parties have committed to autonomously develop and implement Nationally Determined Contributions to contribute to the global goal of reducing emissions (Liu and Raftery 2021). These collaborative initiatives reflect the worldwide dedication to addressing climate change through concrete measures.

As the largest global carbon emitter, China’s escalating greenhouse gas outputs have drawn significant international scrutiny in climate policy discourse. With accelerated urbanization and rapid economic expansion, China’s urban carbon emissions are facing serious challenges (Yu 2021). Conducting a comprehensive analysis of the spatiotemporal dynamics of UCCE can enhance our comprehension of the carbon emission trends, evolutionary trends, and potential convergence patterns (Liu et al. 2022). Focusing on China as the research subject, a thorough examination of the spatiotemporal evolution features of UCCE plays a vital role in understanding its emission patterns, evolving trends, and potential convergence patterns. This not only holds immense academic significance but also offers valuable guidance for the development and implementation of future carbon-reduction policies.

The remainder of the paper proceeds as follows: a literature review is provided in Section 'Literature review', followed by the research methodology in Section ‘Methods’. Section ‘Measurement results of UCEE’ details the measurement results, while Section ‘Spatial disparities and source decomposition of UCEE in China’ examines spatial disparities in UCEE and their determinants. Section ‘Dynamic evolution process of UCEE in China’ traces the temporal dynamics of UCEE, and Section ‘Research on the convergence of UCEE in China’ assesses its convergence characteristics. Finally, Section ‘Discussion’ and Section ‘Policy implications and Conclusion’ summarizes the findings and discusses policy implications. Figure 1 provides a visual representation of the analysis framework developed in this paper.

Fig. 1: Analysis framework.
figure 1

This figure outlines the overall research process of this paper. Firstly, academic research progress is sorted out through a literature review. Secondly, the research design is developed using the methods of SBM-DEA, kernel density estimation, Dagum Gini coefficient, and convergence modeling. Thirdly, the results are presented in four aspects: carbon emission efficiency measurements, spatial differences, dynamic evolution trends, and convergence analysis. Finally, the research conclusions, discussions, and policy implications of this paper are presented.

Full size image

Literature review

Research on carbon emission efficiency (CEE) can be divided into three main areas: measurement methods of CEE, spatiotemporal evolution of CEE, and convergence of CEE.

Measurement methods of CEE

Diverse regions exhibit variations in carbon-reduction pathways due to diverse economic development models (Zheng et al. 2019). Relying solely on the total carbon emission quantity for measuring carbon-reduction efficiency lacks scientific rigor (Zhang et al. 2020). Certain research efforts have formulated carbon emission calculations for energy consumption, drawing upon the 2006 IPCC Guidelines (Wang et al. 2022; Zhang et al. 2020). In recent academic research, the analytical approaches of SFA (parametric frontier estimation) and DEA (non-parametric benchmarking) have redefined the quantification of sustainability indicators (Dong et al. 2022). These approaches are frequently utilized in existing research to assess UCEE. For instance, a three-stage DEA framework was employed to assess CEE within China’s construction sector (Zhang et al. 2021). The CEE of 251 Chinese cities from 2003 to 2018 was quantified using a nonconvex Data Envelopment Analysis model (Yu and Zhang 2021). A recent evaluation of CEE in 32 carbon-neutrality-committed developed economies applied the super-efficiency Slack-Based Measure (SBM) methodology (Dong et al. 2022). Furthermore, a dual-method approach combining Data Envelopment Analysis (DEA) and Directional Distance Function (DDF) frameworks was utilized to assess CEE (Trinks et al. 2020). Employing an enhanced non-radial directional distance function (NDDF) approach, a study constructed a comprehensive CEE index to evaluate total-factor CEE across China’s 30 provincial-level industrial sectors (Cheng et al. 2018). The evaluation of provincial CEE in China was conducted using the slacks-based Malmquist-Luenberger productivity index methodology. (Huang et al. 2020). These studies demonstrate that DEA has become an increasingly authoritative technique for measuring CEE across various contexts.

Spatiotemporal evolution of CEE

Research investigating the spatiotemporal evolution of CEE is frequently analyzed across multiple administrative scales, such as national, provincial, and urban(Dong et al. 2022; Meng and Yu 2023; Zhang et al. 2020; Zhang et al. 2023). At the national scale, longitudinal patterns in CEE across OECD countries were analyzed, with an assessment of interdependencies between metropolitan developmental trajectories and decarbonization efficacy over time (Wang et al. 2021). At the provincial level, industrial CEE across 30 Chinese provincial administrative divisions from 1998 to 2015 was evaluated applying the min-SBM approach, followed by spatial econometric techniques to identify convergence patterns and determinants (Yang et al. 2021). Through the division of China’s 31 provinces into geospatial clusters, the spatiotemporal dynamics of CEE were examined, revealing distinct evolutionary characteristics (Cui et al. 2021). At the urban scale, the spatiotemporal evolution of UCEE in China was investigated through the construction of traditional and spatial Markov probability transition matrices (Wang et al. 2020). A study of 13 cities in China’s Beijing-Tianjin-Hebei region revealed moderate CEE levels in the area (Xue et al. 2022). Additional analyses have further explored regional variations and methodological advancements in CEE assessment(Liu et al. 2020; Zhang et al. 2020).

Convergence of CEE

Research on the convergence of CEE typically integrates variables including economic openness, population size, economic development, industrialization, urbanization, and green technology as control variables to examine their effects on the convergence of CEE. (Dong et al. 2021; Zheng et al. 2019). These studies generally believe that technological progress (Chen et al. 2020), urbanization level (Li et al. 2022; Zhang et al. 2017; Zhou et al. 2021), green technological innovation (Dong et al. 2022), and energy consumption structure (Li et al. 2021) have a positive impact on the convergence of CEE, while industrial structure (Zheng et al. 2019), stock market value, and FDI (Nguyen et al. 2021) have a weak negative impact on it. Additionally, some studies have explored the club convergence of CEE. For example, the convergence of demand-side and geography-based carbon emission intensity across 70 economies was examined (Bhattacharya et al. 2020). Three convergence indices were applied to analyze the convergence characteristics of China’s agricultural CEE across 30 provinces (Liu and Yang 2021). The club convergence of CEE was systematically investigated through a methodological framework integrating Markov chains, spatial Markov models, and Moran’s I tests (Tang et al. 2021). Generally speaking, when conducting analysis related to the convergence of CEE, economic and social factors such as urbanization level, green technology innovation, foreign direct investment, and economic development level will be introduced into the model analysis as important control variables.

Despite the remarkable progress made by academics in carbon emission studies, there are still some shortcomings, mainly in the following areas. Firstly, the challenge lies in the difficulty of achieving a standardized methodology for calculating CEE. Presently, several approaches exist for assessing CEE, such as DEA, super-efficiency DEA, and CFM, among others. However, there is a lack of unified measurement standards and methods. Secondly, research on the convergence patterns of CEE remains scarce. Existing studies generally consider the impact of a single influencing factor on CEE. Limited research has comprehensively analyzed the convergence of UCEE, both nationally and regionally, while taking into account various economic and social development factors.

Methods

Super-efficient SBM-DEA model

This paper employs the DEA model to evaluate the UCEE of 282 Chinese cities. The traditional DEA model, initially proposed to assess relative efficiency through proportional adjustments to inputs or outputs, was later criticized for its potential misalignment with real-world production dynamics (Charnes et al. 1978; Banker et al. 1984). To overcome these limitations, the SBM model and its super-efficiency variant were introduced, enabling more nuanced evaluations of non-linear and non-directional efficiency attributes (Tone 2001, 2002). Building on these advancements, this paper adopts the SBM super-efficiency model with undesirable outputs (Tone 2004) to assess UCEE. This approach improves measurement accuracy by incorporating real-world production constraints, such as undesirable outputs like carbon emissions. The model is expressed as follows:

$$\rho =\,\min \frac{1-\tfrac{1}{m}{\sum }_{i=1}^{m}\tfrac{{s}_{i}^{-}}{{x}_{ik}}}{1+\tfrac{1}{{s}_{1}+{s}_{2}}\left({\sum }_{r=1}^{{s}_{1}}\tfrac{{s}_{r}^{g}}{{y}_{rk}^{g}}+{\sum }_{r=1}^{{s}_{2}}\tfrac{{s}_{r}^{b}}{{y}_{rk}^{b}}\right)}$$
(1)
$$s.t.\left\{\begin{array}{c}{x}_{k}=X\lambda +{s}^{-}\\ {y}_{k}^{g}={Y}^{g}\lambda -{s}^{g}\\ {y}_{k}^{b}={Y}^{b}\lambda +{s}^{b}\\ \lambda ,{s}^{-},{s}^{g},{s}^{b}\ge 0\end{array}\right.$$
(2)

Where \(\rho\) denotes the UCEE metric, m signifies the count of input indicators, while \({s}_{1}\) and \({s}_{2}\) represent the respective counts of desirable and undesirable output indicators. \({x}_{ik}\), \({y}_{rk}^{g}\), and\({y}_{rk}^{b}\) respectively represent the input vector, expected, and undesired output vectors. \(X\), \({Y}^{g}\), and \({Y}^{b}\) are the input, desired output, and undesired output matrices, respectively, λ is the weight vector; \({s}^{-}\), \({s}^{g}\), and \({s}^{b}\) are the slack variables of the input, desired output, and undesired output, respectively.

Capital investments, workforce allocation, and energy utilization serve as crucial input factors, significantly contributing to the production process. Applying the DEA framework to evaluate UCEE demands the construction of a multidimensional indicator system. The specific indicators for calculating CEE are detailed in Table 1.

Table 1 UCEE accounting framework for 282 cities in China.
Full size table

Dagum Gini coefficient decomposition

This paper adopts the Dagum Gini coefficient (DG coefficient) methodology to quantify and dissect the disparities in UCEE across regions. This methodology comprehensively takes into account the spatial nuances of each region, offering an enhanced version of the traditional Gini coefficient approach. The DG coefficient and its decomposition method break down the total Gini coefficient into three parts (Dagum 1997). The intra-group disparity highlights the level variations within a region, whereas the inter-group disparity underscores the gaps between regions. Additionally, the hypervariable density captures the cross-sectional overlap among regions, mirroring the relative disparity. The methodology for calculating the DG coefficient involves the following steps:

$$G=\frac{{\sum }_{i=1}^{k}{\sum }_{h=1}^{k}{\sum }_{j=1}^{{n}_{j}}{\sum }_{r=1}^{{n}_{h}}|{y}_{ji}-{y}_{hr}|}{2{n}^{2}\overline{y}}$$
(3)

Where \(G\) is the total Gini coefficient of UCEE of Chinese cities, \({n}_{j}\) and \({n}_{h}\) represent the number of cities in region j and region h, respectively, n represents the number of cities, k represents the number of divided regions, \(\overline{y}\) represents the average UCEE of all cities, \({y}_{ji}\) and \({y}_{hr}\) respectively denote the UCEE of the ith city in region j and the rth city in hth region, respectively. In addition, the total Gini coefficient can be further decomposed into three parts: intra-group difference contribution \({G}_{{\rm{w}}}\), inter-group net value difference contribution \({G}_{{\rm{nb}}}\) and hypervariable density contribution \({G}_{{\rm{t}}}\) (Dagum 1997).

$$G={G}_{{\rm{w}}}+{G}_{{\rm{nb}}}+{G}_{{\rm{t}}}$$
(4)

Kernel density estimation

Employing the KDE curve to explore the dynamic shifts in UCEE across Chinese cities serves as a valuable complement to the DG coefficient decomposition, enhancing our understanding of the intricate regional dynamics and evolutionary patterns that the latter might overlook. The KDE curve representing the UCEE of region j is defined by a specific functional form, as outlined below:

$$f({y}_{j})=\frac{1}{{N}_{j}h}\mathop{\sum }\limits_{i=1}^{{N}_{j}}K\left(\frac{{y}_{ji}-\overline{{y}_{j}}}{h}\right)$$
(5)

Where \({N}_{j}\) represents the number of cities in region j, \({y}_{ji}\) represents the UCEE of the ith city in region j, \(\overline{{y}_{j}}\) represents the average UCEE of cities in region j; K(·) is the kernel function, and h is the bandwidth.

Convergence model

The convergence model fundamentally operates through two methodological paradigms: σ-convergence analysis and β-convergence analysis. σ-convergence refers to the trend where the deviation of UCEE in various regions from the mean gradually decreases over time. This paper operationalizes σ-convergence assessment through the relative dispersion metric, and the calculation formula is as follows:

$$\sigma =\frac{\sqrt{{\sum }_{i=1}^{{N}_{j}}{({y}_{ij}-\overline{{y}_{ij}})}^{2}/{N}_{j}}}{\overline{{y}_{ij}}}$$
(6)

Where \({N}_{j}\) represents the number of cities in region j, \({y}_{ij}\) represents the UCEE of the ith city in region j, and \(\overline{{y}_{ij}}\) represents the mean UCEE of cities in region j.

β-convergence test is a method based on the perspective of growth rates. Considering the significant spatial correlation features of UCEE in different regions, this paper simultaneously introduces spatial econometric models for β-convergence analysis. Common spatial econometric models include the Spatial Error Model (SEM), Spatial Durbin Model (SDM), etc. SEM offers the advantage of a simple and intuitive model specification, which is easy to understand and estimate, and it effectively addresses spatial dependencies that are not captured by the dependent or independent variables. However, a limitation of SEM is that it only accounts for spatial dependence in the error term, neglecting potential spatial lag effects in the dependent or independent variables, which may result in model specification bias. SDM has the advantage of simultaneously incorporating spatial lag effects in both the dependent and independent variables, allowing for a more comprehensive capture of spatial dependence. Nonetheless, the disadvantages of SDM are that the model contains more parameters, which makes it more complicated to estimate and interpret.

Absolute β-convergence refers to judging whether there is a convergence trend in UCEE without considering factors that significantly affect UCEE. The formal representation of absolute β-convergence is expressed through the following econometric specification:

$$OLS:\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+{\mu }_{i}+{\eta }_{t}+{\varepsilon }_{i,t}$$
(7)
$$SEM:\begin{array}{cc}{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+{\mu }_{i}+{\eta }_{t}+{u}_{i,t}\quad{u}_{i,t}=\lambda \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}\end{array}{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)$$
(8)
$$\begin{array}{l}SDM:\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+\rho \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)\\ \qquad\qquad\qquad\qquad\quad+\,\gamma \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}{\mathrm{ln}}\,{y}_{i,t}+{\mu }_{i}+\,{\eta }_{t}+{\varepsilon }_{i,t}\end{array}$$
(9)

Where \({y}_{i,t}\) and \({y}_{i,t+1}\) represent the UCEE of city i in periods t and t + 1, respectively. β is the convergence coefficient. The convergence rate is given by \(-\,\mathrm{ln}(1-|\beta |)/T\). \(\rho\) stands as the coefficient of spatial autocorrelation, λ serves as the spatial error coefficient, γ represents the spatial autocorrelation coefficient of the independent variable, \({w}_{ij}\) is the spatial weight matrix, \({\mu }_{i}\), \({\eta }_{t}\), and \({\varepsilon }_{i,t}\) represent region effects, time effects, and the error term, respectively.

Conditional β-convergence integrates variables that drive variations in UCEE into the convergence framework, allowing for an assessment of whether a convergence trend emerges when accounting for these influencing factors. \({X}_{i,t+1}\) represents the set of control variables, and the model is as follows:

$$OLS:\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+\delta {X}_{i,t+1}+{\mu }_{i}+{\eta }_{t}+{\varepsilon }_{i,t}$$
(10)
$$\begin{array}{l}SEM:{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+\delta {X}_{i,t+1}+{\mu }_{i}\\\qquad\qquad\qquad\qquad\quad+\,{\eta }_{t}+{u}_{i,t} {u}_{i,t}=\lambda \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)\end{array}$$
(11)
$$\begin{array}{l}SDM:\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)=\alpha +\beta \,{\mathrm{ln}}\,{y}_{i,t}+\rho \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}\,{\mathrm{ln}}\left(\frac{{y}_{i,t+1}}{{y}_{i,t}}\right)\\\qquad\qquad\qquad\qquad\quad+\,\gamma \mathop{\sum }\limits_{j=1}^{n}{w}_{ij}{\mathrm{ln}}\,{y}_{i,t}+\delta {X}_{i,t+1}+\,{\mu }_{i}+{\eta }_{t}+{\varepsilon }_{i,t}\end{array}$$
(12)

Combined with existing studies in academia (Dong et al. 2021; Wang et al. 2021; Xie et al. 2021), this paper uses economic level, industrial structure, foreign direct investment level, urbanization rate and green technology innovation as control variables in the conditional β-convergence test. Economic level (EL), measured by per capita GDP; industrial structure (IS), measured by the level of industrial rationalization; foreign direct investment (FDI), calculated as the proportion of annual utilized foreign capital relative to a region’s gross domestic product; urbanization rate (UR), calculated as the share of urban population relative to the total population within a region; green technology innovation (GTI) is quantified through the ratio of eco-friendly inventions to the annual total patents filed within the city.

Selection of study objects

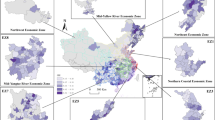
The division of the four major regions is primarily based on the China Statistical Yearbook. According to this source, Eastern China includes 10 provinces, Central China comprises 6 provinces, Western China encompasses 12 provinces, and Northeastern China consists of 3 provinces (Fig. 2).

Fig. 2: Regional division map of China’s four major regions.
figure 2

This figure outlines the selection of study objects. The division of the four major regions is primarily based on the China Statistical Yearbook. According to this source, Eastern China includes 10 provinces—Beijing, Tianjin, Hebei, Shanghai, Jiangsu, Zhejiang, Fujian, Shandong, Guangdong, and Hainan, Central China comprises 6 provinces—Shanxi, Anhui, Jiangxi, Henan, Hubei, and Hunan; Western China encompasses 12 provinces—Inner Mongolia, Guangxi, Chongqing, Sichuan, Guizhou, Yunnan, Tibet, Shaanxi, Gansu, Qinghai, Ningxia, and Xinjiang, and Northeastern China consists of 3 provinces—Liaoning, Jilin, and Heilongjiang.

Full size image

Data sources

In this study, carbon emission data were obtained from the China City Statistical Yearbook and the China Urban Construction Statistical Yearbook for various years. Energy consumption data were sourced from the China Energy Statistical Yearbook for the corresponding years. The remaining data were collected from the Chinese Research Data Services Platform (CNRDS).

Measurement results of UCEE

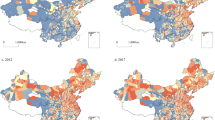
This research employed ArcGIS to produce spatial maps illustrating the distribution of UCEE among 282 cities, employing the natural breaks classification technique to categorize the efficiency scores of these cities into five distinct groups. Figure 3 portrays the geographical variation of UCEE over the years 2011, 2014, 2016, and 2019 among 282 cities in China, revealing the following insights:

  1. (1)

    Chinese UCEE exhibits a noticeable “club convergence” characteristic. During the observation period, cities with high UCEE are mainly situated within high-growth economic corridors, notably the eastern coastal industrial belt, the Guangdong-Hong Kong-Macao Greater Bay Area, the central Yangtze River urban cluster, and the Chengdu-Chongqing economic circle. Cities displaying lower UCEE are predominantly situated in Northeastern China and Western China, as well as the Inner Mongolia Autonomous Region. This “club convergence” phenomenon is primarily attributed to the spatial progression of China’s economic development, gradually advancing from the eastern coastal regions towards the central and western inland areas. The eastern coastal regions exhibit significantly higher levels of openness to international trade and faster advancement in new industrialization compared to the Central China and Western China.

  2. (2)

    This concentration of talent, capital, and technological advancements in the eastern coastal regions has fueled a swift enhancement in UCEE of these cities. Eastern cities consistently demonstrate superior UCEE levels, averaging at 0.407 over the observed timeframe. There are considerable variations in UCEE between the Central China and Western China. The Northeastern China consistently records lower UCEE levels, averaging at 0.336 over the entire observation period. The rapid economic growth in Eastern China since the reform and opening-up, fueled by advanced manufacturing and service sectors, likely accounts for its consistently higher UCEE. Inland regions of the Central China and Western China might experience a lag in the application of green carbon-reduction technologies, but the evolution of regional integration strategies allows these areas to quickly adopt and apply advanced production technologies from more developed regions. Therefore, the Central China and Western China exhibit noticeable trends in UCEE variation. The Northeastern China, possibly influenced by the transformation of its industrial base in the past, has seen a reduction in industrial capacity, leading to a relatively lower UCEE.

Fig. 3: Spatiotemporal distribution map of UCEE in China.
figure 3

This picture reports the characteristics of the spatial distribution of UCEE in China. The four subplots (a–d) illustrate the spatial distribution of UCEE across 282 Chinese cities in the years 2011, 2014, 2016, and 2019, respectively. Utilizing the Natural Breaks Classification, the UCEE values of these cities are categorized into five distinct groups: [0.025–0.138], [0.139–0.239], [0.240–0.315], [0.316–0.400], and [0.401–1.024]. Blank areas denote missing data.

Full size image

Spatial disparities and source decomposition of UCEE in China

Disparities in UCEE within each region

Table 2 presents the intra-group Gini coefficients calculated using the DG coefficient for UCEE across 282 cities nationwide and the four regions. The national average intra-group Gini coefficient pertaining to UCEE stood at 0.178 over the study’s duration. Except for minor increases in individual years, it exhibited an overall trend of fluctuating decline. This suggests that the disparities in UCEE among cities nationwide are gradually diminishing, indicating a decreasing level of imbalance. From a regional perspective, the average intra-group Gini coefficient in the Eastern China and Central China falls below the national average, suggesting a relatively lower degree of imbalance within these areas. The Western China’s average intra-group Gini coefficient, standing at 0.182 and topping all regions, continues to show an upward trajectory since 2016. The primary factor contributing to this trend stems from accelerated growth within the Chengdu-Chongqing economic circle, which has made the disparities between cities in the Western China. The gap in development quality has further widened, and the pace of urban industrial transformation and the strides in urban carbon emission reduction are becoming increasingly inconsistent.

Table 2 Changes in the Gini coefficient across the country and four regions.
Full size table

Disparities in UCEE among regions

Figure 4 depicts the inter-group disparities in UCEE among cities in the four regions, as quantified by the DG coefficient. Regarding the overall development trend, the shaded area in Fig. 4 exhibits a consistent decline. This indicates that over time, the differentiation features among regions are gradually diminishing. Some regions can rapidly improve UCEE through the development of green technologies and adjustments in industrial structure. Although certain areas experience a slower improvement in UCEE due to regional policies, the overall differences in UCEE among regions are consistently decreasing.

Fig. 4: Changes in the inter-group Gini coefficient among the four regions in China.
figure 4

This figure depicts the inter-group disparities in UCEE among cities in the four regions, as quantified by the Dagum Gini coefficient. The decrease in the area of the shaded portion of the graph indicates that the value of the inter-group Dagum Gini coefficient between the two regions is decreasing, which suggests that the disparities between the regions are getting smaller.

Full size image

Sources and contributions of disparities in UCEE across regions

The overall variation in the sample data can be segmented into three components. Figure 5 illustrates the absolute values and relative proportions of each of these components. Analysis of the variations in contribution rates among the three components reveals that hypervariable density becomes the primary source of contribution. As urban industries transition towards a low-carbon paradigm, the widening disparities in UCEE among cities contribute to the polarization of efficiency within respective regions. Areas with superior UCEE encompass cities with relatively lower efficiency, whereas regions with inferior UCEE include cities that exhibit higher efficiency. This phenomenon of overlapping UCEE contributes to the spatial imbalance of UCEE.

Fig. 5: Sources of spatial disparities in UCEE in China.
figure 5

By using the Dagum Gini coefficient and its decomposition, the overall variation in the sample data can be divided into three components: intra-group disparity, inter-group disparity, and hypervariable density. This figure illustrates the absolute values and relative proportions of each component. Panel a presents the absolute magnitudes of each components, while Panel b illustrates their corresponding proportional distributions.

Full size image

Dynamic evolution process of UCEE in China

The use of the DG coefficient decomposition is helpful in identifying regional disparities and specific sources of UCEE in both the nationwide and the four regions. Nevertheless, it falls short in capturing the dynamic evolution traits of carbon UCEE within individual regions. To overcome this limitation, this paper adopts the KDE approach, leveraging attributes like distribution position, peak shape, ductility, and peak count in the KDE curve to unravel the dynamic evolution of UCEE among Chinese cities.

Figure 6 shows the specific kernel density estimation results, and Table 3 reports the corresponding dynamic evolution characteristics.

Fig. 6: Dynamic evolution trend chart of UCEE in China.
figure 6

This figure shows the specific kernel density estimation results. The five subplots (a–e) in the figure depict the dynamic evolution trend of UCEE for the nationwide, Eastern China, Central China, Western China, and Northeastern China, respectively. In the three-dimensional surface plot, the x-axis represents UCEE, the y-axis denotes the chronological progression (year), and the z-axis quantifies the kernel density values.

Full size image
Table 3 Distribution characteristics of KDE curves of UCEE across the country and four regions.
Full size table
  1. (1)

    Distribution Location. The nationwide KDE curve for UCEE nationwide shows a rightward shift, indicating continuous improvement in UCEE across most Chinese cities, reflecting the success of China’s “dual carbon” policy. Regionally, the Eastern China and Central China exhibit significant rightward shifts, while Western China initially shifts leftward before trending right. In contrast, the Northeastern China’s curve shifts leftward, highlighting the carbon-reduction challenges faced by the Western China and Northeastern China, which require further UCEE enhancements.

  2. (2)

    Main Peak Shape. At the nationwide level, as well as in the Eastern China and Central China, the main peak of the KDE curve shows a significant upward trend and increased width, indicating reduced variation in UCEE among cities and a convergence of disparities. The Western China experienced a downward trend and increased width but rebounded after 2015, ultimately showing an upward trend. In the Northeastern China, the main peak exhibits a downward slope and increased breadth, reflecting rising disparities in UCEE and significant differences in energy-saving and carbon-reduction achievements among cities.

  3. (3)

    Ductility. The KDE curves for the nationwide level and the four regions display right-skewed tails, indicating the presence of cities with significantly higher UCEE within each region. Nationally, as well as in the Eastern China and Central China, the ductility shows a converging trend, suggesting a narrowing gap between extreme and average values. In contrast, the Western China and Northeastern China exhibit divergent ductility, with certain cities consistently maintaining lower UCEE levels and persistent disparities compared to the regional average.

  4. (4)

    Number of Peaks. Nationally, as well as in the Eastern China and Central China, the KDE curves maintain a unimodal shape, indicating low levels of differentiation and the absence of polarization. In Western China, the curve transitions from a dual-peak to a multi-peak configuration, reflecting a shift from polarization to diverse UCEE levels. In the Northeastern China, the curve evolves from a single peak to a dual-peak pattern, with a clear separation between peaks, underscoring significant spatial polarization.

Research on the convergence of UCEE in China

σ-convergence test

UCEE exhibits significant disparities among different cities and regions. This paper utilizes the coefficient of variation as a metric to quantify σ-convergence, enabling an analysis of the spatial convergence patterns of UCEE from a stock-based perspective. Table 4 reports the σ-convergence results of UCEE for 282 cities nationwide and the four major regions. Nationally, the coefficient of variation for UCEE fluctuates between 0.313 and 0.392, showing an overall downward trend and σ-convergence characteristics. Regionally, the Eastern China has the lowest average coefficient of variation (0.289), reflecting rapid economic development and reduced disparities in UCEE. The Central China (averaging 0.306) exhibits a declining trend in most years, indicating σ-convergence and improved UCEE. In contrast, the Western China has the highest average coefficient (0.458), with values rising from 0.287 in 2011 to 0.637 in 2018, highlighting increasing internal disparities and the absence of σ-convergence. The Northeastern China shows a fluctuating trend, ultimately achieving σ-convergence with a lower final coefficient compared to the initial value.

Table 4 σ-convergence test results across the country and four regions.
Full size table

β-convergence test

(a) Absolute β-convergence. Table 5 reports the spatial absolute β-convergence results for 282 cities across the country and four regions. There may be disparities in the spatial effect patterns of UCEE in different parts. Firstly, the presence of spatial effects on the absolute β-convergence of UCEE at the nationwide level and within the four regions is assessed through LM tests. Secondly, the final spatial econometric model specification was selected through rigorous LR tests and Wald tests. Subsequently, random effects or fixed effects are selected according to the results of the Hausman test. Finally, the specific form of the fixed effects is chosen based on the tests.

Table 5 Absolute β-convergence test results across the country and four regions.
Full size table

The results from Table 5 indicate:

  1. (1)

    Absolute β-convergence in UCEE is observed at both national and regional scales, and all coefficients remain statistically negative. This implies that, without considering other significant factors, there is a convergent trend in UCEE at both the nationwide and regional perspectives. Consistent with β-convergence theory, initially disadvantaged cities exhibit accelerated catch-up rates in UCEE, ultimately leading to long-term equilibrium alignment across urban systems.

  2. (2)

    In terms of convergent rates, the UCEE convergence varies between the nationwide and the four regions. The nationwide convergent rate is 0.102, with the rates in the Eastern, Central, and Northeastern China being below the nationwide mean at 0.079, 0.100, and 0.049, respectively. Conversely, the Western China exhibits a higher convergent rate, surpassing the nationwide average at 0.158.

  3. (3)

    The nationwide and four regions exhibit distinct spatial effects. The spatial autocorrelation coefficients for the nationwide, Eastern China, and Central China are significantly positive, indicating that changes in UCEE in one city are positively influenced by changes in neighboring cities within the same region.

(b) Conditional β-convergence. The aforementioned analyses assume constant economic, social, and natural factors, which deviate from real-world conditions. Therefore, further investigation into conditional β-convergence is warranted, considering the dynamic interplay of economic, social, and natural factors. Table 6 reports the results of spatial conditional β-convergence for 282 cities nationwide and four regions. According to the results in Table 6:

Table 6 Conditional β-convergence test results across the country and four regions.
Full size table
  1. (1)

    The conditional β-convergence analysis reveals statistically significant negative coefficients (p < 0.01) for UCEE at both national and regional scales. This implies that, even when accounting for economic level, foreign investment intensity, industrial structure, urbanization rate, and the level of green technological innovation, empirical results confirm persistent UCEE convergence toward equilibrium states across national and regional scales.

  2. (2)

    The convergence rates across all regions have shown improvement compared to those under absolute β-convergence. This empirically validates the theoretical appropriateness of the selected control variables in capturing conditional convergence dynamics. Specifically, the Western China exhibits the fastest convergence speed at 0.171, exceeding the national mean (0.108). The Central China’s convergence speed is slightly below the national average, at 0.107. Meanwhile, the Eastern China and Northeastern China display convergence speeds of 0.084 and 0.06, respectively.

  3. (3)

    From a spatial perspective, the spatial autocorrelation coefficients for the nationwide level, Eastern China, Central China, and Western China are 0.645, 0.408, 0.774, and 0.295, respectively. The results demonstrate the presence of positive spatial spillover effects in these regions, which can drive improvements in UCEE in neighboring areas. In contrast, the spatial autocorrelation coefficient for the Northeastern China is −0.525, indicating a negative spatial spillover effect. This suggests significant disparities in development levels within the Northeastern China, potentially reflecting a “Matthew effect” where stronger areas become stronger and weaker areas become weaker.

Discussion

This paper employs an integrated analytical framework combining the super-efficiency DEA model, the DG coefficient, the kernel density estimation, and the spatial convergence model to systematically examine UCEE patterns across 282 Chinese cities during 2011–2019, uncovering critical insights into spatial disparities, temporal trends, and regional convergence mechanisms of UCEE.

Discussion of regional differences

This paper found that the UCEE in China shows a decreasing trend of “East—Center—West—Northeast,” which aligns with established literature in the field (Liu et al. 2023; Shen et al. 2024). The Eastern China has a significant lead in UCEE due to its developed economy and high technological level, while the Western China has a lower efficiency and prominent intra-group differences due to its lagging economic advancement and dependence on resource-intensive industries (Yang et al. 2022). The intra-group differences in the Central China widened after 2016, which may be related to the lack of green technology upgrading in industrial transfer(Shi et al. 2022), while the Northeastern China has low efficiency and smaller differences due to its single economic structure(Liu et al. 2023). The observed convergence across regions likely reflects the implementation of China’s coordinated regional development strategy, demonstrating its measurable impact on reducing spatial inequalities. The hypervariable density suggests that the spatial distribution of UCEE has a cross-over phenomenon, reflecting the influence of inter-city economic linkages and technology diffusion(Wen et al. 2018).

Discussion of dynamic evolution

In terms of dynamic evolution, the UCEE of the nationwide, Eastern China and Central China all increased across the examined timeframe, and the intra-regional disparities gradually narrowed, which was closely related to industrial upgrading, technological innovation, and regional coordinated development policies (Wang et al. 2024). The UCEE of the Western China declined first and then increased, which may be rooted in the foundational economic structure privileging energy-demanding production (Yao et al. 2023), whereas the UCEE of the Northeastern China fluctuated and declined, reflecting the difficulty of economic transformation and the reality of a large proportion of traditional industries (Wen et al. 2018). The phenomenon of spatial polarization in both regions may be related to the uneven distribution of resources and differences in policy support (Xu et al. 2022).

Discussion of dynamic evolution

In terms of convergence characteristics, σ-convergence, absolute β-convergence, and conditional β-convergence exist in the nationwide, Eastern China, Central China, and Northeastern China, while only absolute β-convergence and conditional β-convergence exist in the Western China, which is closely associated with significant regional disparities in economic advancement and resource distribution (Wu and Zhao 2025). The Western China and Central China converge faster, which may be related to the narrowing of the technology gap (Cai et al. 2025), while the Northeastern China has the slowest rate of convergence, reflecting its economic transformation and deficiencies in innovation capacity (Li and Wang 2022). The impacts of EL, IS, FDI, UR, and GTI on UCEE are significantly heterogeneous, consistent with previous studies (Lu and Wu 2025; Wan et al. 2025).

Policy implications and conclusion

Policy implications

Building on the empirical evidence, this paper proposes targeted governance recommendations informed by three strategic dimensions:

  1. (1)

    Promote comprehensive and coordinated carbon-reduction policies. The government should adopt differentiated carbon mitigation strategies that account for heterogeneous urban characteristics and developmental priorities across cities. Clear carbon trading rules should be established to encourage nationwide participation, fostering a market-driven mechanism for emission reduction. Enhanced inter-departmental and inter-group collaboration is essential to integrate resources effectively and create a unified policy framework.

  2. (2)

    Implement region-specific carbon-reduction strategies. Tailored policies should be designed to address regional disparities. For less developed regions, support for industrial upgrades and clean technology adoption is crucial to improve carbon efficiency without hindering economic growth. In developed regions, stricter emission controls should target energy-intensive industries, complemented by a “dual control” strategy to manage energy consumption and optimize energy structures.

  3. (3)

    Leverage diverse policy tools for carbon reduction. The government should prioritize industrial restructuring, promoting green transitions in traditional sectors, and fostering high-tech, eco-friendly industries. Attracting foreign investment into clean technologies and advancing green urbanization are also key. Additionally, increased support for eco-innovation initiatives will stimulate greater corporate investment in research and development, driving sustainable progress.

Conclusion

This paper arrives at three fundamental conclusions:

  1. (1)

    UCEE follows a descending pattern from “East—Center—West—Northeast”, with the Eastern China consistently outperforming the nationwide average. Intra-regional disparities are narrowing in the Eastern China but rising in the Central China since 2016, while the Northeast China shows low UCEE and minimal disparities. Inter-group disparities are decreasing, with hypervariable density being the primary source of overall differences due to overlapping UCEE patterns across regions.

  2. (2)

    Nationwide, the Eastern China and Central China show improving UCEE with narrowing intra-regional disparities, while the Western China and Northeast China exhibit complex trends, including spatial polarization and fluctuating UCEE levels.

  3. (3)

    σ-convergence, absolute β-convergence, and conditional β-convergence are observed in most regions except the Western China, which lacks σ-convergence. Convergence rates vary, with Western China and Central China converging fastest, followed by the Eastern China and Northeast China. Economic, industrial, and technological factors significantly influence UCEE changes, showing regional heterogeneity.

Although this paper has made a series of explorations in studying the UCEE in China, it has some noteworthy limitations that should be considered:

  1. (1)

    Limitations in research data: This study performed a spatiotemporal analysis of carbon emissions across Chinese cities, albeit with a limited timeframe due to constraints in data availability. A study with a longer time span could uncover more stable patterns and causal relationships, offering greater analytical depth and comprehensiveness.

  2. (2)

    The depth of research could be expanded: While this paper examined the influence of various factors on conditional β-convergence of UCEE, it did not delve into the specific mechanisms or pathways through which these factors exert their effects. A systematic examination of the distinct mechanisms through which various factors influence UCEE would contribute to providing more practical policy implications for enhancing UCEE.