Introduction

Ribonucleic acid (RNA) is a fundamental molecule for living organisms. In addition to its central role as messenger RNA used in transcription, RNA molecules carry out various biological functions as non-coding RNAs (ncRNAs). ncRNAs include ribosomal RNAs (rRNAs) and transfer RNAs (tRNAs), which probably are most well-known ncRNAs, as well as small nuclear RNAs (snRNAs)1, small nucleolar RNAs (snoRNAs)2, circular RNAs (circRNAs)3, and ribozymes4, which are involved in functions such as gene regulation and modification5,6. The RNACentral database7 currently contains over thirty million ncRNA sequences. ncRNAs are garnered attention also in drug design as new drugs may be designed to inhibit or mimic the activity of functional RNAs8.

To understand functional mechanisms of ncRNA, obtaining tertiary structure information is crucial. However, our knowledge of RNA structures remains limited due to the scarcity of experimentally determined RNA structures. The Protein Data Bank (PDB)9 contains approximately 6000 entries, including RNA molecules, which constitute only about 3% of the entire PDB entries. Out of the 4094 RNA families listed in the Rfam database (v14.8)10, merely 124 (3.0%) have one or more corresponding structures in the PDB.

To bridge the gap between sequence and structure knowledge, computational methods have been developed for predicting the tertiary structure of RNA from the sequence. Conventional methods can be roughly classified into two categories, template-based and energy minimization-based methods. Template-based prediction methods include RNAbuilder11 and ModeRNA12, which utilizes global or local structure information from previously solved homologous RNA molecules. While these methods can build accurate models when an appropriate template is available, a drawback is the limited availability of templates for many cases. On the other hand, energy minimization-based prediction methods, such as SimRNA13 and FARFAR214, overcome the limitation of template-based methods by folding RNA structures through minimization of an energy term. However, this approach has its own drawbacks, which include extensive computational time, especially for large RNA structures, and imperfect energy term that leads to incorrect structures. To address the challenge of model selection arising from an imperfect energy term, a scoring function was specifically designed using deep learning15. More recently, methods were developed that use deep learning. DeepFoldRNA16 takes a multiple sequence alignment (MSA) and predicted secondary structure as inputs and outputs distances between three nucleotide atoms and torsion angles between nucleotides and along the main chain. These constraints are used to build a coarse-grained model by a custom folding simulation, followed by a full-atom reconstruction using SimRNA13 and QRNAS17. trRosettaRNA18 is a deep learning model that takes an MSA and predicted secondary structures as input and predicts various angles and distances along the main-chain and between nucleotides, which serve as constraints for building the full atomic model using pyRosetta19. RhoFold20 is an end-to-end model to directly predict the three-dimensional structure of RNA from an MSA. The MSA is first processed by a pre-trained RNA language model called RNA-FM21.

Here, we introduce NuFold, a de novo RNA structure prediction method, using an end-to-end deep network architecture. This method takes a target RNA sequence and generates a tertiary structure model through a single network trained comprehensively. The network architecture is based on that of AlphaFold2 (AF2)22, a protein structure prediction method that achieved a distinctive performance in CASP14 (Critical Assessment of Structure Prediction) in 202023. Building upon the AF2 architecture, we made significant modifications. Those include accommodations of nucleic acid sequences, to take secondary structures as input, modifications for predicting RNA-specific inter-base angles, distances, and atom positions, and to allow complete flexibility in the RNA structure representation. Our implementation, termed the nucleobase center representation, enables the optimization of angles of all rotatable bonds of nucleobases. This representation allows us to reproduce any flexibility that exists in the base backbone, providing the ground for accurate base conformation modeling. In comparison with above mentioned deep learning-based approaches, NuFold stands out as a unique end-to-end model that directly outputs full atomic models from MSA and predicted secondary structure, unlike many other deep learning models that predict atom-atom distance and angle constraints to use in the subsequent structure-modeling procedure. RhoFold is the only other end-to-end model, which has a similar architecture as NuFold. Apparent differences in the two architectures are that RhoFold uses a language model to process an input MSA while NuFold takes an MSA in a more direct way similar to AF2 and NuFold takes predicted secondary structure information as another input.

RNA structure prediction is, arguably, more difficult than protein counterpart because the molecule is more flexible and available structural data is very limited compared to proteins. We examined several approaches to overcome this difficulty: To increase the number of training data, we employed a self-distillation technique24, where predicted structures which are believed to be accurate enough, are included in a training set. To increase the depth of input MSAs, we incorporated metagenomic sequences, because the use of metagenome was shown to be effective in protein structure prediction25,26. During training, we adopted a dynamic sampling strategy, which schedules a balance of easy and difficult targets27. Furthermore, we also tested a couple of smaller networks, because the training data we have is smaller than protein datasets used in the original AF2. We report approaches that were effective in improving the modeling accuracy. NuFold achieved a full-atom RMSD of 5 Å or less for most of the test targets. With an RMSD of 5 Å or less, NuFold accurately built the conformation almost perfectly, except for flexible terminal and loop regions. Additionally, it was found that utilizing metagenomic sequences for input MSAs and optimizing the number of recycling enhances NuFold’s prediction performance. NuFold is made available in the forms of source code and a Google Colab Notebook to serve both the computational biology community who aim for further development of RNA structure prediction methods and biology researchers who are interested in obtaining structure models for their RNA sequences.

Results

Overview of NuFold

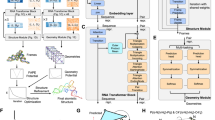
The architecture of NuFold is depicted in Fig. 1a. NuFold is an end-to-end network that predicts the all-atom tertiary structure of RNA from its sequence. NuFold shares the basic framework of deep learning architecture as AF2, which consists of three main modules: the first module, which deals with input data, the second module, the Evoformer blocks, which generates embeddings of the multiple sequence alignments (MSA) collected for the target sequence and residue pairwise information, and the last module, the structure module, which constructs the three-dimensional (3D) structure models of the target RNA. For an input RNA sequence, an MSA is generated by rMSA28 and a predicted secondary structure is generated by IPknot29,30. The Structure Module utilizes Flexible Nucleobase Center Representation shown in Fig. 1b. In the structural module of NuFold, we define the base frame with the following four atoms: O4’, C1’, C2’, and the first nitrogen of the base (N1 for C and U, N9 for G and A). All other atoms are partitioned into ten frames, which are then iteratively bonded using predicted torsion angles on the bonds between frames as a guiding principle (Fig. 1b). As was done in AF2 for amino acids, these definitions are hardcoded for RNA. This representation of RNA nucleotides can reproduce the full dynamics of nucleotide conformations. In Fig. 1c, we show two different conformations of nucleotides, C3’-endo and C2’-endo sugar conformations. These two conformations share about 82% and 10% of nucleotides in known RNA structures and their structures differ by a root mean square deviation (RMSD) of around 0.3 to 0.5 Å31. With the NuFold structure presentation, these two conformations are precisely built with an RMSD of 0.04 Å and 0.03 Å for the C3’-endo and C2’-endo conformations, respectively.

Fig. 1: Overview of NuFold.
figure 1

a The architecture of NuFold. NuFold is an end-to-end architecture for RNA tertiary structure prediction, taking target sequence information and generating corresponding full-atom tertiary structures. The query sequence is initially used to construct an MSA, which, along with predicted secondary structure information, serves as input to the NuFold network. The NuFold network comprises three components: Preprocessing, EvoFormer, a transformer model that extracts co-evolutional information from MSA and embeds it into both single and pair representations; and the structure module, which further processes the embedded information into 3D structures. These processes are iteratively performed in a recycling process to refine predictions. b The network predicts two key components for full-atom structure prediction: the translation and rotation of the base frame, along with a set of torsion angles derived from the base frame. These torsion angles are used to extend new atoms. c Representing two puckering conformations, C3’-endo and C2’-endo conformations. Green and magenta structures represent ground truth and structures built by NuFold, respectively. NuFold predicts torsion angles not only for the main chain or chi angles but also for the ribose ring, allowing for the reproduction of sugar-puckering formations. RMSD of the structures built were 0.04 Å and 0.03 Å, respectively, for C3’-endo and C2’-endo conformations.

Full size image

NuFold was trained on 2860 RNA chains, validated on 48 chains during training, and tested primarily on 36 test RNAs. Entries across the training, the validation, and the test set are non-redundant using a commonly used nucleotide sequence identity cutoff of 80%. These entries originate from RNA entries downloaded from the Protein Data Bank (PDB)9 as of February 28th, 2022. We also used 11101 entries from the bpRNA-1m32 dataset for a self-distillation dataset, which was combined with the training dataset during training. Further details can be found in Methods.

Overall structure prediction performance of NuFold

The structure prediction accuracy for the 36 test targets by different models of NuFold is summarized in Table 1. The first two results, RMSD-centric and GDT-TS-centric, represent outcomes from two network models. The former was selected from a training step that exhibited the smallest average root mean square deviation (RMSD) to the native structure on the validation dataset, while the latter was chosen at a training step demonstrating the highest average Global Distance Test-Total Score (GDT-TS)33 on the validation dataset. RMSD was computed for C1’ atoms in nucleotides. GDT-TS measures overall structural similarity between a predicted and the native structures, ranging from 0 to 1 with 1 indicating exact agreement with the native. These two network models showed similar performance on the test set, folding 25 RNA targets within an RMSD of 6 Å and showing comparable values in average RMSD and GDT-TS. In a direct comparison of the structures generated by these models, the RMSD-centric model generated a lower RMSD (by more than 0.5 Å) structure for four targets, while the GDT-TS centric model generated a lower RMSD structure for two targets. For the remaining 30 targets, the structure generated by both models were within 0.5 Å RMSD, denoted as ties in Table 1. We designated the RMSD-centric model as the baseline due to its better performance compared to the GDT-TS-centric model and used it for comparison with other variants of NuFold.

Table 1 Overall performance of NuFold on the test set using different models
Full size table

Effect of various factors and techniques

In Fig. 2, we investigated how the length of the targets and the depth of input MSAs affected the modeling results of the baseline model. Results from both the test set (blue circles) and the validation set (orange triangles) are shown. In Fig. 2a, we observed a modest correlation between the target length and the modeling accuracy. All small RNA targets shorter than 50 nucleotides (nt) in the test set folded within a 6 Å RMSD, while the fraction of targets with a large RMSD increased for targets with more than 100 nt. The same trend was observed both in the testing and validation sets. Figures 2b, c investigate the effect of the depth of input MSAs in terms of the raw counts of sequences in MSAs (Fig. 2b) and the number of effective counts (Nf)34 of MSAs (Fig. 2c). The effective count of an MSA is the number of non-redundant sequences in the MSA that have similarities below the cutoff of each other. Here, we used 80% as the cutoff of sequence identity to consider if two sequences are redundant or not, which is the standard cutoff value used in the rMSA pipeline. We observed a weak trend that shallow MSAs suffer in modeling results. Out of 23 targets in the test set with less than 100 Nfs in their MSAs, 39.3% of the targets had an RMSD larger than 6 Å. In the validation set, out of 31 targets with less than 100 effective counts, 45.2% of the targets had an RMSD larger than 6 Å.

Fig. 2: The effect of the target length, the MSA depth, recycling, and metagenome MSAs on the modeling accuracy.
figure 2

a–c 36 targets in the test set (cyan circles) and 48 targets in the validation set (orange triangles) are plotted. a RMSD (Å) relative to the length of query RNA sequence and RMSD. b RMSD (Å) relative to the raw count of sequences in MSAs. c RMSD (Å) relative to the number of effective sequences (Nf) in MSAs. d The average RMSD of generated structures relative to the number of recycles (solid lines, left axis, Å) and pLDDT (dashed lines, right axis). The testing data and validation data were shown in cyan and orange, respectively. e The prediction performance comparison between the Baseline model, which utilized three times recycling, and the best structure for each target in all 30 recycle. The performance was measured by RMSD (Å). f The prediction performance comparison between the Baseline model and the best pLDDT model from 11 ± 3 recycles. The performance was measured by RMSD (Å). g The depth of MSAs by the metagenome database search relative to the original MSAs. Meta Only, the MSA from the metagenome search; Concat. is a simple concatenation of the metagenome MSA and the original MSA; Filtered, redundant sequences are removed from the Concat MSA. h The performance comparison between the baseline and the selected structure based on the pLDDT score. The source of the MSA of the selected structure is indicated by different symbols. i Performance changes by differences in MSA depth. A positive Δ MSA indicates that the selected MSA contains more sequences than the baseline MSA.

Full size image

Effect of recycles

Turning our attention back to Table 1, in the middle block labeled as Baseline + , we attempted to improve the modeling accuracy of the NuFold baseline model by increasing the MSA depth by adding metagenome sequences and by increasing the number of recycles.

It has been reported that the increasing the number of recycles in general improves structure prediction accuracy in the case of proteins22,35. Recycle mixes the output atomic coordinates and internal representation vectors from the previous run with the original input and uses them as input for the network (the green box in Fig. 1). During training, zero to three recycles were randomly selected for each batch. In inference, we used three recycles in the baseline model. Here we investigated the effect of up to 30 recycles in RMSD of the predicted structures.

In Fig. 2d, we examined how the average RMSD and pLDDT, the predicted LDDT (local Distance Difference Test)36, which is a measure of the network’s self-evaluation of the model accuracy changed over 30 recycle iterations. In both test (cyan) and validation (orange) cases, the average model accuracy in RMSD (solid lines) improved as more recycles were applied but up to around 10 (the lowest averaged RMSD was achieved at the eighth recycles in the test set and at the eleventh for the validation set). But after that point, the RMSD went worse again with more recycle iterations. On the other hand, pLDDT sharply increased up to around five recycle iterations and continuously went higher as more recycles were accumulated (dashed lines in Fig. 2e, f). Thus, obviously the model becomes overconfident at later iterations of recycles.

In almost all the cases a better model (with a smaller RMSD) was generated in extended iterations of recycles compared to the baseline model that performs three recycles (Fig. 2e). The average RMSD of the best model among extended recycles was 6.38 Å, which is a 0.6 Å improvement from that of the baseline model (6.98 Å). However, selecting the best structure is not easy because pLDDT almost monotonically increases with recycle iterations and does not precisely indicate the best structure (Fig. 2d). In Fig. 2f, on the test set, we selected the highest pLDDT structure from the 8 to 14 recycles, which is ±3 recycles around the 11th recycle, which yielded the lowest average RMSD in the validation set. This strategy made a small improvement in an average RMSD to 6.87 Å, a 0.11 Å improvement from the baseline.

Effect of using metagenome

Subsequently, we used metagenome sequences for MSA construction. The quality of metagenome sequences is not as good as curated sequences in UniProt but it is known that increasing the MSA depth and diversity generally improves modeling accuracy for proteins25,26.

In order to use metagenomic data for MSA, we first created a metagenomic sequence database by combining several metagenomic data sources. We constructed a metagenome sequence database by combining NCBI env_nt, TARA Ocean Metagenome37, MGnify MAG38, and all MGnify contigs, which resulted in a total size of 3.0 Tb. These sources were not included in the rMSA pipeline that we initially used and were 3.2 times larger than the databases used in the original rMSA setting (940 Mb). To search the metagenome database we constructed, we first used the query RNA sequence to search the metagenome database with BLASTn and created a covariance model (CM) with Infernal from the results. Then, we used the CM as input for Infernal’s cmsearch to search the same metagenomic database. We combined the resulting metagenome MSA with the original MSA from rMSA pipeline in two ways, a simple concatenation, named “Concat” and a filtered Concat MSA that removed redundancies with hhfilter. This version is named “Filtered”.

In Fig. 2g, we examined how much sequences were increased in the metagenome MSAs. increase of sequences observed in metagenome the results were shown in Fig. 2g. When we compare the filtered MSA with the original MSA, the depth of MSA increased for 94.4% of the cases (34 out of 36 cases). However, a substantial increase of the MSA depth was observed mainly for cases when the original MSAs already had enough sequences, e.g. over 5000. Out of 25 targets with less than 5000 sequences in their original MSAs, only 15 targets had more than 10 sequence increase.

Next, we examined whether we could utilize metagenome MSAs to improve modeling performance. We ran the baseline NuFold with three metagenome MSAs and the original MSA, generating four structure models. We then selected the model with the highest pLDDT. In Fig. 2h, we compared the RMSD of the selected structure to the structure generated from the original MSA (Fig. 2i). This protocol achieved a better or equivalent RMSD for 34 targets (94.4%), with an overall average RMSD improvement of 0.3 Å. The gain (improvement) in RMSD relative to the change in MSA depth was investigated in Fig. 2i. Increasing the MSA depth did not show a clear improvement in RMSD, but it was evident that the RMSD worsened when the depth decreased. In this experiment, we used metagenome MSAs only as inputs in inference. Training or refining the NuFold model with metagenome data may enhance the interpretation of metagenome data and potentially lead to further performance improvement.

Finally, we combined the recycling strategy and the use of metagenome MSAs. As performed above, using each of four variations of MSAs, the highest pLDDT structure model was selected from the recycle iteration of 8 to 14, then, again the highest pLDDT model among the four structures was selected. This combined approach yielded the best results, an average RMSD of 6.67 Å and an average GDT-TS of 0.456, as reported in Table 1, Baseline+Recycles+Metagenome.

Effect of secondary structure prediction accuracy

We also examined how the accuracy of the secondary structure prediction affects modeling accuracy (Fig. 3). In addition to IPknot, MXfold239 and SPOT-RNA40 were used for this analysis.

Fig. 3: The effect of the secondary structure prediction accuracy.
figure 3

Modeling results (RMSD) of testing targets are shown relative to the F1 score of the predicted secondary structures. The baseline NuFold (Table 1) was used with secondary structure prediction using a IPknot; b MXfold2; c SPOT-RNA. Modeling accuracy of NuFold without MSA input was reported with secondary structure prediction using d IPknot; e MXfold2; f SPOT-RNA. g Comparison between the baseline NuFold with prediction using IPknot and with the correct secondary structure information computed from the PDB files. h Comparison between the baseline NuFold with prediction without secondary structure prediction.

Full size image

For this experiment, we used the same network model that was trained with IPknot prediction. We did not newly train the network specifically with predictions by each method. Figure 3a–c show the RMSD of the test targets relative to the F1 score of secondary structure prediction. With MSA input, a moderate correlation was observed between the F1 score of predicted secondary structure by SPOT-RNA and the RMSD of the predicted tertiary structure, whereas only a very weak correlation was observed for the other two. Pearson’s correlation coefficient was −0.104, −0.174, and −0.595, for IPknot, MXfold2, and SPOT-RNA, respectively. In Fig. 3d–f, we removed the MSA input to try to see a clearer effect of the secondary structure prediction accuracy to the modeling performance. However, the modeling accuracy dropped substantially without MSA, and only a weak correlation was observed. Pearson’s correlation coefficient was -0.245, -0.197, and -0.322, for IPknot, MXfold2, and SPOT-RNA, respectively. Figures 3g, h compare the baseline NuFold with NuFold with two extremes of secondary structure information: the perfectly accurate information computed from the native structure (Fig. 3g) and no secondary structure information (Fig. 3h). It turned out that secondary structure information did not make much improvement in RMSD from the baseline NuFold. Out of 36 targets, 24 were a tie (i.e. RMSD difference less than 0.5 Å) in Fig. 3g while 23 targets were a tie in Fig. 3h. As shown in Supplementary Table 2, the addition of predicted or true secondary structure information improved RMSD on average when compared to Nufold without secondary structure information. However, the improvement was not statistically significant in nearly all cases, except for the prediction with IPknot prediction with no MSA input.

Training with different amounts of self-distillation data

To examine how prediction performance varies with different amounts of self-distillation data, we trained NuFold from scratch using 50%, 33%, and 0% (i.e., no self-distillation data) of the self-distillation dataset and compared the results with the baseline NuFold, which was trained on 100% of the distillation data (Fig. 4). In each batch, the ratio of PDB data to self-distillation data was maintained at 1:3, consistent with the baseline NuFold training. For this analysis, we trained the model with reduced self-distillation data for approximately one month, which is about 25% of the time used in the original training. This allowed us to observe the trend in loss function values. As shown in Fig. 4, both the FAPE loss and the three evaluation metrics improved with more self-distillation data. This indicates that using a larger amount of self-distillation data, which exposes the network to a greater variety of data, is indeed beneficial.

Fig. 4: The effect of the size of self-distillation in training.
figure 4

Loss functions are shown when NuFold was trained using different amounts of self-distillation data: 100% (blue), 50% (orange), 33% (green), 0% (red). In each batch, the ratio of PDB entries to the distillation data was kept at 1:3 as in the baseline NuFold training. Loss values were computed on the validation data set at each step during training. a FAPE Loss (the lower, the better); b RMSD (Å) (the lower, the better); c LDDT Cα (the higher the better); d GDT-TS (the higher the better).

Full size image

Smaller network models

We also trained smaller models than the baseline NuFold. The baseline NuFold has the same size of parameters as the original AlphaFold, with 48 blocks of EvoFormer and 8 blocks of Structure Module. But as available training data is substantially smaller than proteins, we thought simplifying network would make training easier. We prepared models with a half size of Evoformer, 24 blocks, and trained with two size variations of self-distillation data in each batch, 75% and 50% to the original training data from PDB. 75% is the same as the amount used in the baseline NuFold. Results are shown in Small Models section in Table 1. As shown, the average RMSD of the two small models were slightly worse than the baseline. On the other hand, their average GDT-TS was, oppositely, slightly better. Thus, 24 blocks may be sufficient for RNA structure prediction with the currently available data size for future work.

Population-based approaches

Lastly in Table 1, we tested population-based approaches. In a population-based approach, which is also often called an ensemble-based approach, we generate many structures and select a structure as the final prediction using a selection criterion. Population-based approaches have been successful in protein structure prediction field41,42.

We took NuFold models at 385 different checkpoints during training and ran all of them for each target. Then, 385 structures were clustered using LB3Dclust43 with an RMSD cutoff of 1.0 Å. Then, one structure was selected using three different strategies: In the first strategy, from the largest cluster, the structure closest to the average of the all the cluster members was selected. In the second strategy, from the largest cluster, a structure with the highest pLDDT was selected. In the third strategy, the structure with the highest pLDDT was selected from the entire pool of structures.

As shown in the row of Best in the population (Table 1), the structure pool includes a better-quality structure than the baseline by more than 0.5 Å RMSD for 16 out of 36 cases and the average RMSD improved substantially from 6.98 Å to 5.62 Å. However, the two approaches that use clustering resulted in worse than Baseline in all metrics. On the one hand, simply selecting a structure from the pool using pLDDT outperformed Baseline, improving the RMSD by 0.12 Å on average and GDT-TS by 0.009.

Case studies

In this section, we discuss several illustrative examples of predicted RNA structures (Fig. 5). The first example (Fig. 5a) is a 76 nt-long tRNA from Escherichia coli (PDB ID: 2DER chain C). NuFold achieved a full-atom RMSD of 2.88 Å for this target. This structure was very accurately modelled except for the deviation of the 3’ end (in red), including the bases at the anticodon loop. Figure 5b is riboswitch for phosphoribosyl pyrophosphate (PPRP) (PDB ID: 6CK4 chain A) modelled at an RMSD of 2.64 Å. This structure has a pocket for recognizing the ligand PRPP in the area surrounded by blue, orange, and yellow chains. NuFold accurately constructed the overall structure as well as this functionally important region ligand binding site. The next example (Fig. 5c) was a prediction target rp12 in RNA-Puzzles, a 125-base ydaO riboswitch. This was a difficult target with a novel topology at the RNA-Puzzles Round 3 in 2014 when this target was presented44. At that time even the best (lowest) RMSD among all models was over 10 Å. NuFold was able to model the topology correctly, yielding an all-atom RMSD of 3.55 Å. The fourth example (Fig. 5d) is another RNA-Puzzles target, rp06. This target is 168 nt-long, the longest in the test dataset modelled below 6 Å by NuFold (3.10 Å). At the time of RNA-Puzzles round 2, this target had a top all-atom RMSD of 11.4 Å, marking a significant advancement by NuFold. The evaluation report of RNA-puzzles indicated that the absence of a ligand to fill the riboswitch pocket could be the cause of incorrect predictions45, although NuFold was able to understand the conformation from the non-redundant training set without considering the bound ligand.

Fig. 5: Case studies of the predictions of NuFold.
figure 5

The native structures and predicted structures are superimposed and shown in grey and rainbow, respectively. The 5’-terminal and 3’-terminal are shown in blue and red, respectively. a tRNA-Glu of Escherichia coli (PDB: 2DER chain C). 76 nt, RMSD: 2.88 Å. b PPRP riboswitch. (PDB: 6CK4 chain A). 117 nt, RMSD: 2.64 Å. c RNA-puzzle target, rp12. ydaO riboswitch. 125 nt, RMSD: 3.55 Å. d RNA-puzzle rp06. Adenosylcobalamin riboswitch. 168 nt, RMSD: 3.10 Å. e partial structure of the 23S rRNA. (PDB: 5ML7 chain A) 96 nt. An example that improved by increasing the number of recycles. The prediction of baseline is shown on the left (RMSD: 8.70 Å) and the prediction with more recycles is on the right (RMSD 3.39 Å). f twister ribozyme. (PDB: 4OJI chain A) 54 nt. An example that improved by using a metagenome MSA and recycles. Left, the baseline model (RMSD: 4.14 Å); right, the improved model (RMSD 2.23 Å). g RNA-puzzle rp05. lariat capping ribozyme. 188 nt. Left, the native structure; center, the baseline model (RMSD: 22.2 Å); right, model using metagenome MSA with more recycles (RMSD: 11.7 Å). h CRISPR RNA. (PDB: 4U7U chain L). 61 nt, RMSD: 33.0 Å.

Full size image

The next three examples are cases where additional effort over the baseline, i.e. using metagenomes and more recycling, were effective. The first one is 23S rRNA (PDB ID: 5ML7 chain A) (Fig. 5e), a 96 nt-long structure featuring a pseudoknot structure between the middle section (green) and the region of the first stem (red + blue). The baseline method (left) accurately predicted local structures but failed to correctly predict the pseudoknot, resulting in a large gap in its place. This led to an RMSD of 8.70 Å. Through increased recycling, the pseudoknot was almost accurately formed, resulting in an improved RMSD of 3.39 Å. Figure 5f is a twister ribozyme, another target with a pseudoknot (between the middle of the structure in green and the other region in the first stem in red). The baseline model shown on the left has a decent RMSD of 4.14 Å, which was further improved to 2.23 Å by using a metagenome MSA and more recycling.

Figure 5g are models of an RNA-Puzzles target, rp05. It is 188 nt-long, lariat capping ribozyme, which has a unique circular fold with a single pseudoknot. The baseline model (the middle panel) had 33.8% of standard base pairs formed correctly but the overall fold was not correctly built, including the characteristic pseudoknot. That resulted in a large RMSD of 22.2 Å. Using a combination of a metagenome MSA and more recycling, NuFold was able to form the pseudoknot structure correctly; however, the spatial arrangement of the orange region and a stem with red and blue regions was still not quite right, resulting in an RMSD of 11.7 Å.

As the last example (Fig. 5h), we show a target with the largest RMSD in the test set. This is CRISPR RNA (crRNA), a component of an E. coli CRISPR/Cas complex, whose structure has been solved with 11 other proteins. The RMSD of this model was 33 Å due to the long 5’ end tail, which has a different conformation from the crystal structure. But the conformation of this tail is due to interactions with many other proteins of the complex, and it is highly likely that this 5’ end tail forms a different conformation in the isolated state. NuFold correctly recognized base pairs at the 3’ end and folded it. As a result, the fraction of correctly formed Watson-Crick base pairs (INF_WC score used in RNA_Puzzles46) achieved 0.93.

Comparison with other methods

Here we compared the modeling performance of NuFold with five existing methods on the 36 test set targets. Methods compared are in two categories: methods based on energy-minimization, SimRNA13 and FARFAR214, and recent deep learning-based methods, DeepFoldRNA16, trRosettaRNA18, and RhoFold20. For NuFold, we show results from the baseline method as well as the results of the pipeline using four different MSAs that combine metagenome MSAs and more recycling (baseline + recycles + metagenome in Table 1). In Table 2, results of the modeling are summarized with average values for the test set. In addition to metrics that consider global or local backbone similarity, RMSD, and lDDT, we also used the Interaction Network Fidelity (INF) metric as used in RNA-puzzles assessment47. INF considers the entire RNA structure as an interaction network consisting of Watson-Crick (WC) interactions, non-WC interactions, and base stacking. INF_ALL considers all three types of interactions while INF_WC and INF_stack consider the specified interaction type only. INF is defined as the Matthews correlation coefficient (MCC) of this network between the reference and predicted structures. A high INF score indicates that relative positions of bases in a model are well reproduced. Figure 6 shows the distributions of these metrics in the box plots.

Table 2 The performance comparison between NuFold and other methods
Full size table
Fig. 6: Benchmark result to compare prediction methods.
figure 6

Results on the 36 test RNAs are shown in the box plot. Individual points show results of each test RNA. The center line of the box shows the median, two ends of the box show the first and the third quantile, and the whiskers extend to the minimum and maximum values within 1.5 times the interquartile range. Individual data points outside this range are shown as outliers. a RMSD; b LDDT; c INF_WC; d INF_ALL.

Full size image

NuFold clearly outperformed SimRNA and FARFAR2, two conventional methods, which are top performers in RNA-Puzzles, in all the metrics (Table 2, Fig. 6). When compared with deep learning-based methods, NuFold showed slightly worse values overall in terms of global (RMSD) and local main-chain structure, i.e. lDDT. On the other hand, we found that NuFold performed as well or better than other methods in terms of INF scores. For example, NuFold showed the highest average INF_stack and INF_all scores among all the methods. This may be perhaps due to the NuFold’s unique structure representation, the nucleobase center representation, which places the base frame at the C1’ atom, the connection to the base, and the use of all atoms instead of the coarse-grained models more frequently used in other methods16,18. Since C1’ is close to the base, the learning may have focused more on the correct placement of bases in RNAs.

Performance on RNA targets in CASP15

To further evaluate the performance of NuFold in comparison to existing methods, we ran NuFold on twelve RNA targets in CASP15. As the dataset used in NuFold development was constructed before the CASP15 start date, it would be appropriate to compare NuFold with CASP15 participants in the RNA category. Results are reported in Supplementary Table 1 in Supplementary Fig. 3. LDDT, which indicates local structure quality, and GDT-TS, which evaluates global structure quality, are reported in Supplementary Table 1.

NuFold achieved the highest LDDT values among all submitted server models for five out of twelve targets. When compared to the highest-ranked server group, UltraFold_Server, NuFold outperformed them on six of the twelve targets. In terms of GDT-TS, NuFold also secured the highest values for five targets and outperformed UltraFold_Server on seven targets. If NuFold were ranked among the participants (Supplementary Fig. 3), it would have been the top-ranked automatic server and the leading group utilizing machine learning techniques. Therefore, despite not excelling in all CASP15 targets, NuFold would have been highly competitive in the group rankings.

Prediction of RNA dimers with linker trick

Lastly, we tried to model RNA dimers with NuFold. Since NuFold is designed for single chain RNA structure prediction, we adopted the linker trick48,49,50, where two sequences are connected by dummy sequence and provided to NuFold as the input. The linker trick is an idea that was applied to Alphafold when it first came out for protein multimer structure prediction. We concatenated two RNA sequences in a complex with a linker sequence of 10, 30, or 50 Ns in between, where N is as an unknown nucleotide. The NuFold network is expected to open a space for Ns but not to output any atom coordinates for them. MSAs of the two RNAs are simply concatenated with gaps placed at the linker nucleotides. For a RNA dimer target, we applied the NuFold scheme with recycles and metagenomes. We used four different MSAs containing metagenomes, and for each of them output models from 8th to 14th recycles. This procedure was repeated for the three different linker lengths, which yielded in total of 84 ( = 4 × 7 x 3) structures. Then, the structure with the highest pLDDT was selected.

We folded 11 RNA dimers with NuFold with the linker trick. These dimers included all four dimer targets from the past RNA_Puzzles and seven more dimers selected from PDB, which are RNA-only dimer entries that have 10 or more interchain base pairs. Table 3 summarizes the results. For six targets, NuFold was able to fold into correct overall topology, achieving an RMSD of within 6 Å. In Fig. 7, we presented four examples of RNA dimer models. The first two examples, Fig. 7a, b, are successful cases. The first example (Fig. 7a) is a double strand helical structure of dimerization initiation site of genomic HIV-1 RNA. This regular structure is well modelled, including bases that flipped out from the double strand structure, achieving an RMSD of 1.71 Å. The second example (Fig. 7b) is an RNA_Puzzles target r01, a regulatory motif from the thymidylate synthase mRNA. This target also features double-strand structure but with some irregularity in the local main-chain conformation. While overall double strand was modelled properly, both the 5’ and 3’ ends of the two chains as well as the irregular main-chain conformation in the middle of the structure deviated from the reference structure. these deviations resulted in an RMSD of 3.41 Å. In both cases (Fig. 7a, b), almost all the base pairs between chains were formed correctly, with 90.0 % (18/20) and 84.2 % (16/19) accuracy, respectively.

Table 3 Overall performance of NuFold on the 11 dimer targets
Full size table
Fig. 7: Examples of RNA dimer structure prediction.
figure 7

The native (gray and black) and the predicted structure (rainbow, or green and cyan) are superimposed. a dimerization initiation site of genomic HIV-1 RNA (PDB: 462D). 46 nt, RMSD: 1.71 Å. b a regulatory motif from the thymidylate synthase mRNA. RNA-Puzzles target rp01 (PDB: 3MEI). 46. nt; RMSD: 3.41 Å. c Lariat-capping ribozyme with DP2 stem loop (PDB: 6G7Z). 186 nt; RMSD: 8.05 Å. d Hammerhead Ribozyme with a synthetic inhibitor strand. RNA-puzzle target rp15. 68 nt; RMSD: 14.8 Å.

Full size image

The third example (Fig. 7c) is a Lariat-capping ribozyme with shortened DP2 stem loop, the largest dimer target with sequences 132 nt-long and 54 nt-long. For this dimer, both chains, major component (green) and DP2 stem loop (cyan), were modelled overall correctly with RMSDs of 4.13 Å and 4.11 Å, respectively. However, the relative orientation was slightly wrong, resulting in an overall RMSD of 8.05 Å for the complex. Local structures are almost correctly built with only a major difference of the angle of a stem relative to the other chain. 76.9% (10/13) of base pairs were formed correctly. The final example (Fig. 7d) is a structure model of a hammerhead ribozyme with a synthetic inhibitor strand, illustrating a case where NuFold failed to predict the correct dimer conformation. For this target, although approximately half of the ribozyme chain (green) was correctly modelled, NuFold missed most of the interchain base pairs, resulting in an RMSD of 14.8 Å.

In Table 3, we showed the length of the linker of the selected models. In Supplementary Fig. 2, we present the distribution of pLDDT and RMSD of all the models with three different linker sizes, 10, 30, and 50 nt. For most of the targets, pLDDT tends to decrease as the linker length increases. Therefore, a model with a 10nt linker was selected for the majority, eight out of eleven targets. RMSD tends to increase as the linker length increases (Supplementary Fig. 2). Consequently, the selected model by pLDDT was best or very close to the best for most of the cases. Exceptions include 2NOK, where the lowest RMSD of 4.58 Å was found among models with a 30nt-long linker, and 6IA2, where the model with a 50nt linker had the lowest RMSD of 2.54 Å. For rp15 and rp19, a model with a 30nt linker was selected, but there a lower RMSD model with a 10nt linker existed.

To summarize, NuFold showed the ability to fold RNA dimers using the linker trick despite not being explicitly trained for complex modeling. The results suggest that similar to AlphaFold2, NuFold structure representation has the potential to predict multimer structures more accurately by explicitly modeling and training for complex structures.

Discussion

In this work, we have introduced NuFold, a novel de novo RNA structure prediction method. NuFold is an end-to-end model that predicts RNA’s all-atom structure from its sequence, offering a flexible nucleobase center representation for precise torsion angle control in the RNA backbone, which enables accurate structure description of any RNA structures. The architecture of NuFold would be a meaningful contribution to the community as most of the current RNA structure prediction methods employ a coarse-grained RNA structure representation. In addition, we investigated how various factors affect the modeling performance, including the use of metagenomic MSA, recycling, self-distillation data, and smaller models, which have not been thoroughly examined in previous works. RNA tertiary structure prediction is still far from perfection, and the thorough investigation of the factors will be of great value for the evolution of the development of future methods.

We observed a correlation between MSA depth and model accuracy. Additionally, we confirmed that introducing metagenomic MSA and utilizing more recycling contributes to improved modeling accuracy. We also found that generating multiple models enabled us to produce better structures. These findings are consistent with the behavior of state-of-the-art prediction methods for protein structure. Moreover, our analysis revealed that inputting secondary structure predictions does not significantly improve tertiary structure prediction. This aligns with findings from the AlphaFold2 paper, which showed that adding templates as input did not substantially improve protein structure prediction accuracy22. We provided further discussion regarding the predicted secondary structure input with Supplementary Fig. 4.

The comparison with other RNA 3D structure prediction methods showed that NuFold performed clearly better than energy minimization-based methods, but it performed slightly worse than some recent deep learning-based methods. One possible reason is that the training data size was not sufficient for this fully atomic detailed model. The deficiency of training data is a challenge for any RNA structure prediction methods, but it might be more critical for NuFold, which models full atom structures directly from a deep neural network. To address this issue, it would be important to incorporate different data modalities, such as experimental data that provide insights into RNA secondary structure, such as DMS-MaPseq51 and SHAPE-MaP52.

Incorporation of multi-chains, RNAs and proteins, is another future extension of NuFold as the conformation of an RNA is affected by interactions with other molecules. In addition to RNAs and proteins, modeling with small compounds is an important extension as RNAs are emerging targets for drug discovery.

Methods

Details of the NuFold architecture

The network architecture of NuFold is illustrated in Fig. 1a. In the preprocessing step, which generates inputs for the network, NuFold incorporates predicted secondary structure information along with an MSA for a target RNA. Instead of amino acids, NuFold considers 4 + 3 letter types, which are four standard nucleotides, unknown, gaps, and masked position. MSAs are constructed via the rMSA pipeline28 with default parameters. This pipeline identifies similar sequences from the RNA central database, NCBI nt database53, and Rfam database10, which has in total of ~490 Mb of sequences, using BLAST54 and Infernal55, which searches a database with a covariance model that embeds the sequence consensus with a Hidden Markov model and RNA secondary structure.

The secondary structure of a target RNA is predicted using IPknot29,30 as it can predict pseudo-knots. While AF2 relies on template structures from the PDB, we included secondary structure information because the availability of RNA structures in the PDB is limited. In AF2, inter-residue distances and dihedral angles are derived from templates. For RNA, secondary structure provides base pair information, analogous to residue contact information for proteins. To account for the lack of confidence or significance scores in IPknot’s output, we incorporated stochasticity in the IPknot pipeline. In the modified IPknot, 10% of constraints in the integer programming are discarded and base pairs are computed. This process was repeated ten times, and the resulting ten binary base-pairing matrices were averaged to provide the likelihood of base pairing between specific bases. The resulting LxL matrix, where L represents the length of the RNA chain, is the input feature for the predicted secondary structure. The network was trained with predicted secondary structure.

The EvoFormer block is essentially the same as AF2 except that we consider the seven letters to represent RNA sequences. We also tried smaller numbers of layers as we discuss later in the results.

In NuFold, we adopted C1’carbon to deal with tasks originally associated with Cα for proteins in AF2, such as to compute lDDT-Cα, and N1/N9 for tasks of Cβ, e.g. computing a distogram. We also modified auxiliary heads that predict structural features of RNAs to guide training to deal with RNA structures that are more flexible than proteins. The number of the distogram heads was increased to predict distances between three atom types, between C1’, C4’, and P, unlike AF2 which only considers Cβ distances. Moreover, the network architecture of the auxiliary heads was changed to three convolutional layers instead of a single linear layer in AF2. We also added another auxiliary head to predict inter-nucleotide torsion angles, which helps the network to understand the correct base orientations, which is a crucial detail to fold RNA. The inter-nucleotide torsion angles were defined on C1’i-Ni-Nj-C1j’ atoms where i and j are the index of nucleotides and N is the nitrogen in the base which is connected to C1’. This network was implemented with the same linear layer network as the distogram heads of AF2.

Training of NuFold

Some distinctive changes were introduced in the AF2’s training procedure for NuFold. Our loss function was:

$${Loss}=0.3\,{{{{\rm{L}}}}}_{{{{\rm{dist}}}}}+0.3\,{{{{\rm{L}}}}}_{2{{{\rm{Dangle}}}}}+1.0\,{{{{\rm{L}}}}}_{{{{\rm{FAPE}}}}}+2.0\,{{{{\rm{L}}}}}_{{{{\rm{MSA}}}}}+0.1\,{{{{\rm{L}}}}}_{{{{\rm{angle}}}}}+0.01\,{{{{\rm{L}}}}}_{{{{\rm{lDDT}}}}}$$
(1)

\({L}_{{dist}}\) represents the aggregation of cross-entropy losses from three distogram heads, aiming to predict 40 evenly spaced distance bins spanning from 2 Å to 22 Å. \({L}_{2{Dangle}}\) represents a loss from an auxiliary head for predicting torsion angles between pseudo-bonds of two bases. This is a new loss term specific for RNA structures, which evaluates prediction of 24 even-sized bins with cross-entropy loss. \({L}_{{FAPE}}\), \({L}_{{MSA}}\), \({L}_{{angle}}\), and \({L}_{{lDDT}}\) encompass the Frame Aligned Point Error (FAPE) loss, which is computed over backbone and sidechain atom coordinates, MSA masked-nucleotide prediction loss, torsion angle loss, which evaluates all torsion angle predictions between main-chain frames, and pLDDT local environment prediction accuracy loss36, respectively. We retained these components in AF2 without modification. After the training with Eq. (1) was saturated, we applied a fine-tuning training step. In the fine-tuning, we introduced a structural violation loss, denoted as \({L}_{{viol}}\), which penalizes atom clashes and irregular bond lengths.

$${Loss}= 0.3{L}_{{dist}}+0.3{L}_{2{Dangle}}+1.0{L}_{{FAPE}}+2.0{L}_{{MSA}}+0.1{L}_{{angle}} \\ + 0.01{L}_{{lDDT}}+1.0\,{L}_{{viol}}$$
(2)

We used the Adam optimizer56 with a learning rate of 1e-3 for the initial training phase and 1e-4 for fine-tuning. Unlike AF2, our training did not incorporate a warm-up step. The batch size was set at 16, with gradient accumulation and gradient clipping applied at 0.01.

Datasets

RNA tertiary structures were collected from the Protein Data Bank (PDB)9 as of February 28th, 2022. Our selection criteria included structures solved with X-ray crystallography or Cryo-electron microscopy with a resolution better than 5.0 Å and a sequence length ranging from 10 to 1500 nucleotides. Then, we applied two structural criteria: Since NuFold does not consider interactions with proteins or other RNAs, we only kept RNA structures that have at least 10 consecutive bases that are not in close spatial proximity (within 5.0 Å) to other RNAs or proteins. We also required an RNA structure to contain one or more standard Watson-Crick base pairs in regions that do not interact with other RNAs and proteins. Applying these criteria yielded 3237 RNA.

To this set, we added 34 RNA chains that were modeling targets in the past RNA-Puzzles rounds47 and performed sequence clustering to remove redundant sequences. We used single linkage clustering with global sequence identity. Chains with a sequence identity exceeding 80% were grouped together. This process resulted in a total of 499 clusters. From these clusters, 403 (80.8 %), 48 (9.6 %), and 48 (9.6 %) clusters were allocated for training, validation, and testing, respectively. Then, from the test set, we excluded 12 RNA-Puzzles targets that are multimers, since we primarily test the modeling performance for monomer RNAs. This resulted in a final test size of 36 targets. The clusters on the training dataset were expanded to encompass all the structures, which are 2860 chains in the training dataset. During training, each cluster in the training set was sampled with equal frequency, but a sequence in a cluster was chosen randomly so that we could use more structures than using only a cluster representative. On the other hand, one entry from each validation cluster was chosen before the training has started and fixed, so that we always monitor performance of NuFold on the same validation set.

We employed the bpRNA-1m32 dataset to construct a self-distillation dataset following the principles of Noisy Student learning24, which utilize the unlabeled data as training data by labeling them using a teacher network that trained on the labeled dataset. The need for a larger dataset was driven by the desire to enhance generalization performance, given the relatively small number of examples in the clean PDB dataset. Similar to our approach with the PDB dataset, we conducted sequence clustering on the bpRNA-1m dataset and selected 11197 sequences distinct from those in the PDB dataset. Subsequently, we used trRosettaRNA18 to predict three-dimensional structures for these sequences, focusing on those with one or more Watson-Crick base pairs. This process yielded a total of 11101 structures, which served as our self-distillation dataset. In the NuFold training, the ratio of PDB entries and self-distillation data was 1:3 in a batch, i.e. self-distillation data comprised 75% of the training data in each batch.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.