Operando microimaging of crystal structure and orientation in all components of all-solid-state-batteries

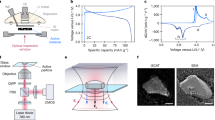
Abstract

Solid-state batteries can outperform conventional lithium-ion batteries in terms of energy density and safety, yet their widespread commercialisation remains hindered by challenges in ionic conductivity, interfacial resistance, and manufacturing. A comprehensive understanding of interactions between the electrodes, the electrolyte, and the packaging during battery operation is crucial. Still, it remains overlooked due to the lack of characterisation methods to measure these components simultaneously. Here, we perform a holistic investigation of a compact all-solid-state battery using operando synchrotron 2D X-ray micro-diffraction imaging. We image in real time and simultaneously the lattice parameters and crystal orientation of the dense LiCoO₂ positive electrode material, the Ti current collector and the electrodeposited Li metal at the negative electrode. We reveal that the reaction mechanism of LiCoO₂ depends on the crystal orientation, and that, in dense electrodes as opposed to porous ones, the delithiation is limited by the formation of a Li-rich insulating interface. Li metal is found to form large crystals whose orientation and number change during plating/stripping: from a heteroepitaxial growth on the Ti current collector at the beginning of charge to a random orientation distribution after 3 µm of Li is plated. These results demonstrate the power of X-ray diffraction imaging to link reaction mechanism and grain orientation in multiple battery components during non-equilibrium processes.

Introduction

Due to several advantages, there is a strong drive to transition from Li-ion to solid-state batteries. Solid-state electrolytes are less flammable, minimising thermal runaway risks, and have a higher Li⁺ transference number, which reduces polarisation and dendrite formation - key to enabling high-energy-density Li metal negative electrodes¹. Energy density can be further enhanced by minimising inactive components, such as conductive additives in electrodes, binders, current collectors, and the negative electrode itself, as Li plating/stripping directly on the current collector offers the highest energy density^2,3,4. The ultimate goal is an all-electrochemically active (AEA), anode-free solid-state battery^5,6. Such a design maximises energy density and minimises electrode-electrolyte interfaces, reducing interphase formation, which leads to polarisation and degradation. Key challenges include (1) identifying factors that limit power and capacity in additive-free positive electrodes and (2) improving the reversibility of Li metal plating/stripping.

On the positive electrode side, slow diffusion is often cited as a limitation for charge transport across the electrode depth, causing Li concentration buildup at electrode-electrolyte or electrode-current collector interfaces^5,7. Electron and Li⁺ transport involve bulk and grain boundary contributions, along with tortuosity due to porosity and grain orientation. Identifying rate-limiting processes through electrochemical methods or simulation is possible but requires high-quality experimental validation⁸, particularly operando characterisation that maps Li concentration profiles and crystal orientation in real time. On the negative electrode side, poor Li plating/stripping reversibility in solid-state batteries stems from issues like voids at the electrode/electrolyte interface, dendrites, or porous layers⁹. These morphologies depend on electrolyte composition, substrate nature, Li grain orientation, pressure, and current density¹⁰. However, limited techniques exist to characterise Li metal microstructure, leaving electrodeposition mechanisms poorly understood and hindering targeted improvements¹¹. Advancing this field requires real-time tracking of Li morphology and grain orientation across multiple crystals during plating/stripping.

Many papers review the need for more operando characterisations for solid-state batteries¹². Globally, an operando technique capable of spatially resolving crystallographic grain structures and orientations with microscale resolution within the components of a solid-state battery while cycling is lacking. In this work, we fill this gap by showing how operando 2D micro X-ray diffraction (2DµXRD) imaging at the synchrotron can provide a holistic visualisation of dynamic processes limiting AEA anode-free solid-state batteries. During a 2DµXRD imaging experiment, 2D maps of the whole battery stack are acquired in less than 5 minutes. Each pixel of the maps contains a 2D diffraction detector image giving access to crystalline structure and grain orientation. We study the limiting processes to fast charge and full discharge capacity in the AEA LiCoO₂ electrode, the archetypal positive electrode material for portable electronics and microdevices. Moreover, we observe Li morphology and texture during 1^st plating and stripping, characterising the dynamics of coherently structured lithium domains that develop at the separator-current collector interface, while monitoring cell casing deformation.

Results

2DµXRD imaging: a method capable of mapping phase and orientation distribution in multiple battery components

Operando 2DµXRD imaging is performed on a dense AEA anode-free solid-state microbattery (Fig. 1a) composed of a 20 µm dense LiCoO₂ (LCO) positive electrode, 4 µm LIPON solid-state electrolyte, and 500 nm Ti acting as the anodic current collector on which Li plates during charge. The electrochemical stack is 40 µm thick × 2 mm wide x 350 µm long (z, x, y directions, respectively). The full battery stack is scanned in 5 min with a 1 × 1 µm X-ray beam, and diffracted X-rays are collected after the battery on a 2D detector. Each pixel of the resulting map contains a detector image composed of Debye Scherrer rings whose position on the detector informs about the presence, the lattice parameters and the orientation of the crystalline materials scanned. With this experiment, all crystalline battery components can be mapped separately, as exemplified for LCO, Li, Ti, Au and parylene shown in Fig. 1bc. Moreover, inhomogeneous intensity along the Debye Scherrer ring is observed, which is characteristic of textured materials (Fig. 1a). For pristine LCO, exemplarily, the Debye Scherrer ring corresponding to the (003) LCO Bragg reflection is composed of six intensity strips at different azimuths, corresponding to six LCO crystal orientations as depicted in Fig. 2abc. Four of the six orientations feature Li diffusion planes almost perpendicular to the electrode surface (LCO^⊥ - 20° between the electrode surface and the Li diffusion planes), which is ideal for Li diffusion out of the electrode. Some LCO crystals are oriented with the diffusion channel almost parallel to the film, labelled LCO^∥. Focusing on the texture in the electrode depth (Fig. 2de), most of the film is composed of LCO^∥ and LCO^⊥ with approx. 1:1 ratio apart from the bottom, which features a significantly larger amount of LCO^⊥. This is consistent with a distinct morphology near the current collector, characterised by smaller grains resulting from the initial nucleation phase of the PVD deposition. This orientation inhomogeneity does not have a strong influence, as observed by the absence of depth-dependent reaction mechanism (detailed in the next sections). Overall, we demonstrate that 2DµXRD imaging can image in real space the crystal parameters and orientation of several crystalline battery components (positive electrode, negative electrode, current collector, packaging). In the following sections, the dynamic evolution of the cell components will be studied starting with the positive electrode material.

Fig. 1: Principle of operando 2DµXRD imaging of all battery components.

a Schematic of the operando 2DµXRD imaging experiment. b Typical diffraction pattern integrated from the detector image. c Selective component (x,z) maps showing where the LCO, Li, Ti, Au and parylene are located in the cell, obtained by plotting the intensity of the (003)_LCO, (110)_Li, (100)_Ti, (111)_Au and (020)_parylene diffraction peaks, respectively. For each pixel, the normalized intensity of each peak is represented using a colour bar. The images of the battery shown in c are measured during the battery charge at 0.5 mAh.cm^-2 capacity. Source data for 1b are provided as a Source Data file.

Fig. 2: Using the detector image to get information on the crystal orientation.

a Schematic of LCO crystal structure with the Co, Li and O atoms in blue, green and red, respectively. The CoO₆ octahedral are represented in blue. b Typical 2D detector image, when the X-rays are focused on pristine LCO, zoomed around the discontinuous (003)_LCO Debye-Scherrer ring. It is composed of six intensity spots at different azimuths, namely: 25°, 90°, 160°, 205°, 275°, 345°. d Same detector image as in c but in the (azimuth, Q) space. Each intensity spot originates from a different crystal orientation as schematically represented on the panel. The grey line represents the horizontal plane (PCB substrate). d Map of the (003)_LCO peak intensity and e map of the LCO^∥:LCO^⊥ peak intensity ratio in the pristine LCO electrode.

The effect of crystal orientation on cell parameter evolution in LiCoO2 during delithiation

The AEA battery is charged in 2.3 h using a constant applied potential of 4.3 V (Fig. 3a). Final charging capacity reaches the expected value of 1.4 mAh.cm² (Figure S1). Converting capacity into composition, this corresponds to the average delithiation from LiCoO₂ to Li_0.5CoO₂. Cell parameter c is determined from the (003)_LCO position for each pixel during charge (Fig. 3b and Figure S2). Maps of the c parameter (Fig. 3c) evidence a clear biphasic transition at the beginning of charge for both LCO^⊥ and LCO^∥. Indeed, high and low c parameter phases coexist at the electrode level corresponding to the well-known insulator to metal transition between 0.95 <x < 0.75 for x in Li_xCoO₂¹³. However, the c parameter changes from 14.0 Å to 14.13 Å for LCO⊥ and from 14.0 Å to 14.04 Å for LCO∥ (Fig. 3d). In porous electrodes, the c parameter of LCO changes by 0.17 ± 0.02 2.82. across the biphasic transition^13,14, which is consistent with the c parameter evolution of LCO^⊥ but not LCO^∥. During subsequent charging, the c parameter of both LCO⊥ and LCO∥ increases homogeneously across the entire electrode, reaching 14.32 Å for LCO⊥ and 14.12 Å for LCO∥ at the end of charge. To have a full picture of the lattice parameter variations, (110) diffraction spots for LCO^⊥ and LCO^∥ grains, observable on the detector at 90° and 210° azimuths, respectively, are analysed and the variations of a lattice parameter determined (Fig. 3d, Figure S3). LCO^⊥ and LCO^∥ have slightly different a parameter values in the pristine state due to detector calibration (Figure S4), namely 2.8090 Å and 2.8082 Å respectively, but both decrease by 0.005 Å at the end of charge, which is comparable to literature^13,14. Overall, the a parameter variation, which is directly connected to the CoO₆ shrinkage during delithiation and hence the state of charge (SoC), is similar for LCO^⊥ and LCO^∥, showing that both crystal orientations undergo a similar delithiation level of Li_0.5CoO₂. That is consistent with the average composition calculated from electrochemistry. Therefore, we conclude that the c lattice parameter versus Li concentration relationship for LCO^∥ differs substantially from that of LCO^⊥. This is an intriguing observation whose origin is still unknown. Indeed, there are no equivalent works in which the phase diagram during Li insertion/extraction is investigated for different crystal orientations. We hypothesise that the discrepancy between LCO^⊥ and LCO^∥ could be due to mechanical effects (see SI for discussion), but these findings definitely call for further investigations.

Fig. 3: LCO^⊥ and LCO^∥ structural mapping during charging.

a Current (black) and capacity (red) of the AEA battery during potentiostatic charge at 4.3 V. The square symbols mark specific times during the charge labelled with Latin letters. b Colour map of the c parameter as a function of time during charging (data is shown for a pixel at the top of the electrode). c c parameter spatial maps measured for LCO^⊥ and LCO^∥ (top and bottom lines respectively) and shown for different times during the charge. Times, labelled as Latin numbers (I, II, III etc.), are shown in a). Each pixel is 33 x 1 µm in the horizontal and vertical direction, respectively. Map size is 1.36 mm×40 µm (horizontal x vertical). d shows the average c (top) and a (bottom) lattice parameter variations for LCO^⊥ and LCO^∥, respectively. Different coloured lines correspond to different time during the charge (I to VII). e Experimental and modelled Li concentration profiles during biphasic transition in plain and dotted line, respectively. Calculations of the error bars of the experimental Li concentration is detailed in the methods. Source data for 3a,d,e are provided as a Source Data file.

Is Li diffusion limiting the charge in AEA LCO positive electrode?

Modelled and experimental Li concentration profiles across the depth of the electrodes during the biphasic reaction are compared in Fig. 3e. Modelled Li concentration is obtained using a partial differential equation Newman-type model using the electrode potential profile and the diffusion coefficient as inputs⁷. Experimental Li concentration is estimated by calibrating the changes of a lattice parameter of LCO^⊥ with Li concentration using reference data from literature¹³ (Figure S5). The experiment confirms a series of modelling observations during the biphasic transition, such as (1) position of the phase boundary, (2) its constant propagation speed of 10 nm.s^-1 and (3) concomitant out-of-equilibrium delithiation of the Li poor phase. After the phase transition, Li concentration is found to be homogeneous in LCO during the rest of delithiation, which agrees with the modelling results. The absence of Li concentration gradients in the solid solution region shows that Li⁺/e^- diffusion is not limiting the charge speed. Moreover, new insights that current modelling approaches cannot predict are obtained from the experimental data. One might expect Li to diffuse faster in LCO^⊥ due to the ideally oriented channels, and hence see the Li-poor/Li-rich phase boundary propagate faster amongst the LCO^⊥ grains. However, this is not the case; indeed, the same phase boundary speed of 10 nm s^-1 is found for LCO^⊥ and LCO^∥. One possible explanation for this observation could be the absence of percolation pathways amongst the LCO^⊥ grains across the electrode thickness. Additionally, the experimental interface between Li-rich and Li-poor phase is broader compared to the modelled one (Fig. 3e). The presence of a broad interface (6 µm) between Li-rich and Li-poor phases can be due to (1) particle by particle lithiation mechanism which has been observed for biphasic transition allowing to reduce interfacial energy^8,15, (2) low grain boundary diffusion and fast bulk diffusion, (3) heterogeneous tortuosity. Overall, our results show no diffusion limitation during the delithiation of a 20 µm dense LiCoO₂ positive electrode under potentiostatic conditions, even in the presence of heterogeneous grain orientation and grain boundaries. This calls for the utilisation of 2DµXRD imaging to investigate even higher energy density devices, e.g. (1) thicker LCO layers such as the 120 µm LCO film used in primary batteries reported et Yue et al.¹⁶ or (2) device charged at higher applied potential where it is suggested that inhomogeneous lithium distribution during 4.6 V cycling induces severe bulk-to-surface concentration gradients associated to capacity fade^17,18.

What is limiting discharge capacity?

Constant applied potential charge is followed by a constant current discharge at i = 2 µA – corresponding to 4 C (Fig. 4a). c parameters for both LCO^⊥ and LCO^∥ decrease constantly and homogeneously at the electrode level (Fig. 4b, c), showing the absence of Li concentration gradient during most of the discharge. However, spatial heterogeneity is observed at the end of discharge, corresponding to the metal-to-insulator transition onset, with the insulating phase clearly observed at the top surface of the electrode (Fig. 4c) and appearing concomitantly with a rapid decrease of electrode potential down to the cut-off electrode potential (3 V). During the rest following the discharge, the insulating phase progressively disappears. The phase fraction of the insulating phase at the top pixels of the electrode reaches approximately 50% when the insulating phase is present over the first five surface pixels (5 microns). The simulated Li concentration and electrode potential curve also feature a concomitant drop and insulating phase formation towards the end of discharge, suggesting that these two observations are correlated. Due to the low diffusion in the insulating phase, its surface rapidly reaches the maximum Li concentration, shutting down the charge transfer reaction. As a result, Li intercalation proceeds mainly through remaining Li-poor grains, the fraction of which is reduced as the Li-rich phase nucleates. A smaller amount of Li-poor phase at the electrode/electrolyte interface for a constant current leads to a drastic increase of the current density, hence polarisation, driving the electrode potential down, ultimately reaching the cut-off electrode potential. The disappearance of the Li-rich phase during rest is due to Li concentration homogenisation in the film thickness, showing that Li-rich formation at this state of charge and at 4 C is kinetically driven as Li concentration reaches Li_0.75CoO₂. The formation of the insulating phase at the electrolyte/electrode interface is limiting the discharge capacity of our AEA battery. Note that there is a large spread of 1^st cycle coulombic efficiency for other LCO solid-state AEAB, ranging between 60 and 88% mostly due to differences in film thickness^{7,19,20,21,22}. Nevertheless, the first cycle coulombic efficiency in LCO porous electrode for Li-ion battery is systematically higher (91–99%) (see Table S1)^{21,23,24,25,26}. We hypothesise that this is due to a higher Li-poor surface available for the charge transfer reaction due to the higher interface area between active material and electrolyte in classical porous electrodes, compared to all electrochemically active ones (Schematic Figure S6). Therefore, possible improvement strategies to design better performing microbatteries could be to (1) remove the phase transition in LCO by chemical doping²⁷, (2) increase the active surface by 3D electrode architecture.

Fig. 4: LCO^⊥ and LCO^∥ structural mapping during discharging.

a Voltage (black) and capacity (red) of the AEA battery during the galvanostatic discharge. b Colour map of the averaged c parameter as a function of time during discharging (data is shown for a pixel at the top of the electrode). c c parameter spatial maps measured for LCO^⊥ and LCO^∥ (top and bottom line respectively) and shown for different times during the discharge. Times, labelled as Latin numbers (VIII, IX, X etc.), are shown in a. Each pixel is 33 × 1 µm in the horizontal and vertical direction, respectively. Map size is 1.36 mm × 40 µm (horizontal x vertical). d shows the average c (top) and a (bottom) lattice parameter variation for LCO^⊥ and LCO^∥, respectively. Different coloured lines correspond to different time during the discharge. e Experimental and modelled Li concentration profile during biphasic transition in plain and dotted line, respectively. Calculations of the error bars of the experimental Li concentration is detailed in the methods. Source data for 4a,d,c are provided as a Source Data file.

Imaging dynamic changes in Li metal texture and morphology

At the negative electrode side, Li metal, Ti current collector, parylene encapsulation and Au diffraction signals are analysed in detail, starting with interpreting typical detector images (Fig. 5a). First, all components are textured as shown by the absence of continuous Debye-Scherrer rings. (100)_Ti Debye-Scherrer rings feature an intense spot at 90° azimuth together with weaker intensity spots observed at 30°, 150°, 210° and 330° (Fig. 5a, Figure S7). Hence, the chemically deposited Ti layer is textured with most of the [100]_Ti perpendicular to the film surface (Figure S8). Regarding Li metal, while (110)_Li, (200)_Li, and (220)_Li are observable, analysis is focused on the highest intensity (110)_Li (Figures S9-10-11). A typical detector image after azimuthal integration (Fig. 5a) features narrow (110)_Li spots showing that the diffracted intensities originate from single crystals. Moreover, Li metal diffraction spots appear at a wide range of different azimuths without evident texture at first glance.

Fig. 5: Mapping anode side-component evolution during cycling.

a Typical detector images around the (110)_Li, (100)_Ti, (111)_Au, (020)_parylene rings. b Spatial maps of the Li, Ti, Au, and parylene positions during the charge and discharge shown in orange, red, purple and blue respectively. For each material, the colour corresponds to the normalized intensity of the (110)_Li, (100)_Ti, (111)_Au and (020)_parylene⁴⁶. Times, labelled as Latin numbers (I, II, III etc.), are shown in c. Each pixel is 33 ×1 µm in the horizontal and vertical direction, respectively. Map size is 1.36 mm × 40 µm (horizontal x vertical). c Li metal layer thickness calculated from the average Ti current position (dotted orange) and from the electrochemistry (plain black line). Source data for 5c are provided as a Source Data file.

Next, Li, Ti, Au and parylene are imaged in real space during plating (Fig. 5b). We observe that Ti current collector (red pixels) moves upward as Li plates underneath (orange pixels) and its displacement exactly corresponds to the expected Li metal layer thickness (Fig. 5c). Interestingly at the end of charge, the Ti current collector appears thicker compared to the beginning of charge due to bending presumably induced by Li growth. (110)_Li intensity in the Li layer is not homogeneous, featuring regions without any intensity (white regions in Fig. 5b). This is not due to the absence of Li metal, as a continuous Li metal layer is observed by cross-section SEM (Figure S12), but to the absence of grains in diffraction conditions. Moreover, the intensity is present mainly as vertical stripes frequently running along the whole Li layer thickness. Finally, comparing the maps at 45 and 100 minutes (V and VII Fig. 5c), corresponding to the middle and end of charge, respectively, it can be observed that grains are not at the same position, suggesting a complex dynamical evolution of the microstructure. These observations indicate that most Li metal grains are long, feature a unique crystallographic coherent domain all along the Li metal layer thickness, and move/rotate during electrodeposition.

The existence of large coherent domains in the Li layer thickness agrees with recent in situ electron microscopy reports²⁸. However, the dynamic nature of the Li metal layer and the statistical description of the evolution of Li metal grain orientation have never been observed before. Therefore, a more quantitative description is obtained by analysing each detector image (as a function of position and time), e.g. Li diffraction peaks are extracted, counted and their azimuths determined (Fig. 6a, see methods). Looking at the distribution of azimuths as a function of time (Fig. 6b), we find a wide range of different azimuths, and hence crystal orientations, with some observable pattern suggesting an existing texture of the Li metal layer. Indeed, from 0 to 50 minutes most of the Li metal crystals have azimuths broadly gathered around 0°, 60°, 120° and 180°, with an apparent absence of 30°, 90° and 150° oriented crystals (Fig. 6c). Beyond 50 min (0.80 mAh cm²), the texture changes drastically since crystals with 30°, 90° or 150° azimuths are observed (Fig. 6d). These observations are consistent with Li being oriented initially with respect to Ti, following the epitaxial orientation described by Burgers orientation relationship (001)_Ti//(110)_Li - [100]_Ti//[111]_Li (Figures S13-14, SI)^29,30. As the Li layer grows, the effect of Ti orientation weakens, in agreement with the observed change of texture after 0.8 mAh.cm² of Li plating (almost 4 microns of Li metal deposited). These results open an excellent research opportunity since being able to image Li texture in real time is crucial to accelerate the control of parameters influencing Li metal deposition (i.e. current collector texture, current density, pressure, nature of the solid electrolyte interphases - SEI). Current knowledge in the field indicates that a highly [110] oriented Li surface would be ideal because it shows less pronounced dendrite/inhomogeneous deposition thanks to a higher in-plane Li diffusion (see SI for a more detailed discussion)³¹.

Fig. 6: Quantitative analysis of Li microstructure evolution.

a Left panel is a detector image in the (azimuth, Q) space zoomed around the position of the (110)_Li Bragg peak. Right panel is a zoom around one Bragg spot and the 2D gaussian fit of the peak in red contour lines. b Azimuths of all the fitted (110)_Li peaks for all positions as a function of time. Purple, pink and blue dotted rectangles are regions of interest which are going to be analysed in more details in c–e. c, d Are histograms of the (110)_Li azimuths from 0 to 50 min and 100–150 min, respectively. e Zoom of b in which the individual grains are plotted with different colours highlighting the presence of ‘ephemeral’, ‘unstable’ and ‘stable’ Li metal grains. f Total number of Li grains in diffraction conditions (in diff.), number of new grains in diffraction conditions (new in diff.) and number of grains moving out of diffraction conditions (out. Diff) in red, orange and purple, respectively observed over the entire battery during the electrochemical sequence. Black plain line is the voltage profile. Source data for 6c–f are provided as a Source Data file.

Tracking the orientation of individual Li grains during plating/stripping is difficult because most grains rotate/move out of diffraction conditions in a few minutes (‘ephemeral’ grains in Fig. 6e). Some grains remain invariant over most of the plating (“stable” grains in Fig. 6e). To capture the motion of Li metal grains, total and new grains in diffraction conditions are counted (Fig. 6f). Total number of grains increases rapidly at the beginning of charge up to approx. 90 and decreases during the rest of the electrochemical sequence (80 grains - end of charge, 40 grains - discharge and rest). The number of new grains ranges from 30 to 10 in charge–discharge, respectively, representing a significant fraction of the observed grains ( < 30 %), showing the dynamic nature of the Li grains in the negative electrode. Some of these observations can be rationalised in light of ex situ observations performed on liquid-based batteries³², since there are few reports on the Li nucleation and growth in solid-state batteries³³. First, a high number of Li grains nucleate due to the relatively high current density at the beginning of the potentiostatic charge (1 mAh cm²), then, as the Li metal layer grows, Li metal grains grow, leading to the reduction of the grain number³⁴ (SI for more details). Measuring operando grains moving out of diffraction conditions calls for further technical development to track grains as they move, hence having access to Li mechanical deformation, which is crucial to build a chemo-mechanical understanding of Li deposition in solid-state batteries.

Discussion

We have applied operando 2DµXRD imaging on an AEA solid-state battery to monitor the crystal structure and orientation of both the positive and the negative electrodes. The novelty of our findings relies on the unique combination of several characteristics of operando 2D-µXRD imaging: (1) operando ( < 5 min), (2) microimaging, (3) crystal structure determination, (4) crystal orientation information, (5) probing several hundreds of grains, (6) measuring most of the battery components simultaneously. This set of capabilities makes operando 2DµXRD advantageous to other existing methods, potentially leveraging a deep understanding of reaction kinetics and limitations. In general, imaging techniques have been essential to advance the knowledge of Li metal deposition. Operando optical microscopy or X-ray tomography have been used to measure Li dendrite growth in transparent solid electrolyte pellets, the displacement of the current collector as Li plates underneath and the formation of voids at the Li metal/electrolyte interface^9,35,36. However, these methods are blind to crystal orientation. Alternatively, transmission electron microscopy (TEM), thanks to electron diffraction, is sensitive to crystal orientation. However, imaging Li crystals is difficult because Li is buried underneath layers of solid electrodes and electrolyte. To lift this challenge, Fuchs et al. have recently successfully combined focused ion beam (FIB) under cryogenic conditions with electron backscatter diffraction²⁸. FIB is used to cut through the sample and expose a fresh Li metal surface. The authors could make up to five images during a 20 h Li deposition/dissolution and showed that Li form large grains, which coarsen during electrodeposition. Some of the drawbacks of this approach are the destructive nature of the analysis, the fact that the sample used in this work is not a realistic battery, and, most importantly, the technique allows the investigation of a limited number of grains (approx. 10) at the broken/FIB surface of the sample. Other key methods bearing structural sensitivity together with 2D/3D mapping capabilities can be found at the synchrotron, mainly benefitting from the high brilliance and coherence of beams produced at 4^th generation sources, e.g., 3D diffraction³⁷, tensor tomography³⁸, dark field X-ray microscopy³⁹, or scanning X-ray diffraction^40,41. These are recently developing at a fast pace and yield a wealth of information, including full 3D morphology and crystal orientation of a group of grains, or high-resolution strain measurement inside crystals. However, they are rarely used in the battery field, and usually require long measurement times, making operando characterisation difficult^38,39,40. For example, dark field X-ray microscopy has been recently used to measure dislocation density in Li metal dendrite growing in a solid-state electrolyte³⁹. This technique measures the mechanical strains developing inside a Li metal grain at the expense of a relatively long measurement time (8 h) and stringent sample environment conditions; hence, it is not easily compatible with realistic operando conditions and raises concerns about the representativeness of the results⁴². Amongst all these experimental tools, operando 2DµXRD imaging is the only method that enables fast scanning of a whole device with microscale resolution, a figure of merit particularly suited to detect metal grains while they form, grow and dissolve. These properties are attained by sacrificing the spatial and reciprocal space information to increase time resolution. In summary, there is an array of methods that have been used to characterise Li metal negative electrode morphology and microstructure, but it is still not enough to understand and master Li metal deposition. Along that line, we believe 2DµXRD imaging will be crucial by providing real-time and spatially resolved observation of crystal parameters and orientation in several components within realistic batteries. The real-time visualisation of metal layer building and dissolution with insights into crystal grain characteristics is crucial to understand interfacial issues in anode-less solid-state batteries and refine our current understanding of electrodeposition processes based on ensemble properties accessed by space-averaged methods, or local morphological probes with insufficient statistical relevance. Moreover, the approach is versatile and can be expanded to different formats as well as beyond Li-ion chemistry, offering a platform for screening the dependence of lithium plating/stripping grain dynamics on geometrical, manufacturing, functional and chemo-mechanical factors.

We have established fast operando 2D-µXRD imaging as a powerful tool to image Li intercalation and Li deposition, accessing crystal grain structure and orientations at the microscale in a real cycling battery. This method was applied to an anode-free all-solid-state battery, the target device for high energy density. We found that fast delithiation of dense LiCoO₂ positive electrode is not limited by diffusion. In contrast, the full lithiation is limited by the formation of an insulating phase at the electrode surface. Design guidelines can be formulated from these direct observations, for example, locally increasing the electrode/electrolyte interfacial area through structuring or texturing could mitigate early intercalation saturation effects and overcome capacity limitation during discharge. At the negative electrode side, we observed the deformation of the current collector, the Li/Ti epitaxial orientation relationship, the presence of large crystallographic coherent domains in Li metal ( > 5 microns), and the fast dynamics of Li metal grains, which occur during plating/stripping and rest. The results presented here demonstrate the use of operando 2DµXRD imaging to spatially resolve morphological/texture/cell parameter changes of most active and inactive cell components, at the microscale but with a ‘field-of-view’ up to the mm, hence giving statistical information on a realistic battery. This is unlocking possibilities to access the details of reaction mechanisms in textured materials or in between device components (i.e., negative-positive electrode correlation), to guide the optimisation of ion diffusion pathways in a variety of energy storage devices where contacting and/or building stable, reversible interfaces between solid materials are key processes.

Methods

Fabrication of thin film batteries

Thin-film batteries (TFBs) were fabricated using sequential layer deposition and patterning via UV photolithography and etching techniques in LETI cleanroom facilities. Film deposition was performed in an ENDURA PVD 200 mm system (Applied Materials) equipped with Ti, LiCoO₂(99.9% purity, Umicore), and Li₃PO₄ (99.9% purity, Umicore) sputtering targets. The deposition tool was linked to an argon-filled glovebox (less than 1 ppm O₂ and H₂O) to maintain controlled conditions during sample transfer and storage. Silicon wafers (200 mm in diameter) were employed as substrates. The deposition parameters are reported in Table 1. SPR 220 photoresist was applied for all photolithography steps, with UV exposure performed using an MA8 mask aligner. Wet etching of LiCoO₂ and LiPON layers was conducted in a 1:1 H₂SO₄:H₂O solution, while Pt layers were etched in a 1:3 HCl:HNO₃ solution. Surface of LCO is 4.8 e^-3cm² with a width and length of 300 µm and 1.6 mm. The LiCoO₂ mass loading is 10.2 mg.cm^-2. Ti top layers were etched in a CHF₃/Ar plasma using a Corial IL200 system. A polymer passivation layer was patterned, and a Ti redistribution layer was deposited as the negative current collector. Substrate thinning was performed through KOH etching. Finally, device singulation was achieved using laser ablation (Coherent GEM 100-CO₂ laser, λ = 10.6 μm, 20 W average power, 2 mm/s). The polymeric battery encapsulation applies the stack pressure, however, it is not controlled/measurable in the current set-up.

Table 1 Deposition conditions for the transparent TFB layers

Scanning Electron Microscopy (SEM) observation

Cross section of thin film batteries was imaged with a MERLIN scanning electron microscope (ZEISS). The image was taken with a 45° tilted sample using 6 kV electron beam energy and 1.1 nA beam current. A 9 nm carbon layer was locally deposited to avoid electrostatic charging and improve the quality of the images.

TFB mounting on PCB for operando characterisation

A specific printed circuit board (PCB) was designed and fabricated for synchrotron operando characterisation. Thin-film battery dies were attached using a UV-cured epoxy. Au wire bonding was carried out to electrically connect batteries to PCB pads.

Electrochemical characterisation of thin film batteries

Electrochemical characterisation of thin film batteries was carried out in an Ar-filled glove box before and after PCB mounting. Unless stated otherwise, electrochemical impedance spectroscopy (EIS), cyclic voltammetry (CV), and galvanostatic charge and discharge (GCPL) experiments were conducted at 25 °C using a VMP3 multi-potentiostat (BioLogic) coupled with the EC-Lab software.

Sample environment of electrochemical cycling during 2DµXRD imaging experiment

Ten microbatteries were positioned on a PCB. The experiment is performed at 22 °C ( + /- 2 °C). Before the experiment, a small current was applied to each battery to check the electrical connection (5 nAh.cm^-²). Some of these batteries were imaged at open circuit voltage using 2DµXRD imaging. The battery with the best image (alignment) and electrochemical test response was selected for operando characterisation. This work shows the electrochemical measurements for the battery measured using operando 2DµXRD imaging. More electrochemical data for other batteries are shown in the supplementary information. Batteries were charged under potentiostatic conditions up to 4.3 V, while the current was measured. Discharge was performed at 4 C with a current of 2 µA (corresponding to a current density of 0.4 mAh.cm²). Note that the current shape obtained during the synchrotron experiment is very similar to the previous test in the lab, as shown in Figure S1.

2DµXRD imaging experiment

2DµXRD mapping was performed on ID13 at the European Synchrotron Radiation Facility (ESRF) using a 1 x 1 µm beam (vertical and horizontal directions, z and x) at 18 keV. The battery was 40 microns thick x 2 mm wide x 350 µm long (z, x, y directions, respectively). The positive electrode, electrolyte, and current collector layer stack was oriented along the z direction. The battery was positioned so that the X-ray beam crosses the battery along the y-axis. During the acquisition, the battery was moved horizontally (x) and vertically (z) to scan the entire electrode stack, producing (x, z) maps of 49 x 49 pixels with a pixel size of 33 ×1 µm in approx. 5 min. The counting time at each position is 0.05 sec (2 min of counting time per map and approx. 3 min of motor movement). “Horizontal fly scans” were performed in which the battery was continuously moved in the x direction from 0 to 1.6 mm while the shutter remained open. Detector images were averaged over 33 µm of battery displacement. Therefore, each detector image is an average in the x direction of 33 µm of the sample. After every horizontal continuous scan, the battery was displaced vertically by 1 µm (in z direction) and a continuous scan in x was performed until the complete 2D maps were produced. This continuous scanning reduces the dose a lot. Indeed, the dose spreads over the 33 µm scanned horizontally. WAXS patterns were recorded using a Dectris EigerX 4 M (2070 x 2167 pixel, 75 micron pixel size). Measured Q range is 0.96 – 6.09 Å^-1. After the sample, the direct beam hits a beam stop approximately at the centre of the detector; therefore, full Debye Scherer rings can potentially be measured, although some shadowing effects come from the sample, as shown in Figure S15. Detector calibration was performed with a reference sample Al₂O₃ using PyFAI⁴³. Sample-to-detector distance calibration was corrected using the Ti current collector peaks. The dose and dose rate for LCO and Li metal are 24 kGy and 4.096 KGy, and 0.651 kGY.s^-1 and 0.1 kGY.s^-1, respectively. This is below the reported threshold of beam damage degradation (see SI for more discussion)^44,45. The calculation were made used the tools developed by Jousseaume et al.⁴⁴.

2DµXRD imaging data analysis

Detector images are azimuthally integrated using PYFAI, transforming the detector image (in pixels) into a map showing the intensity as a function of Q and azimuth (x and y axes). From these maps, the rest of the analysis was performed using a homemade Python-based code. LCO: First, the intensity ratio between LCO^⊥ and LCO^∥ was determined on the pristine battery (Fig. 2c). For this, intensity stripes for (003)_LCO peaks at 90° (LCO^∥) and 160° (LCO^⊥) were integrated over a +/- 10° azimuth range to obtain a ‘classical’ diffraction peak (intensity as a function of Q). Gaussian peak fitting is performed to estimate the peak areas. To obtain the cell parameter evolution as a function of time and orientation (Fig. 3 and Fig. 4), a similar approach was performed on the (003)_LCO and (110)_LCO for all LCO pixels in each map (approx. 96000 detector images treated). Peak position was obtained from the Gaussian peak position. To estimate Li concentration from peak position, three calibration curves of a versus x for x in Li_xCoO₂ were extracted from the literature¹³ (Figure S5). Each calibration curve is used to determine Li concentration. The Li concentration shown in Fig. 3 and Fig. 4 is the average of these three values, while the error bars are the standard deviation. Li metal analysis: The analysis was conducted on the (110)_Li peak, and hence all azimuthally integrated detector images were reduced, focusing on the data in the 2.53 – 2.55 Å^-1 range. The typical data manipulated is a 5-dimensional array (100 time steps, 49 y direction steps, 49 z direction steps, 360 azimuths, 10 pts between 2.53 – 2.55 Å^-1) of the detector intensity. The next step consists of removing the background due to total scattering. This is performed by removing a detector image free of Li metal peaks for each time, y direction and z direction. Then, Li metal peaks on the detector are segmented by thresholding the intensity with 10 times the mean intensity of the detector image in the reduced Q range around the (110)Li, which is mainly composed of the remaining contribution from the background. The (110)_Li peaks are fitted using a 2D Gaussian function (G(Q, Azimuth) allowing to determine the azimuth for each observable Li metal grain. Finally, from the segmented dataset, the number of Li clusters, their size, azimuth and duration are determined. All this data analysis process is performed using homemade Python code, mostly numpy packages.

Li concentration modelling

1D Lithium normalised concentration in cathode ($0 < {c}_{1} < 1$) and electrolyte ($0 < {c}_{1} < 1$) domains are modelled in COMSOL with a variable diffusion coefficient approach as described in Celè et al.⁷.

Lithium flux in LiCoO2 (${\;j}_{1}$) is modelled by a pure diffusion equation:

$$j=-{c}_{1}(1-{c}_{1})\frac{{D}_{1}}{{RT}}\frac{\partial {\mu }_{1}}{\partial x}$$

Where D1(1 − c1) is the self-diffusion coefficient, ${\mu }_{1}$ the chemical potential of lithium inside the cathode, $R$ the gas constant and $T$ the temperature in Kelvin. At the current collector interface, the blocking electrode boundary condition is imposed:

$$j{|}_{x=0}=0$$

At the electrode/electrolyte boundary (x=xlco) a modified Butler-Volmer equation is used to describe the lithium exchange between the two domains:

$$j{|}_{x={x}_{{lco}}}={c}_{1}\left(1-{c}_{2}\right){k}_{1}{e}^{-\left(1-\alpha \right)\eta F/{RT}}-{c}_{2}\left(1-{c}_{1}\right){k}_{2}{e}^{\alpha \eta F/{RT}}$$

Where ${k}_{1}$, ${{k}}_{2}$ are the reaction coefficient, $\alpha$ the charge transfer coefficient, $\eta$ the interface overpotential, and F the faraday constant.

In the electrolyte domain, the flux is described by a drift-diffusion equation

$$j=-{c}_{2}(1-{c}_{2})\frac{{D}_{2}}{{RT}}\frac{\partial }{\partial x}\left({\mu }_{2}-{zF}\phi \right)$$

With $z$ the charge number and $\phi$ the electric potential, which is calculated through the Poisson equation:

$$\frac{\partial \phi }{\partial x}=-\frac{\rho }{{\varepsilon }_{0}{\varepsilon }_{r}}$$

Where $\rho$ is the charge density and ${\varepsilon }_{0},$ ${\varepsilon }_{r}$ the vacuum and relative permittivity, respectively.

Chemical potential in LiCoO2 has been calculated from GITT measurement of the diffusion coefficient as a function of the concentration, while for LiPON the following expression is used:

$${\mu }_{2}={\mu }_{02}+{{{\rm{kT}}}}{N}_{a}{{\mathrm{ln}}}\left(\frac{{c}_{2}}{1-{c}_{2}}\right)$$

Where ${{{\rm{k}}}}$ is the Boltzmann constant and ${N}_{a}$ the Avogadro constant. All equations are casted in weak form and directly implemented in the COMSOL weak-PDE model interface to be numerically solved.