Introduction

Qubit connectivity is a primary feature of any quantum computing technology. It represents the architectural arrangement of the qubits within the quantum processor and indicates the number of qubits with which any other qubit can interact. Highly-connected structures are favorable since two-qubit gates between arbitrary qubits require a smaller gate count and hence more complex problems can be solved with lower circuit depth1,2,3,4,5,6,7,8,9. On the other hand, high qubit connectivity comes at the expense of technological complexity. Therefore, scaling while maintaining high connectivity is a challenge being faced by many quantum computing technologies. All-to-all connectivity has been demonstrated by photonic10 as well as ion-trap11,12 qubits, but the distributed nature of these technologies puts serious challenges on the path to scaling. On the other hand, solid-state systems, such as superconducting13 and quantum dot spin qubits14, can exhibit 2d hardware topologies, which could be compactly integrated on a chip. This allows for colocating classical support electronics and offers an alternative path to scaling.

Implementations of 2d grids with nearest neighbor connectivity are desirable as this would allow for fault-tolerant quantum computing via the surface code15 without additional gate overhead. However, scaling 2d nearest neighbor grids in solid-state systems poses substantial contact routing challenges and complicates the integration of classical support electronics in the qubit plane16,17. Quantum-classical integration would require levels of 3d integration unseen to date18 although important progress has been made in that direction19. Therefore, solid-state platforms explore scaling with sparse 2d connectivity20,21,22 and several works have explored optimized methods for running quantum algorithms on sparsely-connected hardware graphs23,24,25.

Particularly for silicon spin qubits, progress has been made in the last few years demonstrating high-fidelity single- and two-qubit gates in SiGe26,27,28,29,30,31 and silicon metal-oxide-semiconductor (MOS) structures32,33, as well as high-fidelity initialization and readout in SiMOS34,35,36,37. Further, the first few-qubit processors38,39 and architecture proposals18,20,40,41,42 are beginning to emerge. Next steps will be focused towards scale-up, for which the use of industrial complementary metal-oxide-semiconductor (CMOS) processes is expected to play an important role17. In particular, modules containing industry-manufactured bilinear arrays of quantum dots (QDs) using split-gate nanowire transistor technology are readily manufactured and their qubit properties are widely being tested in experiments43,44,45,46. These modules should provide a platform to demonstrate a 1d quantum processor in silicon. One-dimensional processors allow running early noisy intermediate-scale quantum (NISQ) algorithms23,47 or demonstrating logical qubits48. How best to scale this technology to allow for optimized operation of quantum algorithms with minimal compilation overhead is therefore an important question.

Here, we present thoughts on how to scale QD chains of 1d split-gate transistors by combining them into 2d arrays with sparse connectivity. For this purpose, we introduce a hardware junction which enables coupling between horizontally and vertically oriented arrays of split-gate transistors via spin shuttling49. Given this junction element, we consider possible 1d and 2d architectures and investigate their suitability for implementing NISQ algorithms with minimal compilation overhead of two-qubit operations. As a result of our consideration, we propose a modular 2d spin-qubit architecture with unit cells consisting of diagonally-oriented squares where nanowires form the edges and junctions the corners of a square. We then investigate compilation strategies for the proposed 2d architecture and demonstrate a square-root scaling of the compilation overhead, which outperforms the linear overhead of 1d devices, not only asymptotically, but also down to its smallest building block which is likely to be investigated first in future experiments. The compilation results further allow for balancing the trade-off between the compilation overhead and creating space in between the qubit modules which can be beneficial for colocation of classical control and readout electronics20,50,51 and alleviating contact routing issues18,41,52,53. Finally, while reducing compilation overhead is mainly useful for NISQ applications, we believe the proposed architecture should be compatible with recent proposals42,48 to operate similar architectures at fault-tolerance. Overall, this should provide a compelling path to scaling, which could be manufactured with industrial CMOS processes.

Results

Topology of the proposed architecture

We start by introducing the hardware topology of the proposed architecture, before describing the detailed embodiment in silicon and discussing compilation strategies in subsequent sections. The core element of the architecture is a bilinear array of QDs using CMOS split-gate nanowire transistors. This gives rise to a 1d arrangement of m qubits along a line (each with an ancilla qubit for readout as will be explained later), in which neighboring qubits can be involved in two-qubit operations as visualized in Fig. 1a, where the m = 4 dots indicate qubits and the black lines indicate possible two-qubit operations among neighbors. An additional building block is provided by a junction element which can join up to four linear segments in a perpendicular manner, as depicted in Fig. 1b. In principle, a two-qubit operation can be executed between any two qubits involved in the junction as indicated by an orange line connecting the qubits. As explained in more detail in the following section, each two-qubit operation across the junction requires 6 additional spin shuttling steps. We consider the regime in which these coherent shuttling steps are fast, invoking negligible overhead as compared to the two-qubit operation. We note that each qubit can only be involved in a single two-qubit operation at a time.

Fig. 1: Hardware topology of the proposed architecture.
figure 1

a Linear segment of m = 4 qubits (dots) connected by two-qubit operations (lines), representing split-gate transistors along a nanowire. b Hardware junction joining four linear qubit segments. Orange lines indicate two-qubit operations combined with spin shuttling. c Unit cell of the proposed architecture with m = 4 qubits in each segment. d Hardware graph of the proposed architecture with dx = 2 and dy = 3 unit cells in x and y directions, respectively.

Full size image

The unit cell of the proposed architecture is then provided by squares, with linear segments along the edges and junctions at the corners of each square, as in Fig. 1c. To form the complete architecture, we join dx squares in one direction and dy in the perpendicular direction. For convenience, we define the two directions as x and y. The complete architecture and x and y directions are show in Fig. 1d. Since each square contains 4m qubits and the device consists of dxdy squares, each device contains

$$N=4m{d}_{{{{\rm{x}}}}}{d}_{{{{\rm{y}}}}}$$
(1)

qubits. We note that a crucial feature of the proposed architecture is the tilted orientation of squares at an angle of 45∘ in each unit cell, which minimizes the compilation overhead as will be explained later on.

Architecture embodiment in silicon

In the following, we introduce the embodiment of the proposed architecture in silicon and the corresponding control schemes in more detail. We focus on an implementation based on electron spins hosted in gate-defined QDs, but note that a similar proposal can be described for hole spin qubits. Readers interested only in the compilation techniques are advised to skip ahead.

Architecture embodiment in silicon: split-gate submodules

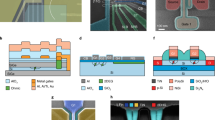
The principal building block of our proposal is the split-gate transistor45,54,55,56. It consists of an undoped silicon-on-insulator nanowire of height h and width w (typically 10 nm and 60 nm, respectively). The central part of the nanowire is gated by two metallic surface electrodes of length lg (typically 40–60 nm) which are isolated from the channel by the gate oxide (SiO2) of thickness t (typically 6 nm); see Fig. 2a, b. The gate stack is typically formed by 5 nm of TiN followed by 50 nm of polycrystalline silicon. The rectangular cross-section of the channel, as seen in Fig. 2b, is covered by the pair of split gates which are separated by a face-to-face distance Sgg ( ≈ 30 nm) and enable local electrostatic control of the nanowire. At deep cryogenic temperatures, when positive (negative) voltages are applied to the gates, few-electron (hole) QDs form in the top-most corners of the device due to the corner effect57,58,59, as shown in Fig. 2b. Charges can be drawn into the QDs from charge reservoirs formed of highly doped silicon located at each side of the split gate (source and drain in a). The qubit that we consider here is the spin of a single electron (or hole) confined to one of the two corner dots whose quantization axis is defined by placing the structure in a magnetic field. The other spin is used as an ancilla for readout as described later on. Hence a split-gate defines one qubit with a readout ancilla. The architecture can be scaled up by fabricating a series of split-gate transistors placed along the axis of the silicon nanowire, as depicted in Fig. 2c. The tunnel coupling along and across the nanowire is engineered by selecting the physical dimensions of the structure. In particular, w primarily determines the coupling across the nanowire whereas Svv determines the coupling along the nanowire. These values can be tuned globally by applying a potential to the silicon handle wafer (or back gate)60. Fine tuning could be achieved with more advanced gate layouts including a dedicated tunnel coupling gate module above the space between QD gates. The split-gate edge-to-edge separation Svv ( ≈ 40–60 m) is set to enable sizable exchange coupling between spins, which we use to generate two-qubit interactions. Overall, the module results in a bilinear array of QDs. Given that the two QDs of each split-gate transistor encode one qubit—one dot contains a qubit spin and the other an ancilla spin for readout—the structure embodies a one-dimensional chain of silicon spin qubits of length m, as described in the previous section.

Fig. 2: Split gate submodules.
figure 2

a Top view of a single split-gate nanowire transistor, with highly-doped source and drain ohmic contacts in blue, metallic split gates (G1 and G2) in orange, Si3N4 spacer in green and buried oxide in black. b Schematic cross section of the split-gate transistor along the dashed line in a. The gates and silicon nanowire are isolated by the gate oxide of thickness t. The metal gate stack TiN(5 nm)/Polycrystalline silicon (50 nm) is represented in pink. Sgg indicates the edge-to-edge separation of the split gates. The silicon nanowire height and width are h and w, respectively. The purple regions represent schematically the QD wavefunctions. BOX stands for buried oxide. The vertical black arrow represents the direction of the external magnetic field. c An 8 split-gate 1d submodule. Dashed lines highlight a one-qubit split gate subset. Svv indicates the edge-to-edge separation between splits and lg the gate length. d Energy spectrum versus energy detuning of the two-spin system in a tunnel-coupled DQD. Both energy and detuning are normalized by the \(\left\vert \uparrow \downarrow \right\rangle -\left\vert S(20)\right\rangle\) tunnel coupling, ts. The diagram is simulated using a 5% g-factor difference and an average Zeeman energy of three times ts. e–i Schematic of operating 3 qubits in a 2 × 3 QD array formed by 3 split gates as indicated by dashed lines. Initialization e, f, one-qubit gates g, two-qubit exchange interaction h, and readout via Pauli spin blockade i.

Full size image

Next, we explain control, readout and initialization of the 1d modules in detail. We base our explanation on the energy spectrum of the coupled two-spin system in the single spin basis as a function of the QD energy detuning, ϵ, and a finite magnetic field; see Fig. 2d. At large positive detuning with respect to the (11)-(20) charge hybridization point, the ground state of the system corresponds to the intradot singlet, \(\left\vert S(20)\right\rangle\). Here the (nm) notation refers to the charge distribution among the two QDs, i.e., dots are occupied with n and m charges, respectively. At negative detuning, the ground state of the system is the (11) charge configuration whose spin degeneracy is broken by the external magnetic field. We consider the QDs to have a tunnel coupling energy ts and present different g-factors due to the variability of the Si/SiO2 interface61, which further breaks the degeneracy of the \(\left\vert \uparrow \downarrow \right\rangle\) and \(\left\vert \downarrow \uparrow \right\rangle\) states. Here, the first spin refers to the spin with the lower g-factor (see the Hamiltonian in Supplementary Note 1). Although not strictly necessary for the operation of the processor, we consider that larger Zeeman energy differences exist across the nanowire than along the nanowire, which could be achieved by creating an asymmetry in the gate structure. Using magnetic materials on the gate stack on one side of the split or placing the splits offset with respect to the nanowire axis59 may produce a difference in the Meissner effect at the location of the QDs. We use the energy spectrum to describe processes involving QDs within a split-gate and QDs on the same corner of the nanowire in different splits.

Architecture embodiment in silicon: initialization

We start with the 1d module loaded with one charge in each QD. Charges can be drawn in from reservoirs at the periphery following established methods62. To initialize to a known spin state, QDs in each split gate are positively detuned until the system relaxes to the \(\left\vert S(20)\right\rangle\) state (Fig. 2e). Then, the system is pulsed towards negative detuning adiabatically with respect to the \(\left\vert \uparrow \downarrow \right\rangle\)-\(\left\vert S(20)\right\rangle\) coupling and non-adiabatically with respect to the \(\left\vert \downarrow \downarrow \right\rangle\)-\(\left\vert S(20)\right\rangle\) coupling (not shown in d), to initialize the QDs in the splits in the \(\left\vert \uparrow \downarrow \right\rangle\) state (Fig. 2f).

Architecture embodiment in silicon: single-qubit operations

In the case of electron spins in isotopically purified silicon QDs, spins present long coherence times (\({T}_{2}^{* }\, > \,100\,\mu\)s and T2 = 28 ms)63. This feature enables high control fidelity via electron spin resonance (ESR) techniques64,65 with typical Rabi frequencies of 1 MHz and fidelity in excess of 99%32. Manipulation occurs for QDs on the same side of the nanowire which are now initialized to the \(\left\vert \uparrow \downarrow \right\rangle\) state.

The ESR implementation for the proposed architecture is inspired by Ref. 66. It requires placing the structure inside a broadband 3D microwave cavity designed to deliver an oscillatory magnetic field perpendicular to the external magnetic field at the location of the chip 67,68. The cavity is designed to have a quality factor Q ≤ 100 to cover the range of potential qubit frequencies associated with the typical variations of the g-factor of electrons in MOS devices, Δg/g ≈ 10−2 (Ref. 69.) The variability, associated with spin-orbit coupling, can be minimized by applying the external magnetic field along the [100] axis70. To reduce the number of necessary frequencies to control the system and minimize cross-talk, we make use of the Stark shift. A g-factor modulation of δg/g ≈ 10−3 (Ref. 61) can be obtained by gate voltage tuning and allows lumping the qubit frequencies into N = Δg/δg bins. Then N-1 frequencies are sufficient to cover the full qubit frequency range. Selected qubits are tuned in and out of resonance with the relevant frequency (fESRi) using gate voltage pulses at the qubit gate71. ESR allows two-axis control (X and Y gates) by controlling the duration of the gate voltage pulse and the phase of the microwave excitation.

In the case of hole spin qubits, the larger spin-orbit coupling when compared to electron spins allows for all-electrical control via individual microwave voltage signals applied directly to the relevant QD gates72,73. The spin coherence is relatively lower, with \({T}_{2}^{* }\) values of up to 7.1 μs reported74, but the faster Rabi frequencies, of up to 150 MHz, have enabled X and Y rotation with fidelity in excess of 99%73,75.

Architecture embodiment in silicon: two-qubit operations

We propose engineering two-qubit gates between spins on the same corner of the nanowire by means of the spin–spin exchange interaction (Fig. 2h). The exchange interaction can be modulated electrostatically by applying a differential mode voltage on the two relevant neighboring gates that brings the system close to ϵ = 0; see Fig. 2d, h. In the limit where the differential mode voltage pulse increases the exchange coupling to a value much larger than the Zeeman energy difference between spins, a \(\sqrt{{\rm{S}}{\scriptstyle{\rm{WAP}}}}\) or Swap gate can be implemented by timing the duration and depth of the interaction pulse76,77—see Supplementary Note 2. Alternatively, when the size of the modulation is smaller, such that the exchange coupling strength remains below the Zeeman energy difference, a CPhase gate could be implemented65 with fidelity above fault-tolerant thresholds29,30,31. In this article, we focus on the former gate but note that the Swap gate can be synthesized from a combination of CPhase and single qubit gates.

Architecture embodiment in silicon: readout

Spin readout is based on spin-dependent tunneling from the (11) to the (20) charge configurations, i.e., Pauli spin blockade78. More particularly, the state \(\left\vert \uparrow \downarrow \right\rangle\) is allowed to tunnel to the \(\left\vert S(20)\right\rangle\) state, whereas all remaining two particle spins states are blocked18,79; see Fig. 2d, i. To detect this tunneling process, we suggest using dispersive readout80. In each split, the gate of the ancilla is connected to a lumped-element electrical resonator which is driven at its natural frequency, f0. At ϵ = 0, the readout point, cyclic tunneling between \(\left\vert \uparrow \downarrow \right\rangle\) and \(\left\vert S(20)\right\rangle\), driven by the oscillatory resonator voltage, manifests in an additional quantum capacitance that loads the resonator producing a spin-dependent frequency shift that can be readily detected with standard methods81,82,83,84,85. On the other hand, at the readout point, the \(\left\vert \downarrow \downarrow \right\rangle\) state does not tunnel under the oscillatory voltage of the resonator giving no signal. This difference in polarizability allows discerning the two computational states (\(\left\vert \uparrow \downarrow \right\rangle\) and \(\left\vert \downarrow \downarrow \right\rangle\)). We note that enhanced spin-orbit coupling can promote fast relaxation between the \(\left\vert \downarrow \uparrow \right\rangle\) state and the singlet38,86 but the state is outside our computational basis. Further, enhanced spin-orbit coupling can couple the \(\left\vert \downarrow \downarrow \right\rangle\) and the singlet states leading to a measurable signal at that additional anticrossing87,88. By operating at \(\bar{g}{\mu }_{{{{\rm{B}}}}}B\, > \,{t}_{{{{\rm{s}}}}}\), even in these systems readout can be performed. In this proposal, we have chosen to have a readout ancilla per qubit such as each qubit can be read with one tunnel step only. However, other arrangements may be possible in which ancillas may be used as computational qubits. To reduce the number of resonators required for readout, time-division multiplexing techniques could be implemented in conjunction with floating gate arrangements as previously described52 and laid out in Supplementary note 3.

Architecture embodiment in silicon: junctions

Coupling of silicon nanowire qubits in the second dimension has been proposed via floating gates89 and microwave resonators90. Here, we propose a hardware junction which allows for coupling 1d submodules of split-gate transistors in 2d. The junction consists of etched silicon-on-insulator in quadrangular form, as can be seen in the central region of Fig. 3a. The exact shape and gate layout of the junction can vary to accommodate different levels of interconnection, reduce cross talk, and shuttling bottlenecks (see Supplementary Note 4). Here, we present a square junction that enables connecting up to four submodules at an angle of 90∘, 180∘, or 270∘. On top of the junction, we place a series of metallic gates with the same gate stack as the split-gate transistors. We propose a five-gate structure arranged in cross geometry—one central square gate flanked by four square gates of the same footprint. The characteristic dimensions of the junction are indicated in Fig. 3b, with submodule-to-edge-gate separation in \({x}^{{\prime} }\)(\({y}^{{\prime} }\)) directions Lq (≈40 nm), the gate length in the \({x}^{{\prime} }\)(\({y}^{{\prime} }\)) directions Ll (≈80 nm), and a junction gate-to-gate separation Ld (≈40 nm). The gate length and pitch are in line with the fabrication requirements for the 1d sub-modules. For the junction, we suggest gate contact over active, a feature available in 10 nm node technology. The junction is invariant under rotations by 90∘.

Fig. 3: Junction and shuttling sequence.
figure 3

a Schematic diagonal view of the junction connecting two \({x}^{{\prime} }\) and two \({y}^{{\prime} }\) submodules. b Top view of the junction. c Shuttling sequence from \({x}^{{\prime} }\) submodule at the left to \({y}^{{\prime} }\) submodule at the bottom. Arrows indicate three consecutive spin shuttling operations (i–iii), followed by a Swap operation, and another three consecutive spin shuttling operations (v–vii). d Same as c, abstracted. e Hardware topology of the junction. Qubits (dots) of \({x}^{{\prime} }\) and \({y}^{{\prime} }\) submodules are connected via six shuttling and one Swap operations (lines).

Full size image

The purpose of the junction is to create a shuttling path for electrons49,91 at the edges of the 1d submodules to be moved around the junction in the \({x}^{{\prime} }\) and \({y}^{{\prime} }\) directions on demand using the appropriate gate voltages sequence. These electrons can be moved to be in exchange coupling proximity with the electrons at the edge of another submodule where a two-qubit gate will be performed. We illustrate the operation of the junction using an \({x}^{{\prime} }{y}^{{\prime} }\) coupling example in Fig. 3c: (i) Shuttle the electron under the top-rightmost gate in the left module \({x}^{{\prime} }\), to the left gate in the junction by applying a differential voltage between the two gates49. (ii) Shuttle from the left gate to the central gate of the junction. (iii) Shuttle from the central gate to the bottom gate of the junction. (iv) Implement a two-qubit gate between the electron under the bottom gate in the junction and the electron under the left-topmost gate in the \({y}^{{\prime} }\) module, as described above. (v–vii) Shuttle the electron back following the reverse process. The corresponding abstracted hardware topology and the same shuttling sequence are presented in Fig. 3d. Although in this work we consider two-qubit interactions between spins confined to different types of QDs (a corner QD in a submodule and a planar QD in the junction), the shuttling process above can be modified to produce two-qubit interactions between planar QDs which have been demonstrated29,30,65,76.

As discussed in Supplementary Note 5, we consider the regime in which spin shuttling operations are performed coherently and much faster than the two-qubit operation in step (iv). Any two qubits of a junction can be involved in a two-qubit operation between them and, since shuttle operations are assumed to have negligible overhead, two two-qubit operations can be run in parallel. Overall, this reasoning allows for abstracting the junction element into the simplified hardware graph depicted in Fig. 3e.

Regarding the quality of the shuttling process, it has been argued that conveyor mode shuttling could lead to a phase error of less than 10−3 for typical values of electron spins in MOS QDs (a correlation length on the variation of the spin splitting of 20 nm and homogeneous coherence times, \({T}_{2}^{* }\ge 20\, \mu\)s) as long as the transfer occurs adiabatically with a velocity not less than 0.1 ms−1 (the transfer length here is ≈400 nm)92.

Compilation methods

We now present compilation methods for deploying NISQ-type quantum algorithms on the proposed architecture, following standard approaches. We assume that algorithms are given by a quantum circuit which consists of initialization, followed by a sequence of one- and two-qubit operations, and readout, suitable for execution on a fully-connected device. While most of these operations are readily available on the proposed architecture, the sparse connectivity will prohibit execution of two-qubit gates between arbitrary pairs of qubits that are not directly connected by an edge of the hardware graph. To address this issue, compilation methods re-express a given quantum circuit through an equivalent circuit readily amenable to the sparse hardware topology. More specifically, before executing a given two-qubit gate, one generally applies a sequence of Swap gates to shuttle the relevant qubits along the hardware graph until they reach neighboring positions. Once neighboring positions are reached, the two-qubit gate is executed and the sequence of Swap gates is reverted to promote the relevant qubits back to their original position. In applying this compilation strategy, the resulting quantum circuit accumulates a compilation overhead characterized by the number of additional Swap gates, NSWAP, and the increased circuit depth, Nd. Both quantities represent important quality metrics for the compilation which should be minimized as is possible to avoid additional decoherence and infidelities introduced through the additional Swap gates on NISQ devices. We note that the proposed architecture uses two \(\sqrt{{\rm{S}}{\scriptstyle{\rm{WAP}}}}\) gates to implement the Swap operation.

In what follows, we focus on two major compilation scenarios: (i) The case of moving two arbitrary qubits together along the hardware graph. This covers the general case where each two-qubit operation is addressed individually and usually gives reasonable estimates for the compilation overhead. (ii) The case of rearranging qubits in an arbitrary permutation. This compilation method could also be, for example, useful for variational algorithms93 from chemistry94,95 and finance96 which repeatedly execute some number of up to ⌊N/2⌋ two-qubit operations in parallel. For such algorithms, the compilation must efficiently permute qubits into configurations which allow for executing the relevant two-qubit operations in parallel, even on the sparse hardware topology. To implement such permutations efficiently, one repeatedly applies a layer of Swap operations during which up to ⌊N/2⌋ Swap gates are executed in parallel. Ultimately, this can result in significantly lower circuit depth than simply addressing each two-qubit operation individually. We note that being able to apply such a layer of two-qubit operations is less general than arbitrary rearrangement and thus further reductions may be possible for this specific case.

Finally, we compare our compilation methods to two important limiting cases—a 1d device which could be fabricated by joining nanowire submodules along one dimension, as depicted in Fig. 4a, and a 2d rectangular device consisting of lx by ly qubits with nearest-neighbor connectivity, as depicted in Fig. 4b.

Fig. 4: Qubit layouts.
figure 4

a Linear layout with N = 8 and b rectangular layout with nearest-neighbor connectivity with (lx, ly) = (8, 4). Qubits are depicted as circles and lines indicate pairs between which a two-qubit operation is feasible.

Full size image

Compilation methods: case I – moving two qubits together along the shortest path

The compilation method for case I (as in, e.g., Ref. 97) requires iterating over all two-qubit operations of a given input circuit and, for each pair of qubits involved in a two-qubit operation, (a) determining the shortest path connecting the two qubits and subsequently (b) executing Swap gates to connect the qubits along the shortest path, executing the two-qubit operation and shuttling qubits back to their original position. Finding the shortest path, i.e, the distance, between a pair of qubits can efficiently be implemented in polynomial time using, e.g., Dijkstra’s algorithm98.

The compilation overhead of this algorithm is determined by the length of the shortest path, l, connecting the pair of qubits involved in each two-qubit operation along the hardware graph. In particular, the overhead of Swap gates accumulated per two-qubit gate is given by NSWAP = l − 1 while the increased circuit depth per two-qubit operation will be given by \({N}_{{{{\rm{d}}}}}=\lceil\frac{l-1}{2}\rceil\), assuming that Swap gates on different pairs of qubits can be applied simultaneously. To compare further the compilation overhead for different devices, we compute the average (\(\bar{l}\)) and maximal (\({l}_{\max }\)) distances between qubit pairs in a given topology. For the linear layout with N qubits, we have

$${\bar{l}}_{{{{\rm{lin}}}}}=\frac{1}{3}(N+1),\quad {l}_{{{{\rm{lin}}}},\max }=N-1.$$
(2)

For a rectangular grid of lx by ly qubits, we find that \({\bar{l}}_{{{{\rm{rec}}}}}=\frac{1}{3}({l}_{{{{\rm{x}}}}}+{l}_{{{{\rm{y}}}}})\) and \({l}_{{{{\rm{rec}}}},\max }={l}_{{{{\rm{x}}}}}+{l}_{{{{\rm{y}}}}}-2\) and specifically for the square grid with \({l}_{{{{\rm{x}}}}}={l}_{{{{\rm{y}}}}}=\sqrt{N}\) we have

$${\bar{l}}_{{{{\rm{rec}}}}}=\frac{2}{3}\sqrt{N},\quad {l}_{{{{\rm{rec}}}},\max }=2(\sqrt{N}-1).$$
(3)

Finally, considering the proposed architecture for dx = dy, the average and maximal qubit distances are

$$\begin{array}{l}{\bar{l}}_{2{{{\rm{d}}}}}=\frac{1}{45(N-1)}\sqrt{\frac{m}{N}}\left[21{N}^{2}+5\left(m+\frac{2}{m}\right)N \vphantom{\left(\sqrt{{m}^{3}}+\frac{2}{\sqrt{m}}\right)}\right.\\ \quad\quad\quad\left.-15\left(\sqrt{{m}^{3}}+\frac{2}{\sqrt{m}}\right)\sqrt{N}+34{m}^{2}+20\right],\\ \qquad\quad \simeq \frac{7}{15}\sqrt{mN},\\ \qquad\quad {\bar{l}}_{2{{{\rm{d}}}},\max }=\sqrt{mN}.\end{array}$$
(4)

For details of the derivation, see Supplementary Note 6. For the limiting case \(m=\frac{N}{4}\), we see that

$${\bar{l}}_{2{{{\rm{d}}}}}=\frac{{N}^{2}}{4(N-1)},\quad {\bar{l}}_{2{{{\rm{d}}}},\max }=\frac{N}{2},$$
(5)

and thus, as expected, the device exhibits linear scaling behaviour. However, its performance is still better than that of the linear device due to the ring-shaped arrangement of qubits.

We visualize the aforementioned compilation overheads expressed via mean and maximal qubit distances in Fig. 5a, b as a function of increasing qubit number. These figures illustrate several important properties, which we comment on in the following. The linear configuration (labeled 1D) clearly exhibits a linear scaling of the compilation overhead, while the rectangular device with nearest neighbor connectivity (labeled 2D) exhibits a square-root scaling. The compilation overhead of the proposed architecture inherits the favorable square-root scaling of 2d hardware topologies, making the proposed architecture favorable over 1d devices. Interestingly, the compilation overhead of the proposed device never exceeds the compilation overhead of the linear architecture, even for the smallest devices dx = dy = 1, 2, 3, …. This is useful as first experimental realizations of the proposed architecture would start from small prototypes. Finally, for increasing sparsity m = 4, 8, 16, …, the compilation overhead of the proposed architecture does increase; however, it never exceeds the overhead of the linear device. This allows for balancing the trade-off between compilation overhead and creating space in between the qubit modules which can be beneficial for colocation of classical support electronics (see Supplementary Note 3).

Fig. 5: Compilation overhead of Case I.
figure 5

This is expressed via a average and b maximum shortest path as a function of the number of qubits for different layouts—a (1D) linear layout, a (2D) rectangular device with nearest neighbor connectivity with lx = ly and the proposed architecture in a square arrangement dx = dy with m = 4, 8, and 16. Lines indicate the scaling and dots indicate qubit numbers which can be realized by an actual device.

Full size image

Compilation methods: case II—rearranging qubits in arbitrary permutations

We now consider the cost of permuting all qubits at once, making use of sorting networks1,2. We begin by recalling qubit permutations on linear and rectangular devices3,4 as these underlie the compilation method for the proposed sparse architecture.

We first consider permutations on 1d linear devices with N qubits using parallel neighbor sort99, as depicted in Fig. 6a. First, each node of the hardware graph is assigned an index v = 1, …, N in ascending order, and each qubit is labeled by its final position. Consecutive layers of Swap operations are then applied in up to N steps. For odd steps 1, 3, …, qubits on node pairs (v, u) ∈ {(1, 2), (3, 4), …} are compared and a Swap operation is applied if the final destination of qubit v is larger than the final destination of qubit u. For even steps 2, 4, …, the same process occurs for qubits in node pairs (v, u) ∈ {(2, 3), (4, 5), …}. With this method, any permutation can be implemented in a maximum of N layers leading to an increase in the circuit depth of

$${N}_{{{{\rm{d}}}}}=N.$$
(6)

The maximum number of Swap operations needed is

$${N}_{{{{\rm{SWAP}}}}}=\frac{N(N-1)}{2}.$$
(7)

It is clear that it is possible for one or two qubits to be required to move N − 1 places and thus the method here produces a result close to the worst-case minimum. An alternative is to use bubble sort or insertion sort, but the maximum depth increases to 2N − 31,2.

Fig. 6: Qubit permutations.
figure 6

These are shown for a linear and b rectangular devices. a Parallel neighbor sort for a linear device with N = 4 qubits using 4 consecutive layers of Swaps. Qubits (circles) are labeled by final positions as marked by gray numbers. Orange lines indicate qubit pairs which are compared at a given iteration and swapped, if in the wrong order. b Permuting N = 9 qubits (circles) in a square layout. Graph positions are labeled in gray. Labels on qubit circles indicate the final row and column of each qubit. The permutation is implemented by consecutively using parallel neighbor sort along (i) columns, (ii) rows, and (iii) columns, as highlighted by orange lines.

Full size image

Next, we consider permutations on a rectangular device of N = lxly qubits with nearest neighbor connectivity. We follow the algorithm of Ref. 4, which consists of the following three steps: (i) Rearrange the qubits in each column using parallel neighbor sort such that each row contains exactly one qubit with final destination in each column 1, 2, 3, …, lx. (ii) Rearrange the qubits in each row using parallel neighbor sort such that all qubits are in the correct column. (iii) Rearrange the qubits in each column using parallel neighbor sort such that each qubit is in the correct final location. We note that column and row can also be interchanged in the above steps. An example visualizing the method is shown in Fig. 6b.

Once step (i) provides an arrangement such that each row contains exactly one qubit with final destination in column 1, 2, 3, …, lx, an implementation of steps (ii) and (iii) using parallel neighbor sort is simple. The challenge is to see that an efficient implementation of step (i) is always possible. This was shown in Refs. 3,4 using Hall’s matching theorem100 and will be discussed in more detail in its adaption to the proposed architecture with sparse 2d connectivity below. The overhead of the discussed method originates from consecutively using parallel neighbor sort on (i) columns (ii) rows and (iii) columns. This results in a maximum of

$${N}_{{{{\rm{d}}}}}=2{l}_{{{{\rm{y}}}}}+{l}_{{{{\rm{x}}}}}$$
(8)

layers of Swap gates and

$${N}_{{{{\rm{SWAP}}}}}=\frac{1}{2}{l}_{{{{\rm{x}}}}}{l}_{{{{\rm{y}}}}}({l}_{{{{\rm{x}}}}}+2{l}_{{{{\rm{y}}}}}-3)$$
(9)

total Swap gates. Specifically, for the square \({l}_{{{{\rm{y}}}}}={l}_{{{{\rm{x}}}}}=\sqrt{N}\), this gives

$${N}_{{{{\rm{d}}}}}=3\sqrt{N}$$
(10)

and

$${N}_{{{{\rm{SWAP}}}}}=\frac{3}{2}N(\sqrt{N}-1).$$
(11)

We now extend the method of Ref. 4 to the proposed architecture with sparse 2d connectivity. The method is based on the definition of generalized rows and columns as depicted in Fig. 7a, b, respectively. In essence, this results in 2dy rows and 2dx columns with 2mdx and 2mdy qubits respectively, where any given row and column share m qubits. Having defined these generalized rows and columns, we note that every qubit can conveniently be labeled by a combination of its column index, ax = 1, …, 2dx, and its vertical position, y. Equivalently, we could choose to label a qubit by its row index, ay and its horizontal position, x. The coordinates x and y can be seen in Fig. 1d. With generalized rows and columns in place, we describe the corresponding compilation algorithm for implementing qubit permutations. Each qubit, in its initial location, carries a label (ax, y), indicating its final position. An arbitrary qubit permutation can then be implemented using the following three steps: (i) Rearrange the qubits in each generalized column using parallel neighbor sort such that each set of qubits with fixed coordinate y contains exactly one qubit with final destination in each column ax = 1, 2, 3, …, 2dx. (ii) Rearrange the qubits in each generalized row using parallel neighbor sort such that all qubits are moved into the correct column according to their column index ax. (iii) Rearrange the qubits in each generalized column using parallel neighbor sort such that each qubit is in the correct y location along the columns. An example visualizing the method is given in Fig. 8. We note again that, once step (i) provides an arrangement such that each set of qubits with vertical position y contains exactly one qubit with final destination in column ax = 1, 2, 3, …, 2dx, an implementation of steps (ii) and (iii) using parallel neighbor sort is straightforward. The challenge is again to see that an efficient implementation of step (i) is always possible. The procedure to achieve this is illustrated in Fig. 8e–g and shall now be explained in more detail. To begin with, a bipartite graph of 4dx nodes is constructed, l ∈ 1, …, 2dx on the left and 2dx nodes r ∈ 1, …, 2dx on the right. Nodes on the left indicate columns in which a qubit is located initially. Nodes on the right indicate columns to which a qubit should be routed. To build the graph, one adds an edge (l, r) to the bipartite graph for each qubit initially located in column l and having final destination in column r. An example is given in Fig. 8e. We note that, since we have 2mdy qubits located in each column initially and since we will have 2mdy qubits with final destination located in each column, the bipartite graph has 2mdy edges incident to each node. Since some qubits may originate and end up in the same column, the bipartite graph can have multiple edges connecting the same nodes.

Fig. 7: Labeling of the proposed architecture.
figure 7

The generalized a rows and b columns m = 4, dx = 2 and dy = 3 are shown. Qubits of the same color are in the same row or column. Lines indicate between which qubits a two-qubit gate can be applied.

Full size image
Fig. 8: Qubit permutation on proposed architecture with dx = 2, dy = 1, and m = 2.
figure 8

a–d Qubits (circles) labeled by their final destination (y, ax) in the block are permuted using parallel neighbor sort along generalized (i) columns, (ii) rows, and (iii) columns as indicated by black solid as opposed to gray dashed lines. Gray labels next to the qubits index current qubit positions. e Bipartite graph corresponding to step (i). Nodes on the left and right indicate qubits with origin and final destination in columns 1, 2, 3, and 4 respectively, while edges represent the corresponding qubit. f Same as e with virtual nodes s, t. g Matchings extracted from e. The yth matching determines qubits routed to position y. An edge (l, r) of yth matching indicates that a qubit of column l destined for column r is to be routed to position y.

Full size image

Next, to determine how qubits should be arranged along columns in step (i), one extracts 2mdy perfect matchings \({{{{\mathcal{M}}}}}_{{{{\rm{y}}}}}\) with y = 1, …, 2mdy from the bipartite graph. A perfect matching \({{{{\mathcal{M}}}}}_{{{{\rm{y}}}}}\) is a set of edges such that each node of the bipartite graph is connected to exactly one edge of the matching. See Fig. 8g for examples showing one possible set of perfect matchings for the bipartite graph in Fig. 8e. Finding 2mdy perfect matchings for the given type of bipartite graph is always possible due to Hall’s matching theorem100. In the bipartite graphs that arise due to our compilation problem, each node has the same number of incident edges, a sufficient condition for Hall’s matching theorem to hold. Matchings can efficiently be found using the Ford-Fulkerson algorithm98. To this end, one attaches virtual nodes s and t to all nodes on the left and right of the bipartite graph, respectively, and determines a minimal network flow from s to t; see Fig. 8f. Finding a minimal flow configuration reveals one matching at a time. Successively removing edges of a matching from the bipartite graph and repeatedly running the Ford-Fulkerson algorithm will reveal all matchings \({{{{\mathcal{M}}}}}_{{{{\rm{y}}}}}\) with y = 1, …, 2mdy, as visualized in Fig. 8g. Finally, to route qubits in step (i), one selects qubits which move to vertical position y by iterating over the edges of the yth matching \((l,r)\in {{{{\mathcal{M}}}}}_{{{{\rm{y}}}}}\). Here, each edge (l, r) signifies that in the generalized column l a qubit destined for the generalized column r should be moved to vertical position y. Since edges in each set of matchings \({{{{\mathcal{M}}}}}_{{{{\rm{y}}}}}\) point to exactly one final destination per vertical position y, the fact that 2mdy matchings exist ensures that step (i) arranges the qubits in each column so that each row contains exactly m qubits with final destination in column 1, 2, 3, …, 2mdx.

We close this section by evaluating the compilation overhead. Considering the succession of parallel neighbor sorts along (i) generalized columns of length 2mdy, (ii) generalized rows of length 2mdx, and (iii) again generalized columns of length 2mdy, the maximum number of required layers of Swap gates is given by

$${N}_{{{{\rm{d}}}}}=4m{d}_{{{{\rm{y}}}}}+2m{d}_{{{{\rm{x}}}}}$$
(12)

and the maximum total number of Swap gates by

$${N}_{{{{\rm{SWAP}}}}}=2m{d}_{{{{\rm{x}}}}}{d}_{{{{\rm{y}}}}}(2m{d}_{{{{\rm{x}}}}}+4m{d}_{{{{\rm{y}}}}}-3).$$
(13)

For the specific case dx = dy = d, and using Eq. (1), we have

$${N}_{{{{\rm{d}}}}}=6md=3\sqrt{mN}$$
(14)

and

$${N}_{{{{\rm{SWAP}}}}}=6m{d}^{2}(2md-1)=\frac{3}{2}N(\sqrt{mN}-1).$$
(15)

We compare the compilation overhead of the proposed architecture with sparse 2d connectivity to the linear and rectangular hardware graphs in Fig. 9. Again, the linear configuration (labeled 1D) exhibits a linear scaling of the compilation overhead, while the rectangular device with nearest neighbor connectivity (labeled 2D) exhibits a square-root scaling. The compilation overhead of the proposed architecture inherits the favorable square-root scaling of 2d hardware topologies, making the proposed architecture favorable over 1d devices. Interestingly, the compilation overhead of the proposed device never exceeds the compilation overhead of the linear architecture for dx = dy ≥ 2. For device structures with dx = dy = 1, the compilation overhead of the proposed architecture can be reduced by recognizing that the rearrangement of the sparse device can always be handled with a single parallel neighbor sort, by arranging the qubits along a single line. This ensures that the compilation overhead for the proposed architecture never exceeds the compilation overhead of the 1d architecture even for the smallest devices. This is useful as first experimental realizations of the proposed architecture would start from small prototypes. Finally, for increasing sparsity m = 4, 8, 16, …, the compilation overhead of the proposed architecture does increase; however, it again never exceeds the overhead of the linear device. This allows for balancing between compilation overhead and creating space in between the qubit modules which can be beneficial for colocation of classical support electronics.

Fig. 9: Compilation overhead for arbitrary rearrangement of qubits given by maximum number of layers of Swap gates as a function of the number of qubits for (1d) linear qubit chains, (2d) rectangular nearest-neighbor grids and the proposed architecture for dx = dy = d with m = 4, 8 and 16.
figure 9

Lines indicate scaling and dots indicate qubit layout which exist. Crosses indicate the reduced compilation overhead by using a single parallel neighbor sort for devices with dx = dy = 1. Such devices consist of a square of qubits, as seen in Fig. 1c.

Full size image

Discussion

Inspired by the challenge of scaling up existing silicon quantum hardware, we investigate compilation strategies for sparsely-connected 2d qubit arrangements and propose a spin-qubit architecture with low compilation overhead. Our considerations are inspired by silicon nanowire split-gate transistors which form finite 1d chains of spin-qubits, allowing for the execution of two-qubit operations such as Swap gates among neighbors. Adding to this, we describe a silicon junction which can couple up to four nanowires at one end into 1d or 2d arrangements via spin shuttling and Swap operations. Given these hardware elements, we propose a modular 2d spin-qubit architecture with unit cells consisting of diagonally-oriented squares with nanowires along the edges and junctions at the corners.

The junction geometry opens space between modules to route the gate lines and/or to place cryogenic classical electronics in the quantum processor plane20,50. Fabricating the qubits and the classical control layer using the same technology is appealing because it will facilitate the integration process, improving feedback speeds in error-correction protocols, and offer potential solutions to wiring and layout challenges16,101,102,103,104,105. Integrating classical and quantum devices monolithically, using CMOS processes, enables the quantum processor to profit from the most mature industrial technology for the fabrication of large-scale circuits51. We show that this architecture allows for compilation strategies which inherit the favorable square-root scaling of compilation overhead in 2d structure and outperform the best in class compilation strategy of 1d chains, not only asymptotically, but also down to the minimal structure of a single square. This result shows that scaling silicon nanowires into 2d structures will have benefits early on, even in experimental demonstrations of the smallest prototypes, thus encouraging building the proposed junction element and expanding silicon architectures into 2d arrangements.

Going beyond the proposed architecture for spin qubits, the proposed method of generalized rows and columns can be applied to many other 2d architectures. In some cases, where rows and columns are not obvious, this could be made to work by introducing branches along a column and row, as illustrated in Fig. 10. As branches lead to three-way junctions within a row and/or column the overhead may, of course, be different. Overall, this shows that the method of generalized rows and columns is a useful compilation strategy not only for spin qubits but also many other architectures such as, for example, IBM’s heavy-hex for superconducting qubits.

Fig. 10: Labeling of an alternative sparsely-connected device.
figure 10

It is constructed from the linear segments and four-way junctions shown in Fig. 1a, b respectively. The generalized a rows and b columns are shown. Qubits are represented by dots and lines indicate between which qubits a two-qubit gate can be performed. Qubits of the same color are in the same row or column. For this device, the rows and columns have branches, which may increase the overhead of the Case II method.

Full size image

We wished to present compilation methods for the device for two quite general situations for which we could obtain an upper bound on the number of layers of SWAP gates to allow comparison to other architectures. The compilation strategies presented here act to demonstrate the square-root scaling in overhead due to routing for the sparsely-connected device, and the advantage of using this device over one with a 1d structure. Many other architecture-aware compilation methods exist and show good results [e.g.,5,6,7,8,106]. Circuit re-synthesis9 provides another option. Alternatively, it may be beneficial to consider a compilation method designed with the desired algorithm in mind [e.g.,25,107]. However, the distance between qubits will clearly affect the overhead introduced through such compilation methods, and thus the results presented here provide some indication of their likely performance.

In exploring strategies to reduce the compilation overhead we focus on the utility of the proposed architecture for the NISQ era. In that, future investigations should be directed to exploring the utility of the proposed architecture for fault-tolerant quantum computation. Positive indications towards this long-term goal are provided by recent work considering error correction along a line48 as well as the possibility of adapting the ideas of the spider-web array42 and operating each nanowire with a single-qubit connected in an angled rectangular lattice with highly coherent shuttle operations.

Finally, while our work provides thoughts on how to scale one-dimensional QDs into a sparse two-dimensional array, it leaves fundamental questions of feasibility to future research. Firstly, if operated for near-term applications, how many SWAP and shuttling operations could the architecture tolerate, before the results become inaccurate? Recent work investigating the feasibility of VQE algorithms in the presence of noise indicates the need for two-qubit gate fidelity well above the fault-tolerance threshold108. As such, the proposed architecture, which adds overhead through SWAP and shuttling operations, will likely require even higher two-qubit fidelities to become a scalable solution for NISQ algorithms. Similarly, if operated in a manner like Ref. 42, what fidelity would the individual shuttling operations need to achieve for overall fidelities to be above the fault-tolerance threshold? Recent work investigating surface codes on sparser grid-like architectures109 indicates that this will likely require gate and shuttling fidelities higher than those of the standard surface code, but it remains subject of future investigations to determine these fidelities. Finally, is it feasible to operate the one-dimensional lines of quantum dots as one perpetual qubit in the manner of Ref. 48? If so, would it then be feasible to exchange information between such qubits via the tunneling junctions? All these questions remain the subject of future work.