Predicting the compressive strength of self-compacting concrete by developed African vulture optimization algorithm-Elman neural networks

Abstract

The compressive strength of concrete depends on various factors. Since these parameters can be in a relatively wide range, it is difficult for predicting the behavior of concrete. Therefore, to solve this problem, an advanced modeling is needed. The aim of the literature is to achieve an ideal and flexible solution for predicting the behavior of concrete. Therefore, it is necessary to develop new approaches. Artificial Neural Networks (ANNs) have evolved from a theoretical method to a widely utilized technology by successful applications for a variety of issues. Actually, ANNs are a strong computing tool that provides the right solutions to problems that are difficult to use conventional methods. Inspired by the biological neural system, these networks are now widely used for solving a wide range of complicated problems in civil engineering. This study’’s target is evaluating the performance of developed African vulture optimization algorithm (DAVOA)-Elman neural networks (ENNs) by considering different input parameters in predicting the self-compacting concrete compressive strength. Hence, once 8 parameters and again to get as close as possible to the prediction conditions in the laboratory, 140 parameters entered to the improved version of Elman Neural Networks as input. According to the results, the element network has the lowest mean squares of the test error in predicting the compressive strength of 7 and 28 days in 100 repetitions. Further, in predicting both compressive strengths, the element grid with the Logsig-Purelin interlayer transfer function has the lowest test error, which determines the optimal transfer function. Moreover, the results showed that DAVOA as a reliable tool with time and cost savings have high power in predicting the desired characteristics. Also, in predicting both 7-day and 28-day compressive strength, networks built with 140 parameters have a 74.54 and 70.44% improvement in test error over 8-parameter networks, respectively, which directly affects this effect. Further parameters are considered as input to the network error rate in predicting the desired properties.

Today, concrete is one of the most utilized materials in construction. For this reason, it is so significant to study the behavior and strength of concrete¹. Self-compacting concrete is a concrete with high efficiency and non-separation that can be poured in the desired location, fill the mold space and surround the reinforcement without the need for mechanical compaction². In general, self-compacting concrete is made with ordinary concrete materials, and in some cases, in addition to relatively large amounts of super-plasticizer, a viscous additive is used to make it³. The type, quality and amount of materials used in concrete construction are the most significant factors in the compressive strength of concrete. For example, parameters such as water to cement ratio, type and amount of chemical and mineral additives can be mentioned. Since these parameters can be in a relatively wide range, it is difficult for predicting the behavior of concrete. Therefore, to solve this problem, an advanced modeling is needed⁴.

Making concrete without the need for vibration has been an important goal for concrete professionals who can achieve this goal by using additives and changing the mixing ratio of components, and eliminate concrete defects due to compaction operations. The invention of self-compacting concrete has been the result of these efforts. According to the definition of Bartos, self-compacting concrete is concrete that moves by its own weight and is able to completely fill the molds and maintain its homogeneity without the need for any vibration and even in spite of dense rebar⁵. The important advantages of this concrete are elimination of vibration operation, ease of concreting, increase of execution speed, ensuring proper compaction, especially in narrow sections with compact rebar, optimal strength to aggregate separation, ability to create smooth and beautiful finished surfaces. Finally, various projects of architecture on the facade, as well as reducing noise pollution in the workplace and the urban environment noted⁶. Therefore, due to the high use of self-compacting concrete, they thought of modeling it using artificial neural networks. One of the most beneficial means for achieving this purpose is the artificial neural network, which is derived from the concept of biological Neural Networks. The neural network model is in fact a complex nonlinear regression model that can be used for predicting the behavior of concrete at the lowest laboratory cost⁷.

The reason for choosing the artificial neural network model is that unlike the classical methods that exist in statistical theories, in these networks, no specific model or function with limiting assumptions is needed to linearize the problem. These networks are considered as a powerful and unique tool for unconventional or impossible analysis.

One of these is the detection of nonlinear systems⁸. In the last few decades, when computers have made it possible for implementing computational algorithms, in order to simulate the computational behavior of human beings, many research works have been started by several scientists, whose outcomes are in the field of artificial intelligence and in the computational intelligence subcategory is classified as Artificial Neural Networks⁹. In concrete technology field, it can be said that so far many researchers have designed different models of Artificial Neural Networks for predicting the different features of different concretes. Hameed et al. Used Artificial Neural Networks for predicting compressive strength and high-strength concrete slump¹⁰.

Abellán et al.¹¹ utilized a neural network for predicting the modulus of elasticity of normal concrete and high strength. Surayadi et al.¹² estimated the 28-day compressive strength of their compacted concrete. To do this, 120 laboratory data were considered for the training phase, 50 data for the validation phase, and 80 data for the experimental phase, for a total of 250 laboratory data were collected. The amount of cement, fine-grained, coarse-grained and fly ash, the ratio of water to cement, and chemical additives were defined as 6 inputs and the compressive strength as a single output of the neural network. By changing the number of layers and neurons, they reached a network with a hidden layer and 5 neurons as an artificial neural network with appropriate architecture. Ramachandra et al. used Artificial Neural Networks for predicting the compressive strength and flexural strength of polymer concrete include fly ash¹³. Utilization of an artificial neural network in MATLAB for predicting the compressive strength of concrete with recycled aggregates by some researchers. Training and experimental data for Artificial Neural Network development were accumulated utilizing 139 datasets obtained from 14 article resources. The improved Artificial Neural Network utilizes 6 input characteristics: water to cement ratio, water absorption, fine particles, coarse grains, recycled coarse grains, and water to total material ratio. The type of network used in this study is neural network after error propagation. Mean square error (MSE) was utilized as a measure to stop artificial neural network training. The results show that ANN is an efficient model to be used as a tool for predicting the compressive strength of concrete with recycled aggregates, which consists of various kinds and recycled aggregates resources¹⁴.

A review on the application of machine learning/deep learning methods for modelling the concrete/fiber-reinforced concrete at elevated temperatures was conducted in¹⁵. These methods were categorized according to the type, technical features, and research applications. Nguyen et al.¹⁶ proposed the semi-empirical formulas for strength predictions of concrete. Non-dimensionalization and optimisation techniques were used to solve this problem. The concrete strength of five datasets was predicted successfully with high accuracy. The lowest value of (R²) was 0.8567 for Dataset 1 and the highest one was 0.9555 for Dataset 3. In¹⁷, a MA framework was developed to estimate the parameters of antenna systems. A periodic switching scheme was studied to balance between global and local search. DE and NFS were used as global and local optimizers respectively. MDE-NFS algorithm was proposed to improve the energy efficiency of antenna systems. Mahmood et al.¹⁸ conducted an analysis of the experimental outcomes related to the compressive strength of hand-mixed cement-grouted sands by employing a range of mathematical methodologies. The compression strength evaluated in accordance with the BS standard was found to be 72% greater than that of the identical mix assessed under the ASTM standard. Emad et al.¹⁹ developed the impact of mix proportions on the compressive strength of ultra-high performance fiber reinforced concrete, considering multi-scale models to predict the compressive strength. A difference-based method for constructing the compressive strength targets was also proposed. Albaijan et al.²⁰ employed Silica nano powder to increase the strength of concrete, considering eleven machine learning methods to estimate the uniaxial compressive strength of nanosilica concrete. A graphical user interface was also developed for the concrete’s uniaxial compressive strength estimation. The statistical evaluation indicated that all models demonstrated commendable accuracy in relation to the experimental outcomes; however, the decision tree regressor model exhibited the lowest accuracy, reflected by a correlation coefficient of 0.68. Fakhri et al.²¹ explored the capabilities of twelve machine learning algorithms to forecast the tensile strength of geopolymer concrete subjected to different curing conditions. The results from both laboratory experiments and machine learning analyses indicated that the geopolymer concrete formulated with 30% fly ash and 70% ground granulated blast slag, combined with 14 mol of NaOH and subjected to an oven curing process at 300 °F for a duration of 28 days, demonstrated enhanced tensile strength.

Serray et al. modeled the new features of self-compacting concrete utilizing a Neural Network method²². In a 2019 study, Rajshwari et al. used compressive strength data from concrete containing large volumes of fly ash, collected from previous experimental research, to model 270 databases were gathered from previous studies, of which twelve were used for the neural network test phase. An ANN model with eight input parameters (ie cement value, fly ash value, ratio of water to adhesives, value of superplasticizer, amount of fine aggregate, amount of coarse and sample, and type of fly ash) was constructed for predicting the compressive strength of concrete. Along with weights and biases were adjusted by try and error for achieving a model with better performance.

Correlation coefficients for training and test data were 96.9% and 98%, respectively, indicating that Artificial Neural Network can be utilized for predicting the strength of HVFA concrete²³. Balf et al.²⁴ used 169 mixing schemes and 11 input neural network parameters that accurately predicted the 28-day compressive strength of self-compacting concrete containing chemical and mineral additives.

Today, self-compacting concrete is a concrete with high efficiency and non-separation that can be poured in the desired location, fill the mold space and surround the reinforcement without the need for mechanical compaction. The compressive strength of concrete depends on various factors. Since these parameters can be in a relatively wide range, it is difficult for predicting the behavior of concrete. Therefore, to solve this problem, an advanced modeling is needed. The aim of the literature is to achieve an ideal and flexible solution for predicting the behavior of concrete. Therefore, it is necessary to develop new approaches. In this regard, ANNs are a strong computing tool that provides the right solutions to problems that are difficult to use conventional methods. This study's target is evaluating the performance of DAVOA-ENN by considering different input parameters in predicting the self-compacting concrete compressive strength. Table 1 compares the work done in this research with similar literature.

Table 1 Comparison of the work done in the research with similar literature.

The neural network used in this study is the recursive network of the element; where, 275 and 549 mixing designs were collected from valid articles for predicting the compressive strength of 7 and 28 days of self-compacting concrete, respectively. The research was conducted in two series. In the first series, 140 parameters affected by the strength characteristic of concrete were entered into the network as introduced, which is unique among the papers presented in the field of predicting the properties of concrete. The reason for choosing this number of parameters is to build a comprehensive model for self-compacting concrete with a significant extent, along with simulating more and more prediction conditions to laboratory conditions by using more influencing factors that are actually available in laboratory conditions. In the second series, for investigating the effect of selected input parameters on the accuracy of the network in predicting the desired properties, the researcher reduced the parameters to 8 inputs. In this study, MATLAB neural network toolbox was used to construct and train neural networks. The network has an input, an output, and a hidden layers. The neurons number in the input layer is equivalent to the number of input parameters, i.e. 140 neurons, and in the output layer is equivalent to the desired single parameter, i.e. compressive strength of 7 or 28 days.

In summary, in the current research, the following objectives are considered:

• (i) Evaluation of the performance of the elemental dynamic Neural Network in predicting the self-compacting concrete compressive strength, especially in a situation where the scope of work is high due to the large volume of parameters and mixing scheme used. This research clearly shows the high potential and reliability of this network in terms of forecasting.

• (ii) Illustrating the effect of network optimization (performing the steps taken in the research) on increasing the accuracy of predicting the desired feature.

• (iii) The performance of the constructed networks varied when more parameters were considered as entered. Hence, once 8 parameters and then in order to simulate with real test conditions, 140 parameters are entered as element networks. Then, between the results obtained from the optimal networks with 8 and 140 entries, it was caught in the case form, which is the best network (selected network). Finally, the outcomes gained from the selected networks were compared with the laboratory outcomes.

• (iv) Making an almost comprehensive model for predicting compressive strength of 7 and 28 days of self-compacting concrete, even if the model includes a design of different mixtures of different types of self-compacting concrete (not just one type of self-compacting concrete). The maximum number of parameters that could be collected in this study was collected to conduct the research in a more comprehensive context.

Compressive strength of concrete

Compressive strength is one of the most significant features of hardened concrete. When tensile strength or shear strength is important in places, compressive strength is utilized for estimating the required properties³⁵. In other words, many various properties of concrete are determined by the compressive strength of concrete and are related to this characteristic, including specific gravity, permeability, durability, abrasion strength, sulfate strength, tensile strength, and some other concrete properties. Like other concrete, achieving the compressive strength of self-compacting concrete is possible through costly and time-consuming tests. Therefore, in this research, in order to achieve this important property of self-compacting concrete, the Artificial Neural Network is used with the aim of reducing the performance of laboratory work. In this study, MATLAB neural network toolbox was used to construct and train neural networks. The network has an input, an output, and a hidden layer. The neurons number in the input layer is equivalent to the number of input parameters, i.e. 140 neurons, and in the output layer is equivalent to the desired single parameter, i.e. compressive strength of 7 or 28 days. There is no specific rule for determining the number of neurons in the hidden layer, and trial and error is commonly used. In this study, according to the instructions provided in the literature, the number of neurons in the hidden layer was considered at least twice the number of parameters of the input layer, which varies from 30 to 300 neurons to determine the optimal number of neurons. The training algorithm used in the network is equal to the DAVOA due to the vastness of the network and the large number of neurons. The interlayer transfer function is set to the network default, tangsig-tangsig.

The selection of ENN over Multilayer Perceptron (MLP) and Feedforward (FF) models was motivated by several distinctive advantages that ENN offers for predicting the compressive strength of self-compacting concrete. ENN incorporates recurrent connections through feedback loops from the hidden layer to the context units. This allows the network to maintain a memory of previous states, which is beneficial for capturing temporal dependencies and dynamic patterns in the data that are not accessible to MLP and FF models. ENN is well-suited for modeling dynamic systems and processes where the current state depends on previous inputs. The prediction of concrete compressive strength involves complex interdependencies among variables, making ENN a suitable choice for capturing these relationships more effectively than static models like MLP and FF.

The architecture of ENN is designed to handle sequential data more efficiently. In our study, the historical and sequential nature of the input parameters can be better learned and represented through ENN’s recurrent structure, potentially improving predictive accuracy. Further, the context units in ENN help in better generalization of the learning model by considering both the current and past input information, leading to more robust predictions, especially in cases where the data has inherent time-dependent characteristics. While MLP and FF models are powerful in handling non-linear relationships, they lack the inherent memory capability and dynamic modeling features that ENN provides. In our tests, ENN demonstrated superior performance in capturing the intricacies of the data, which can be attributed to its recurrent nature. By leveraging the strengths of ENN, we aim to achieve higher accuracy and reliability in predicting the compressive strength of self-compacting concrete, addressing the dynamic and interdependent nature of the involved parameters.

The choice of the DAVOA over other optimization algorithms was driven by several key factors that align with the needs of our study on predicting the compressive strength of self-compacting concrete. DAVOA is known for its rapid convergence rates and efficient search capabilities. It effectively balances exploration and exploitation during the optimization process, making it suitable for complex, high-dimensional problems like predicting concrete properties. The algorithm is adaptable and can handle various constraints and objective functions. This flexibility allows it to be applied to diverse problems, including those with non-linear relationships such as those found in concrete strength prediction. Moreover, DAVOA has demonstrated robustness in handling noise and uncertainty in data. Given the variability and complexity of factors affecting concrete compressive strength, this characteristic is particularly beneficial.

Previous studies have shown that DAVOA outperforms or is competitive with other optimization algorithms, such as Genetic Algorithms (GA) and Particle Swarm Optimization (PSO), in terms of accuracy and computational efficiency. These comparisons support its effectiveness in applications similar to ours. The utilization of DAVOA in this context offers a novel approach, contributing to the innovation of optimization techniques used in civil engineering applications. Its application demonstrates the potential for newer algorithms to improve predictive modeling in material science. By choosing DAVOA, we aim to leverage these strengths to enhance the predictive accuracy and efficiency of our neural network models, ultimately providing more reliable and insightful results for the compressive strength of self-compacting concrete.

Methodology

Elman neural network

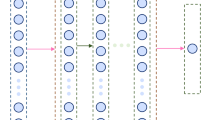
The Elman Neural Network is a recursive network originally introduced by Elman in 1990. This network is not only able to transfer data forward but also to transfer information backward³⁶. This network has a feedback loop from the hidden layer to the input layer³⁷. This feedback loop allows the network to form various time patterns. The element neural network is usually referred to as a special type of feed-forward network that has additional memory and a recursive loop. These networks are often used to identify or generate time outputs in nonlinear systems³⁸. Here, the optimized version of the Elman Neural Network is utilized for predicting the compressive strength of concrete. This network possesses 4 main layers containing the input, the context, the hidden, and the output layer. The principal sections of the network are related to the feed-forward Neural Networks like the connections in the input layer (${W}_{h}^{i}$), the hidden layer (${W}_{h}^{h}$), and the output layer (${W}_{h}^{o}$) are such as the multi-layer neural network. Figure 1 demonstrates a comprehensive form of the Elman Neural Network.

Fig. 1

The Elman neural network.

The Elman Neural Network contains an additional layer named context layer (${W}_{h}^{c}$) in which the inputs come from the outputs of the hidden layers for storing the hidden layer amounts in the past stage. This could be seen in Fig. 1. The input layer and the output layers dimension are supposed n, i.e. $x^{1} (t) = [x_{1}^{1} (t),x_{2}^{1} (t),...,x_{n}^{1} (t)]^{T}$ and $y(t) = [y_{1} (t),y_{2} (t),...,y_{n} (t)]^{T}$ the dimension for the context layer is assumed m. In this network, the ${l}^{th}$ input layer and the ${k}^{th}$ hidden layer are according to the following equations:

$$\begin{array}{*{20}l} {u_{i} \left( l \right) = e_{i} \left( l \right),} \hfill \\ {i = 1,2,...,n} \hfill \\ \end{array}$$

(1)

$$\begin{array}{*{20}l} {v_{k} \left( l \right) = \mathop \sum \limits_{j = 1}^{N} \omega_{kj}^{1} \left( l \right)x_{j}^{c} \left( l \right) + \mathop \sum \limits_{i = 1}^{n} \omega_{ki}^{2} \left( l \right)u_{i} \left( l \right)} \hfill \\ {k = 1,2,...,N} \hfill \\ \end{array}$$

(2)

where ${\omega }_{kj}^{l}\left(l\right)$ presents the i^th and j^th weights of the hidden layers from the ${o}^{th}$ node and ${x}_{j}^{c}\left(l\right)$ presents the signal that is come from the ${k}^{th}$ context layer node. Therefore, for the input layer i, the weight of the hidden layer k is gained by ${\omega }_{kj}^{2}\left(l\right)$. The hidden layer output ultimate amount which is fed to the context layer is demonstrated as below:

$$W_{k} \left( l \right) = f_{o} \left( {\overline{v}_{k} \left( l \right)} \right)$$

(3)

where

$$\overline{v}_{k} \left( l \right) = \frac{{v_{k} \left( l \right)}}{{{\text{max}}\left( {v_{k} \left( l \right)} \right)}}$$

(4)

where ${\overline{v} }_{k}(l)$ demonstrates the hidden layer normalized amount. Therefore, the context layer output is as below:

$$\begin{array}{*{20}l} {C_{k} \left( l \right) = \beta C_{k} \left( {l - 1} \right) + W_{k} \left( {l - 1} \right),} \hfill \\ {k = 1,2,...,N} \hfill \\ \end{array}$$

(5)

where ${W}_{k}$ is the obtain of the self-connected feedback between (0,1). As a result, the ENN output layer is according to the following equation:

$$\begin{gathered} y_{o} \left( l \right) = \mathop \sum \limits_{k = 1}^{N} \omega_{ok}^{3} \left( l \right)W_{k} \left( {\text{l}} \right), \hfill \\ {\text{o}} = 1,2, \ldots ,{\text{n}} \hfill \\ \end{gathered}$$

(6)

where ${\omega }_{ok}^{3}\left(l\right)$ presents the weight of the connection from the k^th layer into the o^th layer. For improving the Elman Neural Network structure, Ren et al.³⁹ have presented the method according to the pseudocode as follows:

where the learning rate is demonstrated by $\mu$, the constant amount is presented by $c$, and the present epoch is shown by $t$. The next level for optimizing the improved Elman Neural Network based on the Improved African vulture optimization algorithm.

Improved African vulture optimization algorithm

Perception

An optimization algorithm is utilized for accessing the most desirable solution for a special kind of problem⁴⁰. The principal method is to utilize traditional techniques for the problems, such as linear programming and nonlinear programming, Hamiltonian approaches are some kinds of these techniques⁴¹. The traditional approaches give accurate optimum solutions and they can be utilized to solve complex and nonlinear problems. Nowadays, the traditional techniques profitability has been declining due to the enhancing the optimization problems complexity⁴². Newly, the researchers discover novel types of optimization algorithms, which are helpful for solving optimization problems that are no necessary for solving their gradients⁴³. These approaches are based on nature and new types of them will be introduced⁴⁴. These methods are identified as metaheuristics. Some metaheuristics are such as follows:

Black Hole (BH), Lion Optimization, Chimp Optimization Algorithm (CHOA), World Cup Optimization (WCO) Algorithm⁴⁵, and African Vultures Optimization Algorithm.

African vulture optimization algorithm

The African Vulture Optimization Algorithm is a metaheuristic algorithm and inspired by vultures preying. The only bird of all life on our planet that can rise to an altitude of more than 11,000 m. At this altitude, birds try to fly long distances with the help of minimal current. This species is named after a German zoologist, Edward Gyps rueppellii, an African vulture of the Hawk family, a genus of vultures. The second name was Rupel. Vultures are very common in the northern and eastern parts of the African continent. The location of birds in a particular area depends largely on the number of herds. The African vulture is a very large bird of prey. Its body length is 1.1 m, its wingspan is 2.7 m and its weight is 4–5 kg. It is very similar in appearance to the neck, so its second name is Gyps rueppellii. The bird has limited the same small head covered with light downwards, the same elongated hooked beak with gray wax, the same long neck with feathers, and the same short tail. Vulture feathers above the body are dark brown and below it is a lighter red. The primary tail and feathers on the wings and tail are very dark, almost black. The eyes are small, have a yellow–brown iris. The legs of the bird are short, relatively firm, dark gray, with long, sharp claws. Males are no different in appearance from females. In young animals, the color of the feathers is slightly lighter.

The vulture's lifestyle attracts Abdollahzadeh et al. for working on describing a new metaheuristic method to solve optimization problem. To initialize the population size, achieve the same amount for whole vultures, and exploring the most desirable vulture in whole collections, and take the best solution for whole groups. It is modeled as below:

$$H\left( i \right) = \left\{ {\begin{array}{*{20}l} {Best~volture~1,~} \hfill & {~if~Z_{i} = f_{1} } \hfill \\ {Best~volture~2,~~} \hfill & {if~Z_{i} = f_{2} } \hfill \\ \end{array} } \right.$$

(7)

where ${f}_{1}+{f}_{2}=1$ $, {f}_{1}$ and ${f}_{2}$ describe the factors in the range of (0, 1) which is measured before optimization. The Roulette wheel are applied to model the most desirable solution selection probability and choosing the group's most desirable solution according to the following equation:

$$z_{i} = \frac{{G_{i} }}{{\mathop \sum \nolimits_{j = 1}^{m} G_{i} }}$$

(8)

where $G$ demonstrates the efficiency of the vultures. If α-numeric parameter is near to 1, the β-numeric is near to 0, and vice versa.

Searching the vulture's famine rate. They are flowing highly and searching for food and by losing the energy it is tries to reach the free meal. This is modeled as the following formulation:

$$l = d \times \left( {\sin^{\gamma } \left( {\frac{\pi }{2} \times \frac{{iter_{i} }}{{{\text{max}}_{iter} }}} \right) + \cos \left( {\frac{\pi }{2} \times \frac{{iter_{i} }}{{{\text{max}}_{iter} }}} \right) - 1} \right)$$

(9)

$$G = \left( {2 \times \delta + 1} \right) \times s \times \left( {1 - \frac{{iter_{i} }}{{{\text{max}}_{iter} }}} \right) + l$$

(10)

where $\delta$ describes the accidental amount between the 0 and 1, $ite{r}_{i}$ demonstrates the current iteration, a fixed number set that is belong to optimization performance and created the performance and exploitation phase is demonstrated by $s$, the whole iteration number is shown by ${\text{max}}_{iter}$, $y$ is the accidental amount between 0 and 1, and $d$ is the accidental amount between -2 and 2. If s reduces to 0, the vulture is hungry, and if it grows to 1, it is satisfied. In vulture's algorithm involve accidental section by 2 various designs and a factor ${R}_{1}$ for choosing the plane by amount in the range of (0, 1). Food exploring is formulated as follows:

$$\begin{gathered} {\text{If}}\;R_{1} \ge rand_{{R_{1} }} : \hfill \\ H\left( {i + 1} \right) = BV\left( i \right) - T\left( i \right) \times H \hfill \\ \end{gathered}$$

(11)

$$\begin{gathered} {\text{If}}\;R_{1} < rand_{{R_{1} }} : \hfill \\ H\left( {i + 1} \right) = BV\left( i \right) - H + rand_{2} \times \left( {\left( {ub - lb} \right) \times rand_{3} + lb} \right) \hfill \\ \end{gathered}$$

(12)

where

$$T\left( i \right) = \left| {U \times BV\left( i \right) - H\left( i \right)} \right|$$

(13)

where $Z$ describes the vultures shift accidently for safeguard food from another's vultures and is discovered by $U=2\times rand$, lower bound is demonstrated by $lb$ and upper bound is shown by $ub$, $BV$ includes the most desirable vultures, and $ran{d}_{2}$ and $ran{d}_{3}$ demonstrate 2 accidental amounts among (0, 1).

If $\left|H\right|<1$, utilization happen. This includes 2 section by 2 designs which are strong-minded with 2 factors of ${R}_{2}$ and ${R}_{3}$ that are between 0 and 1. The first section of utilization begins with $0.5<\left|H\right|<1$. 2 designs include revolve fly. If $|H|\ge 0.5$, it will demonstrate the good energy of the vulture content. The vulture that is weak can attempt to support from powerful vultures. it is modeled according to the following equation:

$$H\left( {i + 1} \right) = T\left( i \right) \times \left( {H + rand_{4} } \right) - j\left( t \right)$$

(14)

$$j\left( t \right) = BV\left( i \right) - H\left( i \right)$$

(15)

where $ran{d}_{4}$ describes an accidental amount in the range of (0, 1).

The vultures' spiral movement are as following equations:

$$y_{1} = BV\left( i \right) \times \left( {\frac{{rand_{5} \times H\left( i \right)}}{2\pi }} \right) \times \cos \left( {H\left( i \right)} \right)$$

(16)

$$y_{2} = BV\left( i \right) \times \left( {\frac{{rand_{6} \times H\left( i \right)}}{2\pi }} \right) \times \sin \left( {H\left( i \right)} \right)$$

(17)

$$H\left( {i + 1} \right) = BV\left( i \right) - \left( {y_{1} + {\text{y}}_{2} } \right)$$

(18)

where $ran{d}_{5}$ and $ran{d}_{6}$ are between 0 and 1. Two vultures attack various kinds of vultures to the food storage, and competitive effort are applied to place food. If $\left|H\right|<0.5$, this term can be determinate. At first $ran{d}_{{R }_{3}}$ is between 0 and 1. If $ran{d}_{{R}_{3}}\ge {R}_{3}$, the design is to accrue different kinds of vultures over the food resource. If $ran{d}_{{R}_{3}}<{R}_{3}$, the violent siege-fight is performed. Most of the time they are hungry, which creates a big competition for food them. This is mathematically formulated according to the following equation:

$$B_{1} = BestVilture_{1} \left( i \right) - \frac{{BestVilture_{1} \left( i \right) \times H\left( i \right)}}{{BestVilture_{1} \left( i \right) - H\left( i \right)^{2} }} \times H$$

(19)

$$B_{2} = BestVilture_{2} \left( i \right) - \frac{{BestVilture_{2} \left( i \right) \times H\left( i \right)}}{{BestVilture_{2} \left( i \right) - H\left( i \right)^{2} }} \times H$$

(20)

where $BestViltur{e}_{1}\left(i\right)$ and $BestViltur{e}_{2}\left(i\right)$ recognize the most desirable vulture for the first the second groups, H(i) presents the vulture current vector position and is gained as the following equation:

$$H\left( {i + 1} \right) = \frac{{B_{1} + B_{2} }}{2}$$

(21)

If $|F|<0.5$, the anterior strong vultures waste their power therefore, they can't withstand against the others. Other vultures go savage for reaching the food. They go in different direction from the chief vulture. This is formulated as the follows:

$$H\left( {i + 1} \right) = BV\left( i \right) - \left| {j\left( t \right)} \right| \times H \times Levy\left( j \right)$$

(22)

where modification phase defines the Levy fight (LF):

$$LF\left( x \right) = \frac{a \times \sigma }{{100 \times \left| b \right|^{2} }}$$

(23)

$$\sigma = \left( {\frac{{{\Gamma }\left( {1 + \zeta } \right) \times \sin \left( {\frac{\pi \zeta }{2}} \right)}}{{{\Gamma }\left( {1 + \zeta_{2} } \right) \times \zeta \times 2\left( {\frac{\zeta - 1}{2}} \right)}}} \right)^{{\frac{1}{\zeta }}}$$

(24)

where $a$ and $b$ describe 2 accidental amount in the range of (0, 1), and $\zeta$ describes a constant is set 1.5.

Developed African vulture optimization algorithm (DAVOA)

However, the African vulture optimization algorithm is a new algorithm by encouraging outcomes, it has some constraints like accidental substituting of weak vultures in the exact exploration part. This can perform a slow junction in the algorithm. Since this method is novel, there is no prescribed regulation for resolving the problem^46,47. The opposition-based learning (OBL) mechanism is used for creating right trade-off among the development and exploration through the research process and for making better the candidates variance. Firstly, the weak vultures by wrong cost esteem in every iteration are taken to bring up to date their situation according to the following techniques.

$$\begin{gathered} R_{1} < rand_{{R_{1} }} \hfill \\ H\left( {i + 1} \right) = \left\{ {\begin{array}{*{20}c} {BV\left( i \right) - H + r_{1} \times \sin \left( {r_{2} } \right) \times \left| {r_{3} \times H_{best}^{i} - H_{worst}^{i} } \right|, r_{4} < 0.5} \\ {BV\left( i \right) - H + r_{1} \times \cos \left( {r_{2} } \right) \times \left| {r_{3} \times H_{best}^{i} - H_{worst}^{i} } \right|, r_{4} \ge 0.5} \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(25)

where ${H}_{best}^{i}$ and ${H}_{worst}^{i}$ define the most desirable and the most disagreeable solution for group number $i$, and ${r}_{1}, {r}_{2},{r}_{3},{r}_{4}$ are estimated according to the following formulation for determining the new situation updating of the vultures.

$$r_{1} = a - itr \times \left( \frac{a}{N} \right)$$

(26)

$$r_{2} = 2\pi \times rnd$$

(27)

$$r_{3} = 2 \times rnd$$

(28)

$$r_{4} = rnd$$

(29)

where the current iteration is described by $itr$, number of iteration is demonstrated by $N$, $rnd$ is an accidental amount in the range of (0, 1), $a$ is a invariable amount match 2. Secondly, the Opposition-based learning (OBL) algorithm is utilized. If $rnd$ is lesser than the invariable amount,$c$, define the recently updated groups and their matching opposite new groups and taking the most desirable solution from them according to their purpose amounts. The purpose rating is performed by newly updated groups, by considering the Opposition-based learning and the position update, the African vulture optimization Algorithm will be more desirable⁴⁸. The main purpose of Opposition-based learning is to estimate the better resolution and its opposite amount at the identical time and to take the most desirable candidate solution from them according to the objective amounts. The opposite amount for a particular vulture x_i, are according to the following equation:

$$\overline{x}_{i} = U_{b} + L_{b} - x_{i} ,$$

(30)

$$x_{i} \in \left[ {L_{b} ,U_{b} } \right]$$

(31)

where $L$_b $\text{and }U$_b are the lower bounds and upper of the research area.

Substantiation of the algorithm

4 test function are used for DVOA validation. The DAVOA has been attained 4 standard test systems and the results has been compared with some algorithm, Lion optimization algorithm (LOA)⁴⁹, Multi-verse optimizer (MVO)⁵⁰, Black hole (BH)⁵¹, the AVOA⁵², and Emperor penguin optimizer (EPO)⁵³. The setting parameters of these algorithm are indicated in Table 2. The applied test function utilized in this investigation is demonstrated in Table 3.

Table 2 Setting parameters of the presented algorithm.

Table 3 The applied test function.

The proportion of algorithm is between 0 and 30. The equality study to the algorithm is according to the mini amount, max amount, basic amount, and the standard diversion value (std) that is shown in Table 4. This Table designates the validation outcome of the investigated algorithms.

Table 4 The substantiation result of the studied algorithms.

According to Table 4, IAVOA possesses the lower Mean amount for whole investigated method. Also low and up constraints amount of the presented algorithm are lower in comparison with the other algorithms. These test function's purpose is to reach the Min amount, the IAVOA has the better outcome. Furthermore, based on the comparison among other methods, IAVOA has is the most desirable and has more reliability and efficacy.

Data preparation

For the lead research, 275 mixing designs (data pairs) for 7-day compressive strength and another 549 mixing designs for predicting 28-day strength of self-compacting concrete were considered. It is noteworthy that initially 140 parameters affecting the strength characteristics of self-compacting concrete were considered as inputs for networks. The reason for this choice is that the author has tried to provide a comprehensive model that includes different types of self-compacting concrete (not just one type, taking into account a large part of the factors involved in the self-compacting concrete compressive strength). To evaluate the self-compacting concrete, and on the other hand to bring the prediction conditions very close to the laboratory conditions by considering as many details as possible, in order to evaluate the precision of the constructed networks in predicting the characteristic and finally the outcomes. Compare if the network has only a limited number of effective parameters. These parameters are:

• Specifications of used sand such as quantity, maximum size, specific gravity, water absorption percentage, grain size, shape of consumption which includes completely rounded corner, rounded corner, relatively rounded corner, sharp corner, relatively sharp corner.

• Consumption characteristics of sand include parameters such as quantity, specific gravity, water absorption percentage, and granulation.

• Grain style includes grain size, specific gravity, quantity, water absorption percentage, maximum size

• Recycled materials include quantity, related chemical analysis, and specific gravity.

• Dry and wet curing conditions.

• Specifications of used cement are the amount of cement, specific gravity and chemical analysis of the used cement.

• Superplasticizer contains PH value, amount of solid particles, specific gravity.

• Pozzolans (fly ash, natural zeolite, metakaolin, microsilica) including amount, specific gravity and chemical analysis of each pozzolan.

• Specifications of limestone powder include quantity, specific gravity, and relevant chemical analysis.

• Specifications of consumable fibers include type, length, diameter, tensile strength, specific gravity and relevant shape.

• Nano silica includes the amount, specific gravity and amount of solids.

• The amount of water consumed.

• The amount of viscosity modifier and its specific gravity.

• The amount of water reducing agent and its specific gravity.

• Operating temperature.

Regarding the method of identifying the chemical analysis of the mentioned materials to the model, it should be said that the chemical analysis of the relevant material is entered in Excel software so that each element is placed in a column of Excel and is introduced as input to the network. The same procedure was used to identify the granulation, with the difference that instead of the element, the relevant sieve number was entered in each column. For example, Table 5 shows how to identify the cement profile of the model. The outputs in question are also 7 and 28 days self-compacting concrete compressive strength, which are in Mega Pascal. For predicting each strength, 85% of the data pairs were used for network training and the other 15% for network testing. It should be noted that for the value of the pair of educational and experimental data, five data heads were randomly selected and the mean difference of the means and the mean difference of the standard deviation of each series were calculated and finally the series with the lowest difference of both statistical parameters He had the mentioned and entered the network as a selected series (candidate).

Table 5 Identify cement specifications to the model.

Network architecture, error function and correlation coefficient

In this study, MATLAB neural network toolbox was used to construct and train neural networks. The network has an input, an output, and a hidden layers. The neurons number in the input layer is equivalent to the number of input parameters, i.e. 140 neurons, and in the output layer is equivalent to the desired single parameter, i.e. compressive strength of 7 or 28 days. There is no specific rule for determining the number of neurons in the hidden layer, and trial and error is commonly used. Some researchers in their research have provided relationships for determining the number of hidden layer neurons, examples of these relationships are given in Table 6, in which Ni, Nh, and No are equivalent to the number of neurons in the input, output, and Is hidden. In this study, according to the instructions provided by Kanellopoulas and Wilkinson⁵⁴, the number of neurons in the hidden layer was considered at least twice the number of parameters of the input layer, which varies from 30 to 300 neurons to determine the optimal number of neurons. The training algorithm used in the network is equal to the DAVOA due to the vastness of the network and the large number of neurons. The interlayer transfer function is set to the network default, tangsig-tangsig.

Table 6 The proposed equations to determine the neurons number in the hidden layer.

The appropriate and usable error function in this study is the MSE function, which is the most common function in the study of neural network performance, which is given in Eq. (32). Also, correlation coefficient R was used to show the relationship between the network output and laboratory values, which is obtained according to Eq. (33).

$$MSE = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \left( {t_{i} - o_{i} } \right)^{2}$$

(32)

$$R = \frac{{\left( {n\sum t_{i} o_{i} - \sum t_{i} \sum o_{i} } \right)}}{{\sqrt {\left( {n\sum t_{i}^{2} - \left( {\sum t_{i} } \right)^{2} } \right)\left( {n\sum o_{i}^{2} - \left( {\sum o_{i} } \right)^{2} } \right)} }}$$

(33)

In both relations,$t$, the actual amount, $o$, the predicted amount and $n$, the number of data. Smith stated the following interval for R:

• When $|R|\ge 0.8$, there is a powerful between 2 sets of variables.

• When $0.2\le |R|\le 0.8$, there is a relation between 2 sets of variables.

• When $|R|\le 0.8$, there is a weak relation between 2 sets of variables.

It should be noted that for predicting the compressive strength by the element grid, raw steps, minimum maximum preprocessing, the maximum number of consecutive attempts, and determining the optimal transfer function was performed, which is described in the secondary network settings.

Secondary network setting

Data normalization

Normalize the data to minimize the effect of scale differences between different parameters and ensure that the parameters are the same. In fact, if large inputs are provided to the network, even with small neurons in the network, the sum of weighted inputs to the next layer neuron will increase and the problem of not training will occur. Therefore, to conduct this research, the data were normalized in the range of (0.1) using commands (5) and (6).

$$\left[ {pn,ps} \right] = mapminmax\left( {p,0,1} \right)$$

(34)

$$\left[ {tn,ts} \right] = mapminmax\left( {t,0,1} \right)$$

(35)

$p$, is the network input and $t$, is the desired goal of the network. Normalized inputs and targets, are returned in $pn, tn$, respectively. $ps$, $ts$ they include the setting parameters of this preprocessing, and the reverse and apply functions are used to return the normalized parameters back to their original state. Note that to perform this step, in order to show the effect of minimum–maximum preprocessing on the mean square error in the number of different neurons, once a pair of data without preprocessing and raw and again with the application of minimum preprocessing into the network were. Tables 7 and 8 show the results of the element grid for both states in both compressive strengths. As can be seen in both compressive strengths, the mean square error is lower in the case where the minimum–maximum preprocessing is used, which is a sign of higher network accuracy due to the use of this preprocessing. The optimal number of neurons with respect to the lowest MSE error rate for each strength between the raw state and the minimum–maximum (for both strengths the minimum error value corresponds to the minimum–maximum state) specified in the table, for a 7-day compressive strength of 180 neurons And 28 days equals 270 neurons.

Table 7 Results from the application of raw and minimum–maximum preprocessing for 7-day compressive strength by using DAVO algorithm.

Table 8 Results from the application of raw and minimum–maximum preprocessing for 28-day compressive strength by using DAVO algorithm.

Determining the maximum consecutive attempt

In the two raw stages and the minimum–maximum, the number of consecutive attempts is set to the network default of 6 repetitions. At this stage, the accuracy of the network was evaluated on 10, 50, 100, 500 itterations. These numbers are randomly selected and do not follow a specific rule. The purpose of this work is to select an iterative in which the grid has the lowest mean square error. The results are shown in Fig. 2. The network has the lowest test error for 7-day compressive strength at 50 repetitions, and for 28-day compressive strength at 100 repetitions, and the lowest test error is 11.69 and 18.59, respectively.

Fig. 2

Diagram of test error in terms of maximum consecutive attempts at 7 and 28 days compressive strength.

Determining the optimal transfer function

The interlayer transfer function in this network in all raw stages, minimum maximum, and maximum consecutive attempts are initially set to the default of tangsig-tangsig network, but in this final step, a combination of 9 possible modes of transfer functions, logsig, tansig, and purline is checked to obtain the optimal transfer function that has the lowest mean square error of the test error. The results of applying different transmission functions between two layers and their effect on network error rate are given in Table 9. As can be seen, the element neural network in 7, 28-day compressive strength with Tansig–sTansig transfer function between the two layers, has the best accuracy and consequently the lowest mean square error in the test mode, which is 11.69 and 18.59, respectively.

Table 9 Results of the effect of different transfer functions between 2 layers in predicting compressive strength of 7 and 28 days of self-compacting concrete.

The second series of research

In the second series of research, the number of input parameters to networks is significantly reduced. In other words, in order to determine the effect of selected input parameters on the test error of networks in predicting the desired characteristic, part of the factors affecting the compressive strength of concrete is ignored and all details are not considered and only 8 more general parameters that often In most articles, different concretes are used for predicting the strength of modeling. These parameters that due to laboratory experiments and using the results of related articles used in this field were selected include the following: The amount of consumed sand, specific gravity of sand, the amount of consumed sand, specific gravity of sand, amount of consumed cement, Specific weight of cement, amount of superplasticizer used, water to cement ratio. The neurons' number in the input layer is equivalent to the number of network input parameters, i.e. 8 neurons, and the number of neurons in the output layer is equal to the single output parameter, i.e. 7 or 28 days compressive strength, and the number of neurons in the hidden layer is up to 2 times the number of neurons in the input layer. (From 4 to 16 neurons) is variable. It should be noted that all the steps are the same as the first series, here only the results of each step are given. Tables 8 and 9 demonstrate the outcomes of the application of crude pretreatment and minimum and maximum for compressive strength of 7 and 28 days, respectively. As can be seen, as in the first series, both strengths have the least maximum improvement in test error by applying preprocessing. The optimal number of neurons in 7-day compressive strength is equal to 16 neurons and in 28-day strength is equal to 12 neurons. In Fig. 3, the mean squares of the network test error are observed in the maximum number of consecutive attempts. According to the diagram, the element network has the lowest mean squares of the test error in predicting the compressive strength of 7 and 28 days in 100 repetitions. Table 10 shows the results of the effect of changing the transfer functions between the two layers in predicting the compressive strength of 7 and 28 days of self-compacting concrete, which was determined. In predicting both compressive strengths, the element grid with the Logsig-Purelin interlayer transfer function has the lowest test error, which determines the optimal transfer function (Table 11).

Fig. 3

Diagram of test error in terms of maximum consecutive attempts at 7 and 28 days compressive strength.

Table 10 Results from the utilization of raw and minimum–maximum preprocessing for 7-day compressive strength by using DAVO algorithm.

Table 11 Results from the utilization of raw and minimum–maximum preprocessing for 28-day compressive strength by using DAVO algorithm.

The Min–Max normalization was applied to all input features before training the neural networks. This preprocessing step was crucial in ensuring that the DAVOA-ENN models could effectively learn from the data and provide accurate predictions for the compressive strength of self-compacting concrete. The normalization process played a vital role in enhancing the model's performance by providing a consistent and stable input dataset. This approach facilitated the effective training of the neural networks and contributed to the robustness and accuracy of the predictions (Table 12).

Table 12 Results of the effect of different transfer functions between 2 layers in predicting compressive strength of 7 and 28 days of self-compacting concrete.

Discussion and results

Comparison of the results of both series of studies by applying DAVOA in predicting compressive strength of 7 and 28 days of self-compacting concrete

Table 13 demonstrates the results of predicting the self-compacting concrete compressive strength for both series of research with 140 and 8 input parameters. The results show that in predicting both compressive strengths, element networks with 140 input parameters have a lower average test error compared to networks with 8 inputs, which indicates the higher accuracy of these networks in predicting the output. So that this rate of improvement of the average network test error, which is of great importance and the lower it is, is a sign that the result of the network prediction is close to reality (laboratory conditions), in 7-day compressive strength with 140 inputs 74.54 Percent and in 28-day compressive strength is 70.44% compared to the network with 8 inputs.

Table 13 Results of 7 and 28 days compressive strength of self-compacting concrete with 140 and 8 input parameters.

Figure 4 shows the correlation diagram of the laboratory data with the results of the selected network (meaning the network with the MSE of the test is less (here for both strengths, the network with 140 inputs) is shown for both strengths. Figure 4a and b corresponds to the 7-day and 28-day compressive strengths in network test mode, respectively, and Fig. 5 a and b corresponds to network training mode. As it turns out, the values obtained during the training and testing of the DAVOA have a high correlation with the laboratory values, which indicates the proper performance of the selected optimal networks made in predicting the properties.

Fig. 4

Correlation diagrams of laboratory data with selected network results in training mode for (a) 7-day compressive strength (b) 28-day compressive strength.

Fig. 5

Correlation diagrams of laboratory data with selected network results in test mode for (a) 7-day compressive strength (b) 28-day compressive strength.

Figure 6a and b compares the results of the 7 and 28-day compressive strength predictions of self-compacting concrete by the German network with 140 inputs as the selected network with real-time laboratory data. As can be seen in the diagrams, the results obtained from the element grid in predicting the 7 and 28 days strength of self-compacting concrete are very close to the results obtained in the laboratory. This indicates that the optimized element grid is very high and ultimately its reliability in predicting both 7 and 28 days compressive strength of self-compacting concrete. Table 14 shows the complete specifications of both selected optimal networks.

Fig. 6

The difference between (a) 7-day compressive strength of laboratory with selected network (b) 28 days compressive strength of laboratory with selected network.

Table 14 The complete specifications of both selected optimal networks.

To evaluate the performance of the DAVOA-ENN models in predicting the compressive strength of self-compacting concrete, we employed several statistical indices, including: (1) RMSE (Root Mean Square Error) measures the average magnitude of prediction errors, (2) MAE (Mean Absolute Error) provides the average absolute difference between predicted and actual values, (3) MAPE (Mean Absolute Percent Error), expresses error as a percentage of actual values, (4) R (Correlation Coefficient) the correlation coefficient indicates the strength and direction of the linear relationship between predicted and actual values, (5) the a20 index measures prediction accuracy within a 20% error margin (refer to^58,59,60), (6) AAE (Average Absolute Error) is another measure of average error magnitude, and (7) VAF% (Variance Accounted For) shows the percentage of variance in the data explained by the model. Table 15 shows these results.

Table 15 Additional statistical indices results.

By incorporating these additional indices, we provide a comprehensive evaluation of the DAVOA-ENN models. The metrics demonstrate the robustness and predictive accuracy of our approach in determining the compressive strength of self-compacting concrete. The inclusion of AAE and VAF% offers further insights into the model’s performance, highlighting its ability to accurately capture the variability and dynamic nature of the data.

Taylor diagram

In addition to the statistical indices presented, we have utilized a Taylor diagram to visually assess the performance of the DAVOA-ENN compared to other models like Multilayer Perceptron (MLP) and Feedforward (FF) models. The Taylor diagram provides a comprehensive visualization of the metrics. The radial distance from the origin on the Taylor diagram represents the correlation between model predictions and observed data. A higher correlation coefficient indicates a stronger linear relationship. Further, the distance along the x-axis reflects the standard deviation of model predictions, allowing for comparison with the observed data's standard deviation (Fig. 7).

Fig. 7

Taylor diagram to visually assess the performance of the DAVOA-ENN compared to other models like Multilayer Perceptron and Feedforward models.

Although not directly plotted, RMSE can be inferred from the distance between the model points and the reference point on the x-axis. The Taylor diagram clearly illustrates the comparative performance of the models, showing that the DAVOA-ENN model achieves the highest correlation and a standard deviation closest to the observed data, indicating superior predictive accuracy and consistency.

The inclusion of the Taylor diagram enhances the interpretability of our results, providing a visual summary of the model's performance in relation to the observed data. This comprehensive comparison facilitates a deeper understanding of each model's strengths and areas for improvement, supporting the robustness and reliability of the DAVOA-ENN approach in predicting the compressive strength of self-compacting concrete.

Usability of algorithms for other materials

The DAVOA-ENN models developed in this study have been specifically tailored for predicting the compressive strength of self-compacting concrete. However, the underlying architecture and optimization strategies are generalizable and can potentially be adapted to other materials with some considerations and modifications.

• (1) Feature engineering

  The input features used for predicting the compressive strength of concrete are specific to the properties of concrete mixtures. When applying the models to other materials, it is essential to identify and incorporate relevant input features that capture the characteristics and behaviors of the new material.

• (2) Transfer learning

  Transfer learning can be employed to leverage the knowledge gained from training on concrete data and apply it to new materials. This involves using the pre-trained model as a starting point and fine-tuning it with new data specific to the material in question.

• (3) Recalibration and training

  If the new material exhibits significantly different properties, it may be necessary to recalibrate the model by re-training it from scratch using a dataset representative of the new material. This ensures that the model accurately captures the unique properties and behaviors of the material.

Recalibration Process is based on: (i) Data collection: Collect a comprehensive dataset that includes relevant input features and target outputs for the new material. The quality and quantity of data play a critical role in model performance, (ii) Model fine-tuning: If transfer learning is feasible, fine-tune the existing model using the new dataset. This involves adjusting model parameters and layers to better capture the nuances of the new material, and (iii) Validation and testing: Validate the recalibrated model using a separate dataset to ensure its accuracy and reliability. Testing with unseen data helps assess the model's generalization capabilities.

The flexibility of the DAVOA-ENN architecture allows for potential adaptation to other materials, given that appropriate input features are identified and sufficient data is available. While transfer learning offers an efficient approach for adapting models, in some cases, re-training from scratch may be necessary to ensure the highest accuracy and applicability to new materials.

Limitations and future directions

The DAVOA-ENN models have shown significant promise in predicting the compressive strength of self-compacting concrete, yet several limitations remain. One primary limitation is the data dependency, where the accuracy of the models is contingent upon the quality and comprehensiveness of the datasets used. Insufficient or biased data can lead to inaccurate predictions, highlighting the need for extensive and representative datasets to ensure robust model performance. Additionally, the complexity of the neural network architecture can result in increased computational costs and longer training times, which may challenge real-time applications or situations where computational resources are constrained. While adaptable, the models are specifically trained on self-compacting concrete data, and applying them directly to other materials without appropriate adjustments could lead to suboptimal outcomes. Moreover, the models are sensitive to hyperparameters, such as learning rate and neuron configurations, necessitating careful tuning to achieve optimal performance.

To address these limitations, future research should focus on enhanced data collection to compile larger and more diverse datasets, thereby improving the models' robustness and generalization capabilities. Exploring hybrid models that integrate DAVOA-ENN with other machine learning techniques could enhance predictive accuracy and reliability. Furthermore, the implementation of automated hyperparameter optimization methods, such as Bayesian optimization or genetic algorithms, could streamline the model tuning process and boost overall performance. Investigating cross-material transfer learning strategies could facilitate adaptation to new materials and reduce the need for extensive retraining. Lastly, developing lightweight and efficient versions of the models for deployment in real-time applications would expand their practical utility, such as in on-site quality control, thereby broadening their applicability in the field of material science and engineering.

Conclusion

Today, self-compacting concrete is a concrete with high efficiency and non-separation that can be poured in the desired location, fill the mold space and surround the reinforcement without the need for mechanical compaction. The compressive strength of concrete depends on various factors. Since these parameters can be in a relatively wide range, it is difficult for predicting the behavior of concrete. Therefore, to solve this problem, an advanced modeling is needed. The aim of the literature is to achieve an ideal and flexible solution for predicting the behavior of concrete. Therefore, it is necessary to develop new approaches. In this regard, ANNs are a strong computing tool that provides the right solutions to problems that are difficult to use conventional methods. This study's target is evaluating the performance of DAVOA-ENN by considering different input parameters in predicting the self-compacting concrete compressive strength. The neural network used in this study is the recursive network of the element. 275 and 549 mixing designs were collected from valid articles for predicting the compressive strength of 7 and 28 days of self-compacting concrete, respectively. The research was conducted in two series. In the first series, 140 parameters affected by the strength characteristic of concrete were entered into the network as introduced, which is unique among the papers presented in the field of predicting the properties of concrete. The reason for choosing this number of parameters is to build a comprehensive model for self-compacting concrete with a significant extent, along with simulating more and more prediction conditions to laboratory conditions by using more influencing factors that are actually available in laboratory conditions. In the second series, for investigating the effect of selected input parameters on the accuracy of the network in predicting the desired properties, the researcher reduced the parameters to 8 inputs. The main results are:

• (i) The element grid, despite the use of different sources that are expected to increase the grid error due to the extent, was able for predicting the compressive strength of self-compacting concrete with high accuracy.

• (ii) When the inputs to the network are more complete and comprehensive and contain a large number of factors affecting the feature, the network is able for predicting the desired property with high accuracy, so that in this study the test error rate of DAVOA with 140 inputs for 7 and 28 days compressive strength of self-compacting concrete was 11.69 and 18.59, respectively.

• (iii) For the network with inputs were 45.95 and 62.91, respectively, which were calculated as above in Optimized element with 140 inputs compared to 8 inputs for both strengths with 74.54 and 70.44% improvement in test error, respectively, the reason is that the input parameters are more comprehensive and more details are considered during optimal network modeling.

• (iv) According to the results of this study, the element grid has a high potential in predicting the self-compacting concrete compressive strength. Also, the more complete the effective input parameters given to the optimal network, in other words, the more accurate the identification and application of input factors affecting the desired output during network construction, the results of network prediction to the results obtained from laboratory conditions will get closer and consequently, the network will predict the desired property with less error and higher accuracy.

The findings open avenues for further exploration into hybrid optimization techniques that can be applied to neural networks in various domains. The methodology developed in this study can be adapted and extended to other engineering materials, encouraging research into cross-material prediction models and transfer learning strategies. Future research could also focus on improving the efficiency of the algorithm to enable its application in real-time scenarios. The application of the DAVOA-ENN model provides a practical tool for engineers and researchers to predict the compressive strength of self-compacting concrete with high accuracy, facilitating more efficient material design and quality control processes. The model's adaptability suggests potential use in diverse material science applications, supporting innovations in construction and material engineering. The ability to accurately predict material properties can lead to cost savings and improved safety in construction practices.