Multiscale wavelet attention convolutional network for facial expression recognition

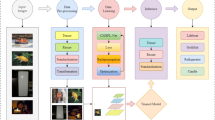
Abstract

Deep learning techniques, particularly Convolutional Neural Networks (CNNs), have been widely recognized as effective tools for facial expression recognition applications. The accuracy of facial expression recognition application requires further enhancement. Main work and effects of this study are as follows: First, the first convolutional layer of CNN is substituted with a Multi-scale Convolutional (MsC) layer, resulting in the proposal of the Multi-scale CNN (MCNN). Experimental results indicate that MCNN achieves an average accuracy improvement of 1.339% over CNN. Second, a wavelet Channel Attention (wCA) mechanism is incorporated after the first pooling layer of CNN, leading to the proposal of the wCA-based CNN (wCA-CNN). Experimental results demonstrate that wCA-CNN achieves an average accuracy improvement of 1.414% over CNN. Third, by substituting the first convolutional layer of the CNN with the MsC layer and incorporating wCA mechanism after the first pooling layer, the wCA-based Multi-scale CNN (wCA-MCNN) is introduced. Experimental results reveal that wCA-MCNN achieves an average accuracy improvement of 2.921% compared to CNN. Fourth, the Residual Network (ResNet18) is selected as a baseline model and improved accordingly. Compared to ResNet18, the accuracy of the proposed MsC-ResNet18, wCA-ResNet18, and MsC-wCA-ResNet18 improved by 0.845%, 0.835%, and 1.810%, respectively. Fifth, all the above proposed methods are evaluated by two datasets: the Facial Expression of Students in Real-Class (FESR) dataset collected from our real classroom and the Karolinska Directed Emotional Faces (KDEF) dataset.

Introduction

Deep learning methods, such as Convolutional Neural Networks (CNNs), have demonstrated greater effectiveness in facial expression recognition (FER) compared to traditional machine learning approaches¹. CNN-based methods are widely applied across various fields: In the medical domain, CNNs are utilized to identify patients’ emotional states², such as pain, anxiety, and depression. Furthermore, CNNs have been effectively adopted to expedite real-time image processing in medical diagnostics, particularly for tumor and cancer detection, thereby improving the accuracy and efficiency of diagnostic workflows³. In intelligent driving, CNNs improve devices’ capacity to interpret users’ emotional states⁴, such as issuing reminders to prevent driver fatigue and enhance safety. Moreover, CNN-based models excel in detecting driver drowsiness by analyzing facial features, including the eyes and mouth, enabling precise real-time evaluations of driver alertness and improving road safety⁵. In the educational field, CNNs are adopted to detect students’ emotions⁶, such as their levels of attention and areas of interest. Furthermore, CNNs have proven effective in classifying students’ facial expressions as ‘Understanding’ or ‘Not Understanding,’ facilitating more precise real-time evaluations of their engagement and comprehension during lectures⁷.

The motivations of this study are as follows: First, to find effective methods for facial expression recognition in classroom. Second, to achieve better performances such as accurate etc. of facial expression recognition methods. Third, to validate the effects of proposed improvements using more facial expression datasets.

Related studies on CNN-based facial expression recognition methods are summarized as follows: First, Lawpanom et al.⁸ proposed the Homogeneous Ensemble CNN (HoE-CNN), which combines multiple similar CNNs (e.g., DCNN⁹, EfficientNetB2¹⁰, ResNet50¹¹, etc.) to improve generalization and classification performance, particularly in online learning environments. Softmax outputs from each model are integrated to produce the final prediction. Second, Helaly et al.¹² developed a deep FER system based on enhanced ResNet18 using transfer learning. They evaluated several pre-trained models (MobileNet¹³, DenseNet121¹⁴, ResNet101¹¹, etc.) on FER2013 and CK + datasets, selecting ResNet18 for optimization. Improvements included residual blocks, batch normalization, dropout, and global average pooling, achieving 83% accuracy on FER2013 and 98% on CK+. Third, Ramya et al.¹⁵ introduced a system for recognizing students’ emotions in online classes using a fine-tuned AlexNet and shallow CNN, extracting features from 3D facial LBP and LDP. Features were fused via Canonical Correlation Analysis (CCA), and expressions classified using a multi-class SVM, reaching 87.69% accuracy on the Bosphorus dataset.

The limitations of the above studies can be summarized as follows: First, the performance metrics of the models, including precision, recall, F1 score, and accuracy, require further enhancement^16,17. CNNs often struggle to accurately capture subtle variations, leading to incorrect recognition results, particularly when handling fine-grained details, such as small facial expressions or subtle changes in emotion. This limitation is largely due to the inability of traditional convolutional layers to effectively process fine-grained features¹⁸. Second, the generalization capability of the models requires significant improvement¹⁹. While CNN models perform well on public facial emotion datasets, their effectiveness often diminishes when applied to real-world datasets. Variations in individual facial features and observation angles significantly impact recognition rates. Furthermore, the scale limitations of traditional convolutional layers hinder the model’s ability to effectively capture multi-scale facial features, which are essential for robust emotion recognition²⁰. Third, the application scenarios remain limited, with most studies primarily focusing on online classroom environments^21,22. In online classes, emotion recognition systems function effectively under controlled conditions, with only minor issues observed. However, in offline classroom environments, emotion recognition is influenced by various factors, including variations in facial observation angles and environmental changes.

The main contributions of this study are outlined as follows: First, a Multi-scale Convolutional Neural Network (MCNN) and a MsC-ResNet18 are proposed. The first convolutional layer of the baseline models (AlexNet and ResNet18) is replaced with a multi-scale convolutional (MsC) layer. Second, a wavelet Channel Attention-based Convolutional Neural Network (wCA-CNN) and a wCA-ResNet18 are introduced. The wavelet Channel Attention (wCA) mechanism is incorporated after the first pooling layer of the baseline models. Third, a wavelet Channel Attention-based Multi-scale Convolutional Neural Network (wCA-MCNN) and a MsC-wCA-ResNet18 are presented. The first convolutional layer of the baseline models is replaced with the MsC layer, and the wCA mechanism is additionally incorporated after the first pooling layer. Finally, the proposed models are validated using both the Facial Expression of Students in Real-Class (FESR) dataset and the publicly available Karolinska Directed Emotional Faces (KDEF) dataset²³.

The remainder of this paper is organized as follows: the next section introduces the MCNN and MsC-ResNet18 models. This is followed by a description of the wCA-CNN and wCA-ResNet18 models. Then, the combined models, wCA-MCNN and MsC-wCA-ResNet18, are discussed. Subsequently, the experimental setup is outlined, including datasets, hyperparameter settings, ablation studies, and comparisons. A comprehensive discussion is provided, covering failure cases, computational efficiency, robustness, comparative analysis with related methods, distinctions from prior work, and future research directions. Finally, the study is concluded.

MCNN and MsC-ResNet18 models

The primary focus of this section is outlined as follows: First, the structures of the baseline models are introduced. Second, the structures of the MCNN and MsC-ResNet18 models are presented. Third, the forward propagation process of the MCNN is detailed.

The structures of the baseline models

The structures of the baseline models used in this study are illustrated in Figs. 1 and 2: First, the ReLU activation function is applied to the convolutional and hidden layers. Second, the SoftMax activation function is adopted in the output layer. Third, no activation functions are applied to the input or pooling layers. Fourth, each convolutional layer in ResNet18 is succeeded by a batch normalization layer. The forward propagation mechanisms of AlexNet and ResNet18 have been elaborated in previous studies^24,25.

Fig. 1

The structure of CNN,$\:\:Conv(k,\:s,\:p)$ denotes a convolutional layer with kernel size $\:k$, stride$\:\:s$, and padding$\:\:p$. $\:Maxpool(k,\:s,\:p)$ represents a max pooling layer with window size $\:k$, stride $\:s$, and padding $\:p$.$\:\:FC$ denotes a fully connected layer.

Fig. 2

The structure of ResNet18, including each layer of ResNet18 and the residual connection.

Structure of the MCNN and MsC-ResNet18

The limitations of CNNs in capturing fine-grained details can be summarized as follows: The kernel size of the first convolutional layer is typically large, potentially resulting in the loss of fine-grained details. Larger kernels primarily capture the overall structure of the image, often overlooking smaller and more intricate details. This limitation further restricts the local receptive field of neurons, diminishing the model’s capability to capture fine-grained information and generalize effectively.

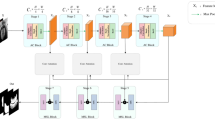
The advantages of the multi-scale convolutional (MsC) layer are summarized as follows: This study uses a convolutional layer that integrates multiple kernel sizes (3 × 3, 5 × 5, 7 × 7), forming the MsC layer. The use of kernels with different sizes allows the capture of image information at multiple scales. This approach enables the model to learn richer and more diverse features. Consequently, the generalization ability and robustness of the model are significantly enhanced. In this study, the MsC layer is adopted to replace the first convolutional layer of the baseline models, leading to the proposal of MCNN and MsC-ResNet18.

The architecture of the MCNN model is illustrated in Fig. 3. The architecture of the MsC-ResNet18 model is depicted in Fig. 4.

Fig. 3

The structure of MCNN, including each layer of MCNN: multi-scale convolution layer, convolutional layer, pooling layer, fully connection layer.

Fig. 4

The structure of MsC-ResNet18, including each layer of MsC ResNet18 and the residual connection.

Forward propagation of the MCNN

Forward propagation of the MsC layer

The MsC layer is capable of extracting features at multiple scales while preserving global information and maintaining fine-grained details. The mathematical formulation of the MsC layer is expressed as follows:

$$\:{O}^{2}=multiscaleconv\left({O}^{1}\right)=concat\left[conv\left({O}^{1},{\omega\:}_{1}\right),conv\left({O}^{1},{\omega\:}_{2}\right),\cdots\:,conv\left({O}^{1},{\omega\:}_{r}\right)\right]$$

(1)

$$\:conv\left({O}^{1},{\omega\:}_{r}\right)=\sum\:_{c=1}^{C}\sum\:_{u=0}^{k-1}\sum\:_{v=0}^{k-1}{\omega\:}_{r,c,u,v}\cdot\:{{O}^{1}}_{s\times\:i+u-p,\:\:s\times\:j+u-p,c}+{b}_{r}^{2}$$

(2)

.

$\:{O}^{1}$ represents the output of the input layer. The operation $\:conv\left({O}^{1},\:\:{\omega\:}_{r}\right)$ applies the convolution kernel $\:{\omega\:}_{r}$ to the feature map $\:{O}^{1}$, which produces an output feature map. The kernels $\:{\omega\:}_{1},{\omega\:}_{2},\cdots\:,{\omega\:}_{r}$ have different sizes. The $\:concat\left(\right)$ function is used to combine multiple output feature maps along the channel dimension. $\:i,j$ is the pixel value position. $\:r$ is the channel number of the output feature map. The weight $\:{\omega\:}_{r,c,u,v}$ is at position $\:(u,v)$ in the $\:c$-th input channel of kernel $\:r$. The value $\:{{O}^{1}}_{s\times\:i+u-p,\:\:s\times\:j+u-p,c}$ is the pixel at position $\:(s\times\:i+u-p,\:\:s\times\:j+v-p)$ in the $\:c$-th channel of the feature map. $\:C$ represents the total number of channels in the input feature map. $\:k$ represents the size of the convolution kernel. The parameter $\:s$ represents the stride of the kernel. The parameter $\:p$ represents the padding size, and $\:{b}_{r}$ is the bias term of the kernel. $\:{O}^{2}$ is the output of MsC Layer.

Forward propagation of the convolutional layer in the MCNN

The convolutional layer applies convolution operations to the output feature maps from the previous layer using convolutional kernels to extract meaningful features. The mathematical formulation for the convolutional layer in MCNN is provided in Eq. (3):

$$\:{O}_{mn}^{l}=conv\left({O}^{l-1},{w}^{l},m,n\right)=\:{\sum\:_{i=0}^{{size}^{l}-1}\sum\:_{j=0}^{{size}^{l}-1}{O}_{m+i,n+j}^{l-1}\cdot\:w}_{ij}^{l}+{b}^{l},\:l\ge\:4$$

(3)

.

$\:{O}_{mn}^{l}$ is the output value of the neuron at position $\:(m,n)$ in the $\:l$-th layer feature map. $\:{O}^{l-1}$ is the output feature map from the previous layer ($\:l-1$). $\:{w}_{ij}^{l}$ is the convolution kernel for the $\:l$-th layer, it is a two-dimensional matrix. $\:conv\left({O}^{l-1},{w}^{l},m,n\right)$ refers to the convolution operation performed by the layer on $\:{O}^{l-1}$ using the kernel $\:{w}^{l}$. $\:{size}^{l}$ indicates the size of the convolution kernel (i.e., its width and height). $\:{b}^{l}$ is the bias term for the $\:l$-th layer.

The output of the convolutional layer undergoes nonlinear activation through the ReLU function, as described in Eq. (4):

$$\:ReLU\left({O}_{mn}^{l}\right)=max\left(0,{O}_{mn}^{l}\right)=\:\left\{\begin{array}{c}0,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{O}_{mn}^{l}\le\:0\\\:{O}_{mn}^{l},\:\:if\:{O}_{mn}^{l}\:>0\:\end{array}\right.$$

(4)

.

Forward propagation of the pooling layer in the MCNN

The pooling layer is defined by its capacity to downsample the feature maps generated by the convolutional layer. The primary objectives of pooling are to reduce the spatial dimensions of the data, preserve essential features, minimize computational complexity, and mitigate overfitting. The mathematical computation of the pooling layer in the MCNN is provided in Eq. (5):

$$\:{O}_{i,j}^{l}=maxpool\left({O}_{i,j}^{l-1}\right)={max}\left({O}_{{size}^{l}\times\:\left(i-1\right)+m,{size}^{l}\times\:\left(j-1\right)+n}^{l-1}\right),m,\:n=1,\dots\:,{size}^{l};\:l\ge\:3$$

(5)

.

For example, $\:x=\left[\begin{array}{cc}\begin{array}{cc}{x}_{11}&\:{x}_{12}\\\:{x}_{21}&\:{x}_{22}\end{array}&\:\begin{array}{cc}{x}_{13}&\:{x}_{14}\\\:{x}_{23}&\:{x}_{24}\end{array}\\\:\begin{array}{cc}{x}_{31}&\:{x}_{32}\\\:{x}_{41}&\:{x}_{42}\end{array}&\:\begin{array}{cc}{x}_{33}&\:{x}_{34}\\\:{x}_{43}&\:{x}_{44}\end{array}\end{array}\right]$, the result after applying the pooling layer can be calculated using Eq. (6):

$$\:maxpool\left(x\right)=\left[\begin{array}{cc}max({x}_{11},{x}_{12},{x}_{21},{x}_{22})&\:max({x}_{13},{x}_{14},{x}_{23},{x}_{24})\\\:max({x}_{31},{x}_{32},{x}_{41},{x}_{42})&\:max({x}_{33},{x}_{34},{x}_{43},{x}_{44})\end{array}\right]$$

(6)

.

Forward propagation of the fully connected layer in the MCNN

In the MCNN, the input of the fully connected layer is derived from the output $\:{O}_{mn}^{9}$ of the last pooling layer, which is flattened into a one-dimensional vector. The relationship is expressed by Eq. (7):

$$\:{O}_{i}^{9}={O}_{mn}^{9},m=int\left(\frac{i}{{size}^{10}}\right)+1,n=i-{size}^{10}\times\:\left(m-1\right))$$

(7)

The final output of the fully connected layer is $\:{\widehat{y}}_{n}$. The value of $\:{\widehat{y}}_{n}$ can be obtained by calculating from Eq. (7) to Eq. (19):

$$\:{O}_{n}^{10}=\sum\:_{i=1}^{{size}^{10}}(\:{O}_{i}^{9}\cdot\:{w}_{in}^{10}+{b}_{n}),\:n=\text{1,2},\dots\:,\:{size}^{11}$$

(8)

$$\:{O{\prime\:}}_{n}^{10}=ReLU\left({O}_{n}^{10}\right)=\left\{\begin{array}{c}0,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{O}_{n}^{10}\le\:0\\\:{O}_{n}^{10},\:\:if\:{O}_{n}^{10}>0\end{array}\right.$$

(9)

$$\:{O}_{m}^{11}=\sum\:_{n=1}^{{size}^{11}}(\:{O{\prime\:}}_{n}^{10}\cdot\:{w}_{nm}^{11}+{b}_{m}),\:m=\text{1,2},\dots\:,\:{size}^{12}$$

(10)

$$\:{O{\prime\:}}_{m}^{11}=ReLU\left({O}_{m}^{11}\right)=\left\{\begin{array}{c}0,\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if\:{net}_{m}^{12}\le\:0\\\:{net}_{m}^{12},\:\:if\:{net}_{m}^{12}>0\end{array}\right.$$

(11)

$$\:{O}_{j}^{12}=\sum\:_{m=1}^{{size}^{12}}({O{\prime\:}}_{m}^{11}\cdot\:{w}_{mj}^{12}+{b}_{j}),\:j=\text{1,2},\dots\:,\:{size}^{13}$$

(12)

$$\:{O{\prime\:}}_{j}^{12}=softmax\left({O}_{j}^{12}\right)=\frac{{e}^{{O}_{j}^{12}}}{\sum\:_{j=1}^{{size}^{12}}{e}^{{O}_{j}^{12}}}$$

(13)

$$\:{\widehat{y}}_{n}={O{\prime\:}}_{j}^{12}$$

(14)

Loss calculation

In this study, the cross-entropy loss function is adopted to measure the difference between the predicted labels and the true labels. When the predicted value $\:{\widehat{y}}_{n}$ for each input sample closely approximates its corresponding true label $\:{y}_{n}$, the loss value decreases. This indicates that the predictions align more closely with the true labels, suggesting that the model demonstrates good training data fit. The mathematical expression for the cross-entropy loss function is presented in Eq. (15):

$$\:L=-\sum\:_{n=1}^{J}{y}_{n}log({\widehat{y}}_{n})$$

(15)

.

wCA-CNN and wCA-ResNet18 models

The primary contributions of this section are outlined as follows: First, the wavelet Channel Attention (wCA) mechanism is incorporated after the first pooling layer of the baseline models, leading to the proposal of the wavelet Channel Attention-based Convolutional Neural Network (wCA-CNN) and wCA-ResNet18, whose structures are illustrated. Second, the forward propagation process of the wCA-CNN is detailed.

Structure of the wCA-CNN and wCA-ResNet18

In this study, we proposed a wavelet Channel Attention (wCA) module, which is integrated by Channel Attention module and wavelet transform function. And the Morlet wavelet family is adopted as the core function for nonlinear activation in the wCA. Considering the simplification and computational efficiency of the module, we use an approximate real-valued form of the Morlet wavelet function: $\:cos\left(1.75t\right)\cdot\:\text{e}\text{x}\text{p}(-t)^{2}/2)$, which helps improve the model’s sensitivity to minor feature changes.

According to the above Morlet wavelet family, we design a parameterized first-order Morlet wavelet transform as $\:y\left(x\right)=cos\left(1.75(x-b)/a\right)\cdot\:\text{e}\text{x}\text{p}(-(x-b)/a)^{2}/2)$, where the trainable translation ($\:b$) and scaling ($\:a$) parameters are introduced to perform scale transformation on the input $\:\left(x\right)$. And it has the ability of nonlinear transformation and multi-scale extraction, which is suitable for visual tasks such as FER.

According to the above $\:y\left(x\right)$, the wavelet coefficients are used to generate channel attention weights: First, global average pooling and max pooling are applied to obtain channel-wise statistics, respectively. Second, a $\:1\times\:1$ convolution is used to reduce the channel dimension for extracting channel features. Third, the channel features are performed for nonlinear transformation by the Morlet wavelet transform function $\:y\left(x\right)\:$to enhance or suppress the effect of specific channels. Fourth, another $\:1\times\:1$ convolution is used to restore the original the channel dimension. Finally, the channel weights are obtained through the Sigmoid function.

The wCA-CNN and wCA-ResNet18 are proposed by integrating wCA module after the first pooling layer. The architecture of the wCA-CNN model is illustrated in Fig. 5. The architecture of the wCA-ResNet18 model is illustrated in Fig. 6. The architecture of the wCA is depicted in Fig. 7.

Fig. 5

The structure of wCA-CNN, including each layer of the the wCA-CNN: convolutional layer, wCA mechanism, pooling layer and fully connection layer.

Fig. 6

The structure of wCA-ResNet18, including each layer of wCA-ResNet18 and the residual connection.

Fig. 7

The structure of wCA, including pooling layer, convolutional layer, Morlet wavelet transform function, sigmoid function.

Forward propagation of the wCA

This section primarily explains the forward propagation process of the wCA mechanism. Figure 7 illustrates the wCA mechanism, and its forward propagation process is outlined as follows:

(1) Channel Attention Weight Based on Global Max Pooling.

The primary purpose of global max pooling is to extract the largest feature element from each channel, thereby emphasizing locally prominent features within an image. The forward propagation formula for the global max pooling operation in the wCA mechanism is expressed as follows:

$$\:{O}_{{m}_{c}}=GMP\left({O}_{c}\right)={max}_{1\le\:i\le\:{size}^{l},1\le\:j\le\:{size}^{l}}\left({O}_{i,j,c}\right),\:\:c=\text{1,2},\dots\:,C$$

(16)

.

$\:{O}_{{m}_{c}}$ is the output feature map at the $\:c$-th channel. $\:{O}_{i,j,c}$ is the value of the feature map at position $\:(i,\:j)$ in the $\:c$-th channel from the previous layer. The final output feature map has a size of $\:(C,\:1,\:1)$, which represents the global maximum value of each channel. $\:{O}_{c}$ is the feature map from the previous layer with a shape of $\:(C,size,size)$, where $\:C$ is the number of channels, and $\:size$ refers to the height and width of the feature map, respectively.

The input to the first convolutional layer of the wCA is the output of the global max pooling layer, and the forward propagation formula for the first convolutional layer is as follows:

$$\:{O}_{k}{\prime\:}=\:\sum\:_{c=1}^{C}{\omega\:}_{k,c}\cdot\:{O}_{{m}_{c}},\:\:k=\text{1,2},\dots\:,\frac{C}{ratio};c=\text{1,2},\dots\:,C$$

(17)

.

The size of the convolution kernel is $\:(\frac{C}{ratio},\text{C},\:1,\:1)$, where $\:{\omega\:}_{k,c}$ represents the weight of the convolution kernel between $\:k$ output channel and $\:c$ input channel, $\:{O}_{k}{\prime\:}$ denotes the value of the $\:k$ channel of the output feature map, with a dimension of $\:(\frac{C}{ratio},\:1,\:1)$.The $\:ratio$ is a constant value, set to 4.

Nonlinear activation is applied through the wavelet transform activation function:

$$\:\varPsi\:\left({O}_{k}{\prime\:}\right)=cos(1.75\cdot\:\frac{{O}_{k}{\prime\:}-b}{a})\cdot\:{e}^{\frac{-{\left(\frac{{O}_{k}-b}{a}\right)}^{2}}{2}}$$

(18)

.

$\:\varPsi\:\left(\right)$ denotes the Morlet wavelet basis function, where $\:a$ and $\:b$ represent the trainable scale factor and shift factor, respectively.

The forward propagation formula for the second convolutional layer in the wCA mechanism is expressed as follows:

$$\:{O}_{c}{\prime\:}=\:\sum\:_{k=1}^{\frac{C}{ratio}}{\omega\:}_{c,k}\cdot\:\varPsi\:\left({O}_{k}{\prime\:}\right),\:\:c=\text{1,2},\dots\:,C;\:k=\text{1,2},\dots\:,\frac{C}{ratio}$$

(19)

.

The size of the convolution kernel is given by $\:(\text{C},\frac{C}{ratio},\:1,\:1)$, where $\:{\omega\:}_{c,k}$ represents the weight of the convolution kernel between the $\:c$-th output channel and the $\:k$-th input channel. $\:{O}_{c}{\prime\:}$ denotes the value of the $\:c$-th channel in the output feature map, which has dimensions of $\:(C,\:1,\:1)$, the ratio is a constant, set to 4.

(2) Channel Attention Weight Based on Global Average Pooling.

The primary function of global average pooling is to compute the average across all spatial positions within each channel, thereby capturing the global background information of the entire image. The forward propagation formula for global average pooling is expressed as follows:

$$\:{O}_{{a}_{c}}=GAP\left({O}_{c}\right)=\frac{1}{size\times\:size}\sum\:_{i=1}^{size}\sum\:_{j=1}^{size}{O}_{i,j,c},\:\:c=\text{1,2},\dots\:,C$$

(20)

.

$\:{O}_{{a}_{c}}$ denotes the value of the output feature map at the $\:c$-th channel. $\:{O}_{i,j,c}$ is the value of the feature map at position $\:(i,\:j)$ in the $\:c$-th channel from the previous layer. $\:size$ refers to the dimensions of the feature maps $\:{O}_{c}$, representing its width and height. The size of the final output feature map is $\:(\frac{C}{ratio},\:1,\:1)$, corresponding to the global average for each channel.

The input to the first convolutional layer of the wCA is equivalent to the output of the global average pooling. The forward propagation formula for the first convolutional layer is expressed as follows:

$$\:{{O}_{k}}^{{\prime\:}{\prime\:}}=\:\sum\:_{c=1}^{C}{\omega\:{\prime\:}}_{k,c}\cdot\:{O}_{{a}_{c}},\:\:k=\text{1,2},\dots\:,\frac{C}{ratio};c=\text{1,2},\dots\:,C$$

(21)

.

$\:{{O}_{k}}^{{\prime\:}{\prime\:}}$ denotes the value of the $\:k$-th channel of the output feature map, which has dimensions of $\:(C,\:1,\:1)$. The $\:ratio$ is a constant, set to 8, and $\:{\omega\:{\prime\:}}_{k,c}$ represents the weight of the convolution kernel.

Nonlinear activation is applied using the wavelet transform activation function:

$$\:\varPsi\:\left({{O}_{k}}^{{\prime\:}{\prime\:}}\right)=cos\left(1.75\frac{{{O}_{k}}^{{\prime\:}{\prime\:}}-b}{a}\right)\cdot\:{e}^{\frac{-{\left(\frac{{{O}_{k}}^{{\prime\:}{\prime\:}}-b}{a}\right)}^{2}}{2}}$$

(22)

.

The forward propagation formula for the second convolutional layer of the wCA is expressed as follows:

$$\:{{O}_{c}}^{{\prime\:}{\prime\:}}=\:\sum\:_{k=1}^{\frac{C}{ratio}}{\omega\:{\prime\:}}_{c,k}\cdot\:\varPsi\:\left({{O}_{k}}^{{\prime\:}{\prime\:}}\right),\:\:c=\text{1,2},\dots\:,C;\:k=\text{1,2},\dots\:,\frac{C}{ratio}$$

(23)

.

$\:{{O}_{c}}^{{\prime\:}{\prime\:}}$ denotes the value of the c-th channel of the output feature map, which has dimensions of $\:(C,\:1,\:1)$. The $\:ratio$ is a constant, set to 4, and $\:{\omega\:{\prime\:}}_{c,k}$ represents the weight of the convolution kernel.

(3) Fusion of Channel Weights of Features.

A fused feature weight is obtained by summing the weight $\:{O}_{c}{\prime\:}$, derived from global max pooling, and the weight $\:{O}_{c}{\prime\:}{\prime\:}$, derived from global average pooling. This fused feature weight incorporates both global and local features of the image, offering a more comprehensive channel weight distribution for the model. The $\:Sigmoid ({\upsigma\:})$ function is then applied to regulate the weight values, ensuring they fall within the range [0, 1]. $\:{O}_{w}$ represents the output of the feature map $\:{O}_{c}$ after adjusting the channel weights through the wCA module, and its calculation formula is:

$$\:{O}_{w}={O}_{c}\cdot\:\sigma\:\left({O}_{c}{\prime\:}+{{O}_{c}}^{{\prime\:}{\prime\:}}\right)={O}_{c}\cdot\:\frac{1}{1+{e}^{-({O}_{c}{\prime\:}+{{O}_{c}}^{{\prime\:}{\prime\:}})}}$$

(24)

.

wCA-MCNN and MsC-wCA-ResNet18 models

The main objectives of this section are as follows: First, the MsC layer replaces the first convolutional layer in the baseline model, and the wavelet Channel Attention (wCA) is added after the first pooling layer. The wavelet Channel Attention-based Multi-scale Convolutional Neural Network (wCA-MCNN) is proposed, along with the MsC-wCA-ResNet18, and their structures are shown. Second, the forward propagation of the wCA-MCNN is described.

Structure of wCA-MCNN and MsC-wCA-ResNet18

By combining the advantages of the MsC layer and the wCA, both the wCA-MCNN and the MsC-wCA-ResNet18 enable multi-scale feature extraction and dynamic weighted fusion. The MsC layer extracts feature information from the input image at multiple scales, which is subsequently selectively weighted by the wCA. This approach considers the importance of each channel and integrates the multi-scale feature extraction capabilities of the wavelet transform. As a result, the model can learn more distinctive features. In contrast to the straightforward feature combination in MCNN and MsC-ResNet18, the channel weights of feature maps at multiple scales are adjusted through the wCA. The weight adjustment enables the model to focus more on channels with critical information while suppressing irrelevant or redundant features. This enhances the model’s performance and allows it to perform classification tasks more effectively.

The structure of the wCA-MCNN is illustrated in Fig. 8. The structure of the MsC-wCA-ResNet18 is illustrated in Fig. 9.

Fig. 8

The structure of wCA-MCNN, including each layer of wCA-MCNN: multi-scale convolutional layer, convolutional layer, pooling layer, wCA mechanism, fully connection layer.

Fig. 9

The structure of MsC-wCA-ResNet18, including each layer of MsC-wCA-ResNet18 and the residual connection.

Forward propagation of the wCA-MCNN

The similarities between wCA-MCNN, CNN, MCNN, and wCA-CNN are as follows: the MsC layer, convolutional layer, pooling layer, and fully connected forward propagation in wCA-MCNN are consistent with those in MCNN, whereas the wCA in wCA-MCNN is identical to that in wCA-CNN. The forward propagation formula for the wCA-MCNN has been described in the previous section.

Experiments

The main content of this section is as follows: First, the datasets used for the experiments are introduced; second, the hyperparameter configuration for the experiments is provided; third, the results of the experiments are analyzed and compared.

Datasets

In this study, we constructed a novel dataset named Facial Expression of Students in Real-Class (FESR) shown in Fig. 10, which captures spontaneous student expressions in natural classroom environments. Videos were recorded in our real classes using fixed-position cameras. The participants in the dataset are undergraduate students aged between 18 and 22, with an approximately balanced gender distribution (1:1 male-to-female ratio).

Images of facial regions were cropped from the video frames using face detection algorithm (RetinaFace²⁶). A total of 6,809 images were collected, with 5,438 used for training, 685 for validation, and 686 for testing. All images are resized to 224 × 224 pixels. Each image was labeled manually to five emotional categories: surprise, joy, neutral, bored, and upset.

The FESR dataset has several challenges as follows: Face in some images may be partially blocked or covered. (e.g., by classroom objects such as laptops or desks). Differences in head positions because students sit at different angles. The lights on the faces of different students are not the same. These characteristics make FESR a useful and realistic dataset for testing how well facial expression recognition systems work in real classroom settings.

Examples of representative images from each emotion category are shown in Fig. 10 (a), and the distribution of image counts per category is visualized in Fig. 10 (b).

Fig. 10

FESR dataset, (a) shows the category pictures of FESR dataset, including surprise, joy, neutral, bored, frustrated; (b) shows total number of images in each category.

The KDEF (Karolinska Directed Emotional Faces) dataset is used in this study. The KDEF dataset contains seven types of facial emotions: surprised, fearful, disgusted, happy, sad, angry, and neutral. Each emotion is presented from five different angles. The use of standardized images helps reduce variations, making the research results more reliable and reproducible. In this study, 2,348 images are used for training, 294 for validation, and 294 for testing purposes. All images have a resolution of 562 × 762 pixels. Figure 11 (a) shows examples of each emotion, while Fig. 11 (b) illustrates the distribution of images for each emotion in the training set.

Fig. 11

KDEF dataset, shows the category pictures of FESR dataset, including surprise, fearful, disgust, happy, sad; angry and neutral; (b) shows total number of images in each category.

Hyperparameter configuration

In the following experiments, the hyperparameter settings are as follows: Dropout is applied to prevent overfitting, with a dropout rate of 0.5 in the first fully connected layer and 0.3 in the second fully connected layer. Batch normalization is applied after the second convolutional layer ($\:Batch\_Norm1=192$) and the fifth convolutional layer ($\:Batch\_Norm2=256$). The early stopping method is adopted in the model. The model performance is automatically monitored during training, and training is halted if the loss does not decrease by more than a specified minimum change ($\:delta=0.00001$) after a patience period of 30 epochs, thereby preventing overfitting.

Hyperparameters are configured in Table 1.

Table 1 Hyperparameter configuration.

Ablation study

To evaluate the effectiveness of the proposed modules, ablation study on two proposed methods: wCA-MCNN and MsC-wCA-ResNet18 are designed.

Ablation study 1: removing the wCA module from wCA-MCNN and MsC-wCA-ResNet18, we obtain MCNN and MsC-ResNet18.

Ablation study 2: removing the MsC (Multi-scale Convolutional) layer from wCA-MCNN and MsC-wCA-ResNet18, we obtain wCA-CNN and wCA-ResNet18.

Ablation study 3: removing both the MsC layer and the wCA module from wCA-MCNN and MsC-wCA-ResNet18, we obtain fundamental baseline models.

Ablation study on FESR dataset

The validation accuracy and loss curves of CNN and its improved variants on the FESR dataset are presented in Fig. 12. These curves reflect the performance trends during the training process.

Fig. 12

Loss and accuracy of CNN, MCNN, wCA-CNN, wCA-MCNN on the validation set of FESR dataset.

The parameters of model, which have the lowest loss on validation set, were saved. Then, the saved parameters were used on the test set. The performance metrics of all compared models on test set of FESR are showed and compared in Table 2.

Table 2 The results of CNN, wCA-CNN, MCNN, and wCA-MCNN on the test set of FESR.

First, MCNN outperforms CNN, and this improvement has been demonstrated. On the FESR test set, the average precision, recall, F1 score, and accuracy of MCNN are 2.680%, 1.620%, 0.020572, and 1.370% higher than those of CNN, respectively.

Second, wCA-CNN outperforms CNN, and this improvement has been demonstrated. On the FESR test set, the average precision, recall, F1 score, and accuracy of wCA-CNN are 4.224%, 1.162%, 0.025922, and 1.196% higher than those of CNN, respectively.

Third, wCA-MCNN outperforms both MCNN and wCA-CNN, and this improvement has been demonstrated. On the FESR test set, the average precision, recall, F1 score, and accuracy of wCA-MCNN are 2.866%, 0.500%, 0.017064, and 1.140% higher than those of MCNN, respectively. Furthermore, the average precision, recall, F1 score, and accuracy of wCA-MCNN are 1.322%, 0.958%, 0.011714, and 1.314% higher than those of wCA-CNN, respectively.

The validation accuracy and loss curves of ResNet18 and its improved variants on the FESR dataset are presented in Fig. 13. These curves reflect the performance trends during the training process.

Fig. 13

Accuracy and loss of 5TPs on validation set of FESR.

The model parameters corresponding to the lowest validation loss during training were saved and used for testing on the test set. The average performance metrics of ResNet18 and its improved variants on the test set of FESR dataset are summarized and compared in Table 3.

Table 3 The results of ResNet18, MsC-ResNet18, wCA -ResNet18, and MsC- wCA ResNet18 on the test set of FESR.

First, the effectiveness of the MsC layer in improving ResNet18 has been validated. On the FESR test set, precision increased by 1.984%, recall increased by 0.321%, F1 score increased by 0.011451, and accuracy improved by 1.009%.

Second, the effectiveness of wCA in improving ResNet18 has been validated. On the FESR test set, precision increased by 1.592%, recall increased by 0.425%, F1 score increased by 0.010461, and accuracy improved by 0.717%.

Third, the combined effectiveness of the MsC layer and wCA in improving ResNet18 has been validated. On the FESR test set, precision increased by 4.951%, recall increased by 2.861%, F1 score increased by 0.039472, and accuracy improved by 2.396%.

Ablation study on KDEF dataset

The validation accuracy and loss curves of CNN and its improved variants on the KDEF dataset are presented in Fig. 14. These curves reflect the performance trends during the training process.

Fig. 14

Loss and accuracy of CNN, MCNN, wCA-CNN, wCA-MCNN on the validation set of KDEF dataset.

The parameters of model, which have the lowest loss on validation set, were saved. Then, the saved parameters were used on the test set. The performance metrics of all compared models on test set of KDEF are shown and compared in Table 4.

Table 4 The results of CNN, wCA-CNN, MCNN, and wCA-MCNN on the test set of KDEF.

First, the performance of MCNN outperforms that of CNN. On the KDEF test set, the average precision, recall, F1 score, and accuracy of MCNN are 1.664%, 1.632%, 0.016092, and 1.632% higher than those of CNN, respectively.

Second, the performance of wCA-CNN outperforms that of CNN. On the KDEF test set, the average precision, recall, F1 score, and accuracy of wCA-CNN are 1.450%, 1.428%, 0.014232, and 1.428% higher than those of CNN, respectively.

Third, the performance of wCA-MCNN outperforms both MCNN and wCA-CNN. On the KDEF test set, the average precision, recall, F1 score, and accuracy of wCA-MCNN are 1.574%, 1.700%, 0.017178, and 1.700% higher than those of MCNN, and 1.788%, 1.904%, 0.019038, and 1.904% higher than those of wCA-CNN, respectively.

The accuracy and loss curves on validation set of ResNet18 and its improved variants on the FESR dataset are presented in Fig. 15. These curves reflect the performance trends during the training process.

Fig. 15

Accuracy and Loss of 5TPs on validation set of KDEF.

The parameters of model, which have the lowest loss on validation set, were saved. Then, the saved parameters were used on the test set. The performance metrics of all compared models on test set of FESR are shown and compared in Table 5.

Table 5 The results of ResNet18, MsC-ResNet18, wCA -ResNet18, and MsC- wCA ResNet18 on the test set of KDEF.

First, the effectiveness of the MsC layer in improving ResNet18 has been validated. On the KDEF test set, precision increased by 0.626%, recall increased by 0.680%, F1 score increased by 0.006884, and accuracy improved by 0.680%.

Second, the effectiveness of wCA in improving ResNet18 has been validated. On the KDEF test set, precision increased by 0.885%, recall increased by 0.952%, F1 score increased by 0.009538, and accuracy improved by 0.952%.

Third, the combined effectiveness of the MsC layer and wCA in improving ResNet18 has been validated. On the KDEF test set, precision increased by 1.131%, recall increased by 1.224%, F1 score increased by 0.012376, and accuracy improved by 1.224%.

Confusion matrix

Confusion matrix on KDEF dataset

The confusion matrix offers an intuitive representation of the relationship between the model’s predictions and the true labels, illustrating how the models vary in identifying different categories. The confusion matrices for CNN, wCA-MCNN, ResNet18, and MsC-wCA-ResNet18 on the KDEF dataset are presented in Fig. 16.

Fig. 16

Confusion matrices for each method on FESR dataset.

According to Fig. 16, the following analysis can be made:

First, the baseline model has limitations in the differentiation of complex expressions. CNN confuses different negative emotions. For example, it mixes up ‘angry’ and ‘disgust’ with mistake rates of 9.5% (4/42) and 2.4% (1/42). It also wrongly predicts ‘fear’ as ‘sad’ in 7.1% of cases (3/42). Although ResNet18 is better learn deeper features through residual structures, it also confuses ‘fear’ with ‘surprise’, resulting in a confusion rate of ‘fear’ and ‘surprise’ still being as high as 12.2% (5/41).

Second, combining the MsC layer with the wCA module greatly improves the model’s performance. The wCA-MCNN can merge features at different scales, for example, eyebrow raising (a large feature) and slight mouth twitching (a small feature). This lowers the mistake rate for ‘fear’ by 33.3% (from 3 to 2) and increases the accuracy for ‘neutral’ by 7.1% (from 38 to 41). The MsC-wCA-ResNet18 focus more on important regions (like the eyes), reducing the confusion between ‘fear’ and ‘surprise’ by 40% (from 5 to 3). It also improves the accuracy for ‘disgust’ from 97.6% (41/42) to 100% (42/42).

Confusion matrix on FESR dataset

The confusion matrices for CNN, wCA-MCNN, ResNet18, and MsC-wCA-ResNet18 on the FESR dataset are presented in Fig. 17.

Fig. 17

Confusion matrices for each method on FESR dataset.

According to Fig. 17, the following analysis can be made:

First, baseline model has limitations when distinguishing complex expressions. The accuracy of the CNN for low-intensity expressions (such as ‘bored’) is only 64.3% (20/31), the confusion rate between it and ‘surprise’ reaches 6.5% (2/31), and 6.7% (9/305) of the ‘joy’ category is misjudged as ‘surprise’ in CNN. Although ResNet18 increased the recognition rate of ‘neutral’ to 98.4% (193/196), the misjudgment rates of ‘bored’ and ‘surprise’ still reached 9.7% (3/31).

Second, combining the MsC layer with the wCA module can improve performance of the model. For example, wCA-MCNN gives more importance to high-frequency details (like wrinkles at the corners of the mouth when someone is happy) and low-frequency patterns (like a relaxed face when someone is bored). This made the accuracy of recognizing ‘joy’ go up by 4.9% (from 278 to 293). Also, the number of times ‘joy’ was confused with ‘surprise’ dropped by 55.6% (from 9 to 4). The MsC-wCA-ResNet18 keeps a perfect accuracy of 100% (193/193) for ‘neutral’, and it became better at telling apart ‘bored’ from other emotions. For emotions like “surprise,” the misjudgment rate dropped from 7.9% (6/89) to 2.2% (2/89).

Comparative experiments with other methods

To further verify the applicability of the proposed method, we expanded the comparison scope. More relevant methods published recently in a real unconstrained environment, including DDMAFN²⁸, MLCL-Net²⁹, ResEmoteNet³⁰, MA-Net³¹, and CDERNet³², were selected for comparation.

In order to maintain the reliability of the experimental results, the same experimental setup is adopted. All relevant methods mentioned above were simulated on the KDEF and FESR datasets. The accuracy and loss of the validation set during the training process of relevant methods, wCA-MCNN and MsC-wCA-ResNet18 on the KDEF and FESR datasets were compared. The results are shown in Fig. 18.

Fig. 18

comparison with other methods.

The parameters of each model, which can get the lowest loss on validation set, were saved and used on the test set. The average values of the all-experimental results were recorded in Table 6, which are compared with wCA-MCNN and MsC-wCA-ResNet18.

Table 6 The comparative results proposed methods with other methods on both datasets.

The following conclusions can be drawn from Fig. 18; Table 6:

First, wCA-MCNN and MsC-wCA-ResNet18 have better stability during the training process compared to other methods. In the five experiments, there were no significant differences in the accuracy curve and loss value curve of the validation set. MLCL-Net and DDMAFN showed obvious fluctuations in five experiments, and there was a situation where there was a large deviation in the results of a certain experiment.

Second, the accuracies of wCA-MCNN and MsC-wCA-ResNet18 are better than the other related methods. Although in FESR, the performance of wCA-MCNN only exceeds that of DDMAFN and is weaker than other methods such as ResEmoteNet. On the FESR dataset, MsC-wCA-ResNet18 achieves the highest accuracy (97.664%) and F1 score (0.952918), outperforming all baseline models including MA-Net and CDERNet. On the KDEF dataset, the performances of both wCA-MCNN and MsC-wCA-ResNet18 are superior to other methods. Among them, MsC-wCA-ResNet18 achieved the highest values in Precision (97.510%), Recall (97.483%), F1 score (0.974806), and Accuracy (97.484%), demonstrating superior generalization and robustness under complex conditions.

Discussion

To provide a thorough and nuanced discussion, this section covers six aspects: First, failure cases are analyzed to understand the limitations of the model. Second, the computational cost is evaluated to assess the model’s efficiency. Third, the model’s robustness under real-world challenges is examined. Fourth, a comparative analysis is conducted against other related methods. Fifth, distinctions between our model and previous approaches are critically analyzed. Sixth, possible directions for future work are discussed.

Failure case analysis

At the early stage of this research, we explored an alternative approach by proposing the wavelet Squeeze-and-Excitation (wSE) module, which integrates the Morlet wavelet function with the Squeeze-and-Excitation (SE) mechanism. The MCNN was employed as the baseline model, adding the wSE module after the first pooling layer of MCNN, resulting in wavelet Squeeze and Excitation based Multi-scale Convolutional Neural Network (wSE-MCNN). However, this is a failure case that wSE cannot stably improve the performance of MCNN. The experimental results of this failed case are presented in Table 7.

Table 7 Results of failure case.

According to Table 7, the results show that wSE-MCNN outperforms MCNN on the FESR dataset. However, the performance of wSE-MCNN is worse than MCNN on the KDEF dataset.

The reason for the above failure case can be analyzed as follows: The wSE module modifies the original SE structure by replacing the ReLU activation with a Morlet wavelet transform function. It is difficult for wSE module to capture the complete and important image information within the channel only by relying on global average pooling, which leads to unstable attention weights and insufficient generalization ability.

To solve the above problem, wavelet-based Channel Attention (wCA) module is proposed. The wCA uses a dual-branch pooling strategy (global average and max) and a feature fusion scheme using $\:1\times\:1$ convolutions, allowing the wavelet transformation to operate on a richer and more diverse set of channel statistics. This design effectively balances global context and significant local features, leading to improved generalization across datasets.

Computational cost analysis

The number of parameters and Floating-point Operations Per second (FLOPs) of the baseline model, the proposed methods in this paper, and other related methods are recorded in Table 8, where the unit of measurement $\:\text{M}$ means one million ($\:{10}^{6}$) and G means Giga ($\:{10}^{9}$).

Table 8 Comparison of calculation costs.

As shown in Table 8, the wCA-MCNN and MsC-wCA-ResNet18 models demonstrate distinct trade-offs between recognition accuracy and computational efficiency, depending on their architectural configurations. Although MCNN has a relatively large parameter count (57.6406 M) and floating-point operations (1.1385G FLOPs), the inclusion of the wCA module in wCA-MCNN introduces only a negligible increase in model size and complexity (57.6509 M/1.1386G). This observation underscores the lightweight nature of the wCA module, which leverages global pooling, 1 × 1 convolutions, and a Morlet-wavelet-inspired nonlinear transformation. These characteristics make wCA highly compatible with existing backbone networks in a plug-and-play manner.

Moreover, MsC-wCA-ResNet18 achieves significantly higher recognition accuracy but incurs a notably larger computational cost (FLOPs: 8.7320G) than ResNet18 (1.8235G). This substantial increase in FLOPs primarily stems from the MsC layer, which simultaneously applies multiple convolutional kernels of varying sizes (e.g., 3 × 3, 5 × 5, 7 × 7) and concatenates their outputs along the channel dimension. While this multi-scale representation enables richer spatial feature extraction and improves model generalization, it substantially increases the number of intermediate feature maps and associated operations.

While the MsC layer contributes to performance gains, its computational inefficiency suggests that further structural optimization, such as kernel reparameterization or grouped convolutions, may be needed to balance its expressive power and cost. In contrast, the wCA module proves to be an efficient and scalable attention mechanism, adding only marginal computational burden while significantly enhancing channel-wise feature recalibration.

Robustness under Real-World challenges

The attention maps on facial images of wCA-MCNN and MsC-wCA-ResNet18, generated by GradCAM, are shown in Fig. 19, providing valuable information for the most concerned facial regions of models for facial expression recognition.

Fig. 19

The visual attention maps of the proposed methods.

According to Fig. 19, both models can capture meaningful facial regions. The wCA-MCNN mostly focus on the center of the face (such as eyes, nose, and mouth). These parts are usually the most helpful for recognizing facial expressions. This means wCA-MCNN can get key emotional information without using much computing power. The MsC-wCA-ResNet18 model pays attention to more parts of the face. It focuses on not just the main features, but also the cheeks, jaw, and forehead, which shows that it has a better ability to understand the expression of the entire face.

However, real-world environments present challenges that can influence the effectiveness of attention-based models. People might move their heads, cover their faces with hands or glasses, or be in poor lighting. These factors may cause attention mechanisms to become unstable or focus on irrelevant regions. For instance, in some samples, attention may shift toward hands or background, weakening the model’s discriminative ability. Although both wCA-MCNN and MsC-wCA-ResNet18 demonstrate decent performance and spatial attention capabilities, their success in real-world applications still depends heavily on the quality of inputs.

Comparative analysis with other related methods

The following discussions can be made from Fig. 18; Tables 6 and 7:

First, the MsC-wCA-ResNet18 model has the best performance. The MsC-wCA-ResNet18 consistently achieves better performance on all testing metrics, such as F1-score of 0.952918 and an accuracy of 97.664% on KDEF, and an F1-score of 0.974806 and an accuracy of 97.484% on FESR, which are better than MA-Net and CDERNet. The performance of wCA-MCNN is better than DDMAFN and ResEmoteNet, particularly in terms of accuracy. For instance, on the FESR dataset, wCA-MCNN reaches an accuracy of 94.968%, which is better than DDMAFN (93.258%) and ResEmoteNet (83.532%). These results highlight the better effects of MsC layer combined with the wCA module, which is helpful for the multi-scale extraction of features and the emphasis of important features by the model.

Second, the advantage of the proposed method is its clear and modular architecture. Compared with such models as ResEmoteNet and MA-Net, our design is much easier to expand. This is not only beneficial for ablation and diagnostic analysis, but also allows researchers to integrate MsC layer or wCA modules into other backbone networks with minimal effort.

Third, the disadvantage of MsC-wCA-ResNet18 is a high computational cost. MsC-wCA-ResNet18 incurs 8.7320 GFLOPs and is significantly higher than most methods despite having relatively moderate number of parameters (11.29 M). This increased complexity is primarily due to the added MsC layer, which can enhance feature capture ability. Although it can bring better accuracy, the high processing cost could make it difficult to apply in the real-world, especially where resources are limited.

Analysis of the distinction from prior work

Compared with the prior work (Ref^8,12,15)., the key distinctions are as follows:

First, Ref⁸. improves accuracy by using a multi-model ensemble, training multiple CNNs independently and combining their outputs for robustness. In this study, our method optimizes the single model, which can reduce computational cost and improve interpretability.

Second, Ref¹². enhances a single model by modifying the ResNet18 architecture under transfer learning. In this study, our approach emphasizes module-level enhancements, with MsC capturing fine-grained multi-scale features and wCA adaptively recalibrating channel importance, rather than simply adjusting the backbone.

Third, Ref¹⁵. adopts a hybrid method, which combined deep features of CNN with handcrafted descriptors like LBP, followed by classification such as SVM. In this study, our all-in-one deep learning framework makes training and predictions simpler. Because our framework does not have the problem of integrating multiple algorithms.

Future work and research directions

Some directions of future work can be explored as follows: First, expanding the dataset to encompass a broader range of classroom scenarios (such as collecting facial emotion data across different grades and classes) will be crucial for improving the model’s generalization in real-world educational settings, which will help address domain shifts and ensure robustness in complex, dynamic environments. Second, to apply on resource-constrained platforms, model lightweighting is a key objective. It can be achieved by replacing standard convolutions with efficient alternatives like Ghost Modules or by employing knowledge distillation to transfer knowledge from high-capacity teacher networks to compact student models. Finally, further refinement of the Multi-scale Convolutional layer and wavelet Channel Attention module is warranted. Such as dilated convolution can replace the standard convolution in MsC layer to reduce computational cost, and the incorporation of feature fusion gates in the wCA module to enhance the sensitivity of model.

Conclusion

This paper aims to improve the performance of deep learning methods in facial expression recognition. CNN and ResNet18 are adopted as baseline models, and multi-scale convolutional (MsC) layer and wavelet Channel Attention (wCA) module are introduced. Finally, wavelet channel Attention-based Multi-scale Convolutional Neural Network (wCA-MCNN) and MsC-wCA-ResNet18 are proposed.

All models were experimented on the public KDEF dataset and Facial Expression of Students in Real-class (FESR) dataset. The proposed methods are verified in the face expression recognition task of classroom in real-world.

Ablation experiments showed that all improvements in this study are effective. Several recently published and related methods were selected to compare with our proposed methods. The experimental results show that the method proposed in this paper has better performance on both the KDEF dataset and the FESR dataset.