Introduction

The economic operating conditions of electrical power systems pose one of the most significant challenges. The key lies in selecting optimal control variables and system quantities. The resolution of optimal power flow (OPF) remains a persistent challenge within the realm of electric power systems. The problem of the OPF in electrical networks is a nonlinear optimization problem that was introduced by Cf. Carpenter in 19621. The OPF has gained significant research attention as an important topic. It involves determining the optimal adjustment of control variables to optimize specific objective functions. OPF addresses the optimization of discrete and continuous control variables, encompassing minimizing of generation fuel costs and active power losses while improving voltage deviation, enhancing voltage stability, and ensuring system security with satisfying both equality and inequality constraints. Consequently, numerous researchers have focused on finding solutions to the OPF problem using both classical and metaheuristic optimization algorithms2.

Due to the complexity of the non-convex and non-differentiable objective functions (OFs) encountered in the OPF problem, classical methods such as linear programming, Newton methods, dynamic and interior-point methods have proven inadequate. As a result, metaheuristic optimization algorithms have been developed to efficiently tackle these complexities and attain the global optimum solution3. Over the past few decades, metaheuristic algorithms have exhibited successful and extensive application in solving various electric power system problems, including the multi-objective OPF problem4. Examples of such metaheuristic optimization algorithms include genetic algorithm (GA)5, particle swarm optimization (PSO)6, whale optimization algorithm (WOA)7, ant colony optimization (ACO)8, artificial bee colony (ABC)9, gray wolf optimizer (GWO)10, Physics-informed neural networks11, adaptive differential evolutionary algorithm12, firefly algorithm (FA)13, moth-flame optimization (MFO)14, cuckoo search algorithm15, adaptive seeker optimization algorithm16, JAYA optimizer17, marine predators algorithm (MPA)18, hybrid PSO and FA19, modified coyote optimization algorithm (MCOA)20, salp swarm optimization (SSO) algorithm21 and circle search algorithm (CSA)22.

Over the past few years, numerous researchers have dedicated their efforts to exploring advanced solutions for the power system’s OPF problem. Some notable studies in this area are outlined below: in23, multi-objective firefly algorithm with CPA was suggested for solving the MO-OPF problem. In24, DE algorithm was integrated with effective constraint handling techniques are introduced for OPF problem solution. Using AMTPG-JAYA technique, a single-objective OPF was optimized in25. Additionally, Table 1 presents improved methods, different objectives functions applied on different systems. This table presents several studies that attempt to reach the best solution to the OPF problem.

Table 1 Some metaheuristic algorithms presented recently for solving OPF problem in some literature review.
Full size table

The research gap in the previously reported methods are the classical deterministic optimization techniques that offer solutions with well-understood convergence properties and analytical foundations. However, these approaches assume differentiability and convexity yield suboptimal or infeasible solutions. The search-based methods have the following challenges: The missing of guaranteed convergence to a global optimum; The effectiveness of the previous methods is dependent on the selection and tuning mechanism of population size, inertia weights, and mutation rates for each algorithm; The random behavior of such algorithms produces limiting reproducibility and consistency; The associated computational burden is affected by the large-scale systems; these metaheuristics generally do not incorporate uncertainty handling mechanisms,

This paper addresses the OPF problem by simultaneously optimizing multiple objectives. These are minimizing the active power loss, fuel cost, emission, voltage deviation at the load buses, and ameliorating voltage stability index (VSI) while accounting for both equality and inequality constraints. In this line, the current paper finds the optimal operational output of power generation units that covers the load requirements considering the artificial rabbits’ optimization (ARO) is employed to find the solution of the considered OPF problem. The effectiveness of the proposed algorithm is evaluated through a comprehensive comparison study with the existing works in literature. Six standard IEEE power systems were also used with 22 different cases studied for testing the ARO performance in solving the OPF problem. Also, this paper extends its validation on different size large-scale test systems standard systems. It was proven that the routine of ARO has robust, and superior competitive performance compared with others at fine convergence rates. Significant technical and economic improvements are acquired.

The significant contribution of this paper can be summarized as follows:

This paper proposes multi-dimension optimal operation solution of the optimal power flow problem using ARO method.

The validation and effectiveness of the proposed algorithm is evaluated on small scale and large-scale IEEE power systems.

Statistical analyses are procced to prove the has robust, and superior competitive performance compared with others at fine convergence rates.

Sensitivity analyses in terms of varied population size and iteration number are also provided for sample systems.

Significant technical, economic and environmental improvements are achieved compared with several previous optimization techniques.

The remaining sections of this paper are structured as follows: Section “Problem formulation” introduces the formulation of the OPF problem. Section “Proposed solution methodology” illustrates the proposed ARO algorithm. In Section “Experimental simulations”, briefly introduces the simulation results, analysis of the experiment and the best compromise using the IEEE test systems. Section “Numerical simulation applications” provides a discussion of these results, while Section “Conclusion” serves as the conclusion, summarizing the main research findings and suggesting future trends.

Problem formulation

The main objective of the OPF problem is to optimize system objectives while adhering to predefined constraints. Solving the OPF leads to the determination of optimal control variable settings. In this context, we introduce a compact formula that facilitates the control of specific research challenges. Mathematically, OPF can be expressed as41,42:

Objectives

The general expression for multiobjective optimization problem can be expressed in the following set of equations, Eqs. (1)-(4), which are :

$$\:{min}{f}_{i}\left(x,u\right)=\left\{{f}_{1}\left(x,u\right),{f}_{2}\left(x,u\right),{f}_{3}\left(x,u\right),\dots\:\dots\:.{f}_{n}\left(x,u\right)\right\},\:\:i=\text{1,2},\dots\:\dots\:.,{N}_{obj}$$
(1)

where, \(\:{f}_{i}\left(x,u\right)\) in Eq. (1) is the objective function to be optimized, with Nobj representing the total number of objectives.

The objective functions in Eq. (1) are subjected to operational constraints that are represented in Eqs. (2) and (3). Both constraints are defined in terms of equality and inequality, are expressed as \(\:g\left(x,u\right)\) and \(\:h\left(x,u\right)\) respectively. Equation (4) represents the lower and upper limits for each of dependent and control variables z (‘x’ and ‘u’), represent vectors of dependent and control variables, respectively19

$$\:{g}_{i}\left(x,u\right)=0$$
(2)
$$\:{h}_{i}\left(x,u\right)\le\:0$$
(3)
$$\:zmin\:<z<zmax$$
(4)

The vectors (x) and (u) can be expressed as follows:

$$\:{x}^{T}=\left[{P}_{G1},\:{V}_{L1}\dots\:{V}_{{LN}_{pq}},\:{Q}_{G1}\dots\:{Q}_{{G}_{NG}},{S}_{L1}\dots\:{S}_{{L}_{Nl}}\right]$$
(5)
$$\:{u}^{T}=\left[{P}_{G2}\dots\:.{P}_{{G}_{NG}},\:{V}_{G1}\dots\:{V}_{{G}_{NG}},\:{{T}_{1}\dots\:{T}_{{L}_{Nt}},Q}_{C1}\dots\:{Q}_{{C}_{NC}}\right]$$
(6)

where \(\:{P}_{G1}\) signifies the real power of the chosen slack bus, while \(\:{V}_{{LN}_{pq}}\) denotes the voltage at load buses. \(\:{Q}_{{G}_{NG}}\) refers to the generation reactive power. \(\:{S}_{{L}_{Nl}}\) denotes the apparent power passes in transmission lines3. VG1, \(\:{T}_{1}\), QC1 and PG2 represent the voltage, transformer tapping ratio, reactive/active power generation at PV buses, respectively. NG, NC and Nt stand for the count of generator units, reactive power compensators, and regulating transformers, respectively.

This paper aims to attain three distinct advantages for the power system, categorized as economic, technical, and environmental categories.

Economic category

The 1st economic OF in this context seeks to minimize the cumulative fuel cost of the power-generating units, denominated in $/h, as outlined in Eq. (7). The pursuit of economic advantages involves the minimization of fuel costs related to generating units, which is mathematically stated as a function of the active generating power ‘\(\:{P}_{gi}\)’ and the cost coefficients ‘ai, bi and ci’ of ith generator units43.

$$\:\text{M}\text{i}\text{n}\:{F}_{1}={\sum\:}_{i=1}^{{N}_{g}}{a}_{i}\text{P}{{\text{g}}_{i}}^{2}+{b}_{i}\text{P}{\text{g}}_{i}+{c}_{i}\text{\$}/\text{h}\text{r}$$
(7)

Technical category

The technical advantages within power systems encompass the reduction of active power losses, the improvement of voltage stability indices, and the enhancement of the voltage profile through the reduction of the deviation of the voltage at load buses from the target voltages at these buses3.

Minimization of active power losses.

The 2nd technical OF is designed to achieve the minimization of power losses PL in all transmission lines ‘Nl’, as described in Eq. (8).

$$\:{\:Min\:F}_{2}\left(x,u\right)={P}_{L}=\sum\:_{k=1}^{{N}_{l}}\left({G}_{k}\left({V}_{i}^{2}{+V}_{j}^{2}-2{V}_{i}{V}_{j}cos{\delta\:}_{ij}\right)\right)\left(\text{M}\text{W}\right)$$
(8)

where, Vi and Vj are the voltages at buses i and j, \(\:{\delta\:}_{ij}\) is the voltage angle variation between bus i and j that connect the line l and Gk is the conductance of branch k between bus i and j.

Minimization of total voltage deviation.

The 3rd technical OF focuses on reducing voltage deviations \(\:\varDelta\:V\) at the load buses \(\:{\varvec{N}}_{\varvec{p}\varvec{q}}\:\)to improve the voltage profile at these locations, as in Eq. (9).

$$\:{\:Min\:F}_{3}\left(x,u\right)=\varDelta\:V=\:\sum\:_{i=1}^{Npq}\left|{V}_{i}-\:1\right|$$
(9)

  • Improving voltage stability index.

The 4th technical OF aims to improve the Voltage Stability Index (VSI) by minimizing the L-index, which is described in Eqs. (10) to (12) as follows:

$$\:{\:Min\:F}_{4}\left(x,u\right)=Min\:\left(VSI\right)=Min\:\left(\text{max}\left({L}_{j}\right)\right),\:j=1,\:2,\:\dots\:\:{N}_{b}$$
(10)
$$\:{L}_{j}=\left|1-{\sum\:}_{i=1}^{{N}_{g}}{F}_{\text{ji}}\frac{{V}_{i}}{{V}_{j}}\angle\:\left({\theta\:}_{\text{ij}}+{\delta\:}_{i}-{\delta\:}_{j}\right)\right|$$
(11)
$$\:{F}_{\text{ji}}=-{\left[{Y}_{\text{LL}}\right]}^{-1}\left[{Y}_{\text{LG}}\right]$$
(12)

Where, Fji is considered an element of complex matrix F that is given from the sub-matrices of admittance YLL and YLG, Ng is number of generators, δi and δj are voltage phase angles of buses i and j. The matrices Y1 and Y2 are the system sub-matrices44.

Environmental category

The 5th OF is concerned with reducing emissions. The objective of minimizing the total emission level is pivotal for realizing environmental benefits within the power system. The total emission from generating units is calculated in ton/hour as in Eq. (13)1

$$\:{Min\:F}_{5}={\sum\:}_{i=1}^{Ng}1{0}^{-2}\left({\alpha\:}_{i}+{\beta\:}_{i}{P}_{{gi}}+{\gamma\:}_{i}\:{{P}_{gi}}^{2}\right)+\left|{\zeta\:}_{i}{exp}[{\lambda\:}_{i}Pgi]\right|\:\text{T}\text{o}\text{n}/\text{h}\text{r}$$
(13)

where, \(\:{\alpha\:}_{i},{\beta\:}_{i},{\gamma\:}_{i},{\zeta\:}_{i},{\lambda\:}_{i}\) are the emission coefficients of generator i, \(\:{P}_{gi}\:\)represents the active power generated by the power unit situated at bus i, with Ng representing the total number of generators.

Constraints

To achieve the optimal objectives most efficiently, it is essential to consider the operational constraints outlined in the active and reactive power flow as in Eqs. (14) and (15).

$$\:Q_{gi} - Q_{Li} + Q_{Ci} - V_{i} \sum \: _{{j = 1}}^{{N_{b} }} V_{j} \left( {G_{{{\text{ij}}}} {\text{sin}}\theta _{{{\text{ij}}}} - B_{{{\text{ij}}}} {\text{cos}}\theta _{{{\text{ij}}}} } \right) = 0,\:{\text{i = 1}},{\text{2}}, \cdots {\text{N}}_{{{\text{PQ}}}}$$
(14)
$$P_{{gi}} - P_{{Li}} - V_{i} \sum \: _{{j = 1}}^{{N_{b} }} V_{j} \left( {G_{{{\text{ij}}}} {\text{cos}}\:\theta _{{{\text{ij}}}} {\text{ + B}}_{{{\text{ij}}}} {\text{sin}}\:\theta _{{{\text{ij}}}} } \right) = 0,\:{\text{i = 1}},{\text{2}}, \cdots {\text{N}}_{{\text{b}}} {\text{ - slack}}$$
(15)

The inequality operational constraints outlined are maintained within the designated minimum and maximum bounds for each constraint, as indicated in Eqs. (16)– (18), ensuring the preservation of generator limitations. Equations (19)-(20) ensure the constrained operation of tapping points for transformers and shunt reactive power compensators. The voltage profile is kept within permissible operating limits, as specified in Eq. (21). Furthermore, Eq. (22) maintains the secure operation of transmission lines by constraining power flow within an acceptable range46.

$$\:{{\:\text{P}}_{{\text{g}}_{\text{i}}}}^{\text{m}\text{i}\text{n}}\le\:{\text{P}}_{{\text{g}}_{\text{i}}}\le\:{{\text{P}}_{{\text{g}}_{\text{i}}}}^{\text{m}\text{a}\text{x}\:}$$
(16)
$$\:{{\text{Q}}_{{\text{g}}_{\text{i}}}}^{\text{m}\text{i}\text{n}}\le\:{\text{Q}}_{{\text{g}}_{\text{i}}}\le\:{{\text{Q}}_{{\text{g}}_{\text{i}}}}^{\text{m}\text{a}\text{x}}$$
(17)
$$\:{{\:\text{V}}_{\text{g}\text{i}}}^{\text{m}\text{i}\text{n}}\le\:{\text{V}}_{\text{g}\text{i}}\le\:{{\text{V}}_{\text{g}\text{i}}}^{\text{m}\text{a}\text{x}}$$
(18)
$$\:{{\:\text{T}}_{\text{i}}}^{\text{m}\text{i}\text{n}}\le\:{\text{T}}_{\text{i}}\le\:{{\text{T}}_{\text{i}}}^{\text{m}\text{a}\text{x}}$$
(19)
$$\:{{\text{Q}}_{{\text{c}}_{\text{i}}}}^{\text{m}\text{i}\text{n}}\le\:{\text{Q}}_{{\text{c}}_{\text{i}}}\le\:{{\text{Q}}_{{\text{c}}_{\text{i}}}}^{\text{m}\text{a}\text{x}}$$
(20)
$$\:{{\text{V}}_{\text{L}\text{i}}}^{\text{m}\text{i}\text{n}}\le\:{\text{V}}_{\text{L}\text{i}}\le\:{{\text{V}}_{\text{L}\text{i}}}^{\text{m}\text{a}\text{x}}$$
(21)
$$\:{{\:\text{S}}_{\text{L}\text{i}}}^{\text{m}\text{i}\text{n}}\le\:{\text{S}}_{\text{L}\text{i}}\le\:{\text{S}}_{\text{L}\text{i}}^{\text{m}\text{a}\text{x}}$$
(22)

The collective function F in Eq. (23) consists of 5 individual OFs; F1, F2, F3, F4 and F5, which can be formulated as follows:

$$\:F={\text{w}}_{1}.\:{\text{F}}_{1}+{\text{w}}_{2}.\:{\text{F}}_{2}+{\text{w}}_{3}.\:{\text{F}}_{3}+{\text{w}}_{4}.\:{\text{F}}_{4}+{\text{w}}_{5}.\:{\text{F}}_{5}$$
(23)

Where w1, w2, w3, w4, w5 are the weight factors where w1+w2+w3+w4+w5 equal 1.

Proposed solution methodology

A recent algorithm ARO47, which was created from the survival strategies of rabbits in nature, as rabbits are herbivores that feed mainly on grass, forbs, and leafy weeds. There are two simulated strategies that have been devised detour eating and haphazard hiding. The initial approach, detour eating, seeks to deter predators from discovering rabbit nests by steering clear of grass consumption near their burrows. This tactic aligns with the well-known Chinese idiom: “rabbits do not eat the grass near their own nest.” This strategy is commonly referred to as exploration. Additionally, rabbits possess a broad field of vision, with a significant portion dedicated to scanning, enabling them to effortlessly locate food across expansive areas.

The alternative strategy is termed exploitation or random hiding. Rabbits consistently endeavor to reduce the risk of capture by potential threats. Their expertise in creating burrows allows them to elude hunters and predators. Rabbits construct multiple burrows in proximity to their nest, selecting one at random as a refuge from potential threats. However, there are instances where rabbits may experience energy depletion. Situated at the lower end of the food chain and facing numerous predators, rabbits must conserve energy for survival. This is achieved through switching between foraging and random hiding48. The mathematical model of the ARO described as follow47.

  1. (a)

    Detour foraging (exploration).

In this approach, rabbits are avoiding eating grass in close proximity to their burrows. Instead, they explore each other’s areas haphazardly in search of food. This behavior involves continual adjustments of their positions in relation to other rabbits within the group, introducing an element of disturbance. A model has been suggested to describe this strategic behavior.

$$\:{\overrightarrow{\:V}}_{i}\left(t+1\right)={\overrightarrow{\:x}}_{j}\:\left(t\right)+R.\:\left({\overrightarrow{\:x}}_{i}\:\left(t\right)-{\overrightarrow{\:x}}_{j}\:\left(t\right)\right)+round\left(0.5\:.\:\left(0.05+{r}_{1}\right)\right).{n}_{1},\:\:i,j=1,\dots\:..,n\:and\:j\ne\:i$$
(24)
$$\:R=L.c$$
(25)
$$\:L=(e-{e}^{{\left(\frac{t-1}{T}\right)}^{2}}.\:\text{s}\text{i}\text{n}(2\pi\:{r}_{2})$$
(26)
$$\:c\left(k\right)=\left\{\begin{array}{c}1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if k=g\left(l\right)\\\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:else\end{array}\right.\:\:\text{k}=1,\dots\:\dots\:,\:\text{d}\:\text{a}\text{n}\text{d}\:\text{l}=\:1,\dots\:\dots\:.,\:[{r}_{3\:}.\:d]$$
(27)
$${\text{g}}={\text{ rand perm }}\left( {\text{d}} \right)$$
(28)
$$\:{n}_{1}\sim N\left(\text{0,1}\right)$$
(29)

where, the intrant position of the ith rabbit at time t + 1 is denoted as \(\:{\overrightarrow{\:V}}_{i}\left(t+1\right)\), \(\:{\overrightarrow{\:x}}_{j}\left(t\right)\)represents the position of the ith rabbit at time t. In this context, n refers to the size of the rabbit population, while d indicates the dimension of the problem. T represents the maximum number of iterations. The function [\(\:.\:]\) corresponds to the ceiling integer function. The function rand perm generates a random permutation of integers ranging from 1 to d. Additionally, r1, r2, and r3 are three random numbers belong to (0,1). The running length, denoted as l, signifies the movement pace during the detour foraging process. Lastly, n1 subject to the standard normal distribution. Equation (24) demonstrates that search individuals engage in a random exploration based on the positions of other individuals. This behavior allows a rabbit to move far from its own territory and venture into the territories of other rabbits. Notably, when a rabbit visits the nests of others instead of its own nest, it makes a significant contribution to the exploration process and enhances the ability of the ARO algorithm to detect global search.

During each iteration in the ARO algorithm, the rabbit generates multiple burrows (d burrows) in a randomized manner around its current position across each dimension of the search space. The purpose of creating these burrows is to provide hiding options for the rabbit, reducing the likelihood of being targeted or attacked. The specific jth burrow for the ith rabbit is generated by:

$$\:{\overrightarrow{\:b}}_{i,j}\left(t\right)={\overrightarrow{\:x}}_{j}\:\left(t\right)+H\:.\:g.\:{\overrightarrow{\:x}}_{i}\:\left(t\right),\:\:i=1,\dots\:..,n\:and\:j=1,....,d$$
(30)
$$\:H=\:\frac{T-t+1}{T}\:.\:{r}_{4}$$
(31)
$$\:{n}_{2}\:\sim\:N\left(\text{0,1}\right)$$
(32)
$$\:g\left(k\right)=\left\{\begin{array}{c}1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if k=j\\\:\:\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:else\:\:\:\:\:\:\:\:\:\end{array}\right.\:\:\text{k}=1,\:\dots\:\dots\:,\:\text{d}\:\:\:\:\:\:\:\:\:\:$$
(33)

Based on Eq. (30), the d burrows are generated within the vicinity of a rabbit along each dimension. The hiding parameter H plays a crucial role, gradually decreasing linearly from 1 to 1/T throughout the iterations, with the addition of random perturbations. This parameter determines the size of the neighborhood in which the burrows are initially created. Initially, a larger neighborhood is considered, but as the iterations progress, this neighborhood gradually decreases in size.

When seeking shelter, rabbits employ a random selection strategy from their available burrows. To mathematically represent this random hiding behavior, Eqs. (34)-(36) are employed:

$$\:{\overrightarrow{\:V}}_{i}\left(t+1\right)={\overrightarrow{\:x}}_{i}\:\left(t\right)+R.\:\left({r}_{4}\:{\overrightarrow{.\:b}}_{i,r}\left(t\right)-{\overrightarrow{\:x}}_{i}\:\left(t\right)\right),\:\:i=1,\dots\:..,n$$
(34)
$$\:g\left(k\right)=\left\{\begin{array}{c}1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:if k=[{r}_{5\:}.\:d]\\\:\:\:0\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:else\:\:\:\:\:\:\:\:\:\end{array}\right.\:\text{k}=1,\:\dots\:\dots\:,\:\text{d}\:$$
(35)
$$\:{\overrightarrow{\:b}}_{i,r}\left(t\right)={\overrightarrow{\:x}}_{j}\:\left(t\right)+H\:.\:{g}_{r}.\:{\overrightarrow{\:x}}_{i}\:\left(t\right)$$
(36)

In the given equation, \(\:{\overrightarrow{\:b}}_{i,r}\left(t\right)\)represents a randomly chosen burrow for hiding from the set of d burrows available to the rabbit. The variables r4 and r5 represent two random numbers within the range of (0, 1).

Referring to Eq. (34), the ith search individual aims to update its position towards the selected burrow from the d burrows. Once either the detour foraging or random hiding is successfully executed, the position of the ith rabbit is updated according to the following expression:

$$\:{\overrightarrow{\:x}}_{i}\left(t+1\right)=\left\{\begin{array}{c}{\overrightarrow{\:x}}_{i}\left(t\right)\:\:\:\:\:\:\:\:f\:\left(\:{\overrightarrow{\:x}}_{i}\left(t\right)\right)\:\:\le\:\:\:f\:\left(\:{\overrightarrow{\:v}}_{i}\left(t+1\right)\right)\:\:\:\:\:\:\:\:\:\:\:\\\:{\overrightarrow{\:v}}_{i}\left(t+1\right)\:\:\:\:\:f\:\left(\:{\overrightarrow{\:x}}_{i}\left(t\right)\right)\:\:>\:\:f\:\left(\:{\overrightarrow{\:v}}_{i}\left(t+1\right)\right)\:\:\:\:\:\end{array}\right.$$
(37)
  1. (b)

    Exploration to exploitation.

The switching from exploration to exploitation is carried by the energy factor of the proposed ARO as:

$$\:A\left(t\right)=4(1-\frac{t}{T})\:ln\frac{1}{r}$$
(38)

where “r” represents a randomly generated number that falls in the range between 0 and 1.

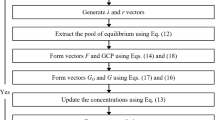
The ARO behavior of rabbits varies depending on the energy factor A(t). When A(t) is greater than 1, rabbits are inclined to explore different foraging areas randomly during the exploration phase. This is referred to as “detour foraging.” Conversely, when A(t) is less than or equal to 1, rabbits are motivated to exploit their burrows randomly during the exploitation phase, resulting in “random hiding.” As the number of iterations increases, A gradually decreases, which enables individuals within the rabbit population to alternate between detour foraging and random hiding behaviors. These updates efficiently continue until the termination criterion is met, at which point the best solution is identified and returned48. Further details of the flow chart of ARO algorithm are shown in Fig. 1.

Fig. 1
figure 1

Flowchart of ARO.

Full size image

Experimental simulations

Test systems

Experiments were conducted using six IEEE standard power systems: the IEEE 30-bus system and the IEEE 57-bus system are considered two small size systems and IEEE 300, 1354, 3012, and 9241 as large test systems. In the IEEE 30-bus system, there were 6 generation buses, 21 loads, 41 branches, 4 tap changers, and 3 shunt capacitors. On the other hand, the IEEE 57-bus system consisted of 7 generation buses, 80 branches, 17 tap changers, and 3 shunt capacitors. The other four systems are considered large-scale systems, are chosen to test the proposed algorithm and assess the performance of it. For the proposed ARO algorithm, the population size was set to 100, and the maximum number of iterations was set to 200 with the IEEE-30 bus system and 300 with IEEE-57 bus system. The dimensions of the problem were determined based on the specific tested power system being considered.

Defination of studied cases

Table 2 reports the classification of the studied cases. These cases were classified into different categories based on the following criteria: technical, economic, and environmental. By organizing the cases into these categories, a comprehensive analysis was carried out to assess the performance of the different objective functions and evaluate the benefits achieved in terms of technical, economic, and environmental aspects. The ARO algorithm was tested on both single and multi OFs for the OPF problem. Additionally, these objective functions were combined in double, triple, and multi-objective formulations. The algorithm’s effectiveness was evaluated based on its ability to optimize the aforementioned objectives in these complex systems.

Table 2 Definition of the OPF cases studied of single and multi-OF frameworks.
Full size table

Numerical simulation applications

This section reports the numerical simulation results for the defined cases studied in Table 2. There are 22 cases that were analyzed, as outlined in Table 2, encompassing two small-sized test systems and four large-scale test systems spanning a range of 300 to 9241 buses. The performance of ARO was assessed against recent published algorithms. The simulation was carried out on a Core I7 laptop with 8 GB of RAM. The proposed ARO was implemented and evaluated using MATLAB R2020a.

The first test system

The analysis focuses on the first test system, IEEE 30-bus, investigating 14 different cases that encompass up to 5 OFs. For cases 1–5, Tables 3 and 4 outline respectively the values of single OF cases and the associated settings of the system control variables. In Case 1, the primary OF1 is minimizing the fuel cost. The simulation analysis shows that the fuel cost achieved is reported as $798.943 per hour. For Case 2, the focus shifts towards decreasing the load-buses voltage deviation. The simulation results reveal that by employing the ARO algorithm, a voltage deviation (VD) of 0.093 per unit is obtained. In Case 3, the voltage stability index is reported as 0.109 p.u. This index provides an indication of the system’s voltage stability. Case 4 achieves the lowest power loss of 2.881 MW. This means that the system operates with minimal power dissipation. Furthermore, Case 5 demonstrates the lowest emission rate observed, which amounts to 0.2047 tons/kg. This indicates a more environmentally friendly operation.

Figures 2 exhibit favorable convergence characteristics when utilizing the ARO algorithm in all investigated cases for Cases 1–5. These figures illustrate the convergence behavior of the ARO algorithm. The convergence curves clearly indicate that the ARO algorithm rapidly converges to the optimal solution and maintains stability thereafter. Table 5 compares the ARO algorithm and recent optimizers that were customized from the literature. Also, the proposed ARO algorithm consistently delivers the most competitive solutions for various objectives. This comparison highlights the superiority of the ARO algorithm in optimizing the system’s performance.

Table 3 Single OFs of the first test system using ARO (Cases 1–5).
Full size table
Table 4 Control variables of single objective functions for IEEE 30-bus test system using ARO.
Full size table
Table 5 Comparison between ARO & recent optimization algorithms for single ofs, (Cases 1–5).
Full size table

To consider multiobjective functions including bi-, tri- and four objective functions, Table 6 reports the results for Cases 6–14. The table provides an overview of the outcomes achieved through the optimization process for each case, considering multiple objectives. The results reported in Table 6 constitute objectives followed by the control variables of the tested cases. The simulation results using the proposed ARO algorithm are compared to other related works in the literature23,49,52,53,54,55. Table 7 shows that the proposed ARO leads to the most efficient solutions for the considered Cases 6–9. Figure 3 shows Pareto sets for Cases 7 and 9. Cases 10–12 address three objectives functions by the proposed ARO algorithm. The results are tabulated in Table 8. In Case 10, three objectives, fuel costs, voltage deviation, and power losses are carried out. Case 11 focuses on minimizing fuel costs, power losses, and emission levels, while Case 12 optimizes fuel costs, voltage deviation, and emission levels simultaneously. The effectiveness of the proposed ARO algorithm is validated compared with the reported results in23,52,53,55,56. Table 9 clearly demonstrates that the proposed ARO algorithm leads to improved fuel costs and power losses compared to PSO-SSO52 in Case 10.

Fig. 2
figure 2

The convergence curves for the single objective cases (Cases 1–5). (a) fuel cost (Case 1), (b) voltage deviation (Case 2), (c) Voltage stability (Case 3), (d) Power losses (Case 4), (e) Emission minimization (Case 5).

Full size image

Furthermore, in Cases 11–12, the economic, technical, and environmental benefits surpass those achieved by PSO, SSO, PSO-SSO52, and MOAD53. The Pareto solutions for Cases 10–12 are illustrated in Fig. 4. The simulation results obtained by the ARO and are compared with other methods, Objectives ECHIT24, PSO29, PSO-SSO29, SSO29, I-NSGA-III42, MODA57 and Jaya56, is presented in Table 9. In Case 13, the optimization is performed simultaneously for fuel costs, voltage deviation, power losses, and emission levels. Case 14 involves considering five objective functions. In both cases, Acceptable economic, technical, and environmental benefits are achieved compared to the competitive algorithms PSO-SSO and MODA. These comparative studies validate the effectiveness and capability of the proposed ARO algorithm.

Table 6 OPF solution and control variables for IEEE-30 bus system using the ARO algorithm for cases 6–14.
Full size table
Table 7 ARO and recent optimizers from the literature for multi-OFs for (Cases 6–9).
Full size table
Fig. 3
figure 3

Bi-objective Pareto set of OPF: (a) Fuel costs and power losses (Case 7); (b) Fuel costs and voltage deviation (Case 9).

Full size image
Table 8 Results obtained by ARO and other optimizers for tri-OFs.
Full size table
Fig. 4
figure 4

Tri-objective Pareto set of OPF in the first test system: (a) Fuel costs, power losses, and emission (Case 11); (b) Fuel costs, Voltage deviation, and emission (Case 12).

Full size image
Table 9 ARO against recent optimizers for cases 13 and 14 for the IEEE 30-bus system.
Full size table

Simulation results of IEEE 57-bus system

The 2nd test system, IEEE 57-bus system, has seven generation buses and 80 branches. The data is reported in59. To evaluate the capability of the ARO algorithm in handling single and multi-objective functions (OFs). In Cases 15 and 16, a single objective function was applied to minimize fuel costs (OF1) and power losses (OF2), respectively. Case 17 involved bi-objectives, aiming to optimize both OF1 and OF2 simultaneously. Lastly, in Case 18, three objectives, OF1, OF2, and OF3 are optimized simultaneously. Cases 15–18 present three algorithms called PSO, MFO and the proposed ARO. It was proven that the ARO has high ability, efficiency, and effectiveness compared with other competitive algorithms.

Table 10 presents the simulation results of the OPF problem for Cases 15–18, comparing the proposed ARO algorithm with two other competitive algorithms. In Case 15, the ARO algorithm achieved the lowest fuel costs of $41,672.88 per hour, while the PSO and MFO algorithms resulted in fuel costs of $41,727.01 and 41,695.26 $ per hour, respectively. Thus, it is evident that the ARO algorithm yields the minimum fuel costs. For Case 16, the proposed ARO algorithm reported an active power loss of 9.076 MW. In Case 17, the ARO algorithm produced the best results with fuel costs of $41,689.29 per hour and an active power loss of 13.89 MW. Finally, in Case 18, the optimal results were obtained using the ARO algorithm, resulting in fuel costs of $41,703.31 per hour, an active power loss of 14.356 MW, and a voltage deviation of 0.967 p.u. The settings of control variables for ARO against recent optimization algorithms applied on IEEE-57 bus test system for Cases 15–18 is shown in Table 11.

Table 10 Simulation results obtained by ARO and recent optimization methods for cases 15–18.
Full size table
Table 11 The settings of control variables for ARO against recent optimization methods for cases 15–18.
Full size table

Table 12 displays a comprehensive comparison between the proposed ARO algorithm and recent well-known algorithms in the literature. Additionally, Fig. 5 illustrates the convergence curves of ARO compared with three competitive methods in literature. Convergence curves clearly indicate that ARO exhibits a faster convergence rate than the others. Furthermore, Table 13 presents the statistical indices extracted from 50 runs of each algorithm specifically for Case 15. It is worth noting that ARO demonstrates the best fuel costs as well as lower STD, which serve as reliable indicators of the effectiveness of the proposed ARO algorithm.

Table 12 Simulation results of ARO and recent optimization methods for cases 15–18.
Full size table
Table 13 Statistical indices of ARO in case 15 using different algorithms compared with ARO for 50 trials based on fuel costs minimization in $/h.
Full size table
Fig. 5
figure 5

Rate of fuel cost convergence of Case 15 using ARO versus different methods.

Full size image

Simulation results for large scale test systems

To validate the proposed ARO algorithm, the large-scale test systems are emulated in Cases 19–22 based on four systems with number of buses more than/equal 300 bus. These systems encompass power systems with varying numbers of buses. The primary data for the tested system was adapted from the MATPOWER 6.2 package59.

Table 13 presents the cost minimization of four cases, Cases 19–22, obtained by the ARO algorithm compared to those obtained by the MATPOWER 6.2 package for large scale power systems called IEEE 300-bus, the 1354pegase, 3012-bus, and 9241pegase test system. This comparison validates the scalability and efficiency of the ARO algorithm.

For the IEEE 300 bus, the fuel costs achieved using ARO amount to 508,324.16 $/h, whereas the MATPOWER package yields fuel costs of 719,692.27 $/h. The proposed ARO algorithm achieves a reduction of 29.34% in fuel costs compared to MATPOWER. In the case of the 1354pegase, the fuel costs OF using the proposed ARO equals 74,477.68 $/h $/h, while the MATPOWER 6.2 simulator yields fuel costs of 74,069.35 $/h. The proposed ARO algorithm reports a slight increase of 0.55% compared to MATPOWER.

For the third large-scale system, the ARO algorithm achieves fuel costs of 1,950,577 $/h, whereas the MATPOWER 6.2 simulator yields fuel costs of 2,591,706.57 $/h. The proposed ARO algorithm achieves a reduction of 24.73% in fuel costs compared to MATPOWER. Similarly, results are acquired for the 4th large-scale test system, the proposed ARO algorithm results in fuel costs of 166,233.12 $/h, while the MATPOWER 6.2 simulator reports fuel costs of 315,912.43 $/h with a reduction of 47.38%.

Figures 6.a-6.d show the convergence curves for the four tested large-scale systems. Then, we can conclude that the proposed ARO has succeeded in achieving an economical solution, the economical reduction lies in the range of 24.73–47.38%, of the OFP even for most of the large-scale systems (Table 14).

Table 14 Costs reduction for large scale test grids by ARO and competitive methods cases 19–22.
Full size table
Fig. 6
figure 6

Convergence rates for large scale test systems.

Full size image

Sensitivity analysis

The sensitivity of the proposed ARO algorithm is carried out on the basic on the variation of population size and the maximum number of iterations. Two standard test systems, IEEE 30 bus and IEEE 57-bus, are selected as the most system used for solving OPF problem as benchmarking test systems. The developed simulation tested aim at minimization the fuel cost to explain the convergence characteristics with changing population size (P). Figure 7 (a) and (b) illustrates the sensitivity of convergence rate to population size. Additionally, statistics indices are reported with different number of iterations (Iter) by performing 50 independent runs with each variation. The sensitivity of ARO to maximum number of iterations is reported in Table 15 at the two test systems.

Fig. 7
figure 7

Convergence rates at different population sizes; (a) IEEE 30-bus system, (b) IEEE 57-bus system.

Full size image
Table 15 Statistical indices of ARO with various numbers of iterations (50 times).
Full size table

Conclusions

This paper has successively solved the multi-dimensional OPF problem through finding the optimal operation settings associated with the power generators’ outputs. Single and multi-objectives frameworks have been considered. The objectives considered achieve the main power systems requirements involving technical and economic issues and respecting the limitation of environmental rules and bounds for emission-clean power grids. In this line, the Artificial rabbits’ optimization is devoted to finding the solution of the OPF problem. The effectiveness of the proposed algorithm is evaluated through a comprehensive comparison study with the existing works in literature. With six IEEE standard power systems, 22 different cases are implemented for testing the ARO performance in solving the OPF problem. Also, this paper extends its validation on different size large-scale test systems standard systems. It was proven that the routine of ARO has robust, and superior competitive performance compared with others at fine convergence rates. Significant technical and economic improvements are acquired as 24.73 -47.38% four large scale test systems. Numerical simulations have been implemented on small, medium, and large test systems and accentuate that ARO algorithm is superior in solving such complex OPF problems compared with other methods in the literature. Added to that, the ARO algorithm has a fast rate of convergence than other previous algorithms that make it an estimated algorithm in solving complex engineering problems. In future research, two aspects to be considered as dealing with various emergency events like N-1 contingency and preparing sufficient control actions to solve the impacts of these emergencies. In the second issue is to solve the OPF using upgraded optimization methods. Added to the previous issues, the future studies aim at incorporating uncertainties associated with renewable energy sources, load variations, and emerging new technologies such as electric vehicles and storage systems.