Enhancing MPPT optimization with hybrid predictive control and adaptive P&O for better efficiency and power quality in PV systems

Abstract

Recently, there has been a focus on renewable energy sources such as solar power. These grid-connected systems play a significant role in meeting energy demand and mitigating global warming. Despite these numerous benefits, the stability and quality of power are the main drawbacks facing these energy systems. Boost converters are used to maximize the power output of the photovoltaic system and power the load. The maximum power point tracking (MPPT) strategy based on the perturb and observe (P&O) algorithm is often used to control the inverter. This strategy yields unsatisfactory results in terms of operational performance and durability. This paper presents a new MPPT strategy for a photovoltaic inverter to improve power quality, stability, and dynamic performance. This new strategy is based on combining modified finite control set model predictive control (MFCS-MPC) with an adaptive P&O algorithm. This proposed strategy differs from the conventional strategy and some existing strategies in terms of robustness, operational performance, and dynamic response. MATLAB/Simulink was used to build and validate a comprehensive mathematical model of the studied system. The effectiveness, efficiency, and performance were studied under different operating conditions. The results show that using the designed MPPT approach achieves a total harmonic distortion of 1.22%, significantly outperforming the conventional P&O algorithm (6%) and complying with IEEE-519 standards. Also, using this designed MPPT approach improves tracking response time by an estimated 35% and reduces overshoot by 28%, ensuring stability under rapid changes in radiation. Furthermore, the new weighted cost function in MFCS-MPC reduces switching losses by 15% while maintaining harmonic suppression. These results highlight the effectiveness of the proposed MPPT approach and its ability to improve system properties compared to the conventional MPPT approach, making it a reliable solution for other energy applications such as wind energy and electric vehicles.

Introduction

The world currently faces significant challenges in balancing environmental protection and economic development. The massive increase in energy demand has significantly depleted traditional energy sources, such as oil and natural gas, creating several problems¹. The most prominent of these problems, which has become a concern for governments, is the phenomenon of global warming². As a result of the consequences that countries are now suffering from, scientists have emphasized the importance of using renewable energy sources (RESs) as a suitable and effective solution for providing electricity³. As is well known, RESs are free, naturally replenished, and inexhaustible. Currently, RESs meet approximately 17% of global energy demand, and this figure is expected to rise to mitigate the negative impacts associated with the use of traditional sources⁴. RESs of various types play a crucial role in achieving environmental and economic balance. Photovoltaic (PV) energy systems have emerged as a crucial solution for renewable energy, but their widespread adoption faces ongoing challenges in energy conversion efficiency⁵.

PV energy systems offer a clean alternative to fossil fuels. Innovations such as perovskite solar cells and bifacial solar panels, which enhance efficiency and lower costs, are notable technological developments in this sector. Governments around the world have recently begun offering numerous attractive incentives, such as tax breaks and subsidies, to encourage the adoption of solar energy, thereby boosting the spread of this industry. PV systems can also be integrated with smart grid technology to improve energy distribution and management. Relying on solar PV energy in power generation systems can mitigate global warming². This energy helps non-petroleum-producing countries reduce their energy dependency and lower the costs of electricity production and consumption. Moreover, reliance on this energy source contributes significantly to the growth of the industrial sector, providing job opportunities in production, installation, and maintenance. Recently, these energy systems have received significant attention, with serious research being conducted to develop this sector and enhance the recyclability of solar panels.

There are several challenges facing the use of solar energy in the energy sector. The most prominent of these challenges lies in maximizing the energy obtained from solar energy and power quality (PQ). Furthermore, the high cost of solar panels is a major challenge that increases the cost of electricity production and consumption. As is well known, maximum power point (MPP) tracking (MPPT) is the control strategy used to maximize power in solar systems⁶. This strategy is characterized by simplicity, ease of implementation, and lower costs.

According to the work done in⁷, MPPT technology is a crucial technique for maximizing power output efficiency and ensuring that non-linear electrical sources operate at their peak power. MPPT technique improves the performance of PV systems by tracking and optimizing this point. However, the author⁸ argues that the output power of PV modules is nonlinear and highly dependent on atmospheric factors such as temperature and radiation, creating several challenges that cause several problems at the grid level, such as power fluctuations. Therefore, it is necessary to develop new strategies for the MPPT approach to increase total power production, improve reliability, and enhance efficiency, especially under changing climatic conditions⁹. Other challenges remain: balancing system stability with monitoring accuracy, especially when controlling PV power plant fluctuations and minimizing power losses. Achieving this balance is essential to ensuring maximum energy conversion without compromising the long-term reliability and efficiency of solar power systems. In¹⁰, the incremental conductance (IC) method is used to implement an MPPT technique for PV systems. This method compares the instantaneous conductance (I/V) of a PV array with its incremental conductance (dI/dV) to determine whether the operating point is approaching the maximum power point (MPP). This strategy has several drawbacks, including unsatisfactory operational performance compared to modern strategies, especially in terms of dynamic response and power ripples. In¹¹, a perturb and observe (P&O) algorithm-based MPPT strategy is proposed for controlling a PV system. This strategy adjusts the operating point of the solar panel to maximize power output by introducing a perturbation (slight change) in the panel voltage or current and observingthe output power. Based on this observation, the direction of the disturbance is adjusted to move toward the MPP. Compared to current strategies, this strategy yields unsatisfactory results, particularly in terms of power ripples, necessitating the search for another, more efficient strategy.

By scanning the existing literature in the field of solar energy, several research gaps are noted, the most prominent of which are: (1) there is a wide scope for improving the quality of energy generated from solar systems by exploring system behavior and control techniques through simulation studies. (2) There is a need to develop efficient control algorithms that take into account realistic PV cell models and parametric changes that will help improve stability problems. (3) There is a need to expand the use of predictive controllers with a greater degree of flexibility in controlling PV systems. (4) There is a potential to benefit from the integration of the P&O algorithm and predictive controller to enhance the effectiveness and competence of the MPPT strategy.

Currently, new techniques are being used to improve MPPT in PV systems. The most prominent of these modern strategies are neural networks (NN)¹² and fuzzy logic controllers (FLCs)¹³, whose use relies heavily on experience and experimentation. These strategies exploit nonlinearity in system performance through learning. These nature-inspired strategies offer significant performance and the potential to improve PV system properties. However, using these strategies requires effort and time to achieve good results. As is well known, there is no mathematical basis that facilitates the use of FLC and NNs, making their implementation difficult. On the other hand, model-based predictive control (MPC) has been used to control renewable energy systems^14,15. This strategy relies on predicting the future behavior of the system under study, which allows for precise and time-varying control.

PV system control is generally a research area that poses theoretical and practical problems to ensure efficient and stable operation, with distinct technological concerns such as interactions, environmental uncertainty, stability, nonlinearity, etc. To achieve the above goals, a control technology must be developed that addresses these challenges. Among the many systems proposed in the literature, predictive control is the most suitable for developing an MPPT strategy. Given the performance and simplicity of the P&O algorithm, several researchers have proposed new strategies for P&O algorithm. This study proposes a combination of the adaptive P&O approach and predictive control to obtain a new strategy with the potential to improve energy quality and robustness. This combination has not been investigated before, making the work of great significance.

There is a growing need for innovative MPPT techniques that simplify implementation, reduce reliance on inverters, and improve switching frequencies. This paper presents an improved strategy for MPPT optimization in PV systems, using a finite set predictive control (FCS-MPC) model to address inherent nonlinearity and dynamic uncertainty in PV output characteristics. In this work, the FCS-MPC approach is applied to optimize the MPPT strategy of a PV system. The application of the FCS-MPC approach to the MPPT strategy is the first major contribution of this paper. Furthermore, the FCS-MPC approach is combined with the adaptive P&O algorithm to obtain an approach with high operational performance and high robustness. This resulting algorithm dynamically adjusts the step size, reducing it near the MPP to reduce fluctuations and increasing it farther from the MPP to accelerate convergence. The second major contribution of this paper is the FCS-MPC-P&O-based MPPT strategy. This strategy features high performance, fast dynamic response, and high robustness, making it a suitable solution for solar PV systems and other energy systems such as wind power.

The proposed strategy provides a good balance between detection accuracy and operating speed, as well as reliable performance under a variety of environmental conditions, both normal and abnormal. The study also proposes an additional modification of the FCS-MPC cost function, adding a weighted term responsible for the deviation of the current and optimal switching frequencies, making the work of great significance in the field of control. This modification constitutes the third major contribution of the paper. On the other hand, this modification reduces switching losses and harmonic distortions simultaneously, enhancing overall performance and system stability. This designed strategy was implemented in the MATLAB environment under various operating conditions. The results obtained demonstrate that the proposed technique offers significant improvements in achieving fast dynamic response, increasing stability margins, and improving PQ compared to the conventional approach and some related work.

The main objectives achieved by this work can be summarized in the following points:

• Significantly improving tracking speed and system stability compared to the traditional approach.

• Significantly reducing the THD of current compared to the traditional approach.

• Overcoming the drawbacks and problems of the traditional MPPT approach.

• Significantly improving energy efficiency, stability, and reliability compared to the traditional strategy.

The paper is structured in six sections. Section “Related works” reviews various related works using different control techniques in MPPT optimization, showing the advantages and drawbacks of previously published methods. In “Proposed system configuration”, the proposed configuration system is explored, providing critical information on the system parameters that deal with the PV system’s modeling and the boost converter’s mathematical model. Section “Control strategies modeling” presents the modeling of the control strategies, including the modified P&O algorithm and the implementation steps of the proposed FSC-MPC. Section “Simulation results and discussion” presents the graphical and numerical results of the two approaches using the MATLAB environment under various operating conditions. Section “Conclusions” presents the main results, highlights their significance, and suggests future research directions to ensure a comprehensive study of the proposed MPPT optimization approach for PV systems.

Related works

Several previous research studies have also been conducted to determine the best techniques for achieving optimum power output and quality in PV systems. However, many of these methods fall short of the proposed approach in response time and total harmonic distortion (THD) areas. In¹⁶, the authors proposed an integral backstepping control (IBC) for microgrid-connected PV systems, which was robust. Although the method guarantees stability and high-performance tracking, the implementation process involves many parameters of fine-tuning, which may be too complex for PV systems that contain various uncertain and variable conditions. In¹⁷, the authors proposed the application of fuzzy sliding mode control (SMC) and PI controller to a single-stage grid-connected PV system that enhances the PQ by providing compensation for the disturbing signal and voltage. However, it isn’t easy to implement in real time due to the tuning requirement and the need for more computational time. Other works that handled direct power control for PV systems using a simplified super-twisting control presented in¹⁸ provided simple control schemes and higher efficiency. However, it does not directly incorporate PQ improvements for non-ideal grid conditions; it provides insufficient information for grid-connected and standalone systems. SMC technique for the regulation of peak power demand in¹⁹ contributes to a remarkable enhancement in the energy conversion of PV systems. However, the method has problems at this stage of the model; for example, it is hard to implement changes in environmental factors such as variation in irradiance. In²⁰, the MPC technique was used to optimize the performance of grid-connected PV systems. Although it improved the integration of the PV system and the MPPT performance, the method has a high computational load and time delay, and hence, poor dynamic performance is present in the place of the fluctuating voltage, which has raised the THD value. In²¹, a model-free controller (MFC) of three-phase grid-connected PV systems was introduced to enhance the stability and reliability of the system. However, due to the time-varying features of the method and the inability to adjust the operating conditions in real applications, the application is quite impractical for real-world applications with different operating conditions. The use of hybrid MPPT-based metaheuristic techniques was also investigated in²², where this paper sought to present enhancements to tracking in partially shaded conditions. However, the techniques still fail to work in grid-connected and standalone systems, particularly in systems with unsteady irradiance, and hence, they take longer to work in dynamic conditions. The authors in²³ have presented a synergetic control approach for enhancing the power quality of PV systems. Although the approach increased voltage stability and decreased harmonics, the system’s poor performance in responding to external disturbances was a major drawback. A butterfly optimization algorithm-based control, an inspired MPPT algorithm for PV systems, was proposed in²⁴ to optimize the energy output in steady-state conditions. However, the approach may not be effective under rapidly changing environmental conditions and is slow to react to real-time system changes, which affect the THD. Different MPPT techniques-based algorithms, particle swarm optimization (PSO), and grey wolf optimization (GWO) have been verified experimentally in²⁵, and they showed better performance in partially shaded conditions. However, these algorithms incur high-speed computational costs and always have large delays in response compared to their large-scale applications and other advanced metaheuristic techniques. In²⁶, golf optimization was used to optimize the MPPT technique under partially shaded conditions or zones. Although the method gave better tracking precision, it suffers from slow response time while tracking continually changing light levels and, therefore, cannot be good for systems with large variances. In²⁷, the authors proposed an adaptive IC algorithm for the MPPT technique in PV systems. This design has some added benefits regarding energy extraction, but it entails a very complicated system implementation and is not very versatile across various applications. In²⁸, a combination of genetic algorithm and backstepping control is proposed to improve the MPPT properties of a PV system. This proposed strategy exhibits high performance and robustness and is implemented in MATLAB using partially shaded PV panels. The results obtained showed that the designed approach yielded good results in terms of reference tracking, PQ, and robustness. However, despite this performance, the approach has several drawbacks that limit its deployment. The most prominent of these drawbacks are its complexity, difficulty of implementation, high costs, and the presence of a significant number of gains compared to the traditional approach. In²⁹, the PSO algorithm-based MPPT technique was proposed as a suitable solution for improving the characteristics of a PV system. The PSO algorithm was used to calculate the gain values ​​of the MPPT strategy, allowing for a significant increase in performance and efficiency compared to the conventional MPPT approach. This designed strategy yielded greater efficiency compared to the conventional MPPT technique in dealing with partial shading situations. However, ripples in the power level were observed, searching for a more efficient strategy ongoing. Neuro-fuzzy algorithm is combined with the PSO algorithm in³⁰ to overcome the problems of the MPPT strategy of PV systems using battery storage systems. The proposed MPPT strategy has several advantages, most notably high efficiency and high robustness. However, it is more complex than the traditional MPPT approach. The effectiveness of this strategy was verified using MATLAB under various operating conditions. The results showed that this strategy yielded satisfactory operational performance compared to the traditional strategy, making it a promising solution. This strategy has drawbacks, the most notable of which are its complexity and the lack of any rules that facilitate the implementation of the neuro-fuzzy algorithm. As is well known, the neuro-fuzzy algorithm relies on experimentation and experience, which requires considerable time and effort to achieve satisfactory results. In³¹, the author compared three different strategies for approaching the MPPT of a PV system. These strategies are MMPT-IC, MPPT-PO, and super-twisting SMC technique-based MPPT techniques. After providing a mathematical model for each strategy, the three strategies were implemented in the MATLAB environment under various operating conditions. The simulation results were carefully analyzed, allowing the advantages and disadvantages of each control method to be extracted based on the test results. All conducted tests indicate that the super-twisting SMC technique-based MPPT technique outperforms other strategies in improving PV system performance. Despite this performance, some drawbacks limit its widespread adoption, the most prominent of which is the chattering phenomenon. This phenomenon affects the control system, reducing its lifetime. Another work³² addressed improving the performance and efficiency of the MPPT strategy for PV systems. In this work, a combination of NNs and backstepping control was proposed to obtain a robust and reliable controller that can improve the properties of the MPPT strategy. This proposed strategy differs from the conventional approach in terms of performance, efficiency, robustness, and dynamic response. The graphical results of all tests demonstrated the effectiveness of the NN-backstepping controller-based MPPT technique in improving PV system characteristics compared to the classical MPPT approach. However, this designed strategy has drawbacks that limit its use in other industrial applications, the most prominent of which are its complexity and the presence of a significant number of gains. In³³, the effectiveness and efficiency of applying the crow search algorithm to the MPPT strategy of the PV system are discussed. This algorithm is used to calculate the gain values ​​of the MPPT approach. Simplicity, ease of implementation, and fast dynamic response are the most prominent features of the designed strategy. The effectiveness and efficiency of the designed approach are verified using MATLAB under uniform and shading conditions. The obtained results highlight the robustness, effectiveness, efficiency, and operational performance of the crow search algorithm-based MPPT technique compared to the conventional MPPT technique.

Another scientific research addressed the topic of the MPPT strategy and highlighted its disadvantages in³⁴, where the strategy was used based on the MPP voltage limit to control the PV cell’s voltage and generate the required duty cycle directly using a mathematical expression, which results in a high convergence speed, avoiding the drift problem, and the absence of MPP fluctuations. A series of simulation and experimental tests were conducted to validate and verify the tracking performance of the proposed MPPT strategy under rapid changes in solar radiation. The effectiveness and performance of this designed strategy were studied compared to the IC algorithm in terms of tracking accuracy. Experimental and simulation results demonstrated that the proposed strategy outperforms the IC approach in several aspects, such as response time and the ripple problem. The designed approach achieves a tracking efficiency of up to 99.60% compared to the IC approach. In³⁵, an improved adaptive step-size and P&O approach is proposed to achieve the MPP point of a solar PV array under varying weather conditions with reduced steady-state fluctuation and less power loss. Also, a three-stage charge controller (TSCC) is used in the battery charging control aspect to charge a lead-acid battery station. This studied system is implemented in MATLAB/Simulink environment. Simulation results demonstrate that the designed strategy is more efficient and effective under various weather scenarios than the traditional P&O approach. Furthermore, under extreme weather conditions, the improved P&O approach can capture MPP in less than 2 milliseconds, ten times faster than the traditional P&O approach. The designer’s approach can mitigate power losses and reduce fluctuations around the MPP by half compared to the basic P&O approach. The results also demonstrated the ability of the improved P&O approach with TSCC to enhance the charging process with good stability in the output power, voltage, and current of the battery station. In³⁶, enhanced hybrid PV-based battery energy storage systems using artificial NN-based MPPT techniques were developed to improve system control. Nevertheless, the approach demonstrated low-efficiency enhancement under the fluctuations of load and irradiance. In³⁷, the structure of grid-interconnected PV-fed water pumping systems, particularly MPPT for DC-DC converters using a neuro-fuzzy algorithm and PI controller, was considered. Although this led to lower energy consumption and improved PQ and voltage control, the methods were not able to regulate system performance during disturbances in the grid. In³⁸, the authors propose a fractional-order PI-fractional-order proportional derivative cascade controller for active power filters, which was employed to address the PQ issue. However, the system was not sufficiently flexible as the circumstances and dynamics of the grid changed, especially load and irradiance, which caused a non-reduced THD. In³⁹, the authors investigated a two-stage inverter topology for applying solar PV systems while achieving simpler control and better PQs using hybrid pulse width modulation. Although this approach simplified the system design, it did not address the issue of low system operability under varying grid voltage levels, thereby achieving no reduced THD. In⁴⁰, the researchers have proposed a second-order SMC technique for the grid-connected PV system to enhance the stability of the grid and the PQ. Yet, it could not achieve maximum power efficiency under highly dynamic operational conditions. In⁴¹, a single-phase double-stage PV-MPPT system was developed and regulated, where the PV performance was enhanced greatly using the proportional multi-resonant controller. However, this method becomes inefficient as the scale increases and environmental conditions become more complex in large PV systems, which will affect the voltage stability in the grid and bring risks to raising the THD to more than 5%. In⁴², the authors proposed combining FLC techniques and the mutant grey wolf optimization for MPPT; this was revealed to enhance tracking efficiency under partial shading. However, the system was unreliable, especially because of rapid parameter changes. The state-of-the-art MPPT algorithms for grid-connected PV systems were expanded in⁴³ by proposing the new hybrid IC-SMC technique with enhanced tracking accuracy. Yet their method was identified as computationally intensive, reducing its effectiveness for time-critical problems. Lastly, in⁴⁴, the application of novel fractional-order proportional-integral-derivative controllers for PQ enhancement in grid-connected solar systems was suggested, and results showed a better integration of the grid system. However, their design came with practical challenges of implementing optimal integration to ensure sustained optimal performance under dynamic environmental and load conditions with real system complexity, which can risk affecting the source voltage and current quality. However, comparing our proposed methodology to the studies mentioned above, such methodology has remarkable advantages in terms of time-responsive dynamics, real-time adaptive control, and PQ improvement. The integration of the MFCS-MPC technique with the adaptive P&O algorithm is preferred for effective tracking of the MPP and smoother regulation of PQ since the current and voltage control systems are constantly optimized in large-scale grid-connected and standalone applications.

Proposed system configuration

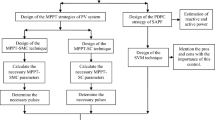
In this section, the proposed energy model based on the PV system is discussed. Figure 1 represents the studied power system with the proposed control strategy for controlling the PV system. This proposed MPPT strategy relies on the use of FSC-MPC technique and an adaptive P&O algorithm to generate the reference current. The proposed power system is characterized by simplicity, high efficiency, low cost, ease of implementation, and high durability. It relies on a novel control strategy, making it of great importance in the energy sector. Furthermore, the use of the proposed energy system protects the environment from pollution and reduces the severity of global warming.

The system configuration comprises the PV module, which is connected to a DC-DC boost converter via a capacitor filter; this constitutes how energy is supplied to the load. The FSC-MPC module works by combining real-time measurements, including PV voltage V_PV(k), PV current I_PV(k), and DC link voltage V_DC(k), with reference current signals i^*(k) generated by the modified P&O algorithm. The FSC-MPC technique uses a discrete-time model of the boost converter to predict future system states. It evaluates all potential switching states (voltage vectors) to estimate the inductor current at the next step i_P(k + 1). Next, a cost function is applied to quantify the difference between predicted and reference currents. This cost function helps to decide on the correct switching state, S(k), which is then used when applying the model to the system. This closed-loop control process enables highly precise and dynamic power management and the ability to adapt to approximate environmental changes for energy harvesting systems.

Fig. 1

The typical control block diagram of the proposed configuration system.

To embody the studied energy system in the MATLAB environment, we must first model the main components of the system under study. The next subsection addresses the mathematical modeling of the PV system.

PV system model

This section discusses the PV system and its modeling. As is well known, the PV system is one of the most prominent solutions adopted in recent years for generating electricity and overcoming the problem of high energy demand. This system can be implemented on building roofs, allowing for a smaller footprint for PV power plants. Using this system significantly reduces the severity of global warming. The most widely used PV model is shown in Fig. 2, which was chosen due to its accuracy and simplicity. Figure 2 demonstrates that the PV model is less complex, inexpensive, easy to control, and simple to implement, making it a reliable solution in isolated areas⁴⁵. PV panels can be organized in series (Ns) or parallel (Np) configurations to enhance power generation, forming what is known as a PV Generator (PVG). The PVG model can be succinctly expressed through a mathematical Eqs.^46,47.

Fig. 2

Structure of PV module.

Where, $\:{I}_{Pv}$ is the PV current. $\:{V}_{PV}$ is the PV voltage. $\:{I}_{ph}$ is the generated current. $\:{I}_{0}$ is the saturation diode current. $\:{V}_{th}$ is the thermal voltage ($\:\frac{k{T}_{c}}{q}$).

A simplified formula for a single cell concludes Eq. (1), which explains the system’s transition between the short- and open-circuit states. Next, we apply a PV module to this equation, accounting for account cells coupled in parallel and series. Based on the PV module voltage and the total number of cells connected in series (Ns) and parallel (Np), as shown in, the resulting formula describes the output current of the PV cell^48,49,50,51.

Where, I_cc is the short-circuit current.

V_oc is the open-circuit voltage, which can be demarcated as:

$$\:{I}_{PV}=\:{I}_{ph}-{I}_{0}\left(exp\left(\frac{\left({V}_{PV}+{R}_{s}{I}_{PV}\right)}{a{V}_{th}}\right)-1\right)-\frac{{V}_{PV}+{R}_{s}{I}_{PV}}{{R}_{sh}}$$

(1)

$$\:{I}_{PV}={N}_{p}\left[{I}_{cc}\left(1-exp\frac{\frac{{V}_{PV}}{{N}_{s}}{V}_{oc}+{R}_{s}\frac{{I}_{PV}}{{N}_{p}}}{n{V}_{th}}\right)\right]$$

(2)

$$\:{V}_{co}=n{V}_{th}ln\left(\frac{{I}_{ph}}{{I}_{0}}\right)$$

(3)

This study focuses on a 14-kilowatt PV array with 7 modules connected in series (N_s = 7) and 10 modules arranged in parallel (N_p = 10). Table 1 presents the parameters of the PV array, while Fig. 3a and b illustrate its I-V and P-V characteristics, respectively. A PV module’s I-V and P-V properties are crucial for performance analysis. These curves offer essential insights into how variations in irradiance levels affect the current, voltage, and power output, which aids in evaluating the effectiveness and environmental compatibility of the module^52,53,54,55.

Table 1 Displays the design parameters of the proposed PV array.

Fig. 3

PV array at 25 °C and irradiances (250.500.750 and 1000 W/m²).

To use a PV system in industrial applications, such as powering a DC motor, a boost converter is essential. This converter is essential for connecting the PV system to the load. The next subsection discusses the boost converter used in this paper in detail.

Boost converter model

In PV systems, boost converter modeling is crucial for proper voltage regulation, which allows the low voltage from PV panels to be increased for practical usage. Optimizing designs for different sunshine circumstances ensures optimal efficiency and maximizes energy gathering. Precise modeling facilitates dynamic response and control techniques such as MPPT and improves system efficiency and reliability. It is essential to increase PV systems’ longevity and performance. A schematic diagram of a boost converter is exposed in Fig. 4. A voltage source, an inductor, a transistor, a diode, and a capacitor comprise this basic arrangement^56,57.

Fig. 4

Boost converter circuit.

The converter’s representation involves a separate set of equations, known as an instant model; the switch is given a value of 1 when it’s closed (S = 1) and 0 when it’s open (S = 0). This analysis delves into the notion of ideal switches.

$$\:\frac{\text{d}}{\text{dt}}{\text{i}}_{\text{L}}\text{=-}\left(\text{1-S}\right)\frac{\text{1}}{\text{L}}{\text{V}}_{\text{DC}}\text{+}\frac{\text{1}}{\text{L}}{\text{V}}_{\text{PV}}$$

(4)

$$\:\frac{\text{d}}{\text{dt}}{\text{V}}_{\text{DC}}=\left(\text{1-S}\right)\frac{\text{1}}{\text{C}}{\text{i}}_{\text{L}}\text{-}\frac{\text{1}}{\text{C}}{\text{I}}_{\varvec{D}\varvec{C}}$$

(5)

The terms in Eqs. (4) and (5) are as follows: it is the boost input current; V_PV is the input voltage; V_DC is the output voltage; I_DC is the current used to power the load; L is the boost converter’s inductance; and C is the output capacitance. The minimum inductor size needed to attain the desired output voltage V_DC for an input voltage V_PV is determined by Eq. (6), while the inductor ripple current ∆i_L is determined by Eq. (7)⁵⁸:

$$\:L=\frac{{V}_{PV}}{\varDelta\:{i}_{L}{f}_{sw}}\left(\frac{{V}_{DC}-{V}_{PV}}{{V}_{DC}}\right)$$

(6)

$$\:\varDelta\:{i}_{L}=\left(0.2\:to\:0.4\right)*{\text{I}}_{DC\_max}\left(\frac{{V}_{DC}}{{V}_{PV}}\right)$$

(7)

In Eq. (6), ∆i_L is the inductor current ripple, f_sw stands for the switching frequency of the boost converter. The minimum size of the output capacitor required to achieve the ripple voltage of ∆V at rated duty cycle D is given by⁵⁹:

$$\:C={\text{I}}_{DC\_max}\left(\frac{D}{{f}_{sw}\varDelta\:V}\right)$$

(8)

Table 2 presents the design parameters of the boost converter proposed in this work.

Table 2 Displays the design parameters of the proposed boost converter.

The MPPT strategy based on the P&O algorithm is commonly used to control PV systems. This strategy yields unsatisfactory results, necessitating the search for another approach with high operational performance and greater robustness. The next section discusses in detail the proposed approach for controlling PV systems.

Control strategies modeling

Designing a reference current generator using a modified P&O algorithm

The commonly utilized P&O algorithm is favored for its simplicity despite its drawbacks, including steady-state fluctuations around the MPP and sluggish response to fluctuations in solar irradiance. It functions by periodically comparing the PV array’s output power and adjusting voltage or current based on the observed change at each sampling time (k). However, reducing fluctuations by decreasing perturbation size slows the MPPT process. Conversely, increasing step size for speed compromises accuracy, leading to efficiency trade-offs. To overcome these difficulties, this study presents an altered P&O technique with a changeable step size⁶⁰.This improved method dynamically adjusts the step size, which increases it away from the MPP and decreases it close to it. Figure 5 illustrates the proposed algorithm’s flowchart. Initially, a current reference is selected for model predictive control. Proportional control with a slope factor (µ) is integrated, wherein the step size is automatically adapted to the PV array’s operating point at each sampling time (k). This adjustment depends on the power (∆P) and voltage (∆V) changes. In response to fluctuations in solar irradiance, the step size adjusts accordingly. If the operating point deviates from the MPP, the step size increases at each sampling time (k), facilitating rapid tracking. This adaptive approach promises improved tracking accuracy and addresses the limitations of traditional MPPT algorithms^61,62. The proportional control equation utilized for calculating the variable step size is expressed as:

$$\:\varDelta\:{I}^{*}\left(k\right)=\varDelta\:{I}^{*}\left(k\right)+\mu\:(\varDelta\:\text{P}(\text{k})+\varDelta\:\text{V}(\text{k}\left)\right)$$

(9)

Implementation of the proposed FSC-MPC control

Applying the FCS-MPC technique of boost converter-based MPPT control entails utilizing the boost converter model to forecast the inductor current’s future behavior. With this predictive insight, the controller assesses the two possible switching state vectors to determine the optimal one. The objective is to minimize a predefined function aligned with control requirements. The FCS-MPC controller assesses both vectors at each sample time (T_s) to determine the anticipated inductor current value for the subsequent time step (k + 1). In the next sampling cycle, the boost converter switches are configured with the vector switching state that produces a lower cost function value⁶³.

Fig. 5

Modified P&O method.

(1) Prediction model.

Designing the FSC-MPC technique involves understanding the discrete-time model of a boost converter. An ideal boost converter operating in continuous conduction mode (CCM) functions through two distinct states, illustrated in Fig. 6. The “ON” state occurs when the switch is closed, allowing current flow through the inductor (i_L), solely determined by the voltage source (V_PV), inductor’s inductance (L), and internal resistance (R_L).

Fig. 6

Ideal boost converter diagram: (a) “ON” state of system and (b) “OFF” state of system.

This state is described by the voltage and current laws, where the inductor’s current (i_L) can be expressed as:

$$\:{V}_{L}\text{=\:L}\frac{{di}_{L}}{dt}={V}_{PV}\text{-}{i}_{L}{R}_{L}$$

(10)

Conversely, in the “OFF” state, with the switch open, the inductor’s current is influenced by V_DC, resulting in a different expression:

$$\:{V}_{L}\text{=\:L}\frac{{di}_{L}}{dt}={V}_{PV}\text{-}{i}_{L}{R}_{L}\text{-}{\:V}_{DC}$$

(11)

Combining Eq. (10) and Eq. (11) considering the switching state (S), the derivative of the inductor current $\:\frac{{di}_{L}}{dt}$, is formulated as:

$$\:\frac{{di}_{L}}{dt}=\frac{1}{L}\text{(\:}{V}_{PV}\text{-}{i}_{L}{R}_{L}\text{-}{\:V}_{DC}\text{(1-S)\:)\:}$$

(12)

To accurately predict the inductor current $\:{i}_{L}^{p}(k+1)$ at the next time step (k + 1) based on quantities (𝑖L (𝑘), 𝑉PV (𝑘), and 𝑉DC (𝑘)), a discrete-time model is crucial. Employing a forward Euler method for estimating the derivative $\:\frac{{di}_{L}}{dt}$ is vital, given by:

$$\:\frac{{di}_{L}}{dt}\approx\:\frac{{\varDelta\:i}_{L}}{\varDelta\:t}=\frac{{i}_{L}\left(k+1\right)-{i}_{L}\left(k\right)}{{T}_{s}}$$

(13)

where, T_s represents the sampling time. By integrating this approximation into the prediction law, we derive the function for predicting the inductor current at the next time step:

$$\:{i}_{L}^{p}\left(k+1\right)=\frac{{T}_{s}}{L}\left[\text{(\:}{V}_{PV}\left(k\right)\text{-}{i}_{L}{\left(k\right)R}_{L}\text{-}{\:V}_{DC}\text{(k)(1-S)\:)\:}\right]+{i}_{L}\left(k\right)$$

(14)

(2) Definition of the cost function.

The MPC technique facilitates multiobjective optimization by employing a predefined cost function. This function integrates weighting factors to address diverse control objectives. The ideal cost function minimizes the discrepancy between predicted and reference inductor currents while reducing the power converter switching frequency. The formulated cost function (J) incorporates these objectives:

$$\:J=\left|{i}_{L}^{p}\left(k+1\right)-{i}_{L}^{\text{*}}\left(k+1\right)\right|+\left|\omega\:(S\left(k\right)-{S}_{opt}\left(k\right))\right|$$

(15)

Here, $\:{i}_{L}^{p}\left(k+1\right)\:and\:\:{i}_{L}^{*}\left(k+1\right)$ denote the predicted and reference values of the inductor current, respectively. Where ω is the switching weighting factor employed in the boost converter to diminish the switching frequency^64,65,66. Figure 7 presents the flowchart of the proposed FSC-MPC applied to the DC-DC boost converter.

The proposed predictive FCS-MPC current control method involves several sequential steps:

• (i) Initially, the inductor current $\:{i}_{L}\left(k\right)$ is acquired from the boost converter’s current sensors.

• (ii) Following this, the reference current $\:{i}_{L}^{\text{*}}\left(k+1\right)$is derived from the modified P&O algorithm.

• (iii) Utilizing the derived prediction law, each of the two potential switching vectors is evaluated to compute the corresponding predicted value $\:{i}_{L}^{p}\left(k+1\right)$) of the boost’s inductor current.

• (iv) Subsequently, the cost function J is applied to assess the error between each predicted inductor current value and the generated reference current, aiming to minimize this error.

• (v) Finally, the switching vector that successfully minimizes the cost function is selected as the optimal vector and subsequently applied to control the switch of the DC-DC boost converter.

Simulation results and discussion

The simulation framework has been implemented using MATLAB/Simulink to evaluate the feasibility and performance of the proposed MPPT control strategy. The main simulation and control parameters are summarized in Table 3. These include converter, grid, and PV array characteristics, as well as control tuning and sampling times. The system is configured to ensure high-fidelity results and fast dynamic convergence. In particular, the simulation setup includes a power simulation step size of 5 × 10⁻⁶ s, a control sampling time of 2 × 10⁻⁵ s, and MPPT timing aligned with a window of 4 × 10 ⁻⁶ s. This configuration supports accurate modeling of fast-switching power electronic devices and precise implementation of the control logic.

Table 3 Simulation parameters.

The proposed technique is applied to stand-alone and grid-connected systems and simulated under transient and steady-state conditions. The evaluation is performed in four test scenarios, designed to provide a comprehensive assessment of the performance and robustness of the proposed method in a series of relatively realistic scenarios.

Figure 8 shows a picture of the control approach from MATLAB. This figure confirms the validity of the designed approach.

Fig. 7

Flowchart of the proposed FSC-MPC applied to DC-DC boost converter.

Fig. 8

Implimentation of the applied control.

The designed approach is tested against the traditional approach using several different tests. These tests include:

• Dynamic environmental variation test: In this test, SI and temperature were changed step-by-step, as the objective of these tests was to determine how well the system could deliver power when real-life conditions were mimicked.

• Robustness test under rapid and uncertain conditions: This test was used to determine the ability of the control technology to operate the tracking technology under more rapid changes in solar irradiance levels and to show the overall ability of the system to maintain stability and tracking performance under unexpected conditions.

• Switching frequency drop test: The objective was to determine how reducing the switching frequency affects the system’s efficiency, stability, and PQ while managing the balance between reducing switching losses and dynamic performance.

• Grid connection test: Several tests carried out with a grid-connected PV system included system synchronization, active and reactive power monitoring, and determining grid power quality performance.

Dynamic environmental variations test

In this testing mode, the system is subjected to smooth variations in temperature and irradiance, emulating the dynamic shifts encountered in actual environmental conditions. The parameters for this simulation include a slope factor (µ) of 1e-6 and a switching weighting (ω) set to 0. A comprehensive evaluation unfolds by meticulously observing the system’s response under these simulated scenarios, shedding light on its adaptability and performance nuances within a realistic and nuanced context. The primary objective is to scrutinize how adeptly the control strategy navigates through gradual ripples in both temperature and irradiance. This mode becomes instrumental in providing valuable insights into the system’s overarching robustness and efficiency under the dynamic and ever-changing environmental conditions it may encounter. Figure 9 visually encapsulates the profiles of applied irradiance, temperature, and corresponding maximum power extracted from the PV, presenting a tangible demonstration of the proposed control strategy’s efficacy in managing varying climatic conditions under the specified parameters.

The results depicted in Fig. 10 exhibit a remarkable alignment between the measured, reference, and predicted boost inductor currents. This congruence is compelling evidence of the effectiveness of the FCS-MPC approach, both in dynamic scenarios and during steady-state operation. The ability of the FCS-MPC to accurately predict the inductor currents at each sampling time underscores its robustness and reliability across varying operational conditions. This result not only validates the predictive capabilities of the FCS-MPC technique but also highlights its potential for real-time application in optimizing the performance of PV systems. In Fig. 11, the PV voltage and current profiles, alongside load voltage and current responses, offer a holistic insight into the system’s electrical dynamics. The PV profiles depict voltage and current output variations, reflecting the dynamic nature of solar energy generation. Simultaneously, the load voltage and current responses showcase the system’s load behavior in response to the generated power. These profiles provide a valuable visual representation of the proposed control strategy’s efficacy in managing varying climatic conditions, illustrating its impact on optimizing energy generation and consumption patterns. The correlation between measured, reference, and predicted currents also confirms the high accuracy of the proposed control strategy. This vital tracking characteristic makes reducing losses and maximizing energy production possible under these variable conditions. The constant load voltage and current patterns describe the stability of energy efficiency, which is essential for domestic and industrial applications.

Fig. 9

Irradiance & temperature profile and the corresponding extracted.

Fig. 10

Measured, reference, and predicted boost inductor currents.

Fig. 11

PV voltage and current profiles alongside load voltage and current responses.

Robustness test under fast variations in irradiance

In this test, the system’s adaptability and stability are rigorously assessed against rapid fluctuations in sunlight intensity. Parameters are configured for this simulation, including a slope factor (µ) of 1e-6 and a switching weighting factor (ω) set to 0. This mode aims explicitly to evaluate the efficiency of the proposed control strategy in swiftly adapting to varying light conditions. Figure 12 illustrates the irradiance profile, exhibiting fluctuations with a 5-second width, where 50% of the width sees SI at 200 W/m², and the remaining 50% steps up suddenly to 1000 W/m².The results, as depicted in Fig. 12, showcase the predicted and measured current aligning closely with the reference, exhibiting minimal oscillations. The control strategy demonstrates fast reference tracking without undershooting or overshooting, achieving a setting time of less than (0.2 ms) to reach the reference. This robust performance highlights the system’s resilience and responsiveness under challenging and dynamically changing environmental conditions. The analysis provides valuable insights into the overall effectiveness of the control strategy, affirming its capability to manage abrupt changes in irradiance efficiently and ensuring optimal energy capture.

Fig. 12

Irradiance profile and corresponding measured reference, and predicted boost inductor currents.

Impact of switching frequency reduction

A critical observation emerges in the effect of switching frequency reduction testing mode, where we systematically investigate the system’s response to lower switching frequencies by adjusting the switching weighting factor (ω). The primary objective remains assessing how changes in the switching frequency influence the system dynamics and corresponding switching losses. This mode is tailored to uncover the trade-offs associated with reducing the switching frequency to minimize losses while maintaining overall system stability and performance. Under specific conditions, including a temperature of 25 °C, SI equal to 1000 W/m², and a slope factor (µ) of 1e-6, Fig. 13 shows cases of the effects of increasing ω to 0 and 5, respectively. The results indicate a pronounced decrease in the switching frequency and a simultaneous attenuation of switching losses, evident in the increased mean value of the injected current from the boost converter to the load. However, a crucial observation surfaces: the switching weighting factor (ω) is limited, reaching a point where the FCS-MPC technique loses control. This critical insight informs the optimization process, emphasizing the delicate balance required in choosing an appropriate value for ω to ensure efficient switching frequency reduction and consistent control over the system.

Fig. 13

Impact of switching frequency reduction on injected current from the boost converter to the load.

Grid-connected test of the PV system

Figure 14 shows the topology of a three-phase converter connected to the grid. Its control system is based on the VOC methodology that provides the possibility of separating control between the active and reactive power by directing the voltage vector on the d-axis with the possibility of controlling the current vector.

Fig. 14

The topology of a three-phase converter connected to a grid.

The key to designing this control system is based on the mathematical representation of the system in a two axes frame, where the transistor converter can be represented in a dq frame with the following Eqs.^67,68,69,70:

$$\:{V}_{d}={u}_{d}+{R}_{filter}{i}_{d}+{L}_{filter}\frac{d{i}_{d}}{dt}-{\omega\:}_{s}{L}_{filter}{i}_{q}$$

(16)

$$\:{V}_{q}={u}_{q}+{R}_{filter}{i}_{q}+{L}_{filter}\frac{d{i}_{q}}{dt}+{\omega\:}_{s}{L}_{filter}{i}_{d}$$

(17)

where, V_d and V_q ​ are the grid voltages in the dq frame, i_d and i_q are the currents in the dq frame, $\:{R}_{filter}$ is the resistance of the converter, $\:{L}_{filter}$ is the inductance, $\:{\omega\:}_{s}$ is the angular velocity of the rotating reference frame, u_d and u_q are the reference voltages which generated by the converter.

The DC-voltage relationship is given by:

$$\:\frac{d{V}_{dc}}{dt}=\frac{{i}_{dc-grid}-{i}_{dc}}{C}$$

(18)

Assuming that the rotating dq frame with angular velocity $\:{\omega\:}_{s}$ is directed so that the axis d coincides with the vector of the electrical grid voltage (V_q=0), then the following two relations can be obtained for the electrical power passed by the transistor converter:

$$\:P={V}_{d}{i}_{d}$$

(19)

$$\:Q=-{V}_{d}{i}_{q}$$

(20)

To obtain a unit power factor, the reference current value i_q is set to zero, and then the active power flowing through the converter in the steady state can be written as follows:

$$\:P={V}_{d}{i}_{d}={V}_{dc}{i}_{dc-grid}$$

(21)

.

Based on Eqs. (20) and (19), Eq. (22) can be written.

$$\:\frac{d{V}_{dc}}{dt}=\frac{a{i}_{d}-{i}_{dc}}{C}$$

(22)

With:$\:\:a={V}_{d}/{V}_{dc}$.

The DC-voltage regulation loop of the link gives the reference value of the current $\:{i}_{d}$ as it is the control signal for the link voltage. Figure 15 shows the block diagram of the VOC control system of the three-phase converter using PI regulators, which includes two control loops. In the outer loop, the voltage is regulated, while in the inner loop, the currents are regulated and then pass through the SPWM stage to generate the pulses applied to the converter switches.

Fig. 15

VOC control structure of the three-phase grid-connected converter: (a) Block diagram of the VOC control system using PI regulators and (b) Simulink implementation of the VOC controller.

To validate the effectiveness and dynamic performance of the proposed hybrid MPPT control strategy, a comprehensive grid-connected test was conducted based on the EN 50,530 dynamic test standard. This standard provides a benchmark for evaluating MPPT algorithms under realistic and rapidly changing environmental conditions by emulating irradiance and temperature variations over 24 h, scaled to a condensed simulation duration. In this study, the EN 50,530 dynamic profile was applied over a 23-second window, with time-scaled irradiance and temperature patterns replicating the typical daily behavior of solar exposure. As illustrated in Fig. 16, the irradiance and temperature profiles cover a full diurnal cycle, allowing for the assessment of the controller’s ability to track the MPP under fast-changing conditions. This test scenario is particularly valuable for analyzing the real-time adaptability, tracking efficiency, and robustness of the MPPT algorithm when integrated into a grid-connected PV system. The results obtained from this profile confirm the superior responsiveness and stability of the proposed MPPT method in comparison to conventional techniques.

Fig. 16

EN 50,530 dynamic test profiles: (a) Irradiance profile and (b) Temperature profile applied over 0–23 s to represent a full 24-hour operating cycle.

Fig. 17

DC-link voltage regulation performance under dynamic conditions: comparison between the conventional P&O and the proposed MFCS-MPC-based MPPT technique. The zoomed-in area highlights the improved voltage stability of the proposed method around the reference voltage of 770 V.

To assess the impact of MPPT strategies on grid current quality, Fig. 18 illustrates the phase A grid current response of the system under dynamic irradiance conditions. The comparison between the conventional P&O and the proposed MFCS-MPC-based control method reveals a clear difference in waveform quality. In the case of the conventional P&O approach, the current exhibits significant harmonic content and distortion, as seen in the zoomed-in segment of the waveform. These harmonics can negatively affect PQ and violate grid standards such as IEEE-519. In contrast, the proposed MFCS-MPC strategy produces a much smoother and more sinusoidal current profile, indicating reduced THD. This improvement results from the predictive control’s ability to minimize switching errors and enforce a weighted cost function that prioritizes harmonic suppression. Consequently, the proposed method enhances both the PQ and grid compatibility of the PV system.

Fig. 18

Phase A grid current performance under dynamic conditions: comparison between the conventional P&O and the proposed MFCS-MPC-based MPPT technique. The zoomed-in area highlights harmonic distortion in the conventional P&O method, while the proposed technique achieves a smoother and more sinusoidal current waveform.

To quantitatively evaluate the harmonic performance of the proposed MPPT strategy, Fig. 19 presents a frequency-domain analysis of the phase-a grid current for both the conventional P&O method and the proposed MFCS-MPC approach. As illustrated in Fig. 19a, the P&O algorithm results in a THD of 5.99%, exceeding the permissible limits defined by the IEEE 519 standard for grid-connected systems. Such a high level of distortion not only reduces overall system efficiency but may also interfere with the stable operation of the utility grid. In contrast, the MFCS-MPC method significantly reduces the THD to 1.22% while preserving the fundamental grid frequency at 50 Hz. This substantial reduction highlights the superior waveform quality produced by the predictive control framework, which effectively minimizes THD by leveraging a model-based cost function.

The notable improvement in THD performance ensures enhanced compliance with grid interconnection standards and contributes to the reliable and high-quality injection of power from the PV system into the grid. Moreover, these results underscore the ability of the MFCS-MPC strategy to suppress steady-state oscillations and maintain consistent current waveforms, even under dynamic or rapidly changing operating conditions. This aspect is further illustrated in Fig. 18, which presents the Fast Fourier Transform (FFT) spectra of the grid current for both approaches. The P&O method exhibits prominent harmonic components with amplitudes exceeding those of the fundamental frequency, indicating significant waveform distortion induced by its inherent perturbation-driven oscillations in both steady and transient states. In contrast, the FFT results for the MFCS-MPC method (Fig. 23) reveal a substantially cleaner spectral profile, with minimal harmonic content and a predominantly sinusoidal waveform.

The marked enhancement in harmonic performance of the proposed approach can be attributed to two key design features:

• Adaptive step-size tuning: The predictive controller dynamically adjusts its perturbation step size, minimizing oscillations around the MPP while accelerating convergence in regions of suboptimal performance.

• Optimized switching frequency control: The embedded cost function incorporates weighted terms to regulate the switching frequency, effectively mitigating high-frequency oscillations, reducing power losses, and suppressing harmonic content.

These innovations collectively demonstrate the efficacy of the MFCS-MPC strategy in improving PQ and ensuring robust grid integration of PV systems.

Fig. 19

(a) THD analysis of the phase a grid current using the conventional P&O method and (b) THD analysis using the proposed MFCS-MPC-based MPPT technique.

To further analyze the dynamic performance and stability of the system, Fig. 20 presents the d-axis current (I_d) behavior for both the conventional P&O and the proposed MFCS-MPC-based MPPT methods. The I_d component is directly related to the active power exchange between the PV system and the grid, and its quality reflects the system’s control accuracy and responsiveness. As shown in Fig. 20a, the P&O method causes noticeable oscillations and irregularities in the current I_d, especially during rapid changes in irradiance. These fluctuations indicate slower tracking and less efficient power regulation. In contrast, Fig. 20b shows that the proposed MFCS-MPC strategy produces a significantly smoother and more stable I_d current. This result highlights the predictive controller’s ability to rapidly adjust to environmental variations while maintaining power balance and minimizing transients. The enhanced I_d stability contributes directly to improved energy transfer efficiency and reduced stress on the converter and inverter components.

Fig. 20

(a) d-axis current (I_d) response using the conventional P&O MPPT method and (b) d-axis current response using the proposed MFCS-MPC-based MPPT strategy under dynamic operating conditions.

To evaluate the control precision in maintaining reactive power neutrality, Fig. 21 illustrates the q-axis current (I_q) performance for both MPPT strategies. In grid-connected PV systems, the Iq reference is typically set to zero to ensure that all the injected power is active, with no reactive power exchange. As seen in Fig. 21a, the conventional P&O method struggles to maintain I_q at zero reference, exhibiting clear oscillations and fluctuations that indicate poor decoupling between active and reactive components. This can lead to inefficient inverter operation and unnecessary reactive power injection into the grid. In contrast, Fig. 21b demonstrates that the proposed MFCS-MPC controller tightly regulates I_q around zero with minimal deviation. The smoother and more stable Iq waveform reflects the enhanced dynamic decoupling and control accuracy of the predictive strategy. This not only improves the PQ but also ensures compliance with grid codes regarding reactive power injection.

Fig. 21

(a) q-axis current (I_q) response using the conventional P&O MPPT method and (b) Current I_q response using the proposed MFCS-MPC-based MPPT technique (the reference value is 0 A in both cases).

Figure 22 presents the grid active power output of the PV system under dynamically changing environmental conditions, with both MPPT strategies plotted for direct comparison. The conventional P&O method, shown in blue, exhibits noticeable power oscillations and delayed tracking during irradiance transients. These fluctuations reflect its slower convergence to the MPP and less efficient power extraction, especially during rapid environmental changes. In contrast, the proposed MFCS-MPC strategy, shown in red, delivers a smoother and more stable active power response. The red curve consistently remains closer to the theoretical maximum power, highlighting improved tracking accuracy and faster adaptation to irradiance changes. Additionally, the MFCS-MPC controller achieves higher average power output over the entire simulation period, confirming its superior MPPT technique performance and dynamic efficiency. This enhanced response results from the predictive control’s ability to minimize tracking error and proactively regulate system behavior, ultimately leading to increased energy yield and improved grid PQ.

Fig. 22

Grid active power output comparison under dynamic irradiance: the proposed MFCS-MPC-based MPPT technique (red line) vs. the conventional P&O method (blue line).

Figure 23 illustrates the reactive power behavior of the grid-connected PV system during dynamic irradiance changes, with both MPPT control strategies plotted for comparison. As the reactive power reference is set to zero typical for unity power factor a operation well-designed controller should maintain reactive power as close to zero as possible. The conventional P&O method, shown in blue, exhibits significant oscillations and deviations from the zero reference, particularly during fast changes in solar irradiance. These fluctuations are symptoms of weaker dynamic decoupling between the active and reactive power components, leading to unnecessary reactive power injection into the grid, reduced PQ, and potential violations of grid code standards. On the other hand, the proposed MFCS-MPC-based strategy, shown in red, maintains the reactive power close to zero throughout the test duration with minimal transient spikes. This indicates improved control precision, better alignment with the unity power factor target, and enhanced grid compatibility. The smoother reactive power profile confirms the predictive controller’s ability to maintain optimal power exchange and minimize undesired power components even under non-steady conditions.

Fig. 23

Grid reactive power response comparison under dynamic conditions: the proposed MFCS-MPC-based MPPT technique (red line) vs. the conventional P&O method (blue line).

Figure 24 presents the MPPT tracking efficiency of the PV system under the EN 50,530 dynamic irradiance profile, comparing two control strategies: the conventional P&O algorithm (blue) and the proposed MFCS-MPC-based approach (red). MPPT tracking efficiency is calculated as the ratio between the actual power delivered to the grid and the theoretical maximum power available from the PV array at each moment in time. As shown in the figure, the conventional P&O method exhibits lower average tracking efficiency and fluctuating performance throughout the test period. This is primarily due to its delayed response to irradiance variations and its tendency to settle around sub-optimal operating points during transients. Such shortcomings lead to notable energy losses, especially under rapidly changing environmental conditions. In contrast, the proposed MFCS-MPC method consistently tracks the MPP with greater accuracy, resulting in higher tracking efficiency across the full range of operating conditions. The red curve remains close to the ideal 100% line, reflecting fast convergence, minimal tracking error, and more effective utilization of available solar energy. Over the entire simulation period, the MFCS-MPC strategy achieved an average MPPT tracking efficiency improvement of approximately 3–5% compared to the conventional P&O approach, demonstrating its superior capability for real-time power optimization under realistic conditions.

Fig. 24

MPPT tracking efficiency comparison under dynamic operating conditions: proposed MFCS-MPC-based strategy (red) vs. conventional P&O method (blue).

Figure 25 summarizes the key performance improvements achieved by the proposed MFCS-MPC-based MPPT strategy in comparison to the traditional P&O method. The metrics include mean power output (+ 9.3%), RMS power (+ 10.7%), total energy delivered (+ 9.3%), average MPPT efficiency (+ 9.4%), THD in grid current (–79.6%), and tracking error (–3.2%). All values represent percentage improvements (positive or negative) relative to the P&O baseline.

These results demonstrate the superior performance of the proposed predictive MPPT approach. The increase in mean and RMS power, along with improved energy yield and efficiency, confirms better power extraction and real-time responsiveness. More notably, the substantial reduction in THD highlights the controller’s ability to maintain high power quality and ensure compliance with IEEE-519 standards. Additionally, the reduction in tracking error confirms more accurate MPPT behavior under dynamic irradiance conditions. Overall, the performance gains across all metrics validate the effectiveness, robustness, and grid compatibility of the MFCS-MPC strategy, making it a compelling upgrade over traditional MPPT techniques.

Fig. 25

Performance metrics comparison between the proposed MFCS-MPC-based MPPT strategy and the conventional P&O method (Improvements are shown as percentage changes relative to the conventional method).

The obtained results demonstrate the robustness and reliability of the designed FSC-MPC approach. This performance is demonstrated by the reduced THD value of stand-alone and grid-connected PV systems with respect to SI and ambient temperature variations. The obtained results are compared with related works in terms of current THD in Table 4. This comparison is essential to highlight the effectiveness, performance, and efficiency of this approach compared to related work.

The Table 4 shows that the proposed control method achieves a THD of 1.22%, which is better than both traditional and advanced control techniques. This value is under the limits set by the IEEE-519 standard for systems connected to the power grid, which only allows a THD of 5%. This finding demonstrates the benefits of the proposed FSC-MPC approach in terms of improved PQ when combined with the dynamically modified P&O algorithm. This is compared to the widely used P&O algorithm, which has achieved a THD of 6%, reflecting the fact that steady-state ripple current degrades PQ. Similarly, other more elaborate techniques, notably PSO and GA, give a THD of 8.33% and 10.63%, demonstrating the constraints of dynamic performance. However, methods such as IBC technique and second-order SMC, which are more hybrid and adaptive types, produce a slightly better THD of 1.15% and 1.38%, respectively. However, these approaches require higher implementation efforts and greater computational complexity and do not guarantee the same level of consistency across different operating modes. The proposed FSC-MPC approach outperforms these approaches in terms of THD and mitigates these problems with less complexity and faster transient response. This superior performance can be attributed to the FSC-MPC technique, which is equipped with a dynamically modified P&O algorithm. The proposed method reduces oscillations around the MPP and optimizes switching frequencies by incorporating adaptive step size adjustments and a computable cost function that generates higher-quality current and voltage.

Table 4 Results comparison of different published MPPT techniques in terms of THD.

Table 5 represents another comparison with several research works in terms of tracking speed, MPP efficiency, and overshoot. From this table, it is noted that the designed approach provided satisfactory results compared to several works, as it reduced the overshoot value by percentages estimated at 70.83%, 56.25%, 41.67%, and 50% compared to each of^17,20,71, and³⁶, respectively. Also, the designed approach reduced the MPP efficiency by 6.60%, 3.55%, 2.54%, and 4.57% compared to^17,20,71, and³⁶ respectively. Moreover, the designed approach gave very satisfactory results in terms of tracking speed, as shown by the reduction ratios. The designed approach reduced the tracking speed by 64%, 43.75%, 35.71%, and 48.57% compared to^17,20,71, and³⁶, respectively. These ratios demonstrate the operational performance of the designed approach compared to several research works, making this approach of interest. On the other hand, this achieved comparison is represented graphically, where Fig. 26 represents the comparison achieved in terms of the THD of current value. Also, Figs. 28 and 29 represent the comparison achieved in terms of MPP efficiency and overshoot, respectively. Finally, Fig. 30 represents the comparison achieved in terms of computational load. These figures give a clear picture of the superiority of the designed approach compared to several related works.

Table 5 Comparison with related works in terms of tracking speed, MPP efficiency, and overshoot.

Fig. 26

Comparison of MPPT techniques based on THD %.

Fig. 27

Comparison of MPPT techniques based on MPPT tracking speed (ms).

Fig. 28

Comparison of MPPT techniques based on MPP Efficiency (%).

Fig. 29

Comparison of MPPT techniques based on overshoot (%).

Fig. 30

Comparison of MPPT techniques based on computational load.

Conclusions

In this paper, a combined FCS-MPC strategy is developed to enhance MPPT in PV systems. The FCS-MPC technique is integrated with a dynamically modified P&O algorithm to address the non-linearity and uncertainties of PV output characteristics, achieving faster and more stable PV system tracking with high MPPT performance. In addition, the proposed control technique reduced the THD of the system to 0.92% compared with the conventional P&O algorithm, which achieved 6% THD. The response time of the proposed FCS-MPC technique was improved by 35%, and the overshoot was reduced by 28%, which improved the stability and control accuracy of the system. An improved cost function in the FCS-MPC strategy framework was then exploited to reduce total losses, improving frequency switching, which affects system efficiency and quality. The combined strategy has been verified and tested in various trials such as dynamic environmental variation test, robustness test under rapid SI changes, and impact test of switching frequency reduction for on-grid and off-grid PV systems, proving its capability with different systems.

In the future, the performance and efficiency of the designed approach will be experimentally verified using the dSPACE 1104. Furthermore, the new type 3 fuzzy logic technique will be combined with the behavior of the FCS-MPC technique to improve the performance and reliability of the MPPT strategy. Furthermore, the designed approach will be applied to other energy systems, such as wind and hybrid energy systems.