Introduction

Over the past five decades, wide-bandgap semiconductors (Eg > 1.43 eV), such as CdMnTe, CdSe, CdTe, CdZnSe, CdZnTe, GaAs, HgI2, and TlBr, have been considered for room temperature gamma and X-ray detector applications as their elemental compositions are mutually soluble, forming homogeneous solid solutions without altering their individual crystal structures1,2,3,4,5,6,7,8,9,10. However, one of the primary challenges in fabricating detectors from these materials is the difficulty of growing chemically pure and structurally perfect crystals1,11,12. This process can introduce defects such as sub-grain boundary networks, inclusions, precipitates, and nonuniform compositions, which inhibit the performance of detectors10,11,12. Various approaches have been employed to address these obstacles and optimize detector performance, including compound doping, combining binary materials to synthesize ternary, quaternary, or higher-order solutions, and modifying the growth methodology10. Still, the presence of active point and extended defects/impurities continues to be a primary inhibitor of the charge-transport properties in these detectors.

Among all these materials, CdTe has been one of the most studied due to its high atomic number, high density, higher resolution, very low leakage current, large cover area, and wide electronic bandgap (Eg = 1.44 eV), which enables room-temperature operation13,14,15. However, the performance of CdTe detectors is limited by the presence of structural defects, impurities, Te inclusions, precipitates/anti-sites (TeCd, Te at Cd sites), and complexes of cadmium vacancies (VCd)16. The addition of 10 atomic % of Zn has been the primary candidate for improving the performance of CdTe, forming Cd0.9Zn0.1Te16,17,18,19,20. Here, distinct advantages of Cd0.9Zn0.1Te over CdTe were found through the reduction in the density of the carrier traps (VCd, TeCd), complexes such as TeCd(VCd), as well as a notably wider bandgap (Eg = 1.57 eV)21,22. However, the mass production of Cd0.9Zn0.1Te detectors has still been constrained by the formation of sub-grain boundary networks and Te inclusions generated during the growth and post-growth phases of the material processing, which adversely affect the performance of the detectors23.

Recently, the addition of selenium in the CZT matrix has been found to be effective in reducing concentrations of Te inclusions and sub-grain boundary networks and achieved better compositional homogeneity, resolving some of the long-standing issues pertaining to CZT24,25,26. Here, the resulting quaternary material CdZnTeSe (CZTS) with a composition of 2 atomic % of Se has been found to be sufficient in reducing the performance limiting defects, while compositions of ~ 1.5% Se in CZTS matrix still exhibit a high concentration of Te inclusions similar to that of pure CZT27,28. Currently, a better understanding of the system parameters that impact the formation of Te inclusions and sub-grain boundaries is necessary to optimize crystal growth process protocols to minimize their impact on device performance. Studies on microscopic techniques capable of mapping the size, density, and spatial distribution of Te inclusions within pure CZT and CZTS are essential for developing a more complete understanding of the mechanisms behind Te-inclusion formation and the influence of Se doping on their development.

While a variety of optical techniques, including Raman and photoluminescence spectroscopic characterization, have been utilized to evaluate Te inclusions in CZT and CZTS29,30,31,32,33,34,35, the spatial resolution of these techniques is typically constrained by the diffraction limit to several hundreds of nm for light in the visible spectral range. Moreover, while Te inclusions have also been characterized using scanning probe microscopy18,20, these techniques alone are not capable of developing a full picture of the cause and electronic effects associated with Te inclusions in these materials, including strain, band bending, and the local work function, which enable these inclusions to act as traps for free carriers in radiation detection devices. To understand the effects of Te inclusions in detail, here we report multimodal characterization of Te inclusions in Cd1–xZnxTe and Cd1−xZnxTe1−ySey.

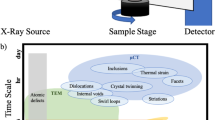
As depicted in Fig. 1, to combine the advantages of optical and scanning probe microscopic imaging and provide for additional information on the effects of secondary phases, we perform multimodal microscopic surface imaging and analysis of the optical and electronic properties of Te inclusions in CZT and CZTS matrices. Confocal Raman microscopy was employed to differentiate between the vibrational response of bulk CZT/CZTS and Te inclusions. Utilizing IR scattering-scanning near-field optical microscopy (IR s-SNOM) techniques in the mid-IR spectral range, we demonstrate for the first time a mapping of the location, size, and geometric distributions/concentration of Te inclusions with few-nm spatial resolution via measurement of the local IR optical response of the surface. In addition, Kelvin Probe Force Microscopy imaging was subsequently performed on Te inclusions and grain boundaries to measure their associated surface potential and band bending. We provide a comparative analysis of these techniques and utilize the combined information on the location, vibrational response, and work function of the Te inclusions to better understand how micro- and nano-scale inclusions inhibit carrier flow in radiation detector devices.

Fig. 1
figure 1

Multimodal imaging of a single Te inclusion within a bulk Cd0.9Zn0.1Te0.985Se0.015 crystal. (a) Optical microscopy image with correlated (b) Raman spectral mapping can be utilized to image large inclusions with a diffraction limited resolution of several hundred nm. (c) Nanometer-scale resolution scanning probe imaging techniques can then be employed using conventional AFM, which maps the topography of the Te inclusion (a). (d) Optical coupled IR s-SNOM imaging can be applied to observe nanoscale variations of the inclusion’s infrared optical response, while electrical (e) KPFM imaging can be used to relate information on the relative variations of the surface potential associated with the presence of a Te inclusion. The scale bar is 5 μm for all images.

Full size image

Results

Crystal growth

CZT and CZTS crystals of two-inch diameter were grown by the Traveling Heater Method (THM), adopting the same growth parameters reported earlier for Cd0.9Zn0.1Te0.98Se0.02 growths25. To facilitate the easy location and study of Te inclusions, pure CZT crystals were utilized for most characterization measurements (unless otherwise noted). CZT crystals exhibit a significantly higher density of Te inclusions. Se doped samples were also studied to investigate the relationship between Se doping and the size and distribution of Te inclusions. Se doping compositions of CZTS matrix of less than 1.5% have still been found to exhibit a high concentration of Te inclusions similar to that of CZT26,28. For the purposes of studying the formation and electronic structure of Te inclusions, we specifically chose the composition of Cd0.9Zn0.1Te0.985Se0.015 for characterization.

Confocal Raman microscopy

Confocal microscopic characterization was first employed to locate large, µm-scale Te inclusions. While diffraction limited in its spatial resolution, these optical microscopy techniques can be utilized to visualize the location and distribution of large Te inclusions and verify material composition by observing their Raman response. Figure 2 displays correlated optical and Raman imaging of a ~ 8-µm Te inclusion in a bulk CZT sample. Here, confocal Raman imaging enables mapping of the spectral variations of the vibrational signatures of both bulk CZT/CTZS and Te inclusions, which denotes changes in their structural configuration. Such confocal Raman characterization represents a versatile means of performing an initial characterization to identify the composition of a sample surface as it is noncontact and nondestructive for low laser fluences, allowing for point-by-point mapping of a surface’s structural response30. In previous studies, Te inclusions were identified and quantitatively analyzed using micro-Raman spectroscopy on CdTe and CdZnTe. Specifically, Te inclusions exhibit two prominent Raman modes around 121(A1) and 141(E) cm−1, along with a weak mode around 92 (E) cm−1. The 92 cm−1 line is generally associated with the presence of a trigonal lattice of metallic Te17,29,30. In CdTe, longitudinal optical (LO) and transverse optical (TO) phonon modes at 168 and 141 cm−1 are expected.17,29,30. Other peaks around 272 cm−1 (elemental Te) and 328 cm−1 (2LO CdTe) were identified, while the origin of these peaks has yet to be assigned32. Micro-Raman imaging was carried out using a confocal Raman microscope (Horiba XploRA PLUS) with 532-nm laser excitation at an approximate power of 1 mW and total exposure times of no more than 10 s. Raman mappings were obtained by scanning a confocal laser illumination spot using an automated X–Y sample translation stage.

Fig. 2
figure 2

micro-Raman mapping and spectroscopy of Te inclusion embedded within bulk CZT crystal. (a) Optical microscopy image with correlated (b) line-trace of the Raman response over an individual Te inclusion showing the intensity variation and spectral shifts of the Raman response. The location of the line trace is marked by green dashed line in panel (a). A comparison of the Raman spectra measured at (c) a Te inclusion (position marked by the red circle in (a) and (d)) and the bulk CZT (position marked by black circle in (a)). Integrating the Raman response over a spectral range spanning from 110 to 150 cm−1, the intensity variation of the Raman response increases by a factor of ~ 6 × at the Te inclusion with respect to the bulk CZT.

Full size image

As displayed by the correlated optical microscopy and Raman intensity mapping images in Fig. 2a, b, the Raman response of Te inclusions exhibits several characteristic differences from the surrounding bulk CZT crystal. We observe the expected three characteristic lines at 93.2, 121.9, and 141.4 cm−1 (Fig. 2c) associated with trigonal Te at the inclusion location. Notably, we observe that the intensity of the ~ 121 and ~ 141 cm−1 Raman peaks exhibit a drastic intensity increase at the inclusion site. Integrating the Raman response between 110 and 150 cm−1, we observe an approximately 6 times larger response above the Te inclusion than the surrounding bulk CZT crystal.

In bulk CZT adjacent to the Te inclusion, we observe two peaks at 124.2 and 142.5 cm−1 (Fig. 2d), which are weaker in intensity and slightly shifted from those of the Te inclusion. Moreover, we observe a very weak and broad peak at 97 cm−1. While all three of these Raman peaks correspond to trigonal phase Te outside the inclusion, their small intensity and spectral shifts indicate that these peaks result from Te precipitations distributed throughout the bulk CZT crystal. The two peaks at 121.9 and 142.5 cm−1 are associated with trigonal Te and commonly observed in the bulk CZT matrix, albeit with very low intensity, and have been reported to increase with incident laser exposure due to Te secondary phase enrichment on the surface17. The observed spectral broadening is likely associated with strain-induced effects that depend on the size and possibly the shape of the few nanometer-sized precipitates.

Figure 2b displays a line trace of the spectral response over an individual Te inclusion site showing the intensity variation and spectral shifts of the Raman response. As a result of its significantly increased Raman scattering cross-section, Raman imaging represents a simple, non-contact means of quickly identifying the presence of microscale Te inclusions on the surface of CZT and CZTS crystals.

IR near-field microscopy

Having mapped regions containing large or elevated concentrations of Te inclusions with µm scale spatial resolution, co-located scanning probe characterization techniques can further be employed to map the distribution of Te inclusions with nanometer spatial resolution. By pairing scanning probe characterization with further optical and/or electronic excitation of the surface, additional information on the optoelectronic response of the Te inclusions and their impact on the surrounding bulk CZT and CZTS crystal can be mapped and identified. To perform high-resolution imaging of large Te inclusions and identify the presence of sub-µm inclusions along sub-grain boundaries, IR s-SNOM techniques were first employed to simultaneously map variations in the topographic and optical response of the substrate. IR s-SNOM provides a non-destructive means of transducing the mid-IR optical response of a surface with nanometer spatial resolution through the measurement of scattering from the mutual polarization of an atomic force microscopy (AFM) probe with the sample surface directly beneath it, typically induced via illumination by an external IR laser light source36. The resolution of IR s-SNOM characterization of the optical response is proportional to the radius of curvature of the AFM probe tip, which for most commercially available probes is on the order of 10–20 nm. For imaging in the mid-IR spectral range, this means achieving spatial resolutions that are up to ~ 1000 × lower than the diffraction limit.

To map the presence and geometric distribution of Te inclusions within CZT and CZTS substrates, s-SNOM characterization was implemented in the mid-IR spectral range (\(\lambda =10\,\mu\)m) using Pt-coated AFM probes (Arrow-NCPt). Although the room-temperature absorption coefficient at 10 \(\mu\)m is less than 0.01 cm−1 for high-resistivity CZT37, there are significant advantages resulting from operation in the mid-IR due to the higher reflectivity of Te with respect to the surrounding CZT/CZTS matrix, allowing µm and nm length-scale Te inclusions to be easily identified through the enhanced optical scattering intensity by the AFM probe. As feedback of the AFM probe with the surface is maintained through the use of tapping mode AFM, the near-field scattering signal can be filtered out from other scattering contributions from the macroscopic focal area through the implementation of lock-in filtering of the scattering signal at the higher harmonics of the AFM probe’s dither motion \(n{\Omega }_{m}\), where \({\Omega }_{m}\) represents the resonance frequency of the probe’s fundamental bending eigenmode and \(n=\text{2,3},4,\) represents the higher harmonic being monitored through lock-in filtering38,39. Information on the amplitude and phase of the s-SNOM scattering amplitude can be performed through the implementation of pseudo-heterodyne interferometry40,41.

As shown in Fig. 3 panels (a,b), Te inclusions can be easily identified using s-SNOM imaging and are characterized by both a significant increase in the s-SNOM scattering amplitude (~ 2 ×) and a reduction in the s-SNOM scattering phase (~ 0.1 rad). These relative shifts in the s-SNOM signal are associated with an increased optical polarizability of the surface and a reduced absorption by the surface beneath the AFM probe. Such signal contrast variation is expected for Te inclusions as Te exhibits a high reflectivity and low absorption in the mid-IR spectral range42,43. With the ability to precisely image Te inclusions, we can further correlate their presence near sub-grain boundaries within the bulk crystal. Panels (c, d) and (e–g) show small Te inclusions located along sub-grain boundary interfaces within the bulk crystal denoted by the blue dashed line. As illustrated in Fig. 3e–g, while the topographic variation associated with Te inclusions can be minimal, the strong signal variation in the optical response can easily identify their presence along a sub-grain boundary.

Fig. 3
figure 3

IR s-SNOM mappings of Te inclusions embedded within bulk CZT crystals. (a, b) Topography and associated s-SNOM scattering amplitude images recorded over a large hexagonal Te inclusion embedded in a bulk CZT crystal. Panels (c, d) and (e–g) demonstrate imaging of the spatial correlation of the presence of Te inclusions with grain boundaries (blue-dashed line). (c, d) shows topography and s-SNOM amplitude of a Te inclusion located at a sub-grain boundary. Panels (e–g) show topography, s-SNOM amplitude, and s-SNOM phase of a series of Te inclusions located along a sub-grain boundary (blue dashed line) in a bulk CZT crystal. All IR s-SNOM data were recorded using lock-in filtering at the 3rd harmonic of the AFM dither frequency (\(3{\Omega }_{d}\)).

Full size image

Kelvin probe force microscopy

While IR s-SNOM nanoscale optical imaging can identify and map the presence of micro-and nano-meter length scale Te inclusions, Kelvin Force Probe Microscopy (KPFM) imaging has a further advantage as it can measure the variation of the surface potential between bulk CZT and CZTS crystals and Te inclusions. Additionally, it can be used to visualize the impact of Te inclusions on the work function of the surrounding bulk CZT and CZTS matrix through the identification of band bending effects. KPFM measures the contact potential difference (CPD) between a conducting AFM tip and a sample’s surface enabling nanoscale visualization of variations of a CZT/CZTS surface’s work function induced via the presence of Te inclusions. Having located and characterized individual nanoscale Te-inclusion sites with IR s-SNOM, KPFM measurements were subsequently carried out using FM-KPFM feedback. Here, following the line measurement of the sample surface topography, the AFM probe is lifted above the sample by a lift height of 60 nm and retraced above the sample surface. During this lift-mode trace, the AFM probe (Bruker PFQNE-AL) is mechanically driven at the resonance frequency of its fundamental bending eigenmode (\({\Omega }_{\text{m}}\cong 300\) kHz) while a \({V}_{AC}\)~ 3 V AC-bias at a frequency of \({\upupsilon }_{\text{AC}} \sim\) 2 kHz is applied between the sample and the AFM probe. In addition, a variable DC voltage, \({V}_{DC}\), is added to \({V}_{AC}\) to reduce the amplitude of observed AFM probe oscillations occurring at sideband frequencies of \({\Omega }_{\text{m}}\pm {\upupsilon }_{\text{AC}}\). AFM probe oscillations occurring at these sideband frequencies result from the electrostatic interaction between the AFM probe with the surface and are minimized when \({V}_{DC}\) is equal to the contact potential difference (\({V}_{CPD}\)) between the probe and the sample surface. \({V}_{CPD}\) can in turn be expressed as the difference in work function, \(\Phi\), between probe material and the sample surface: \({V}_{CPD}=\Delta\Phi /\text{e}=({\Phi }_{\text{sample}}-{\Phi }_{\text{probe}})/\text{e}\), where \(\text{e}\) is the electron charge44. Using newly exfoliated highly oriented pyrolytic graphite (HOPG) as a reference material for the contact potential difference (\({\Phi }_{\text{HOPG}}=4.68\) eV)45, the work function of bulk CZT/CZTS was found to be ~ 4.95 eV, in relative agreement with the range of observed work functions13,46.

Figure 4a, b displays a representative KPFM characterization of a hexagonal Te inclusion located within a bulk of CZTS crystal. Similar to previous studies20,47, we observe the presence of the Te inclusion is characterized by a significant relative increase in the CPD (~ 240 mV) relative to the surrounding bulk CZTS crystal. Illustrated in Fig. 4d, this measurement aligns with models of the trapping of free charge carriers by Te inclusions. Interestingly, our KPFM images further reveal a region of increased CPD within the bulk crystal surrounding Te inclusions. Performing an exponential fit of the CPD of the bulk crystal near the Te defect, \(\Delta\Phi \left(\text{x}\right)=\text{A}\cdot \text{exp}(-|\text{x}-{\text{x}}_{0}|/{\Gamma }_{\text{x}})\), a quantitative measurement of the magnitude and spatial extent of band bending behavior could be made in regions within the bulk CZTS crystal proximal to Te inclusions. Here, \({\text{x}}_{0}\) denotes the spatial position of the edge of the Te inclusion, while \(\text{A}\) and \({\Gamma }_{\text{x}}\) represent the magnitude and decay constant of the exponential fit to the experimentally observed band bending near the Te inclusion. An example of one such fit is displayed in Fig. 4c as shown by the blue dashed line indicating a ~ 1.55 \(\upmu\)m band bending decay constant. Analyzing 18 fits of this band bending effect over multiple Te inclusions, we find the magnitude of this band bending effect to have a mean of ~ 110 mV with a standard deviation of 60 mV. The decay constant, \({\Gamma }_{\text{x}}\), of the exponential fits was found to have a mean of 1.75 µm with a standard deviation of 1.1 µm. This observation of band bending effects further underscores the detrimental role that Te inclusions can play to carrier transport in CZT and CZTS crystals, as free charge carriers passing within several \(\upmu\)m of Te inclusions can be funneled via band bending into carrier trap sites.

Fig. 4
figure 4

KPFM mapping image of a hexagonal Te inclusion within a bulk CZTS crystal. (a, b) Topography and KPFM potential images, respectively. (c) Line trace showing the spatial variation of the CPD as the location denoted by the dashed white line in panels (a, b). The dashed blue line displays an exponential fit of band bending in the bulk crystal in proximity to the inclusion. (d) Illustration of the band bending induced carrier funneling to Te-inclusion trap sites.

Full size image

While the formation of Te inclusions is known to correlate with the presence of sub-grain boundaries in bulk CZT and CZTS crystals, KPFM imaging of these inclusions further revealed that the sub-grains themselves can exhibit slight variations in surface potential. Figure 5 displays two examples of KPFM mapping across a single sub-grain boundary present within a bulk CZT crystal sample. Here the mean difference in the CPD between the two sub-grains is revealed to be ~ 85 mV. Currently, the precise origin of these variations in the surface potential is unknown but could be attributable to variations in the crystallographic orientation and/or variations in the relative electrical resistivity in adjacent grains caused by different effects of the surface processing conditions, including the topography.

Fig. 5
figure 5

(a) Topography and corresponding (b) KPFM imaging of surface potential changes of Te inclusion defects located along a sub-grain boundary located in a bulk CZT crystal. Zoom in (c) topography and (d) KPFM scans of the area marked by the white box in (a, b), illustrating the surface potential change, which occurs at the sub-grain boundary (blue dashed line). (e) Line-trace of the variation of the surface height and measured KPFM contact potential difference along the white line shown in (c, d). Moving from the grain on the left to the grain on the right, the surface topography varies by only a few nanometers while the surface potential increases by ~ 85 mV.

Full size image

The presence of the mV-scale variations in the work function of the material could illustrate an additional barrier to efficient free carrier motion through crystals. Here, grains with higher work functions may act as shallow energy barriers to free carrier motion, as charges within these grains must overcome a low energy barrier to pass on to neighboring grains. Additionally, the Te inclusions along the sub-grain boundary and the linear features are expected to produce some effects on band bending at the Te/CZT interface and the region near the sub-grain boundary, leading to potential changes in the transport properties for carriers propagating through these volumes.

Summary

While bulk CZT and CZTS crystals have been considered as strong candidates for the realization of room-temperature gamma and X-ray detectors, their performance is often limited by the presence of structural defects in the form of Te inclusions and sub-grain boundaries. Here, the detrimental effects of Te-rich secondary phases depend strongly on the size and concentration of Te inclusions due to trapping effects, particularly the creation of non-uniformity in charge-collection properties. Relatively large micron-scale inclusions tend to be more detrimental than the smaller nm-scale inclusions48. However, previous optical imaging modalities have been unable to identify the presence and concentration of nm-scale inclusion features. We demonstrate the combination of confocal microscopy and Raman spectroscopic characterization with scanning probe microscopy techniques (IR s-SNOM and KPFM) for: (1) the multimodal identification of the presence and nanoscale spatial distribution Te defects and grain boundaries, and (2) the characterization of the local opto-electronic response of these defects and their effect on the surrounding bulk crystal. We find IR s-SNOM to be an effective technique at identifying nanoscale Te defects along grain boundaries, which would otherwise be unobservable with traditional confocal microscopy techniques. Further KPFM characterization reveals the elevated work function of Te defects, the spatial extent of band bending in the surrounding bulk crystal, and the presence of mV variations of the work function between opposing sides of grain boundaries. The utilization of these methods to further characterize CZT and CZTS crystals may provide feedback for the further optimization of crystal growth protocols and, via related improvements in detection efficiency, more widespread use of these materials as room-temperature radiation detectors.