Introduction

The number of elderly persons is rapidly increasing every year, and the birth rate is also decreasing1. As the society enters a super-aged phase, the severity and implications of sarcopenia among the elderly are becoming increasingly recognized2. As a result, mobility is decreased, causing various cardiovascular diseases such as myocardial infarction, cerebral infarction, and stroke, resulting in hemiplegia or even death, leading to a rapid increase in geriatric diseases3.

As these cases rapidly increase, various services such as an expansion of nursing homes and the development of wearable robot platforms are being actively carried out to increase medical and welfare benefits for the elderly. In particular, research on various wearable robots aims to enhance the walking performance of users. Wearable lower limb robots can be broadly classified into exoskeleton robots4,5,6,7,8, soft exosuits9,10,11,12, and orthotic devices13,14,15,16,17 based on their function and structure. Exoskeleton robots are further categorized into treadmill-based18,19 and overground walking-based robots20,21,22 depending on the usage environment and the condition of the user. Treadmill-based robots are primarily used in indoor environments such as rehabilitation centers and are designed for patients with stroke, spinal cord injuries, musculoskeletal impairments, and balance disorders. Overground walking-based robots are suitable for both indoor and outdoor environments and are classified based on the range of joints they support from an orthotic perspective, including hip orthosis (HO), knee-ankle-foot orthosis (KAFO), and hip-knee-ankle-foot orthosis (HKAFO). The type of exoskeleton robot applied to a patient is determined by orthotic classification, the stage of injury, and the type of disability.

Research on gait cycle prediction is a crucial factor in maximizing the performance of lower limb wearable robots, as it supports natural walking for users and enhances safety23,24,25. A common approach involves utilizing force sensing resistors (FSRs) as insole sensors to determine the user’s gait phase26,27,28. This method is widely used in exoskeleton robots that mechanically integrate the foot, such as KAFO and HKAFO. However, in modular exoskeleton robots like HO, which do not include the foot, incorporating insole sensors can present challenges, such as wearability issues. To address these limitations, research has been conducted on gait phase estimation (GPE) algorithms that utilize joint data and cyclic movement patterns. GPE primarily utilizes the adaptive frequency oscillator (AFO) theory or the phase portrait method. AFO refers to an oscillator that learns the frequency of periodic input signals and adjusts its parameters accordingly. It predicts the gait cycle by recognizing repetitive movement patterns. UCLouvain developed a primitive-based control framework using AFO, which provides reference torque through a virtual musculoskeletal model29. The AFO algorithm is specialized for a consistent walking speed within a treadmill environment, which limits its applicability in overground settings. Samsung developed the particularly-shaped adaptive oscillator (PSAO), which estimates the gait cycle by analyzing joint angles30. However, PSAO has limitations due to its complex initial setup and parameter tuning, which hinder its generalizability across diverse user populations. Another research example is the phase portrait method, which predicts the stance/swing state of gait by deriving the gait cycle as a pattern. Georgia Tech Research Institute used encoder sensors and inertial measurement unit (IMU) sensors attached on the thigh of the robotic hip exoskeleton (RHE) and the linear gait pattern was predicted using convolutional neural network (CNN) based GPE algorithm31. These methods require large-scale training datasets and high-performance computational resources, which pose practical limitations for implementation on embedded systems. To address these limitations, enhanced GPE algorithms have been proposed that enable real-time application in embedded assistive devices. Texas A&M University collected the angle and integral of the thigh that used the IMU sensors attached to the powered transfemoral prostheses, and developed the GPE algorithm using an integral and phase-shifted method32. Korea Advanced Institute of Science and Technology (KAIST) attached the IMU sensors on the thigh, developed the GPE algorithm utilizing the estimated hip angle and angular velocity, and also validated the GPE algorithm performance through the experiment using the force plate33. Research on GPE algorithms has continuously explored various approaches, including data normalization and deep learning techniques, to predict gait phases in a linearized pattern.

Figure 1
figure 1

Overview the clinical trials of GPE-based muscle support algorithm for RHE; (a) gait rehabilitation training system. (b) hip angle and angular velocity according to gait cycle. (c) torque profile stages. (d) GPE and torque profile.

Full size image

In the study, a GPE-based muscle support algorithm, optimized for embedded and portable environments, is applied to a robotic hip exoskeleton (RHE) to compare gait support performance between two groups: elderly individuals with sarcopenia and patients with brain lesions.

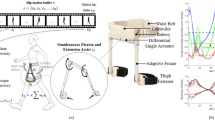
The gait rehabilitation system consists of a robotic hip exoskeleton (RHE), a lift device, insole sensors, and a photoplethysmogram (PPG) sensor. The training protocol comprises two standard gait rehabilitation tests: the 10-meter walk test (10MWT) and the 6-minute walk test (6MinWT). In the 10MWT, walking time, cadence, and speed are measured, while in the 6MinWT, walking distance, cadence, and speed are assessed (Fig. 1a). During these tests, the RHE system collects hip joint angle and angular velocity data (Fig. 1b). The hip joint support system provides real-time adjustable torque profiles to modulate muscle support levels dynamically (Fig. 1c).

Typically, walking rehabilitation outcomes are assessed using metrics such as time or velocity in the 10MWT, and distance in the 6MWT34,35. In the study, in addition to measuring temporal and spatial variables such as time and distance to capture quantitative changes, we also consider qualitative improvements using indicators such as walking speed and cadence. Walking speed is a widely accepted indicator of functional mobility, as it reflects a subject’s ability to ambulate independently and efficiently in daily life. It is also correlated with community ambulation levels and has prognostic value for rehabilitation outcomes. Cadence, defined as the number of steps per minute, is often used to evaluate gait symmetry and balance, as deviations from normal cadence can indicate compensatory strategies, neuromuscular impairments, or balance deficits. Furthermore, walking distance in the 6MWT serves as a reliable marker of cardiopulmonary endurance and overall walking capacity, while reduced time or increased velocity in the 10MWT indicates improvements in short-distance functional walking performance.

The optimized torque profile is generated based on predicted gait trajectories produced by the GPE algorithm, which adapts to the user’s gait cycle (Fig. 1d). This algorithm uses hip joint angle and angular velocity data and applies a low-pass filter to transform the inherently elliptical phase portrait trajectory into a circular and linearized form. This transformation compensates for the nonlinear characteristics of gait prediction. The resulting phase variable is normalized to a 0–1 gait cycle, enabling robust and consistent phase estimation for real-time torque modulation. As a result, the proposed GPE algorithm provides both robustness and adaptability in gait cycle estimation, supporting its potential for clinical implementation in diverse rehabilitation settings.

The RHE with a GPE-based muscle support algorithm aims to evaluate its applicability for individuals who are capable of walking. Therefore, the hypotheses of the study are as follows: (1) When gait rehabilitation training is performed while wearing the RHE, walking time in the 10MWT decreases, and walking distance in the 6MinWT increases, resulting in a significant improvement in gait performance. (2) Among the individuals wearing the RHE, those with lower initial gait performance (e.g., lower walking speed in 10MWT and shorter walking distance in 6MinWT) exhibit a relatively greater improvement in walking speed and walking distance after gait rehabilitation training compared to those with higher initial gait performance.

The contributions of the study can be summarized as follows:

  • Development of a GPE-based muscle support algorithm : To address the issue of nonlinearity in gait cycle prediction, an enhanced GPE algorithm was applied to provide improved muscle support.

  • Implementation of a personalized torque control system : PPG sensor feedback was utilized to enable optimized muscle support tailored to individual users.

  • Validation through clinical trials : A six-day clinical trial was conducted with elderly individuals and patients with brain lesions, demonstrating significant gait improvements in 10MWT and 6MinWT evaluations.

  • Applicability to various exoskeleton robot platforms : The proposed method was shown to be applicable not only to the RHE platform but also to various lower-limb rehabilitation exoskeleton robots.

Figure 2
figure 2

Representative kinematic and dynamic data of the hip joint during exoskeleton-assisted walking. (a) Group A: a participant with sarcopenia, assistive torque level 2. (b) Group B: a participant with brain lesions, assistive torque level 7. Each plot includes hip joint angle, angular velocity, gait phase estimation (GPE), and assistive torque.

Full size image
Table 1 Results for gait rehabilitation training (10MWT and 6MinWT) and absence or presence of robotic hip exoskeleton (No RHE and RHE) according to groups A and B.
Full size table

Results

To evaluate the effects of gait rehabilitation training with and without RHE in elderly and brain lesion patients, the training results were categorized into basic training effects (No RHE) and robotic-assisted effects (RHE). In the 10MWT, time, cadence, and speed were analyzed, while in the 6MinWT, distance, cadence, and speed were compared between the pre-test and post-test (as shown in Table 1).

Figure 3
figure 3

Results for 10MWT/6MinWT pre-test and post-test and absence of robotic hip exoskeleton (No RHE) according to groups A and B. Upper plots indicate the gait rehabilitation training for 10MWT ((a) time, (b) cadence, and (c) speed). Lower plots indicate the gait rehabilitation training for 6MinWT ((d) distance, (e) cadence, and (f) speed). The increase/decrease rate and p-value are indicated through graphs. p-value is expressed as follows; \(*: P<0.05,\,**: P<0.01\).

Full size image

Comparison of gait features between two groups

Kinematic differences: Hip angle and angular velocity

A comparative kinematic analysis was conducted using representative cases of a participant with sarcopenia (Fig. 2a) and another with brain lesions (Fig. 2b), focusing on hip joint behavior. In the case of the participant with sarcopenia, the hip joint angles on both the left and right sides exhibited clear periodicity with consistent amplitude, and the angular velocity profiles showed symmetrical patterns across sides. In contrast, the participant with brain lesions demonstrated periodic hip joint angles on both sides; however, the pattern characteristics differed significantly between the left and right limbs. Additionally, the angular velocity signals displayed noticeable asynchrony, indicating disrupted coordination.

Dynamic and phase-related differences: GPE and hip torque

From a dynamic perspective, the participant with sarcopenia (Fig. 2a) exhibited a linear and stable gait phase estimation (GPE) pattern, which contributed to the generation of a well-regulated torque profile. In this case, the assistive torque level was set to 2. In contrast, the participant with brain lesions (Fig. 2b), with an assistive level of 7, showed distorted GPE patterns, likely resulting from asynchronous hip joint movements. This irregularity in phase progression adversely affected the consistency and magnitude of torque generation.

These representative examples illustrate typical gait patterns observed in each group after hip exoskeleton-assisted walking. While individual differences persist, both groups showed overall improvements in gait coordination and joint control, as further detailed in the quantitative analysis (see Table 1).

Walking performance results for 10MWT

In the No RHE condition, the time for Groups A and B decreased by 4.88% (p = 0.15) and 27.08% (p = 0.04), respectively (Fig. 3a–c). The pre-test values were 3.28 ± 0.68 s for Group A and 5.76 ± 3.19 s for Group B, while the post-test values were 3.12 ± 0.34 s and 4.2 ± 0.98 s, respectively. The cadence for Groups A and B increased by 1.78% (p = 0.14) and 7.23% (p = 0.045), with pre-test values of 125.44 ± 6.92 steps/min for Group A and 111.4 ± 15.06 steps/min for Group B, and post-test values of 127.67 ± 7.18 steps/min and 119.45 ± 13.43 steps/min, respectively. The speed for Groups A and B increased by 4.28% (p = 0.12) and 24.04% (p = 0.009), with pre-test values of 5.14 ± 0.56 mph for Group A and 3.12 ± 1.01 mph for Group B, and post-test values of 5.36 ± 0.74 mph and 3.87 ± 0.83 mph, respectively.

In the RHE condition, the time for Groups A and B decreased by 10.53% (p = 0.004) and 26.32% (p = 0.002), respectively. The pre-test values were 3.8 ± 0.56 s for Group A and 6.04 ± 1.59 s for Group B, while the post-test values were 3.4 ± 0.37 s and 4.45 ± 1.23 s, respectively (Fig. 4a–c). The cadence for Groups A and B increased by 2.87% (p = 0.04) and 10.36% (p = 0.013), with pre-test values of 119.29 ± 6.8 steps/min for Group A and 105.65 ± 15.39 steps/min for Group B, and post-test values of 122.71 ± 6.29 steps/min and 116.6 ± 13.53 steps/min, respectively. The speed for Groups A and B increased by 11.11% (p = 0.004) and 28.32% (p = 0.002), with pre-test values of 4.23 ± 0.61 mph for Group A and 2.79 ± 0.76 mph for Group B, and post-test values of 4.7 ± 0.53 mph and 3.58 ± 0.8 mph, respectively.

Walking performance results for 6MinWT

In the No RHE condition, the distance for Groups A and B increased by 0.67% (p = 0.45) and 14.04% (p = 0.14), respectively (Fig. 3d–f). The pre-test values were 281.58 ± 44.33 m for Group A and 232.15 ± 61.71 m for Group B, while the post-test values were 283.48 ± 27.48 m and 264.75 ± 43.86 m, respectively. The cadence for Groups A and B increased by 0.48% (p = 0.43) and 4.34% (p = 0.21), with pre-test values of 117.27 ± 7.07 steps/min for Group A and 106 ± 12.31 steps/min for Group B, and post-test values of 117.83 ± 6.69 steps/min and 110.6 ± 11.83 steps/min, respectively. The speed for Groups A and B increased by 0% (p = 0.49) and 17.91% (p = 0.09), with pre-test values of 4.77 ± 0.74 mph for Group A and 2.96 ± 0.87 mph for Group B, and post-test values of 4.77 ± 0.51 mph and 3.49 ± 0.73 mph, respectively.

In the RHE condition, the distance for Groups A and B increased by 10.59% (p = 0.046) and 22.02% (p = 0.04), respectively (Fig. 4d–f). The pre-test values were 223.54 ± 37.03 m for Group A and 198.48 ± 45.75 m for Group B, while the post-test values were 247.21 ± 24.7 m and 242.19 ± 40.53 m, respectively. The cadence for Groups A and B increased by 4.8% (p = 0.007) and 8.14% (p = 0.1), with pre-test values of 109.09 ± 4.66 steps/min for Group A and 97.1 ± 12.36 steps/min for Group B, and post-test values of 114.33 ± 4.37 steps/min and 105 ± 12.51 steps/min, respectively. The speed for Groups A and B increased by 7.23% (p = 0.085) and 25.19% (p = 0.03), with pre-test values of 4.01 ± 0.5 mph for Group A and 2.58 ± 0.73 mph for Group B, and post-test values of 4.3 ± 0.44 mph and 3.23 ± 0.68 mph, respectively.

Figure 4
figure 4

Results for 10MWT/6MinWT pre-test and post-test and presence of robotic hip exoskeleton (RHE) according to groups A and B. Upper plots indicate the gait rehabilitation training for 10MWT ((a) time, (b) cadence, and (c) speed). Lower plots indicate the gait rehabilitation training for 6MinWT ((d) distance, (e) cadence, and (f) speed). The increase/decrease rate and p-value are indicated through graphs. p-value is expressed as follows; \(*: P<0.05,\,**: P<0.01\).

Full size image

Discussion

Group A consisted of elderly participants, where the effect of gait rehabilitation training without the robotic device (No RHE) was minimal. However, with the robotic device (RHE), both 10MWT and 6MinWT showed statistically significant improvements. In other words, when walking without the robotic device, there was little difference in pre-test and post-test results for 10MWT and 6MinWT. However, when using the robotic device, a significant difference was observed, indicating that the participants successfully adapted to robotic gait training. Group B consisted of individuals with brain lesions, where 10MWT in the No RHE condition showed statistically significant improvements, and both 10MWT and 6MinWT in the RHE condition demonstrated statistically significant results. This indicates that, even without the robotic device, 10MWT showed a noticeable difference between pre-test and post-test. Additionally, when using the robotic device, significant differences were observed in both 10MWT and 6MinWT, confirming the effectiveness of robotic-assisted gait training. When comparing the results of the two groups, it was observed that participants generally adapted well to robotic gait training. Additionally, individuals with greater walking difficulties (Group B) showed a higher rate of improvement in both gait rehabilitation effectiveness without RHE (No RHE) and the robot-assisted training effect (RHE). Furthermore, in the No RHE condition, even though the pre-test and post-test results were not statistically significant, the substantial difference in the improvement rate suggests a clinically meaningful change. These findings align with the initial hypotheses: (1) When gait rehabilitation training is performed while wearing the RHE, walking time in the 10MWT decreases, and walking distance in the 6MinWT increases, resulting in a significant improvement in gait performance. (2) Among the individuals wearing the RHE, those with lower initial gait performance (e.g., lower walking speed in 10MWT and shorter walking distance in 6MinWT) exhibit a relatively greater improvement in walking speed and walking distance after gait rehabilitation training compared to those with higher initial gait performance.

It was observed that the pre-test and post-test results with RHE showed lower performance compared to the pre-test and post-test results without RHE (No RHE). The primary reason for this appears to be the relatively heavy weight of the robot, which may have caused psychological discomfort for the users during walking. Additionally, environmental factors such as the short six-day clinical trial period and the consecutive training schedule may have contributed to this result by providing insufficient time for users to adapt to the robot or leading to accumulated fatigue.

The recruited participants included elderly individuals and patients with brain lesions, with a variety of conditions; however, they were generally selected based on having gait impairments. The study provided useful insights into the trend that individuals with greater walking difficulties benefit more from robot-assisted gait rehabilitation training. However, it was observed that the standard deviation value of the gait rehabilitation training results was relatively large. This is likely due to the diversity of lesions among the participants in the study. In future studies, if participants are recruited with more uniform lesion types, the range of standard deviation values of gait rehabilitation training results is expected to decrease.

The participants in the clinical trial underwent gait rehabilitation training using a lift and RHE over a six-day period and successfully completed the training without any safety incidents. When performing gait rehabilitation training while being suspended by the lift and wearing the RHE, participants were able to walk naturally in straight-line distances. However, at turning points, the lift was perceived as an obstacle, causing stiffness and psychological discomfort in the trainees. The lift system was generally effective in ensuring safety during gait rehabilitation training, except for certain sections. Since the rehabilitation training gait data collected during the clinical trial included turning points, the reliability of the data was somewhat low but still helpful in identifying trends. Resolving these issues to some extent is expected to enhance the reliability of gait rehabilitation training data in future studies.

The low-pass filter-applied GPE algorithm was found to be effective in compensating for nonlinearity issues in gait prediction. Additionally, it was confirmed that the GPE algorithm is useful as an indicator for distinguishing the beginning and end of gait cycles. However, the predictive trajectory of the GPE algorithm is expected to be influenced by the gait performance of individuals wearing the RHE robot, determining whether it appears linear or nonlinear. In particular, the more non-linear the predictive trajectory, the greater the likelihood that the timing of the assistive force in the applied strength-support algorithm will be misaligned. This misalignment may result in counterproductive forces for the wearer, which can interfere with their movement. To address this issue, it is necessary to implement a personalized phase portrait technique, adjusting the trajectory from an elliptical shape to a more circular form. Future research aims to integrate deep learning technology into the low-pass filter-enhanced GPE algorithm to generate personalized phase portraits, thereby further improving the algorithm’s performance. Moreover, this study has demonstrated the potential application of the GPE algorithm not only for elderly individuals wearing the RHE but also for patients with brain lesions and other lower-limb disabilities.

The torque profile provided by the robot was adjusted in real-time and applied to the user. In general, minimal torque assistance was provided to individuals with slower walking speeds or weaker muscle strength, while higher levels of muscle support were offered to those with faster walking speeds and more developed muscle strength. Additionally, a counter-based muscle support algorithm was implemented, where flexion torque was applied to one side while simultaneously providing extension torque to the opposite side. Among the RHE users with good walking performance, adaptation to this support method was relatively quick. However, for users with poor walking performance, PPG sensor monitoring revealed a rapid change in heart rate, indicating potential discomfort or strain. Based on these findings, the intensity of muscle support was adjusted accordingly during gait training. In the future, we aim to develop a system that incorporates real-time feedback from physiological signals such as electrocardiogram (ECG) and electromyography (EMG) to automatically tune the muscle support algorithm, ultimately providing a personalized torque profile for each user.

Through the clinical trial results of the study, we compared gait performance under No RHE and RHE conditions and confirmed that the rate of gait performance improvement varied depending on the participants’ initial walking ability after undergoing gait rehabilitation training with RHE. Additionally, the study demonstrated the potential effectiveness of the GPE based muscle support algorithm. In the future, we plan to conduct feasibility study of robotic gait rehabilitation clinical trials by applying the GPE algorithm-based muscle support system to various exoskeleton robot platforms, including a lightweight RHE platform and a full-body exoskeleton robot platform.

Table 2 Participant’s information.
Full size table
Figure 5
figure 5

This is the experimental protocol for the 10MWT and 6MinWT. A total of seven days of gait training is conducted. On Day 1, primary and secondary endpoints are conducted. From Day 2, the pre-test is conducted, which included both unassisted gait rehabilitation training (No RHE) and robot-assisted gait rehabilitation training (RHE). From Days 3 to 6, gait rehabilitation training is performed exclusively using RHE. On Day 7, the post-test is conducted, including both unassisted gait rehabilitation training (No RHE) and robot-assisted gait rehabilitation training (RHE), along with assessments of primary and secondary endpoints. To prevent fall-related accidents during gait training, all participants wear a safety lift system while gait.

Full size image

Methods

Experimental methods

Participants

A total of 22 participants are recruited from two institutions and classified into two groups: the elderly group (n=12) and the brain lesion patient group (n=10). The brain lesion patient group in the study include individuals with various diagnoses; however, they are generally considered cases in which lower limb muscle weakness resulted from brain lesions. The study participants are screened based on the following criteria to ensure eligibility. Participants are screened according to the following criteria to determine eligibility for inclusion. The common inclusion criteria are as follows: (1) adults over 19 years old; (2) upper limb function grade \(\ge\) 4 according to the Medical Research Council (MRC) scale; (3) ability to walk independently: Functional Ambulation Category (FAC) scale 2–436; (4) gait impairment due to frailty, leading to difficulty in independent standing and walking; (5) hip flexion and extension strength graded 2–4 according to the MRC scale in both lower limbs37; (6) spasticity assessment indicating a Modified Ashworth Scale (MAS) score of 0–2 (no spasticity to mild spasticity) for hip flexion and extension movements in both lower limbs; (7) medically stable enough to undergo at least one hour of gait rehabilitation training per day; (8) ability to read and provide informed consent for participation in the study. Common exclusion criteria are as follows: (1) Body Mass Index (BMI) \(\ge\) 35 \(kg/m^2\); (2) physical characteristics incompatible with the assistive device used in the study; (3) presence of an implanted cardiac device, such as a pacemaker or automatic defibrillator37; (4) medically or neurologically unstable conditions; (5) inability to stand due to bilateral lower limb paralysis or spinal instability; (6) severe pain preventing independent walking.

A description of all participants is reported in Table 2. Group A has 12 subjects (4 men and 8 women), with an average age of 72.17 ± 6.15 years, an average height of 158.67 ± 10.97 cm, and an average weight of 59.67 kg ± 12.24 kg. Group B has 10 subjects (6 men and 4 women), with an average age of 63.6 ± 6.2 years, an average height of 161.89 ± 8.73 cm, and an average weight of 64.48 kg ± 12.63 kg.

The study was approved by the Institutional Review Board (IRB) of Chungnam National University Hospital (CNUH 2023-04-021-005) and Korea University Ansan Hospital (2023AS0185). All procedures involving human participants were conducted in accordance with the Declaration of Helsinki and relevant institutional guidelines and regulations. All participants provided voluntary informed consent, and it was explicitly explained that their decision not to participate would not affect their treatment or result in any disadvantages.

Protocol

The experimental protocol is illustrated in Fig. 5. The GPE-based muscle support algorithm is applied to RHE, and tests are carried out in elderly people or patients with brain lesions using the 10-meter walk test (10MWT) and the 6-minute walk test (6MinWT). Group A (the elderly group) was recruited from one institution, while Group B (the brain lesion patient group) was recruited from another. The walking pathway was secured as a straight-line space of 15 meters and 7.5 meters, respectively. For the safety of the participants, gait training is performed with the participants suspended in a lift system. The training sessions are divided into seven rounds. On Day 1, primary and secondary endpoints are conducted. On Day 2, the pre-test is conducted as follows: In the No RHE condition, participants perform two gait rehabilitation trainings in 10MWT, rest, and then one gait rehabilitation training in 6MinWT. Afterward, they have time to wear the robotic device and take a rest. In the robot-assisted gait rehabilitation training (RHE) condition, participants perform two gait rehabilitation trainings in 10MWT, rest, and then one gait rehabilitation training in 6MinWT. From Days 3 to 6, only robot-assisted gait rehabilitation training (RHE) is conducted. Participants perform two rounds of gait rehabilitation training in 10MWT and then take a break. In 6MinWT, gait rehabilitation training is performed 2 to 3 times depending on the participant’s condition, with a break in between. On Day 7, after the post-test, primary and secondary endpoints are assessed. The post-test follows the same process as the pre-test.

Figure 6
figure 6

(a) Robotic hip exoskeleton (RHE). The encoder sensor measures the user’s kinematics during walking. (b) The insole sensor was developed from Digitsole. The DSPod calculates the user’s foot kinematics in real-time. The original insole contained a brand logo, which has been removed for publication to avoid trademark issues. (c) The Photoplethysmogram (PPG) sensor measures the heart rate.

Full size image

Hardware platforms

Robotic hip exoskeleton (RHE)

The RHE used in the study provides assistance torque tailored to the user’s walking motion. The robot consists of a main controller, battery, two BLDC motors (EC45flat, Maxon, Switzerland), two motor controllers, and two encoders (as shown in Fig. 6a). The assistive torque can support up to a maximum of 12 Nm. The overall dimensions of the robot are \(485\times 330\times 500\) mm, and it weighs approximately 4.3 kg. When used in assistant mode, the operating time is more than 2 hours. The battery is a 24 VDC lithium-ion battery. The waist section can accommodate sizes up to 36 inches and is adjustable via a belt mechanism. The thigh part is reinforced with a plastic cover on the front and wraps around the thigh, secured with fastening components. The hip joint includes two passive degrees of freedom for adduction/abduction, allowing a range of motion from − 5 to 5 degrees. Additionally, it features two active degrees of freedom for extension/flexion, enabling a range of motion from − 25 to 100 degrees. The muscle support mode can be operated through the right switch button, and the user’s muscle support amount can be adjusted through the left switch button. The amount of muscle support is divided into a total of seven levels.

Insole sensor

To verify the effectiveness of robot performance, tools that verify walking performance, such as metabolic cost38, and electromyography (EMG), are generally required. The insole sensor (Digitsole Pro System, Digitsole, France) is a motion analysis solution developed for healthcare professionals, designed to analyze users’ gait and running patterns, thereby assisting in the evaluation and rehabilitation of musculoskeletal disorders and sports-related injuries (as shown in Fig. 6b). The insole device weighs approximately 71 g and is available in six different sizes. The integrated DSPod is an IMU-based sensor module that operates for up to 35 hours in active mode and requires approximately 2 hours and 30 minutes for a full charge. This sensor module is attached to the insole and is designed for easy detachment, allowing compatibility with various insole sizes.

In the study, insole sensors are used to collect linear gait indicators, specifically the spatio-temporal parameters of symmetry, cadence, and speed. Symmetry, which reflects the left-right balance during walking, is utilized as a measure for evaluating the effectiveness of rehabilitation. Cadence, based on walking rhythm and the number of steps per minute, is used to assess the degree of functional recovery. Speed, an indicator of overall gait efficiency, serves as a key criterion for verifying the effectiveness of robot-assisted rehabilitation training. The product was verified as a user-friendly gait analysis tool by comparing its performance with the Vicon system, a motion analysis system39.

Photoplethysmogram (PPG) sensor

The photoplethysmography (PPG) sensor (Polar OH1, Polar Electro Oy, Finland) is a healthcare device that utilizes light to record changes in the area where arteries pass (as shown in Fig. 6c). The principle of the PPG sensor is based on emitting LED light onto blood vessels. As blood flows, the expansion and contraction of the vessels cause variations in light reflectance. The reflected light is detected by a photodetector, and the resulting signal is analyzed to measure heart rate.

In the study, the device is connected to a PC via Bluetooth and is used for real-time monitoring. It can store up to 200 hours of training data and supports continuous operation for up to 12 hours on a single charge. The device is worn as an armband, enabling real-time collection and monitoring of heart rate data40. The user’s resting heart rate is first measured and set as the baseline heart rate. Subsequently, while wearing the robot, the user adjusts the level of assistive force in real-time during walking. The assistive level at the point when the user’s heart rate stabilized is determined and designated as the final assistive force setting41,42.

Figure 7
figure 7

The control block diagram overview of robotic hip exoskeleton (RHE). It is divided into five stages; low-pass filter (LPF), STOP and GO algorithm, gait phase estimation (GPE) algorithm, torque profile, and friction compensation.

Full size image

Assistance strategy for RHE

Block diagram of control system

The control block diagram of RHE is shown in Fig. 7 and it is divided into five stages as follows. The angle and angular velocity are collected through the encoder sensor in real-time. This is RAW data with noise, and the noise is removed through a low-pass filter (LPF) step. The noise-removed data distinguishes the start and end points of muscle support through the STOP and GO algorithm. The GPE algorithm operates at the start point of muscle support, and the gait cycle is predicted. In the torque profile stage, a torque profile of the hip joint is constructed based on the muscle support cycle and amplitude previously analyzed through gait analysis. The friction compensation stage is carried out simultaneously with the muscle support period, helping the thigh link to move smoothly. Finally, the reference current commanded from the high-level control drives the hip joint motor in conjunction with the feed-back current, which acts as a current controller to move the robotic hip exoskeleton.

Low-pass filter (LPF)

The angle and angular velocity data collected from encoders in real-time walking are RAW data collected through CAN communication, which contains noise and affects the calculations of the implemented algorithms. Additionally, the phase portrait represented based on angle and angular velocity data exhibits an elliptical shape, which impacts the results of the GPE algorithm. To address the issues, the noise in the angle and angular velocity data is reduced using the following Eq. (1).

$$\begin{aligned}&\tilde{x}_{t}=(1-\alpha )\cdot x_{t}+\alpha \cdot \tilde{x}_{t-1} \end{aligned}$$
(1)

where \(\tilde{x}_{t}\) represents the filtered value, \(\alpha\) is the coefficient of the LPF, \({x}_{t}\) is the RAW data, and \(\tilde{x}_{t-1}\) is the value before filtering.

STOP and GO algorithm

To distinguish the starting and ending points of muscle support, STOP and GO algorithm is needed at the beginning before starting walking. The angle and angular velocity of the encoder are used to determine the starting and ending points of muscle support. At the stage when muscle support begins, the gait cycle is predicted through the GPE algorithm, and the muscle support of the hip joint is assisted according to the cycle and amplitude of the torque profile established based on the GPE algorithm. At the point when muscle support ends, the support timing of friction compensation and GPE algorithm is turned off.

Algorithm 1
figure a

STOP and GO algorithm

Full size image

Gait phase estimation (GPE) algorithm

Heel strike corresponds to the 0% point in the gait cycle and is a crucial indicator of the start of walking. Identifying the starting point of walking facilitates the setup of robot control. From the perspective of gait kinematics, maximum hip flexion or extension is sometimes considered the initial gait event23,43,44. In the study, heel strike occurs at the point of maximum hip flexion, and at this moment, the gait cycle is set to 0% through the GPE algorithm stage. At the start of walking, the angle and angular velocity of the hip joint are collected through an encoder mounted on the sagittal plane of the hip joint. The RAW data appears as a distorted oval in the phase portrait. To solve the problem, a low-pass filter is used on the data to improve the ideal cosine and sine waveforms. It appears as a circle in the phase portrait. Using Eqs. (2)–(5) in the improved phase portrait, the gait cycle is predicted from zero to one (as shown in Fig. 8).

$$\begin{aligned}&k=\frac{\left| \dot{\tilde{\theta }}_{max}-\dot{\tilde{\theta }}_{min} \right| }{\left| \tilde{\theta }_{max}-\tilde{\theta }_{min} \right| },\end{aligned}$$
(2)
$$\begin{aligned}&\alpha =\frac{\left| \tilde{\theta }_{max}+\tilde{\theta }_{min} \right| }{2},\end{aligned}$$
(3)
$$\begin{aligned}&\beta =\frac{\left| \dot{\tilde{\theta }}_{max}+\dot{\tilde{\theta }}_{min} \right| }{2},\end{aligned}$$
(4)
$$\begin{aligned}&\phi =\frac{atan2(k(\tilde{\theta }-\alpha ), \dot{\tilde{\theta }}-\beta )}{2\pi } \end{aligned}$$
(5)

where \(\tilde{\theta }\), \(\dot{\tilde{\theta }}\) is the filtered angle and angular velocity of the hip joint motor, respectively. k is the scale coefficient of normalizing factor, \(\alpha\) is the median value of \(\tilde{\theta }\), \(\beta\) is the median value of \(\dot{\tilde{\theta }}\). \(\phi\) is a phase variable that can be calculated using the arc-tangent function that is bounded on [0, 1]. Constraints: \(\phi =\phi +1\,(if\,\phi <0)\).

Torque profile and friction compensation

As a result of analyzing the cycle of flexion/extension moment produced by the human hip joint when walking, based on the gait cycle, an extension moment occurs in 0 to 60% of the stance section, and a flexion moment occurs in the swing section 60–100%. The timing of torque assistance for supporting thigh muscle function was determined based on the gait cycle predicted by the GPE algorithm. Based on the previously predicted GPE algorithm, a torque profile is constructed with extension torque in the 20–60% and flexion torque in the 60–100%. The amplitude of the torque profile (\(\tau _{p}\)) is set so that it could be adjusted manually using a button because the strength of the muscle produced by the thighs varies from person to person. The assistive torque is divided into seven discrete levels based on the motor specifications. Each level corresponds to a predefined percentage of the maximum torque, arranged in descending order. For example, Level 4 delivered 70% and Level 1 delivered 30% of the maximum torque. The assistive level for each user is dynamically adjusted according to their physiological signals (PPG) and conditions such as fatigue or stress.

The structure of the motor transmits power through a mechanical system that is mechanically combined, such as a motor, harmonic gear, and shaft. Frictions in these mechanical systems are divided into static friction and viscous friction, and a friction compensation model is considered to overcome the effects of these frictions. In the study, the speed-current graph of the motor used in the robotic hip exoskeleton is collected, and unlike the existing friction compensation models such as Coulomb and viscosity, Stribeck, and LuGre friction compensation models, a curve-fitting model is derived and applied as a friction compensation model. The friction compensation value (\(\tau _{f}\)) is linked to the torque profile (\(\tau _{p}\)) and transmits the torque value (\(\tau _{r}\)) to the RHE, thereby supporting muscle strength to the user (as shown in Eq. (6)).

$$\begin{aligned} \tau _{r}=\tau _{p}+\tau _{f} \end{aligned}$$
(6)

where \(\tau _{r}\), \(\tau _{p}\), and \(\tau _{f}\) is torque value of RHE, the torque profile, and friction compensation value, respectively.

Figure 8
figure 8

The process for gait phase estimation (GPE) algorithm. The collected hip angle (\(\theta\)) and angular velocity (\(\dot{\theta }\)) are expressed as a phase variable (\(\phi\)), and the trajectory changes depending on whether LPF is applied (gray: before LPF application, orange: after LPF application). This is converted to a 0-1, expressing the gait cycle.

Full size image

Difference ratio (DR)

To compare the pre-test and post-test in unassisted gait rehabilitation training (No RHE) and robot-assisted gait rehabilitation training (RHE), the difference ratio (DR) is derived using the following Eq. (7).

$$\begin{aligned}&Difference\;ratio\,(\%)=\frac{V_{post}\,-\,V_{pre}}{V_{pre}}\,\times \,100 \end{aligned}$$
(7)

where \(\textit{V}_{pre}, \textit{V}_{post}\) represents the pre-test and post-test values, respectively. Difference ratio (DR) is expressed as the rate of increase or decrease by comparing post-test performance to pre-test performance. A positive sign indicates an increase, while a negative sign represents a decrease.

Statistical analysis

Target number of subjects

The sample size was determined based on previous RHE clinical study37 and using G*Power ver. 3.1.9.745. According to the results of a prior RHE study, when 14 participants underwent a 5-day training program, the primary outcome, the 6-minute walk test (6MinWT)46, showed a \(13\pm 6\%\) increase in walking distance. Based on this, the standard deviation for a pairwise t-test was calculated as 22.44, and the effect size was set at 0.62. Under a two-tailed null hypothesis, with a significance level (\(\alpha\)) of 0.05 and a statistical power (\(1-\beta\)) of 0.8, the calculated sample size was 23 participants. Based on this calculation, participants were recruited across two institutions to ensure the required sample size was met.

Clinical outcome data

Statistical analysis is conducted based on insole data collected from the same group, comparing the presence or absence of a robotic device and pre-test and post-test data. Since the data is assumed to follow a normal distribution, a paired t-test is performed. This test is used to calculate the mean difference between the two datasets and evaluate whether the difference is statistically significant. Furthermore, a one-tailed test examines whether one condition was greater or less.