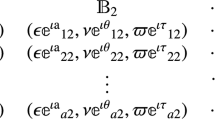Smart system for forecasting financial outcomes and supporting strategic choices

Abstract

In a period characterised by swift technological changes, choosing the most suitable strategic initiative presents a significant challenge for organisations aiming for long-term financial sustainability and competitive advantage. This research introduces a Smart Decision Support System that combines financial forecasting with a comprehensive multi-criteria decision-making (MCDM) framework to assess various strategic options in the face of uncertainty. The opinion weight criteria method (OWCM) is utilised to ascertain the relative significance of evaluation criteria through expert opinions, thereby minimising bias and ensuring equitable weight distribution. The complex picture fuzzy set (CPFS) framework effectively addresses uncertainty in expert judgements, providing superior modelling capabilities for hesitation and imprecision relative to traditional fuzzy environments. A novel ranking approach, termed mixed aggregation by comprehensive normalisation technique (MACONT), is developed to prioritise alternatives. This method integrates the strengths of both additive and multiplicative aggregation, facilitating a balanced and comprehensive assessment. The proposed framework includes a comprehensive sensitivity analysis to assess the influence of different criteria weights on the final rankings, thereby validating the stability and robustness of the results. The model is also evaluated against established MCDM methods such as ERUNS, AROMAN, and WASPAS to ensure consistency, reliability, and practical applicability. The findings indicate that the proposed approach reliably produces stable rankings in various scenarios, providing decision-makers with a robust and flexible tool for strategic planning in dynamic and uncertain contexts.

Introduction

The concept of financial resilience has gained considerable significance in a volatile and interconnected global econom¹. Financial resilience refers to the ability of an entity whether individual, organisational, or systemic to anticipate, prepare for, respond to, and recover from financial shocks while maintaining or improving its performance. In light of the prevailing economic uncertainty and financial risks across multiple sectors, enhancing financial resilience has become a vital objective for policymakers and practitioners. Recent research has emphasised the complex attributes of financial resilience, which include cognitive abilities, financial literacy, digital skills, and organisational agility². Mundi and Vashisht³ highlight the significant role of cognitive abilities in shaping individual financial resilience, particularly in emerging markets. The results demonstrate that individuals with higher cognitive abilities exhibit enhanced skills in processing financial information, making informed decisions, and adapting to economic challenges. Mishra et al.⁴ highlight the importance of digital financial literacy, especially for women, demonstrating that enhanced digital skills lead to improved financial decision-making and resilience.

Resilience at the organisational level is often associated with performance outcomes. Zahedi et al.⁵ present a comprehensive classification of the key factors affecting financial resilience, which encompasses risk management practices, capital adequacy, adaptive capacity, and leadership preparedness. The relationship between financial literacy and sustainable performance has received significant scholarly focus. Seraj et al.⁶ identify entrepreneurial resilience as a crucial mediator between financial knowledge and business sustainability. Research among Saudi entrepreneurs indicates that resilient entrepreneurs utilise financial literacy more effectively to navigate market uncertainties and sustain business performance over time. In supply chain management, resilience fulfils two roles. Tufan et al.⁷ examine the influence of agility and resilience in supply chains on financial performance, particularly in dynamic and crisis-prone environments. Their findings indicate that organisations that invest in flexible and responsive supply chain structures experience reduced vulnerability to disruptions, alongside improved profitability and competitiveness.

In the context of rapid technological change, financial institutions and enterprises face significant challenges in making informed strategic decisions amid uncertainty, complexity, and intense competition. Conventional decision-making methods, despite their merits, frequently encounter challenges in assimilating extensive heterogeneous data, addressing ambiguity in expert assessments, and maintaining transparency in the evaluation of various technological options. Recent studies have explored hybrid frameworks for multi-criteria decision-making in financial contexts to enhance decision quality and reduce uncertainty. For instance, Işık et al.⁸ proposed a hybrid framework for assessing the performance of Pakistani commercial banks, integrating multiple evaluation criteria to generate robust rankings and actionable insights. Their approach demonstrated the effectiveness of combining qualitative and quantitative factors in financial performance assessment. Similarly, Yüksel et al.⁹ developed an AI-driven hybrid fuzzy decision-making framework to support sustainable investment decisions in carbon capture technologies. Their work highlights how artificial intelligence can dynamically incorporate uncertainty and evolving criteria, improving decision reliability in complex, technology-driven financial scenarios. These studies collectively underscore the potential of hybrid MCDM and AI-based methods in addressing multi-dimensional financial decision-making problems, providing a foundation for extending such approaches in the current research. Hao and Yang¹⁰ proposed a multiple-output quantile regression neural network to improve prediction accuracy for complex datasets, enabling simultaneous estimation of multiple conditional quantiles. Consequently, there is an increasing need for intelligent, structured, and adaptive systems that can predict financial outcomes and assist in strategic decision-making with enhanced accuracy, robustness, and interpretability. Emerging technologies, including machine learning (ML), deep learning (DL), blockchain, and the internet of things (IoT), exhibit significant potential for improving financial forecasting and operational efficiency. The selection and prioritisation of these technologies for strategic implementation necessitate a systematic approach that considers various, often conflicting, evaluation criteria. Factors including forecast accuracy, data security and integrity, scalability, cost efficiency, and regulatory compliance significantly impact the strategic value of each technology. Implementing these trade-offs requires sophisticated multi-criteria decision-making techniques that can manage uncertainty and incorporate expert judgement.

This study proposes a smart evaluation framework that integrates the OWCM for assessing the relative importance of criteria, the MACONT for aggregating performance scores, and a CPFS environment to manage uncertainty in decision data. This study has the following primary objectives:

• To develop a comprehensive decision-support framework aimed at forecasting financial outcomes and facilitating strategic technology selections.

• To utilise the OWCM for assessing the relative significance of various evaluation criteria.

• To implement the MACONT for the robust aggregation of performance scores.

• Utilising a CPFS environment facilitates the modelling and management of uncertainty in expert evaluations.

• To assess a range of strategic technological options based on various pertinent decision criteria.

• To determine the optimal technological option for improving financial decision-making in uncertain conditions.

• The objective is to establish a replicable methodology for multi-criteria evaluation within the framework of emerging financial technologies.

• This study aims to illustrate the practical applicability of the model using a case study inspired by real-world scenarios.

Literature review

MCDM methods have developed alongside advancements in mathematics and computational technology. This section presents a critical analysis of key research contributions in fuzzy set theory and its applications, with a specific focus on CPFS.

Foundations of fuzzy set theory and MCDM

The fuzzy set theoretical framework, established by L.A. Zadeh¹¹, is fundamentally grounded in the notion of membership grades, which function as instruments for managing uncertainty. Atanasov¹² subsequently enhanced this Agency with IFSs, where the emphasised membership degree is paired with a non-membership degree. The various forms of representation enabled the effective use of IFS in multiple areas, such as pattern identification, managerial decision-making, and market trend forecasting.

Yu et al.¹⁴ investigated developmental mechanisms in IFS theory from a dynamic perspective. The research elucidated the evolution of IFS, thereby improving understanding of its use in various dynamic systems and decision-making scenarios. Distance measures play a crucial role in assessing Intuitionistic Fuzzy Sets (IFSs), particularly in the domains of pattern recognition and clustering. Sahu et al.¹⁵ utilised PiFS and rough set theory in the context of career selection decisions. This research highlights hybrid distance measures that improve the precision of modelling decision problems characterised by conflicting criteria. This research is pertinent to our study, as the combination of fuzzy logic and rough set methodologies improves the accuracy of identifying student preferences and mental health risk factors. Singh and Kumar¹⁶ introduced a multi-criteria group decision-making framework that integrates quality function deployment with Pythagorean fuzzy sets. This study presents a systematic method for managing group decision-making situations, facilitating the integration of varied perspectives and uncertainties into the ultimate decision. The use of PiFS in group decision-making corresponds with the methodology of this study, which aims to incorporate various expert perspectives in evaluating student mental health interventions.

The CPFS enhances classical fuzzy set theories to effectively manage elevated levels of uncertainty, hesitation, and contradiction in decision-making scenarios. This framework incorporates complex-valued membership, abstention, and non-membership degrees, making it suitable for real-world problems characterised by ambiguity and imprecision in information. Liu et al. citeliu2021 contributed significantly to this field by introducing power aggregation operators under CPFS, thereby improving the modelling of expert opinions in group decision-making. Mehmood and Liu¹⁸ introduced operators based on the Frank t-norm and t-conorm to enhance aggregation capabilities, addressing both optimistic and pessimistic decision-making attitudes. The practical significance of CPFS has been demonstrated across various domains. Tian et al.²⁰ introduced an adaptive tempered reversible jump algorithm for Bayesian curve fitting, improving convergence and flexibility in nonparametric regression models. Zhu et al.²² proposed novel distance measures within the CPFS framework, enhancing its utility for clustering and classification tasks, and highlighting its significance in soft computing for pattern recognition and medical diagnosis. Furthermore, CPFS has been integrated into artificial intelligence systems. Jan²³ conducted a mathematical analysis of generative adversarial networks using CPF soft information, showing that CPFS enhances the interpretability and robustness of AI models in uncertain data contexts. CPFS has evolved into a multifaceted instrument for multi-attribute decision-making, relevant in diverse fields such as healthcare, artificial intelligence, sustainability, and clustering. The continuous development of aggregation operators, distance measures, and hybrid models is expected to improve the ability to address uncertainty in complex systems.

A review of OWCM and MACONT approaches

The OWCM, as proposed by Mandil et al.²⁴, introduces a novel criteria weighting framework that addresses a persistent problem of logical inconsistency in MCDM. Unlike traditional methods pairwise comparison models, OWCM eliminates the need for reciprocal matrices or consistency ratios. OWCM employs direct expert opinions and aggregates them without iterative adjustments, ensuring consistency, reducing computational complexity, and enhancing practical applicability in real-world decision-making contexts. The OWCM approach has been widely implemented and adapted across various disciplines. Elsayed and Arain²⁵ developed an integrated framework within the healthcare sector that merges OWCM and CODAS through the application of triangular neutrosophic sets for the assessment and selection of healthcare waste treatment devices. This combination utilised the simplicity and consistency of OWCM, while the neutrosophic environment enhanced the management of ambiguous and uncertain data, commonly found in healthcare decision-making processes. The research by Mohamed²⁶ illustrates an innovative application of OWCM, employing it within a trapezoidal soft set-based OWCM-RAM framework. This study analysed public perceptions of integrating the Metaverse to improve traffic safety. OWCM played a crucial role in processing opinion-based criteria in a complex, soft information environment, demonstrating its adaptability and effectiveness in advanced computational settings. Karamoozian et al. have contributed significantly to multi-criteria and uncertainty-based decision-making in engineering and construction domains. The study applied a probability-based Pareto-optimal approach to evaluate braking systems²⁷. They also explored risk assessment of occupational safety in construction projects under uncertain information²⁸. A hybrid DEMATEL-ANP and LCA model has been utilized for selecting optimal pipe materials in hydrocarbon pipeline projects, demonstrating the integration of multi-criteria analysis with sustainability considerations²⁹. Xiong et al.³⁰ explored learning economic model predictive control using clustering and kernel-based Lipschitz regression, enhancing real-time control in dynamic economic systems. Additionally, a novel fuzzy decision-making approach was proposed for green supplier selection in construction, emphasizing environmental and operational priorities³¹. These works highlight the applicability of hybrid MCDM and fuzzy-based approaches for robust decision-making in complex and uncertain environments.

Smarandache et al.³² expanded the method’s application in cybersecurity by integrating OWCM with a Tree Soft Set approach to evaluate blockchain security under uncertain conditions. Their study showed that OWCM can adjust to hierarchical and structurally complex MCDM environments while remaining robust against vague or partially known data, highlighting its suitability for uncertainty modelling paradigms. Jing et al.³³ proposed a patent text-based product conceptual design decision-making approach, fusing incomplete evaluation semantics and scheme beliefs to support innovative design decisions. Sun et al.³⁴ investigated habitual decision-making and strategies to change entrenched user behavior, providing insights for decision support systems targeting behavioral interventions. Delice et al.³⁵ provided a basis for further advancements like OWCM by clarifying the challenges inherent in decision-making amid vagueness and linguistic uncertainty. Their hybrid approach utilising MC-HFLTS in conjunction with MAIRCA and MABAC methods for waste container site selection demonstrates an increasing demand for efficient criteria weighting models like OWCM. The initial efforts demonstrated the need for effective tools that can integrate complexity, expert involvement, and model transparency. The OWCM method has evolved from a theoretically sound weighting approach to a flexible decision-support tool suitable for diverse applications. The integration of CODAS, RAM, Tree Soft Sets, and neutrosophic theories has proven effective, with applications in healthcare, intelligent transportation systems, cybersecurity, and waste management. OWCM demonstrates consistent advantages, including the absence of inconsistency, reduced cognitive load, and compatibility with fuzzy, soft, and neutrosophic logic frameworks, thus improving the MCDM landscape.

A new category of methods has developed regarding aggregation and final ranking, distinguished by thorough normalisation and multi-faceted assessment. Lu and Wu³⁶ revisited intelligent auditing from a data science perspective, emphasizing the use of AI and machine learning techniques to enhance audit quality and efficiency. Ayan and Abacıoğlu³⁷ performed a bibliometric analysis revealing a rising trend in the application of methods including WASPAS, MABAC, EDAS, CoCoSo, and MACONT in modern decision science, especially within industrial and service sectors. Their findings indicate that MACONT is a developing methodology that provides strong, scalable, and flexible evaluation in MCDM. Yang et al.³⁸ developed an integrated consensus-reaching process for product appearance design, combining trust and empathy relationships to improve collaborative design decisions. Dhumras and Bajaj³⁹ presented a modified EDAS model that employs picture fuzzy soft Dombi operators to mitigate imprecision in robotic agrifarming, highlighting the significance of flexible aggregation operators in practical applications. Shakeel et al.⁴⁰ introduced a multi-stage decision support system that employs the innovative intuitionistic fuzzy CIMAS-AROMAN method for the assessment of visual energy platforms in the UK. Xiang et al.⁴¹ proposed a linear programming-based fuzzy AROMAN method for assessing the development of the digital economy in provincial regions. This study introduces a comprehensive decision-making framework for multi-criteria evaluation that employs fuzzy logic and optimisation methodologies.

Biswas et al.⁴² presented the ERUNS method for ranking firms in the energy sector, showing that nonlinear standardisation enhances accuracy and relevance in comparative performance assessments. This facilitates the role of MACONT in overseeing complex assessments where traditional linear aggregation methods may misrepresent the underlying data structure. Wieckowski et al.⁴³ presented an adaptive electric vehicle selection model that employs RANCOM and ESP-SPOTIS, highlighting an increasing reliance on adaptive and modular aggregation models for sustainable transportation decision-making. Research demonstrates a clear advancement in MCDM towards hybrid, intelligent, and adaptable models. The authors propose integrating AI-driven expert modelling, LOPCOW-based objective weighting, and MACONT-based ranking to create a decision support system characterised by transparency, efficiency, and applicability to various real-world challenges.

Research gap

The process of selecting strategic technology investments, especially in emerging fields like machine learning, blockchain, and deep learning, encounters various limitations in the current literature.

• Although financial forecasting models and MCDM techniques have been extensively utilised separately, there is a scarcity of research that combines AI-based forecasting with systematic multi-criteria evaluation to establish a comprehensive decision-making framework for strategic investments.

• Current literature frequently utilises classical fuzzy sets, intuitionistic fuzzy sets, or Pythagorean fuzzy sets. These approaches exhibit limited capacity to effectively capture multi-dimensional uncertainty and hesitancy in expert opinions, particularly in contexts where multiple components of truth, falsity, and indeterminacy coexist. CPFS provide enhanced information representation; however, their application in strategic investment contexts remains largely unexamined.

• Numerous studies rely exclusively on subjective weighting or solely on objective weighting. A scarcity of methods exists that systematically integrate expert consensus while minimising bias, exemplified by the OWCM, which has been applied minimally in high-uncertainty strategic decision contexts.

• Traditional additive or multiplicative aggregation models are frequently employed independently, which may distort outcomes when conflicting criteria are present. The MACONT, which integrates both additive and multiplicative components, has not been addressed in previous research within the strategic technology selection field.

• Limited research rigorously examines the stability of rankings across different weight variations and normalisation methods, thereby reducing confidence in the decision outcomes. To emphasize the theoretical contribution of the proposed decision support system, Table 1 compares it with existing MCDM methods and its individual components.

Table 1 Comparative overview of existing MCDM methods and the proposed decision support system .

Motivation

Organisations today face significant opportunities and challenges in selecting strategic technological investments amid ongoing digital transformation. Technologies including machine learning, blockchain, deep learning, and hybrid AI systems possess the capacity to transform business processes, improve decision-making abilities, and ensure long-term financial sustainability. The swift advancement of these technologies, along with market volatility, regulatory challenges, and environmental issues, renders strategic selection a complex and critical endeavour. Conventional decision-making methods frequently do not adequately account for this complexity due to three primary factors:

• The absence of integration between forward-looking financial forecasting and systematic multi-criteria evaluation results in decisions that rely solely on historical performance or qualitative perceptions.

• Limited uncertainty modelling techniques are employed, which fail to adequately represent the varied opinions and hesitancy of multiple stakeholders in high-impact strategic investments.

• Their approach depends on either entirely subjective or entirely objective weighting, neglecting the importance of a balanced method that integrates expert consensus and reduces bias.

Considering these limitations, there is a significant requirement for an intelligent, uncertainty-aware decision-support framework that integrates:

• Utilisation of AI in financial forecasting to predict the long-term effects of investment decisions.

• Advanced fuzzy modelling, particularly CPFS, is utilised to represent multi-dimensional uncertainty in expert opinions.

• OWCM for hybrid objective and subjective weighting.

• MACONT facilitates balanced and robust aggregation of various evaluation criteria.

This paper addresses the need for a methodologically robust and practically applicable decision-making framework that assists organisations in selecting optimal technological strategies amidst uncertainty, thereby ensuring competitive advantage and sustainable financial growth.

Contributions of the study

This study presents the following key contributions:

• An integrated framework is proposed that combines the OWCM for establishing balanced criterion weights with the MACONT for robust ranking of alternatives in the presence of uncertainty.

• This represents an early application of CPFS in the realm of strategic technology selection for forecasting financial outcomes. CPFS facilitates the representation of expert evaluations with increased dimensionality, encompassing positive, neutral, and negative membership degrees alongside their corresponding phase terms.

• The proposed method assesses eight advanced technological alternatives, including machine learning, blockchain, deep learning, hybrid AI systems, and other emerging solutions, based on ten clearly defined criteria that include financial, operational, security, scalability, and sustainability factors.

• This study integrates AI-driven financial forecasting into the decision-making process, contrasting with existing works that focus solely on qualitative or historical assessment. It enables organisations to evaluate both short-term and long-term impacts of their strategic choices.

• The framework is validated via a case study inspired by real-world scenarios, showcasing its applicability, robustness, and capacity to manage uncertainty in multi-stakeholder contexts.

• The findings provide practical guidance for managers, policymakers, and technology strategists to facilitate informed, transparent, and sustainable decisions regarding technology adoption and investment planning.

Structure of the paper

This paper is structured as follows. Section 2 outlines the essential concepts and mathematical framework of CPFS, emphasising their appropriateness for addressing multi-dimensional uncertainty in decision-making contexts. Section 3 outlines the proposed decision-support algorithm, which incorporates the OWCM for weight determination and the MACONT for ranking alternatives in the context of uncertainty. Section 4 presents a case study that evaluates eight strategic technological alternatives based on ten decision criteria, illustrating the applicability of the proposed framework. Section 5 presents the results and discussion, encompassing sensitivity analysis, comparative validation, and managerial implications. Section 6 concludes the paper by summarising the key findings and outlining future research directions.

Complex picture fuzzy sets

Definition 2.1

A CPFS $\mathfrak {S}$ on a universe Y is expressed in the form:

$$P=\left\langle \left( {\mathbbm {A}}, \varrho ({\mathbbm {A}}) \textrm{e}^{\iota \beth ({\mathbbm {A}})}, \xi ({\mathbbm {A}}) \textrm{e}^{\iota \Omega ({\mathbbm {A}})}, \vartheta ({\mathbbm {A}}) \textrm{e}^{\iota \Phi ({\mathbbm {A}})}\right) \mid {\mathbbm {A}} \in Y\right\rangle$$

where $\iota =\sqrt{-1}, \varrho ({\mathbbm {A}}), \xi ({\mathbbm {A}}), \vartheta ({\mathbbm {A}}) \in [0,1]$ are amplitude terms and $\beth ({\mathbbm {A}}), \Omega ({\mathbbm {A}}), \Phi ({\mathbbm {A}})$ $\in [0,2 \pi ]$ are the phase terms of membership, neutral membership, and non-membership degrees, respectively, which are restricted by the conditions $\varrho ({\mathbbm {A}})+\xi ({\mathbbm {A}})+\vartheta ({\mathbbm {A}}) \le 1$ and $\beth ({\mathbbm {A}})+\Omega ({\mathbbm {A}})+\Phi ({\mathbbm {A}}) \le 2 \pi$, for all ${\mathbbm {A}} \in Y$. The degree of rejection of ${\mathbbm {A}}$ in $\mathfrak {S}$ is given as follows:

$$\pi ({\mathbbm {A}})=\left( 1-\varrho ({\mathbbm {A}})-{\xi }({\mathbbm {A}})-\vartheta ({\mathbbm {A}})\right) \textrm{e}^{\iota \left( 2 \pi -\beth ({\mathbbm {A}})-\Omega ({\mathbbm {A}})-\Phi ({\mathbbm {A}})\right) },$$

for all ${\mathbbm {A}} \in Y$.

Definition 2.2

This paper presents an interpretation of the complement, inclusion, intersection, and union operations for any two CPFSs within a universe Y.

$$\begin{aligned} {\mathbb {F}}_{1} \cap {\mathbb {F}}_{2} = \Bigg \langle \Bigg ( {\mathbbm {A}},&\min \left( \varrho _{{1}}({\mathbbm {A}}), \varrho _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \min \left( \beth _{{1}}({\mathbbm {A}}), \beth _{{2}}({\mathbbm {A}})\right) }, \\&\max \left( \xi _{{1}}({\mathbbm {A}}), \xi _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \max \left( \Omega _{{1}}({\mathbbm {A}}), \Omega _{{2}}({\mathbbm {A}})\right) }, \\&\max \left( \vartheta _{{1}}({\mathbbm {A}}), \vartheta _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \max \left( \Phi _{{1}}({\mathbbm {A}}), \Phi _{{2}}({\mathbbm {A}})\right) } \Bigg ) \,\Bigg |\, {\mathbbm {A}} \in Y \Bigg \rangle \end{aligned}$$

$$\begin{aligned} {\mathbb {F}}_{1} \cup {\mathbb {F}}_{2} = \Bigg \langle \Bigg ( {\mathbbm {A}},&\max \left( \varrho _{{1}}({\mathbbm {A}}), \varrho _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \max \left( \beth _{{1}}({\mathbbm {A}}), \beth _{{2}}({\mathbbm {A}})\right) }, \\&\min \left( \xi _{{1}}({\mathbbm {A}}), \xi _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \min \left( \Omega _{{1}}({\mathbbm {A}}), \Omega _{{2}}({\mathbbm {A}})\right) }, \\&\min \left( \vartheta _{{1}}({\mathbbm {A}}), \vartheta _{{2}}({\mathbbm {A}})\right) \textrm{e}^{\iota \min \left( \Phi _{{1}}({\mathbbm {A}}), \Phi _{{2}}({\mathbbm {A}})\right) } \Bigg ) \,\Bigg |\, {\mathbbm {A}} \in Y \Bigg \rangle \end{aligned}$$

$$\begin{aligned} \begin{aligned} {\mathbb {F}}_{1} \subseteq {\mathbb {F}}_{2} \quad \text {if and only if} \quad&\varrho _{{1}}({\mathbbm {A}}) \le \varrho _{{2}}({\mathbbm {A}}), \quad \xi _{{1}}({\mathbbm {A}}) \le \xi _{{2}}({\mathbbm {A}}), \quad \vartheta _{{1}}({\mathbbm {A}}) \ge \vartheta _{{2}}({\mathbbm {A}}), \\&\beth _{{1}}({\mathbbm {A}}) \le \beth _{{2}}({\mathbbm {A}}), \quad \Omega _{{1}}({\mathbbm {A}}) \le \Omega _{{2}}({\mathbbm {A}}), \quad \Phi _{{1}}({\mathbbm {A}}) \ge \Phi _{{2}}({\mathbbm {A}}), \quad \forall {\mathbbm {A}} \in Y. \end{aligned} \end{aligned}$$

$$\begin{aligned} \bar{\mathbb {F}} = \left\langle \left( {\mathbbm {A}}, \vartheta ({\mathbbm {A}}) \, \textrm{e}^{\iota \Phi ({\mathbbm {A}})},\ \xi ({\mathbbm {A}}) \, \textrm{e}^{\iota \Omega ({\mathbbm {A}})},\ \varrho ({\mathbbm {A}}) \, \textrm{e}^{\iota \beth ({\mathbbm {A}})} \right) \;\Big |\; {\mathbbm {A}} \in Y \right\rangle \end{aligned}$$

Definition 2.3

For a complex picture fuzzy number (CPFN), the score function $\mathbb {S}(\mathrm (G))$ is defined as follows:

$$P = \left( \varrho \textrm{e}^{\iota \beth },\ \xi \textrm{e}^{\iota \Omega },\ \vartheta \textrm{e}^{\iota \Phi } \right) ,$$

is defined by the following equation:

$$\begin{aligned} \mathbb {S}(\mathrm (G)) = (\varrho - \xi - \vartheta ) + \frac{1}{2\pi } (\beth - \Omega - \Phi ), \end{aligned}$$

(1)

The value of $\mathbb {S}(\textrm{G})$ lies within the interval $[-2, 2]$. This function is utilised to compare and rank different CPFNs.

Definition 2.4

The accuracy function H for a CPFN, defined as

$$P = \left( \varrho \textrm{e}^{\iota \beth },\ \xi \textrm{e}^{\iota \Omega },\ \vartheta \textrm{e}^{\iota \Phi } \right) ,$$

is given by:

$$\begin{aligned} \mathbb {H}(\mathrm (S)) = (\varrho + \xi + \vartheta ) + \frac{1}{2\pi } (\beth + \Omega + \Phi ), \end{aligned}$$

(2)

The output of $\mathbb {H}(\textrm{S})$ is contained within the interval [0, 2]. This function enhances the score function by offering further insight when two CPFNs produce the same scores.

Ranking Rule: Let ${\mathbb {G}}_1$ and ${\mathbb {G}}_2$ be two CPFNs. The sequence among them is established in this order:

• If $\mathbb {S}({\mathbb {G}}_1) > \mathbb {S}({\mathbb {G}}_2)$, then ${\mathbb {G}}_1$ is ranked higher than ${\mathbb {G}}_2$.

• If $\mathbb {S}({\mathbb {G}}_1) < \mathbb {S}({\mathbb {G}}_2)$, then ${\mathbb {G}}_1$ is ranked lower than ${\mathbb {G}}_2$.

• If $\mathbb {S}({\mathbb {G}}_1) = \mathbb {S}({\mathbb {G}}_2)$:

  • If $\mathbb {H}({\mathbb {G}}_1) > \mathbb {H}({\mathbb {G}}_2)$, then ${\mathbb {G}}_1$ is preferred over ${\mathbb {G}}_2$.

  • If $\mathbb {H}({\mathbb {G}}_1) < \mathbb {H}({\mathbb {G}}_2)$, then ${\mathbb {G}}_2$ is preferred over ${\mathbb {G}}_1$.

  • If $\mathbb {H}({\mathbb {G}}_1) = \mathbb {H}({\mathbb {G}}_2)$, then both CPFNs are considered equivalent.

Definition 2.5

Let ${\mathbb {F}}_{1} = \left( \varrho _{{1}} \textrm{e}^{\iota \beth _{{1}}},\ \xi _{{1}} \textrm{e}^{\iota \Omega _{{1}}},\ \vartheta _{{1}} \textrm{e}^{\iota \Phi _{{1}}}\right)$ and ${\mathbb {F}}_{2} = \left( \varrho _{{2}} \textrm{e}^{\iota \beth _{{2}}},\ \xi _{{2}} \textrm{e}^{\iota \Omega _{{2}}},\ \vartheta _{{2}} \textrm{e}^{\iota \Phi _{{2}}}\right)$ be two CPFNs. Then, their score and accuracy functions are defined respectively as:

$$\begin{aligned} \begin{aligned} \mathbb {S}({\mathbb {G}}_1)&= (\varrho _{1} - \xi _{1} - \vartheta _{1}) + \frac{1}{2\pi }(\beth _{1} - \Omega _{1} - \Phi _{1}), \\ \mathbb {S}({\mathbb {G}}_2)&= (\varrho _{2} - \xi _{2} - \vartheta _{2}) + \frac{1}{2\pi }(\beth _{2} - \Omega _{2} - \Phi _{2}), \\ \mathbb {H}({\mathbb {F}}_1)&= (\varrho _{1} + \xi _{1} + \vartheta _{1}) + \frac{1}{2\pi }(\beth _{1} + \Omega _{1} + \Phi _{1}), \\ \mathbb {H}({\mathbb {F}}_2)&= (\varrho _{2} + \xi _{2} + \vartheta _{2}) + \frac{1}{2\pi }(\beth _{2} + \Omega _{2} + \Phi _{2}). \end{aligned} \end{aligned}$$

To compare the two CPFNs, we apply the following criteria:

• If $\mathbb {S}({\mathbb {G}}_1) < \mathbb {S}({\mathbb {G}}_2)$, then ${\mathbb {G}}_1$ is ranked lower than ${\mathbb {G}}_2$.

• If $\mathbb {S}({\mathbb {G}}_1) > \mathbb {S}({\mathbb {G}}_2)$, then ${\mathbb {G}}_1$ is ranked higher than ${\mathbb {G}}_2$.

• If $\mathbb {S}({\mathbb {G}}_1) = \mathbb {S}({\mathbb {G}}_2)$, the comparison is based on the accuracy function:

  • If $\mathbb {H}({\mathbb {F}}_1) < \mathbb {H}({\mathbb {F}}_2)$, then ${\mathbb {G}}_1$ is less informative than ${\mathbb {G}}_2$.

  • If $\mathbb {H}({\mathbb {F}}_1) > \mathbb {H}({\mathbb {F}}_2)$, then ${\mathbb {G}}_1$ is more informative than ${\mathbb {G}}_2$.

  • If $\mathbb {H}({\mathbb {F}}_1) = \mathbb {H}({\mathbb {F}}_2)$, then ${\mathbb {G}}_1$ and ${\mathbb {G}}_2$ are considered equivalent.

Definition 2.6

Let ${\mathbb {F}}_{1} = \left( \varrho _{{1}} \textrm{e}^{\iota \beth _{{1}}}, \xi _{{1}} \textrm{e}^{\iota \gamma {\mathbb {F}}_{1}}, \vartheta _{{1}} \textrm{e}^{\iota \Phi _{{1}}} \right)$ and ${\mathbb {F}}_{2} = \left( \varrho _{{2}} \textrm{e}^{\iota \beth _{{2}}}, \xi _{{2}} \textrm{e}^{\iota \gamma {\mathbb {F}}_{2}}, \vartheta _{{2}} \textrm{e}^{\iota \Phi _{{2}}} \right)$ be two CPFNs. Then:

$$\begin{aligned} { \begin{aligned} {\mathbb {F}}_{1} \otimes {\mathbb {F}}_{2}&= \left\langle \varrho _{{1}} \textrm{e}^{\iota \beth _{{1}}} \cdot \varrho _{{2}} \textrm{e}^{\iota \beth _{{2}}}, \right. \\&\quad \left( \xi _{{1}} + \xi _{{2}} - \xi _{{1}} \xi _{{2}} \right) \textrm{e}^{\iota 2 \pi \left( \frac{\Omega _{{1}}}{2 \pi } + \frac{\Omega _{{2}}}{2 \pi } - \frac{\Omega _{{1}}}{2 \pi } \frac{\Omega _{{2}}}{2 \pi } \right) }, \\&\quad \left( \vartheta _{{1}} + \vartheta _{{2}} - \vartheta _{{1}} \vartheta _{{2}} \right) \textrm{e}^{\iota 2 \pi \left( \frac{\Phi _{{1}}}{2 \pi } + \frac{\Phi _{{2}}}{2 \pi } - \frac{\Phi _{{1}}}{2 \pi } \frac{\Phi _{{2}}}{2 \pi } \right) } \Bigg \rangle \end{aligned} } \end{aligned}$$

(3)

where

$$\begin{aligned} \varrho _{{1}} \textrm{e}^{\iota \beth _{{1}}} \cdot \varrho _{{2}} \textrm{e}^{\iota \beth _{{2}}} = \varrho _{{1}} \cdot \varrho _{{2}} \textrm{e}^{\iota 2 \pi \left( \frac{\alpha {\mathbb {F}}_{1}}{2 \pi } \cdot \frac{\alpha }{2 \pi } \right) }. \end{aligned}$$

(4)

Similar expressions hold for $\xi _{{1}} \textrm{e}^{\iota \gamma {\mathbb {F}}_{1}} \cdot \xi _{{2}} \textrm{e}^{\iota \gamma {\mathbb {F}}_{2}}$ and $\vartheta _{{1}} \textrm{e}^{\iota \Phi _{{1}}} \cdot \vartheta _{{2}} \textrm{e}^{\iota \Phi _{{2}}}$.

$$\begin{aligned} \bar{\mathbb {F}}_{1} = \left\langle \left( {\mathbbm {A}}, \vartheta _{{1}}({\mathbbm {A}}) \textrm{e}^{\iota \Phi _{{1}}({\mathbbm {A}})}, \xi _{{1}}({\mathbbm {A}}) \textrm{e}^{\iota \gamma {\mathbb {F}}_{1}({\mathbbm {A}})}, \varrho _{{1}}({\mathbbm {A}}) \textrm{e}^{\iota \beth _{{1}}({\mathbbm {A}})} \right) \mid {\mathbbm {A}} \in Y \right\rangle . \end{aligned}$$

(5)

$$\begin{aligned} \begin{aligned} {\mathbb {F}}_{1} \vee {\mathbb {F}}_{2} =&\langle \left( {\mathbbm {A}}, \max \left( \varrho _{{1}}({\mathbbm {A}}), \varrho _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \max \left( \beth _{{1}}({\mathbbm {A}}), \beth _{{2}}({\mathbbm {A}}) \right) } \right. \\&\quad \min \left( \xi _{{1}}({\mathbbm {A}}), \xi _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \min \left( \Omega _{{1}}({\mathbbm {A}}), \Omega _{{2}}({\mathbbm {A}}) \right) }, \\&\quad \left. \min \left( \vartheta _{{1}}({\mathbbm {A}}), \vartheta _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \min \left( \Phi _{{1}}({\mathbbm {A}}), \Phi _{{2}}({\mathbbm {A}}) \right) } \right) \\&\mid {\mathbbm {A}} \in Y \rangle \end{aligned} \end{aligned}$$

(6)

$$\begin{aligned} \begin{aligned} {\mathbb {F}}_{1} \wedge {\mathbb {F}}_{2} =&\left\langle \left( {\mathbbm {A}}, \min \left( \varrho _{{1}}({\mathbbm {A}}), \varrho _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \min \left( \beth _{{1}}({\mathbbm {A}}), \beth _{{2}}({\mathbbm {A}}) \right) } \right) , \right. \\&\quad \max \left( \xi _{{1}}({\mathbbm {A}}), \xi _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \max \left( \Omega _{{1}}({\mathbbm {A}}), \Omega _{{2}}({\mathbbm {A}}) \right) }, \\&\quad \max \left( \vartheta _{{1}}({\mathbbm {A}}), \vartheta _{{2}}({\mathbbm {A}}) \right) \textrm{e}^{\iota \max \left( \Phi _{{1}}({\mathbbm {A}}), \Phi _{{2}}({\mathbbm {A}}) \right) } ) \\&\quad \mid {\mathbbm {A}} \in Y \rangle \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned} {\mathbbm {A}} {\mathbb {F}}_{1} = \left\langle \left( 1 - \left( 1 - \varrho _{{1}} \right) ^{{\mathbbm {A}}} \right) \textrm{e}^{\iota 2 \pi \left( 1 - \left( 1 - \frac{\alpha {\mathbb {F}}_{1}}{2 \pi } \right) ^{{\mathbbm {A}}} \right) }, \xi _{{1}}^{{\mathbbm {A}}} \textrm{e}^{\iota 2 \pi \left( \frac{\gamma {\mathbb {F}}_{1}}{2 \pi } \right) ^{{\mathbbm {A}}}}, \vartheta _{{1}}^{{\mathbbm {A}}} \textrm{e}^{\iota 2 \pi \left( \frac{{1}}{2 \pi } \right) ^{{\mathbbm {A}}}} \right\rangle , \quad {\mathbbm {A}} > 0. \end{aligned}$$

(8)

$$\begin{aligned} {\mathbb {F}}_{1}^{{\mathbbm {A}}} = \left\langle \varrho _{{1}}^{{\mathbbm {A}}} \textrm{e}^{\iota 2 \pi \left( \frac{\alpha }{2 \pi } \right) ^{{\mathbbm {A}}}}, \left( 1 - \left( 1 - \xi _{{1}} \right) ^{{\mathbbm {A}}} \right) \textrm{e}^{\iota 2 \pi \left( 1 - \left( 1 - \frac{\gamma {\mathbb {F}}_{1}}{2 \pi } \right) ^{{\mathbbm {A}}} \right) }, \left( 1 - \left( 1 - \vartheta _{{1}} \right) ^{{\mathbbm {A}}} \right) \textrm{e}^{\iota 2 \pi \left( 1 - \left( 1 - \frac{\beta {\mathbb {F}}_{1}}{2 \pi } \right) ^{{\mathbbm {A}}} \right) } \right\rangle , \quad {\mathbbm {A}} > 0. \end{aligned}$$

(9)

$$\begin{aligned} {\mathbb {F}}_{1} \oplus {\mathbb {F}}_{2} = \left\langle \left( \varrho _{{1}} + \varrho _{{2}} - \varrho _{{1}} \varrho _{{2}} \right) \textrm{e}^{\iota 2 \pi \left( \frac{\alpha {\mathbb {F}}_{1}}{2 \pi } + \frac{\beth _{{2}}}{2 \pi } - \frac{\beth _{{1}}}{2 \pi } \frac{\beth _{{2}}}{2 \pi } \right) }, \xi _{{1}} \textrm{e}^{\iota \gamma {\mathbb {F}}_{1}} \cdot \xi _{{2}} \textrm{e}^{\iota \Omega _{{2}}}, \vartheta _{{1}} \textrm{e}^{\iota \Phi _{{1}}} \right\rangle . \end{aligned}$$

(10)

Theorem 2.1

Let ${\mathbb {F}}_{1}=\left( \varrho _{{1}} \textrm{e}^{\iota \beth _{{1}}}, \xi _{{1}} \textrm{e}^{\iota \Omega _{{1}}}, \vartheta _{{1}} \textrm{e}^{\iota \Phi _{{1}}}\right)$ and ${\mathbb {F}}_{2}=\left( \varrho _{{2}} \textrm{e}^{\iota \beth _{{2}}}, \xi _{{2}} \textrm{e}^{\iota \Omega _{{2}}}, \vartheta _{{2}} \textrm{e}^{\iota \Phi _{{2}}}\right)$ be two CPFNs, $0 \le {\mathbbm {A}}, {\mathbbm {A}}_{1}, {\mathbbm {A}}_{2} \le 1$. Then the following hold:

• $\left( {\mathbb {F}}_{1}^{{\mathbbm {A}}_{1}}\right) ^{{\mathbbm {A}}_{2}} = {\mathbb {F}}_{1}^{{\mathbbm {A}}_{1} {\mathbbm {A}}_{2}}$.

• ${\mathbbm {A}}\left( {\mathbb {F}}_{1} \oplus {\mathbb {F}}_{2}\right) = {\mathbbm {A}} {\mathbb {F}}_{1} \oplus {\mathbbm {A}} {\mathbb {F}}_{2}$.

• ${\mathbbm {A}}_{1} {\mathbb {F}}_{1} \oplus {\mathbbm {A}}_{2} {\mathbb {F}}_{1} = \left( {\mathbbm {A}}_{1} + {\mathbbm {A}}_{2}\right) {\mathbb {F}}_{1}$.

• $\left( {\mathbb {F}}_{1} \otimes {\mathbb {F}}_{2}\right) ^{{\mathbbm {A}}} = {\mathbb {F}}_{1}^{{\mathbbm {A}}} \otimes {\mathbb {F}}_{2}^{{\mathbbm {A}}}$.

• ${\mathbb {F}}_{1}^{{\mathbbm {A}}_{1}} \otimes {\mathbb {F}}_{1}^{{\mathbbm {A}}_{2}} = {\mathbb {F}}_{1}^{{\mathbbm {A}}_{1} + {\mathbbm {A}}_{2}}$.

Comparison of CPFS with other fuzzy extensions

CPFS represent an advanced extension of classical fuzzy models by incorporating complex-valued membership degrees. While traditional fuzzy frameworks such as Intuitionistic Fuzzy Sets (IFS), Pythagorean Fuzzy Sets (PyFS), Fermatean Fuzzy Sets (FFS), and Picture Fuzzy Sets (PFS) have significantly contributed to uncertainty modelling, CPFS enhances this ability by adding a phase term to each component, thus capturing both magnitude and direction of expert hesitation (Table 2).

Table 2 Comparison of different fuzzy set extensions.

Advantages of CPFS:

• CPFS represents each membership component as a complex number, enabling richer representation of ambiguity through both amplitude and phase.

• The complex plane allows experts to express varying degrees and directions of hesitation more precisely than real-valued sets.

• CPFS becomes a special case of Picture or Fermatean fuzzy sets when the phase component equals zero, demonstrating its generality.

• The inclusion of phase information provides finer discrimination between alternatives that appear similar under simpler fuzzy models.

• In multi-criteria decision-making, CPFS ensures more stable and differentiated ranking outcomes.

Disadvantages of CPFS:

• Complex-valued operations require higher computational resources compared with PFS or FFS.

• Interpretation difficulty: The phase component may not be easily interpretable by practitioners unfamiliar with complex mathematics.

• Assigning meaningful phase angles can introduce additional subjectivity into expert evaluation.

Developing a decision support system using OWCM and MACONT under CPFs environment

In the proposed decision support framework, a collection of alternatives, represented by ${{M^{\kappa }}_i}$ $(i = 1, 2, \ldots , a)$, is evaluated against b essential criteria, denoted as ${\mathbb {C}_j}$ $(j = 1, 2, \ldots , b)$. The evaluations are performed by a set of f domain experts, denoted as ${\mathcal {E}_k}$ $(k = 1, 2, \ldots , f)$, with individual weights assigned according to their expertise and normalised to satisfy $\sum _{k=1}^{f} w_k = 1$. CPFS-based evaluations provide a thorough representation of expert opinions by considering both magnitude and phase-related uncertainties. The criterion weights are determined using the OWCM, which incorporates expert consensus, while the MACONT method is utilised to rank alternatives.

Algorithm

Step 1: A decision-making problem encompasses criteria $\mathbb{C}_{j} = \mathbb{C}_{1} ,\mathbb{C}_{2} , \ldots ,\mathbb{C}_{x}$ and alternatives $M_{i}^{k} = M_{1}^{k} ,M_{2}^{k} , \ldots ,M_{0}^{k}$. Decision-makers utilise CPFNs to asses alternatives $M_{i}^{k}$ according to each criterion $\mathbb{C}_{j}$. The evaluations are represented in a CPFNs $M = \left[ {\mathbb{C}_{{ij}} } \right]_{{0 \times x}}$, where $\mathbb{C}_{j}$ denotes the evaluations of the i-th alternative under the j-th criterion.

In Table 3, the seven CPFNs linguistic terms used by DMs are defined.

Table 3 Linguistic terms and corresponding CPFSs.

The linguistic terms and their corresponding CPiFVs were determined based on expert evaluations and existing scales from the CPFS literature. Each linguistic term represents a qualitative assessment level (e.g., Excellent, Good, Fair), which is expressed as a complex-valued triplet $(\mu e^{i\theta _\mu }, \nu e^{i\theta _\nu }, \pi e^{i\theta _\pi })$, where $\mu$, $\nu$, and $\pi$ denote the membership, non-membership, and neutral degrees, respectively, and $\theta$ represents their phase in the complex plane.

Softmax function

Step 2: In CPF sets, each element denotes an evaluation value attributed to a particular criterion within the decision-making framework. The contribution of each element is quantified through score computation, which is subsequently utilised to evaluate the performance of each perspective as outlined in Eq. 11.

$$\begin{aligned} {\aleph }_{j}={\left\{ \begin{array}{ll}\Pi _{i=1}^{j-1}{\wp }_{i}& j=2,3,...,n\\ 1& j=1 \end{array}\right. } \end{aligned}$$

(11)

where,

$$\begin{aligned} \wp = (\varrho - \xi - \vartheta ) + \frac{1}{2\pi } (\beth - \Omega - \Phi ), \end{aligned}$$

(12)

Step 3: Evaluate each decision maker listed in Table 4 and assign weights according to Eq. 13). The scores are determined based on the roles and responsibilities assigned to each decision-maker within the decision-making process.

$$\begin{aligned} \mathbb {E}_{k}^{j}=\mathbb {E}_k(j,{\aleph }_1,{\aleph }_2,...,{\aleph }_n)=\frac{\exp \left( \frac{{\aleph }_{j}}{\beta }\right) }{\sum _{j=1}^{n}\exp \left( \frac{{\aleph }_{j}}{\beta }\right) },k>0. \end{aligned}$$

(13)

Table 4 Characteristics of decision makers (DMs) in the case study.

Step 4: Integrate data from all tables to create a aggregated group for the expert-derived combined CPFNs. The integration is conducted by the complex picture fuzzy sets Aczél–Alsina weighted average (CPFSAAWA) operator⁴⁶, as specified in Eq.14).

$$\begin{aligned} \begin{aligned} {CPFSAAWA}(\mathscr {K}_{1}, \mathscr {K}_{2}, \cdots , \mathscr {K}_{n}) = \left( \begin{array}{c} \left( 1 - e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (1-\varrho _{l}) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) e^{2\pi \left( 1 - e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (1-\beth _{l}) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) }, \\[10pt] \left( e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (\xi ) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) e^{2\pi \left( e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (\Omega ) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) }, \\[10pt] \left( e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (\vartheta _{l}) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) e^{2\pi \left( e^{-\left( \displaystyle \sum _{l=1}^{n} {{\mathbb {E}_{k}}^{j}} \left( -\log (\Phi _{l}) \right) ^{\mathbb {E}} \right) ^{\frac{1}{\mu }}} \right) } \end{array} \right) \end{aligned} \end{aligned}$$

(14)

Step 5: The subsequent step entails the computation of the aggregated score matrix as outlined in Eq. (15).

$$\begin{aligned} \P = (\varrho - \xi - \vartheta ) + \frac{1}{2\pi } (\beth - \Omega - \Phi ), \end{aligned}$$

(15)

Opinion weight criteria method

The OWCM is a methodology that employs expert input to determine objective criterion weights derived from subjective evaluations. This method is particularly advantageous in decision-making scenarios where expert opinions are essential but may vary in consistency and emphasis. The procedure comprises the following steps:

Step 6: To make the scores comparable, they are normalised column-by-column. To create the normalised matrix $\partial _{ij}$, each element ${\P }_{ij}$ is split by the highest score in its associated column:

$$\begin{aligned} \partial _{ij} = \frac{{\P }_{ij}}{\max ({\P }_{:j})} \end{aligned}$$

(16)

This makes the criterion dimensionless and consistent for further analysis by guaranteeing that all scores lie inside the range [0, 1].

Step 7: For every criteria, the average score ${\S }_j$ is calculated for all experts. This average serves as a standard by which to measure variations in the opinions of experts.

$$\begin{aligned} {\S }_j = \frac{1}{m} \sum _{i=1}^{m} {\P }_{ij} \end{aligned}$$

(17)

Step 8: The squared difference between each normalised value and its corresponding mean is calculated in order to evaluate the departure of individual assessments from the mean.

$$\begin{aligned} {\nabla }_{ij} = \left( \partial _{ij} - {\S }_j \right) ^2 \end{aligned}$$

(18)

This quantifies the range of expert opinions on each criterion.

Step 9: The squared deviations from all experts are added together to determine the overall squared deviation $\mathfrak {F}_j$ for each criteria.

$$\begin{aligned} \mathfrak {F}_j = \sum _{i=1}^{m} {\nabla }_{ij} \end{aligned}$$

(19)

Step 10: We calculate inverse deviation scores $\alpha _j$ by deducting each total deviation from 1 in order to prioritise criteria with higher consensus:

$$\begin{aligned} \alpha _j = 1 - \mathfrak {F}_j \end{aligned}$$

(20)

Step 11: The final weight $w_j$ for each criteria is determined using the normalised inverse deviation values.

$$\begin{aligned} w_j = \frac{\alpha _j}{\sum _{j=1}^{n} \alpha _j} \end{aligned}$$

(21)

The weights combine subjective evaluation with statistical accuracy by taking into account expert importance assessments and their agreement levels. The following multi-criteria decision-making procedure uses the weights obtained from Equation (21) to effectively evaluate and rank the options.

MACONT method

Step 12:

$$\begin{aligned} {\epsilon _{ij}}^{(1)} = \frac{{\P }}{\sum _{i=1}^{m} \left( {\P }\right) } \end{aligned}$$

(22)

Normalisation using the linear sum approach, where each value is scaled proportionately by its total sum across alternatives, as demonstrated in equation 22.

$$\begin{aligned} {\epsilon _{ij}}^{(2)} = \frac{{\P }}{\max _{i} \left( {\P }\right) } \end{aligned}$$

A max-based scale between 0 and 1 is made possible by equation 4, which normalises each value in relation to the maximum in its column.

$$\begin{aligned} {\epsilon _{ij}}^{(3)} = \frac{({\P }) - \min _{i} ({\P })}{\max _{i} ({\P }) - \min _{i} ({\P })} \end{aligned}$$

(23)

The numbers in equation 23 are adjusted to the [0, 1] range based on their distribution using min-max normalisation.

Step 13:

Weighted aggregation is used to integrate the three normalised matrices into a single decision matrix in the manner described below:

$$\begin{aligned} {\upsilon }_{ij} = \Xi _1 {\epsilon _{ij}}^{(1)} + \Xi _2 {\epsilon _{ij}}^{(2)} + \Xi _3 {\epsilon _{ij}}^{(3)} \end{aligned}$$

(24)

In this context, $\Xi _1, \Xi _2, \Xi _3 \in [0, 1]$ denote weights that indicate the relative significance of each normalisation method, with the condition that $\Xi _1 + \Xi _2 + \Xi _3 = 1$.

Step 14:

First, determine the criterion’s mean value.

$$\begin{aligned} \bar{{\upsilon }}_j = \frac{1}{m} \sum _{i=1}^m {\upsilon }_{ij} \end{aligned}$$

Next, calculate two score types: the weighted product score ${\upsilon }_i$ and the weighted summation score $\varrho _i$:

$$\begin{aligned} \varrho _i = \sum _{j=1}^n {w}_j ({\upsilon }_{ij} - \bar{{\upsilon }}_j) \end{aligned}$$

(25)

This summary, which has been corrected for significance ${w}_j$, quantifies the departure of each alternative from the mean across all criteria.

$$\begin{aligned} {\gimel }_i = \frac{\prod _{e=1}^n ({\upsilon }_e - {\upsilon }_{ie})^{w_e}}{\prod _{f=1}^n ({\upsilon }_{if} - {\upsilon }_f)^{w_f}} \end{aligned}$$

(26)

Using a multiplicative deviation formulation, this score represents relative performance. The criteria ${\gimel }_e > {\gimel }_{ie}$ and ${\gimel }_{if} \ge {\gimel }_f$ are indicated by $e$ and $f$, respectively.

Step 15:

Compute two subordinate comprehensive grades to improve the evaluation of overall performance:

$$\begin{aligned} {\mho }_1(\zeta _i) = {\gimel } \frac{\varrho _i}{\sqrt{\sum _{i=1}^m (\varrho _i)^2}} + (1 - {\gimel }) \frac{{\gimel }_i}{\sqrt{\sum _{i=1}^m ({\gimel }_i)^2}} \end{aligned}$$

(27)

${\mho }_1$ uses the preference parameter ${\gimel } \in [0, 1]$ to integrate the normalised summation and product scores.

$$\begin{aligned} {\mho }_2(\zeta _i) = \wp \max _j \left( {w}_j ({\upsilon }_{ij} - \bar{{\upsilon }}_j) \right) + (1 - \wp ) \min _j \left( {w}_j ({\upsilon }_{ij} - \bar{{\upsilon }}_j) \right) \end{aligned}$$

(28)

${\mho }_2$ evaluates weighted maximum and minimum deviations, adjusted by the preference $\wp \in [0, 1]$, to quantify the extreme behaviour of each alternative.

Step 16:

Combine ${\mho }_1(\zeta _i)$ and ${\mho }_2(\zeta _i)$ into the final score as:

$$\begin{aligned} \eta (d_i) = \frac{1}{2} \left( {\mho }_1(\zeta _i) + \frac{{\mho }_2(\zeta _i)}{\sqrt{\sum _{i=1}^m ({\mho }_2(\zeta _i))^2}} \right) \end{aligned}$$

(29)

The final score provides a thorough evaluation of each alternative’s extreme and worldwide performance. Based on their final comprehensive ratings, the options are arranged in decreasing order $\eta (d_i)$. The option with the highest value of $\eta (d_i)$ is considered the best alternative. The computational procedure of the proposed framework is outlined in Fig.  1.

Fig. 1

Proposed algorithm workflow for evaluating performance of forecasting financial.

Statement of the problem

Organisations in all sectors are under tremendous pressure to use emerging technologies for strategic resilience, operational efficiency, and competitive advantage in the present era of digital transformation. There are previously unheard-of chances for innovation and performance optimisation due to the quick development of machine learning (ML), deep learning (DL), blockchain, cloud computing, the internet of things (IoT), and robotic process automation (RPA). Nevertheless, decision-makers find it difficult to choose the best option that fits organisational goals, resource limitations, and operational realities because to the extreme diversity and complexity of these technologies. Furthermore, adopting technology in strategic efforts requires weighing a number of, sometimes contradictory, factors, including accuracy, scalability, security, implementation cost, integration feasibility, and sustainability effect. The uncertainty and ambiguity included in stakeholder judgements and expert opinions further compound the difficulty. In these situations, decisions are rarely clear-cut or binary; instead, they are influenced by subjective opinions, insufficient data, and differing levels of assessment confidence. Such complicated, ambiguous, and interconnected judgements are frequently difficult for traditional MCDM systems to capture and analyse efficiently. Because of this, businesses run the danger of investing in less-than-ideal solutions or underusing transformational technology, which can result in lost opportunities, inefficient operations, and a decline in competitiveness in rapidly evolving markets.

There is little evidence of integrated decision frameworks that concurrently compare a large number of competing strategic initiatives under real-world uncertainty, despite the fact that previous research has examined technology selection in discrete domains, such as implementing blockchain for financial transparency or machine learning for predictive analytics. Current approaches frequently use deterministic scoring, lack advanced normalisation techniques, and ignore the complex relationships between criteria. Furthermore, sophisticated fuzzy set extensions that may efficiently describe the degrees of positive, neutral, and negative evaluations while maintaining the capacity to manage multi-dimensional uncertainty. The decision-making literature is severely limited by this gap, especially when it comes to high-stakes strategic planning in technologyintensive industries. The development of a strong, adaptable, and uncertainty resilient assessment framework that can methodically consider a wide range of factors, capture expert opinions in all their complexity, and produce trustworthy evaluations of rival strategic technology options is therefore urgently needed. Such a system must use the power of complex image fuzzy sets to manage subjective uncertainty while integrating sophisticated weighting mechanisms, such the OWCM, with allinclusive normalisation approaches MACONT.

Alternatives definition and functional overview

This study assesses eight strategic technological alternatives, labelled as ${M^{\kappa }}_{1}$–${M^{\kappa }}_{8}$, each providing distinct capabilities to improve financial forecasting and facilitate strategic decision-making in uncertain environments. The definitions and operational mechanisms of each alternative are outlined below:

• ${M^{\kappa }}_{1}$: Robotic process automation (RPA) RPA utilises software bots to automate repetitive, rule-based financial tasks, including data entry, reconciliation, and report generation. This minimises human error, enhances efficiency, and allocates human resources to more valuable tasks. It addresses operational inefficiencies and manual workload bottlenecks effectively⁴⁷.

• ${M^{\kappa }}_{2}$: AI-powered customer personalization platform This platform utilises AI algorithms to assess customer behaviour, preferences, and transaction histories, facilitating customised product offerings and focused financial guidance. Real-time personalisation enhances client engagement and loyalty, optimises cross-selling and up-selling opportunities, and addresses challenges related to customer retention⁴⁸.

• ${M^{\kappa }}_{3}$: Cloud ERP system for operations optimization Cloud-based Enterprise Resource Planning systems consolidate essential financial and operational processes into a single platform that is accessible from any location. They enhance the efficiency of accounting, budgeting, and supply chain management, thereby accelerating decision-making and lowering IT maintenance expenses. These systems tackle scalability challenges and facilitate real-time performance monitoring⁴⁹.

• ${M^{\kappa }}_{4}$: Hybrid AI + blockchain infrastructure This integrated solution merges the predictive and analytical capabilities of AI with the transparency and security attributes of blockchain technology. Artificial intelligence examines data recorded on the blockchain to provide actionable insights, whereas blockchain technology guarantees data integrity and auditability. This synergy enhances decision accuracy and trust, thereby mitigating risks associated with data quality and manipulation⁵⁰.

• ${M^{\kappa }}_{5}$: Machine learning (ML) for predictive analytics Machine learning models employ historical and real-time financial data to discern patterns, trends, and correlations, facilitating predictive insights. Supervised and unsupervised learning algorithms enable machine learning to predict future market trends, evaluate credit risks, and enhance investment strategies. This method tackles the issues of volatility and data complexity through the continuous retraining of models using updated data⁵¹.

• ${M^{\kappa }}_{6}$: IoT-integrated financial monitoring IoT sensors and devices gather real-time operational and transactional data, which is integrated into financial monitoring systems for immediate analysis. This integration enhances asset tracking, inventory management, and fraud detection capabilities. Monitoring based on IoT effectively tackles the issue of delayed data availability and improves proactive risk management⁵².

• ${M^{\kappa }}_{7}$: Blockchain-based financial transparency system Blockchain technology provides a decentralised and immutable ledger for the documentation of financial transactions, thereby improving transparency and trust. Smart contracts facilitate the automation of compliance and settlement processes, thereby minimising fraud and operational risks. This approach addresses data tampering and audit inefficiencies by employing cryptographic verification and distributed consensus mechanisms⁵³.

• ${M^{\kappa }}_{8}$: Deep learning for automated decision-making Deep learning architectures, including convolutional and recurrent neural networks, analyse large-scale, unstructured financial data to facilitate automated and adaptive decision-making. These models are capable of detecting anomalies, predicting asset price fluctuations, and generating investment recommendations, thereby surpassing human cognitive limitations in processing large datasets⁵⁴.

Criteria definitions

This study employs ten evaluation criteria to assess strategic initiatives aimed at forecasting financial outcomes and facilitating strategic decisions. Each criterion is delineated below, accompanied by its function in addressing pertinent challenges.

• Accuracy of forecasting ($\mathbb {C}_1$): Assesses the system’s capacity to produce accurate financial forecasts. High accuracy reduces decision-making risks by minimising prediction errors that may result in financial losses.

• Scalability ($\mathbb {C}_2$): Denotes the ability of the system to manage growing amounts of data and transactions while maintaining performance levels. Scalability guarantees sustained relevance as business operations grow.

• Data security ($\mathbb {C}_3$): Evaluates the capacity to safeguard sensitive financial and operational information against unauthorised access or breaches. Robust data security measures mitigate financial fraud and cyber threats.

• Integration capability ($\mathbb {C}_4$): This assessment examines the effectiveness of integrating the system with current IT infrastructure, legacy systems, and other business applications. High integration capability mitigates operational silos and improves cross-departmental collaboration.

• Implementation cost ($\mathbb {C}_5$): Assesses the comprehensive expenses associated with technology adoption, encompassing hardware, software, and human resources. Monitoring implementation costs is essential for preventing budget overruns and optimising return on investment.

• Adaptability to market changes ($\mathbb {C}_6$): Demonstrates the system’s adaptability to swiftly evolving financial and market conditions. High adaptability reduces the risk of obsolescence and facilitates agile decision-making.

• Decision-making speed ($\mathbb {C}_7$): Evaluates the duration required by the system to process inputs and generate actionable recommendations. Accelerated decision-making facilitates prompt interventions in unstable markets.

• Transparency ($\mathbb {C}_8$): Assesses the transparency and comprehensibility of system outputs, guaranteeing that decisions are clear to stakeholders. Transparency fosters trust and aids in resolving compliance and audit issues.

• User-friendliness ($\mathbb {C}_9$): Assesses the ability of end-users to utilise and gain advantages from the system without requiring significant technical training. An intuitive system minimises operational errors and enhances adoption rates.

• Sustainability ($\mathbb {C}_{10}$): Evaluates the environmental and social implications of the technology alongside its financial performance. Sustainability-oriented systems are aligned with corporate responsibility objectives and assist in fulfilling regulatory obligations.

Experimental results

Step 1: Table 3 lists the linguistic words for criteria and options. Table 5 details the evaluations of each criterion by several decision makers using CPFNs over all potential values ${M^{\kappa }}_{i}$.

Table 5 DM’s evaluation information.

Step 2: Equations 13 and 11 are used to calculate the score values and matrix data for each matrix that decision makers provide.

$$\begin{aligned} \wp _{ij}^{1}=\begin{bmatrix} 0.4109 & 0.1800 & 0.3228 & 0.2246 & 0.4791 & 0.2637 & 0.1409 & 0.0691 & 0.0223 & 0.3732 \\ 0.4000 & -0.0554 & 0.5909 & -0.0109 & 0.6237 & -0.0900 & 0.4437 & 0.3428 & -0.0791 & 0.4932 \\ 0.2746 & 0.3409 & 0.2846 & 0.3700 & 0.3037 & 0.2291 & 0.1437 & 0.3809 & -0.0172 & 0.4637 \\ 0.2528 & 0.5446 & 0.2900 & 0.2937 & -0.1391 & 0.5909 & -0.0200 & 0.3846 & 0.2805 & 0.4119 \\ 0.5009 & -0.1600 & 0.1937 & 0.5528 & 0.2346 & 0.0091 & 0.5028 & 0.4237 & 0.3315 & -0.1560 \\ -0.0600 & 0.6937 & 0.3346 & 0.2709 & 0.0600 & 0.2328 & 0.1191 & 0.3237 & 0.1337 & 0.1720 \\ 0.2014 & 0.1519 & 0.4128 & 0.0434 & 0.5031 & 0.2795 & 0.2128 & 0.4495 & -0.0763 & 0.6519 \\ 0.1639 & 0.2409 & 0.3000 & -0.0074 & 0.0929 & 0.3605 & 0.2923 & -0.0568 & 0.4900 & 0.2315 \\ \end{bmatrix} \end{aligned}$$

$$\begin{aligned} \wp _{ij}^{2}=\begin{bmatrix} 0.4246 & 0.2991 & -0.0391 & 0.2500 & 0.4037 & 0.0700 & 0.2409 & 0.3546 & 0.4923 & -0.0568 \\ 0.1200 & 0.5846 & 0.4037 & 0.2009 & 0.1000 & 0.5746 & -0.0109 & 0.6328 & 0.0709 & 0.1442 \\ 0.4009 & 0.2837 & 0.2700 & 0.3737 & 0.5046 & 0.4009 & 0.3346 & 0.1291 & 0.0419 & 0.4025 \\ -0.0900 & 0.3609 & 0.4646 & 0.6237 & -0.0900 & 0.0391 & 0.4637 & 0.6046 & 0.2609 & 0.3205 \\ 0.6137 & 0.0100 & 0.2009 & 0.4837 & -0.0609 & 0.3828 & 0.5346 & 0.1900 & 0.3600 & -0.2174 \\ -0.2509 & 0.2309 & 0.6337 & -0.0500 & 0.3309 & 0.4846 & 0.1400 & 0.2009 & 0.2223 & 0.3039 \\ 0.3437 & 0.1120 & 0.1309 & 0.2500 & 0.3326 & 0.1719 & 0.3340 & 0.5695 & 0.0419 & 0.1005 \\ 0.0309 & 0.2832 & 0.2220 & 0.0520 & 0.2194 & 0.3005 & 0.3235 & 0.1712 & 0.2715 & 0.4634 \\ \end{bmatrix} \end{aligned}$$

$$\begin{aligned} \wp _{ij}^{3}=\begin{bmatrix} 0.2628 & 0.6846 & -0.1600 & 0.5309 & 0.0891 & 0.2437 & 0.3909 & 0.5737 & 0.1437 & 0.3632 \\ 0.3800 & -0.2163 & 0.6128 & 0.4646 & 0.4709 & 0.0200 & 0.0891 & 0.3828 & 0.3423 & -0.0377 \\ 0.5737 & 0.5646 & 0.1009 & -0.1409 & 0.4837 & 0.5146 & 0.1900 & 0.4609 & -0.1191 & 0.4723 \\ 0.4546 & 0.3137 & 0.3100 & 0.1128 & 0.4437 & 0.1909 & 0.4446 & 0.1000 & 0.4911 & 0.1015 \\ -0.1800 & 0.3391 & 0.5946 & -0.0200 & 0.0837 & 0.2691 & 0.3128 & 0.1437 & 0.2409 & 0.7323 \\ 0.2309 & 0.5646 & 0.1137 & 0.0591 & 0.0900 & 0.5928 & 0.0409 & 0.6037 & -0.1263 & 0.3805 \\ 0.1111 & 0.4112 & 0.1234 & 0.2317 & 0.3512 & 0.0431 & 0.5022 & 0.0106 & 0.6703 & 0.0329 \\ 0.4725 & -0.1298 & 0.4634 & 0.3015 & 0.1415 & 0.4122 & 0.0706 & 0.3440 & 0.1728 & 0.3506 \\ \end{bmatrix} \end{aligned}$$

Step 3: Equation 13 is used to calculate the softmax function for each matrix provided by DMs, where $\beta =2$.

$$\mathbb {E}^{{k},1}_{ij}= \begin{bmatrix} 0.3311 & 0.3591 & 0.2964 & 0.3494 & 0.3372 & 0.3326 & 0.3315 & 0.3311 & 0.3311 & 0.3311 \\ 0.3269 & 0.3886 & 0.3171 & 0.3252 & 0.3308 & 0.3292 & 0.3269 & 0.3269 & 0.3269 & 0.3269 \\ 0.3495 & 0.2584 & 0.2921 & 0.3472 & 0.3523 & 0.3500 & 0.3495 & 0.3494 & 0.3495 & 0.3495 \\ 0.3292 & 0.3362 & 0.3657 & 0.3409 & 0.3356 & 0.3278 & 0.3287 & 0.3292 & 0.3292 & 0.3292 \\ 0.3249 & 0.4030 & 0.3029 & 0.3263 & 0.3208 & 0.3240 & 0.3249 & 0.3249 & 0.3249 & 0.3249 \\ 0.3384 & 0.2969 & 0.3025 & 0.3373 & 0.3361 & 0.3381 & 0.3383 & 0.3384 & 0.3384 & 0.3384 \\ 0.3350 & 0.3187 & 0.3298 & 0.3382 & 0.3347 & 0.3349 & 0.3350 & 0.3350 & 0.3350 & 0.3350 \\ 0.3362 & 0.2820 & 0.3649 & 0.3471 & 0.3379 & 0.3364 & 0.3363 & 0.3362 & 0.3362 & 0.3362 \\ \end{bmatrix}$$

$$\mathbb {E}^{{k},2}_{ij}= \begin{bmatrix} 0.3290 & 0.3668 & 0.3275 & 0.3277 & 0.3307 & 0.3285 & 0.3289 & 0.3290 & 0.3290 & 0.3290 \\ 0.3398 & 0.2307 & 0.3963 & 0.3671 & 0.3476 & 0.3425 & 0.3400 & 0.3398 & 0.3398 & 0.3398 \\ 0.3385 & 0.3221 & 0.2945 & 0.3390 & 0.3422 & 0.3408 & 0.3396 & 0.3388 & 0.3385 & 0.3385 \\ 0.3568 & 0.1836 & 0.2820 & 0.3310 & 0.3486 & 0.3571 & 0.3569 & 0.3567 & 0.3568 & 0.3568 \\ 0.3092 & 0.4807 & 0.3426 & 0.3212 & 0.3110 & 0.3096 & 0.3092 & 0.3092 & 0.3092 & 0.3092 \\ 0.3457 & 0.2070 & 0.2991 & 0.3292 & 0.3472 & 0.3460 & 0.3458 & 0.3457 & 0.3457 & 0.3457 \\ 0.3255 & 0.4116 & 0.3256 & 0.3237 & 0.3256 & 0.3255 & 0.3255 & 0.3255 & 0.3255 & 0.3255 \\ 0.3445 & 0.2215 & 0.3517 & 0.3487 & 0.3464 & 0.3448 & 0.3446 & 0.3445 & 0.3445 & 0.3445 \\ \end{bmatrix}$$

$$\mathbb {E}^{{k},3}_{ij}= \begin{bmatrix} 0.3399 & 0.2742 & 0.3761 & 0.3229 & 0.3322 & 0.3389 & 0.3396 & 0.3399 & 0.3399 & 0.3399 \\ 0.3333 & 0.3806 & 0.2866 & 0.3077 & 0.3217 & 0.3283 & 0.3331 & 0.3333 & 0.3333 & 0.3333 \\ 0.3120 & 0.4195 & 0.4134 & 0.3138 & 0.3055 & 0.3092 & 0.3109 & 0.3117 & 0.3120 & 0.3120 \\ 0.3140 & 0.4802 & 0.3523 & 0.3280 & 0.3158 & 0.3151 & 0.3144 & 0.3141 & 0.3140 & 0.3140 \\ 0.3659 & 0.1163 & 0.3545 & 0.3525 & 0.3681 & 0.3664 & 0.3659 & 0.3659 & 0.3659 & 0.3659 \\ 0.3160 & 0.4961 & 0.3984 & 0.3336 & 0.3168 & 0.3159 & 0.3159 & 0.3160 & 0.3160 & 0.3160 \\ 0.3395 & 0.2697 & 0.3446 & 0.3381 & 0.3397 & 0.3396 & 0.3395 & 0.3395 & 0.3395 & 0.3395 \\ 0.3194 & 0.4966 & 0.2834 & 0.3042 & 0.3156 & 0.3188 & 0.3191 & 0.3193 & 0.3194 & 0.3194 \\ \end{bmatrix}$$

Step 4: Data from all tables are integrated into a single group in the combined CPFNs Table, which is the result of expert analysis. Equation (14) describes how the CPFSAAWA operator is used to carry out the integration. The results are shown in Table 6.

Table 6 Alternative evaluation.

Step 5: The aggregated score matrix is calculated using Eq. 1), as demonstrated in the matrix below.

$${\P } = \begin{bmatrix} 0.3849 & 0.5588 & 0.1251 & 0.4378 & 0.4729 & 0.3870 & 0.3331 & 0.5393 & 0.3184 & 0.3659 \\ 0.3967 & 0.5167 & 0.5901 & 0.3186 & 0.5152 & 0.4128 & 0.3413 & 0.5458 & 0.1959 & 0.3079 \\ 0.6424 & 0.5744 & 0.3268 & 0.3361 & 0.6294 & 0.5643 & 0.5300 & 0.4053 & 0.0318 & 0.5194 \\ 0.2872 & 0.5857 & 0.5848 & 0.4774 & 0.2455 & 0.4961 & 0.4100 & 0.5547 & 0.4193 & 0.4205 \\ 0.4629 & 0.0375 & 0.4901 & 0.5260 & 0.1478 & 0.2776 & 0.4826 & 0.3074 & 0.3147 & 0.5297 \\ 0.0417 & 0.5969 & 0.4538 & 0.3329 & 0.2439 & 0.5248 & 0.1399 & 0.4871 & 0.1471 & 0.3651 \\ 0.2432 & 0.3357 & 0.4053 & 0.4213 & 0.5060 & 0.2109 & 0.4194 & 0.4871 & 0.4473 & 0.4955 \\ 0.3148 & 0.2109 & 0.3718 & 0.1891 & 0.2068 & 0.4053 & 0.2574 & 0.2054 & 0.4572 & 0.5201 \\ \end{bmatrix}$$

Step 6: By dividing each item by the highest score in the associated column, the score matrix is normalised. According to Equation (16), this procedure adjusts the data between 0 and 1, enabling fair comparison across criteria.

$$\begin{aligned} \begin{bmatrix} 0.5991 & 0.9363 & 0.2120 & 0.8323 & 0.7514 & 0.6858 & 0.6284 & 0.9723 & 0.6964 & 0.6908 \\ 0.6175 & 0.8656 & 1.0000 & 0.6057 & 0.8187 & 0.7316 & 0.6439 & 0.9839 & 0.4284 & 0.5813 \\ 1.0000 & 0.9624 & 0.5538 & 0.6389 & 1.0000 & 1.0000 & 1.0000 & 0.7307 & 0.0696 & 0.9806 \\ 0.4471 & 0.9813 & 0.9911 & 0.9076 & 0.3900 & 0.8792 & 0.7736 & 1.0000 & 0.9170 & 0.7939 \\ 0.7205 & 0.0629 & 0.8306 & 1.0000 & 0.2349 & 0.4920 & 0.9105 & 0.5541 & 0.6883 & 1.0000 \\ 0.0649 & 1.0000 & 0.7691 & 0.6329 & 0.3876 & 0.9300 & 0.2639 & 0.8781 & 0.3217 & 0.6892 \\ 0.3786 & 0.5624 & 0.6868 & 0.8010 & 0.8040 & 0.3737 & 0.7912 & 0.8782 & 0.9783 & 0.9354 \\ 0.4901 & 0.3533 & 0.6301 & 0.3596 & 0.3286 & 0.7182 & 0.4856 & 0.3703 & 1.0000 & 0.9819 \\ \end{bmatrix} \end{aligned}$$

Step 7: Every decision-maker’s average score is calculated for each criterion. The average score, which is determined by Equation (17), represents the overall tendency of assessors with respect to each criterion.

$$\begin{aligned} \begin{bmatrix} 0.2774&0.3417&0.3348&0.3039&0.2968&0.3279&0.2914&0.3532&0.2332&0.3524 \end{bmatrix} \end{aligned}$$

Step 8: The squared deviation from the criteria mean is computed for every normalised input. This phase uses Equation (18) to quantify the dispersion or discrepancy in the assessments.

$$\begin{aligned} \begin{bmatrix} 0.1035 & 0.3536 & 0.0151 & 0.2792 & 0.2067 & 0.1281 & 0.1136 & 0.3832 & 0.2145 & 0.1145 \\ 0.1157 & 0.2745 & 0.4425 & 0.0910 & 0.2724 & 0.1630 & 0.1243 & 0.3978 & 0.0381 & 0.0524 \\ 0.5222 & 0.3853 & 0.0480 & 0.1122 & 0.4945 & 0.4518 & 0.5022 & 0.1425 & 0.0268 & 0.3946 \\ 0.0288 & 0.4091 & 0.4308 & 0.3644 & 0.0087 & 0.3040 & 0.2326 & 0.4183 & 0.4676 & 0.1949 \\ 0.1963 & 0.0777 & 0.2458 & 0.4845 & 0.0038 & 0.0269 & 0.3833 & 0.0404 & 0.2071 & 0.4194 \\ 0.0452 & 0.4334 & 0.1886 & 0.1083 & 0.0082 & 0.3626 & 0.0008 & 0.2755 & 0.0078 & 0.1135 \\ 0.0102 & 0.0487 & 0.1239 & 0.2471 & 0.2573 & 0.0021 & 0.2498 & 0.2756 & 0.5553 & 0.3399 \\ 0.0452 & 0.0001 & 0.0872 & 0.0031 & 0.0010 & 0.1524 & 0.0377 & 0.0003 & 0.5880 & 0.3962 \end{bmatrix} \end{aligned}$$

Step 9: The total deviation, which measures the extent of diversity in expert opinions for a given criteria, is calculated by adding the squared deviations for each criterion. The execution of this follows Equation (19).

$$\begin{aligned} \begin{bmatrix} 1.0671&1.9825&1.5820&1.6898&1.2527&1.5908&1.6443&1.9336&2.1052&2.0254 \end{bmatrix} \end{aligned}$$

Step 10: The total deviation values are inverted to reflect the reliability of criteria with reduced dispersion. A smaller deviation indicates a greater consensus among experts, thus enhancing the criterion’s significance. The transformation is represented in Equation (20).

$$\begin{aligned} \begin{bmatrix} 0.0671&0.9825&0.5820&0.6898&0.2527&0.5908&0.6443&0.9336&1.1052&1.0254 \end{bmatrix} \end{aligned}$$

Step 11: The final set of objective weights for each criteria is obtained by normalising the inverse values to total one. The normalisation procedure, which is described in Equation (21), ensures consistency.

$$\begin{aligned} \begin{bmatrix} 0.0098&0.1429&0.0847&0.1004&0.0368&0.0860&0.0937&0.1358&0.1608&0.14922 \end{bmatrix} \end{aligned}$$

MACONT method

Step 12:

The score matrix is subjected to three methods in order to integrate various normalisation viewpoints. Equation 22 shows how the first approach normalises each element according to the sum of all values in each column. In order to facilitate max-based normalisation, the second technique scales each value in relation to the maximum value in its corresponding column. Equation 23 describes the third method, which uses min-max normalisation to scale data to the [0, 1] range depending on the column’s minimum and maximum values. Tables 7, 8, and 9 provide specifics on the results of normalisation 1, normalisation 2, and normalisation 3.

Table 7 Normalization 1.

Table 8 Normalization 2.

Table 9 Normalization 3.

Step 13:

Weighted aggregation is used to aggregate the three normalised matrices into a single decision matrix. Equation 24 is used to proportionately integrate the contributions of each normalisation technique based on provided weights, and the results are displayed in Table 10.

Table 10 Aggregation of normalizations.

Step 14:

Each criterion’s average value is determined as shown in Eq. (25). For every choice, two scores are computed: the weighted product score and the weighted summation score. According to Eq. (26), these scores represent the relative performance and the deviation from the mean, respectively. Table 11 presents the findings.

Table 11 Mean and relative performance.

Steps 15, 16:

Two subordinate comprehensive grades are computed to better represent overall performance. The initial grade, ${\mho }_1$, combines the normalised weighted summation and product scores via a preference parameter, as outlined in Equation (27). The second grade, ${\mho }_2$, measures the extreme behaviour of each alternative via weighted maximum and minimum deviations, adjusted by an additional preference parameter, as shown in Equation (28). The final score $\eta (d_i)$ is calculated according to Equation 29, with the results displayed in Table 12.

Table 12 Final results.

Sensitivity analysis

The sensitivity analyses presented in Tables 13-16 compare the robustness of four decision-making approaches MACONT, WASPAS, ERUNS, and AROMAN under varying parameter settings for $\mu$ (5-100) and $\beta$ (0.1, 0.5, 0.7, 0.9). For the MACONT method in Table 13, the rankings remain predominantly stable across all parameter combinations, with ${M^{\kappa }}_{4}$ consistently occupying the top position, followed by ${M^{\kappa }}_{8}$ and ${M^{\kappa }}_{7}$, and ${M^{\kappa }}_{1}$ typically ranked lowest. The only deviation is observed at $\beta =0.5$ and $\mu =5$, where ${M^{\kappa }}_{1}$ briefly appears in first place indicating a localized sensitivity to parameter interaction. Apart from this rare case, the method demonstrates high stability, and score magnitudes increase smoothly with higher $\mu$ without disrupting the relative order. In the WASPAS method in Table 14, the ranking is similarly stable, with ${M^{\kappa }}_{4}$ always ranked first and ${M^{\kappa }}_{5}$ consistently last. However, the middle-ranking positions (e.g., ${M^{\kappa }}_{7}$, ${M^{\kappa }}_{2}$) show less variation in score magnitude compared to MACONT, and there is no observable case where parameter changes cause a reordering in the top positions—indicating stability, but also suggesting less sensitivity to detecting small performance shifts. For the ERUNS method in Table 15, the preference order remains entirely unchanged across all parameter combinations, with ${M^{\kappa }}_{4} \succ {M^{\kappa }}_{8} \succ {M^{\kappa }}_{2} \succ {M^{\kappa }}_{7} \succ {M^{\kappa }}_{6} \succ {M^{\kappa }}_{5} \succ {M^{\kappa }}_{1} \succ {M^{\kappa }}_{3}.$This complete stability signifies robustness; however, it may imply a restricted ability to capture subtle variations in alternative performance due to parameter changes, which could diminish adaptability in dynamic decision-making contexts. The AROMAN method presented in Table 16 demonstrates stable rankings, with ${M^{\kappa }}_{4}$ consistently ranked highest and ${M^{\kappa }}_{1}$ ranked lowest. While score magnitudes exhibit minor fluctuations with alterations in $\mu$ and $\beta$, these changes do not significantly affect the ordering, demonstrating a robust insensitivity to parameter variations. A comparative assessment indicates that although all four methods demonstrate significant robustness, MACONT provides a distinctive equilibrium between stability and sensitivity. The controlled sensitivity is beneficial in practical decision-making, as methods need to be both dependable and adaptable to changes in parameters. Consequently, MACONT exhibits enhanced adaptability while maintaining overall ranking robustness, positioning it as the most effective method among the four in the evaluated scenarios. Figure 3 demonstrates the effects of altering the parameters $\mu$ and $\beta$ on the performance scores $M^\kappa _i$ of the alternatives assessed by the MACONT method, highlighting the stability and nuanced sensitivity of the rankings in response to parameter variations. Figure 4 illustrates the impact of varying $\mu$ and $\beta$ on the performance scores $M^\kappa _i$ of the WASPAS method, indicating stable rankings with slight score fluctuations. Figure 5 illustrates the impact of varying $\mu$ and $\beta$ on the performance scores $M^\kappa _i$ obtained from the ERUNS method, demonstrating a consistent and invariant preference order across all parameter configurations tested. Figure 6 illustrates the influence of parameters $\mu$ and $\beta$ on the performance scores $M^\kappa _i$ in the AROMAN method, demonstrating stable rankings with minor variations in score magnitudes. As shown in Fig.  2, the trends of alternatives $M^\kappa _1$ to $M^\kappa _8$ vary with changing $\mu$ and $\beta$ parameters. The figure highlights that $M^\kappa _4$ consistently achieves the highest values across all scenarios, indicating its dominance in the decision-making process.

Table 13 The impact of the parameter ${\mu }$ and $\beta$ on the decision result by MACONT method.

Table 14 The impact of the parameter ${\mu }$ and $\beta$ on the decision result by WASPAS method.

Table 15 The impact of the parameter ${\mu }$ and $\beta$ on the decision result by ERUNS method.

Table 16 The impact of the parameter ${\mu }$ and $\beta$ on the decision result by AROMAN method.

Fig. 2

Effect of $\mu$ and $\beta$ on decision results of $M^\kappa _1$–$M^\kappa _8$ using line graphs.

Fig. 3

Effect of varying $\mu$ and $\beta$ on performance scores $M^\kappa _i$ of alternatives by the MACONT method.

Fig. 4

Effect of varying $\mu$ and $\beta$ on performance scores $M^\kappa _i$ of alternatives by the WASPAS method.

Fig. 5

Effect of varying $\mu$ and $\beta$ on performance scores $M^\kappa _i$ of alternatives by the ERUNS method.

Fig. 6

Effect of varying $\mu$ and $\beta$ on performance scores $M^\kappa _i$ of alternatives by the AROMAN method.

Comparison analysis

The comparative results in Table 17 reveal that, across multiple established methods such as COPRAS⁵⁵, q-ROFHOWAGA with TOPSIS⁵⁶, Hybrid-modified TOPSIS⁵⁷, ELECTRE⁵⁸, CRITIC-MARCOS⁵⁹, and the Delphi method⁶⁰, the optimal alternative ${M^{\kappa }}_{4}$ consistently emerges as the top-ranked choice. This demonstrates a significant level of consensus among different MCDM techniques, thereby enhancing the reliability of the decision outcome. The current models exhibit robust ranking stability; however, the proposed OWCM integrated with MACONT shows a significant advantage. OWCM with MACONT integrates ordered weighting logic, facilitating enhanced prioritisation of criteria according to decision-maker preferences, alongside a complex-number representation that adeptly addresses uncertainty, hesitation, and interdependent evaluation information. In comparison to other proposed OWCM-based integrations like AROMAN, ERUNS, and WASPAS, the OWCM with MACONT achieves the same optimal solution (${M^{\kappa }}_{4}$) while providing a ranking order that demonstrates a more equitable trade-off between high-performing and moderately performing alternatives. This balance is crucial in decision-making contexts where it is important to avoid over-prioritizing any single factor. Additionally, MACONT’s ability to process multi-dimensional and uncertain data while preserving informational richness offers a methodological advantage compared to conventional ranking aggregators. Research conducted by Ali⁵⁹ and Yazdi⁵⁷ indicates that hybrid approaches, which integrate weighting mechanisms with robust aggregation models, frequently surpass traditional methods in intricate decision-making contexts. OWCM with MACONT is notable for its adaptability and capacity to sustain ranking consistency, while enhancing sensitivity to nuanced performance variations among mid-ranked alternatives. This guarantees that the decision-making process is equitable and strategically coherent. Consequently, the agreement among various methods confirms the optimality of ${M^{\kappa }}_{4}$. The proposed OWCM with MACONT approach offers an advanced, reliable, and interpretable decision support tool, rendering it especially appropriate for situations characterised by high complexity, uncertainty, and multi-perspective evaluation.

Table 17 Comparison of proposed operators with some exiting operators.

Discussion of ranking

The integration of hybrid AI and blockchain infrastructure (${M^{\kappa }}_{4}$) results in the highest overall performance, effectively merging predictive accuracy with robust security and transparency. Blockchain provides immutable and verifiable records, whereas AI improves forecasting and pattern recognition capabilities. This combination demonstrates strong regulatory compliance, as blockchain establishes a permanent audit trail, and achieves a high level of innovation due to the ongoing integration of AI and blockchain in finance. The system’s real-time processing capabilities facilitate immediate fraud detection and dynamic financial modelling, significantly impacting operations by minimising manual audits and expediting decision-making. Integration presents challenges stemming from the complexity of merging AI and blockchain systems; however, the long-term return on investment surpasses initial implementation costs, positioning ${M^{\kappa }}_{8}$ as the most strategically advantageous option. Deep learning for automated decision-making (${M^{\kappa }}_{8}$) is ranked second owing to its remarkable forecasting accuracy, utilising sophisticated pattern recognition to identify complex trends. It demonstrates superior capabilities in real-time processing, facilitating prompt responses to market fluctuations, and achieves high marks in innovation due to its advanced algorithms. The blockchain-based financial transparency system (${M^{\kappa }}_{7}$) demonstrates superior security and data integrity, alongside regulatory compliance, due to blockchain technology’s capability to prevent tampering and guarantee comprehensive auditability. It presents significant potential for user adoption in highly regulated industries where trust is critical. Nevertheless, it exhibits lower accuracy in forecasts and a reduced level of innovation when compared to AI-driven solutions, given that blockchain-only systems have reached a relatively mature stage. Real-time processing capabilities remain constrained without integration with advanced analytics engines. Despite challenges related to cost and scalability, ${M^{\kappa }}_{7}$ is the optimal choice for organisations that prioritise trust and compliance over predictive capabilities. Machine learning for predictive analytics (${M^{\kappa }}_{5}$) provides high forecast accuracy at a reduced cost compared to deep learning solutions, presenting a viable option for organisations aiming for a balance between performance and cost efficiency. The integration capability is strong, as machine learning models can be deployed on existing infrastructures with minimal modifications. Nonetheless, its efficacy in real-time processing is limited, and it does not possess inherent security features unless supplemented with additional protective technologies. The innovation level is moderate, given that machine learning is well-established; however, it continues to serve as a cost-effective solution for resource-constrained businesses. The Cloud ERP system for operations optimisation (${M^{\kappa }}_{3}$) demonstrates robust integration capabilities and significant operational impact, facilitating the centralisation of workflows and enhancement of efficiency. User adoption potential may be enhanced through the use of familiar interfaces and centralised data access. Nonetheless, the accuracy of its forecasts is not a primary strength, and its security and data integrity are largely contingent upon the protections provided by the cloud provider. The level of innovation is moderate, given that ERP systems represent a mature technology. ${M^{\kappa }}_{3}$ is well-suited for organisations that emphasise operational efficiency rather than advanced analytics. The AI-powered customer personalisation platform (${M^{\kappa }}_{2}$) demonstrates significant user adoption potential and innovation in customer engagement through the application of AI to customise financial products and services, thereby enhancing satisfaction and retention. Nonetheless, its operational impact is primarily confined to customer-facing functions, providing minimal advantages for enterprise-wide forecasting. Furthermore, it exhibits inferior performance in regulatory compliance and security when contrasted with blockchain-based solutions. IoT-integrated financial monitoring (${M^{\kappa }}_{6}$) provides significant real-time processing capabilities and operational effects, particularly in asset-intensive sectors. IoT sensors deliver real-time financial and operational data, facilitating expedited decision-making. Nonetheless, the accuracy of forecasts is constrained unless integrated with advanced AI analytics, and security remains a concern due to the susceptibility of IoT devices to cyberattacks. Robotic process automation (${M^{\kappa }}_{1}$) is recognised for its cost efficiency, as it automates high-volume, rules-based tasks, thereby decreasing processing time, minimising human errors, and lowering labour costs. The operational impact is significant, as it streamlines workflows and enhances throughput in back-office functions, including invoice processing, data entry, and reconciliations. Nonetheless, it provides limited enhancement to forecasting accuracy and depends on established system safeguards for security. The level of innovation is modest, as RPA is characterised as a mature, incremental technology rather than a transformative one, resulting in reduced competitiveness in innovation-driven assessments.

Limitations of the model

Although the proposed Smart Decision Support System effectively integrates financial forecasting with a comprehensive MCDM framework, several limitations should be acknowledged to ensure a balanced understanding of its scope and applicability.

• Although the CPFS framework effectively manages hesitation and imprecision, some forms of uncertainty–such as incomplete, inconsistent, or rapidly changing data–may not be fully captured. This is particularly relevant in complex or dynamic decision environments.

• While AI-driven financial forecasting provides powerful predictive capabilities, its application in volatile markets has inherent limitations. Models trained on historical data may overfit past patterns and fail to adapt to sudden market shocks, while noisy or incomplete data can reduce prediction accuracy. Extreme events, such as geopolitical crises or regulatory changes, can lead to sharp deviations that AI models may not anticipate. Additionally, many AI models operate as “black boxes,” making interpretation difficult for managers, and real-time implementation demands significant computational resources. Over-reliance on AI predictions without integrating expert judgment may increase risk in dynamic financial environments.

• The framework is developed for a specific strategic decision-making context. Applying it to other industries or domains may require redefinition of criteria, linguistic terms, and normalization procedures to maintain accuracy and relevance.

• Validating the proposed framework across diverse real-world case studies presents several challenges. Different industries and contexts may have varying criteria importance, data availability, and measurement scales, which can affect the generalizability of the results. Collecting consistent, high-quality data across cases is often difficult, and expert judgments may vary significantly, leading to variability in outcomes. Additionally, comparing results across heterogeneous environments requires careful normalization and sensitivity analysis to ensure meaningful interpretation. These challenges highlight the need for adaptable weighting mechanisms and robust validation procedures when applying the framework in practice.

• Criteria such as Innovation Level and User Adoption Potential rely on qualitative judgments that may vary among evaluators, leading to potential inconsistency in scoring.

• While the model considers Integration Capability as an evaluation criterion, it does not explicitly account for hidden implementation costs, time delays, or organisational resistance that can occur during technology adoption.

Overall, these limitations indicate that while the proposed Decision Support System provides a robust, flexible, and theoretically grounded approach for strategic evaluation, its performance can be further enhanced through dynamic weighting mechanisms, adaptive AI retraining, and extensive cross-domain validation in future research.

Theoretical and practical implications

Theoretical implications:

• Integrates OWCM, CPFS, and MACONT into a unified Decision Support System, advancing hybrid MCDM methodology.

• Extends uncertainty modelling by applying CPFS to capture multi-dimensional hesitation and directional uncertainty.

• Introduces a balanced aggregation approach (MACONT) that synthesises additive and multiplicative normalisation, improving rank stability and reducing rank reversal.

• Bridges predictive analytics and decision theory by coupling AI-driven financial forecasting with a structured MCDM framework, enriching theoretical links between forecasting and multi-criteria evaluation.

Practical implications:

• Provides practitioners with a robust Smart Decision Support System to evaluate and prioritise strategic initiatives under uncertainty.

• Enhances decision reliability and transparency by combining objective opinion-weighting (OWCM) with expressive fuzzy representation (CPFS) and stable aggregation (MACONT).

• Offers adaptability for diverse domains (e.g., finance, technology selection, risk assessment) through modular criteria and linguistic-to-CPFS mapping.

• Facilitates scenario testing and sensitivity analysis to assess the robustness of decisions under varying forecasts and weight assumptions, supporting evidence-based strategic planning.

Managerial implications

The findings of this study have several meaningful implications for managers, policymakers, and strategic planners operating in data-driven and uncertainty-prone decision environments. The proposed Decision Support System (OWCM–CPFS–MACONT) not only identifies the optimal alternative among competing options but also provides a transparent and explainable reasoning process for decision-makers. The numerical results highlight the most influential criteria and their relative importance across technological, financial, and operational dimensions. Managers can use these insights to prioritise resources and investments more effectively. For instance, criteria such as integration capability and scalability potential emerged as decisive factors, guiding managers to focus on flexible and interoperable technologies that ensure long-term adaptability. Through the application of complex picture fuzzy sets, the model captures multi-level uncertainty and hesitation inherent in expert evaluations. This enables managers to make risk-informed decisions even when data are incomplete, vague, or volatile–particularly beneficial in dynamic sectors such as finance, manufacturing, and renewable energy systems. By analysing how rankings shift under sensitivity tests, managers can identify stable options that remain effective across multiple scenarios. The results reveal actionable patterns linking performance attributes with outcome stability. Decision-makers can employ the system to simulate different what-if scenarios and evaluate trade-offs between cost, efficiency, and sustainability. This supports operational optimization by ensuring that every selected technology or investment aligns with both short-term goals and long-term strategic priorities. The DSS quantifies the relative performance of alternatives, allowing decision-makers to allocate resources more rationally. Policymakers can adopt the same framework to evaluate technology adoption programs, funding priorities, and infrastructure initiatives while maintaining fairness and transparency in evaluation.

Actionable decision plans

Based on the numerical analysis and robustness results, the following action plans are recommended:

• Identify and strengthen high-impact criteria (e.g., reliability, cost efficiency, and sustainability) before large-scale implementation.

• Use the OWCM weighting results to continuously monitor evolving priorities as market or technological conditions change.

• Apply sensitivity-based feedback loops to re-evaluate strategic options when volatility increases, such as during financial shocks or supply disruptions.

• Integrate the DSS into enterprise information systems for routine performance benchmarking and investment screening.

The proposed framework provides managers with a quantifiable, reproducible, and adaptive evaluation process. By replacing subjective judgments with systematic analysis, it enhances transparency and accountability in decision-making. Furthermore, the visual and numerical outputs of the system can be directly incorporated into corporate dashboards or digital twins for ongoing monitoring and scenario planning. The managerial implications demonstrate that the proposed Decision Support System is not only theoretically sound but also practically valuable for supporting data-driven, uncertainty-tolerant, and forward-looking decision-making in complex operational environments.

Conclusion

This study examined the challenge of identifying the most strategically beneficial financial technology initiative within a context marked by uncertainty, swift innovation, and changing regulatory requirements. A Smart Decision Support System was developed to integrate advanced financial forecasting with a robust MCDM framework. The OWCM was utilised to obtain balanced and unbiased criteria weights based on expert judgements, while the CPFS framework improved the ability to model hesitation and imprecision in qualitative evaluations. The novel MACONT established a balanced ranking mechanism through the integration of additive and multiplicative aggregation methods. The evaluation process identified Hybrid AI + Blockchain Infrastructure as the leading alternative due to its distinctive integration of high predictive accuracy, robust security, transparency, and compliance capabilities. Integrating AI-driven forecasting with blockchain’s immutable record-keeping, ${M^{\kappa }}_{8}$ provides enhanced real-time fraud detection, dynamic financial modelling, and significant operational impact. Although the integration complexity is elevated, the long-term return on investment and strategic advantages surpass the initial difficulties. Comprehensive sensitivity analysis validated the stability and robustness of the rankings under various criteria weight adjustments. Benchmark comparisons with established MCDM methods, including ERUNS, AROMAN, MARCOS, and WASPAS, yielded consistent and reliable results, thereby validating the practical applicability of the proposed framework. The findings highlight the efficacy of the integrated OWCM–CPFS–MACONT approach as a decision-making instrument for organisations confronted with complex investment decisions amid uncertainty. The methodology enhances decision transparency and ensures resilience against fluctuating expert opinions and data ambiguities.

In future work, the proposed framework could incorporate machine learning techniques to dynamically adjust criteria weights based on historical data and emerging trends. This enhancement would improve the adaptability of the decision-support system in rapidly evolving financial and technological environments and provide more robust and timely decision-making guidance. Additionally, future research can explore integrating emerging technologies such as quantum computing to handle large-scale and complex computations more efficiently, as well as addressing multi-stakeholder conflicts in decision-making by incorporating consensus-building and negotiation mechanisms. These advancements could further improve the robustness, scalability, and applicability of the decision-support system across diverse and dynamic environments.