Real time frequency and voltage stabilization in multi area hybrid power systems using hybrid MGOAO optimized PID and FOPID controllers

Abstract

The integrated study of automatic voltage regulation (AVR) and load frequency control (LFC) in a two-area hybrid power system is examined in this research. A new Moss Growth Optimization and Artemisinin Optimization (MGO-AO) algorithm is suggested for the best controller parameter tuning, while a traditional FOPID controller is used as the secondary controller. First, a test system with two-area non-reheat thermal turbines is used to apply the MGO-AO algorithm. The analysis of the joint LFC-AVR problem is then expanded to a combination model. In addition, a high-voltage direct current (HVDC) link is added to the system in addition to the traditional AC tie-line. A battery energy storage system (BESS) is also incorporated to reduce frequency and voltage fluctuations and enhance system stability. When compared to an AC-only network, the AC/DC hybrid transmission system dramatically improves system dynamic performance, according to comparative studies. Robustness is demonstrated for representative disturbances e.g., $\:3\text{\%}$ and $\:5\text{\%}$ step load perturbations in the two regions and a $\:5\text{\%}$ generation loss with a $\:3\text{\%}$ generation increase and for configurations with and without BESS. Comparative analysis against ARO, GWO-PSO, modified SSA, and the standalone MGO and AO shows that the proposed hybrid MGO-AO/FOPID achieves the lowest settling times and overshoots. Hardware-in-the-Loop (HIL) validation on dSPACE MicroLabBox confirms the practical implementability of the unified FOPID scheme.

Introduction

The integrated power system is made up of a complicated network of utilities that act in different ways. Tie-lines are used to move power between these utilities. Regulating changes in terminal voltage and frequency across different areas is important for keeping the interconnected power system safe. Controlling both active and reactive power can help with this regulation. Utilities in the interconnected network must make sure that generation matches demand because the load on the power system changes all the time. When there is a difference between generation and load, the system’s frequency changes. When there is more generation than demand, the frequency goes up above the set value. When demand is higher than generation, frequency goes down. Regulatory actions can fix this problem by changing the levels of generation to match the levels of demand. Also, changing the generator’s field excitation current to meet the system’s reactive power needs keeps terminal voltage changes in check. It is very important to properly control both frequency and terminal voltage in order to keep the system stable as a whole.

Literature review

The Automatic Voltage Regulator (AVR) loop controls terminal voltage, while the Load Frequency Control (LFC) loop controls frequency in systems that are connected to each other. LFC and AVR have been thoroughly evaluated as separate entities. LFC loop keeps the frequency steady in systems that are connected to each other, while the AVR loop keeps the terminal voltage steady. Extensive research has been undertaken on LFC and AVR as separate entities. Fosha and Elgerd first came up with the basic mathematical modeling of thermal systems for LFC in 1970¹. Guha et al. (2017) examined the load frequency control of thermal-hydro systems, neglecting the analysis of system nonlinearities, including governor deadband and governor response characteristics. In studies by Vedat et al.², as well as Morsali et al.^3,4. As secondary regulators, fractional order controllers such as FOPID and FOPI were employed. Particle Swarm Optimization (PSO) is one of several population-based and stochastic methods⁵, Improved PSO (IPSO)⁶, Backtracking Search Algorithm (BSA)⁷, Differential Evolution (DE)⁸, Teaching-Learning Based Optimization (TLBO)⁹, Harmony Search Algorithm (HSA)¹⁰, and hybrid algorithms like HGA-PSO¹¹, have been used in LFC operations to optimize controller parameters. In the work of Mohanty et al.¹², Frequency deviations were handled by intelligent controllers such fuzzy PID, whose parameters were adjusted by a hybrid strategy that used the Imperialist Competitive Algorithm (ICA) and gravitational search with multiple optimization techniques (hMOL-GSA). Hossam-Eldin et al.¹³ proposed a FPIDD $\:{\:}^{2}$controller tuned using a Gradient-Based Optimizer (GBO) for frequency and voltage regulation in a hybrid power system. Ali et al.¹⁴ implemented a Dandelion Optimizer (DO)-based strategy for combined AVR and LFC in a multi-area, multisource power system considering nonlinearities. Kalyan et al.¹⁵ conducted a comparative performance analysis of various energy storage devices integrated into a combined LFC-AVR framework in a multi-area power system. Ali et al.¹⁶ proposed a nature-inspired computational control methodology for simultaneous LFC and AVR regulation in a multi-area interconnected power system. Furthermore, Sahu et al.¹⁷ integrated a PI controller with intelligent controllers for LFC, optimizing the controller gains through various hybrid optimization methods. Khamari et al.¹⁸ and Sahu et al.¹⁹ examined the application of energy storage systems and FACTS devices in LFC, evaluating how well they worked in tandem with secondary controllers. However, neither the integration of renewable energy sources nor the combined effects of LFC and AVR have been fully investigated. However, the body of research on this combination strategy is somewhat small. In the study by Gupta et al.²⁰, A thorough examination of a traditional single-area power system was carried out. Kouba et al.²¹ extended this analysis, excluding Generator Rate Constraints (GRC), to a two-area system with ordinary thermal units. Vijaya Chandrakala and Balamurugan²² employed a simulated annealing technique for hydrothermal systems to stabilize voltage and frequency, however they neglected to take renewable energy integration into consideration. In Rajbongshi and Saikia’s²³ work, for a combined model analysis, a solar thermal unit was incorporated into a multi-area system; nevertheless, popular green energy sources like solar photovoltaic and wind were not taken into account. The authors looked into a multi-area system using hybrid energy sources because of this gap. Area-1 includes conventional sources along with GRC, while Area-2 consists of wind, diesel, and solar PV units for analysis. Recent developments in power system control have underscored the synergy between sophisticated optimization algorithms and STATCOM-based reactive power support to improve frequency stability during the integration of renewable energy sources. Area-1 study looks at both traditional sources and GRC, while Area-2 study looks at diesel, wind, and solar PV units. Recent improvements in power system regulation show that adding more renewable energy sources can keep the frequency stable by using advanced optimization algorithms and STATCOM-based reactive power support. In studies carried out by Kareem M. AboRas²⁴, A Dandelion Optimizer (DO) was used to improve frequency regulation in wind-integrated systems by optimizing a FOPI-PIDA controller that worked with a STATCOM. The DO-optimized STATCOM greatly improved frequency stability in benchmark systems like the IEEE 39-bus network, going beyond what previous MPA-tuned solutions could do. Saqif Imtiaz²⁵ conducted research utilizing a hybrid metaheuristic algorithm that combines the Marine Predator Algorithm (MPA) and the Artificial Hummingbird Algorithm (AHA) to improve a PI-PIDA-controlled STATCOM for microgrid frequency regulation in the event of both symmetrical and asymmetrical failures.

The proposed hybrid method showed a better dynamic response and less frequency deviation.

These studies reinforce the importance of hybrid optimization in modern control design and demonstrate the effectiveness of integrating STATCOM with optimized multi-parameter controllers in enhancing system resilience, particularly for microgrids and systems with high renewable penetration. Further, in studies of Naga Sai Kalyan and Sambasiva Rao²⁶, a combined approach to LFC and AVR in a multi-area hybrid power system was investigated by integrating renewable generation and AC/DC interconnections. This study revealed that incorporating HVDC links and battery energy storage systems (BESS) alongside traditional AC tie-lines significantly enhances dynamic system performance. Although numerous optimization algorithms exist in the literature, this study introduces a novel combinational algorithm called HAO-MGO to optimize controller parameters. Focusing on enhancing system performance during sudden load and generation disturbances. In a test system, the suggested approach is used to control both the terminal voltage and system frequency simultaneously. Ibraheem and Bhatti²⁷ suggest an HVDC link is the driving force behind this study since it is combined with the AC tie-line in parallel and a battery energy storage system (BESS) is included for the first time. Large power transfers over long distances are made possible by the DC link’s implementation, which also reduces the transient stability problems that come with AC tie-lines. Additionally, because the BESS is integrated into the renewable side, it can offer vital support during peak loads and fluctuations in renewable energy.

Research gap and motivation

The reviewed literature reveals several limitations and open challenges in the context of integrated LFC-AVR control under hybrid power systems:

• Fosha and Elgerd¹: Developed foundational LFC models but did not account for system nonlinearities such as GRC and GDB, or voltage control.

• Guha et al.²⁸: Analyzed thermal-hydro LFC systems without considering GRC, GDB, or voltage control dynamics.

• Ali et al.¹⁴: In the study the cascade controllers are indeed effective, they typically separate the voltage and frequency control loops, which does not adequately capture the cross-coupling dynamics inherent in integrated LFC-AVR systems. The proposed controller is a co-designed MIMO PID/FOPID controller, where tuning is performed considering the interdependence of the LFC and AVR subsystems, and cross-effects are embedded in the control law, rather than being treated as isolated dynamics.

• Kalyan et al.¹⁵: The paper focused on comparing the performance of different energy storage devices in a multi-area system. However, it did not employ advanced controller tuning or fractional-order schemes, nor did it explore optimization-based co-design of LFC-AVR controllers.

• Hossam-Eldin et al.¹³: Introduced a robust FPIDD² controller with gradient-based tuning for frequency-voltage control, yet the optimization technique lacked global search ability and did not include BESS, HVDC, or multi-area renewable hybrid scenarios as addressed in the present study.

• Vedat et al.²; Morsali et al.^3,4: Applied fractionalorder controllers like FOPID for frequency control but did not address AVR or their coupling.

• Panda and Mohanty⁵; Barisal and Mishra⁶; Guha et al.⁷; Sahu et al.^8,9; Nandi et al.¹⁰; El Yakine et al.¹¹: Applied various metaheuristic optimizers to LFC but lacked focus on integrated multi-loop tuning or energy storage integration.

• Mohanty et al.¹²; Sahu et al.¹⁷: Implemented intelligent fuzzy-based control for LFC but did not include AVR, HVDC, or BESS.

• Khamari et al.¹⁸; Sahu et al.¹⁹: Introduced FACTS and BESS in LFC scenarios but did not address the co-design of FOPID for LFC-AVR loops.

• Gupta et al.²⁰; Kouba et al.²¹: Studied single and two-area thermal systems but excluded renewable sources, GRC, and AVR integration.

• Vijaya Chandrakala and Balamurugan²²: Applied simulated annealing to hydrothermal systems but overlooked renewables and integrated LFC-AVR dynamics.

• Rajbongshi and Saikia²³: Incorporated solar thermal into LFC, but excluded solar PV, wind, and coordinated voltage control.

• Kareem M. AboRas²⁴: Proposed DO-optimized FOPI-PIDA controller with STATCOM for frequency control but no AVR or hybrid tuning.

• Saqif Imtiaz²⁵: Applied MPA-AHA hybrid optimization to STATCOM-based frequency regulation, but did not address simultaneous voltage control or FOPID tuning.

• Naga Sai Kalyan and Sambasiva Rao²⁶: The combined LFC-AVR with HVDC and BESS was investigated using HAO-MGO, but fractional-order co-design and validation across multiple disturbances were not explored.

The literature review shows that both traditional and intelligent optimization methods have made a lot of progress in coordinating the control of Load Frequency Control (LFC) and Automatic Voltage Regulation (AVR). Many studies have focused on improving frequency regulation by using PI, PID, or fractional-order controllers that have been optimized with algorithms that are inspired by nature such as PSO⁵, DE⁸, and TLBO⁹. Hybrid approaches and energy storage integration have been emphasized in recent studies. For instance, Ali et al.¹⁴ A cascaded Dandelion Optimizer-based controller has been proposed for improved damping under nonlinearities, while Ali et al.¹⁶ LFC-AVR coordination, nature-inspired computations were used. Kalyan et al.¹⁵ Performance of energy storage devices was assessed, but controllers were not optimized. Similarly, Hossam Eldin et al.¹⁶ Optimized a FPIDD $\:{\:}^{2}$controller via gradient methods without exploring hybrid links or renewable resources Although these studies contributed valuable insights, most either lack integrated FOPID control, overlook co-tuning for both LFC and AVR loops, or fail to consider HVDC and BESS together. This motivates the need for a unified control framework that integrates hybrid optimization (MGO-AO), fractional-order control, and modern infrastructure elements to achieve simultaneous voltage and frequency stability in complex, renewable-integrated power systems. The study by Naga Sai Kalyan and Sambasiva Rao²⁶ partially addressed these gaps by integrating HVDC in a two-area hybrid model. Motivated by this, the current work further extends the concept by using a parallel AC/DC interconnection model and a BESS with renewable generation and simultaneous tuning of LFC-AVR FOPID controllers using an improved hybrid algorithm (HAO-MGO). The primary objective of integrating LFC and AVR is to achieve simultaneous frequency and voltage stability in interconnected hybrid systems. As frequency and voltage dynamics are interdependent, their isolated control may cause degraded damping. A unified controller addresses cross-coupling, ensuring improved stability margins and system resilience.

Contribution and paper organization

The key contributions of this paper are summarized as follows:

• 1. Unified control: Development of a unified FOPID-based control strategy for simultaneous regulation of frequency and voltage. Unlike cascaded schemes, our design jointly tunes the LFC and AVR controllers while accounting for cross-couplings (Eqs. 18, 19, 25–27), providing superior damping of both slow and fast modes.

• 2. Hybrid optimization: The MGO-AO algorithm combines AO’s diffusion/mutation (exploration, Eqs. 39 and 40) with MGO’s attraction/mean and local refinement steps (exploitation, Eqs. 42 and 43). This hybrid stops early convergence and finds high-quality solutions.

• 3. Comprehensive tuning: Concurrent optimization of twenty FOPID parameters (5 parameters per FOPID $\:\times\:2$ loops $\:\times\:2$ areas). Each FOPID is defined as.

$$\:G\left(s\right)={K}_{p}+{K}_{i}{s}^{-\lambda\:}+{K}_{d}{s}^{\mu\:}$$

• 4. Integration of HVDC and BESS: The modeling of parallel AC/DC ties (Eqs. 14–19) and the dynamic BESS model with state of charge constraints (Eqs. 34–37) provide rapid corrective measures that are synchronized with governor and excitation control.

• 5. Robustness: Tested for how sensitive it is in different situations, such as when there are step load disturbances, generator failures, or when renewable energy is added.

• 6. Experimental validation: The implementation of Hardware-in-the-Loop (HIL) on the dSPACE MicroLabBox (real-time step, mapped analog/digital input/output) verifies that simulated enhancements are applicable to hardware.

The remainder of the paper is structured as follows: “System modeling” delineates the control framework and system modeling. “Hybrid artemisinin-moss growth technique” addresses the MGO-AO optimization framework. “Results and discussions” delineates the simulation outcomes and comparative analysis. Ultimately, “Conclusion” ends the research.

System modeling

Modeling for LFC loop

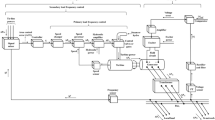
As shown in Fig. 1, the test system being looked at has two connected zones with a capacity ratio of 2:1 and uses both traditional and renewable energy sources. In Area-1, there is a thermal power station, a hydroelectric unit that uses governor response characteristics (GRCs), and a gas-fired power plant. The hydro unit shows rates of 360% and 270% per minute that go up and down, while the thermal unit’s GRC is set at 3% per minute. The dead-zone nonlinearity in the Governor Dead Band (GDB) makes it less sensitive to small changes in frequency.

The Generation Rate Constraint (GRC) limits how quickly generation can change. These effects are necessary for realistic modeling, but if they are not properly taken into account when designing a controller, they can make things less stable. GRC and other nonlinear limits are important because thermal units can’t change their output right away. If you don’t take these limits into account, you might make too optimistic predictions about how well the controller will work. Area-2 has a solar photovoltaic (PV) unit, a wind energy system, and a diesel generator all at the same time. The study by Shankar, Kalyan, and Ravi²⁹ is referenced for the temporal constants and gain parameters of the generating units in Area-1. On the other hand, the production units in Area-2 are based on the research done by Rajbongshi and Saikia²³ and Tasnin and Saikia³⁰. More information can be found in the Appendix. The non-reheat thermal two-area system is first looked at to set a standard and make sure the proposed controller design is correct. Then, the method is used on the hybrid model (AC/DC tie-lines with BESS) to show how adding HVDC and BESS can make things better and more scalable. Combining HVDC cables with AC tie-lines makes it easier to control areas that are far apart.

Unlike AC tie-lines, HVDC links can provide rapid power modulation, thereby improving damping of oscillations and contributing to both frequency and voltage stability. The modified models in Figs. 1 and 2 are taken from original models in Naga Sai Kalyan and Sambasiva Rao²⁶. The transfer function models for each generation unit within the load frequency control (LFC) framework are approximated as follows.

Fig. 1

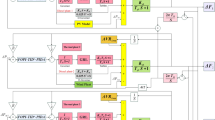
FOPID controlled combined LFC and AVR system. Adopted from reference²⁶.

Follows:

Thermal system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GT}\left(S\right)}{{\Delta\:}{P}_{mT}\left(S\right)}=\frac{\left(1+S{T}_{re}{K}_{re}\right)}{\left(1+{t}_{gr}S\right)\left(1+{T}_{re}S\right)\left(1+{t}_{Tr}S\right)}\end{array}$$

(1)

Hydro system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GH}\left(S\right)}{{\Delta\:}{P}_{mH}\left(S\right)}=\frac{\left(1+S{T}_{rs}\right)\left(1-S{t}_{W}\right)}{\left(1+{t}_{h}S\right)\left(1+{t}_{rh}S\right)\left(1+0.5{t}_{W}S\right)}\end{array}$$

(2)

Gas system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GG}\left(S\right)}{{\Delta\:}{P}_{mG}\left(S\right)}=\frac{(1+XS){\left(1-{t}_{CR}S\right)}^{a}}{(1+YS)(c+bS)\left(1+{t}_{F}S\right)\left(1+{t}_{CD}S\right)}\end{array}$$

(3)

Diesel system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GD}\left(S\right)}{{\Delta\:}{P}_{mD}\left(S\right)}={K}_{D}\frac{\left(1+S{t}_{d1}\right)}{\left(1+{t}_{d4}S\right)\left(1+{t}_{d2}S\right)\left(1+{t}_{d3}S\right)}\end{array}$$

(4)

Wind system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GW}\left(S\right)}{{\Delta\:}{P}_{mW}\left(S\right)}={K}_{W1}{K}_{W2}\frac{\left(1+S{t}_{W1}\right)}{\left(1+{t}_{W2}S\right)\left(1+2S+{S}^{2}\right)}\end{array}$$

(5)

Solar photovoltaic system:

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{GPV}\left(S\right)}{f}={K}_{PV}\frac{1}{1+{t}_{PV}S}\end{array}$$

(6)

Under typical operating conditions, the electricity produced by producing units in the corresponding locations is provided as:

$$\:{P}_{G1}={P}_{GT}+{P}_{GH}+{P}_{GG}$$

(7)

$$\:{P}_{G2}={P}_{GD}+{P}_{GW}+{P}_{GPV}$$

(8)

The change in power generation by both locations is represented as follows for minor load perturbations:

$$\:{\Delta\:}{P}_{G1}={\Delta\:}{P}_{GT}+{\Delta\:}{P}_{GH}+{\Delta\:}{P}_{GG}$$

(9)

$$\:{\Delta\:}{P}_{G2}={\Delta\:}{P}_{GD}+{\Delta\:}{P}_{GW}+{\Delta\:}{P}_{GPV}$$

(10)

The power transfer between regions using just the AC line is shown as

$$\:\begin{array}{c}{P}_{tieAC}={P}_{12}sin\left({\delta\:}_{1}-{\delta\:}_{2}\right)\end{array}$$

(11)

Using only the AC line, the power transmission between regions is displayed as

$$\:\begin{array}{c}\varDelta\:{P}_{tieAC}={T}_{12}\left({\Delta\:}{\delta\:}_{1}-{\Delta\:}{\delta\:}_{2}\right)={T}_{12}\left({\Delta\:}{f}_{1}-{\Delta\:}{f}_{2}\right)\end{array}$$

(12)

The synchronizing coefficient $\:{T}_{12}$ is modeled as

$$\:\begin{array}{c}{T}_{12}={P}_{12}cos\left({\delta\:}_{1}-{\delta\:}_{2}\right)\end{array}$$

(13)

Integrating an HVDC link in parallel with the existing AC tie-line can reduce power flow deviations to some extent. However, it is important to note that HVDC link designs cannot be standardized across different test systems. The specific parameters for the HVDC link, customized for the operation of this test system is given below as

$$\:\begin{array}{c}\frac{{\Delta\:}{P}_{HVDC}\left(S\right)}{{\Delta\:}{P}_{mHVDC}\left(S\right)}=\frac{{K}_{HVDC}}{1+{T}_{HVDC}S}\end{array}$$

(14)

where:

• $\:{\Delta}{P}_{HVDC}\left(S\right)$ is the change in transmitted power via the HVDC link.

• $\:{\Delta}{P}_{mHVDC}\left(S\right)$ is the reference input or modulation signal.

• $\:{K}_{HVDC}$ is the gain of the HVDC link.

• $\:{T}_{HVDC}$ is the time constant of the HVDC link.

The full power flow equations through the tie-line are supplied by

$$\:\begin{array}{c}{P}_{tie12}={P}_{tieAC}+{P}_{tieDC}\end{array}$$

(15)

Equation (15), with minor perturbations, can be changed as:

$$\:\begin{array}{c}\varDelta\:{P}_{tie12}=\varDelta\:{P}_{tieAC}+\varDelta\:{P}_{tieDC}\end{array}$$

(16)

Under step load perturbations, the power flow through the DC tie-line is provided by:

$$\:\begin{array}{c}\varDelta\:{P}_{tieDC}={K}_{DC}\frac{\left(1+{T}_{DC}S\right)}{\left(S\right)}\left({\Delta\:}{f}_{1}-{\Delta\:}{f}_{2}\right)\end{array}$$

(17)

Area Control Error (ACE): Upon integrating AC/DC tie-line, the area control errors (ACE) are modeled as Fig. 2

$$\:AC{E}_{1}={B}_{1}{\Delta\:}{f}_{1}+\left({\Delta\:}{P}_{tieAC}+{\Delta\:}{P}_{tieDC}\right)$$

(18)

$$\:AC{E}_{2}={B}_{2}{\Delta\:}{f}_{2}+\left({\Delta\:}{P}_{tieAC}+{\Delta\:}{P}_{tieDC}\right)$$

(19)

Fig. 2

Test System with AC/DC linkages adopted from reference²⁶.

AVR loop handling

A synchronous generator’s voltage must be kept at a predetermined level by the Automatic Voltage Regulator (AVR). Figure 3 shows the cross-coupling coefficients as well as the AVR system’s comprehensive model. By continually comparing the output voltage (V) with the reference signal (V_ref), the error voltage (DV) is found. After being amplified, the error signal is transmitted to the exciter, which modifies the field excitation of the generator. This procedure improves the system’s stability by enabling quick adjustment of any variations in terminal voltage. The modeling of each subsystem within the AVR is described as follows.

$$\:{G}_{A}\left(s\right)=\frac{{K}_{A}}{1+s{T}_{A}}$$

(20)

$$\:{G}_{E}\left(s\right)=\frac{{K}_{E}}{1+s{T}_{E}}$$

(21)

$$\:{G}_{F}\left(s\right)=\frac{{K}_{S}}{1+s{T}_{S}}$$

(22)

$$\:{G}_{S}\left(s\right)=\frac{{K}_{S}}{1+s{T}_{S}}$$

(23)

The voltage error signal is given by:

$$\:\begin{array}{c}\varDelta\:V=V-{V}_{\text{r}\text{e}\text{f}}\end{array}$$

(24)

Loop modeling using both LFC and AVR

The Automatic Voltage Regulator (AVR) loop in the integrated model is in charge of keeping the terminal voltage at a predetermined level by adjusting field excitation, while the Load Frequency Control (LFC) loop regulates frequency by matching real power generation with load demand.

However, the control activities carried out inside the AVR loop have a big impact on how the LFC operates. The voltage magnitude that develops in a generator $\:{\text{E}}^{{\prime\:}}$ is directly impacted by changes made to the AVR to sustain terminal voltage, which in turn affects the actual power generation.

$$\:\begin{array}{c}{P}_{e}=\frac{\left|V\right|\left|{E}^{{\prime\:}}\right|}{{X}_{s}}sin\left(\delta\:\right)\end{array}$$

(25)

where $\:{X}_{S}$ is the generator synchronous reactance and $\:\delta\:$ is the rotor angle.

When there are load perturbations, the rotor angle ( $\:{\Delta\:}\delta\:$ ) can be changed by altering the real power generation ( $\:{\Delta\:}{P}_{e}$ ), which is determined by:

$$\:\begin{array}{c}\varDelta\:{P}_{e}={P}_{s}\varDelta\:\delta\:+{K}_{1}{E}^{{\prime\:}}\end{array}$$

(26)

where the synchronizing power coefficient is denoted by Pe. Additionally, the rotor angle ($\:\delta\:$) affects the q-axis $\:\left(\text{V}\text{q}\right)$ and d-axis $\:\left(\text{V}\text{d}\right)$ components of the system terminal V. Then terminal voltage is.

Fig. 3

FOPID Controlled AVR system adopted from reference²⁶.

given by

$$\:\begin{array}{c}\varDelta\:V={K}_{2}\varDelta\:\delta\:+{K}_{3}{E}^{{\prime\:}}\end{array}$$

(27)

The generator’s induced voltage is determined by the following factors:

$$\:\begin{array}{c}{E}^{{\prime\:}}=\frac{{K}_{G}}{1+s{\tau\:}_{G}}\left(V-{K}_{4}{\Delta\:}\delta\:\right)\end{array}$$

(28)

where the coefficients $\:\text{K}1,\text{}\text{K}2,\text{}\text{K}3$, and K 4 allow the AVR system to be coupled with generation control loops. The AVR system in Fig. 3 is a modified one taken reference from the original model in Naga Sai Kalyan and Sambasiva Rao²⁶.

Controller design

In this combined model, system response deviations must be regulated by minimizing the Area Control Error (ACE). A robust secondary controller is essential to ensure design simplicity and effective disturbance rejection. While conventional PID controllers are widely used in industrial applications, the Fractional Order PID (FOPID) controller offers enhanced flexibility by introducing fractional orders $\:\lambda\:$ and $\:\mu\:$, enabling better adaptability and improved dynamic performance. PID controllers, although simple, lack sufficient flexibility to cope with LFC-AVR’s nonlinearity, parameter variations, and cross-coupled dynamics. The FOPID controller enhances the flexibility of shaping the system response by introducing integral and derivative orders ( $\:\lambda\:,\mu\:$ ). A mathematical representation of a FOPID controller is given by:

$$\:\begin{array}{c}{G}_{FOPID}\left(s\right)={K}_{P}+{K}_{I}{s}^{-\lambda\:}+{K}_{D}{s}^{\mu\:}\end{array}$$

(29)

Here, $\:\lambda\:$ and $\:\mu\:$ are fractional orders of integration and differentiation. In contrast to integer PID, fractional orders can be used to shape slow and fast dynamics, enabling better balance between robustness and transient response.

For two areas and two loops (LFC and AVR), a total of twenty parameters are tuned simultaneously. Traditional cascaded control ignores cross-coupling, resulting in suboptimal coordination. In addition to improving damping of both slow and fast modes, the unified FOPID ensures that the tuning is coordinated across both loops.

Four well-known objective functions were used to test the suggested controller: integral square error (ISE), integral absolute error (IAE), integral time square error (ITSE), and integral time absolute error (ITAE). These indices provide a quantitative evaluation of system responsiveness by imposing penalties for temporal fluctuations in frequency (Δf_1, Δf_2), tie-line power exchange (ΔP_(“tie” 1,2)), and voltage (ΔV_1, ΔV_2).

Fig. 4

Comparison of different objective functions.

The mathematical definitions of these objective functions are presented as follows:

• Integral square error (ISE): A large deviation is heavily weighted by this index, which penalizes the square of the error throughout the entire period.

$$\:\begin{array}{c}\text{}\text{I}\text{S}\text{E}\text{}={\int\:}_{0}^{T}\:\:{\left[{\Delta\:}{f}_{1}+{\Delta\:}{f}_{2}+{\Delta\:}{P}_{\text{tie\:}\text{1,2}}+{\Delta\:}{V}_{1}+{\Delta\:}{V}_{2}\right]}^{2}dt\end{array}$$

(30)

• Integral absolute error (IAE): Unlike ISE, This index considers the absolute error to avoid penalizing large errors excessively, resulting in a more balanced assessment.

$$\:\begin{array}{c}IAE={\int\:}_{0}^{T}\:\:\left|{\Delta\:}{f}_{1}+{\Delta\:}{f}_{2}+{\Delta\:}{P}_{\text{t}\text{i}\text{e}\text{1,2}}+{\Delta\:}{V}_{1}+{\Delta\:}{V}_{2}\right|dt\end{array}$$

(31)

• Integral time square error (ITSE): This function introduces a time-weighted factor to the squared error, which helps in reducing steady-state error by emphasizing deviations at later time instances.

$$\:\begin{array}{c}\text{}\text{I}\text{T}\text{S}\text{E}\text{}={\int\:}_{0}^{T}\:\:t{\left[{\Delta\:}{f}_{1}+{\Delta\:}{f}_{2}+{\Delta\:}{P}_{\text{tie1,2\:}}+{\Delta\:}{V}_{1}+{\Delta\:}{V}_{2}\right]}^{2}dt\end{array}$$

(32)

• Integral time absolute error (ITAE): Similar to ITSE, this index includes a time-weighting factor, but instead of squared errors, it considers absolute errors, leading to improved transient performance.

$$\:\begin{array}{c}\text{}\text{I}\text{T}\text{A}\text{E}\text{}={\int\:}_{0}^{T}\:\:t\left|{\Delta\:}{f}_{1}+{\Delta\:}{f}_{2}+{\Delta\:}{P}_{\text{tie\:}\text{1,2}}+{\Delta\:}{V}_{1}+{\Delta\:}{V}_{2}\right|dt\end{array}$$

(33)

Among these performance indices shown in Fig. 4; Table 1, the ISE index yielded the best results as it emphasizes large initial deviations, thereby reducing overshoot and settling time. Consequently, ISE was used as the performance index in the MGO-AO optimization process.

Table 1 Best cost values tested under various objective functions.

Battery energy storage system (BESS)

The device that stores energy from both non-renewable and renewable sources and releases it as required is called a battery energy storage system (BESS). The BESS’s primary and secondary dynamics, such as its internal response and the delay brought on by power electronics, are taken into consideration by the second-order model. The transfer function of the BESS is given by:

$$\:\begin{array}{c}{G}_{\text{B}\text{E}\text{S}\text{S}}\left(s\right)=\frac{{K}_{\text{B}\text{E}\text{S}\text{S}}}{\left({T}_{\text{B}\text{E}\text{S}\text{S}}s+1\right)\left({T}_{2}s+1\right)}\end{array}$$

(34)

where:

• $\:{K}_{\text{B}\text{E}\text{S}\text{S}}$ : Gain representing the power capacity of the BESS.

• $\:{T}_{\text{BESS\:}}$ : Primary time constant representing the main energy storage response.

• $\:{T}_{2}$ : Secondary time constant representing delays in power electronics or control.

The BESS input is the control signal u(t) generated by the FOPID controller for frequency management:

$$\:\begin{array}{c}u\left(t\right)={K}_{p}e\left(t\right)+{K}_{i}{D}^{-\lambda\:}e\left(t\right)+{K}_{d}{D}^{\mu\:}e\left(t\right)\end{array}$$

(35)

where $\:e\left(t\right)={f}_{\text{ref\:}}-f\left(t\right)$. The BESS power injection is then defined as:

$$\:\begin{array}{c}{P}_{\text{B}\text{E}\text{S}\text{S}}\left(t\right)=\alpha\:\cdot\:u\left(t\right)\end{array}$$

(36)

To maintain operational safety, the BESS State of Charge (SOC) is dynamically updated:

$$\:\begin{array}{c}SOC(t+1)=SOC\left(t\right)-\frac{{P}_{\text{B}\text{E}\text{S}\text{S}}\left(t\right)\cdot\:{\Delta\:}t}{{E}_{\text{rated\:}}}\end{array}$$

(37)

subject to the constraint:

$$\:SO{C}_{\text{m}\text{i}\text{n}}\le\:SOC\left(t\right)\le\:SO{C}_{\text{m}\text{a}\text{x}}$$

This framework makes sure that the BESS can help while still following storage limits. Its quick response improves the performance of the slower governor and AVR systems, which makes the whole system more stable in changing conditions. The appendix has the BESS settings that were made just for this test system. This model accurately shows how the BESS changes over time, taking into account both its ability to store energy and the time it takes to respond. The new idea is coordination: the HVDC link has an immediate effect on ACE (Eqs. 18, 19), which makes it easier to quickly change the power on the tie line.

The BESS, on the other hand, reacts to changes in frequency by injecting power, but only up to a certain point. This dual solution works better than standard methods that only work on one of them. It makes both frequency and voltage more stable. The BESS charges when the frequency is too high and discharges when it is too low, as long as the state of charge allows it. This happens almost right away. This two-in-one feature improves frequency damping and keeps the bus voltage steady, even when the renewable power changes. This design makes sure that the BESS can help without going over its storage limits. When things change, its quick response works well with the slower governor and AVR processes to make the whole system more stable. The appendix has the BESS settings that were made just for this test system. This model accurately illustrates the temporal evolution of the BESS, considering its energy storage capabilities and response time. The new thing is coordination. The HVDC link has a direct effect on ACE (Eqs. 18, 19), which means that tie-line power can be fixed right away. When the frequency changes, the BESS also limits SOC injections. This dual technique makes both frequency and voltage more stable, which is better than traditional systems that only work on one at a time.

The BESS reacts almost immediately to changes in frequency by charging when the frequency is too high and discharging when it is too low, as long as the SOC limits are met. This dual capability enhances frequency damping and bolsters bus voltage, especially in the context of renewable generation variability.

Hybrid artemisinin-moss growth technique

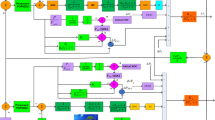
The proposed Hybrid Artemisinin Optimization-Moss Growth Optimization (HAO-MGO) algorithm combines the exploration ability of Artemisinin Optimization (AO) with the exploitation capability of Moss Growth Optimization (MGO) to enhance the convergence and robustness of the optimization process. The flowchart can be see in the Fig. 5.

Initialization

The algorithm begins by initializing a population of $\:N$ candidate solutions, represented as:

$$\:\begin{array}{c}{X}_{i}=\left[{x}_{i1},{x}_{i2},\dots\:,{x}_{id}\right],\:i=\text{1,2},\dots\:,N\end{array}$$

(38)

where $\:{x}_{ij}$ represents the $\:j$-th variable of the $\:i$-th candidate solution in a $\:d$-dimensional search space.

Artemisinin optimization phase

In this phase, the diffusion and propagation mechanism inspired by the artemisinin compound in Artemisia annua plants is applied. The new solution update is given by:

$$\:\begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\lambda\:\cdot\:r\cdot\:\left({X}_{\text{b}\text{e}\text{s}\text{t}}^{t}-{X}_{i}^{t}\right)\end{array}$$

(39)

where − $\:{X}_{i}^{t}$ is the position of the $\:i$-th solution at iteration $\:t.-{X}_{\text{best\:}}^{t}$ is the current best solution. − $\:\lambda\:$ is a diffusion coefficient. − $\:r$ is a random number in $\:\left[\text{0,1}\right]$.

A mutation mechanism is incorporated to enhance diversity:

$$\:\begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\alpha\:\cdot\:\left({X}_{j}^{t}-{X}_{k}^{t}\right)\end{array}$$

(40)

where $\:{X}_{j}^{t}$ and $\:{X}_{k}^{t}$ are randomly selected solutions, and $\:\alpha\:$ is a scaling factor.

The MGO-AO hybridization process applies AO operators (diffusion and mutation; Eqs. 39,40) to diversify the population, followed by MGO operators (Eqs. 42, 43) to refine promising solutions. This sequencing yields a balanced exploration-exploitation trade-off. A stopping rule (Eq. 44) halts optimization when

$$\:\begin{array}{c}\left|f\left({X}_{\text{best\:}}^{t+1}\right)-f\left({X}_{\text{best\:}}^{t}\right)\right|<\epsilon\:\:\text{}\text{o}\text{r}\text{}\:t\ge\:{T}_{\text{m}\text{a}\text{x}}\end{array}$$

(41)

Thus AO avoids local minima while MGO accelerates convergence around optima, producing better controller tuning than either standalone method.

Fig. 5

Flowchart representation of the HAO-MGO optimization for LFC-AVR system.

Moss growth optimization phase

After the exploration phase, the Moss Growth Optimization (MGO) refines the solutions by simulating the growth mechanism of moss, where solutions move towards the best region with adaptive step sizes. The position update is given by:

$$\:\begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\beta\:\cdot\:\left({X}_{\text{best\:}}^{t}-{X}_{i}^{t}\right)+\gamma\:\cdot\:\left({X}_{\text{mean\:}}^{t}-{X}_{i}^{t}\right)\end{array}$$

(42)

where: $\:\beta\:$ is the attraction coefficient towards the best solution. $\:\gamma\:$ controls the convergence towards the mean solution $\:{X}_{\text{mean\:}}^{t}$.

A local exploitation step ensures fine-tuning:

$$\:\begin{array}{c}{X}_{i}^{t+1}={X}_{i}^{t}+\delta\:\cdot\:randn\left(\text{0,1}\right)\end{array}$$

(43)

where $\:\delta\:$ is a small step size, and $\:\text{r}\text{a}\text{n}\text{d}\text{n}\left(\text{0,1}\right)$ is a normally distributed random number.

Stopping criteria

The algorithm iterates until a predefined number of iterations $\:{T}_{\text{max\:}}$ is reached or the objective function improvement falls below a threshold:

$$\:\begin{array}{c}\left|f\left({X}_{\text{best\:}}^{t+1}\right)-f\left({X}_{\text{best\:}}^{t}\right)\right|< \varepsilon \end{array}$$

(44)

where $\:f(\cdot\:)$ is the objective function.

Final solution

Upon termination, the best solution $\:{X}_{\text{best\:}}$ is returned as the optimal result.

The hybrid approach ensures enhanced dynamic performance by improving the transient response of the system while maintaining stability. Specifically, the HAO-MGO technique has been proven to:

• Achieve faster convergence and minimize system errors in comparison to other optimization techniques.

• Provide a more balanced exploration–exploitation trade-off, which helps in avoiding local minima and ensuring global optimality.

• Enhance the robustness of the system against perturbations and load disturbances, thus ensuring reliable operation.

Results and discussions

The transfer function model, which is the subject of Section II’s mathematical modeling, was created using the MATLAB/SIMULINK environment, as seen in Fig. 1. This section provides the performance assessment and simulation results of the suggested Hybrid MGO-AO PID tuning approach for Automatic Voltage Regulation (AVR) and Load Frequency Control (LFC) in a multi-area power system. The system is tested in a variety of scenarios, including loss events, load variations, and the integration of a Battery Energy Storage System (BESS). Table 2 shows the conditions that must be met for the system to work in each case.

Table 2 System operational conditions for each case.

Table 3 shows the lowest and highest values for the FOPID controller settings that were chosen for the simulation. We examine the outcomes by employing essential performance indicators, including:

Table 3 Selected minimum and maximum values of FOPID controller parameters during simulation.

Changes in frequency (Δf_1, Δf_2): Checking to see how well the control method can keep the frequency changes stable in both areas.

Voltage responses ($\:{V}_{1},{V}_{2}$): Evaluating the system’s ability to maintain voltage stability.

• Tie-line power $\:\left({P}_{\text{tie\:}}\right)$: Monitoring power exchange stability between interconnected areas.

• Settling time and overshoot: Measuring the time required for the system to reach a steady state after disturbances.

• Steady-state error: Ensuring minimal deviations from the desired operating conditions.

The performance of Hybrid MGO-AO to that of MGO and AO approaches on their own to show how much better system stability and optimization efficiency have gotten.

The results are discussed for each test case in the following subsections.

Case-1: dynamic response analysis

As disturbances, a step load of 0.03 and 0.05 p.u. are applied in area-1 and area-2, respectively, in case-1 at $\:\text{t}=25\text{}\text{s}$ and $\:\text{t}=50\text{}\text{s}$. The optimal gains obtained are tabulated in Table 4. Responses to frequency deviations, voltage deviations in both regions, and tie-line power deviations of the system have been displayed in Fig. 6. PID controller is used in this test case. Dynamic responses for MGO, AO, and HAO-MGO techniques, including settling time, peak overshoot, and undershoot values, have been presented in Tables 5 and 6. From Fig. 6, we can observe that the Hybrid MGO-AO approach effectively damps frequency deviations and reduces settling time compared to the individual MGO and AO techniques. Specifically, $\:{\Delta\:}{f}_{1}$ stabilizes in 9.4861 s using MGO-AO, whereas MGO and AO take 14.808 s and 10.0409 s, respectively. A similar trend is observed for $\:{\Delta\:}{f}_{2}$, where MGO-AO achieves a settling time of 9.2641 s, outperforming 10.6347 s (AO) and 10.0404 s (MGO). Examining Fig. 6, we notice that voltage deviations are significantly lower with the MGO-AO approach. The settling time for $\:{V}_{1}$ using MGO-AO is 6.6754 s, while AO and MGO result in 10.7816 s and 11.2031 s, respectively. Similarly, $\:{V}_{2}$ stabilizes in 10.4099 s using MGO-AO, compared to 11.1309 s (MGO) and 13.1545 s (AO). The tie-line power exchange between the two areas also exhibits improved stability under the MGO-AO approach. As shown in Fig. 6, $\:{P}_{\text{tie\:}}$ stabilizes in 5.312s, significantly improving over 7.6421 s (MGO) and 10.0521 s (AO). This confirms that the proposed hybrid optimization technique enhances power-sharing stability and reduces oscillations. From these observations, we can conclude that the Hybrid MGO-AO technique demonstrates superior performance in mitigating frequency and voltage fluctuations, ensuring faster settling times and better system robustness under load perturbations.

Table 4 Optimal gains for HAO-MGO, MGO and AO techniques for case-1.

Table 5 Case-1: frequency response comparison of different optimization techniques.

Table 6 Case-1: voltage and tie-line power response comparison.

Case-2: comparative stability analysis

A generation loss of 0.05 and a rise in generation of 0.03 p.u. are applied at $\:\text{t}=50\text{}\text{s}$ and $\:\text{t}=70$ s, respectively, while a step load of 0.03 and 0.05 p.u. in area-1 and area-2 are applied as disturbances at $\:\text{t}=20\text{}\text{s}$ and $\:\text{t}=35\text{}\text{s}$, respectively. The optimal gains obtained are tabulated in Table 7 Frequency deviation responses, volatge deviation response in both the areas and tie-line power deviation responses of the system have been shown in Fig. 7. PID controller is used in this test case. Dynamic responses, such as settling time, peak overshoot and undershoot values, for MGO, AO and HAO-MGO approaches have been presented in Tables 8 and 9. From Fig. 7, it is evident that the MGO-AO-based controller ensures a much faster frequency stabilization compared to the other techniques. To justify the novelty of the proposed MGO-AO algorithm for LFC-AVR co-design, a detailed comparative evaluation was conducted against recent state-of-the-art hybrid metaheuristics, including GWO-PSO, Modified SSA, and ARO, as shown Tables 8 and 9. The gains of the recent algorithms are stated in Table 10. While GWO-PSO and SSA demonstrate good initial convergence, they suffer from premature convergence and higher settling times (e.g., 10.29 s and 9.26 s for $\:{\Delta\:}{f}_{1}$, respectively), along with larger overshoot/undershoot values. ARO, though effective in exploration, exhibits less stable voltage control ($\:{\Delta\:}{V}_{2}$ POS $\:=$ 1.2258) and longer frequency settling ($\:{\Delta\:}{f}_{2}=9.02\text{}\text{s}$). In contrast, the proposed MGO-AO algorithm achieves the best trade-off between exploration and exploitation by integrating the global search capabilities of MGO and the local refinement ability of AO. It records the lowest settling times (8.43 s for $\:{\Delta\:}{f}_{1}$ and 9.02 s for $\:{\Delta\:}{f}_{2}$), minimal peak overshoots ($\:\text{P}\text{O}\text{S};0.014$), and superior voltage and tie-line stability, outperforming all compared techniques. This quantifiable superiority across multiple dynamic indices affirms the necessity and effectiveness of the MGO-AO hybrid over other recently published optimization approaches. Figure 7 further shows that the proposed Hybrid MGOAO controller minimizes tie-line power oscillations and ensures a faster stabilization. This proves that the hybrid optimization strategy is more effective in controlling inter-area power exchange stability. From the above analysis, we can infer that Hybrid MGO-AO outperforms individual MGO and AO techniques and the recent algorithms ARO, GWO-PSO and Modified SSA, achieving faster frequency and voltage stabilization, reduced overshoot, and improved tie-line power regulation under simultaneous generation and load perturbations.

Table 7 Optimal gains for HAO-MGO, MGO and AO techniques for case-2.

Table 8 Case-2: frequency response comparison of different optimization techniques.

Table 9 Case-2: voltage and tie-line power response comparison.

Table 10 Optimal gains for ARO, GWO-PSO and modified SSA techniques for case-2.

Fig. 6

Test system responses for 3% step load perturbation (SLP) in Area 1 and a 5% SLP in Area 2.

Fig. 7

Test system responses for a 5% generation loss in Area 1 along with 3% SLP, and a 3% increase in generation in Area 2 with $\:5\text{\%}$ SLP.

Fig. 8

Frequency, voltage, and tie-line power responses with and without BESS.

Fig. 9

Frequency, voltage, and tie-line power responses with and without BESS.

Case 3: BESS integration with load perturbations

In this test case, the system is analyzed with and without the integration of Battery Energy Storage System (BESS) while introducing Step Load Perturbation (SLP) of 0.03 and 0.05 p.u at $\:\text{t}=25\text{}\text{s}$ and $\:\text{t}=50\text{}\text{s}$ in area 1 and area 2. The optimal gains obtained are tabulated in Table 11. PID controller is used in this test case. The goal is to examine the impact of BESS on system stability under load disturbances. The performance metrics for with and without BESS integration are presented in Tables 12 and 13, while the dynamic responses of frequency ($\:{\Delta\:}{f}_{1},{\Delta\:}{f}_{2}$), voltage ($\:{V}_{1},{V}_{2}$), and tie-line power ($\:{P}_{\text{tie\:}}$) are depicted in Fig. 8. As shown in Fig. 8, integrating BESS significantly enhances frequency stability, leading to reduced frequency deviations and faster settling times. The Hybrid MGO-AO method stabilizes Δf_1 in 9.4861 s, while the AO and MGO methods take 10.0409 s and 14.808 s, respectively. Δf_2 shows a similar pattern, with MGO-AO settling in 9.2641 s, which is faster than AO (10.6347 s) and MGO (10.0404 s). The findings demonstrate that BESS, when combined with MGOAO, accelerates frequency recovery and reduces oscillations. Figure 8 shows that adding BESS makes the voltage more stable. The settling time for V_1 with MGO-AO is 6.6754 s. This is a big improvement over AO (10.7816 s) and MGO (11.2031 s).

Table 11 Optimal gains for PID controller with BESS and without BESS for case-3.

Table 12 Case-3: frequency response comparison.

Table 13 Case-3: voltage and tie-line power response comparison.

Fig. 10

Frequency, voltage, and tie-line power responses with PID and with FOPID.

For V_2, MGO-AO stabilizes in 10.4099 s, while AO and MGO stabilize in 13.1545 s and 11.1309 s respectively, these results show that BESS improves voltage regulation ensuring minimal fluctuations and faster recovery. A significant observation from Fig. 8 is that the integration of BESS reduces tie-line power deviations. The settling time for the MGO-AO method is 5.312 s, while the settling time for AO is 10.0521 s and the settling time for MGO is 7.6421 s. This means that BESS helps to keep the flow of power between connected areas stable, which reduces power imbalances caused by changes in load. The results show that adding BESS makes the system much more stable, especially when it comes to quickly stabilizing frequency and voltage, reducing overshoot, and improving tie-line power control. The Hybrid MGO-AO methodology surpasses the individual MGO and AO methodologies, exhibiting improved oscillation damping and greater resilience in load disturbance situations.

Case 4: BESS integration with load and generation perturbations

In this test case, the system is analyzed with and without the integration of Battery Energy Storage System (BESS) while introducing Step Load Perturbation (SLP) of 0.03 and 0.05 p.u at $\:\text{t}=20\text{}\text{s}$ and $\:\text{t}=35\text{}\text{s}$ in area 1 and area 2, along with a 0.05 p.u of generation loss and a 0.03 p.u of increase in generation at $\:\text{t}=50\text{}\text{s}$ and $\:\text{t}=70\text{}\text{s}$ in area 1 and area 2. The optimal gains obtained are tabulated in Table 14. PID controller is used in this test case. The goal is to examine the impact of BESS on system stability under load and generation disturbances. The performance metrics for with and without are presented in Tables 15 and 16, while the dynamic responses of frequency ( $\:{\Delta\:}{f}_{1}$, $\:{\Delta\:}{f}_{2}$ ), voltage ( $\:{V}_{1},{V}_{2}$ ), and tie-line power ( $\:{P}_{\text{tie\:}}$ ) are depicted in Fig. 9. Table 15 shows that adding BESS makes the system’s frequency much more stable. The settling time of Δf_1 decrease from 8.43137 s to 8.3142 s, while Δf_2 increases from 8.86101 s to 8.53146 s, which means that frequency fluctuations are stabilizing more quickly.

Table 14 Optimal gains for PID controller with BESS and without BESS for case-4.

Table 15 Case-4: frequency response comparison of different optimization techniques.

Table 16 Case-4: voltage and tie-line power response comparison.

Also, the Peak Overshoot (POS) and Peak Undershoot (PUS) measures show BESS make frequency deviations smaller, which shows how well they work to reduce oscillations. Table 16 shows how the voltage and tie-line power change for each configuration. It is clear that adding BESS makes overshoots less likely and settling times better. The system with BESS stabilizes at 6.2837 s for ΔV_1, while the system without BESS stabilizes at 6.599 s. Likewise, for ΔV_2, the time it takes to settle goes from 8.5623 s to 8.3797 s. Also, the tie-line power deviation (ΔP_tie-line) is more stable, as shown by the smaller undershoot from − 0.149 to 0.141.

Figure 9 illustrates a more refined and steady response with BESS incorporation, corroborated by the numerical results. According to the results, BESS enhances frequency and voltage stability by reducing settling times and peak deviations, which is crucial to mitigating disturbances in modern power grids.

Case 5: robustness analysis with FOPID controller

Robustness tests include step load changes (3% in Area 1 and 5% in Area 2), a 5% generation outage at t = 50 s, and a 3% generation increase at t = 70 s. The results show that MGO-AO optimized FOPID is still the best way to keep things stable and stop oscillations. This test case uses a Fractional Order PID (FOPID) controller instead of the usual PID controller. It keeps the same problems and adds the BESS system from Case 4. Table 17 shows the best benefits that can be achieved. The FOPID controller is used in this experiment. The main goal of this study is to see how the FOPID controller affects system performance in terms of voltage regulation, frequency stabilization, and power exchange between ties. We look at frequency changes (Δf_1, Δf_2), voltage differences (ΔV_1, ΔV_2), and tie-line power transfer (ΔP_tie-line) to see how well the FOPID controller works. Table 18 shows how the frequency response of PID and FOPID controllers compares. The FOPID controller has a lower peak undershoot (PUS) for Δf_1, going from 0.2004 (PID) to 0.1919 (FOPID), and for Δf_2, going from − 0.30238 (PID) to − 0.2545 (FOPID). This shows that the damping characteristics have gotten better.

Table 17 Optimal gains for HAO-MGO-PID and HAO-MGO-FOPID for case-5.

Table 18 Case-5: frequency response comparison.

A marginal decrease in peak overshoot (POS) is noted in Δf_1, from 0.01067 (PID) to 0.00982 (FOPID).

However, the POS in $\:{\Delta\:}{f}_{2}$ increased slightly from 0.02823 to 0.0342, indicating that while damping improved, initial overshoot was slightly higher. Settling times remained nearly the same, with $\:{\Delta\:}{f}_{1}$ reducing slightly (8.3142 s to 7.7148 s), while $\:{\Delta\:}{f}_{2}$ showed a minor improvement (8.53146 s to 8.3717 s). Overall, the FOPID controller improves damping performance, but further fine-tuning is needed to minimize the initial overshoot. Table 19 compares the voltage and tieline power response with PID and FOPID controllers. The key observations include settling time improvement, where $\:{\Delta\:}{V}_{1}$ reduces from 6.2837 s (PID) to 5.9175 s (FOPID). Similarly, $\:{\Delta\:}{V}_{2}$ shows a Notable decrease from 8.3797 s (PID) to 7.28762 s (FOPID), signifying an expedited system response. The tie-line power deviation ΔP_tie-line stabilizes more rapidly with the FOPID controller, achieving a time of 6.9507 s compared to 7.07961 s with the PID controller. ΔV_1 shows a decrease in peak overshoot (POS) from 1.177 to 1.124, and ΔV_2 shows the same pattern. The improvements show that the FOPID controller improves the system’s transient response, especially when it comes to stabilizing voltage and tie-line power. FOPID works much better than PID in every case. For example, Δf_1 stabilizes in 7.714 s with FOPID, which is less than the 8.314 s it takes with PID. This shows that there is less overshoot (0.009 pu against 0.106 pu). Similar improvements can be seen in ΔV and tie-line power deviations, which means that the damping is working better. Figure 10 shows how the system with PID and FOPID controllers responds differently.

Table 19 Case-5: voltage and tie-line power response comparison.

The FOPID controller enhances transient stability, reduces settling time, and improves damping. However, frequency overshoot still requires further optimization to achieve a more balanced tradeoff between response speed and overshoot minimization.

Implementation in real time with dSPACE

The suggested FOPID-based control technique for frequency and voltage stability in a multiarea hybrid power system has been validated using the experimental setup shown in Fig. 11. HIL validation was carried out using a dSPACE MicroLabBox 1202. The controller model was deployed from MATLAB/Simulink with a fixed-step ode 3 solver at $\:{T}_{s}=1\text{}\text{m}\text{s}$. Key signals were mapped as follows: $\:\text{A}\text{O}1-\text{A}\text{O}2={\Delta\:}{f}_{1},{\Delta\:}{f}_{2}$; AO3–AO4 $\:=$ terminal voltages $\:{V}_{1},{V}_{2}$; digital I/O $\:=$ event flags. Sixteen-bit analog resolution with 2nd-order anti-aliasing was used. The FOPID computations ran at highest task priority, and data were recorded via Controldesk at $\:1-\text{k}\text{H}\text{z}$ sampling. Real-time traces matched offline simulations within $\:\pm\:5\text{\%}$ in settling time and overshoot, demonstrating feasibility for practical deployment. The dSPACE ControlDesk software is used for model implementation, parameter tuning, and real-time monitoring. The real-time execution of the designed system is managed using MATLAB/Simulink, where the control algorithm is deployed onto the dSPACE platform.

The analog and digital input/output (I/O) interfaces of the MicroLabBox facilitate seamless interaction between the simulated system and the hardware setup. The real-time frequency and voltage response of the PID and FOPID integrated model (case 5) is assessed using oscilloscope-based monitoring, as depicted in Fig. 12, where critical performance parameters, including settling time, overshoot, and steady-state error, are studied. dSPACE MicroLabBox real-time responses confirm FOPID controller’s effectiveness in diminishing fluctuations, improving stability, and achieving faster settling times compared to conventional PID control, as shown by simulation results. Hardware-in-the-loop (HIL) validation is important since it replicates real-time operational conditions, such as computational latencies, measurement noise, and nonlinearities in hardware interfaces. This validates the controller’s effectiveness beyond simulations and indicates preparedness for practical application.

Conclusion

Detailed evaluation of a Hybrid Moss Growth Optimization-Artemisinin Optimization (MGO-AO)-based controller for Automatic Voltage Regulation (AVR) and Load Frequency Control (LFC) has been performed for a multi-area hybrid power system. To assess the impacts of several disturbances, including load perturbations, generation losses, and battery energy storage systems (BESS), five test cases were analyzed.

Fig. 11

LFC-AVR H-I-L experimental setup using dSpace Micro LabBox 1202.

Fig. 12

Verification of the suggested controller’s DSO response.

Simulation experiments show that the Hybrid works better when you cut down on overrun and settling time. The MGO-AO method always made the frequency and voltage more stable. Case 5 showed even more improvements when a Fractional Order PID (FOPID) controller was used instead of a regular PID controller. The FOPID controller outperformed the PID controller by stabilizing faster, reducing frequency deviations, and improving damping characteristics. Fractional order tuning’s ability to adapt made control more precise, which improved the balance between stability and response speed.

AVR Loop’s resilience and optimal control method’s efficiency were demonstrated by the constant voltage in Areas 1 and 2. The combination of BESS and the FOPID controller significantly improved system stability by quickly correcting for fluctuations and maintaining a robust voltage profile. Results show that the proposed hybrid MGO-AO with FOPID controller outperforms the conventional PID controller, thus enabling sophisticated power system control. Future studies could examine AI-based predictive control techniques and real-time adaptive implementations to optimize efficiency. The stability of hybrid systems is enhanced by a unified FOPID tuned by MGO-AO and coordinated with HVDC and BESS. Improvements are consistent under multiple disturbances and validated via HIL experiments, demonstrating its readiness for real-world applications.