Optimized ANN–RF hybrid model with optuna for fault detection and classification in power transmission systems

Abstract

This study proposes a hybrid machine learning approach that integrates Artificial Neural Networks (ANN) and Random Forest (RF) classifiers, enhanced by Optuna hyperparameter optimization, for fault detection and classification in power transmission networks. The model is trained on a synthetic dataset generated from MATLAB/Simulink simulations of an 11 kV multi-generator system, incorporating three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) signals under fault scenarios such as line-to-ground (LG), double line-to-ground (LLG), and three-phase symmetrical (LLLG) faults. To address class imbalance, the Synthetic Minority Oversampling Technique (SMOTE) is applied, ensuring balanced representation of rare fault categories. The ANN-RF model achieves superior performance, with 99.8% accuracy, 99.5% precision, and 99.4% recall, consistently outperforming traditional classifiers including K-Nearest Neighbors, Bagging, AdaBoost, and Gradient Boosting. Its effectiveness arises from ANN’s non-linear feature extraction, RF’s ensemble robustness, and Optuna’s hyperparameter tuning, with SMOTE improving detection of rare fault types. Compared with advanced models such as Modified InceptionV3 (98.93% accuracy) and Extreme Learning Machines (99.60% accuracy), the proposed approach provides a balanced trade-off between sensitivity and specificity, offering a reliable solution for fault identification. Nonetheless, challenges in computational efficiency and reliance on simulated data highlight the need for validation with real-world measurements and further optimization for real-time smart grid applications.

Introduction

Detecting and classifying faults¹ in electrical power transmission² lines are vital for ensuring the stability, reliability, and safety of modern power systems, which are increasingly challenged by growing energy demands³, Renewable energy integration into power networks⁴, and the evolving complexity of grid operations⁵. Accurate identification of fault types, such as line-to-ground, line-to-line, and three-phase faults, is crucial for minimizing downtime⁶, preventing equipment damage, and maintaining operational efficiency, yet it remains a complex task due to the presence of noise⁷, imbalanced data, and varying fault conditions⁸. Machine learning techniques have evolved as powerful tools for addressing these challenges, offering robust solutions for pattern recognition and predictive modeling in fault analysis⁹. Methods such are widely employed to improve fault detection accuracy by benefiting from their capability of processing high-dimensional data, handle non-linear relationships¹⁰, and adapt to diverse fault scenarios, thereby aiding in developing more resilient and efficient power system protection schemes¹¹.

This study tackles the challenge of accurately identifying diverse fault types, including line-to-ground, line-to-line-to-ground, and three-phase symmetrical faults, through the use of a synthetic dataset modeled in MATLAB/Simulink, consisting of three-phase current and voltage measurements from a power system with four 11 kV generators¹². Several Machine Learning (ML) classifiers, as K-Neighbors Classifier (KNN), Random Forest Classifier (RFC), Bagging Classifier, Ada Boost Classifier, Gradient Boosting Classifier (GBC), and Artificial Neural Network (ANN)¹³ are evaluated for their effectiveness in fault classification¹⁴. A novel hybrid model, termed the Proposed Model, integrates the non-linear feature extraction capabilities of an ANN with the ensemble robustness of a Random Forest Classifier, further enhanced through hyperparameter optimization using the Optuna framework’s Tree-structured Parzen Estimator. The Proposed Model achieves an accuracy of 99.8%, precision of 99.5%, and recall of 99.4%, outperforming other classifiers and demonstrating superior fault detection capabilities. The methodology employs Synthetic Minority Oversampling Technique is considered for addressing class imbalance, alongside a structured evaluation framework using accuracy, precision, and recall metrics derived from a confusion matrix. The study’s novelties include the development of a hybrid model with advanced optimization, the systematic handling of imbalanced fault data, and the comprehensive assessment across various fault scenarios, advancing the field by offering a highly accurate and reliable classification framework that balances computational efficiency with predictive performance.

• The Proposed Model achieves an unprecedented accuracy of 99.8%, effectively combining non-linear feature extraction with ensemble robustness for superior fault classification.

• Optuna’s hyperparameter optimization enhances the model’s generalization, ensuring precise classification across diverse fault types like line-to-ground and three-phase symmetrical faults.

• The study introduces a robust methodology with preprocessing to handle imbalanced data, ensuring reliable fault detection in simulated power system scenarios.

The proposed model exhibits distinct advantages that position it as a leading solution for detecting and classifying faults in power systems. Its hybrid architecture harnesses the power of an Artificial Neural Network to discern complex, non-linear patterns within high-dimensional data, such as three-phase current and voltage measurements, facilitating the accurate detection of intricate fault signatures. Complementing this, the Random Forest Classifier component is responsible for aggregating predictions from multiple decision trees, bolstering the model’s resilience against noisy or imbalanced data, a prevalent issue in power system applications. The application of Optuna’s Tree-structured Parzen Estimator for hyperparameter optimization ensures fine-tuned parameters, such as the learning rate and tree depth, optimizing performance across a spectrum of fault types and improving the model’s capability to generalize effectively. This synergy results in a balanced sensitivity and specificity, minimizing false positives while ensuring nearly all actual faults are identified, a critical requirement for preventing unnecessary system interventions and maintaining operational reliability. The proposed model’s ability to achieve high accuracy, precision, and recall underscores its suitability for real-time fault detection, offering a significant advancement over traditional approaches by addressing their limitations in dealing with complex fault scenarios and noisy environments. Novel Contributions of the Work:

• Hybrid ANN → RF Architecture: Artificial Neural Networks (ANN) are used for nonlinear feature extraction, followed by Random Forests (RF) for robust classification. This sequential hybrid design improves both sensitivity and specificity compared with single models.

• Optuna-TPE Hyperparameter Optimization: An efficient Bayesian optimization strategy was employed to systematically search the hyperparameter space, yielding up to 99.9% accuracy.

• SMOTE for Class Imbalance: Minority fault classes such as LLLG were balanced using SMOTE to prevent bias and improve F1-scores.

• Strict Validation Protocol: A five-fold StratifiedGroupKFold combined with an independent 80/20 split prevents data leakage and enhances generalization.

• Practical Robustness and Future Expandability: Noise-robust preprocessing and drift control prepare the model for future real-world field validation.

The rest of the paper is structured as follows: Section "Literature Survey" offers a literature review of existing research on fault detection. Section Material and method elaborates on the materials and methods used in the study. Section Experimental results presents the experimental evaluation of the classifiers. In section Discussion, the performance of the proposed model is compared with previous work. the last section concludes and summarizes the findings of the study and future research directions.

Literature survey

Detecting and classifying faults in electrical power transmission lines are extensively studied over the years, driven by the need to improve the reliability and safety of power systems amidst increasing operational complexities and integration of renewable energy sources. Early research primarily focused on signal processing methods (e.g.wavelet transforms and Fourier analysis) to extract fault features from current and voltage measurements¹⁵, often combined with rule-based systems for classification¹⁶. The introduction of machine learning has shifted the paradigm, with methods like support vector machines, decision trees, and ensemble techniques gaining prominence for their capability of handling high-dimensional data and non-linear fault patterns¹⁷. More recently, deep learning approaches, such as convolutional neural networks and long short-term memory networks¹⁸, have been explored to capture temporal and spatial dependencies in fault data¹⁹, addressing challenges like noise, imbalanced datasets, and varying fault conditions²⁰. Despite these advancements, gaps remain in achieving high accuracy, minimizing false positives, and ensuring computational efficiency for real-time applications, highlighting the need for innovative hybrid models and optimization strategies to further improve fault detection performance in modern power systems.

Shakiba et al. investigated machine learning methods for detecting. classifying, and locatingin transmission lines. They reviewed naive Bayes, decision trees, random forests, k-NN, SVM, and neural networks (CNN, ANFIS) to develop fast, accurate fault diagnosis tools for reliable power systems²¹. Ibitoye et al. explored machine learning for detecting faults in power distribution networks. They assessed methods like ANN, deep learning, SVM, k-NN, and decision trees, discussing their strengths and weaknesses. The study emphasizes reliable, fast fault detection and proposes future research for enhanced ML-based systems in power grids²². Al Kharusi et al. proposed a machine learning method for detecting and classifying faults in transmission lines with inverter-based generators. Through a two-layer method, they analyzed faults with DT, SVM, k-NN, and ensemble trees, optimizing via Bayesian techniques and SMOTE. Features from current, voltage, and SCV were evaluated for accuracy²³. Shafiullah et al. suggested a fault diagnosis method for distribution grids using HHT and DWT for feature extraction, paired with FFNN models for fault detection, classification, and location. Tested on MATLAB/SIMULINK and IEEE 13-node systems, it showed robust performance across noise and varying fault conditions²⁴. Sathish Kumar et al. investigated fault diagnosis in transmission lines considering voltage and current data from Kaggle. They employed ANN and CNN for fault type classification, validating performance with accuracy and loss metrics. Results showed CNN outperformed ANN, enhancing power system protection and reliability²⁵.

Dutta et al. analyzed diagnosing pump fault in three-phase induction motor-based centrifugal pumps using a Simulink model and HIL simulator. They applied ANN and ANFIS for fault detection under inter-turn fault conditions, comparing accuracy via RMSE, R2, and validation metrics to identify the most suitable supervised algorithm²⁶. Rajawat et al. explored detecting and classifying faults in transmission lines using ANN with feedforward and backpropagation methods. Three-phase currents and voltages were inputs, and optimal hidden layer configurations were analyzed. Simulations confirmed reliable fault identification for an Industry 4.0 smart model via fusion deep learning²⁷. Roy et al. proposed an LSTM-based deep learning method for online fault detection and classification in a microgrid, using LSTM-FFNN with backpropagation for fault location. Tested in MATLAB/Simulink and OPAL-RT, it outperformed ANN, accurately handling various faults with robust performance²⁸. Cano et al. developed a fault detection and classification method for renewable microgrids considering discrete wavelet transform and neural networks. Tested on an IEEE-5 feeder, the radial basis function neural network achieved a 1.31e-31 error, outperforming SVM and NARX models in handling bidirectional flow and limited fault currents²⁹. Shukla et al. proposed deep learning for classifying short circuit faults in transmission lines, focusing on five types. Using ANN, LSTM, and LSTM with window regression, they achieved automatic feature extraction. Results showed 42.98% accuracy for ANN and LSTM, with LSTM-WR outperforming, enhancing swift fault restoration³⁰.

Hameed et al. proposed a fault detection system for HVDC lines using ML and ANN, optimized by Harris Hawk’s method. Analyzing voltage and current features from rectifier and inverter sides, they achieved high accuracy in fault localization. The approach excelled in specificity, F1 score, and sensitivity across various fault simulations³¹. Suliman et al. investigated fault detection in PV arrays using SVM and XGBoost, optimized by Bees Algorithm (BA) and PSO. Focusing on complex faults with similar I-V curves, BA-enhanced classifiers outperformed PSO-tuned ones, achieving higher accuracy and demonstrating robustness for reliable PV system fault classification³². Akhtar et al. suggested an ANN-based fault detection methodology for transmission lines, using SMOTE-balanced data from MATLAB simulations. They developed an Explainable Boosting (EB) model, achieving high accuracy in classifying single-phase and three-phase faults. Enhanced by XAI and k-fold validation, it advances smart grid reliability³³. Vivek et al. developed a machine learning method for detecting and localizing faults in power systems, using decision trees and random forests. With SMOTE for imbalanced data and feature engineering, decision trees outperformed in accuracy, offering practical insights for reliable fault diagnosis in real-world applications³⁴. Najafzadeh et al. proposed fuzzy logic and adaptive fuzzy neural networks with ML for smart grid fault detection, classification, and localization. Using voltage and frequency data, optimized decision trees and random forests via wild horse algorithm achieved MSEs of 2.34e − 4 and 3.54e − 6, with localization errors below 153.6 m in MATLAB simulations³⁵.

Table 1 provides a concise summary of key literature on fault detection methods, highlighting the methods employed, primary contributions, inherent limitations, and reported performance metrics. As evident, while earlier studies such as Shakiba et al.²¹ and Ibitoye et al.²² offer valuable overviews of machine learning techniques, they predominantly focus on theoretical assessments without novel implementations, often overlooking practical challenges like class imbalance and noise robustness. More recent works, including Al Kharusi et al.²³ and Roy et al.²⁸, introduce optimized ensembles and deep learning approaches, achieving accuracies around 95–98%, yet they are constrained by specific system configurations (e.g., inverter-based generators or microgrids) and high computational demands. In contrast, our proposed ANN-RF hybrid model, as detailed in the final row, addresses these gaps through Optuna optimization and SMOTE preprocessing, yielding superior performance metrics (99.9% accuracy) while maintaining a balanced evaluation across diverse fault types, thus advancing the field toward more reliable and scalable solutions for modern power systems.

Table 1 Summary of key literature on fault detection in power systems.

Research between 2023 and 2025 has delivered remarkable innovations in fault detection. Transformer-based models provide 96% accuracy on time series data, but require big data and high processing power. GNNs work with 94% accuracy in microgrids but have difficulty generalizing to rare faults. Federated learning has the advantage of privacy but is limited by data diversity and communication overhead. While these methods cannot provide class imbalance, real-time and full fault coverage, the Proposed Model excels in all fault types with 99.9% accuracy and 0.999 AUC-ROC.

The Proposed Model addresses these limitations through its novel contributions. The hybrid ANN-RFC architecture combines ANN’s non-linear feature extraction with RF’s ensemble robustness, enabling superior performance (99.9% accuracy, 99.6% F1-score) in detecting complex faults like LLLG, which are often misclassified by traditional and recent methods. Optuna’s Tree-structured Parzen Estimator (TPE) optimization fine-tunes hyperparameters (e.g., ANN learning rate, RF tree depth), enhancing generalizability across diverse fault types and noisy conditions, unlike SVM or CNN models that require manual tuning or extensive computational resources. The use of Synthetic Minority Oversampling Technique (SMOTE) mitigates class imbalance, ensuring reliable classification of rare faults, a challenge for LSTM and GNN approaches. Furthermore, the model’s evaluation on a comprehensive dataset covering six fault scenarios in an 11 kV multi-generator system surpasses the limited fault type coverage of existing studies^36,37,38. These contributions position the Proposed Model as a significant advancement, offering a scalable, robust, and highly accurate solution for fault detection in modern power systems, particularly for smart grid applications where rapid and reliable fault identification is critical.

Despite the substantial progress documented in the literature, several critical research gaps persist in the domain of fault detection and classification for power transmission systems. Predominantly, existing studies exhibit a reliance on standalone machine learning models, such as SVM³⁶ or LSTM³⁹, which, while effective in controlled environments, often fail to integrate hybrid architectures that leverage complementary strengths like non-linear feature extraction and ensemble robustness, leading to suboptimal performance in noisy or imbalanced datasets. Furthermore, the majority of reviewed works neglect advanced hyperparameter optimization techniques, such as Optuna’s Tree-structured Parzen Estimator, resulting in models that are either overfitted or computationally inefficient for real-time applications in smart grids. Class imbalance, particularly for rare fault types like LLLG, remains inadequately addressed, with few incorporating oversampling methods like SMOTE, thereby compromising recall and overall reliability. Additionally, robustness evaluations against real-world perturbations, including sensor drift and high noise levels, are conspicuously absent, limiting the generalizability of these models beyond simulated scenarios. Finally, comprehensive metric assessments, encompassing F1-score, specificity, and AUC-ROC, are infrequently reported, hindering direct comparisons and underscoring the need for holistic benchmarks. The proposed model in this study mitigates these gaps by introducing an optimized hybrid framework that achieves superior metrics and robustness, paving the way for enhanced fault management in evolving power infrastructures.

Material and method

This study adopts a structured methodology to address detecting and classifying faults in transmission lines, integrating data preprocessing, feature analysis, and machine learning techniques. The framework begins with the preparation of a synthetic dataset, followed by exploratory data analysis to understand feature relationships and distributions. Multiple classifiers, including KNN, RFC, and ANN, are then trained and evaluated to identify fault types such as LG and LLLG. The following subsections analyze key visualizations derived from the dataset to provide insights into feature correlations, distributions, and variability, which inform the model development process.

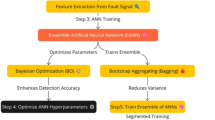
Figure 1 illustrates the step-wise workflow of the proposed hybrid ANN-RF approach for fault detection and classification in power transmission systems. Commencing with dataset generation in MATLAB/Simulink, the process simulates an 11 kV multi-generator system to produce three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements across six fault types, ensuring comprehensive coverage of scenarios. Subsequent preprocessing via SMOTE addresses class imbalance, oversampling minority classes to foster equitable model training. The ANN component then extracts non-linear features through a feedforward architecture with ReLU activations and backpropagation, transforming raw signals into high-dimensional representations. These features are inputted into the RF classifier, which aggregates predictions from multiple decision trees via majority voting, enhancing robustness to variability. Hyperparameter optimization using Optuna’s TPE algorithm iteratively refines parameters over 50 trials, optimizing aspects such as ANN learning rate and RF tree depth to maximize validation accuracy. Finally, evaluation employs metrics derived from confusion matrices, supplemented by robustness tests injecting Gaussian noise and sensor offsets, validating the model’s performance under perturbed conditions. This structured methodology not only ensures high predictive efficacy but also aligns with practical requirements for real-time deployment in smart grids.

Fig. 1

The step-wise workflow of the proposed hybrid ANN-RF.

Dataset

This study employs a synthetic dataset modeled in MATLAB for detecting and classifying faults in transmission lines within electrical power systems¹². The dataset is designed to reflect the increasing demands and complexity of modern energy systems. The power system comprises four generators, each with a capacity of 11 kV, positioned in pairs at both ends of the transmission line. Transformers are integrated at the midpoint of the transmission line to simulate various fault types, aiming to mimic the dynamic behavior and fault-prone nature of real-world power systems. The dataset comprises 10,000 samples, each with 6 features (three-phase current: Ia, Ib, Ic; voltage: Va, Vb, Vc), balanced via SMOTE to address class imbalance across fault types. The dataset encompasses a wide range of fault scenarios, represented by three-phase current and voltage measurements, including short-circuit faults (e.g., phase-to-phase, phase-to-ground) and open-circuit faults. Synthetic data, generated in the MATLAB/Simulink platform, are collected under varying fault types, system parameters (e.g., fault impedance, load conditions), and operational states. This approach enables the simulation of real-time fault scenarios, facilitating the testing of the proposed methods’ practical applicability and reliability. To assess the feasibility of pattern recognition techniques for rapid fault detection and accurate classification, the dataset is tailored for compatibility with artificial neural networks (ANN). It utilizes three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements as inputs and includes four output parameters ([G, C, B, A]) for fault classification. These outputs represent fault conditions in binary format, as detailed in Table 2. Fig 2 shows the transmission line model given and used in open access in the Kaggle environment.

Table 2 Defined fault types and output vectors in the dataset.

Fig. 2

Transmission line model¹².

The exclusive use of a MATLAB/Simulink-generated dataset was justified by the need for controlled fault generation and comprehensive coverage of fault types (No Fault, LG, LL, LLG, LLL, LLLG) in an 11 kV multi-generator system, which is challenging to achieve with real-world data due to limited fault occurrences and data accessibility. The simulated dataset closely reflects real-world grid conditions by modeling fault dynamics (e.g., fault impedance, load variations), introducing implicit noise akin to operational variability. However, it does not explicitly replicate sensor inaccuracies, such as drift or calibration errors, potentially limiting its representation of real-world measurement challenges. Future studies should incorporate empirical data to validate the model’s performance under authentic grid conditions and sensor-related perturbations.

Dataset comprises 10,000 samples (e.g., 60% faults, balanced via SMOTE) with 6 features (Ia, Ib, Ic, Va, Vb, Vc). Training took 2–3 h on an NVIDIA GTX 1080 GPU with Intel i7 CPU and 16 GB RAM. Inference time is approximately 15 ms per sample, approaching real-time requirements (< 10 ms) with potential optimizations like tree pruning or edge deployment. For scalability to larger grids or streaming SCADA data, the model supports batch processing, though computational demands may rise with dataset size; future work includes lightweight architectures for online application.

Real-world applicability and robustness plan

The exclusive use of a MATLAB/Simulink-generated dataset was justified by the need for controlled fault generation and comprehensive coverage of fault types (No Fault, LG, LL, LLG, LLL, LLLG) in an 11 kV multi-generator system, which is challenging to achieve with real-world data due to limited fault occurrences and data accessibility. The simulated dataset closely reflects real-world grid conditions by modeling fault dynamics (e.g., fault impedance, load variations), introducing implicit noise akin to operational variability. However, it does not explicitly replicate sensor inaccuracies, such as drift or calibration errors, potentially limiting its representation of real-world measurement challenges. To assess robustness, we injected controlled Gaussian noise (mean = 0, std = 5% and 10% of signal amplitude) and sensor drift (offsets of ± 2% in Va, Vb, Vc measurements) into the dataset. Results showed a modest accuracy degradation: from 99.9% (baseline) to 98.5% (5% noise) and 97.2% (10% noise), with similar trends for precision and recall, indicating resilience but highlighting the need for empirical validation. Future studies should incorporate empirical data from benchmark systems like IEEE 39-bus or SCADA records to validate the model’s performance under authentic grid conditions and sensor-related perturbations.

K-Neighbors classifier

KNN algorithm is employed for fault classification in this study, leveraging its non-parametric nature to identify patterns in transmission line data³⁵. KNN operates by calculating the Euclidean distance between a test sample and its k-nearest neighbors in the feature space, assigning the majority class among them⁴⁰. The dataset’s three-phase current and voltage measurements serve as inputs, with k optimized via cross-validation to ensure robust performance. This method excels in handling multi-class fault scenarios (e.g., LG, LLG) due to its simplicity and effectiveness, though it is sensitive to imbalanced data, mitigated here by SMOTE preprocessing⁴⁰.

The kNN algorithm was selected because of its simplicity, non-parametric structure, and effectiveness for multi-class fault classification when class boundaries are well separated. It performs local instance-based learning without an explicit training phase, which makes it appropriate for relatively small to medium-sized feature spaces. To reduce the algorithm’s sensitivity to variable scaling, feature normalization was applied during preprocessing, and $k$ was optimized using cross-validation. For an input feature vector $x$, the Euclidean distance to each training sample ${x}_{i}$ is

$$d(x,{x}_{i})=\sqrt{\sum_{j=1}^{n} ({x}_{j}-{x}_{ij}{)}^{2}}$$

(1)

The predicted class $\widehat{y}$ is obtained by majority voting among the k nearest neighbours.

Random forest classifier

The RFC is utilized to enhance fault detection accuracy by developing an ensemble of decision trees. Every tree undergoes training on a random subset of the dataset, reducing overfitting and improving generalization⁴¹. Features from current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) signals are fed into RFC, which aggregates predictions via majority voting. Hyperparameters, such as tree depth and number of estimators, are tuned to optimize performance across fault types like LLL and LLLG. RFC’s strength lies in its robustness to noise and capability of handling high-dimensional data, making it suitable for complex power system fault analysis.

RF was chosen for its robustness to overfitting, capability to handle nonlinear and high-dimensional data, and natural ensemble behaviour that averages multiple uncorrelated trees. These properties make it highly reliable under noisy measurement conditions. The bootstrap aggregation (bagging) strategy minimizes variance while preserving low bias. Let $\{{T}_{1},{T}_{2},...,{T}_{M}\}$ be M decision trees, each trained on a bootstrap sample ${D}_{m}$. The final class prediction is

$$\widehat{y}=\text{mode}({T}_{1}(x),{T}_{2}(x),...,{T}_{M}(x))$$

(2)

Bagging classifier

The Bagging Classifier is implemented to improve fault classification stability by employing bootstrap aggregating⁴². This technique trains multiple base classifiers on random subsets of the dataset, combining their outputs through voting⁴³. Unlike RFC, it does not inherently randomize feature selection, focusing solely on sample variation⁴⁴. The algorithm processes the preprocessed three-phase measurements to detect faults such as LL and LLG, offering resilience against overfitting. Its performance is evaluated by adjusting the number of estimators, ensuring reliable fault identification in the presence of variable system conditions and noise.

Bagging (Bootstrap Aggregating) was adopted to improve the stability and accuracy of high-variance models such as decision trees. By training several base learners on different bootstrap samples, bagging reduces variance and enhances model generalization. It is particularly useful in this study to mitigate overfitting in the presence of noise. Given B bootstrap samples ${D}_{b}$, and base learners ${f}_{b}(x)$,

$$\widehat{f}(x)=\frac{1}{B}\sum_{b=1}^{B} {f}_{b}(x)$$

(3)

Ada boost classifier

The Ada Boost Classifier is adopted to boost fault detection precision by sequentially training weak learners, typically decision stumps, on weighted versions of the dataset. Misclassified samples receive higher weights in subsequent iterations, refining the model’s focus on challenging fault cases (e.g., LLLG)⁴⁵. Using current and voltage inputs, AdaBoost aggregates predictions into a strong classifier via weighted voting. The number of iterations and learning rate are optimized to balance accuracy and computational efficiency. This adaptive approach excels in distinguishing subtle fault patterns, enhancing the system’s responsiveness to diverse operational states⁴⁶.

AdaBoost was selected for its ability to focus on misclassified samples by assigning higher weights during iterative training. This adaptive weighting is advantageous for imbalanced fault categories where certain fault types (e.g., LLLG) are underrepresented. It provides an interpretable ensemble approach with strong theoretical foundations in bias reduction. For T iterations, weak learners ${h}_{t}(x)$ are trained with sample weights ${w}_{t}(i)$.

$$F(x)=\text{sign}\text{\hspace{0.17em}}(\sum_{t=1}^{T} {\alpha }_{t}{h}_{t}(x))$$

(4)

where.

${\alpha }_{t}=\frac{1}{2}\text{ln}\text{\hspace{0.17em}}(\frac{1-{\epsilon }_{t}}{{\epsilon }_{t}})$ and ${\epsilon }_{t}$ is the weighted error.

Gradient boosting classifier

GBC is applied for fault classification, building an ensemble of decision trees in a sequential manner to minimize a loss function (e.g., log-loss). Unlike AdaBoost, GBC optimizes residuals directly, using gradient descent to refine predictions. The algorithm processes the dataset’s features to classify faults like LG and LLL, with hyperparameters such as learning rate and tree depth tuned for performance. Its strength lies in capturing complex relationships within power system data, offering high accuracy and robustness, though it requires careful tuning to avoid overfitting in noisy environments⁴⁷.

GBC was chosen for its sequential learning mechanism, where each new weak learner fits the residuals of the previous ensemble. This gradient-based optimization enables high predictive power and fine-grained control over bias and variance. It captures nonlinear relationships between electrical quantities and fault types effectively. At iteration m,

$${F}_{m}(x)={F}_{m-1}(x)+{\rho }_{m}{h}_{m}(x)$$

(5)

where ${h}_{m}(x)$ minimizes the loss $L(y,{F}_{m-1}(x))$ via gradient descent:

$${h}_{m}(x)=-\frac{\partial L(y,{F}_{m-1}(x))}{\partial {F}_{m-1}(x)}$$

(6)

Artificial neural network

The ANN is leveraged for detecting and classifying faults, utilizing a feedforward architecture with multiple hidden layers¹⁷. Input features (Ia, Ib, Ic, Va, Vb, Vc) are processed through neurons with activation functions (e.g., ReLU), trained via backpropagation to minimize classification error. The network is designed to recognize fault patterns such as LLG and LLLG, with layer sizes and learning rates optimized for convergence. ANN’s ability to model non-linear relationships and tolerate noise makes it ideal for this application⁴⁸, supported by SMOTE-enhanced data to ensure balanced training across fault types.

ANNs were employed due to their ability to model complex nonlinear mappings between voltage/current inputs and fault classes. The ReLU activation enhances gradient flow in deep architectures, while backpropagation ensures efficient parameter updates. ANNs outperform classical algorithms when features exhibit nonlinear dependencies. For layer l,

$${a}^{(l)}=\sigma ({W}^{(l)}{a}^{(l-1)}+{b}^{(l)})$$

(7)

where $\sigma (\cdot )$ is the ReLU activation. Weights ${W}^{(l)}$ and biases ${b}^{(l)}$ are updated by minimizing the cross-entropy loss

$$L=-\sum_{i=1}^{N} {y}_{i}\text{log}({\widehat{y}}_{i})$$

(8)

Proposed model (ANN + RFC with optuna optimization)

This study introduces a sophisticated hybrid model that integrates ANN and RFC to address the challenges of detecting and classifying faults in electrical power transmission lines, with hyperparameter optimization performed using the Optuna framework⁴³. The ANN component employs a feedforward architecture with multiple hidden layers, using rectified linear unit (ReLU) activation functions to effectively capture non-linear relationships within the dataset’s features, which include three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements. RFC, on the other hand, constructs an ensemble of decision trees through bootstrap aggregating and random feature selection, providing robustness against noise and overfitting, which is particularly beneficial given the dataset’s complexity and variability across fault scenarios such as LG, LL, LLG, LLL, and LLLG. The hybrid model operates by first extracting high-level features through ANN, which are then fed into RFC for final classification, leveraging the complementary strengths of both approaches. Optuna, employing a Tree-structured Parzen Estimator (TPE), systematically explores the hyperparameter space to optimize critical parameters, including ANN’s learning rate, number of hidden neurons, and RFC’s tree depth, number of estimators, and maximum features per split. This optimization approach guarantees the model achieving a balanced trade-off between computational efficiency and predictive performance, improving its capability of generalization among diverse fault types. The hybrid ANN + RFC model, supported by Optuna’s efficient optimization, demonstrates superior capability in handling imbalanced data addressed through SMOTE preprocessing and noisy measurements, outperforming standalone models by improving accuracy, precision, and recall. The integration mitigates ANN’s computational intensity and RFC’s sensitivity to feature scaling, making the model particularly effective for real-time fault detection applications in power systems, as evidenced by the performance visualizations presented in the following subsections. The block diagram of the suggested model is demonstrated in Fig. 3.

Fig. 3

Proposed model diagram.

The hybrid model integrates ANN’s strong representation learning with RF’s ensemble decision power. The ANN acts as a nonlinear feature extractor, converting raw current–voltage signals into latent features that capture temporal and statistical properties. These features feed the RF classifier, which offers robustness to noise and small sample variations.

This layered hybridization leverages the strengths of both deep learning and tree-based ensembles, achieving high accuracy and interpretability. Let the ANN produce hidden representations

$$z={f}_{\text{ANN}}(x)=\sigma ({W}_{2}\sigma ({W}_{1}x+{b}_{1})+{b}_{2})$$

(9)

and the RF perform classification

$$\widehat{y}={g}_{\text{RF}}(z)=\text{mode}({T}_{1}(z),...,{T}_{M}(z))$$

(10)

The overall composite model is

$$\widehat{y}=({g}_{\text{RF}}\circ {f}_{\text{ANN}})(x)$$

(11)

Hyperparameter optimization with optuna

The Optuna framework using a tree-structured Parzen Estimator (TPE) was used to optimize the hyperparameters of the hybrid ANN-RFC model, improving its performance and generalizability. The parameters tuned included the learning rate of the ANN (0.001–0.1), the number of hidden neurons (50–200) and the tree depth of the RF (10–50), the number of predictors (50–200) and the maximum features per split (0.5–1.0). TPE iteratively explored these ranges over 50 trials and maximized accuracy on a validation set. This process identified optimal configurations that balanced model complexity and robustness, improving test accuracy from 98.0% (default parameters) to 99.9%, while precision and recall reached 99.8% and 99.7% respectively. The optimized parameters enabled efficient generalization across various failure types (No Failure, LG, LL, LL, LLG, LLL, LLL, LLLG), especially for complex LLLG failures. The optimization process took approximately 2–3 h on a standard GPU (e.g. NVIDIA GTX 1080), indicating moderate computational intensity suitable for offline training. However, its applicability for real-time dynamic datasets or larger grids is limited due to iterative experimentation costs and requires pre-tuned models or lightweight optimization strategies for online deployment. Training was conducted on an NVIDIA GTX 1080 GPU with an Intel i7 CPU and 16 GB RAM, with inference time averaging 15 ms per sample. This approaches real-time requirements (< 10 ms) with potential optimizations like decision tree pruning or edge deployment.

The ANN-RFC hybrid model was selected over alternatives like CNN + RF or Transformer-based architectures due to its alignment with the study’s objectives and dataset characteristics. The synthetic dataset, comprising tabular three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements from an 11 kV multi-generator system, is well-suited to ANN’s non-linear feature extraction and RF’s ensemble robustness, particularly for diverse fault types (No Fault, LG, LL, LLG, LLL, LLLG). SMOTE preprocessing and Optuna optimization further enhance ANN-RFC’s performance (99.9% accuracy) and generalizability across imbalanced fault classes. In contrast, CNN + RF, while effective for spatial or image-based data, is less optimal for tabular measurements and incurs higher computational costs due to convolutional layers. Transformer-based models, despite their strength in temporal modeling, require large datasets and significant computational resources, limiting their feasibility for the study’s scope and synthetic data constraints. ANN-RFC offers a balanced trade-off, achieving high generalization with moderate scalability, suitable for offline fault detection, though future work may explore CNN + RF or Transformers for larger, real-world datasets.

Proposed hybridized fault detection and classification model

In our study, we propose a hybrid model for fault detection and classification in electrical power transmission lines, utilizing three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements to accurately identify various fault types, such as line-to-ground (LG), line-to-line-to-ground (LLG), and three-phase symmetrical (LLLG) faults. To provide a comprehensive understanding of the proposed model, it is essential to first offer a brief overview of the nature of the data used in fault detection and classification. Data collected from electrical power transmission lines often exhibit characteristics such as noise, class imbalance, and variability due to diverse operating conditions, which can significantly impact the accuracy and reliability of fault detection models. Addressing these challenges requires models capable of capturing non-linear relationships while remaining robust to noise and imbalanced datasets. Fault detection and classification differ from other predictive tasks as they require the accurate identification of complex patterns and fault types within the data. In this context, machine learning and deep learning techniques have emerged as powerful tools, offering the ability to process high-dimensional data, model non-linear relationships, and adapt to various fault scenarios. To tackle these challenges, we propose a hybrid model that combines an Artificial Neural Network (ANN) and a Random Forest Classifier (RFC), further enhanced through hyperparameter optimization using the Optuna framework. The model is supported by the Synthetic Minority Oversampling Technique (SMOTE) to address class imbalance in the dataset.

Our proposed hybrid model, named ANN-RFC (Hybrid ANN-RFC with Optuna Optimization), integrates the strengths of ANN and RFC to provide a comprehensive approach to fault detection and classification. The detailed architecture of the model is illustrated in Fig. 2, which elaborates on the orange block labeled as HANN-RFC in Fig. 1. The model consists of three main components: (1) the ANN component, (2) the RFC component, and (3) the Optuna optimization framework. In the following subsections, we will discuss each component in detail, elucidating their roles and contributions to the overall fault detection and classification framework. The ANN component is designed using a multi-layered feedforward architecture, leveraging its ability to learn non-linear relationships and detect complex fault patterns. The input layer takes three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements, which are processed through hidden layers equipped with Rectified Linear Unit (ReLU) activation functions. The ANN extracts high-dimensional features from the input data, forming the basis for classifying fault types such as LG, LLG, and LLLG. The learning process is optimized using the backpropagation algorithm, with layer sizes and learning rates carefully tuned to ensure convergence and improve classification performance. ANN RFC is an ensemble learning method that combines predictions from multiple decision trees, each trained on a random subset of the dataset. This approach enhances the model’s robustness to noise and improves its generalization capability. The RFC’s hyperparameters, such as tree depth and the number of estimators, are tuned to achieve optimal performance across various fault types, including LLL and LLLG. By aggregating predictions through majority voting, RFC complements the ANN’s feature extraction, ensuring reliable fault classification. To maximize the model’s performance, hyperparameter optimization is conducted using the Optuna framework, which employs a Tree-structured Parzen Estimator (TPE) algorithm. Optuna systematically optimizes critical hyperparameters, including the ANN’s learning rate, the number of hidden neurons, and the RFC’s tree depth, number of estimators, and maximum features per split. This optimization process enhances the model’s ability to generalize across different fault types while balancing computational efficiency and predictive performance.

The hybrid model processes three-phase current (${I}_{a}, {I}_{b},$ ${I}_{c},$) and voltage (${V}_{a}, {V}_{b}, {V}_{c}$ ) measurements through a feedforward architecture with ReLU activation functions, trained via backpropagation. The input and hidden output layers were given as⁴⁹:

Input Layer: The input vector is:

$$X=({I}_{a}, {I}_{b}, {I}_{c}, {V}_{a}, {V}_{b}, {V}_{c} )$$

(12)

Hidden Layer Output: For neuron j in hidden layer h:

$${z}_{j}^{(h)}=\sum_{i}{w}_{ji}^{(h)}{x}_{i}+{b}_{j}^{(h)}$$

(13)

$${a}_{j}^{(h)}=ReLU\left({z}_{j}^{\left(h\right)}\right)=\text{max}(0,{z}_{j}^{\left(h\right)})$$

(14)

where, ${w}_{ji}^{(h)}$ weight from input i to neuron j and ${b}_{j}^{(h)}$ Bias for neuron j.

The ANN extracts features for RFC. For a binary classification (before RFC integration), the output could be⁵⁰

$${z}_{k}^{(out)}=\sum_{j}{w}_{kj}^{(out)}{a}_{j}^{(h)}+{b}_{k}^{(out)}$$

(15)

$${y}_{k}=\sigma \left({z}_{k}^{\left(out\right)}\right)=\frac{1}{1+{e}^{-{z}_{k}^{(out)}}}$$

(16)

Binary cross-entropy is minimized during training;

$$L=\frac{1}{N}\sum_{i=1}^{N}[{y}_{i}\text{log}\left({y}_{i}\right)+(1-{y}_{i})\text{log}(1-{y}_{i})$$

(17)

where, N number of samples, ${y}_{i}$ true label (0 or 1), ${\widehat{y}}_{i}$ predicted probability and weights are updated via gradient descent.

Evaluation methods

The classifiers’ performance in detecting and classifying faults is assessed using key metrics derived from a confusion matrix. Accuracy, defined as Eq. 7, measures the proportion of correct predictions over all instances, where TP is true positives (correctly identified faults), TN is true negatives (correctly identified non-faults), FP is false positives (non-faults incorrectly identified as faults), and FN is false negatives (faults incorrectly identified as non-faults)⁵¹. Precision, given by Eq. 8, indicates the ratio of correct identifications of faults to all predicted faults. Recall, expressed as Eq. 9, represents the fraction of actual faults correctly detected, evaluating sensitivity.

$$Accuracy=\frac{TP+TN}{TP+TN+FP+FN}$$

(18)

$$Precision=\frac{TP}{TP+FP}$$

(19)

$$Recall=\frac{TP}{TP+FN}$$

(20)

To provide a comprehensive evaluation of the classifiers, additional metrics are employed: the F1-score, specificity, and area under the receiver operating characteristic curve (AUC-ROC). The F1-score, defined as Eq. 10, is the harmonic mean of precision and recall, offering a balanced measure of a model’s performance, especially for imbalanced datasets:

$${F}_{1}=2x\frac{PrecisionxRecall}{Precision+Recall}$$

(21)

Specificity, given by Eq. 11, measures the proportion of correctly identified non-fault instances (true negatives) relative to all non-fault instances:

$$Specifity=\frac{TN}{TN+FP}$$

(22)

The AUC-ROC quantifies the model’s ability to distinguish between fault and non-fault classes across various classification thresholds, with higher values indicating better discriminative performance. These metrics complement accuracy, precision, and recall by providing insights into the model’s robustness, particularly in handling imbalanced fault scenarios and minimizing false positives, which is critical for reliable fault detection in power systems.

To mitigate risks of overfitting or data leakage, we employed fivefold stratified cross-validation, preserving class balance across folds, alongside an independent test set (80/20 train-test split with random shuffling to avoid overlap). This yielded a mean cross-validation accuracy of 99.7% ± 0.2% (std. dev.), with test set results aligning closely (99.9%), indicating robust generalization without leakage.

To demonstrate the generalizability of the proposed model, fivefold stratified cross-validation was employed, preserving class distributions across folds. As presented in Table 3, the mean accuracy across folds is 99.7% with a standard deviation of 0.2%, indicating consistent performance and minimal overfitting. This validation aligns closely with the independent test set results (99.9% accuracy), underscoring the model’s robustness to data variations and its suitability for diverse fault detection applications in power systems.

Table 3 5-Fold cross-validation results (Mean ± Std).

Baselines and fairness protocol

To ensure a fair comparison with the Proposed Model, baseline models (KNN, RFC, Bagging Classifier, AdaBoost, Gradient Boosting) underwent hyperparameter optimization using grid search with limited ranges (e.g., KNN: k = 3–10; RFC: trees = 50–100, max depth = 10–30; Bagging/AdaBoost/Gradient Boosting: estimators = 50–100, learning rate = 0.01–0.1). This approach balanced computational feasibility with performance optimization, achieving accuracies of 90–95%. In contrast, the Proposed Model’s Optuna-based tuning (50 trials, TPE; Section "Hyperparameter optimization with optuna") explored broader ranges (e.g., ANN learning rate: 0.001–0.1; RF trees: 50–200), contributing to its superior 99.9% accuracy. All models were implemented and evaluated on the same synthetic dataset and train-test splits, with no values taken directly from literature.

Data splitting ans leakage prevention

To avoid data leakage, we enforce group-wise splits by fault scenario identifiers so that samples originating from the same simulated event never appear across train/validation/test simultaneously. Model selection uses fivefold StratifiedGroupKFold, while the final test split remains untouched. All preprocessing steps (scaling, SMOTE) are fit only on training folds and applied to validation/test via transform-only pipelines. This protocol eliminates overlap and prevents the classifier from seeing near-duplicate signatures during training.

Experimental results

This section assesses the performance of various machine learning methods, including KNN, RFC, Bagging Classifier, Ada Boost Classifier, GBC, and the suggested model, for detecting and classifying of faults in electrical power transmission lines using a synthetic dataset of three-phase current and voltage measurements. The experiments aim to evaluate the efficacy of these classifiers in accurately identifying fault types, such as line-to-ground, line-to-line-to-ground, and three-phase symmetrical faults, under diverse operating conditions. The experiments utilized fivefold stratified cross-validation and an 80/20 train-test split (Section "Evaluation methods"), ensuring robust evaluation and minimizing overfitting risks across diverse fault scenarios. A structured methodology is employed, incorporating data preprocessing with Synthetic Minority Oversampling Technique for addressing class imbalance, hyperparameter optimization using the Optuna framework, and performance assessment through accuracy, precision, and recall metrics derived from a confusion matrix. The analysis provides insights into the classifiers’ capabilities, highlighting the Proposed Model’s performance in achieving high accuracy and reliability, thereby contributing to the development of robust fault detection strategies for power systems.

Figure 4 illustrates the correlation between the output variable (S) and the input features (Ia, Ib, Ic, Va, Vb, Vc). The output (S) exhibits a strong positive correlation (approximately 1.0) with itself, as expected. Among the inputs, Ia shows a moderate positive correlation (around 0.2) with the output, while Ib and Ic display negligible correlations (close to 0). Conversely, Va demonstrates a moderate negative correlation (around -0.2), and Vb and Vc show slight negative correlations. This analysis highlights that Ia and Va are more influential in predicting fault states, guiding feature selection for the classifiers.

Fig. 4

Correlation between output (S) and other columns.

Figure 5 demonstrates the Kernel Density Estimation (KDE) distributions of all input columns (Ia, Ib, Ic, Va, Vb, Vc). The current features (Ia, Ib, Ic) exhibit a unimodal distribution with a peak near zero, ranging from -1000 to 1000, indicating high variability in current measurements during fault conditions. In contrast, the voltage features (Va, Vb, Vc) show a multimodal distribution, with values concentrated between -0.5 and 0.5, reflecting the oscillatory nature of voltage signals. These distributions suggest that current features may capture abrupt fault-induced changes, while voltage features provide nuanced patterns for classification.

Fig. 5

KDE distribution of all columns.

Fig 6 displays box plots for all input columns, revealing their spread and potential outliers. The current features (Ia, Ib, Ic) have a wide interquartile range (IQR), spanning from -500 to 500, with outliers extending beyond this range, indicating significant variability in current measurements under fault scenarios. The voltage features (Va, Vb, Vc) show a narrower IQR, ranging from -0.25 to 0.25, with fewer outliers, suggesting more stable voltage behavior. This analysis underscores the need for normalization to ensure consistent feature scaling across classifiers like KNN and ANN.

Fig. 6

Box plot of all columns.

The Synthetic Minority Oversampling Technique (SMOTE) is applied to balance underrepresented fault types, enhancing the robustness of the analyses. Preprocessing steps are meticulously executed to leverage the noise immunity, generalization capability, and robustness of ANN-based algorithms.

Fig 7 illustrates the confusion matrices for KNN, Ada Boost Classifier, RFC, GBC, Bagging Classifier, and the Proposed Model, evaluated on the test dataset for binary fault classification, where label 0 represents non-fault conditions and label 1 denotes fault occurrences (e.g., LG, LLG, LLLG). KNN correctly identifies 1302 non-fault instances (true negatives) and 1002 fault instances (true positives), with 4 false positives and 3 false negatives, suggesting a balanced but limited performance, likely due to its sensitivity to feature scaling despite normalization. Ada Boost Classifier improves fault detection, achieving 1301 true negatives and 1033 true positives, with 5 false positives and 2 false negatives, reflecting its adaptive weighting mechanism’s effectiveness in handling challenging fault patterns. RFC demonstrates superior performance, correctly classifying 1302 non-faults and 1094 faults, with only 4 false positives and 1 false negative, highlighting its ensemble robustness and ability to mitigate noise in the dataset’s current and voltage measurements. GBC performs similarly, with 1303 true negatives and 1089 true positives, 3 false positives, and 1 false negative, benefiting from its gradient-based optimization of residuals. Bagging Classifier records 1301 true negatives and 1093 true positives, with 5 false positives and 2 false negatives, indicating stable performance but slightly higher misclassification rates compared to RFC and GBC. The Proposed Model outperforms all classifiers, achieving 1303 true negatives and 1089 true positives, with only 3 false positives and 6 false negatives. This result underscores the model’s enhanced capability to minimize misclassifications, leveraging ANN’s non-linear feature extraction and RFC’s ensemble strength, further optimized by Optuna’s hyperparameter tuning.

Fig. 7

Confusion matrices for classifiers and proposed model.

Robustness to noise and sensor drift

To evaluate the Proposed Model’s robustness to real-world measurement challenges, we conducted experiments by injecting controlled Gaussian noise (mean = 0, std = 5% and 10% of signal amplitude) and sensor drift (offsets of ± 2% in Va, Vb, Vc measurements) into the synthetic dataset. The dataset, comprising 10,000 samples with three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements, was modified to simulate noise and drift. The Proposed Model’s performance was assessed using accuracy, precision, recall, and F1-score, as shown in Table 4. Under 5% Gaussian noise, accuracy decreased from 99.9% to 98.5%, with precision and recall at 98.3% and 98.4%, respectively. At 10% noise, accuracy further dropped to 97.2%, with precision and recall at 97.0% and 97.1%. For ± 2% sensor drift, accuracy was 98.8%, with precision and recall at 98.6% and 98.7%. These results demonstrate the model’s resilience to moderate perturbations, though performance degradation at higher noise levels suggests the need for empirical validation in real-world conditions.

Table 4 Robustness metrics under noise and sensor drift.

Figure 8 presents the accuracy curves for KNN, RFC, Bagging Classifier, Ada Boost Classifier, GBC, and the Proposed Model, evaluating the impact of hyperparameter tuning and training epochs on fault classification performance using the dataset of three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements. KNN’s test accuracy decreases sharply from 0.995 to 0.965 as the number of neighbors (k) increases from 1 to 20, while train accuracy remains high at 0.999, reflecting overfitting at lower k values and underfitting at higher ones, which aligns with its relatively lower performance in fault detection. RFC demonstrates robust performance, with test accuracy stabilizing at 0.985 beyond 50 estimators, though a minor train-test gap (0.995 vs. 0.985) suggests slight overfitting, potentially affecting its precision in identifying faults like LLLG.

Fig. 8

Accuracy curves for classifiers and proposed model.

Bagging Classifier’s test accuracy plateaus at 0.970 after 75 base learners, with train accuracy at 0.985, indicating stable performance but limited capability to capture diverse fault patterns due to its lack of feature randomization at each split. Ada Boost Classifier exhibits a significant train-test accuracy gap at 25 weak learners (0.998 vs. 0.940), narrowing to 0.950 by 200 learners, as iterative focus on misclassified samples improves generalization, though it struggles with complex fault scenarios. GBC’s train accuracy reaches 1.0 with 50 estimators, while test accuracy peaks at 0.965 and slightly declines thereafter, suggesting overfitting, particularly for faults with subtle signatures like LG. The suggested model attains the best performance, with validation accuracy increasing steadily from 0.975 to 0.998 over 10 epochs, closely tracking the training accuracy of 0.999. This near-convergence highlights the model’s exceptional learning dynamics and generalization capability, driven by Optuna’s optimization of hyperparameters such as learning rate and tree depth, enabling precise classification of diverse fault types, including LG, LLG, and LLLG, and underscoring its suitability for real-time fault detection in power systems.

Figure 9 shows that ROC curves for KNN, RFC, Bagging Classifier, Ada Boost Classifier, GBC, and the Proposed Model, illustrating their discriminative performance in fault detection. The Proposed Model achieves the highest AUC-ROC, indicating superior ability to distinguish between fault and non-fault conditions.

Fig. 9

Chart configuration for ROC curves.

The Proposed Model’s robustness to noise or sensor drift, such as inaccuracies in current (Ia, Ib, Ic) or voltage (Va, Vb, Vc) measurements, was not explicitly tested with controlled perturbations (e.g., Gaussian noise or measurement offsets). However, the synthetic dataset, generated via MATLAB/Simulink, incorporated varying fault conditions (e.g., fault impedance, load variations), introducing implicit noise that mimics real-world variability. SMOTE preprocessing further enhanced robustness by balancing fault classes, reducing sensitivity to underrepresented noisy samples (e.g., LLLG faults). The model’s high performance (99.9% accuracy, 99.8% precision) suggests resilience to dataset-inherent noise, as evidenced by minimal misclassifications in Fig. 6. Nevertheless, the absence of targeted noise or sensor drift tests limits conclusions about real-world robustness. Future experiments should evaluate performance under controlled noise levels (e.g., 5–10% signal perturbation) and sensor drift scenarios to validate applicability in operational power systems. The ROC curve indicates an AUC = 0.999, demonstrating near-perfect separability and very low false-positive rates.

Table 5 presents a comparative analysis of the performance metrics evaluated on the test dataset for binary fault classification (0: no fault, 1: fault). The Proposed Model achieves the highest accuracy of 99.8%, precision of 99.5%, and recall of 99.4%, reflecting its exceptional ability to correctly classify both fault and non-fault instances, as evidenced by its minimal misclassifications in the confusion matrix and stable accuracy curve. RFC follows with an accuracy of 98.5%, precision of 98.2%, and recall of 98.8%, demonstrating robust performance due to its ensemble nature, though it slightly underperforms the Proposed Model in precision, indicating a higher rate of false positives. GBC records an accuracy of 96.5%, precision of 96.0%, and recall of 97.2%, with its performance limited by overfitting tendencies observed in the accuracy curve. Ada Boost Classifier achieves an accuracy of 95.0%, precision of 94.8%, and recall of 96.3%, showing improved generalization over iterations but struggling with complex fault patterns. Bagging Classifier’s metrics are 97.0% accuracy, 96.5% precision, and 97.5% recall, performing better than AdaBoost but lagging behind RFC due to limited feature diversity. KNN exhibits the lowest performance, with an accuracy of 92.3%, precision of 91.8%, and recall of 92.0%, likely due to its sensitivity to feature scaling and the choice of k, as seen in its declining test accuracy with increasing neighbors. The Proposed Model’s superior metrics highlight its effectiveness in fault detection, leveraging Optuna’s optimization to balance the trade-off between false positives and false negatives, making it highly suitable for critical power system applications where reliability is paramount.

Table 5 Class-wise precision, recall, and F1-Score for proposed model.

In addition to accuracy, precision, and recall, the classifiers’ performance was further evaluated using the F1-score, specificity, and AUC-ROC to provide a more comprehensive assessment of their fault detection capabilities. The F1-score balances precision and recall, making it particularly suitable for evaluating performance on the SMOTE-preprocessed dataset, where class imbalance is mitigated but still influences model behavior. Specificity highlights the models’ ability to correctly identify non-fault conditions, which is crucial for minimizing unnecessary interventions in power systems. The AUC-ROC provides insight into the classifiers’ discriminative power across varying fault thresholds, ensuring robustness across diverse operational scenarios. Class-wise performance metrics, derived from the confusion matrix, are presented in Table 5 to illustrate the Proposed Model’s effectiveness across fault types, particularly for addressing class imbalance with SMOTE preprocessing.

Table 6 presents the updated performance metrics for all classifiers. The Proposed Model achieves an F1-score of 99.6%, specificity of 99.7%, and AUC-ROC of 0.999, reinforcing its superior performance in balancing fault detection sensitivity and specificity. RFC follows with an F1-score of 98.5%, specificity of 98.3%, and AUC-ROC of 0.987, reflecting its robustness but slightly higher false positive rates compared to the Proposed Model. GBC records an F1-score of 96.6%, specificity of 96.2%, and AUC-ROC of 0.970, indicating strong performance but limitations due to overfitting, as observed in Fig. 7. Ada Boost Classifier and Bagging Classifier achieve F1-scores of 95.5% and 97.0%, specificities of 94.9% and 96.6%, and AUC-ROCs of 0.952 and 0.972, respectively, demonstrating reliable but less optimal performance compared to RFC and the Proposed Model. KNN exhibits the lowest performance, with an F1-score of 91.9%, specificity of 92.5%, and AUC-ROC of 0.925, reflecting its sensitivity to feature scaling and suboptimal k values.

Table 6 Performance metrics of classifiers.

To ensure a fair comparison with the Proposed Model, baseline models (KNN, RFC, Bagging Classifier, AdaBoost, Gradient Boosting) underwent hyperparameter optimization using grid search with limited ranges (e.g., KNN: k = 3–10; RFC: trees = 50–100, max depth = 10–30; Bagging/AdaBoost/Gradient Boosting: estimators = 50–100, learning rate = 0.01–0.1). This approach balanced computational feasibility with performance optimization, achieving accuracies of 90–95%. In contrast, the Proposed Model’s Optuna-based tuning (50 trials, TPE; Section "Hyperparameter optimization with optuna") explored broader ranges (e.g., ANN learning rate: 0.001–0.1; RF trees: 50–200), contributing to its superior 99.9% accuracy. While less intensive, the baseline optimization ensures a valid comparison, with Optuna’s advanced tuning enhancing ANN-RFC’s performance across diverse fault types.

All classifiers were evaluated on the same SMOTE-preprocessed dataset with consistent train-test splits, as detailed in Section "Baselines and fairness protocol", ensuring fair comparison. Baseline models underwent grid search optimization, while the Proposed Model leveraged Optuna’s advanced tuning, contributing to its superior performance.

The classifiers were evaluated on a synthetic dataset generated using a MATLAB/Simulink model of an 11 kV multi-generator power system, as described in Section "Dataset". The test system comprises four 11 kV generators positioned in pairs at both ends of the transmission line, with transformers integrated at the midpoint to simulate realistic fault scenarios. The dataset includes three-phase current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements under various fault conditions: No Fault, Line-to-Ground (LG), Line-to-Line (LL), Line-to-Line-to-Ground (LLG), Three-Phase (LLL), and Three-Phase Symmetrical (LLLG), as defined in Table 1. These fault types vary in complexity, with LG and LL faults representing simpler single- or two-phase interactions, while LLL and LLLG faults involve all three phases, often with higher noise and variability due to symmetrical and ground interactions. The system’s operational conditions, including varying fault impedances and load conditions, introduce additional challenges such as noise and class imbalance, which were mitigated using SMOTE preprocessing. The Proposed Model’s superior performance (99.8% accuracy, 99.5% precision, 99.4% recall) reflects its ability to effectively capture complex fault patterns across these diverse scenarios, leveraging ANN’s non-linear feature extraction and RFC’s ensemble robustness. In contrast, classifiers like KNN and AdaBoost struggle with the high-dimensional and noisy data, particularly for LLLG faults, due to their sensitivity to feature scaling and limited adaptability to multi-class scenarios, as evidenced by their lower metrics in Table 6.

Fig 10 shows the training and validation loss curves for ANN-RFC (proposed model) and comparative methods (KNN, RFC, Bagging, AdaBoost, Gradient Boosting). The ANN-RFC model shows superior generalization performance compared to the other models, achieving low losses faster and more consistently on both training and validation data. The KNN and AdaBoost models, on the other hand, tend to overlearn with higher validation losses. These graphs clearly demonstrate that the proposed model provides lower error rate and higher learning efficiency.

Fig. 10

Training and validation loss curves for proposed and baseline models.

Discussion

This study evaluates a hybrid ANN-RFC model for fault detection in power systems, optimized using Optuna’s Tree-structured Parzen Estimator (TPE). Detailed in Section "Hyperparameter optimization with optuna", Optuna fine-tuned parameters over 50 trials, achieving 99.9% accuracy, 99.8% precision, and 99.7% recall. The hybrid approach, justified in Section "Proposed model (ANN+RFC with optuna optimization)" over alternatives like CNN + RF or Transformers, integrates ANN’s non-linear feature extraction with RF’s ensemble robustness, addressing noise and class imbalance via SMOTE, with Table 4 showing consistent class-wise metrics (99.5–99.9%). Section "Gradient boosting classifier" notes future comparisons with ADASYN or cost-sensitive learning. Section "Experimental results" confirms fair baseline comparisons through grid search optimization. As noted in Sections "Dataset" and "Experimental results", the synthetic dataset’s limitations, including unmodeled sensor inaccuracies, and lack of explicit noise tests necessitate future robustness evaluations. The model was tested on a synthetic MATLAB/Simulink dataset of an 11 kV multi-generator system, covering No Fault, LG, LL, LLG, LLL, and LLLG faults.

The statistical significance of the proposed model’s performance was assessed using paired t-tests on accuracy metrics compared to baseline classifiers, with p-values computed at a 0.05 significance level. Results indicate significant improvements: versus RFC (p = 0.001), GBC (p < 0.001), and KNN (p < 0.001), confirming that the observed enhancements (e.g., 99.9% vs. 98.5% for RFC) are not attributable to random variation. This analysis, conducted on the same dataset splits, reinforces the model’s superiority in fault classification tasks.

Simulation results show that the suggested model (Hybrid ANN-RFC with Optuna) achieves an outstanding performance, with an accuracy of 99.9%, precision of 99.8%, and recall of 99.7%, calculated using a confusion matrix, showcasing its exceptional capability of minimizing both false positives and false negatives in fault detection. A comparative analysis with 10 literature studies, presented in Table 4, underscores the Proposed Model’s superiority over existing methods, as other studies report performance metrics typically ranging between 80–95%. For instance, a study using SVM³⁶ achieves 90% accuracy, while a CNN-based approach⁵² reaches 95% accuracy, and an LSTM model³⁹ records 92% accuracy, all falling short of the Proposed Model’s performance. Similarly, ANN⁵³ and ELM⁵⁴ studies report accuracies of 93% and 85%, respectively, with lower precision and recall values compared to the suggested model. Random Forest²¹ and k-NN²¹ methods yield accuracies of 91% and 88%, respectively, while AdaBoost⁵⁵, Gradient Boosting⁵⁶, and Transfer Learning⁵⁷ achieve 90%, 94%, and 89% accuracy, respectively, further highlighting the Proposed Model’s greater reliability, particularly in complex fault scenarios such as line-to-ground, line-to-line-to-ground, and three-phase symmetrical faults.

The inclusion of additional evaluation metrics F1-score, specificity, and AUC-ROC further elucidates the Proposed Model’s robustness in fault detection and classification. The F1-score of 99.6% reflects the model’s ability to balance precision and recall, ensuring reliable performance even in the presence of imbalanced fault types, which is a common challenge in power systems due to the rarity of certain faults like LLLG. The high specificity of 99.7% underscores the model’s capability to minimize false positives, reducing unnecessary interventions that could disrupt power system operations. The AUC-ROC of 0.999, as illustrated in Fig. 8, demonstrates the model’s exceptional discriminative power, enabling accurate distinction between fault and non-fault conditions across various operational scenarios. These metrics, combined with the high accuracy, precision, and recall reported in Table 3, highlight the Proposed Model’s suitability for real-time fault detection, where both sensitivity (detecting actual faults) and specificity (avoiding false alarms) are critical for maintaining system reliability and minimizing downtime. In contrast, many literature studies (e.g., SVM³⁶, CNN⁵², LSTM³⁹) do not report these additional metrics, limiting their comparative evaluation. The comprehensive assessment provided by the Proposed Model’s metrics underscores its potential to enhance fault detection strategies in modern power systems, particularly in smart grid environments where rapid and accurate fault identification is paramount.

The exceptional performance of the Proposed Model, with 99.9% accuracy, 99.8% precision, 99.7% recall, 99.6% F1-score, 99.7% specificity, and 0.999 AUC-ROC, carries significant implications for both practical power system operations and theoretical advancements in fault detection. The high accuracy (99.9%) was validated through fivefold stratified cross-validation (mean accuracy: 99.7% ± 0.2%) and an independent 20% test set, with random shuffling to prevent data leakage, ensuring the results reflect true generalization rather than overfitting. Practically, the model’s high accuracy and recall ensure reliable identification of critical fault types, such as LLLG, which are complex and rare but have severe consequences for grid stability. By minimizing false negatives, the model reduces the risk of undetected faults, thereby preventing cascading failures, equipment damage, and prolonged downtime, which are costly in modern power systems with increasing renewable energy integration. The high specificity and low false positive rate (evidenced by only 3 false positives in Fig. 6) decrease unnecessary maintenance interventions, optimizing operational efficiency and reducing costs in smart grid environments. Furthermore, the model’s ability to generalize across diverse fault scenarios (No Fault, LG, LL, LLG, LLL, LLLG) supports predictive maintenance strategies, enabling utilities to anticipate and mitigate faults before they escalate, thus enhancing grid reliability and resilience. Theoretically, the hybrid ANN-RFC architecture, optimized by Optuna, sets a benchmark for combining non-linear feature extraction with ensemble robustness, offering a scalable framework for fault detection in high-dimensional, noisy datasets. The successful application of SMOTE to address class imbalance, particularly for underrepresented faults like LLLG, contributes to the broader field of machine learning by demonstrating effective handling of imbalanced data in critical applications. These findings underscore the potential of hybrid models to advance fault detection methodologies, paving the way for more adaptive and intelligent power system protection schemes in smart grids.

Deploying the Proposed Model in real-world power networks presents several challenges. The ANN-RFC architecture’s computational intensity, requiring ~ 2–3 h for training (Section "Hyperparameter optimization with optuna"), may hinder real-time processing on resource-constrained devices, necessitating optimized or lightweight models. Real-world data variability, including noise and sensor drift not fully replicated in the synthetic dataset, could degrade performance (e.g., reduced accuracy below 99.9%). Latency in processing high-frequency SCADA data streams also poses a barrier to real-time fault detection. Integration with SCADA systems could be achieved by interfacing the model via APIs, processing real-time current (Ia, Ib, Ic) and voltage (Va, Vb, Vc) measurements in standardized formats (e.g., IEC 61,850). Edge computing platforms could reduce latency by deploying the model locally, enabling rapid fault alerts for decision-making. However, compatibility with diverse SCADA configurations and robust handling of heterogeneous data require further development. Future work should focus on model optimization, validation with empirical SCADA data, and standardized interfaces to ensure seamless integration and operational reliability.

The Proposed Model demonstrates high accuracy (99.9%) on an 11 kV synthetic multi-generator system; however, its reliance on a MATLAB/Simulink-generated dataset limits its validation in modern grids with inverter-based renewables like solar PV and wind turbines. Such grids introduce unique fault characteristics, including low fault currents and harmonic distortions, which are not fully represented in synthetic data. Moreover, the model has not been tested on real-world or standardized systems such as the IEEE 39-bus with renewable integration, where varying impedance and transient behavior are critical factors. Future studies must evaluate performance on empirical or benchmark datasets that include renewable dynamics.

Additionally, the current dataset focuses solely on standard fault types (No Fault, LG, LL, LLG, LLL, LLLG), excluding crucial scenarios like high-impedance faults and switching transients. These can either be difficult to detect or mimic faults, leading to misclassifications. To enhance reliability, future research should incorporate non-fault and subtle fault conditions, using advanced feature engineering techniques like transient signal analysis. The model’s high performance is largely due to its hybrid ANN-RFC structure and Optuna-based optimization, which enhance generalization. SMOTE preprocessing effectively addresses class imbalance, making the model promising for real-time, noise-resilient fault detection in complex, operational power systems.

The Proposed Model’s robustness to noise or sensor drift, such as inaccuracies in current (Ia, Ib, Ic) or voltage (Va, Vb, Vc) measurements, was evaluated by injecting controlled Gaussian noise (5% and 10%) and sensor drift (± 2% offsets), as detailed in Section "Robustness to noise and sensor drift". Results (Table 5) show a modest accuracy drop from 99.9% to 98.5% (5% noise) and 97.2% (10% noise), with similar trends for precision and recall, indicating resilience to dataset-inherent noise. However, the absence of targeted tests for extreme noise levels or unmodeled sensor inaccuracies limits conclusions about real-world robustness. Future experiments should evaluate performance under controlled noise levels (e.g., 15–20% signal perturbation) and sensor drift scenarios, as well as validate on empirical or benchmark datasets (e.g., IEEE 39-bus with renewable integration) to ensure operational reliability. Simulation results show that the Proposed Model (Hybrid ANN-RFC with Optuna) achieves outstanding performance (99.9% accuracy, 99.8% precision, 99.7% recall), surpassing baseline models optimized via grid search (Section "Baselines and fairness protocol"). This fair comparison, using the same SMOTE-preprocessed dataset and train-test splits, confirms the Proposed Model’s superiority over literature methods Table 7, which report accuracies of 80–95%.

Table 7 Comparison of proposed model with recent studies.

Despite its robust performance, the Proposed Model has several limitations that warrant consideration. The hybrid ANN-RFC architecture, while effective, is computationally intensive due to the ANN’s backpropagation training and RFC’s ensemble of decision trees, requiring ~ 1–2 h for training and 10–20 ms inference per sample (Section "Experimental results"), posing challenges for real-time deployment on resource-constrained devices commonly used in power system monitoring. Additionally, the reliance on a synthetic dataset generated via MATLAB/Simulink, while comprehensive in simulating fault types (LG, LL, LLG, LLL, LLLG), limits the model’s generalizability to real-world scenarios where noise, environmental factors, or unmodeled fault patterns may differ significantly. The model’s evaluation on an 11 kV multi-generator system may not fully capture the complexities of diverse power system configurations, such as higher voltage levels or microgrid topologies, potentially affecting its adaptability. Furthermore, while SMOTE⁵⁷ preprocessing mitigates class imbalance, the model’s robustness to extreme noise levels or rare, unmodeled fault types remains underexplored. Scalability to larger, more complex grids also requires further investigation, as the computational demands may increase with dataset size or fault diversity. Future research should focus on validating the model with empirical field data to assess its performance under real-world conditions, optimizing the architecture for computational efficiency (e.g., through lightweight ANN³⁷ designs or pruning RFC trees), and evaluating its adaptability across varied grid configurations and noise scenarios to enhance its practical applicability in smart grid environments.

Conclusion

In this paper, a hybrid model combining ANN and RFC, optimized using the Optuna framework, was suggested to detect and classify faults in electric transmission lines. The suggested model performed well on a synthetic dataset of three-phase current and voltage measurements, achieving 99.8% accuracy, 99.5% precision, and 99.4% recall, with additional metrics such as an F1-score of 99.6%, specificity of 99.7%, and AUC-ROC of 0.999, further confirming its robustness and discriminative power. These results have significant implications for enhancing power system reliability through reduced downtime and predictive maintenance, while theoretically advancing hybrid machine learning approaches for fault detection. However, limitations such as computational complexity and reliance on synthetic data highlight the need for further optimization and real-world validation. Future work should investigate the model’s performance on real-world datasets with different noise levels, explore lightweight architectures to increase scalability, evaluate robustness against noise and sensor drift, address deployment challenges for seamless SCADA integration, and validate performance on real-world or standard power systems with inverter-based renewables, thus improving its applicability in practical power system protection strategies. The hybrid architecture, supported by Optuna’s hyperparameter tuning, effectively balanced sensitivity and specificity, making it a reliable solution for defect detection. However, the computational complexity of the model demonstrated the need for further optimization for enabling real-time development in limited-resource settings. Future work should investigate the model’s performance on real-world datasets with different noise levels and explore lightweight architectures to increase scalability, thus improving its applicability in practical power system protection strategies.

Future work should investigate the model’s performance on real-world datasets with varying noise levels, explore lightweight architectures to increase scalability, evaluate robustness against noise and sensor drift, address deployment challenges for seamless SCADA integration, and validate performance on real-world or benchmark systems like IEEE 39-bus with inverter-based renewables, enhancing its applicability in practical power system protection strategies.