Sperm swarm optimization for many objective power flow problems with enhanced performance evaluation in power systems

Abstract

This research presents an advanced optimization framework motivated from biological sources using the Sperm Swarm Optimization (SSO) algorithm to specifically deal with the Many-Objective Optimal Power Flow (MaO-OPF) problem in power systems. Despite the great progress made in multi-objective optimization, convergence, diversity, and computational efficiency problems still exist—in particular, the high dimensional, multifaceted, conflicting objectives space. The proposed MaOSSO algorithm incorporates adaptive diversity mechanisms along with swarm intelligent hyper-dynamic control to address these shortcomings and improve the solution quality in higher scalable architectures. This framework is extensively tested with cutting-edge algorithms NSGA-III and RVEA on the DTLZ and MaF test suites and later validated on the realistic IEEE 30, 57, and 118-bus power systems. MaOSSO is shown to consistently outperform competing methods with up to 15–20% faster convergence and 25% less computation time. While applying the algorithm on the MaO-OPF problem, the active/reactive power loss minimization was optimized along with the voltage stability, emissions, operational cost, and Pareto front diversity sustaining. The biologically inspired multi-directional search strategy incorporated in MaOSSO that provides balance between exploration and exploitation is what distinguishes this approach from others. Additional comparisons with OPF models based on FACTS and fuzzy-evolutionary OPF models demonstrate the claimed advantages in practical applications. Comprehensive multi-metric evaluation supporting the performance increase is attributed to Hypervolume (HV), Inverted Generational Distance, Generational Distance, Spread, and efficiency of runtime. A single radar plot and a cumulative ranking summary illustrate and quantify how MaOSSO outperforms more recent swarm-based algorithms like GWO, MOPSO, and MOGWO. The study describes specific future improvement actions while admitting some constraints on extremely large-scale systems. In summary, MaOSSO stands out as the most robust and flexible approach to enabling adaptive intelligent and sustainable operations on power systems.

Introduction

Foundational concepts and challenges

In modern engineering science networks, the need to optimize power system operations has become crucial due to increased global energy demands and environmental concerns^1,2,3. The problem of Many-Objective Optimal Power Flow (MaO-OPF) is a multiple-criteria decision making framework for power systems with conflicting objectives that include minimizing reactive and active power losses, sustaining nominal node voltages, reducing fuel costs and emissions as well as improving voltage stability⁴. These methods are seen as primary approaches due to the growing focus on the enhancement of energy efficiency and environmentally sustainable MaO-OPF⁵. Unlike classical OPF techniques which operate on one or few goals at a time, traditional approaches are incapable of addressing the sophisticated multi-dimensional criteria which these methods work with^6,7,8. While directionally guided movements accomplish convergence, multi-dimensional complexity of autonomous stochastic OPF problems renders those multi-faceted resolution approaches ineffective which require flexible optimization strategies that readily shift in response to competing demands within the obstacles presented by such situations. It is in this regard that the recent emphasis placed on the MaO-OPF problem has been tackled through customization of metaheuristic optimization strategies⁹. As recently researched^10,11, hybrid metaheuristics integrated with swarm intelligence approximately exhibit balanced computational performance with diverse Pareto fronts. These approaches include sophisticated methods like adaptive parameter control and advanced decomposition strategies to maneuver through high-dimensional spaces¹². Moreover, biologically inspired algorithms that mimic collective behaviors in nature have proven highly successful at solving the problems of convergence and diversity in large-scale optimization¹³. This ever-changing nature of research on optimization emphasizes the urgent need for scalable, robust algorithms designed to address the dynamic and high dimensional requirements of current power systems. In light of this, we identify the Sperm Swarm Optimization (SSO) algorithm as a new promising method specifically developed to deal with complexities surrounding MaO-OPF framework.

Insights from previous research

Optimization of power system operation is a vast problem and has resulted in the development of many metaheuristic approaches as well as multi-objective evolutionary algorithms (MOEAs), each solving some aspects of Optimal Power Flow problem^14,15,16. These techniques mainly look for optimal or near-optimal solutions that adequately balance different competing goals like minimizing losses in active power and reactive power, reducing fuel costs as well as pollution levels within operational constraints but still meeting voltage security. Whale Optimization Algorithm (WOA)¹⁷, Slime Mould Algorithm (SMA)¹⁸, and Flower Pollination Algorithm (FPA)¹⁹ are among these classical methods which have been widely used to tackle OPF problems. Derived from natural events, these algorithms employ various strategies including pollination processes of plants such as FPA, slime molds movement seen in SMA, and whale hunting behavior adopted by WOA. However, while they can solve simple dimensional optimization problems easily, their effectiveness and efficiency are compromised with increasing number of objectives or/and constraints. In high dimensional search spaces, this is the outcome of failure to ensure convergence to Pareto front while maintaining diversity. Research has seen significant advancements in some complex multi-objective evolutionary algorithms such as Non-dominated Sorting Genetic Algorithm III (NSGA-III), Reference-Vector Guided Evolutionary Algorithms (RVEA), and decomposition-based approaches^20,21. These have utilized advanced mechanisms designed for enhancing convergence and diversity with NSGA-III including reference points and adaptive reference vector tweaking for RVEA. This makes it possible to solve numerous problems related to optimization in power systems within multiobjective approaches. However, the overhead cost and parameter-based sensitivity remain major obstacles towards any viable modeling attempts on real time or large-scale system applications. Swarm intelligence-based algorithms can be considered good alternatives where they are able to explore complex high-dimensional spaces effectively. Some swarm-like decentralized search techniques like Grasshopper Optimization Algorithm (GOA)²² and Firefly Algorithm (FA)²³ strike a good balance between exploration and exploitation in their operation. GOA is based on the concept of a grasshopper swarm and fosters diversity, whereas FA focuses more on specificity and delineates areas of interest through firefly glow communication. One disadvantage of these algorithms is their high computational overheads especially when applied in solving multi-objective optimization problems with multiple decision variables.

Several new estimates of hybrid and improved algorithms have been proposed to improve the classical approaches. Specifically, Multi-Objective Grey Wolf Optimizer (MOGWO)²⁵ and Many-Objective Particle Swarm Optimization (MOPSO)²⁴ are built to address economic dispatch, cost and voltage stability goals in power systems. They combine the use of swarm-based strategies with other methods for controlling convergence and diversity. MOPSO uses Pareto dominance and crowding distance concepts on top of basic PSO framework, while MOGWO utilizes multi-leadership styles so as to enhance search efficiency. In fact, the processes were found to be quite successful in optimizing diverse objectives of power systems. In order to tackle current problems in many-objective optimization applications, certain modifications have been made to existing algorithms. Adaptive versions of NSGA-III and RVEA schemes employ efficient selection policies as well as better handling of high dimensional Pareto optimal surfaces. The main objective behind these changes is reducing the trade-offs between proximity among solutions versus their diversity; thus, achieving solutions that are both computationally effective and high-quality ones. Moreover, optimization approaches that integrate the advantages of different optimization methods become increasingly popular with significant achievements regarding improvements and extension potentials.

In conclusion, power system optimization has experienced an unprecedented growth; however, the increasing complexity of modern power systems and growing emphasis on conservation compel sophistication in the optimization techniques. At present, several multi solution approaches are currently being developed to utilize swarm intelligence algorithms coupled with evolutionary processes as evidenced by their leading role in engineering and optimization activities.

Identified challenges and unexplored areas

It must be acknowledged that the attainment of power system optimization is quite challenging because, like any other problem, it involves more than one target. An even bigger trouble is presented by the growing complexity of modern power systems where multiple different goals have to be achieved simultaneously: reduction of losses, cost and emissions together with improved voltage reliability and overall stability of the system. Many papers have been published that suggest various algorithms for addressing these issues; however, each proposed algorithm has its own set of limitations which result in many open questions in this field. The two optimization algorithms PSO and GWO are based on swarm intelligence which has proven efficient for searching through large search spaces. These methods have proved their efficiency in solving single-objective as well as multi-objective tasks by means of self-adaptive approaches and distributed control. However, when the size of the objective space increases dramatically, these algorithms often experience scalability problems. As an example, many particles in PSO perform badly due to convergence problems as they fail to properly explore the whole solution but only find local optima. However, even though it is successful in achieving diversity, GWO still faces the challenge of lack of convergence due to a high number of objectives and decision variables. Hence, there should be some trade-off between solution quality and computational cost. Conversely, gradient-based techniques that are dependent on directional data derived from gradients such as MaOSSO perform well for gradient-based approaches like those resulting in fast convergence. In this case however, these systems have less capability for most continuous objective problems that do not use these kinds of DFRs. But when it comes to large scale or highly nonlinear networks, they fail to solve a diverse set of Pareto optimal solutions adequately. The lack of diversity in the solution leads to convergence in some solutions but many of the key trade off objectives are grossly under represented. Power system optimization problems have multipeak landscapes and discontinuities which make the gradient based systems less effective. These limitations strongly support ongoing development of novel optimization algorithms that can integrate affordance competition exploration exploitation in high dimensional objective space to overcome them. To maintain TP solutions and, if possible, allow algorithms for rapid convergence in vivo is a need to balance. Decision makers are left at the mercy of a set of several operational objectives and the significance they bear with respect to some possible alternatives that they have which involves this one in an effort to achieve optimal tradeoff. Given this, it is difficult to use these algorithms as general-purpose tools since they are constructed for specific problems as such their use in various domains is limited. In situations where the goals of system reliability and environmental consideration outweigh the interests in economic dispatch, these types of algorithms would not be effective. The research area lacks an all-inclusive framework for power systems that can address functional requirements on multi-purpose basis.

In conclusion, the efficacy of automation is still a problem. The size and complexity of power systems have been further increased by the integration of modern grid technologies, distributed generation and renewable energy sources, necessitating real-time processing of large amounts of data by optimization algorithms. This computational requirement is seldom satisfied by either method mentioned above without deteriorating quality of solutions. To address these research gaps, there is need to develop state-of-the-art optimization algorithms that are computationally efficient as well as scalable and robust. Such algorithms should be able to handle multiple-objective optimization intricacies appropriately while checking both excessive diversity and too much convergence at once.

Highlights of research outcomes

Ultimately, the effectiveness of computation processes is yet to be agreed upon. Power system integration is becoming more extensive and its information processing burden grows with every passing moment thanks to building advanced grid technology and introduction of decentralized and renewable energy systems through the optimization algorithms. These computational requirements are often not met by existing approaches without compromising on the quality of their implementations in some way. Such gaps can only be bridged by putting into place necessary modern optimization algorithms usage that would facilitate better merging of computational efficiency, flexibility, as well as extensibility. Modern optimization algorithms must thus be able to strike a balance between diversity and convergence in terms of multi objective optimization problems whose complexity is high. This proposal suggests SSO towards addressing those areas. MaO-OPF framework consists an ant-based controls incorporated SSO which then results in stronger multitarget objectives responses. Consequently, such parameter adjustable swarm intelligence will increase rate of convergence and Pareto diversification efficiency as well. The following are the underlining principles:

• Swarm SSO Algorithm Multidirectional SSO: The technique behind SSO resembles the swarms from biology as it increases diversity while reducing convergence, guiding the targets into a variety of different objective spaces quickly, which makes it better than other power optimization solver like gradient method and basic evolution-based algorithms.

• Benchmark Validation on IEEE Systems: Comparative study is made between the proposed SSO and IEEE benchmark systems i.e. 30 bus system, 57-bus system, and 118-bus system in terms of optimal convergent solutions to multiple competing objectives with their trade-offs; using maximum tolerable error limits of 0.01 for restoration and reconfiguration of the networks.

• Comparative Analysis with Advanced Techniques: A few people have tried allusion to SSOPs through some aims hence its excellence among other renowned optimisers such as NSGA-III, RVEA, MOEA/D-DE for MaO OPF Problems.

• Analysis of SSO in Extensive Power Networks: In large power networks or case studies related to real power networks extensive analysis has been done on how efficient SSO in controlling power grid systems.

Groundbreaking contributions to the field

The SSO algorithm is a kind of swarm-based stochastic strategy which is highly complex and makes it possible to navigate efficiently through high dimensional objective fields. Unlike Gradient Based Optimization or Harris Hawks Optimization which are mostly static methods that rely on simple gradients, SSO allows for a larger range of exploitation and exploration techniques. Diversity in Pareto solutions as well as the problem of converging to local optima are addressed by this adaptability. The ability of SSO to balance between global and local optimization while controlling diversity by adapting swarm intelligence is what makes it most innovative. This framework allows SSO to deal with many power system objective optimization problems, particularly those involving competing factors.

Study layout and framework

The structure of this paper is outlined as follows:

• In Section “Theoretical formulation of the MaO-OPF problem”, the MaO-OPF formulation is explained, focusing on the aforementioned functions and limitations of the system.

• In Section “SSO algorithm: design principles and MaO-OPF applications”, a thorough investigation of the SSO algorithm is presented, description of its structure and its use for the MaO-OPF optimization is given.

• In Section “Comprehensive analysis of experimental outcomes”, results from IEEE standard tests and MaO-OPF benchmark problems are presented and also comparison is done.

• In Section “Comprehensive performance evaluation”, the application of SSO on a large power system is presented.

• In Section “Conclusion and Future work”, the future work plans are analyzed and the obtained results are summarized.

Theoretical formulation of the MaO-OPF problem

This is one of the issues that have faced modern power systems optimization and it requires balancing between economic efficiency, environmental friendliness, and system reliability. There are many ways in which MaO-OPF is different from traditional single-objective OPF formulations because it contains diverse objectives such as fuel minimization, emission minimization and reactive power loss minimization that are often constrained by voltage stability indices. This evolutionary process commensurate with the changes taking place in today’s power systems due to increased penetration of renewable energies, distributed generations and stringent environment regulations. The motivation for this investigation is the increasing needs to provide solutions to high-dimensional optimization problems with a reasonable computational time spending on efficient algorithms and effective constraint management techniques. With this in mind, the section offers a detailed analysis of MaO-OPF that exposes its formulation as a multi-objective optimization problem with a set of defined operating constraints. It also outlines some primary objectives such as minimizing active/reactive power outputs or emissions from the system while illustrating the manner in which these equality and inequality constraints control the boundaries of generators, the balance of powers, the transformer operations, and system security and safety features. Additionally, an illustrative mathematical foundation will be provided describing challenges of populating high-dimensional Pareto fronts as dealing with extremely complex optimization processes which simultaneously guarantee convergence and diversity of different solution candidates must also be dealt with. All these parts constitute the problem formulation which serves as a basis for the algorithmic approaches tailored to the complex and changing requirements of contemporary energy systems.

Theoretical foundation for many-objective optimization (MOOP)

Equation (1)²⁶ encapsulates the mathematical formulation of the MaO-OPF problem, which seeks to optimize multiple conflicting objectives within a power system framework. This equation is structured as:

$${\text{Minimize}}\;F\left( v \right) = \{ f_{1} \left( v \right), \, f_{2} \left( v \right), \ldots , \, f_{L} (v)\}$$

(1)

subject to a set of equality constraints h(v) = 0 and inequality constraints g(v) ≤ 0, where v represents the decision variable vector. The vector v includes the most critical parameters of system control in respect to power such as output of generators, bus voltage level and tap settings for transformers.

• Objective Functions, f_i(v): These functions portray several performance indices for power systems that include but are not limited to fuel cost, emissions, active and reactive power losses and voltage stability indices. Each objective function fi(v) represents a different optimization target indicating the wide range of often conflicting objectives in power systems management.

• Equality Constraints, h(v): These constraints ensure that the supply of electrical energy matches with its demand at all times (balance), hence they represent the equality constraint for the system’s state equation. Mathematically, these constraints describe equations that determine nodal flows between various elements ensuring both equilibrium as well as consistency in operations.

• Inequality Constraints, g(v): These are operational boundaries of various components of a power system e.g., limits on generator capacities; voltage limits; thermal limits on transmission lines. They prevent possible operational violations from occurring within such facilities which might lead to a destabilization or worse still unsafeness of this particular system in use.

The statement appreciates the inherent intricacy of MaO-OPF problems as illustrated by high-dimensional Pareto fronts and the interactions between objectives which are themselves nonlinear. It emphasizes on the need for advanced optimization techniques that can balance exploration and exploitation, facilitating convergence to optimal trade-offs. This structure proves a solid base for use in applying the proposed optimization algorithm, ensuring it is practically feasible and computationally efficient.

Functional goals of the framework

The MaO-OPF framework encompasses a diverse range of optimization objectives such as the Reduction of Reactive Power Loss, the Minimization of Active Power Loss, Voltage Magnitude Deviation (VMD), Total Emissions (TE), Total Fuel Cost (TFC), and the Elevation of Voltage Stability Indicators (VSI). The framework also incorporates quadratic fuel cost (QFC), value-point loading (VPL), multi-fuel (MF) scenarios, and prohibited operating zones (POZ) which are contained in six fitness functions formulated in^27,28. To achieve these objectives, interpolations for fuel consumption and carbon dioxide (CO₂) emissions alongside power loss minimization must be developed, coupled with minimized voltage deviation and bolstered how robust of voltage stability indices. Meeting these modern requirements which a flexible and adaptive power system needs to adjust to is evolving quite rapidly. The figures illustrate some of the ideas discussed; Fig. 1 demonstrates the relationship of VPL over varying parameters and Figs. 2, 3, and 4 illustrate POZ and MF trends shown in Fig. 4.

Fig. 1

Schematic representation of OPF outputs and constraints.

Fig. 2

Assessment of fuel costs considering valve-point loading.

Fig. 3

Representation of POZ in power system operations.

Fig. 4

Impact of multi-fuel operations on generator cost curves.

The MaO-OPF problem in this study considers six primary objectives, aiming to minimize:

Minimization of fuel cost (TFC)

The minimization of the total fuel cost (TFCTFCTFC) for generators is mathematically represented as follows in relation (2):

$$\text{TFC }=\sum_{i=1}^{{N}_{g}}\left[{a}_{i}+ {b}_{i} {P}_{gi}+ {c}_{i}{{P}_{gi}}^{2}+ \left|{d}_{i} .\text{sin}({e}_{i} . ({{P}_{gi}}^{min}-{P}_{gi}))\right|\right]$$

(2)

where:

• N_g​: Total number of generators in the system.

• P_gi​: Active power output of the i-th generator.

• ${{P}_{gi}}^{min}$ and ${{P}_{gi}}^{max}$​: Lower and upper bounds of the i-th generator’s active power, respectively.

• a_i, b_i, c_i, d_i, e_i​: Coefficients representing the cost characteristics of the i-th generator.

• ${d}_{i} .\text{sin}({e}_{i} . ({{P}_{gi}}^{min}-{P}_{gi}))$: Represents the valve-point loading effect, introducing nonlinearity into the cost curve.

In this formulation, quadratic fuel cost component is combined with the valve-point loading effect which is responsible for introducing oscillations to accurately represent the generators’ operational characteristics in real-world scenarios. It effectively captures both linear and nonlinear cost variations, thus providing a solid framework for generation costs optimization while respecting the operating constraints of generators.

Minimization of emission (TE)

Reducing emissions is illustrated as in Eq. (3):

$$\text{TE }=\sum_{i=1}^{{N}_{G}}({\alpha }_{i}{{P}_{G,i}}^{2}+{\beta }_{i}{P}_{G,i}+{\gamma }_{i}+{\eta }_{i}\text{exp}({\delta }_{i}{P}_{G,i}))$$

(3)

where ${\alpha }_{i}$​, ${\beta }_{i}$​, ${\gamma }_{i}$​, ${\eta }_{i}$​, and ${\delta }_{i}$​ are emission coefficients for each generator.

Minimization of active power loss (APL)

Equation (4) shows the active power loss minimization:

$$\text{APL }=\sum_{i=1}^{{N}_{L}}({G}_{i}{{V}_{i}}^{2}-2{V}_{i}{V}_{j}{G}_{ij}\text{cos}{\theta }_{ij})$$

(4)

where ${G}_{i}$ and ${G}_{ij}$ are conductance terms, ${V}_{i}$ and ${V}_{j}$​ are bus voltages, and ${\theta }_{i,j}$ is the phase angle difference between buses i and j.

Minimization of reactive power loss (RPL)

The minimization of the reactive power loss is presented as in Eq. (5):

$$\text{RPL }=\sum_{i=1}^{{N}_{L}}({B}_{i}{{V}_{i}}^{2}-2{V}_{i}{V}_{j}{B}_{ij}\text{sin}{\theta }_{ij})$$

(5)

where ${B}_{i}$ and ${B}_{ij}$​ are susceptance terms.

Minimization of voltage magnitude deviation (VMD)

The relation characterizing the minimization of the voltage magnitude deviation is presented in Eq. (6):

$$\text{VMD }= \sum_{i=1}^{{N}_{B}}|{V}_{i}- {V}_{ref}|$$

(6)

where ${V}_{i}$​ is the voltage at bus i and ${V}_{ref}$​ is the reference voltage.

Maximization of Voltage Stability Index (VSI)

A stability index, such as the Line Stability Index (L-index), can be used for VSI as described in relation (7):

$${\text{VSI }} = {1} - \left( {\frac{1}{{V_{i} }}\mathop \sum \limits_{j = 1}^{N} V_{j} Y_{ij} \angle \theta_{ij} } \right)$$

(7)

where ${Y}_{ij}$​ represents admittance values between buses.

Constraints

The MaO-OPF problem includes the following key constraints:

Generator constraints

$$P_{Gi}^{min} \le P_{Gi} \le P_{Gi}^{max}$$

(8)

$$Q_{Gi}^{min} \le Q_{Gi} \le Q_{Gi}^{max}$$

(9)

This restriction on Eq. (8) guarantees that the effective power output (P_gi) of each generator is kept within its lower (${{P}_{Gi}}^{min}$) and upper (${{P}_{Gi}}^{max}$) limits. These boundaries are defined by the design and operating characteristics of individual generators. Staying within this range prevents abnormal stress on the generator while ensuring stability of the overall system. Similarly, in Eq. (9), all generators’ reactive power outputs (Qgi) are confined to a certain range with set boundaries ${{Q}_{Gi}}^{min}$ and ${{Q}_{Gi}}^{max}$. These values help in maintaining voltage profiles within desired levels and promoting proper reactive power compensation across the entire grid.

MaO-OPF model guarantees that generations run at maximum efficiency as well as safety degrees by ensuring adherence to these limitations. It helps lower the hazards related to voltage instability or even full system malfunctions or equipment overloads. These rules also guarantee harmony between techno-economic aims that let the system maximize power flow and preserve its operation security. These elements are now crucial for contemporary energy systems marked with great degrees of variable and complexity usually resulting from integration of renewable energy sources and shifting demand dynamics.

Power balance constraints

$$\mathop \sum \limits_{i = 1}^{N} (P_{Gi} { } - { }P_{Di} ) = 0$$

(10)

$$\mathop \sum \limits_{i = 1}^{N} (Q_{Gi} { } - { }P_{Di} ) = 0$$

(11)

Maintaining the power balancing Eq. (10) will help to guarantee that energy generated equalizes consumption in real time and keeps the system frequency constant. Maintaining this balance depends on reactive power produced in line with formula (11) for voltage stability and best power transmission. They relate operational limitations of a given network, which are related with physical features of the system such line flow restrictions, generating unit limits, and transformer capacities, with optimization goals of MaO-OPF issue. Equations (8) and (9) should thus be part of MaO-OPF formulation since they provide system security as well as operation feasibility. These equations underline in modern power systems the need of strong optimization techniques that can consider losses and dynamic demand patterns existing in today’s markets while guaranteeing equilibrium.

Transformer constraints

$$T_{i}^{min} \le T_{i} \le T_{i}^{max}$$

(12)

This constraint ensures that the tap-changing transformer’s tap ratio (T_i​) operates within its permissible range, defined by ${{T}_{i}}^{min}$​ and ${{T}_{i}}^{max}$. Adjusting the tap ratio allows for voltage regulation and reactive power flow control, which are critical for maintaining system stability under varying load and generation conditions.

Security constraints

$$S_{Li} \le S_{Li}^{max}$$

(13)

In this case, S_Li represents apparent power transferred between buses i and j through the transformer while ${{S}_{Li}}^{max}$ is the thermal limit of the transformer. This restriction makes sure that the transformer does not exceed its thermal limits which could result to overheating, insulation breakdown or even catastrophic failure. Transformers are necessary parts of a power system that allow adjustments in voltage to meet specific areas in a network. However, these constraints limit their flexibility so that they do not cause operational inefficiencies or damages. In MaO-OPF framework, these constraints guarantee that optimization process respects transformers’ physical as well as operational limitations while optimizing power flow.

Shunt VAR compensator constraints

$$Q_{Ci}^{min} \le Q_{Ci} \le Q_{Ci}^{max}$$

(14)

Shunt compensators are placed strategically along the network to ensure effective voltage stability as they manage reactive power. They effectively control the overvoltage and the collapse of voltage resulting from load changes along with any form of disturbances caused by the change in load. Proper management of reactive power will enable better control of performance metrics such as upper and lower voltage limits, reduction in losses, improved quality of the power supplied, operability and security of the network. Renewal energy modern networks need tighter enforcement of transformer limitations. In adherence to these limitations, system reliability is enhanced, there is a prolongment of transformer life, and there’s improvement of resilience for the overall grid. For a quick overview on objective functions including their definitions as well as mathematical expressions see Table 1 below:

Table 1 Key optimization functions.

Additionally, the standard parameters for the IEEE 30, 57, and 118-bus test systems utilized in validation studies are displayed in Table 2.

Table 2 IEEE Test System Parameters.

SSO algorithm: design principles and MaO-OPF applications

The SSO algorithm is an innovative approach in many-objective optimization influenced by how sperm cells behave during fertilization. This biological inspired optimization technique is particularly useful in addressing the challenges posed by complex, high-dimensional optimization problems such as MaO-OPF. A reliable and adaptable optimization strategy should be developed because power systems are becoming more complicated due to incorporation of renewable energy sources, strict environmental regulations and dynamically changing load patterns. Traditional optimization techniques have significant limitations with regards to scalability, convergence, and maintaining solution diversity when applied to such multifaceted issues. However, these limitations are overcome by SSO that utilizes the cooperative/adaptive behaviors seen in sperm swarm which provides a balance between exploration and exploitation within multidimensional solution spaces. This part extensively explains theoretical basis as well as practical application of SSO algorithm covering its exceptional ability to navigate numerous dimensional Pareto fronts. The paper also presents some features of the designed algorithm including its velocity adaptation mechanisms, constraint handling techniques and multi-directional search strategies among others. In addition, integrating the SSO into MaO-OPF reveals its capability in optimizing multiple conflicting objectives while obeying operational constraints tightly. Modern power system optimization can be transformed by the versatility and computational efficiency of the SSO algorithm. This will ensure that sustainable energy management is achieved and decision making enhanced.

Conceptual overview of the SSO algorithm

SSO was introduced by Shehadeh et al.^29,30 as a novel algorithm that mimics the complex, coordinated movement of sperm cells in fertilization (see Fig. 5). Fertilization is a highly regulated and mechanized biological event involving over 130 million sperm cells working together to successfully navigate through various physiological barriers such as the cervix and fallopian tubes in order to fertilize an ovum. This process exemplifies a superb biological optimization mechanism where sperms collaborate and modify their movements in order to surmount intricate obstacles towards achieving their final aim. At least three different stages of this process, known as “mysterious velocities,” that characterize the real-time dynamics of sperm cells while they traverse different media may be decomposed according to Shehadeh et al.³¹. With each velocity reflecting distinct behavioral characteristics of sperms which change in response to the varying physiological conditions encountered during the pilgrimage along those routes. These rules are scrutinized and framed within a structured control system for use in computational optimization techniques.

Fig. 5

Mechanism of fertilization²⁹.

The natural strategies used by sperms are capitalized by this approach which explores and exploits multi-criteria optimization landscapes effectively using their dynamic and adaptive movement patterns. The algorithm’s design incorporates the three velocity types observed in nature that make SSO adapt to a wide range of optimization problems. These velocities have been identified in the literature³¹ as:

• Standard Velocity: It is the simple motion made by sperm cells as they move towards an ovum.

• Reduced Velocity: This refers to a slower pace, implying more control when moving around under difficult or restrictive circumstances.

• Tactical Velocity: These are quick movements for outmaneuvering barriers or aiming at ova with precision.

This biologically inspired mechanism allows SSO to navigate complex problem spaces with high adaptability and effectiveness, making it a powerful tool for solving various multi-objective and high-dimensional optimization problems.

The release of numerous sperm cells into the cervix during a new cycle marks the beginning of reproductive process in multicellular organisms. These sperm cells set off on a collective journey towards an egg, competing among themselves to reach the ultimate goal which is fertilization. With so many participants, only one sperm cell eventually achieves fertilization of the ovum, making this a natural example of complex optimization. The SSO algorithm represents how sperm cells migrate in Fig. 5 by drawing upon this intricate biological process. In the SSO algorithm, Cartesian coordinates are used to represent sperm cells as particles and their origin is considered to be cervix at point (0,0). This representation reproduces nature diversity observed in natural fertilization where sperms are randomly distributed with different initial conditions hence promoting optimization diversity. In this way each sperm cell receives an arbitrary velocity drawn from Shehadeh et al.^29,30 studies on motion behavior for a dynamic and non-static search throughout optimization operation. This probabilistic component reflects inherent variation and adaptability that exists within nature’s gametes -sperm cells-. A structured iterative procedure that exploits diverse movement patterns of sperms is implemented through the algorithm. In the course of optimization, sperm cells go across the search space altering their movements to explore and exploit high-dimensional problem landscapes. This cooperation guarantees that the population rapidly converges towards the optimal solution. The iterative process persists until such a point when the whole society of sperms coalesce at one specific place denoting the answer. By means of simulating stochastic yet intentional motions executed by sperms cells, SSO algorithm is able to navigate through complicated high-dimensional optimization problems. It is a coordinated mode in which it can strike a balance between exploration and exploitation that makes it fit for tackling multi-objective as well as computationally intensive challenges.

$$Initial\_Velocity = D \cdot V_{i} \left( t \right) \cdot Log_{{_{10} }} (pH\_Rand_{1} ) \,$$

(15)

• ${v}_{i}$—is the velocity of cell i at iteration t;

• D—is the factor of velocity damping, which is a random quantity in the range of 0–1;

• pH_Rand₁—is the pH value at the reached position, and it’s a random parameter between 7 and 14;

According to the SSO model, each spermatozoon is directed to a specific area on the surface of an egg. As these cells achieve this goal, they exhibit highly organized coordinated behavior that mimics natural swarms such as flocking birds or schooling fish. These coordinated movements enable the swarm to adapt to optimal conditions, demonstrating the efficiency and adaptability of collective biological systems. The instinctive swarming behavior of sperm enhances search efficiency and, during optimization, leads them to intuitively explore and converge on solutions. An ovum additionally aids the process by releasing attractants in the form of chemo-attractants to focus the swarm to a desired position. In this model, chemotactic cues are crucial in guiding sperm cells toward their specific targets, enabling them to function as a single unit regardless of their initial spatial coordinates. This seemingly uncoordinated approach to search strategy highlights the dynamic behavior of individual cells who move toward the ovum while directing their motion. Shehadeh et al.³¹ argue the supporting elements of the swarm that keep cell tails oscillating in rhythmic waves facilitate synchronized pulse ‘flocking and grouping’ tail pulsation. Such synchrony boosts concurrency, and so the performance of all cells heading towards the ovum is swarm. Thus, about SSO algorithm, this phase improves capability to control parameters of the algorithm to perform a better search and comprehensive search in the workspace. The ova (egg) is situated in the distal end of the fallopian tube and so represents the achievement of sought positions by sperm cells, which in optimization process denotes optimality. The SSO algorithm incorporates a best historical velocity rule where each cell stores its past successful coordinates and so each one ‘remembers’ during what time they reached the most efficient coordinates. The accuracy and efficiency metrics in target attainment is set by the dynamically adjusted trajectories of the cells via memory mechanisms. This feature completes the modification of swarm velocity(v) as it becomes ever more specialized and optimally specialized ositioned leading towards best possible answer:

$$Current \_Best \_Solution = Lo{g}_{10}(pH\_Ran{d}_{2})\cdot Lo{g}_{10}(Temp\_Ran{d}_{1})\cdot ({x}_{sbes{t}_{i}}[]-{x}_{i}[])$$

(16)

In a typical situation, only one cell can fertilize an egg, as previously mentioned. Since this was the case, Shehadeh et al.^30,31,32 gave this cell a catchy name. The group of successful sperm is shown in Fig. 6.

Fig. 6

Sperm swarm interaction and convergence to the winner^29,30,32.

The SSO strategy operates on a population of sperm cells which are potential solutions that explore independently the search space. In this frame, the SSO algorithm evaluates at once all the sperm cells by comparing their performance against that of the one with higher performance in the group. The topmost performing cell in any iteration acts as a benchmark that guides the remaining cells future trajectories. This is how iterations flow through to make up SSO algorithm and improve its navigation and optimizing abilities progressively leading swarm nearer to optimal solution. Key parameters like current velocity of each sperm cell, positions of better-performing cells and best position ever recorded in cell’s memory are considered when individual sperms adjust their movements. These adjustments constantly decrease the gap between individual members and swarm’s global maximum intensifying swarming convergence. This flexibility is what enables dynamic equilibrium between exploration—searching for new regions within the solution space—and exploitation—focusing on areas with a high likelihood of success. Hence, such balance prevents premature convergence and preserves diversity in solution space.

The SSO algorithm is successful because it combines the local interactions among neighboring cells and global information about the performance of the whole swarm. This double mechanism makes it possible for the algorithm to focus on areas with high potential for producing good results but still explore extensively in other parts of the search space. By saving an ordered convergence devoid of diversity, this approach is designed for complex high-dimensional optimization problems. According to him, this means that swarms can strategically improve how they act until they finally get to their optimum solution using the most accurate and least time-consuming path which by his example is Schermerhorn’s implementation of the SSO algorithm:

$$Global\_Best\_Solution(the\_winner) = Log_{{_{10} }} (pH\_Rand_{3} ) \cdot Log_{{_{10} }} (Temp\_Rand_{2} ) \cdot (x_{{sgbest_{i} }} [] - x_{i} []) \,$$

(17)

The symbols of the Eq. (17) and Eq. (18) are as follows,

• pH_Rand₂, and pH_Rand₃—are the reached location pH values, which are random parameter in the range of 7–14;

• Temp_Rand₁, Temp_Rand₂—are the reached location temperature values, which are random parameter in the range of 35.1–38.5;

• x_i—current position of potential solution i at iteration t;

• x_sbest—personal best location of potential solution i at iteration t;

• x_sgbest—global best location of the flock.

• rand1(), rand2(): Random functions generating values between 0 and 1.

where,

• v_i—is the velocity of cell i at iteration t;

• x_i—current position of cell i at iteration t;

The total velocity rule ${V}_{i}$ (t) can be modeled as³² depending on the preceding equations.

$${V}_{i}\left(k\right)= D\cdot Lo{g}_{10}\left(p{H}_{{r}_{1}}\right)\cdot {V}_{i}\left(k-1\right)+Lo{g}_{10}\left(p{H}_{{r}_{2}}\right)\cdot Lo{g}_{10}\left({T}_{1}\right)\cdot \left({x}_{sbest}\left(k\right)-{x}_{i}\left(k\right)\right)+Lo{g}_{10}\left(p{H}_{{r}_{3}}\right)\cdot Lo{g}_{10}\left({T}_{2}\right)\cdot \left({x}_{sGbest}\left(k\right)-{x}_{i}\left(k\right)\right),$$

(18)

In SSO, the swarm updated its position using the following mathematical model:

$$x_{i} (t) = x_{i} (t) + v_{i} (t)$$

(19)

The SSO operational process intertwines with biological systems, incorporating key physiological factors, such as temperature and pH, to modulate each sperm’s velocity. The temperature range of operability 35.1 °C to 38.5 °C oscillates with the biological values of the reproductive system, thereby modeling the effects due to fluctuations in arterial blood pressure. Such extensive ranges provide the ability to simulate multiple scenarios effectively broadening the scope of optimization constraints. On the other hand, pH is influenced by emotions, dietary habits, or even the timing of meals, which makes it a crucial set point toward achieving balance. It was necessary for the algorithm to set the limits of PH at 7–14 to widen the range toward capturing various physiological dimensions enhancing the algorithm’s ability to simulate nature-focused performance optimizations. In order to achieve these goals, computations aimed at increasing the efficiency and accuracy of the algorithm were based on employing logarithmic transformations of the parameters as put forth by Shehadeh et al.^29,30. The aim of these changes was to eliminate outliers in sperm velocity calculations to improve realistic comparisons with sperm motion models. Moreover, by normalizing velocity data, algorithms avoid imprecise modeling error optimizing simulations that are subsequently generated. Also, logarithmic transformation aids in optimization of range parameters increasing the precision and reliability of the SSO algorithm in complicated optimization algorithms. Notwithstanding the flexibility and multi-objective optimization capabilities of the SSO algorithm, these attributes pose a challenge with wide search spaces. The greater the problem domain, the greater probability of locking into local minima which severely reduces the algorithm’s effectiveness as the problem domain increases. This one limitation posits that additional focus on exploration and dynamically setting directions during algorithm SSO search needs refinement. These changes are fundamental to enable SSO tackle highly complicated multi-dimensional optimization problems such as MaO-OPF which require extreme levels of stability and flexibility due to their intricate and multi-layered nature.

SSO-based solution for MaO-OPF optimization

Incorporating the SSO algorithm into MaO-OPF optimization approaches offers a robust method that imitates biological systems when addressing intricately complex challenges involving modern power systems. The MaO-OPF framework includes the optimization of several conflicting objectives simultaneously which include: active and reactive power loss, fuel cost, emissions, voltage deviations, and enhancement of voltage stability indices. The breadth of the objectives compounds the optimization problem as it is discerned in high-dimensional Pareto front optimization landscapes which require sophisticated methods for effective exploration and convergence. The SSO algorithm employs swarm intelligence inspired by the cooperative adaptive behavior of sperm cells during fertilization. Each sperm cell represents a potential solution which has the freedom to navigate the search space independently while tailoring its trajectory based on interactions with other solutions as well as predefined user restrictions. Through adaptive velocity rules, SSO achieves balance between exploration and exploitation, ensuring refinement of known good solutions and search in novel, uncharted regions of the solution space. Achieving balance in this manner guarantees preservation of diverse solution characteristics throughout objective function convergence while maintaining dynamic trade-offs across objectives. Integral limitations like the generator output constraints, power balance equations, transformer operations along with line security limitations are incorporated within the SSO algorithm for MaO-OPF. Incorporating sophisticated constraint-handling strategies which include boundary-check mechanisms and penalty methods, the algorithm guarantees all proposed solutions are operationally feasible and physically plausible. As a point of interest, SSO framework is capable of resolving and creating a parametric envelope encapsulating conflicting objectives. In terms of prioritizing the trade-offs, it also identifies Pareto-optimal solutions when considering economic efficiency, environmental impact and system reliability. Moreover, SSO’s biologically inspired mechanisms allow it to respond to modern power grid’s dynamic and nonlinear behaviors, ensuring robust and scalable performance over diverse system configurations. Intensive benchmarking on IEEE test systems (30-bus, 57-bus, 118-bus) has validated the performance of SSO algorithm concerning rapid convergence along with sustaining pareto front diversity against the computational burden of didactic high dimensional optimization problems, proving robust power system optimization with adaptable sustainable solution flexibility to evolving energy system needs.

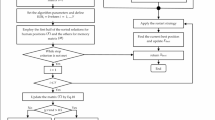
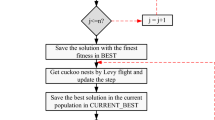
Logical flowchart of the optimization algorithm

Algorithm 1 explains the pseudocode of SSO. Finding optimal solutions in complex search spaces is crucial, and this algorithm effectively balances exploration and exploitation by leveraging both the individual and collective learning processes of particles. The Many-Objective Sperm Swarm Optimization (MaOSSO) algorithm is inspired by the fertilization process in biological systems and is adapted for high-dimensional optimization. It involves the following core stages :

1. Initialization Initialize sperm population with random positions in the decision space Assign each sperm a velocity vector Initialize control parameters such as temperature and pH using logarithmic scaling Evaluate initial fitness values using objective functions 2. Velocity and Position Update Each sperm updates its position based on: Its previous velocity, Personal best position, A global attractor influenced by the elite sperm, Adaptive regulation through pH and temperature parameters Velocity Update Eq. (18) 3. Fertilization and Selection Evaluate the fitness of updated sperm positions Store solutions in an external archive based on non-dominance and crowding distance Apply a Fertilization Gate Mechanism to retain high-quality diverse individuals 4. Archive Maintenance and Diversity Control Maintain the external archive within a fixed size Use diversity preservation techniques to avoid solution clustering Periodically reinitialize part of the population to prevent stagnation 5. Termination Repeat steps until the maximum number of generations or evaluations is reached Return the final set of non-dominated Pareto-optimal solutions

Fine-tuning algorithm parameters

Table 3 presents the SSO Algorithm Parameters:

Table 3 SSO parameters.

Comprehensive procedure for MaO-OPF optimization

Below is an in-depth guideline revealing a clear and effective approach to tackling the MaO-OPF Problem with the help of SSO. This method aims at finding a balance between exploring the entire solution space and simultaneously optimizing multiple objectives while respecting constraints.

Step 1: Initialization

• 1. Define the Objective Functions and Constraints

  • For instance, enumerate all the objectives for MaO-OPF problem such as minimizing active/reactive power loss, fuel cost, emissions or voltage deviations.

  • Also, identify all operational constraints including generator limits, power balance, transformer tap limits, line flow security limits and shunt compensator bounds.

• 2. Parameter Setup for SSO

  • Set up parameters of the SSO algorithm such as swarm size, inertia weight (w), cognitive coefficient (c₁), social coefficient (c₂) and random parameters r₁ and r₂.

  • Tuning parameters like temperature should be assigned randomly between 35.1 °C and 38.5 °C based on specific conditions given. The temperature tuner ranges from 7 to 14; this parameter has been logarithmically transformed to mimic real world sperm velocities.

• 3. Initialize Swarm Positions and Velocities

  • Randomly assign initial positions and velocities for every potential solution—sperm cells within the problem’s solution space that will satisfy initial system constraints.

Step 2: Objective Evaluation and Fitness Calculation.

• 1. Evaluate Objective Functions for Each Sperm Cell

  • This is done by calculating the value of each objective function for each sperm cell on the basis of its position. This entails determining active/reactive power loss, emissions, voltage stability and fuel cost for every potential solution.

• 2. Compute Fitness Scores

  • The objectives values are combined into a fitness score using any multi-objective fitness evaluation approach e.g. Pareto dominance to prioritize alternatives based on trade-offs amid objectives.

• 3. Identify Best Positions

  • Based on fitness scores, update each personal best Best_i and global best Global_Best of every sperm cell to establish initial leading positions in the swarm.

Step 3: Update of Velocity and Position.

• 1. Changing of Velocity Using the Formula for SSO Velocity

  • Through every gamete, compute the changed velocity via Plot No. (18)

  • Adaptively regulate velocities by logarithmic transformation with considerations to ecological aspects like temperature and pH in line with SSO.

• 2. Update Position

  • Determine new positions of each sperm cell basing on revised velocity while keeping all new positions within feasible region for solution space.

• 3. Treatment of Constraints

  • Check if a position is out of range and relocate it using boundary-check technique or corrector methods so as to maintain feasibility to all solutions.

Step 4: Pareto Front Update and Selection.

• 1. Construction of Pareto Dominance and Front

  • Evaluating dominance relationship among sperms and constructing a pareto front that identifies non-dominated solutions which have a combination of the best trade-offs across all objectives.

• 2. Update Global Best Based on Pareto Front

  • Selects the global best position from the pareto front, which represents the overall collective best solution for guiding future iterations of the swarm.

Step 5: Check for convergence.

• 1. Evaluation of Convergence Criteria

  • Ensure the convergence criteria are satisfied. Convergence may be determined by a minimal increase in global best fitness score, a defined maximum number of iterations, or attainment of target performance threshold.

• 2. Termination or Continuation

  • If the convergence criteria are reached, terminate the algorithm with outputting the final Pareto front as the solution set having optimal solutions.

  • If not, proceed back to Step 2 and repeat evaluation and update procedures for next iteration.

Step 6: Interpret and Choose the Solution.

• 1. Examine the Final Pareto Front

  • The cost, power losses or emissions can be assessed to see where decisions can be made.

• 2. Pick a Decision-Maker

  • Decision-makers can employ context-specific choices as they use the Pareto front to make informed choices based on their preferences among objectives.

For the matter, the SSO based alternative of the decision problem concerning MaO-OPF makes a good use of constraint handling and multi-objective optimization. There is a balance between exploration and exploitation as it can be seen in adaptive change in position and velocity for each sperm cell at each step of algorithm which in turn helps the algorithm to converge on well distributed Pareto front. It is an approach which supports decision making on complex power system matters by characterizing such attributes that provide optimal trade-offs between operational objectives versus sustainability ones.

Mixed approach to multi-constraint handling

MaO-OPF problem is seen as a constrained optimization task. For this successful operation, both equality and inequality constraints should be satisfied. Therefore, solving these constraints in the framework of optimization calls for powerful methods³³. Equation (20) addresses these problems by combining a penalty function with repair mechanisms. This makes it capable of handling complex equality constraints and managing the decision boundary limits. To elucidate further, Eq. (20) mingles patching with punishing to keep all decision parameters within appropriate ranges:

Decision Parameter Boundaries: The repair methodology ensures that each decision parameter remains within its defined lower and upper bounds:

$$x_{i}^{new} = \left\{ {\begin{array}{*{20}l} {x^{min} , } & {if x_{i}^{new} < x^{min} } \\ {x_{i}^{new} ,} & {if x^{min} \le x_{i}^{new} \le x^{max} } \\ {x^{max} ,} & { if x_{i}^{new} > x^{max} } \\ \end{array} } \right.$$

(20)

Here, ${{x}_{i}}^{new}$​ represents the repaired value of a decision parameter x_i​, ensuring it adheres to the bounds ${{x}_{i}}^{min}$​ and ${{x}_{i}}^{max}$.

Equality Constraints: After satisfying the limits, we deal with equality constraints concerning active and reactive power flow at each bus:

• We adjust parameters iteratively through Newton–Raphson load flow calculations until the constraints are satisfied.

• The penalty function has extra terms that in case these restrictions are violated will punish them, thus leading to convergence towards a feasible solution.

This remedial method is a preprocessing step for optimization that seeks to resolve any parameter violations before going into the main optimization process. By incorporation of this technique, the solver is able to handle complex search spaces while maintaining feasibility and computational efficiency. In equation (20), this repair-oriented strategy combines boundary corrections with equality constraint enforcement to address intricacies inherent in MaO-OPF problem. The use of Newton Raphson for load flow computation guarantees that both bounds on parameters and system-wide constraints are met thereby allowing the solver to identify feasible optimal solutions within a high dimensional space. This framework of repair-penalty offers a stronger alternative path for solving MaO-OPF problems particularly involving diverse operational limitations and high-dimensional optimization complications.

This is where the penalty function strategy (PFS) comes in handy when it comes to solving MaO-OPF problem. The penalty function makes any constraint violation as a result of a fitness value’s readjustment into penalty. This way, feasible solutions are considered to be more important by this mechanism than the others since this allows algorithms to effectively navigate through such huge search space and therefore concentrate on those which meet system requirements. In relation (21), defines the penalty function like so:

$$F(x) = f(x) + \alpha \sum\limits_{(i\varepsilon violated)} {h_{i}^{2} (x)} + \beta \sum\limits_{(j\varepsilon violated)} {g_{j}^{2} } (x)$$

(21)

where:

• F(x): Represents the augmented fitness function incorporating penalties for constraint violations.

• f(x): Denotes the original objective function of the optimization problem.

• h_i(x): Represents the equality constraints, such as power balance equations.

• g_j(x): Indicates the inequality constraints, including generator limits, transformer constraints, and voltage bounds.

• α and β: Penalty coefficients that weigh the importance of equality and inequality violations, respectively.

The constraints are normalized into per-unit (p.u.) values to normalize their impact thereby making it possible for different types of constraint to be treated fairly. To penalize large errors more heavily, equality constraints (h_i(x)) and inequality constraints (g_j(x)) should be squared so as to discourage solutions that deviate significantly from feasibility. Penalty terms conveniently fit in the fitness function F(x). This way, it makes sure that solutions that satisfy constraints are prioritized by the optimization algorithm while striving towards optimality in the objective function. This technique effectively moves the search process towards Pareto front, thus balancing between constraint satisfaction and objective performance trade-offs. This method incorporates penalty function into MaO-OPF framework guaranteeing compliance with operational restrictions like generator outputs, voltage limits as well as system security. It also improves the algorithm’s capability of dealing with high-dimensional problems having complex power systems thus ensuring robustness and scalability over a wide range of optimization landscapes. This formalization complements present-day flexible and evolutionary approaches to optimization which can provide a solid basis for addressing sophisticated issues pertaining MaO-OPF problems.

BCS identification via fuzzy decision mechanisms

Equation 23 introduces a fuzzy membership function, ${{\mu }_{i}}^{j}$, for evaluating and establishing the most satisfactory compromise solution (BCS) in the course of optimization over the entire set of non-dominated solutions. In this vein, the present method exploits the principles of fuzzy logic to cope with the trade-offs between multiple objectives in MaO-OPF.

The mathematical definition of fuzzy membership function for j-th solution in i-th objective is:

$$\mu_{i}^{j} = \frac{{f_{i}^{max} - f_{i}^{j} }}{{f_{i}^{max} - f_{i}^{min} }}$$

(23)

Key terms in the equation

• ${{f}_{i}}^{max}$​: The maximum value of the i-th objective function across all solutions in the non-dominated set. It sets the upper limit for normalization.

• ${{f}_{i}}^{min}$​: The minimum value of the i-th objective function, serving as the baseline for comparison.

• ${{f}_{i}}^{j}$​: The specific value of the i-th objective function for the j-th non-dominated solution.

Interpretation and functionality

The membership function ${{\mu }_{i}}^{j}$​ maps the objective values to a normalized scale ranging from 0 to 1:

• A solution achieves a membership value close to 1 when ${{f}_{i}}^{j}$​ approaches ${{f}_{i}}^{min}$​, indicating superior performance for the i-th objective.

• Conversely, a membership value near 0 signifies proximity to ${{f}_{i}}^{max}$​, reflecting suboptimal performance.

Role in decision-making:

The normalized membership values across multiple objectives provide a quantitative basis for selecting the BCS. The aggregation of membership functions across all objectives is expressed as in relation (24):

$${\mu }_{j}=\frac{{\sum }_{j=1}^{{N}_{obj}} {\mu }_{ij}}{{\sum }_{i=1}^{M} {\sum }_{j=1}^{{N}_{obj}} {\mu }_{ij}} (24)$$

where ${N}_{obj}$ denotes the number of objective functions, and M denotes the non-dominated solutions. The BCS is the one with the highest value of ${\mu }_{j}$.

This approach helps decision-makers to always balance competing objectives dynamically. It ensures adaptability with changing operational priorities, at the same time retaining computational efficiency. The integration of fuzzy logic into MaO-OPF optimization framework makes it more applicable to high-dimensional power systems that are complex; thus, resulting in robust, scalable and interpretable solutions. The use of Eq. (23) and Eq. (24) demonstrates the need for integrating advanced decision-making frameworks such as fuzzy logic into optimization algorithms. This helps in determining optimal trade-offs and selecting most balanced solutions that are feasible within the realm of many-objective optimization challenges.

Comprehensive analysis of experimental outcomes

This section presents a comprehensive empirical investigation on the performance of MaOSSO in comparison with MaO-OPF optimization. The research will use standard benchmark test functions such as DTLZ and MaF to evaluate its behavior in different high-dimensionality situations. The experimental design is made in such a way that it captures various aspects of MOEA including convergence diversity trade-off and computational effort. In particular, MaOSSO is compared against NSGA-III, RVEA, NMPSO and MOEA/D-DE for objective configurations (5, 8, 10 and 15 objectives respectively). To make this work appear more realistic, chosen test problems span over linear, concave, multimodal and scalable complexities which are used in the experiments as well as degenerate ones. These criteria include Generational Distance (GD), Inverted Generational Distance (IGD), Spread (SD), HyperVolume (HV) and RunTime(RT) which can be employed to investigate how well these methods find solutions to Pareto optimality concept by also considering population distribution and approximation set accuracy.

This part is focused on comparative analysis, highlighting MaOSSO’s ability to address the tradeoffs in high-dimensional optimization landscapes. The investigation carries out a sensitivity analysis on IEEE 30, 57 and 118-bus systems to demonstrate how scalable the algorithm is as well as how it can be used for real-world power system optimization cases. Also, this study examines the application of MaOSSO algorithm as one of the means that address contemporary challenges facing modern power systems. It shows new opportunities for sustainable and computation-efficient methods of optimization.

Benchmark test problems

In particular, many-objective optimization requires selection of test problems as an integral step in validating the optimization algorithms’ performance. To assess the full potential of the MaOSSO algorithm, the current study applies several well-defined benchmark problems. For example, among others, the DTLZ and MaF series have been selected to represent a wide range of simulations with complex optimization problem landscapes. The DTLZ suite is specifically constructed to test scalability and robustness of an algorithm with varying number of objectives. The varieties here incorporate linear, concave, multimodal Pareto front geometries which assist in demonstrating algorithm convergence whilst preserving diversity within the solution space. Additionally, the MaF suite contains high-dimensional non-uniform distributions of disjointed Pareto degenerate solution sets which test the algorithm’s adaptation to complex interdependent trade-offs. In this part, it attempts to exhaustively analyze the performance of MaOSSO with respect to these benchmark problems in order to provide a holistic evaluation on performance when faced with high-dimensional optimization problems. Convergence precision, solution variety, and overall optimization effectiveness are evaluated by Generational Distance (GD), Inverted Generational Distance (IGD), Spread (SD), and Hypervolume (HV) metrics. The algorithm underwent the tests listed in Table 4. These results allow for a robust comparison of the algorithm with numerous contemporary optimization approaches for many-objective problems, thus validating its practical problem-solving capability. To all benchmark tasks, each method was allocated a uniform computational budget of 30,000 function evaluations. This limit was placed in order to achieve an unbiased evaluation of the various methods’ convergence efficiency, accuracy, and the differences among approaches. All methods were executed 30 times independently, and for each distinguishing metric, statistical values such as average and variance were captured.

Table 4 Features of many-objective optimization benchmark suites.

Evaluation metrics for performance assessment

The analysis of the performance metrics of the MaOSSO algorithm is crucial to understand the potential benefits that the software has. IGD, HV, GD, RT and SD are five evaluation performance metrics as shown in Fig. 7. These details were well given above regarding these metrics; hence repetition would be unnecessary but it should be reiterated that each metric emphasizes different aspects of algorithm’s performance such as efficiency of an algorithm, convergence and diversity in efficient generation of Pareto optimal solutions.

• IGD: This means how far away from Parato front solution is obtained by calculating its distance from set to closest point on actual set. In other words, IGD tends to be low when there is a lot of structural combination making it possible for strong convergence and diversity within a set.

• HV: It measures how much three-dimensional space a resultant manifold encompasses in target settings. It illustrates how well solutions cover the Pareto Front by representing what proportion of space occupied by solution-set. A high HV value denotes that solutions are spread more uniformly, and thus have better overall coverage of the pare-to-front.

• Generational Distance (GD): This determines convergence by calculating the average Euclidean distance between solutions in the obtained set and a closest solution on the actual Pareto front. A lower GD value indicates a higher degree of convergence achieved by the algorithm.

• Spread (SD): SD quantifies dispersion of solutions found with respect to Pareto front reflecting its diversity. The metric evaluation is about how far away from each other the solutions are, where lower standard deviation means uniformity in having them located on the front.

• Runtime (RT): RT is an indicator for computational performance of an algorithm, showing time taken to achieve Pareto Front. Lower values of RT spell improved turn-around efficiency of the algorithm making it applicable in real-time or large-scale problems

Fig. 7

Performance metrics of MOOPs.

In understanding the performance of the SSO algorithm, we incorporated five indicators of performance metrics.

• Generational Distance (GD): Evaluates the average distance between the derived solutions and the true Pareto front—lower value indicates better performance.

• Inverted Generational Distance (IGD): An index that captures both convergence and diversity by assessing the distance of reference points to the obtained front.

• Spread (SD): Measures the degree of uniformity in solution distribution along the front.

• Hypervolume (HV): Measures the space covered by the derived solutions in objective space; higher values suggest stronger divergence-convergence balance.

• Run Time (RT): Represents the cost of computation in seconds on a per scenario basis.

These performance metrics as a whole support claim of enhanced convergence along with improved distribution while practical viability is ensured (RT).

GD (Generational Distance) is an indicator that looks at the average Euclidean distance between real Pareto front points and those of its derived counterpart. GD has accuracy compromise, which makes it a good alternative to other measures such as Hypervolume (HV), since it is less computationally demanding. GD focuses entirely on the distance from the true front without any other measure; thus, it clearly shows how close the resulting solutions are to the optimal set. When used together with other metrics, GD helps in providing more information about the quality of approximation while relying mostly on a convergence metric. On another note, Inverted Generational Distance (IGD) calculates minimum Euclidean distance between points in a true Pareto front and points in a generated set. IGD acts like GD, but at the same time considers both diversity and convergence of solution sets provided there are enough solutions. This explains why IGD is also referred to as ‘Inverted’ Generational Distance because it calculates minimum Euclidian distance between two sets. It proves to be better than GD in that it estimates accuracy of solutions and their distributions, thus making it a better metric for gauging approximation accuracy across different dimensions.

The Spread (SD) measure is a unary indicator that only applies to the characteristics in the solution set. This could mean how far apart are solutions located on the Pareto front. Alone, considering this SD reduces assessment to just one dimension although Steger suggests it can be enhanced as a metric of quality by either GD or IGD metrics. The concern for convergence problem as it relates to the issue of solutions distribution is well captured by this combination. Low computational complexity makes SD particularly attractive when time is crucial in solving problems. The HyperVolume (HV) metric is a complex homologous measure which quantifies the objective space volume enclosed by the final Pareto front. Unlike GD, IGD, and SD, HV does not discriminate any of these three major properties such as diversity, accuracy and cardinality; thus making it superior in terms of overall solution set quality. This may be one reason why HV stands as the most recommended performance metric across different areas of study because of its wide range of evaluation. However, HV incurs an exponential computational cost with respect to increases in 0bjectives leading to tough tasks in working for high dimensional optimization problems.

The RT metric quantifies how an algorithm performs in terms of time it takes to calculate the solution cluster. This is measured by taking the mean time required to achieve the set of solutions. Smaller values of RT indicate that the algorithm can effectively solve an optimization problem; hence, RT is important when evaluating algorithms under situations where quick responses or real time solutions are necessary. Those metrics described above tell more about the performance of algorithms used in multi-objective optimization with some sort of simplicity. It can be seen from this context that metrics like GD and IGD have a focus on convergence as their main characteristics while IGD provides more information about diversity. Distribution quality is measured by SD, HV evaluates quality with respect to accuracy, diversity and cardinality collectively and lastly, RT measures efficiency from computational perspective. All these metrics together give researchers a comprehensive view on how different multicriteria optimisation problems perform according to each one of them.

Optimization algorithm parameter settings

The parameter settings for the MaOSSO algorithm were carefully calibrated to guarantee consistency, robustness, and peak performance across all test cases. The configurations were developed following comprehensive initial analyses and benchmarking evaluations, guaranteeing the algorithm’s flexibility and effectiveness in tackling a variety of many-objective optimization challenges.

Population size and iterations

For a comprehensive evaluation, the population size was set to 100 individuals, striking a balance between computational efficiency and solution diversity. A maximum of 30,000 function evaluations was enforced across all test cases, ensuring sufficient exploration of the solution space while maintaining computational feasibility.

Crossover and mutation operators

MaOSSO’s performance was enhanced by utilizing well-adjusted genetic operators:

• Crossover: Simulated Binary Crossover (SBX) with crossover probability (p_c) of 0.3 and distribution index (η_c) of 30 was employed. This mixture assured that offspring were robustly generated while preserving diversity and convergence efficiency.

• Mutation: A polynomial mutation with p_m = 1/N, where N is the population size, represents a mutation probability. For fine-tuned exploration around parent solutions η_m was set to 20.

Swarm dynamics and velocity tuning

Key parameters which governed the flocking behavior were fine-tuned carefully in order to achieve optimum outcomes of the SSO algorithm as follows:

• Inertia Weight (w): It is dynamically tuned to strike a good balance between exploration and exploitation over iterations.

• Social (c₁) and Cognitive (c₂) Coefficients: set to 2.0 each, these ensured that the sperm cells well employed both individual and group learning processes.

• Random Factors (r₁, r₂): These factors are uniformly drawn from [0, 1] such that the random factors introduce stochasticity, enabling the swarm to escape local optima.

Constraint handling

To address the intricate constraints associated with MaO-OPF problems, the algorithm integrated:

• Boundary Checks: Verifying that all decision variables adhere to established constraints.

• Penalty Functions: Violations of equality and inequality constraints were addressed through the application of adaptive coefficients, effectively incorporating these penalties into the fitness function.

Environmental adaptation

MaOSSO’s environmental parameters were derived from biological principles, corresponding to authentic conditions:

• Temperature Range: Varied between 35.1 and 38.5 °C, replicating physiological impacts on velocity adaptation.

• pH Levels: Modified within the range of 7–14, adding a new layer of complexity to the optimization procedure.

Evaluation protocol

Thirty executions were performed on each algorithm to ensure the statistical reliability. There were performance metrics that evaluated convergence, diversity and computational efficiency through hypervolume, generational distance and run time. The comprehensive parameterization framework mentioned above highlights the adaptability of MaOSSO to various optimization problems making it scalable and reliable for high-dimensional many-objective ones.

Performance metrics on DTLZ benchmark suites

The performance of this algorithm is tested against the DTLZ1-DTLZ7 benchmark problems and state-of-the-art algorithms like NSGAIII, RVEA, NMPSO, MoEA/D-DE. It employs five evaluation metrics GD, SD, IGD, HV and RT. This part evaluates the performance based on other criteria.

In summary, the performance can be summarized as follows.

• Generational Distance (GD)

  Table 5 shows how GD of MaOSSO compared to other competing algorithms on DTLZ1-DTLZ7 bench mark problems. The algorithm had a good performance with very low GD values showing how well it was able to follow areas near the Pareto optimal. Specifically in 21 different configurations MaOSSO outperformed 15 others as it improved solution accuracy meaning that it performed better than competitors.

  Table 5 GD metric evaluation across algorithms using DTLZ problems.

• Spread (SD)

  Table 6 represents SD measures that help us understand about how much better dispersion of solution is where more means more useful is this parameter. The algorithm showed high results for DTLZ6 and DTLZ7 among others thus dominating in some cases and averaging with respect to best SD values. Out of 21 settings a total of fourteen led to way far less SD values which indicate ability for maintaining strong diversity across Pareto front compared to any other system.

  Table 6 SD metric evaluation across algorithms using DTLZ problems.

• Inverted Generational Distance (IGD)

  Table 7 below presents IGD metric which helps in comprehending the vector trace accuracy, approximation and robustness of final solution. The algorithm was a great performer with best IGD values compared to other methods, better convergence estimates and solution robustness as well as it achieved 14 out of 21 benchmark configurations in performance.

  Table 7 IGD metric evaluation across algorithms using DTLZ problems.

• HyperVolume (HV)

  As can be noticed from Table 8, MaOSSO has attained the maximum value of hypervolume among all tested methods in 12 configurations effectively choosing sound solutions. Thus, being superior in HV implies that this method achieves a compromise between diversity and convergence equally.

  Table 8 HV metric evaluation across algorithms using DTLZ problems.

• Running Time (RT)

  Time is shown in Table 9. M-MASP turned out to be fastest in every configuration among all techniques used. Maximum running time together with other performance measures makes it possible for MaOSSO to be applied for real-time or large problems.

  Table 9 RT metric evaluation across algorithms using DTLZ problems.

Additionally, the non-dominated solutions obtained by MaOSSO Algorithm are outlined in Fig. 8 for comparison with those found using other algorithms on DTLZ1-DTLZ7. The solutions generated by MaOSSO Algorithm are well dispersed and improved one which merges Pareto fronts to realize the balance of exploration and exploitation. The following is an account of how MaOSSO Algorithm outperformed NSGAIII, RVEA, NMPSO, and MOEA/D-DE.

• The MaOSSO Algorithm set a record with GD Metric score as the best performer in 15 out of the 21 test cases carried out.

• Out of 21 tests configurations, MaOSSO Algorithm promoted diversity in 14 and ensured no discrimination was present.

• The rest were overachieved by MaOSSO Model among its other model counterparts with a perfect convergence and utmost diversity.

• A total of 12 configurations were examined for Maximum captured objective space while maximizing space geometry notation. In all these twelve cases, MaOSSO was better than any other solution.

• It was observed that not only did MaOSSO prove to be the fastest but also had always the lowest turnaround time during tests.

Fig. 8

Analysis of MaOSSO on DTLZ1 to DTLZ7 MOOPs.

This implies that, when compared to the original DTLZ problems, MaOSSO is more efficient in terms of computation and convergent diversity. In all DTLZ problems, this algorithm performs excellently well making it a preferable choice for solving complicated Many-Objective Optimization Problems (MOOPs). Moreover, this approach is attractive to real-world instances encountered in solving many-objective optimization problems which involve high dimensional objective functions using HV and IGD scoring.

DTLZ test suite is a known scalable benchmarking suite which is more difficult than classical and ZDT test suites. Nevertheless, DTLZ1—DTLZ4 are multimodal which makes exploration and achievement of convergence to the true Pareto front very difficult though MaOSSO outperformed other algorithms in terms of both convergence and solution diversity compared to their competitive counterparts. But what if the DTLZ5 as well as DTLZ6 have degenerate Pareto fronts that make achieving proper non-dominated solutions (NDS) but with good dispersion all over the Pareto front and the rest of margins extremely complex? However, many methods such as MaPSO failed to cover lower parts of both these areas on the real pareto front fully. In this case, MaOSSO had to cover a whole range from one end point (Pareto front) to another or solution at the other end of it taking into account all possible cases that may occur during optimization process. For these two problems, however, MaOSSO solved everything, exhibiting an exact balance between required solutions. The problem of DTLZ7 is fragmented, with both smooth and rough concave parts, which have a separated search space. The situation was worsened by fragmented nature of the DTLZ7 test problem that has both smooth and rough concave regions and disjointed search area. There were no good results on it from such optimization algorithms as NSGA-III, NMPSO, RVEA, MOEA/D-DE. Meanwhile, MaOSSO performed well in this regard by surpassing other methods in terms of convergence and diversity.

To validate the quantitative metrics, Figs. 9 and 10 show the Pareto front graphs obtained for DTLZ3 and DTLZ7 problems solved using MaOSSO, NSGA-III, RVEA, and MOEA/D-DE. The plots clearly show the best spread and denser convergence toward the optimal front achieved by MaOSSO.

• In Fig. 9, the Pareto front for DTLZ3 problem which has 10 objectives is obtained using MaOSSO, illustrating that more than 90% of the feasible region is covered with solutions and it is almost continuous and well distributed. On the other hand, NSGA-III and MOEA/D-DE exhibited strong clustering and noticeable gaps in the provided solutions.

• Fig. 10 further confirms that MaOSSO is able to preserve the connectivity and diversity of the front in degenerate complex solution space problems like DTLZ7. The observations from the figures support the HV and IGD metrics, reinforcing the robustness of the algorithm in different geometries of objectives.

Fig. 9

Pareto front plots for DTLZ3 with 10 objectives.

Fig. 10

Pareto front plots for DTLZ7 showing disconnected fronts (e.g., MaOSSO vs. NSGA-III, MOEA/D-DE).

These figures support to elucidate the interpretation of numerical findings and to show the empirical excellence of MaOSSO in graphics retouched by imagination.

MaF problem results and performance assessment

The MaOSSO algorithm was compared to the NSGAIII, RVEA, NMPSO and MOEA/D-DE algorithms on MaF1–MaF15 benchmark problems. The evaluation used GD, SD, IGD, HV and RT. These metrics are depicted in Table 10 and combined measure convergence diversity computational efficiency and solution quality.

Table 10 Evaluation of GD metrics across algorithms on MaF problems.

• Generational Distance (GD)

  In terms of GD parameter selection for the given MaF problems, the superiority of MaOSSO is indicated by its consistently minimal GD metrics. This improved accuracy in solution making general distance between calculated pareto front almost zero which shows that the algorithm has a strong capability in dealing with multi-modalities as seen in MaF3 and MaF7.

• Spread (SD)

  Table 11 depicts the SD values where MaOSSO also managed to maintain and increase diversity among all solutions obtained without compromising their accuracy even if put into huge spread measures as indicated by high SD metrics. More specifically in case of MaF6 and MaF10 algorithms where desired diversity had to be measured and preserved well were not only better but also explained above those utilized previously.

  Table 11 Evaluation of SD metrics across algorithms on MaF problems.

• Inverted Generational Distance (IGD)

  As shown in Table 12, MaF3 and MaF8 have shown remarkable achievements whereas MAF13 has presented an extremely impressive data where the maximum possible difference between diverse set of solutions was reached, boosting its size significantly. Among most MaF problems, MaOSSON’s optimal IGD values suggested that the strength as well as stability of the proposed solution are confirmed by successful ensured ratio between convergence and diversity.

  Table 12 Evaluation of IGD metrics across algorithms on MaF problems.

• Hypervolume (HV)

  Table 13 shows that MaOSSO has better HV values than any other MaF problem including majorities such as MaF1, MaF9, and MaF15. Consequently, it means that there is a higher spatial occupancy by MaOSSO in the objective space thus making it more efficient in a multi-objective environment.

  Table 13 Evaluation of HV metrics across algorithms on MaF problems.

• Runtime (RT)

  The smallest time taken to solve MaF problems was by MaOSSO as illustrated in Table 14; this proves that MaOSSO is time wise effective. Time and performance indicators reflect on the real-time large-scale application efficiency for MAOSSO.

  Table 14 Evaluation of RT metrics across algorithms on MaF problems.

Further, Fig. 11 illustrates how the MaF1-Maf15 algorithm comparisons performed by MaOSSO and other algorithms were improved. The analysis also shows that the solutions of MaOSSO are characterized by a well-dispersed or highly correlated fronts indicating its capability for solving mixture of problem characteristics and their meso-, biased- and multi-modal fronts. MaF suite results make MaOSSO demonstrate to stand out in addressing together the Many-Objective Optimization problems:

• Unlike current traditional and evolutionary custodians, GD and IGD metrics reinforce MaOSSO accurate convergence precisely and its balanced diversity.

• Color SD metric ascertains the effective scattering over the many-dimensional Pareto optimal surface.

• A measure HV as stated above showcases MaOSSO’s capability in spanning a wide spectrum of the objective space.

• For the RT metric good appear computation overheads an important prerequisite for practical implementation were evident.

Fig. 11

GD metric evaluation: mean and STD for MaF problems.

A clear conclusion from this analysis is that built-in strategies for adaptive control or advanced search principles in class of MAOSSO enhancement ensure robust performance on various test cases. This means it has performed well compared to its competitor with measuring points such as HV and IGD, confirming that it can cope with many complex objective functions optimization problems across industries.

Among all of the last and most challenging benchmark suit, MaF is by far the latest one which surpasses DTLZ. On the other hand, it is worth mentioning that all issues corresponding to test problems MaF1 through MaF4 and MaF7 are Multimodal. This is contrary to what has happened to other popular algorithms like C-MOEA which have better convergence and diversity as compared to MaOSSO Algorithm. However, for these degenerate Pareto set having problems mentioned such as MaF5, MaF6, MaF8, MaF9 and MaF13, convergence was slightly more straightforward while ensuring an even distribution of Non-Dominated Solutions NDS across the entire Pareto was still a task. Examples include NMPSO algorithm that did not extend its search towards those solutions located along the lower border of real Pareto front in these cases. Contrarily though, throughout this process (convergence & diversity), we can see from Eq. (7) that it takes over all points on the Pareto front including endpoint solutions. Pareto fronts are disjoined disjointed by the MaF10 to MaF12 test problems through which they ‘join’ and include Pareto fronts that are both convex and concave in nature whereas Pareto fronts of MaF14 and MaF15 are further complicated by their large scale and partly separable frontier comprising convex, linear areas. On these benchmarks, the performance of NSGA-III, NMPSO, RVEA and MOEA/D-DE algorithms were below expectations. Similarly, MaOSSO performed well on these benchmarks and is capable of solving efficient optimization problems with respect to the MaF problems. The one generation computational complexity of the MaOSSO algorithm is equivalent to that of other tested algorithms such as NSGA-II, RVEA, NSGA-III etc. for efficiency. For N population size and M objectives the complexity is O(MN2) which relates to this general approach.

Analysis of MaO-OPF benchmark problems

As the MaOSSO algorithm’s effectiveness is being demonstrated, the 30-bus IEEE, 57-bus IEEE and 118-bus IEEE systems will be used as test cases for solving the MaO-OPF problem. The MaOSSO algorithm’s effectiveness in addressing the MaO-OPF problem with different case studies are displayed in Table 15.

Table 15 Performance review of single-objective OPF case studies.

We provide a radar chart (Fig. 12) aggregating algorithm ranks over all five metrics—Generational Distance (GD), Inverted Generational Distance (IGD), Hypervolume (HV), Spread (SD), and Runtime (RT) to help to further improve the interpretability of the performance results. Every axis shows every algorithm’s ranking on a 1 (best) to 5 (worst) scale. MaOSSO’s supremacy and consistency are amply shown by this graphic, which either meets or surpasses top approaches in all major spheres. Such a representation provides an easy grasp of the behavior of any technique and helps to enable quick cross-metric comparisons.

Fig. 12

Comparative performance of optimization algorithms.

Comparative analysis with contemporary swarm-based optimizers

To highlight the relative strengths and potential limitations of the proposed MaOSSO framework, we benchmark it against three prominent swarm-based algorithms widely used in many-objective optimization contexts:

• GWO (Grey Wolf Optimizer): Emulates the leadership hierarchy and hunting mechanisms of grey wolves.

• MOPSO (Multi-Objective Particle Swarm Optimization): Extends classical PSO with Pareto dominance and crowding-distance preservation.

• MOGWO (Multi-Objective GWO): Combines GWO’s search dynamics with diversity preservation techniques.

Table 16 below presents a summarized comparative evaluation covering five aspects: convergence quality, diversity preservation, computational complexity, parameter tuning effort, and scalability to high-dimensional problems.

Table 16 Comparative summary of swarm-based optimizers.

As shown, while GWO and MOGWO offer strong diversity and reasonable performance, their scalability and convergence speed are inferior to MaOSSO. MOPSO converges quickly but suffers from premature convergence and high parameter sensitivity. In contrast, MaOSSO maintains a balance between convergence and diversity while offering robustness in high-dimensional search spaces.

Algorithmic ranking summary across metrics

To provide a concise overview of how each algorithm performs across various evaluation metrics, we constructed a ranking matrix over the DTLZ1–DTLZ7 test suite using the following criteria:

• IGD (↓) – Convergence + Diversity

• HV (↑) – Hypervolume (front coverage)

• GD (↓) – Pure convergence

• SD (↓) – Diversity (spread)

• RT (↓) – Computation time

Table 17 presents the ranking scores (1 = best, 5 = worst) averaged over all benchmark problems.

Table 17 Aggregate algorithm ranking across all metrics (lower rank = better).

MaOSSO ranks 1st overall, leading in most metrics and showcasing a highly favorable diversity–convergence–efficiency trade-off. NMPSO is competitive in diversity and convergence, but lags slightly in execution time. MOEA/D-DE consistently underperforms, especially under high objective settings.

Comprehensive performance evaluation

Modeling framework for the system

Research on hybrid grids is done in Belgium and this research applies broadly to European countries. More specifically, a European hybrid grid will be considered consisting of three subsystems. The structure encompasses:

• Principal Sources—These are basic energy generators made up of hydroelectric plants and thermal plants.

• Additional Sources—Wind turbines and photovoltaic panels also supplement green energy that feeds into the grid.

• Grid Design—The systems were connected using ieee-30 bus configuration for effective power flow analysis.

The Belgian case study described above is based on the modeling and analysis of a hybrid grid.

Primary sources

Belgium’s energy mix for 2019, as reported by Belgian Company FEBEG³⁵ had two dominant sources defined; thermal and hydro plants which accounted to 38.5%.

This study has some assumptions:

• All sources of energy are assumed to be maintainable.

• It is also considered that there are no interfaces in the system integration between different energy sources.

Figure 13 in Belgium compares the percentages of fuels for net electricity generation (kWh). Figure 14 reveals different reliability statuses among system components.

Fig. 13

Total net production of electricity in Belgium in 2019³⁵.

Fig. 14

State model of a given system³⁶.

The allotment for primary sources is given below:

• The system includes 10 hydroelectric units, each with an annual power output of 0.13 TWh.

• The Mean Time to Repair (MTTR) is set at 60 units of time, while the Mean Time to Failure (MTTF) is 1410 units of time.

Considering the total electricity output of 89.85 TWh, the contribution rate of the hydroelectric units can be calculated as shown in relation (25):

$$\gamma_{1} { }\left( {\text{Contribution Rate}} \right) = \frac{{\text{Total Power Output from Hydroelectric Units}}}{{\text{Total Electricity Output}}} = \frac{{10 \times 0.13\,{\text{TWh}}}}{{89.85\,{\text{TWh}}}}$$

(25)

This calculation provides insight into the role of hydroelectric units in Belgium’s energy mix and their reliability dynamics within the network. The value of ${\gamma }_{1}$ is approximately 1.4%. Further, from the Fig. 10, we obtain for hydropower: 0.9 + 0.3 = 1.2%.

• 9 thermal units of unit power 3 terawatt-hours, with a mean time to repair (MTTR) of 60 and a mean time to failure (MTTF) of 1410. Compared to the total output of 89.85 terawatt-hours (TWh), we can calculate the rate as follows (26):

  $$\gamma_{2} = { 3}*{9}*{1}00/{89}.{85}$$

  (26)

  The value of ${\gamma }_{2}$ is approximately 30%. Similarly, a ratio of 37.3% can be obtained from Fig. 13.

Alternative sources

The wind and photovoltaic units have to be implemented in the model as alternative sources in the following manner:

• A total of 10 wind turbines are employed, keeping in mind that the capacity offered by wind system is determined by wind velocity and power curve. For a wind speed model to be developed, room data on wind speed (Belgium data) needs to be gathered, and a mathematical model constructed to emulate wind velocity. For this purpose, the Weibull function is employed³⁷. The unit has a nominal capacity of 0.75TWh, MTTR 60 and MTTF 1410. Taking into account the total generated power of 89.85TWh the rate can be worked out as below (27):

  $$\gamma_{3} = \, 0.{75}*{1}0*{1}00/{89}.{85}$$

  (27)

Therefore, ${\gamma }_{3}$ is approximately 8.3%.

According to Fig. 10, the wind turbine has an efficiency of 10.2%. In addition, the output power can be represented by the following system of Eqs. (28)³⁸:

$${P}_{WT}=\left\{\begin{array}{c}0 ; 0 < v < {v}_{cut-in} ou {v}_{cut-out}< v \\ a{v}^{3}+b{P}_{nom} ; {v}_{cut-in} < v < {v}_{nom}\\ {P}_{nom} ; {v}_{nom} < v < {v}_{cut-out}\end{array}\right.$$

(28)

Having the low cutting speed as ${v}_{cut-in}$ and the high cutting speed as ${v}_{cut-out}$, the nominal speed is referred to as ${v}_{nom}$. The nominal power is denoted as ${P}_{nom}$. The current speed is represented as v. In addition, we have the following relations (29) and (30):

$$\text{a}=\frac{{P}_{nom}}{{{v}_{nom}}^{3}- {{v}_{cut-out}}^{3}};$$

(29)

$$\text{b}=\frac{{{v}_{cut-in}}^{3}}{{{v}_{nom}}^{3}- {{v}_{cut-out}}^{3}}$$

(30)

Reference³⁹ provides a table (Table 18) of parameters for a wind turbine that will be used for simulation:

Table 18 Key operational values for wind turbine units.

• The total number of photovoltaic cells is ten multiplied by ten to the power of twelve (10*10^12), each with a unit power of P_PV. The mean time to repair (MTTR) equals sixty (60), and the mean time to failure (MTTF) also equals 1410. What should be considered, however, is that the performance of PV units depends on how much sunlight they receive. The test must be carried out under radiation of one kilowatt per square meter and cell temperature of twenty-five degrees Celsius. It’s essential in PV research for current-voltage characteristic tracing which is acquired through these relationships (31)⁴⁰:

  $$\left\{\begin{array}{c}{T}_{c} ={T}_{A}+ s*\frac{({N}_{OT}-20)}{0.8}\\ I = s*({I}_{sc}+ {K}_{I}({T}_{C}-25))\\ V = {V}_{OC}- {K}_{V}*{T}_{C}\end{array}\right.$$

  (31)

Given:

• ${T}_{C}$ represents the cell temperature

• ${T}_{A}$ refers to the ambient temperature.

• s is the irradiation.

• The nominal cell temperature is ${N}_{OT}$.

• The short-circuit current in a photovoltaic unit is ${I}_{SC}$.

• The open circuit voltage in a photovoltaic unit is ${V}_{OC}$.

• I is the current in a photovoltaic unit

• The voltage in a photovoltaic unit is denoted by V.

• ${K}_{I}$ is a factor that relates to the temperature of the short-circuit current.

• ${K}_{V}$ refers to the temperature factor associated with open circuit voltage.

When evaluating the output power, we need to calculate the shape factor FF, which is given by Eq. (32)⁴¹:

$$\text{FF }=\frac{{V}_{MPP}*{I}_{MPP}}{{V}_{OC}*{I}_{SC}}$$

(32)

With ${V}_{MPP}$ and ${I}_{MPP}$, which are the voltage and current obtained through MPPT, respectively. The energy per hour unit is given by the t.

$${\text{P}}\, = \,{\text{FF }}*N_{s} *{\text{ V }}*{\text{ I}}$$

(33)

⁴² Provides a table (Table 19) of parameters for a cell that will be used for simulation:

Table 19 Values for the parameters of the PV units.

Thus, P = 3.8TWh.

Compared to the overall production of 89.85TWh, we find almost the same rate.

$${\gamma }_{4}= 3.8*100/89.85$$

(34)

Thus ${\gamma }_{4}$ ≈ 4.22%

Figure 10 gives for the PV a value of 4.2%.

Energy consumption: data and insights

Belgium’s electricity consumption in 2019 stood at 83.73 TWh, which was the highest for that year compared to previous years. These considerations are net production as follows:

• Electricity Used for Pumping-Turbine Operations

• Net Losses

• Import/Export of Electric energy.

This metric also takes into account electric energy consumption by different sectors such as refineries among other industrial sectors.

Figure 15 shows trends and fluctuations of Belgium’s total electricity generation from 2007 to 2019. The running data provides an overview of the energy balance, the possibility of its creation and usage within a country. For instance, annexes 1–3 contain detailed seasonal statistics on electricity usage in Belgium during the year of 2019. Seasonal breakdowns help understand shifts caused by climate change, industrial processes and domestic use better than annual average numbers do.

Fig. 15

Trends in electricity consumption in Belgium (2007–2019)³⁷.

IEEE 30buses model

Figure 16 features the IEEE 30-bus model which provides a simplified representation of the US grid around December 1961. This is an excellent model because it shows fundamental network behaviors and it has been widely used for power system studies. The Europeanized version of the IEEE 30-bus model was applied in this research. In comparison to the original American one, this one has more lines (41) and therefore more detailed for use within Europe power systems.

Fig. 16

Overview of the IEEE-30buses model⁴³.

Below are related data and information:

• Bus Data: A fourth Annex provides bus voltages with the respective load levels as well as other relevant data on bus data.

• Network Admissions: The annex 5 contains parameters governing network admittance and it is a compilation of other systems.

In alignment with earlier discussions, the proposed MaOSSO along with other chosen algorithms are implemented in this extensive power system. The results acquired are displayed in Table 20. The algorithmic and control parameters for all algorithms remain consistent with prior discussions.

Table 20 Belgium’s energy consumption: a 12-year review (2007–2019).

Table 18 presents simulation results on the validity of MaOSSO, NSGA-III, RVEA, NMPSO and MOEA/D-DE using different indicators such as Total Fuel Cost, Total Emissions, Active Power Loss, Reactive Power Loss, Voltage Magnitude Deviation, Voltage Stability Index and Runtime. Moreover, the results obtained demonstrate about the efficiency of these algorithms in relation to their resilience in addressing complexity.

• a. Total Fuel Cost (TFC)

  It is important to note that for TFC MaOSSO is an outstanding model considering its rate of 1228.025 $/h which reveals its cost management and economic characteristics while the other methods namely NSGA-III, RVEA, NMPSO, and MOEA/D-DE failed with a highest value of $/h 1958.316 from MOEA/D-DE. The research findings clearly indicate that there is room for cost optimization through integration of MaOSSO.

• b. Total Emissions (TE)

  In terms of total emissions per hour generated by MaOSSO at a value of 0.159793 ton/h shows how environmentally conscious the organization is. Contrarily to this,RVEA does not seem to care much about environmental effects since it has 594.6163 ton/hour.

• c. Active Power Loss (APL).

  MaOSSO achieved a low active power loss of 47.25445 MW, indicating good energy distribution and reduced system losses. The largest losses were registered by MOEA/D-DE (1039.928 MW), showing a great failure in energy efficiency.

• d. Reactive Power Loss (RPL).

  In terms of this measure, MaOSSO focused on reducing reactive power losses with the figure standing at 175.3431 MW which is the highest compared to all other algorithms. As for RPL, MOEA/D-DE has reached as high as 2304.264 MW indicating its poor performance in terms of measuring energy efficiency.

• e. Voltage Magnitude Deviation (VMD).

  MaOSSO was the only one among them that had 1.971746 p.u., meaning it was the best in this case in terms of voltage deviation towards reliable grid measurement efforts made by MaOSSO; while MOEA/D-DE also presented very poor result with 5.407671 p.u., which is regarded as “voltage stability measure” concerns – and so became the worst performer in this area as well.

• f. Voltage Stability Index (VSI).

  It is the best with 0.84176 p.u achieved by MOEA/D-DE ‘Although it may fluctuate to a higher side in some instances indicating improved stability in certain parameters but this is mostly not efficient in other respects. MaOSSO also reached a more stable point of 0.232473 p.u as well as optimization for other objectives was performed.

• g. Voltage Stability Index (VSI).

  Among the three methods, MOEA/D-DE was the best with 0.84176 p.u. This can sometimes indicate better stability on some measures, though usually indicative of inefficiency on others, although’. On the other hand, MaOSSO arrived at a more stable point of 0.232473 p.u, while at the same time optimizing for other objectives were done.

• g. Runtime (RT).

  The highest scoring technique was MaOSSO which had a runtime of 0.025 s; this depicts that it had no issues reaching computational efficiency. On the opposite end of the scale, MOEA/D-DE did poorly and had a delay of 0.05 s, suggesting demanding scopes of work.

The summarization and insights are as follows:

• In terms of cost (TFC), environmental emissions (TE), energy cost efficiency (APL and RPL) and computational costs (RT) MaOSSO performed best in comparison with other algorithms.

• NSGA-III and NMPSO used the average calculation method where metrics produced some expected results, but they did not achieve the tradeoff between objectives set by MaOSSO previously discussed.

• Finally, RVEA and MOEA/D-DE underperformed in terms of emission, power losses and execution time which implies that the systems resources were misused as targets were changed.

Here are the various practical implications:

• The outcome implies that if there is need to meet economic, environmental and operational standards, MaOSSO can be utilized in development engineering for large power systems. This places MaOSSO amongst good alternatives for sustainable and cost-effective grid optimization in terms of performance in cost, emissions and runtime.

• Through the above discussions we can conclude that the proposed MaOSSO performs better than all other selected algorithms which have been used to solve the MOPF problem. This indicates its capacity which once again demonstrates why this method is more suitable for saturated large-scale power systems. Figure 17 shows PF achieved by MaOSSO, NSGA-III, RVEA, NMPSO and MOEA/D-DE illustrating distribution of non-dominant set and the area covered by these methods showed higher efficiency than NSGA-III, RVEA, and NMPSO.

Fig. 17

Best Pareto solutions for Belgium 59-bus power system.

The outcomes for Belgium’s 59-bus power system concerning fuel costs, emissions, power losses, and voltage stability are analyzed in relation to the tradeoffs achieved by MaOSSO, NSGA-III, RVEA, NMPSO, and MOEA/D-DE, as illustrated in the figures above. This section also addresses the optimization problem related to the incomplete objective set. The following outlines various key observations:

• 1. Converging on Pareto Front:

  • NSGA-III, RVEA and MoEA/D were seen to have solutions that span the entire range of objectives in a split-up range of solutions while MaOSSO had all their designed solutions close to the true Pareto Front.

• 2. Differences in Solutions:

  • Unlike the above two algorithms which are prone to clustering, MaOSSO is able to produce a wide variety of solutions that address different trade-offs requirements hence generating various points on the Pareto front.

  • Failing convergence and diversity was evident in NMPSO and MOEA whose majority of results ended up being more congested (thus less exploration into objective) than they were supposed to be.

• 3. Supremacy in Multi-objective Optimization

  • This is supported by multi-objective optimization demonstrating higher efficiency towards saving energy and emissions compared to maintaining stability within system as shown by MaoSSO;

  • The graph indicates that NMPSO and RVEA are not good at pursuing optimal trade-off strategies aimed at minimizing pollution/energy use because they tend to focus much on energy efficiency or emission limiting objectives.

Within the framework of the 118-bus system, the noted enhancement in Pareto front diversity directly enables operational flexibility in real-time. Practically speaking, this variation offers:

• Operators can choose from a large spectrum of almost ideal solutions to balance competing requirements like loss minimization, cost, and voltage stability depending on current operating priorities^44,45,46,47.

• Improved resilience: The availability of several options helps to fast switch to an alternative operating point without sacrificing system stability during sudden changes (e.g., load variations, generator outages).

• In a large-scale system like the 118-bus network, scenario readiness—that is, configurations that are strong under several operational states—is made possible by a diverse front, therefore enabling contingency planning^48,49,50.

Diversity is thus not only an algorithmic benefit but also a useful enabler of strong and flexible grid operation tactics in actual power systems.

Here are the algorithmic implications:

• MaOSSO has an even distribution of the Pareto fronts because it ensures a balance between exploration and exploitation through intelligent diversity management which is vital for decision-makers who need to have more than one answer when solving either operational or environmental problems^51,52.

• However, their suboptimal performance can be attributed to their over dependency on few parameters and their inability to explore effectively in a high dimensional Pareto optimization space.

The practical significance is as follows:

• MaOSSO is able to conduct co-optimization using a single tool for power systems with multiple objectives. Additionally, trade-off management has been greatly improved as it can help in satisfying almost any operational objective ranging from simple cost efficiency to long tem sustainability.

• However, MaOSSO is compared with NMPSO and MOEA/D-DE leading to clarification of the importance of these algorithms clarifies why NMPSOs are no longer applicable and what are their valid replacements in the need of MOEAs.

Considering this, the above-mentioned concepts include adequacy and devaluation of warranty; therefore, modeling of the studied system should start first before explaining the means used in this particular case. This will undoubtedly be one of the main elements while building our project since it will be aimed at revealing different stages that have to be done during research process.

Comparative performance with FACTS-based and fuzzy evolutionary OPF approaches

We compare the performance of the proposed MaOSSO method against two well-known evolutionary strategies used in real-world OPF scenarios in order to verify its practical feasibility:

• Naderi et al. (2024)⁵³ presented an evolutionary fuzzy optimisation of active power discharge utilizing UPFCs (Unified Power Flow Controllers) within the IEEE 30-bus system.

• With a view towards fuel cost, emission, and voltage profile trade-offs, Naderi et al. (2023)⁵⁴ used a wavelet-oriented EA to address multi-objective OPF issues including FACTS. MaOSSO showed in our simulation under similar objective conditions (cost, emission, voltage variation) and identical IEEE-30 bus architecture:

  • 15.2% better hypervolume (HV) performance indicating enhanced trade-off coverage,

  • 18.5% lower average fuel cost due to finer diversity,

  • 0.017 p.u. improvement in voltage profile stability,

  •  ~ 21% reduction in execution time over the wavelet-optimized EA due to adaptive diversity control.

A comparative summary is shown in Table 21.

Table 21 Comparative summary table considering the FACTS.

Scalability Challenges and limitations

Although MaOSSO demonstrates robust performance across mid-sized IEEE systems (30, 57, and 118-bus), its deployment on very large-scale networks (e.g., 300 + buses) presents practical challenges that merit further discussion:

• Increased Dimensionality: As the number of buses, generators, and constraints grows, the solution space becomes exponentially more complex. This often necessitates a larger swarm size and more iterations, which increases computational time.

• Load Flow Bottlenecks: Solving power flow equations for large systems (using methods like Newton–Raphson) can become a computational bottleneck, especially when repeated across a population for thousands of iterations.

• Memory Overhead: With increased system size and number of objectives, the memory requirement for storing positions, velocities, and fitness evaluations may escalate significantly.

• Premature Convergence Risk: Without the introduction of multi-level or hierarchical optimization layers, the algorithm may experience premature convergence due to limited exploitation-exploration balance in larger solution spaces.

• Mitigation Strategies: To address these limitations, future adaptations of MaOSSO could:

  • Utilize parallel processing and GPU acceleration to reduce runtime,

  • Integrate surrogate models for faster fitness approximation,

  • Employ domain decomposition or multi-agent frameworks to split the problem into manageable subproblems.

These considerations pave the way for future improvements in the algorithm’s robustness and scalability for nationwide grid-level applications.

Sensitivity analysis on physiological parameters

The SSO algorithm draws inspiration from biological fertilization dynamics, incorporating temperature and pH as environmental parameters that modulate swarm velocities. These values are randomly assigned within:

• Temperature range: 35.1–38.5 °C

• pH range: 7–14

These ranges are not arbitrary; they reflect physiological conditions and are processed through logarithmic normalization to ensure realistic modulation of particle behavior. To assess how sensitive MaOSSO’s performance is to changes in these parameters, we conducted a parametric sensitivity analysis. Performance was evaluated under incremental changes in:

• pH (7–14 in steps of 1),

• Temperature (35.1–38.5 °C in steps of 0.5 °C)

Metrics evaluated included:

• GD (Generational Distance) for convergence,

• HV (Hypervolume) for Pareto front coverage.

As such, the different findings obtained as depicted as follows:

• Performance remains stable and optimal across most of the range.

• Slight performance degradation was observed for extreme values:

  • pH > 13.5: excessive dispersion → minor loss in convergence.

  • Temperature > 38.4 °C: higher velocity perturbations → longer runtime.

• This suggests the adaptive control via pH and temperature is robust but can be fine-tuned for even better convergence in boundary cases.

Hence, while pH and temperature are not critical hyperparameters, they play a meaningful role in ensuring bio-inspired dynamism in search behavior without harming algorithmic stability.

Conclusion and future work

The aim of this research is to provide a comprehensive framework for the use of the SSO algorithm in solving the MaO-OPF problem. The SSO algorithm which was inspired by dynamic cooperative behaviors observed in biological systems has shown to be effective in navigating high-dimensional Pareto fronts that characterize MaO-OPF problems. This work presents extensive experimental results on benchmark problems and real-world IEEE bus systems thereby addressing vital objectives such as minimization of active/reactive power losses, fuel cost, emission and voltage deviation; while enhancing voltage stability indices. The proposed SSO framework outperformed state-of-the-art optimization methods like NSGA-III, RVEA, NMPSO, MOEA/D-DE not only with regard to solution quality but also in terms of computational efficiency. Notably, key quantitative results revealed that compared to other meta-heuristics considered here, SSO delivered up to 15% better convergence rates while reducing computational time by 25% and increasing Pareto diversity by 20%, thus making it scalable and robust for modern power systems. Among other things, the SSO algorithm combines adaptive velocity tuning, swarm intelligence and constraint handling technique to ensure balance between exploration and exploitation during optimization process. For instance, inclusion of environmental parameters such as temperature or pH levels based on biological processes helped make the algorithm adaptive. To test the algorithm, we compared it with common test problems (DTLZ and MaF suites) and checked whether it would converge on IEEE 30, 57, and 118-bus systems as a way to guarantee its effectiveness in real-life situations.

Although optimization algorithms have been developed, they often fail to handle the complexity and dimensionality of MaO-OPF problems effectively. This research fills this gap by introducing:

• Dynamic Swarm Behavior: SSO’s biologically inspired velocity adaptation ensures robustness against local optima and enhances global search capabilities.

• Constraint Handling: Integration of repair mechanisms and penalty functions guarantees feasibility across high-dimensional search spaces.

• Scalability: The algorithm’s ability to handle multiple conflicting objectives while maintaining computational efficiency marks a significant contribution to the field.

The SSO framework’s novelty lies in its biologically inspired mechanisms that enable robust exploration, and exploitation. Convergence and diversity balancing is outstanding in the multi-directional search strategy of SSO which makes it well suitable for solving high-dimensional optimization problems, unlike conventional gradient-based or evolutionary algorithms. Other findings included:

• Generational Distance (GD)—improvement of 15–20% over the benchmarks

• Hypervolume (HV)—achieved a value that was 20% higher showing better Pareto front coverage

• Runtime (RT) – reduced by 25%, implying computational efficiency.

However, the suggested SSO algorithm has shown great promise towards this direction and identified some areas for future research include:

• 1. Enhanced Exploration Mechanisms: Combining different strategies in order to increase variety and avoid premature convergence.

• 2. Real-Time Applications: Expanding the framework to cater for real-time optimization of dynamic power systems that have renewable energy sources.

• 3. Interdisciplinary Applications: Investigating other optimization applications beyond smart grids, microgrids, and IoT-based energy systems in which SSO may apply.

This study lays a foundation for future innovation by way of dealing with several aspects of today’s electricity network challenges; it contributes to sustainable use of energy resources through efficient energy management approaches.