A realistic FastQ-based framework FastQDesign for ScRNA-seq study design issues

Abstract

Single-cell RNA sequencing (scRNA-seq) has emerged as a powerful technology for characterizing transcriptomic profiles at single-cell resolution. It is crucial to consider both the number of cells and sequencing depth during library preparation. The existing methods are primarily simulation-based, rely on Unique Molecular Identifier (UMI) matrix, and have little context in the actual FastQ reads. Here we propose the first FastQ-based study design framework, named “FastQDesign,” which leverages raw FastQ files from publicly available datasets as references and suggests an optimal design within a fixed budget. We demonstrate our framework through a synthetic dataset and applications to nine real-world datasets. Our study underscores the importance of an appropriate design to investigate the biology of heterogeneous cell populations and offers practical guidance considering cost-benefit trade-offs. A high-efficiency software suite is available at https://github.com/yuw444/FastQDesign.

Introduction

Single-cell RNA sequencing (scRNA-seq) has revolutionized genomics research by enabling detailed gene expression profiling at single-cell resolution. This technology provides profound insights into cellular heterogeneity, cell differentiation, and gene regulation, making it essential in modern biology and biomedical research¹. Successful scRNA-seq experiments require careful consideration of critical components, notably the number of cells and the read depth for sequencing. Optimizing these parameters is crucial for deriving meaningful biological insights from scRNA-seq data, as they significantly influence the experiment’s accuracy, sensitivity, and cost-effectiveness.

Existing approaches to scRNA-seq experiment design are primarily simulation-based and rely on the Unique Molecular Identifier² (UMI) matrix. For instance, scDesign³ generates a synthetic UMI matrix learning from the real UMI count matrix. Zhang et al.⁴ determined the optimal sequencing depth to be around one UMI per cell per gene using empirical Bayes derivation. scPower⁵ models the relationship between sample size, cell number per sample, sequencing depth, and the power of detecting differentially expressed genes for a selected cell type using a pseudobulk matrix approach. Sun et al.⁶ proposed the probabilistic framework scDesign2 to capture gene correlations via copula framework. ScDesign3⁷ employs a generalized additive model to account for the location, scale, and shape of each feature in the dataset, including gene expression, pseudotime, and spatial coordinates.

While UMI-based approaches have been widely adopted, they overlook a key aspect of scRNA-seq experimental design-how to translate the design from the UMI matrix to the corresponding raw FastQ reads⁸. During library preparation, UMIs are added to sequences before PCR amplification, enabling accurate transcript abundance measurement without amplification bias. This means that multiple FastQ reads can share the same UMI within the same FastQ file. However, due to amplification bias, different UMIs may have varying numbers of corresponding reads⁹. Therefore, assuming a universal read-to-UMI ratio for all transcripts does not accurately reflect the true data structure.

Furthermore, existing approaches often explore a limited range of design options, primarily focusing on specific cell type frequencies or differentially expressed markers within a single cell type. In contrast, real scRNA-seq datasets are far more diverse and complex, encompassing a wider variety of cell types and biological processes. Due to the nature of simulation-based methods, parametric models are imposed on gene expression counts, such as Poisson, Zero-Inflated Poisson, Negative Binomial, and Zero-Inflated Negative Binomial, which may not fit the data well and do not capture real biological complexity^10,11.

To address these challenges, we present a statistical framework “FastQDesign" capable of efficiently learning knowledge from large-scale publicly available scRNA-seq datasets, and providing practical study design guidance based on total FastQ reads rather than UMI counts. Our framework utilizes the downsampling technique^12,13,14 and we propose comprehensive stability indices to evaluate performance across various aspects, including cell clustering, marker genes for cell subgroups or condition comparisons (such as control [wildtype] versus experimental [knock-in, knock-out, exposure]), and pseudo-temporal ordering of cells. Moreover, we propose a practical cost-benefit analysis that allows investigators to intuitively explore a wide range of feasible study designs and identify the optimal solution that best resembles the reference dataset while considering a fixed budget and flexible cost calculations. FastQDesign allows investigators to tailor experiments to achieve the expected similarity to the reference for their specific biological questions.

Here, simulation studies and demonstrations through real datasets are provided to evaluate the performance of FastQDesign. We also address the need for appropriate study design despite the popularity of reference-based annotation tools, such as Azimuth¹⁵.

Results

FastQDesign framework for designing scRNA-seq experiments

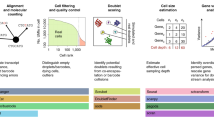
Although sequencing costs have dropped significantly over the past decade, understanding the effects of cell numbers and FastQ read counts per cell remains crucial in scRNA-seq experiments. Efficient allocation of financial resources can significantly benefit researchers. FastQDesign aims to provide practical guidance for scRNA-seq experiments by focusing on FastQ read counts and cell numbers. Our framework consists of three main steps, outlined below and illustrated in Fig. 1.

Fig. 1: The framework of FastQDesign.

Step 1, we prepare both the FastQ reference dataset and the pseudo-design dataset downsampled from the FastQ reference dataset. The reference dataset can be from a publicly available resource, such as GEO. After the cellranger’s alignment process, the barcode and the alignment detail (BAM file) are transferred to our proposed algorithm fastF to generate the pseudo-design dataset. It first processes the cell barcode one at a time, selecting it only if the current random number n is less than the given subsampling cell number ratio N until finished the entire barcodes list; then processes the BAM file one read at a time, and checks: i) if the current random number r is less than the given subsampling read depth ratio R, ii) if the current read is confidently mapped to the transcriptome (i.e., whether it is noise), iii) if the read belongs to the selected cell barcodes. Note that both n, r ∈ Uniform(0, 1) are simulated from a random number generator (RNG). The filtered reads are then encoded to the SQLite database to generate the UMI matrix from the pseudo-design dataset. Step 2, we compare the stability of the pseudo-design sample from three aspects, cell clustering, marker genes, and pseudotime, by the adjusted rand index(ARI), Jaccard index, and Kendall’s τ index (details are in Methods). We define the similarity as the average of these three indices. We obtain the grid of similarity by varying cell number and read depth, where each dot is the average of 10 repeated measurements. A shape-constrained additive model(SCAM) is fitted to smooth the surface. Step 3, cost-benefit analysis for optimal designs. The colored-coded curves stand for different flow cell capacities. In particular, the purple curve is the budget function, any designs under it are feasible(black), otherwise, it is not attainable(grey). The design with a diamond shape surpasses the similarity threshold(red straight line) and has a minimal cost, which is optimal cost design. The design with a star shape under the budget(blue vertical line), achieves the optimal similarity. The designs are one-to-one correspond in both scatter plots.

Step 1: Prepare the reference and obtain pseudo-design samples

The initial step involves utilizing the raw FastQ reads from the reference dataset. Software suite Cellranger¹⁶ from 10X genomics processes these FastQ reads through transcriptome alignment, cell barcode¹⁷ clustering, and deduplication of PCR artifact to produce: a barcode file containing all cell barcodes, a BAM file with alignment information for each read in FastQ files, and an UMI matrix showing gene expression levels for all genes in each cell. Subsequently, pseudo-design datasets with a lower number of cells and shallower sequencing depth are subsampled from the FastQ reference data using a downsampling technique. To facilitate this subsampling procedure efficiently, we have developed a software tool named fastF (see details in Methods).

Step 2: Evaluate the similarity between pseudo-design datasets and the reference dataset

For any given combination of a subsampled number of cells and the number of reads in a pseudo-design dataset, we compare it with the reference dataset by measuring the stability of cell clusters, cluster marker genes, and pseudo-temporal ordering of cells (pseudotime)¹⁸. We further define a similarity index as the average value of all proposed stability indices. This approach allows us to generate a three-dimensional similarity surface that represents the overall similarity score between the pseudo-design dataset and the reference dataset, as a function of the cell number percentage (N) and FastQ read depth percentage (R) relative to the reference FastQ dataset. For simplicity, we refer to N as cell number and R as read depth in the following discussion.

Step 3: Two-dimensional design optimization given the budget or similarity constraint

The search for the optimal design, represented by the combination of N and R, can be framed as a two-dimensional optimization problem. The design cost for a scRNA-seq dataset can be formulated as a function of N and R and treated as a regularity constraint in the optimization. In other words, we aim to identify a design that achieves the best similarity with the reference dataset within the budget. Two design strategies are evaluated: shared and individual designs. A shared design enables multiple researchers to utilize a sequencing flow cell through multiplexing technology, while an individual design allocates the entire flow cell for a single experiment. Along with cost constraints, we can also impose a similarity constraint aimed at identifying a design that achieves a specified level of similarity at the minimum cost.

In the following, we used a non-obese diabetic (NOD) mouse dataset to demonstrate the utility of our proposed framework. This dataset is composed of two strains of mice, NOD.Foxp3-EGFP (wildtype) and NOD.Tnfrsf9-/-.Foxp3-EGFP (CD137 knock-out), to determine the effect of CD137 deficiency on regulatory CD4 T and CD8 T cells respectively in NOD mice. Pancreatic islet cells were pooled from 6 mice for each strain and Foxp3+ CD4 T cells (Tregs) and CD8 T cells were isolated for scRNA-seq. In summary, there are 4176 T cells, 30,157,639 UMI counts, and 383,303,345 raw FastQ reads.

Pre-processing of FastQ reads for downstream analysis

We first define several key terminologies to evaluate the quality of the dataset: i) Total FastQ read counts: the total number of reads generated from the sequencing experiment; ii) Valid cell numbers: the number of detected cell-associated barcodes identified by Cell Ranger¹⁹; iii) Denoised FastQ read counts: the FastQ reads that originate only from valid cell barcodes; iv) Valid FastQ read counts: the denoised reads that are confidently mapped to the transcriptome (see Method for details); v) Used cells: the number of cells that pass the quality control criteria of the Seurat pipeline; vi) Valid UMI counts: the total UMI counts derived from valid cells, note that only valid reads are considered for UMI counting¹⁶; vii) Used UMI counts: the UMIs that belongs to the used cells.

In this dataset, there were 182,474,081 FastQ reads from the wildtype sample (AI), 93.64% of which belong to 2, 804 valid cells from the cellranger¹⁶ pipeline. In addition, 69.33% were valid read counts, with about 45,115 valid FastQ reads per valid cell. There were 200,829,264 FastQ reads from the knockout sample (BM), 68.10% of which were confidently mapped to the transcriptome in 2991 valid cells. Subsequently, 1927(68.72%) wildtype and 2249(75.19%) knockout cells passed quality control in the Seurat¹⁵ pipeline. In total, 68.68% FastQ reads, 5795 cell barcodes, and 39,544,501 UMI counts were valid. These statistics are summarized in Fig. 2a–c and Supplementary Table 1–3.

Fig. 2: Summary of a non-obese diabetic mouse FastQ reference dataset with two strains of 6 mice, with AI (1927 cells) and BM (2249 cells).

a–c The counts of FastQ reads, cell number, and UMI in each strain and overall. Not every FastQ read belongs to a real cell barcode, so we denoised those FastQ; Next, not every denoised FastQ could confidently map to the transcriptome, only the valid FastQ read does. Later, some cell barcodes are filtered out due to quality control, left with the actual used cells with actual used UMI counts. d The UMAP of the reference dataset, which partition into 4 clusters. e The distribution of conditions in the UMAP. f The dot plot of the canonical marker in each cell subtype, dot colored with average expression, sized by the expressed percentage in the cluster. g The distribution of the number of duplications per UMI. h The trend of UMI recover rate as the read depth change, both FastQ reference and UMI matrix are measured. i The distribution of the number of read variations per cell barcode. j The benchmark test to generate one pseudo-design dataset with 50% cells and 50% of FastQ read depth, the traditional approach could achieve the goal with a combination of three tools, the proposed fastF could do it all at once. Results are measured in terms of CPU time, memory usage, and cache usage.

After pre-processing using R package Seurat, four clusters were identified as shown in Fig. 2d. The distribution of AI and BM are demonstrated in Fig. 2e. Meanwhile, clusters 0,1,2, and 3 were identified as regulatory CD4 T cells, effector CD8 T cells, naíve/memory CD8 T cells, and proliferating cells, respectively, through the canonical gene markers as shown in Fig. 2f. We used these four well-separated clusters as our reference dataset to demonstrate our proposed subsampling procedure for future study design consideration.

Non-linear relationship between total UMI counts and read depth

We investigated the relationship between raw FastQ reads and UMI count matrix. The existing UMI-centric approaches^6,7 implicitly assumed UMI counts would have a linear relationship with the number of reads. In other words, a constant inflation scalar is applied to inflate UMI counts to the targeted number of FastQ reads. However, as shown in Fig. 2g, the corresponding number of FastQ reads per UMI has a wide range between 1-70 (with a mean of 6.36 and variance of 15.84) in our reference dataset, suggesting a constant inflation scalar may not be appropriate for real data.

To investigate this further, we downsampled the dataset at 10%, 20%, …, 90% of total reads and summarized the resulting total number of UMIs. In Fig. 2h, we found that the fraction of UMI recovered from the subsampling of FastQ follows a slow-declining non-linear relationship with the subsampling rate as most UMIs have more than one corresponding read. In comparison, we subsampled from the entire UMI matrix, the trend presents a linear relationship as the exact percentage of UMI counts is recovered. These suggest the need to take into account the corresponding number of reads for each UMI rather than simply assuming a linear relationship between total UMI counts and total read counts when designing a scRNA-seq experiment.

fastF - A breakthrough development for downsampling FastQ reads and obtaining UMI matrix

Existing subsampling pipelines for FastQ reads, such as seqtk, subSeq^20,21, can only downsample FastQ reads globally in R and lacks precise control over cell identities N. Due to sequencing errors²², multiple cell barcodes can correspond to the same unique cell barcode (see details in Methods). This is illustrated in Fig. 2i, where the distribution has a mean of approximately 50. Consequently, when utilizing existing parsing tools on the FastQ file without considering the correction of the cell barcode to downsample cell identities in FastQ reads N, the same group of cell barcodes may not be retained. Additionally, the choices of N and R are not independent when using tools that can only downsample read depth, i.e. there will be an implication on cell numbers(N) when varying read depth(R). For example, the subsample with R = 0.2 could result in fewer than 100% cells population (N = 1) before imposing precise control on the number of cells.

To overcome these issues and further improve the efficiency of the downsampling process, we developed a high-efficiency software fastF for downsampling from the reference FastQ dataset (see details in Methods). To demonstrate the computing efficiency of fastF, we conducted a benchmark test by sampling 50% of FastQ reads while retaining 50% of cells and obtaining the UMI matrix. This was compared between fastF and a combination of existing pipelines, including sampling FastQ reads on BAM file using samtools²³ and awk²⁴, converting the resulting BAM file to UMI matrix using umi_tools²⁵. We evaluated CPU time, memory, and storage cache usage of fastF. As summarized in Fig. 2j, fastF outperformed the existing pipeline in these metrics, with a 73.3% reduction in CPU time; a 96.1% reduction in memory usage; and a 72.4% reduction in storage cache usage, see Code availability for reproducibility. Thus, fastF significantly improved the computational efficiency for subsampling FastQ reads.

The stability of cell clustering in pseudo-design dataset

We first evaluated the impact of varying cell numbers (N) and read depth (R) on cell cluster identification. In Fig. 3a, we subsampled only 10% of the original FastQ reads using fastF with all cells in the original data, obtaining its corresponding UMI matrix, and repeating the Seurat pipeline to identify the updated cluster membership for each cell. We compared them with the cluster membership identified in the full dataset (Fig. 2d) by using adjusted random index²⁶ (ARI) (see details in Methods). Only a few cells exhibit different cluster assignments between the pseudo-design dataset and the reference, which indicates stable cell clustering identification even with just 10% of the total reads (FastQ N = 100% R = 10%, ARI = 0.945). On the other hand, we performed the downsampling procedure to the UMI matrix directly, and the resulting cell cluster is widely disturbed as shown in Fig. 3b (UMI N = 100% R = 10%, ARI  = 0.671). Lastly, we evaluated the effect of cell number by reducing it to 10% while keeping all reads, shown in Fig. 3c (FastQ N = 10% R = 100%, ARI = 0.857), suggesting that cell number has a bigger impact on the stability of cell clustering compared to the read depth in this reference dataset.

Fig. 3: Visualizations of stability of pseudo-design datasets.

a–c The UMAPs of the FastQ sample with 10% read depth of all cells, the UMI sample with 10% read depth of all cells, 10% cell and total read depth, were colored with the consistency of cell clustering match with the reference. d–f The pairwise minimal p-value's of each gene among the clusters from the samples and the reference, x is $-\log 10(p\_val\_adj)$ in the reference, y is the same value in the sample, only the significant DE genes in either reference or samples are shown. g–i The pairwise minimal p-value's of each gene between the condition within the cluster from the samples and the reference, only the significant DE genes in either reference or samples are shown. j, k The impact of varying read depth, and cell numbers on ARI and Jaccard indexes, 10 simulations were conducted at each setting.

The stability of cluster marker genes in pseudo-design dataset

Next, we evaluated the stability of cluster marker genes among the clusters between the pseudo-design dataset and reference dataset, using the same three settings as previously : i) FastQ N = 100% R = 10%, ii) UMI N =;100% R = 10% and iii) FastQ N = 10% R = 100%. We calculated the Jaccard index²⁷(see details in Methods) between the cluster marker genes identified in the pseudo-design dataset and the cluster markers genes in the reference dataset, using the same adjusted p-value cutoff 0.05 (see details in Methods). As shown in Fig. 3d-i, adjusted p-values in  − log10 scale are compared between the two datasets. For setting i), The agreement between the cluster marker genes in the pseudo-design dataset and the full dataset was strong, as most of the cluster marker genes were shared between both datasets (Jaccard =  0.53). In setting ii), the agreement was much weaker, where most of the cluster marker genes of the reference are no longer significant in the pseudo-design dataset, suggesting that 10% UMI counts are too shallow (Jaccard = 0.09). While the agreement was strong in setting iii) (Fig. 3f, Jaccard = 0.61), the magnitude of adjusted p-values was noticeably weaker in the pseudo-design dataset compared to the reference dataset. This suggests that the number of cells primarily influences the scale of p-values, but has less effect on the presence or absence of cluster marker genes. Under these three settings, read depth had a greater impact on the stability of cluster marker genes than the number of cells.

Similar to cluster marker genes, we used the Jaccard index to quantify the stability of between-condition (AI vs. BM) marker genes. As shown in 3g–i, we observed similar trends on N and R as measured in cluster marker genes. However, the signals are much weaker in between-condition marker genes in this reference dataset. This suggests the current N and R are less saturated on keeping the stability of between-condition markers.

Stability indices as a function of N and R

To systematically understand the effects of cell numbers and read depth on the stability indices (ARI and Jaccard index), we performed the stability analysis under various settings. In Fig. 3j, we subsampled various levels of FastQ reads (R = 90%, …, 10%) while keeping the total cell number fixed, with 10 repeats for each setting, and an average of 10 repeats taken. As expected, all indices consistently decrease as the read depth decreases. Notably, as summarized in the previous section, the impact of reads on the ARI is significantly weaker than on the Jaccard index. Additionally, the decline in the Jaccard index occurs much more rapidly in UMI subsampling compared to FastQ subsampling.

Next, we performed the stability analysis by varying the numbers of cells (N = 90%, …, 10%) while keeping the total FastQ reads or UMI counts unchanged, with 10 repeats for each setting. As shown in Fig. 3k, the trends between the subsampling of FastQ reads and UMIs are mostly equivalent because only the number of cells was affected. The impact of varying numbers of cells on the Jaccard index is also larger than ARI. Especially, Jaccard index is swiftly down as cell numbers drop when comparing across conditions, suggesting the vital role of cell number on the Jaccard of condition.

Two-dimensional optimal design with constraints

In Fig. 4a, the average of 10 repeats of each stability index under subsampling FastQ with different combinations of N and R is displayed as contour plots. The ARI is less affected by the change of R compared to N, whereas the Jaccard index of cluster marker genes is affected by both N and R.

Fig. 4: Contours plots of stability index and optimal designs.

a Contour plots of median indexes of pseudo-design datasets. The missing upper right corner is due to the pseudo-design dataset with N = 1.0 and R = 1.0 is the reference itself. b The fitted contour plots of median indexes of pseudo-design datasets. c, d Each circular dot represents a possible design, the colored-coded curves stand for different flow cell capacities, such as 10M, 80M, and 200M. In particular, the purple curve is the budget($7500) function, any designs under it are feasible(black), otherwise, it is not attainable(grey). The design with a diamond shape surpasses the similarity threshold(red straight line) and has a minimal cost, which is an optimal cost design. The design with a star shape under the budget(blue vertical line), achieves the optimal similarity. The designs are one-to-one correspond in both scatter plots. e, f The possible design only lies on the curves, which refer to the individual design, the entire flow cell capacities are used. Only the flow cell with its curve under the budget curve is feasible.

We defined a similarity score S as a function of N and R, calculated as the mean of all stability indices, representing an overall stability measurement for the pseudo-design dataset to the full dataset. (see details in Method). To further smooth the two-dimensional surface, we fitted a shape-constrained additive model (SCAM)²⁸ with these grid points, which allows a monotonically decreasing pattern as N and R decrease(see details in Method). Fitted values are shown in Fig. 4b.

Note that our goal is to identify an optimal design (a combination of N and R) that can achieve the highest similarity score with a given budget or a desired similarity score. To achieve this, we can formulate this problem as a two-dimensional optimization problem with respect to N and R given either constraint. The cost function primarily consists of two components: library preparation and sequencing costs. Library preparation includes sample preparation, Gel Bead-in-Mulsion generation, reverse transcription and cDNA amplification, and library construction. Sequencing cost can be calculated largely in two types: shared design or individual design, where the main difference is that the shared design only requires the proportional cost of the used flow cell capacity, while the individual design uses the entire flow cell and covers the whole cost for sequencing (see details in Methods). For the demonstration purpose, we assumed three flow cell capacities for sequencing: small, medium, and large with total reads as of 10M, 80M, and 200M, and prices at $1000, $2000, and $3000, respectively. The library preparation cost is assumed at $5,000. The fixed budget for the experiment is $7500 and the desired minimal similarity is 0.75. To further increase the practicality, we convert the ratios N and R into the corresponding valid cells ${N}^{{\prime} }$ and valid reads per valid cell ${R}^{{\prime} }$ in the designs (see details in Methods).

For the shared design, as shown in Fig. 4c, d, feasible designs (combinations of ${N}^{{\prime} }$ and ${R}^{{\prime} }$) are determined by the selected flow cell capacity (small, medium, or large) and the budget. Assuming we used the largest capacity option (200M total reads), the sequencing cost calculation is based on $15 per million reads ($3,000/200). When the constraint is the fixed budget (e.g., $7500), the design for the highest similarity score is achieved at ${N}^{{\prime} }=5,750$, ${R}^{{\prime} }=18,240$, with a cost of $7,290.53 and an 86.40% similarity score. We can also set the constraint as the minimum level of similarity (e.g., 0.75), then the design for the minimum cost is achieved at ${N}^{{\prime} }=4,025$, ${R}^{{\prime} }=9,120$ with the corresponding cost of $5,801.69 and a 0.75 similarity score.

For the individual design, feasible designs are very limited according to the selected flow cell capacity (small, medium, or large), as shown in Fig. 4e, f, only the designs that lie on the curves of capacities are available. Interestingly, both optimal designs (fixed budget or fixed similarity score) achieved the same design with ${N}^{{\prime} }=5,175$, ${R}^{{\prime} }=10,618$, the corresponding similarity score is 80.6%, and the cost is $7000 using the flow cell with medium capacity (80M total reads).

FastQDesign is validated by simulation studies

Next, we conducted a simulation study to verify that the optimal design suggested by our proposed downsampling framework can be used for a future design. While several tools exist for simulating single-cell RNA-seq FastQ-read level data, such as Minnow²⁹, ScSimRead³⁰, none allow for the simulation of FastQ files with specified underlying truths, such as the number of cell subtypes, the degree of distinction between them, which, though useful, does not address this specific need. Alternatively, we first simulated the UMI matrix by R package splatter³¹. We then drew each UMI duplication number from the negative binomial distribution with a mean of 8 and a standard deviation of 40 (fitted from our reference NOD mouse dataset, shown in Fig. 5a) to represent the corresponding valid FastQ reads for each UMI as in real data.

Fig. 5: FastQDesign is validated by simulation studies.

a The histogram of the negative binomial (2, 0.2) vs the empirical distribution of UMI duplication in Fig 2g. b The Splatter simulated 1M, 5 clusters cell population. c A sample of a cell population with 5K cells, which served as the reference dataset in the simulation. d The contour plots of the Jaccard index. We regard the samples from the population as the true future design and then compare it with the true DE gene in the population, hence the resulting Jaccard index is the underlying truth of the future design. FastQDesign, scDesign2, scDesign3: The Jaccards between the reference and pseudo-design samples, generated by FastQDesign, scDesign2, and scDesign3. The root mean square error of Jaccard is calculated between the pseudo-design dataset and the underlying truth. e, f The benchmark test result for generating a pseudo-design dataset with 50% of cells, and 50% of FastQ read depth, comparing FastQDesign, scDesign2, and scDesign3. g ARI index between pseudo-design dataset and the reference when using FastQDesign. scDesign2 and scDesign3 could not map the generated dataset into the reference, so ARI is unavailable.

One population of 1 million cells with 5 distinct cell types and 300 genes was simulated as shown in Fig. 5b, including 901,993,779 valid UMI counts with selected parameters (see details in Methods). We referred to this dataset as “population" and mimicked the case that any future design is a random draw from this population dataset. Continued, we drew a random sample of FastQ reads (UMI duplication) as the reference dataset from the population, with only 5000 cells and 2% read depth, resulting in 640,294 UMI counts, as shown in Fig. 5c. Then, the proposed downsampling framework was applied to this reference dataset.

As shown in Fig. 5d, we constructed four two-dimensional surfaces of Jaccard index: i) subsampled datasets directly from the population dataset versus the population dataset (N and R matched to pseudo-designs of reference dataset), which served as the simulated truth; ii) pseudo-design datasets by FastQDesign compared to the reference dataset; datasets simulated by iii) scDesign2 and iv) scDesign3 respectively compared to the reference dataset. In order to align the comparison, scDesign2 and scDesign3 utilize the corresponding info between UMI counts and FastQ read provided by FastQDesign, to ensure these three methods are comparing under the same N and R. To further evaluate the performance across methods, the root mean square error (RMSE) between i) and the surface derived from each method was used. Under the simulation, we found RMSE of FastQDesign is 0.092, scDesign2 is 0.087, and scDesign3 is 0.064, which suggests FastQDesign shows comparable performance to scDesign2 and scDesign3.

Besides, we compared our approach to scDesign2⁶ and scDesign3⁷ in terms of computational efficiency for generating a pseudo-design dataset with 50% of the cells and 50% of the read depth of the reference dataset (see details in the Methods section). FastQDesign is much faster in generating the pseudo-design dataset and has the lowest memory usage amount of the three as shown in Fig. 5e, f. Note that scDesign2 and scDesign3 are simulation-based methods, therefore the simulated dataset does not have corresponding cell IDs matched to the reference dataset, and we could not compare the stability of cell clustering using ARI. However, because FastQDesign generates pseudo-design samples from downsampling procedures, which kept the same cell ids retrievable, ARI can still be calculated on FastQDesign, shown in Fig. 5g.

Real data examples

In this section, we demonstrate FastQDesign on different applications using two published mouse datasets. In the first dataset example, the investigator aimed to identify differences between wildtype (WT) and knock-in samples, while in the second dataset example, the cells were collected from two different time points and investigated cell differentiation using pseudotime analysis.

FastQDesign on wildtype vs. knock-in dataset

Warshauer et al.³² investigated a de novo germline gain-of-function mutation in the transcriptional regulator STAT3 and identified in cases of neonatal type 1 diabetes in a comparison of wildtype and engineered knock-in mouse models.

The raw data were downloaded from GEO: GSE173415. For the wildtype sample, there were 640,918,954 raw reads and 13,471 valid cells after running the cellranger pipeline, with 438,784,526 reads passing quality control (valid rate is 68.46%), resulting in an average of 32,573 valid reads per valid cell. For the knock-in sample, there were 535,006,146 reads and 12,644 valid cells after running the cellranger pipeline, with 350,143,132 reads passing quality control (valid rate is 65.45%), resulting in an average of 27,693 valid reads per valid cell. Subsequently, 12,618 wildtype and 11,115 knock-in cells passed the pre-processing step in the Seurat pipeline (see details in Methods).

In Fig. 6a–c, we defined 9 cell clusters by using canonical markers and clustering analysis. Wildtype and knock-in cells are well-distributed in each cluster. Figure 6d shows the results after applying FastQDesign to this dataset, where the ARI stays high even with N = 50% and R = 50%, suggesting heterogeneous cell populations in this reference data. The stability of cluster marker genes also stays high during 0–30% reduction of N and R. However, the stability sharply declines after reaching less than half N and R. Noticeably, the stability of between-group gene markers started to drop even with 90% of cells, suggesting much weaker signals compared to cluster marker genes. The overall similarity remains relatively steady, with a larger impact by the reduction of N.

Fig. 6: Design summary of the comparison between wildtype (WT, 12,618 cells) and knock-in (KO, 11,115 cells) in the neonatal type 1 diabetes mouse model.

a, b The UMAPs of an example of wildtype vs. knockin group, with 9 clusters. c The dot plot of canonical gene markers in each cluster. d Contour plots for different indexes from FastQDesign framework. e–h Cost-benefit analysis for shared and individual designs from FastQDesign.

For cost-benefit analysis, we assumed three flow cell capacities are available as of 100M, 400M, and 800M reads in total; sequencing costs for each flow cell are $2000, $4000, and $6000, respectively; the library cost is $5,000. Given the budget of $10,000 and the desired overall similarity of 0.75, the resulting independent and shared designs are shown in Fig. 6e–h. Under the shared design, the flow cell with the largest capacity (800M reads) is always used as it has the smallest average cost per read. The optimal design with budget constraint is ${N}^{{\prime} }=18,270$ and ${R}^{{\prime} }=24,320$, with an optimal similarity of 80.90%, and an actual cost of $9,967.13. Whereas the optimal design with similarity constraint is ${N}^{{\prime} }=10,440$ and ${R}^{{\prime} }=18,240$ with an overall similarity index of 76.00%, and an actual cost of $7,128.77. For the individual design, the flow cell with 400M reads capacity was chosen. The optimal designs under the budget and overall similarity constraints are identical (${N}^{{\prime} }=13,050$ and ${R}^{{\prime} }=20,564$, with an overall similarity index of 78.22%, and an actual cost of $9000).

FastQDesign on time-series dataset

Zander et al.³³ investigated the mechanisms by which CD4+ T cells regulate CD8+ T cell differentiation during chronic infection. They performed single-cell RNA sequencing on CD8⁺ T cells specific for the GP33-41 peptide of lymphocytic choriomeningitis virus at days 8 and 30 post-infection to comprehensively characterize the heterogeneity of the CD8⁺ T cell response to chronic viral infection.

We downloaded the data from GEO: GSE129139. For the day 8 sample, there were 164,476,395 raw reads and 2063 valid cells after running the cellranger pipeline, with 106,152,740 reads passing quality control (valid rate is 64.54%), resulting in an average of 51,455 valid reads per valid cell. For the day 30 sample, there were 141,995,403 raw reads and 1879 valid cells after running the cellranger pipeline, with 88,220,298 reads passing quality control (valid rate is 62.13%), resulting in an average of 46,951 valid reads per valid cell. Subsequently, 2001 cells from the day 8 sample and 1876 cells from the day 30 sample passed the preprocessing step in the Seurat pipeline (described in Method).

As shown in Fig. 7a, we defined four cell populations based on top cluster marker genes (Fig. 7b). Fig. 7c shows the distribution of cells from day 8 and day 30 samples, indicating partial similarity and distinction likely related to the different time period of viral infection. Figure 7d shows the pseudotime trajectory derived from R package monocle3³⁴ (see details in Methods). We summarized the stability indices in Fig. 7e, where ARI is robust to the change of Rand mainly affected by the change of N, Jaccard index decreases similarly in both N and R. In addition to these two indices, we also used the non-parametric correlation statistic, Kendall’s τ, to measure the stability of estimated pseudotime from monocle3. As expected, Kendall’s τ is more sensitive to N and is less affected by the change of R. Overall, the similarity index is more affected by N than R in this reference dataset.

Fig. 7: Design summary of time series dataset that investigated T cell differentiation during chronic infection in day 8 (2001 cells) and day 30 (1876 cells).

a The UMAP of the time series reference dataset, colored by the cluster. b The same UMAP but colored by time point. c The dot plot of canonical marker genes in each cluster. d The UMAP with pseudotime inferred by monocle3. e Contour plots for different indexes from FastQDesign framework. In particular, Kendall’s tau is added to measure the consistency of pseudotime between the pseudo-design dataset and reference dataset. f-i Cost-benefit analysis for shared and individual designs from FastQDesign.

The cost-benefit analysis results are summarized in Fig. 7f, i. As in the previous example, we assumed three flow cell capacities are available with 10M, 40M, and 100M total reads respectively; sequencing cost for each flow cell is $1000, $2000, and $3000 respectively; the library preparation cost is $5000. The budget is $7500 and the desired similarity index is 0.75. Under the shared design, the flow cell with the largest capacity (100M reads) is always used as it has the smallest average cost per read. The optimal design with the budget constraint is ${N}^{{\prime} }=2,730$ and ${R}^{{\prime} }=4,930$ per cell, with an optimal similarity of 75.33%, and an actual cost of $5,636.63. Whereas the optimal design with the similarity constraint is ${N}^{{\prime} }=3,510$ and ${R}^{{\prime} }=14,790$ per cell, with an overall similarity index of 88.90%, and an actual cost of $7,455.56. Under the individual design, the 40M reads flow cell was chosen. The optimal designs under the budget and overall similarity constraints are identical(${N}^{{\prime} }=2,340$ and ${R}^{{\prime} }=10,842$, an overall similarity index of 83.20%, and an actual cost of $7000).

Can cell annotation tools replace the need for proper study design?

A common misconception among users is that cell annotation tools can reliably recover cell clustering and annotate subgroups regardless of the query dataset’s number of cells and read depth. While these tools are popular, we observed that their performance can be inconsistent when applied to the same dataset with varying sizes in number of cells or read depth. To demonstrate this effect, we used Azimuth¹⁵, a widely adopted reference-based annotation tool that maps a query dataset onto a relevant reference dataset for cell annotation prediction.

There is limited research on how study design factors such as number of cells and read depth can impact the performance of Azimuth. To fill this gap, we examined the NOD mouse reference dataset and used the Adjusted Rand Index to compare Azimuth’s annotation predictions between a pseudo-designed subset and the full reference dataset (see Methods for details). As illustrated in Fig. 8, annotation predictions vary significantly depending on the number of cells and read depth of the query dataset, highlighting the need of a well-considered study design can not be ignored even with reference mapping tools.

Fig. 8: The prediction stability of Azimuth.

a–c The UMAPs of AI and BM reference dataset, with predicted cell annotations from Azimuth, using different cell subtype resolutions, where L1 has 7 cell types, L2 has 30 cell types, L3 has 57 cell types respectively. d The contour plots of ARI for predicted cell annotations from Azimuth between the reference and pseudo-design datasets according to different resolutions (L1, L2, or L3).

Summary of additional six reference datasets

For a comprehensive demonstration of FastQDesign, we have downloaded six reference datasets from 10X Genomics^{35,36,37,38,39,40}. All datasets targeted at least 5K cells when designing the experiment, and were across different species, such as mus musculus and home sapiens, and six different organs, including brain, heart, jejunum, liver, PBMC, and lung (see details for data pre-processing in Methods). In Table 1, we summarized the raw FastQ reads, percentage of valid FastQ reads, valid cells and valid UMI counts for each dataset. The cost-benefit analysis for each dataset is also provided (based on shared design, flow cell capacity of 200M reads with cost $3000, and similarity constraint is set as 0.75). Interestingly, different dataset shows different impact of N and R to the overall similarity measurement, for example, the optimal design of dataset Brain5k suggests less impact in N compared to R whereas the optimal design of dataset Pbmc5k suggests both N and R can be largely reduced and still achieve desirable performance. We compared the costs calculated between suggested optimal design by FastQDesign and each corresponding reference dataset, and observed some dataset can use considerable lower cost to achieve similar performance, for example, dataset Brain5k, Heart5k, Pbmc5k and Lung5k show approximate one-third of the original cost can be reduced. Whereas in dataset Jejunum5k, the cost difference between optimal design and reference dataset is minimal, indicating the input N and R is not enough (especially N) to provide a stable inference to reveal the complexity of the data. In other words, for a future design based on this dataset the investigator would know, based on suggestions from FastQDesign, input N and R (from reference dataset) is not enough and could consider to increase N and R, with more focus in the direction of N.

Table 1 The summary table presents six additional reference datasets from 10X Genomics. Summary statistics regarding FastQ reads, cell barcodes, and UMI barcodes are provided. Cost-benefit analysis is performed for each dataset and the optimal shared design is summarized, with a minimum overall similarity constraint is set to 0.75, along with costs calculated for the optimal shared design and for the original reference dataset respectively, assuming the same unit price

Discussion

In this study, we demonstrated the needs of considering FastQ reads rather than UMI count matrix for scRNA-seq study design, by showing: firstly, UMI recovery rate can remain high even though the read depth drops significantly, as shown in Fig. 2h, as there are always multiple reads corresponding to the same UMI due to the design of the sequencing library; secondly, the number of corresponding reads for each UMI has a wide range of distribution due to the PCR bias during the library preparation, as shown in Fig. 2g. In conclusion, a stability analysis based on UMI count matrix would result in acquiring deeper sequence depth because UMI count matrix is equivalent to the case of very shallow sequencing depth where each UMI only has one corresponding read. When calculating the cost for study design, methods solely based on UMI count matrix do not have an accurate estimate of actual reads needed for the design due to the ignorance of corresponding reads per UMI.

Existing tools for the scRNA-seq study design are simulation-based. In other words, those methods impose parametric models on certain parameters such as the distribution of gene expression level per gene and the differences between different cell populations. Properly setting these parameters for these methods is challenging. In addition, as single-cell research evolves, a greater variety of data from different conditions, organisms, and tissues becomes available. It is unclear whether these simulation-based methods can find settings that match certain types of data. In contrast, our proposed tool, FastQDesign, is designed to extract empirical information from any input data (either FastQ or UMI count matrix), allowing it to adapt to the rapidly increasing number of publicly available datasets, such as those on GEO database.

We have also demonstrated the coveat of the widely-used reference-based annotation tool - Azimuth. To our surprise, not only sequencing depth but also the number of cells largely affect the annotation performance of Azimuth. Due to the wide popularity of this annotation tool, many investigators may overly rely on it and ignore the need to consider a proper study design. Another pitfall of relying on Azimuth is that only cell cluster annotation is available, but information other than that is not guaranteed, such as cluster marker genes. In our study, we have comprehensively shown that both the change of N and R impact the stability of cluster annotation, cluster marker genes, and pseudo-temporal ordering of cells. In short, our results show the limitation of Azimuth and suggest proper consideration of study design is necessary.

To the best of our knowledge, there is no efficient software that performs subsampling directly on FastQ reads with selection on both cell number and read depth, while producing the corresponding UMI count matrix. Existing tools are limited to subsampling based solely on read depth and do not provide a straightforward way to handle reads from single-cell data, where cell-specific metadata and precise control over cell counts are essential. Additionally, subsampling within a UMI matrix would not yield valid FastQ reads or maintain metadata integrity, which is critical in the FastQDesign framework. fastF was developed to address these specific challenges. It enables users to specify both the number of cells and the read depth during FastQ subsampling, and efficiently generates the associated UMI count matrix, ensuring compatibility with downstream data analysis. fastF demonstrates significant improvements in computing time, memory usage, and storage requirements, overcoming the bottlenecks associated with alignment and metadata handling in traditional approaches. We anticipate that fastF will serve as a valuable tool for researchers who need flexible and accurate subsampling capabilities in single-cell studies using FastQ reads. While we acknowledge there exist other scRNA-seq pre-processing pipelines, such as alevin-fry⁴¹, and kb-python⁴², FastQDesign’s performance can not be evaluated on them due to their incompatibility in generating BAM file for our downsampling procedure.

In the simulation study, we evaluated the performance between FastQDesign, scDesign2, and scDesign3 by comparing the RMSE of Jaccard index between the surface derived from simulated truth and the surface derived from each method. Our method achieved comparable performance with other two simulation-based methods, and in addition to Jaccard index, we evaluated aspects of stability such as cell population using ARI, and pseudo-temporal cell ordering using Kendall’s tau. We have also demonstrated FastQDesign in various real data examples as reference dataset, such as NOD mice dataset, K392R dataset, time-series dataset, and 6 datasets provided by 10x genomics. Based on our cost-benefit analysis, as expected, the number of cells and reads depth may have different impact on the stability in different reference dataset, which again suggests a customized study design given different reference dataset. In addition, according to a different goal/constraint such as fixed budget or certain level of similarity to achieve, the choice of number of cells and reads depth also vary.

There are often multiple samples in a dataset. In this study, we rely on preprocessing procedures such as normalization (using SCTransform function in R Seurat package) and batch effect removal technique (IntegrateData function in R Seurat package) to handle variation across multiple samples. Another important consideration of study design is related to the rare cell populations. According to different clustering results, one may have more cell populations or less cell populations identified. As we demonstrated in real data examples, more clusters could pose more challenge to achieve desirable stability metrics. In some cases, rare cell populations might appear, as shown in Supplement Fig. 3, there is one small cell cluster in our AIBM reference dataset with only 21 cells. When N = 0.6 and R = 1.0, this small cell subcluster can no longer be identified and results in ARI=0.71, although the rest of cell population is well-reserved. In our default pipeline, the small cell clusters (number of cells less than 100) will be removed from the reference dataset, to mitigate the instability of the subsample procedure.

As the demonstrated framework, the success of study design relies on the choice of an appropriate reference. Users should select the reference dataset carefully, and we recommend that it should capture the major biological diversity relevant to their study of interest. Like other reference-based approaches, it relies on the assumption that the reference dataset includes enough number of cells and enough sequencing depth for cell populations of interest. Meanwhile, FastQDesign provides pre-trained similarity surfaces from the reference datasets that are publicly available on the 10X Genomic website. Investigators can specify the costs for library preparation and the available flow cell capacities with their price tags from their local sequencing facilities. By combining the similarity surface and the provided cost functions, the optimal designs can be identified accordingly. An intuitive interface is provided for investigators to explore different options to find the optimal design that meets their needs. One major limitation is that there are only nine pre-trained reference datasets available for investigators to use directly. However, investigators can utilize their own reference dataset of interest to train the similarity surface using our software. In the near future, we plan to expand the selection of reference datasets to include various organisms, tissues, and conditions, enabling investigators to use them directly without handling the raw data and training the data themselves. As another limitation, our current tool only applies to studies using 10X Genomics Single-Cell sequencing UMI-based protocols, while many other protocols, such as non-UMI-based SMART-seq and UMI-based methods like Drop-seq and CEL-Seq, also exist. In our future work, we will support these protocols by generalizing our tool fastF to facilitate downsampling procedure across different protocols. Ultimately, our goal is to create a comprehensive scRNA-seq study-design Atlas.

Methods

Reference alignment

Since all of the reference data in this study used 10X Genomics platform, the software Cell Ranger (version 7.0.0)⁴³ is used for the reads alignment, with default parameters. The main outputs from Cell Ranger are the folder filtered_feature_bc_matrix and BAM file possorted_genome_bam.bam. The folder includes the UMI matrix, indicating the number of unique UMIs per gene per cell, which forms our reference UMI count matrix. The BAM file includes the cell barcode and the alignment details of each FastQ read in the sequencing library. They are characterized by barcode tags, such as CB for corrected cell barcode, UB for corrected UMI, and alignment tags, such as GX for gene id, xf for extra alignment flags.

fastF: An ultra-efficient FastQ sampling tool

The cell barcode of one unique cell may have many variations in the FastQ file due to sequencing errors²². For example, the true cell barcode AGCTAGCTAGCTAGCT may appear as AGCCAGCTAGCTAGCT, TGCTAGCTAGCTAGCT, or AGCTAGCTAGCTAGCC as random mismatches because of error. As summarized in Fig. 2i, the number of variations of each cell barcode in the FastQ reference is calculated using umi_tools(1.1.6)²⁵. In summary, sampling on the FastQ reference data at the desired percentage of number of cells and read depth requires four essential steps: i) identifying the true cell barcode; ii) parsing the FastQ reads according to each unique cell barcode and sampling cell barcodes and read depth at desired percentage; iii) aligning FastQ reads to the reference genome; iv) summarizing the results into UMI count matrix. Leveraging the existing pipeline is viable but computationally costly as shown in Fig. 2j. To overcome these challenges, we developed a software fastF that can efficiently subsample FastQ reads at specified N and R and produce the corresponding UMI count matrix. It uses the existing alignment results from the BAM record to assess alignment quality, extract cell barcodes and UMIs, identify aligned genes, and summarize valid reads for each pseudo-design sample, supporting the FastQDesign framework.

In Fig. 1, fastF utilizes the outputs from cellranger: i) barcode file contains one corrected cell barcode at each line; ii) BAM file contains tags of the corrected cell barcode(CR), reads quality validation(xf), and gene alignment(GX). It first samples the desired percentage (N) of cell barcodes to form a cell barcode candidate pool by deciding if the random number n < N. We then process the BAM one read at a time. If the random number r < R, the desired percentage of read depth, then check if this read belongs to the candidate pool, if not, it is a noise to the pool, otherwise we check for read quality. If it is valid, we encode the corresponding cell barcode, gene alignment, and UMI into the SQLite⁴⁴ database for summarising the UMI matrix. Meanwhile, it produces the exact number of valid cell barcodes for the given parameters(N). The numbers of valid FastQ reads (R) after de-noising and passing the quality check.

fastF sample FastQ reads in the BAM files, and derive the corresponding UMI matrix at a specified percentage of N and R. It uses the standard C libraries, for instance, htslib⁴⁵ for BAM file streaming, zlib⁴⁶ for writing and reading gz file, mt19937ar⁴⁷ for random number generation, SQLite database for summarizing. To enhance the efficiency of the downsampling process, the desired cell barcode list and feature list were stored in a hash table to accelerate matching during filtering. To further reduce memory usage and improve the speed of summarizing the UMI matrix, cell barcodes and UMIs were encoded in binary format. For example, the nucleotides were encoded as follows: A = 00, C = 01, G = 10, and T = 11. This way, four base pairs occupy only 1 byte, compared to 4 bytes in their text format. The pseudo-code is presented in Algorithm 1 (see details in Supplementary file). With these considerations, fastF is ultra-efficient in run time, RAM consumption, and cache usage.

In conclusion, fastF allows specifying the desired percentage of cells and read depth, and outputs barcodes.tsv.gz, features.tsv.gz, and matrix.mtx.gz, similar to the cellranger output, which can be utilized directly by popular scRNA-seq data analysis pipelines, such as Seurat¹⁵ and monocle3³⁴. Meanwhile, it produces the exact number of valid cell barcodes for the given parameters(N and R), the numbers of denoised, valid FastQ reads in the metadata of matrix.mtx.gz. In Supplementary Fig. 2, we present how the number of detected genes changes with respect to cell numbers and read depths.

Statistics and reproducibility

Data pre-processing

The UMI matrices from both reference and pseudo-design datasets have the same data preprocessing steps. From the UMI matrix, we leverage the Seurat¹⁵ data analysis pipeline and perform data normalization, dimension reduction, cell clustering, and differential expression gene identification. In particular, Seurat::SCTransform⁴⁸ was used in the normalization step. Seurat version 4.3.0.1 is used throughout this study.

When preparing the reference for the comparison, we have customized parameters for each used reference dataset, such as the number of unique express genes, nFeature_RNA, the UMI counts, nCount_RNA, the percentage of mitochondrial gene expression, percent.mt, as shown in Supplementary Table 1. However, in their pseudo-design datasets, the quality control parameters for cells are no longer needed as the reference cells could serve as the validation set for the later stability comparison.

Stability of cell clustering

Cell clustering is a vital component of scRNA-seq analysis as it will determine the cell population membership for each single cell. In practice, the number of clusters needs to be carefully chosen to reflect underlying cell populations of interest. For example, we defined four clusters in the demonstrated reference dataset in Fig. 2d–f. In order to compare the clustering result in the pseudo-design dataset, we need to make sure the number of clusters between the two datasets is the same. However, the R function FindClusters from Seurat could not guarantee the number of clusters in the pseudo-design datasets by specifying the parameter res. Hence we developed a root searching algorithm that identifies the parameter res in the FindClusters until the desired number of clusters is achieved. This is implemented in an R function FixedNumClusters from our developed R package FastQDesign.

To quantify the stability of clustering results between the reference dataset and the pseudo-design dataset, we propose to use adjusted random index²⁶ (ARI). Specifically, ARI is a measure of agreement between two partitions. It compares the cell partitions in reference and pseudo-design samples and quantifies the degree of agreement, reflecting cell group stability. When two partitions are independent, the expected value of ARI is 0. Conversely, it is 1 when two partitions fully agree. Furthermore, its calculation is based on the overlapping cells between the reference and pseudo-design sample, say v cells. Let the original partition X = {X₁, X₂, ⋯  , X_k} and the sample partition Y = {Y₁, Y₂, ⋯  , Y_l}, where k and l are the numbers of clusters in the reference and pseudo-design sample, respectively, where X_i, Y_j are the set of cells with cluster membership i, j accordingly. Let ∣X_i∣ = a_i, ∣Y_j∣ = b_j, ∣X_i ∩ X_j∣ = v_ij. Then, the adjusted random index is calculated as

$$ARI=\frac{{\sum }_{ij}\left(\begin{array}{c}{v}_{ij}\\ 2\end{array}\right)-\left[{\sum }_{i}\left(\begin{array}{c}{a}_{i}\\ 2\end{array}\right){\sum }_{j}\left(\begin{array}{c}{b}_{j}\\ 2\end{array}\right)\right]/\left(\begin{array}{c}v\\ 2\end{array}\right)}{\frac{1}{2}\left[{\sum }_{i}\left(\begin{array}{c}{a}_{i}\\ 2\end{array}\right)+{\sum }_{j}\left(\begin{array}{c}{b}_{j}\\ 2\end{array}\right)\right]-\left[{\sum }_{i}\left(\begin{array}{c}{a}_{i}\\ 2\end{array}\right){\sum }_{j}\left(\begin{array}{c}{b}_{j}\\ 2\end{array}\right)\right]/\left(\begin{array}{c}v\\ 2\end{array}\right)}.$$

Stability of marker genes

The Jaccard index²⁷ is used to quantify the similarity between two sets. Once the cell clusters are established, the next step is to identify differentially expressed (DE) genes for each cluster (also called cluster marker genes). This is done by using the R function FindAllMarkers. We took the minimum p-value for each gene if multiple p-values were available due to comparisons across different clusters. To define significant genes, we use two criteria: i) the adjusted p-value adj_p_val <0.05, ii) the maximum percentage of cells expressed in the groups of comparisons (reported as pct.1 and pct.2 in Seurat)  >0.2, iii) the absolute value of the average of $\log 2$ fold change between the two groups, $| avg\_\log 2FC| > 0.3$.

Let D_i be the set of cluster marker genes of i-th cluster in the reference dataset, D_j be the set of cluster marker genes of j-th cluster in the pseudo-design dataset. The Jaccard index is defined as

$$J=\frac{\left| \left(\mathop{\bigcup }_{i = 1}^{k}{D}_{i}\right)\bigcap \left(\mathop{\bigcup }_{j = 1}^{l}{D}_{j}\right)\right| }{\left| \left(\mathop{\bigcup }_{i = 1}^{k}{D}_{i}\right)\bigcup \left(\mathop{\bigcup }_{j = 1}^{l}{D}_{j}\right)\right| }.$$

The Jaccard index measures the overall agreement of cluster marker genes between the reference and the pseudo-design dataset. When the cluster marker genes between two datasets are identical, the Jaccard index is 1, whereas it is 0 when they are mutually exclusive.

Cell pseudotime calculation

The pseudotime is calculated using R functions order_cells and learn_graph from the package monocle3 with default parameter settings. The cell embedding UMAP is inherited from the R object created by Seurat pipeline. To automate the root node selection for the pseudo-design samples, one can also specify the root cells by providing cell IDs, the leaf node with the biggest overlapping with the provided root cells will be the root node; the biggest leaf node will be the root node in the case where none of the root cells is part of the leaf nodes. For the root node selection process, a wrapper function FastQDesign::RootNodeSelect is made. By default, the biggest leaf node is chosen as the root node when root cells are unavailable.

In the reference, we first identify the root cells and then use them as the root cells for each pseudo-design sample to calculate the pseudotime. A wrapper function FastQDesign::FindPseudotime calculates the pseudotimes for both the reference and the pseudo-design sample. In particular, monocle3_1.0.0 is used throughout the paper.

Similarity surface construction

The similarity of one experimental design is defined as the measure of agreement between the pseudo-design sample and the reference data set. This measure can be expressed as the weighted average of the above three evaluation indexes as follows:

$$S=\frac{1}{{w}_{1}+{w}_{2}+{w}_{3}}\left\{{w}_{1}ARI+{w}_{2}Jaccard+{w}_{3}\tau \right\},$$

where w_i is the user-defined weight for the ith metric. The assignment of weights depends on the primary focus of the study. For example, w₁ should be given a higher value if detecting cell clusters is the primary focus; likewise, if identifying cluster marker genes is the primary focus then w₂ should be assigned higher weight; note that w₃ can be even set to 0 if studying pseudotime ordering is not needed. Throughout the paper, we set equal weights as w₁ = w₂ = w₃ = 1 for simplicity. Note that S has a range of [0, 1], whereas S gets bigger, and the design becomes more powerful. Under the fixed budget, the optimal design is reached when this measurement is the maximum.

With a systematic downsample cycle, a series of measurements will be obtained, i.e., (ARI, Jaccard, τ). First, we create a grid of N and R with N = 0.1, 0.2, …, 1.0 and R = 0.1, 0.2, …, 1.0. At each joint coordinate, such as N = 0.1andR = 0.3, we run 10 repeated cycles of the downsampling process and evaluate the correspondent indexes. Then, we take the median of each index against the variability. Next, with the choice of w₁, w₂, w₃, 100 groups of (S, N, R) established. Last, we build a 3D smoothing surface from the grids for the later continuous estimation.

Throughout the paper, we used the percentage of the cells (N) and the percentage of the original depth (R) to generalize similarity surface demonstration. In the actual design, we have reflected these ratios to the true valid cell numbers(${N}^{{\prime} }$) and valid FastQ reads count per valid cell(${R}^{{\prime} }$) in each pseudo-design dataset, both ${N}^{{\prime} }$ and ${R}^{{\prime} }$ can obtain or calculated from fastF (see details in Supplement). For example, there are 5796 (N_valid) valid cells, and 45,115 (R_valid)valid FastQ reads per valid cell in AI and BM datasets, ${N}^{{\prime} }=ceiling({N}_{valid}\times 0.1)=580$ when N=0.1; However, ${R}^{{\prime} }$ may vary due to each cell may have a different number of valid FastQ reads, but it should be close to R_valid × R when N_valid is large.

As observed from the three reference datasets, similarity increases as N and R increase. Therefore, we fitted a shape-constrained additive model (SCAM)²⁸ to the 99 simulated grid points $(S,{N}^{{\prime} },{R}^{{\prime} })$ to ensure that similarity is monotonically increasing with respect to both ${N}^{{\prime} }$ and ${R}^{{\prime} }$. We used scam(similarity  ~ s(${N}^{{\prime} }$, k=10, bs = “mpi") + s(${R}^{{\prime} }$, k=10, bs = “mpi"), df_similarity) to fit the scam model in R package scam version 1.2–14, where df_similarity contain three columns, ${N}^{{\prime} }$, ${R}^{{\prime} }$, and similarity. Later, we used its predict function to estimate the similarity of any given pair of $({N}^{{\prime} },{R}^{{\prime} })$.

Furthermore, to match the flow cell capacity, we need to inflate the product of ${N}^{{\prime} }\times {R}^{{\prime} }$ by the FastQ read-valid ratio q. It is estimated by

$$\hat{q}=\frac{{M}_{valid}}{{M}_{total}},$$

where M_valid is the number of valid FastQ reads passed the quality check in the reference, and M_total is the total number of FastQ reads.

Cost-benefit analysis

The overall cost $g({N}^{{\prime} },{R}^{{\prime} })$ for a 10X Genomics experiment is composed of library preparation cost(C_prep), and the sequencing cost(C_seq) for a flow cell with the read capacity of a.

• Library preparation: Multiple samples can be prepared in the same library by using feature barcode technology (CellPlex kit).

• Sequence Cost: There are multiple Illumina sequence platforms. Each platform has its flowcell category, which comes with different capacities.

Also, we consider two design schemes: i) shared design, where the partial flowcell capacity may be used; ii) individual design, where only the entire flowcell capacity may be used; In the first scheme, the sequencing facility could combine multiple libraries from their queries as needed to share a flow cell with multiplexing technology. Although the second scheme is straightforward, its choices of flowcell capacities are limited. So, we name the first scheme a shared design and the second an individual design. Then we construct a constraint function for each design under the budget b as follows,

$${g}_{1}({N}^{{\prime} },{R}^{{\prime} }) = \frac{\frac{{N}^{{\prime} }\times {R}^{{\prime} }}{\hat{p}}}{a}\times {C}_{seq}+{C}_{prep} \, < \, b\\ {g}_{2}({N}^{{\prime} },{R}^{{\prime} }) = I\left(\frac{{N}^{{\prime} }\times {R}^{{\prime} }}{a\times \hat{p}}==1\right)\times I\left({C}_{prep}+{C}_{seq} \, < \, b\right)=1.$$

Under the shared design, where ${N}^{{\prime} }\times {R}^{{\prime} }$ is the needed valid FastQ reads for the recommended design, we inflated this number by the valid rate $\hat{p}$ from the reference, to reflect the actual total FastQ reads required to obtain this many valid reads for the sequencing library. Then, the corresponding cost is according to the usage fraction $\frac{\frac{{N}^{{\prime} }\times {R}^{{\prime} }}{\hat{p}}}{a}$, which needs to be smaller than the budget b. The individual design is similar, we need both the usage fraction to be 1 and the cost under the budget.

We then locate the optimal designs under these two schemes respectively. Technically, we are solving a constrained two-dimensional optimization problem where S is the target function, g₁, g₂ are the constraints. Since the constraints are flat planes, the optimal design is essentially determined by the gradient rather than the magnitude of the similarity surface. With the similarity surface, we can calculate the predicted similarity for a given choice of $({N}^{{\prime} },{R}^{{\prime} })$. So, we simplify the problem to a greedy search algorithm. We first provide a list of combinations of $({N}^{{\prime} },{R}^{{\prime} })$ that satisfy the constraints; among these options, we locate the pair that provides the best-predicted similarity as the optimal similarity design, and the most inexpensive pair as the optimal cost design.

Simulation study

In the simulation, we used R package Splatter³¹ (version 1.25.0) to simulate the population with batchCells rep(10000, 100), batch.facLoc 0.05, batch.facScale 0.05, lib.loc 7, dropout.type “experiment", dropout.mid 1.3, dropout.shape -4, nGenes 300, and seed 926.

Later, we considered the UMI duplication number follows NB(2, 0.2), this distribution is fitted from the non-obese diabetic (NOD) mouse dataset. When drawing the sample from the UMI matrix, we draw all UMI duplications(equivalent to valid FastQ reads) instead of the UMI itself. The read depth ratio relative to the reference is comparable to the probability of including each UMI duplication. In particular, these procedures were wrapped in FastQDesign::DownSample.

Since scDesign2 and scDesign3 do not acknowledge the FastQ read depth when generating samples, to ensure a fair comparison, both of them use the resulting UMI counts from FastQDesign::Downsample as the target UMI counts, scDesign2::fit_model_scDesign2 used to fit the model, scDesign2::simulate_count_scDesign2 to simulate the pseudo-design dataset. A series of commands scDesign3::construct_data, scDesign3::fit_marginal, scDesign3::fit_copula, scDesign3::extract_para, scDesign3::simu_new are performed. In particular, R packages scDesign2(version 0.1.0) and scDesign3(version 0.99.5) are used for the simulation.

Compare the stability of predicted annotation from Azimuth

Azimuth¹⁵ is a reference-based annotation tool that takes query data and annotates the cell population annotation based on selected reference data. The “pbmcref¹⁵" is chosen to be the reference for our query datasets from the NOD mouse example. We used the function RunAzimuth from R package Azimuth to predict the cell cluster annotation for our reference dataset. We also performed the same procedure for each pseudo-design dataset from different combinations of N and R. In particular, Azimuth(version 0.5.0) is used throughout the paper.

We used ARI to quantify the stability of the predicted cell subtypes derived from Azimuth between full reference and pseudo-design dataset. Three cell subtype partitions (referred to as L1, L2, and L3 in Fig. 8) are provided from the R object “pbmcref" according to different resolutions defined by Azimuth.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.