Neuronal mismatch responses to auditory stimuli in the dorsal hippocampus of anesthetized rats

Abstract

The hippocampus is classically linked to memory, yet increasing evidence points to a broader role in perceptual inference and deviance detection. Predictive coding theories propose that perception minimizes mismatches between expected and actual sensory input, expressed in neural signatures such as mismatch negativity (MMN) and P300. Although MMN arises mainly from sensory and prefrontal cortices, the hippocampus is anatomically interconnected with both and may also contribute to prediction error processing. We recorded single- and multi-unit activity and local field potentials (LFPs) from DG and CA1 in urethane-anesthetized rats during an auditory oddball paradigm and a no-repetition control sequence to dissociate prediction error from repetition suppression. Approximately 20% of hippocampal neurons were sound responsive, and a subset showed deviant selectivity. Spiking activity predominantly reflected prediction errors, while LFPs revealed complementary contributions from repetition suppression and prediction error. Early LFP components were enhanced for randomly presented deviants, whereas later components within the P300 latency range were stronger for predictable deviants, indicating temporally distinct phases of error signaling and top-down modulation. These findings identify the hippocampus as an active contributor to auditory deviance detection and support a hierarchical model in which hippocampal circuits participate in predictive sensory processing beyond memory.

Introduction

The ability of the brain to detect and respond to unexpected sensory stimuli is essential for adaptive behavior. Predictive coding theory posits that perception is not a passive process, but rather an active inference mechanism in which the brain continuously generates predictions about incoming sensory information and minimizes the mismatch between expected and actual inputs¹. Within this framework, mismatch negativity (MMN) and the P300 component have been widely studied as neural signatures of prediction error and stimulus evaluation. MMN, typically observed in event-related potentials (ERPs), reflects automatic detection of deviations from regular sensory patterns², while P300, especially its subcomponents P3a and P3b, is associated with attentional reorientation and context updating^3,4.

Although MMN and P300 have been extensively examined in auditory and somatosensory cortices, their roles in hippocampal circuits remain elusive. Given the established involvement of the hippocampus in spatial navigation⁵, associative learning, and memory formation⁶, it is crucial to investigate its potential contribution to predictive processing. It has been known for nearly 30 years that the hippocampus plays a broader role in perception and novelty detection^7,8, integrating past experiences to anticipate and evaluate incoming sensory input^9,10. The hippocampus may thus support predictive coding by providing a contextual framework that shapes expectations and guides behavior^8,11,12.

The hippocampus is suggested to lie at the apex of the cortical processing hierarchy, even in the context of predictive functions¹³, it integrates and relays information across sensory and prefrontal regions. Anatomically and functionally, it is well-positioned to encode predictions, prediction errors, or both, due to its reciprocal connections with the auditory cortex¹⁴ (AC), prefrontal cortex¹⁵ (PFC), thalamus¹⁶, and entorhinal cortex¹⁷. A recent and elegant study in the visual domain shows that hippocampus represents prediction errors early during learning but predictions at later stages of learning¹⁸, backing the findings of a previous study¹⁹. Furthermore, the hippocampal subfields also appear to support distinct roles in predictive processing: Cornu ammonis 1 (CA1) is implicated in sequence learning and novelty detection^12,20,21, while the dentate gyrus (DG) supports pattern separation, distinguishing between highly similar inputs, a crucial mechanism for sensory discrimination^22,23,24.

The classical oddball paradigm, which presents low-probability deviant tones among repetitive, high-probability standards, has become a common tool for studying mismatch responses^2,4. Human imaging and electrophysiological studies have reported hippocampal responses to sound deviations^{21,25,26,27,28}, and animal research similarly suggests hippocampal involvement in novelty detection using ERP and LFP recordings^29,30,31,32. Moreover, single- and multi-unit studies in rodents have shown that hippocampal neurons respond to auditory stimuli^33,34,35,36. While these studies were not explicitly framed within predictive coding theory, their findings align with concepts of expectancy violation, novelty detection, and associative learning^37,38,39.

While previous studies have reported mismatch responses using event-related potentials (ERP) to auditory stimuli in the rat hippocampus³¹, the present work advances this line of research by examining these responses at the neuron level. It distinguishes between prediction error and repetition suppression, investigates expectation signaling within a predictive coding framework, and identifies distinct contributions from different hippocampal subfields. In this study, we recorded single- and multi-unit activity as well as local field potentials (LFPs) from CA1 and DG in urethane-anesthetized rats under the oddball paradigm. To disentangle prediction error from repetition suppression, we also employed cascade and many-standards control sequences^40,41. Our results reveal that a subset of hippocampal neurons (~20%), respond to auditory stimuli, with nearly a quarter of these showing stronger responses to deviant and control tones. These effects were especially pronounced in DG, supporting a role for the hippocampus in deviance detection and predictive auditory processing that extends beyond its traditional functions^42,43 in memory and spatial navigation.

Results

To understand the role of dorsal hippocampus in auditory processing, we recorded sound-evoked neuronal activity from 27 rats under urethane anesthesia (Fig. 1A). We focused on the Cornu Ammonis 1 (CA1) and Dentate Gyrus (DG) subfields of the hippocampal formation.

Fig. 1: Experimental design and histology of recorded neurons.

A Schematic representation of an experimental setup for extracellular recording of auditory-evoked responses in a rat brain. A schematic lateral view where the hippocampus is shown in violet. Stimuli were sequences of 75 ms pure tones played by a speaker coupled to one of the ears. Red arrows represent a possible pathway for auditory information during the experimental session. B Coronal hippocampal section, 4.5 mm caudal from bregma, with electrolytic lesions in Cornus ammonis 1 (CA1) and dentate gyrus (DG). Scale bar, 500 µm. Electrophysiological recordings were made using either multichannel or tungsten electrodes. C A classical oddball sequence (top) consists of a number of repetitions of a standard tone (STD), with a deviant tone (DEV) at a different sound frequency occurring with low probability. In the current study, only the last STD tone before a DEV tone was used for analysis. To account for the different responses to both sound frequencies, another oddball sequence was played with the STD and DEV roles inverted (second panel). We also used cascade (third and fourth panels) and many-standard sequences (bottom) as non-repetition controls. D Mismatch responses recorded following this procedure (DEV, deviant; STD, standard; CTR, control) can be decomposed in 3 indices (iPE, index of prediction error; iRS, index of repetition suppression; iMM, index of neuronal mismatch). E Coronal section of the hippocampus, indicating the location of CA1 and DG regions. The red line indicates the approximate location of the multichannel probe. F Enlarged view of the DG with the electrode probe overlaid, showing the approximate position of recording sites across different sublayers (gl: granule cell layer; Hilus: hilus (polymorphic layer); CA3: cornu ammonis, area 3; ml: molecular layer). G LFP traces from all recorded channels in one animal (n = 30 channels in 1 rat), aligned to deviant stimulus onset (0 ms), which include the standard tone before the deviant (left vertical blue line), the deviant (vertical red line) and the standard tone after the deviant (right vertical blue line). Channels where units exhibited significant CSI are traced in red. H Time-amplitude plot of LFP activity across channels (n = 30 channels in 1 rat), revealing prominent oscillatory activity in the hilus and granule cell layer (in the infrapyramidal blade). Red and blue lines above the plot indicate deviant and standard tone presentations, respectively. The underlying data for this Figure can be found in Supplementary Data 1.

We recorded a total of 824 units, 138 single units, and 686 multiunits, of which 321 were histologically located in CA1 and 503 in DG. Figure 1B shows two representative examples of electrolytic lesions in the CA1 and DG (arrowheads).

To test whether neurons were sensitive to auditory stimuli, we recorded neuronal responses during sound stimulation. We define auditory-responsive neurons as those units exhibiting a mean activity during the analysis window (250 to 650 ms) at least two standard deviations above the mean activity in the 125 ms preceding reference window (100-225 ms). Following this criterion, we identified 177 neurons (21%) that exhibited auditory responses after noise burst stimulation. We found at least one auditory-responsive neuron in all 27 recorded rats. Among them, 63 neurons (35.6%) were histologically located in CA1 across 23 rats, and 114 neurons (64.4%) were located in DG across 12 rats, with 7 rats contributing to both subfields. These auditory-responsive neurons also responded to pure tones, although when recording the frequency response areas, we found no preference for any sound frequency. This suggests that hippocampal neurons are primarily influenced by the contextual aspects of auditory stimulation rather than the physical properties of the sound stimuli.

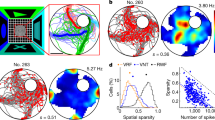
When analyzing the response to an auditory oddball paradigm (Fig. 1C), 43 (24.3%; across 9 rats) of these auditory-responsive hippocampal neurons (21 units in CA1 out of 6 rats and 22 units in DG out of 5 rats, with 2 rats contributing to both) exhibited a lower response to the repetitive, standard stimuli (STD) and a significantly higher response to the deviant sound (DEV). We term these CSI-significant units, since they were determined using the common SSA index (CSI). Figure 2 illustrates the responses of example neurons to the deviant (DEV, shown in red) and standard tone (STD, shown in blue), along with their corresponding locations in the DG and CA1, as well as raster plots of these neurons, showing a higher response rate in CA1, compared to DG.

Fig. 2: Schematic of left coronal sections with example PSTHs and Dot Raster plots.

The left column shows a schematic drawing of representative coronal sections, with their position relative to bregma shown below them. Dots indicate the approximate locations where we recorded CSI-significant neurons. Darker outlined numbered dots mark the locations of selected example neurons, with their corresponding PSTH and dot raster plots. Responses to deviant tones (DEV) are shown in red, while the responses to standard tones (STD) preceding the deviant are shown in dark blue; responses to all other standard tones are shown in light blue (dot raster plot). The underlying data for this Figure can be found in Supplementary Data 1.

In the following sections, we present the results from recordings of auditory-responding neurons, focusing on those showing significantly stronger responses to the deviant than to the standard, i.e., contextual modulation (CSI-significant).

Context-dependent responses in CA1 and DG

To explore the mechanisms of stimulus specific adaptation (SSA) in the hippocampus, we first compared responses obtained under the auditory oddball paradigm (Fig. 1C) by plotting peri-stimulus histograms (PSTH), as shown in Fig. 3. As explained previously, 177 out of the 824 units recorded (27 rats) showed significant responses to sounds, and we refer to them as hippocampal auditory-responsive units. In these units, auditory responses (Fig. 3A) began on average around 237 ms after stimulus onset, lasted until 662 ms, and peaked at 387 ms. When subtracting the mean STD response from the DEV response (purple, Fig. 3A bottom) to visualize when the DEV response was higher than the STD (DEV–STD > 0), we observed that the DEV response exceeded the STD response for 450 ms, from 237 ms to 687 ms after stimulus onset. These units showed a significantly higher DEV response around 337 ms (p < 0.001; t-test with Holm-Bonferroni correction for multiple comparisons; Fig. 3A).

Fig. 3: Average PSTH of auditory-responsive and CSI-significant neurons.

Average PSTH responses (mean ± SEM) to DEV tones are shown in red, while average responses to STD tones are shown in blue. The subtraction of the mean STD response from the DEV response (DEV – STD) is shown in purple. The vertical bar on the left of the plots indicates the duration of the sound. The shaded area along the lines represents the SEM error. Statistical significance is denoted by a thick line above the X-axis. A Average response of auditory-responsive units (n = 177; 27 rats). B Average response of CSI-significant units (n = 43; 9 rats). C Average response of CSI-significant units located in CA1 (n = 21; 6 rats). D Average response of CSI-significant units located in DG (n = 22; 5 rats). E Comparison of the average DEV response of CSI-significant units in CA1 vs. DG. F Comparison of the average STD response of CSI-significant units in CA1 vs. DG. The underlying data for this Figure can be found in Supplementary Data 2.

Within the CSI-significant subset (n = 43; see above), auditory responses lasted 475 ms, starting at 237 ms, continuing until 712 ms, and peaking at 362 ms (Fig. 3B). The DEV – STD plot showed positive responses for 425 ms, from 262 ms to 687 ms. The DEV response was significantly different from the STD response for most of the period between 312 and 542 ms (p ≤ 0.01). By subfield, responses spanned ~237–687 ms in both CA1 and DG (lasting for about 450 ms; Fig. 3C, D, respectively). Units in DG reached peak activity at 337 ms, 100 ms earlier than those in CA1. When we subtracted the mean STD response from the DEV response, CA1 units showed a statistically significant difference between DEV and STD responses at 312 ms (p = 0.008; Fig. 3C, bottom), whereas DG units exhibited the most significant difference from 512 to 537 ms (p = 0.002; Fig. 3D, bottom). In DG, the DEV response exceeded the STD response between 262 ms and 687 ms after stimulus onset, while in CA1, this difference began slightly earlier at 237 ms and extended to 687 ms.

Next, we compared responses to the DEV condition (Fig. 3E) and the STD condition (Fig. 3F) between DG and CA1. After applying a t-test and Fisher’s correction for combined probability across multiple comparisons, in the DEV comparison, we found that the largest difference between subfields occurred at ~337 ms, aligning with the DG peak response. For the STD comparison, the largest difference between subfields occurred around 550 ms (Fig. 3F), however, the responses were very noisy and close to the baseline. To test whether CA1 and DG showed differences in onset latencies, we used a 50-ms window to determine a stable onset response time. DEV onsets did not differ between subfields (CA1: 341.250 ± 30.633 ms; CI = [277.134, 405.366]; n = 20; DG: 314.423 ± 26.923 ms; CI = [255.763, 373.083]; n = 13; Wilcoxon rank-sum, p = 0.383; effect Cliffs_delta = -0.085). Neither did STD onset latencies differ (CA1: 439.167 ± 58.932 ms; CI = [312.769, 565.564]; n = 15; DG: 287.500 ± 62.375 ms; CI = [154.551, 420.449]; n = 16, Welch’s t-test, p = 0.0877; effect Hedges_g = 0.617).

Comparing CA1 and DG mismatch (DEV-STD) onset latency, showed similar starting points (CA1: 356.62 ± 37.04 ms SEM; CI = [278.098, 435.138]; n = 17; DG: 323.21 ± 12.76 ms SEM; CI = [295.643, 350.785]; n = 14; Welch’s t-test, Bonferroni-adjusted, p = 0.4041). Medians differed by −50 ms (CA1 median = 362.50 ms; DG median = 312.50 ms). Thus, while DG peaks earlier on DEV trials (Fig. 3E), the emergence of the DEV–STD difference occurs at comparable times across subfields.

Periodic oddball modulates DG activity

To examine whether the units recorded in hippocampus code for some form of regularity, we employed a variation of the classic random oddball paradigm (Fig. 4A), namely, the periodic auditory oddball paradigm, where groups of 9 standard tones followed by 1 deviant tone are repeated overtime as a frozen token of stimuli, as shown in Fig. 4B. Both paradigms used the same stimuli and probabilities, the periodicity of the deviant being the only difference. This periodic auditory oddball establishes expected uncertainty (low temporal entropy, since the position of the deviant is predictable), whereas the classic random oddball imposes unexpected uncertainty (trial-wise unpredictability). Thus, comparing periodic vs. random isolates the impact of temporal predictability on hippocampal responses. This periodic auditory oddball was presented immediately after the random oddball paradigm. Figure 4C displays the average response of all CSI-significant units to both the periodic- and random oddball stimuli (n = 20; 9 tracks in 3 animals). 75% of these units were in DG. Interestingly, we observed a significant difference in the neuronal response that emerged just as the deviant tone was presented (Fig. 4C; t-test with Holm-Bonferroni corrections for multiple comparisons, p = 0.04 at 37.5 ms histogram center). However, comparing the normalized spike counts for the DEV, CTR (control stimuli), and STD tones between the random and periodic oddball responses during the analysis window did not reveal a significant difference (Fig. 4E). Activity in the pre-analysis window (25 to 50 ms) was significantly lower for periodic than for random sequences (t-test with Holm-Bonferroni correction, p = 0.0025). This is summarized in a pre-stimulus bar chart (Fig. 4D).

Fig. 4: Differences between periodic and random oddball paradigm responses.

A Schematic of a classical oddball sequence. It includes many repetitions of a standard tone (STD, light blue) and rare deviant tones (DEV, red) at a different frequency, with the STD immediately before each DEV shown in dark blue. B Schematic of a periodic oddball sequence. It uses repeating blocks of nine STDs followed by one DEV as a fixed frozen, ten-tone cycle over time; for illustration purposes only four STDs are shown. C Average PSTH of CSI-significant units recorded using multichannel probes from both CA1 (n = 5; 2 rats) and DG (n = 15; 3 rats), centered at the onset of deviant tones (0 ms, red). The plot includes the responses to the standard tones before and after a deviant (blue). Vertical bars indicate the duration of sounds. The response (mean ± SEM) during a random oddball sequence is shown with a continuous trace, while the mean response during a periodic oddball is displayed with a dashed trace. The shaded area along the lines represents the SEM error. Statistical significance for the comparison between random and periodic sequences is denoted by a thick black line above the X-axis. Note that the only statistical difference occurs during the presentation of the deviant tone (25–50 ms), marked by a circled D. D Bar plots representing the normalized spike counts for the 25–50 ms time window. E Bar plots representing the normalized spike counts for each experimental condition (red, deviant; blue, standard; green, control), using the analysis window (250-650 ms); no periodic/random difference is observed. Error bars indicate ± SEM. Asterisks indicate significance from a t-test with Holm–Bonferroni correction (**p < 0.01; ***p < 0.001). The underlying data for this Figure can be found in Supplementary Data 2.

Prediction error index as the main contributor to the mismatch negativity index in CSI-significant units

Of 177 hippocampal auditory-responsive units (CA1: 63 units in 23 rats; DG: 114 units in 12 rats), 43 units showed significant CSI—21 in CA1 (6 rats) and 22 in DG (5 rats).To assess how these units responded to the DEV stimuli, we computed the frequency-specific SSA index (SI) and the CSI Fig. 5A (left) illustrates scatter plots of the SI (graph plots SI for f₁, x-axis versus f₂, y-axis), where non-CSI-significant (auditory-responsive after excluding CSI-significant) units appear in a lighter shade, while significant-CSI units are represented in a dark tone. In CA1, non-CSI-significant units are more broadly dispersed, whereas CSI-significant units cluster predominantly in the upper-right quadrant, indicating that both frequencies in the sequence respond more to deviant stimuli than standard stimuli. In DG, non-CSI-significant units tend to concentrate around zero, with all but one CSI-significant unit positioned in the upper-right quadrant, again indicating a preference for deviant sounds. Points in the upper right quadrants denote stimulus-independent modulation; most CSI-significant units fall here, consistent with stimulus-non-specific deviance detection, meaning that the DEV–STD difference is consistent across frequency identities rather than tied to a particular frequency.

Fig. 5: CSI selectivity and mismatch-related responses across CA1 and DG.

A Left panels display scatter plots of the frequency-specific SSA index (SI) for f₁ (x-axis) vs. f₂ (y-axis) in CA1 (top; n = 63; 6 rats) and DG (bottom; n = 107; 5 rats). Lighter shades denote non-CSI units (auditory-responsive after excluding CSI-significant), while CSI-significant units appear in a darker tone. Units in the top right quadrant show higher response to the deviant for both frequencies. Right panels show histograms of the common SSA Index (CSI) for CA1 (top) and DG (bottom). Red vertical lines represent the mean of the distribution. B Left panels show the distributions of the index of neuronal mismatch (iMM) for CA1 (top; n = 126; 6 rats) and DG (bottom; n = 214; 5 rats), with lighter colors representing non-CSI-significant units (auditory-responsive after excluding CSI-significant) and darker colors indicating CSI-significant units. Middle panels display the index of prediction error (iPE) and right panels the index of repetition suppression (iRS). These results show that prediction error is the main contributor to neuronal mismatch both in CA1 and DG. Red vertical lines mark each distribution’s median: the dashed line is the median of non-CSI-significant units, while the solid line indicates the median of CSI-significant units. Asterisks indicate that the median differs from zero according to a two-sided sign test with Bonferroni correction; *p < 0.05, **p < 0.01, ***p < 0.001. The underlying data for this Figure can be found in Supplementary Data 3.

Figure 5A (right panels), displays histograms for the distribution of CSI values. As expected, the median CSI of CSI-significant units was significantly larger than zero both in CA1 (0.213; IQR: [−0.0799, 0.6811]; 95% CI: [0.139,0.3006];p < 0.001; two-sided sign test, n = 21) and DG (0.271; IQR: [0.0446, 1]; 95% CI: [0.2213,0.4493]; p < 0.001, n = 22). This was not the case for non-CSI-significant units in DG (0.020; IQR: [−0.1400, 0.6056]; 95% CI: [0.0035,0.0457]; p = 0.11, n = 114), nor CA1 (-0.0196; IQR: [−0.2431, 0.0690]; 95% CI: [−0.0463,0.0036]; p > 1, n = 63). To avoid CSI-driven bias, we computed all summary metrics on the subset of auditory-responsive but non-CSI-significant units and tested median effects with two-sided sign tests (Bonferroni-corrected across indices).

We compared the auditory-evoked responses in each condition (STD, DEV, CTR), in the form of 3 indices (as shown in Fig. 1D): index of Neuronal Mismatch (iMM = DEV–STD), index of Prediction Error (iPE = DEV–CTR) and index of Repetition Suppression (iRS = CTR–STD). Thus, the iMM quantifies the overall neuronal mismatch response, and by means of comparing it to a control sequence, the iPE identifies the component of the mismatch response that is attributed to predictive error signaling (or genuine deviance detection), and the iRS estimates the extent to which repetition of the STD suppresses activity. In CA1 (non-CSI-significant), SI, CSI, iMM, iPE, and iRS distributions were not significantly different from zero after correction. In DG (non-CSI-significant), SI showed a small positive effect (r = 0.31; p = 0.033 two-sided sign tests with Bonferroni-corrected across indices), whereas CSI, iMM, iPE, and iRS distributions were not significantly different from zero. These analyses are shown with less-saturated colors in the revised figure to distinguish them from the full and CSI-significant subsets. For the broader non-CSI-significant pool, iMM (DG > CA1: r = –0.28; p < 0.001) and iPE (DG > CA1: r = –0.19; p = 0.0067) differed, while iRS did not (p = 0.418). Within the CSI-significant subset, none of the CA1–DG contrasts reached significance (iMM p = 0.129; iPE p = 0.343; iRS p = 0.611; all |r| ≥ 0.63 using a signed-rank tests), probably do to having a smaller sample size.

Figure 5B illustrates non-CSI-significant units in light colors, while CSI-significant units appear in darker tones. All neuronal mismatch indices exhibit a normal distribution (Fig. 5B), as confirmed by a Kolmogorov-Smirnov test (p < 0.001). iMM values for CSI-significant units range from −0.3 to 0.8 in CA1 and from 0.1 to 1 in DG (Fig. 5B, magenta), and in both cases the median values were significantly largen than zero (CA1: 0.230; IQR: [−0.2445, 0.7693]; 95% CI: [0.1686,0.3125]; p < 0.001; DG: 0.3366; IQR: [−0.0939, 1]; 95% CI: [0.2012,0.4565]; p < 0.001; two-sided Wilcoxon rank-sum test). The main contributor to iMM was iPE (Fig. 5B, orange), which in both hippocampal areas reached high values (CA1: 0.2030; IQR: [−0.5759, 0.7730]; 95% CI: [0.1210,2243]; p < 0.001; DG: 0.3032; IQR: [−0.4763, 1]; 95% CI: [0.1667,0.4059]; p < 0.001). On the other hand, iRS (Fig. 5B, cyan) showed values much smaller, only being significantly larger than zero in DG (CA1: 0.0211; IQR: [−0.4630, 0.8786]; 95% CI: [−0.0148,0.1136]; p = 0.07; DG: 0.0671; IQR: [−0.1649, 0.6243]; 95% CI: [0.0361,0.1241]; p = 0.002).

These results show evidence of strong auditory mismatch in the spiking responses of both CA1 and DG, which could be mostly attributed to an enhanced response to the deviant sounds.

LFP mismatch reflects distinct contributions of prediction error and repetition suppression across subfields and time

Next, we recorded and analyzed the local field potentials (LFPs), which measure the average synaptic activity in local circuits, in an attempt to correlate spiking responses with global responses. Figure 1E shows a coronal section of the hippocampus highlighting the location of a multichannel recording. CSI-significant units were predominantly found in the DG, particularly in the granule cell layer, followed by the hilus and molecular layer (Fig. 1G, with CSI-significant units marked in red). Similarly, the largest LFP amplitudes were observed in the hilus and granule cell layers of the DG (Fig. 1H).

The left column of Fig. 6A-C presents the average response across all multichannel recordings (Fig. 6A; n = 268; 9 tracks from 3 animals), along with the average responses for LFPs in CA1 (Fig. 6B; n = 3 from 1 animal) and DG channels (Fig. 6C; n = 13 from 3 animals) where significant CSI units were recorded. To directly compare responses to DEV and STD stimuli, we plotted their average waveforms (Fig. 6, middle column) and computed the difference waveform (shown in purple). We observed no prominent deflections in response to the standard tone prior to the deviant in any of the averaged traces. In the combined average across all channels (Fig. 6A, middle panel). The DEV–STD difference was statistically significant (p < 0.05; t-test with Holm-Bonferroni correction) across several time windows, including an early time window where the DEV response was more negative than the STD (~100–250 ms) and a late one were the DEV response was more positive than the STD (~400-800 ms) with peak amplitude at 578 ms.

Fig. 6: LFP responses, predictive coding indices and Random vs Periodic Oddball response.

A The average LFP traces (mean ± SEM) across all multichannel recordings (n = 268; 9 tracks in 3 animals) are shown on the left panel, with the response to the STD condition in blue, DEV in red, and CTR in dark green. As in previous figures, vertical bars indicate the tone presentations. The middle panel shows the comparison of the response to the DEV vs STD conditions, the subtraction of the mean STD response from the DEV response (DEV–STD) is shown in purple. Black bars above the x-axis indicate pointwise DEV > STD significance (t-tests, Holm–Bonferroni). The average LFP amplitude (mean ± SEM) for each stimulus condition during the analysis window (250–650 ms) is shown in the right panel, where asterisks indicate significant differences among conditions after a t-test with holm-Bonferroni correction. B, C Same as in (A), but using data from channels where CSI-significant units were recorded in CA1 (n = 3, 2 tracts in 2 animals) and DG (n = 13, 6 tracts in 3 animals), respectively. Error bars indicate ± SEM. D Violinplots of the distributions of predictive coding indices (iMM, neuronal mismatch index; iPE, index of prediction error; iRS, index of repetition suppression). For all multichannel recordings (n = 268; 9 tracks in 3 animals) on the left, CA1 (n = 3; 2 tracks in 2 animals) in the middle panel, and DG (n = 13, 6 tracts in 3 animals) on the right panel. Indices whose average is different from zero are indicated by asterisks; *p  <  0.05, **p  <  0.01, ***p  <  0.001. E Average of all DG LFP (n = 13, 6 tracts in 3 animals), showing the response elicited by both the periodic and random oddball auditory paradigm of channels that had units with significant CSI. The response to the periodic oddball is shown as a dashed line, whereas the response to the random presentation is represented by a continuous line. The shaded area along the lines is the SEM error. Statistical significance for the comparison between random and periodic sequences is denoted by a thick black line above the X-axis. The underlying data for this Figure can be found in Supplementary Data 3.

In CA1 (Fig. 6B), the DEV response was significantly different from the STD condition across most of the trial. It included two early periods where the DEV response was more negative than the STD (~120–220 ms and 330-450 ms), an early period where DEV was more positive (~230–330 ms), as well as a late period where the DEV response was more positive (~480–850 ms) with peak amplitude at 571 ms. In DG (Fig. 6C), the DEV response was significantly different from the STD condition across most of the trial. It included two early periods where the DEV response was more negative than the STD (~100–200 ms and 350–400 ms) and a late period where the DEV response was more positive ( ~ 500–800 ms) with peak amplitude at 579 ms.

The right panels in Fig. 6 show the corresponding mean amplitudes during the analysis window. The LFP amplitude of the DEV condition was significantly larger than that for the STD and CTR conditions for all the recorded channels (Fig. 6A, right panel; p < 0.001 and p = 0.0015, respectively; t-test with Holm-Bonferroni correction, n = 268). In DG, the LFP amplitude significantly differed among the DEV, STD, and CTR conditions, and all indices were significantly larger than zero (Fig. 6C, right panel). On the other hand, no significant differences were observed among LFP mean amplitudes in CA1 bar chart, this may be due to the small number of channels included in the sample (Fig. 6B, right panel; n = 3).

We also calculated the LFP-based predictive coding indices. When considering all multichannel recordings (Fig. 6D, left panel), both the mean iMM and iPE indices were significantly greater than zero (iMM = 0.0793 ± 0.0172, p < 0.001; IC = [0.0454, 0.1131]; iPE = 0.0583 ± 0.0170, p = 0.002; IC = [0.0248, 0.0918]; n = 268), whereas the iRS index was not (iRS = 0.0210 ± 0.0159, p = 0.56; IC = [-0.0103, 0.0522]; n = 268). In CA1 (Fig. 6D, center panel), iMM and iRS were significantly greater than zero (iMM = 0.3977 ± 0.0832, p = 0.0107; IC = [0.2709, 0.6641]; iRS = 0.2309 ± 0.0556, p = 0.0042; IC = [0.3437, 0.5078]; n = 3), but the iPE index did not reach significance (iPE = 0.1668 ± 0.0554, p = 0.08; IC = [−0.0848, 0.1684]; n = 3). On the other hand, in DG (Fig. 6D, right panel) both iPE and iRS were significantly greater than zero (iPE = 0.1639 ± 0.0553, p = 0.006; IC = [0.0461, 0.2874]; iRS = 0.2231 ± 0.0537, p = 0.006; IC = [0.1097, 0.3521]; n = 13), with iRS showing a higher mean than iPE, and the iMM index was also significantly above zero (iMM = 0.3870 ± 0.0812, p = 0.028;; IC = [0.2164, 0.5789]; n = 13).

With only 3 channels in CA1 and 13 in DG (Fig. 6D), DG showed larger iPE than CA1 (medians: DG 0.210 vs CA1 0.017; U = 9, p = 0.568; Cliff’s δ = −0.54; Hedges’ g = −0.64), indicating a large but non-significant shift toward stronger deviance responses in DG. By contrast, CA1 exhibited greater iRS (CA1 0.436 vs DG 0.292; U = 34, p = 0.286; δ = +0.74; g = 0.99). A Welch’s unequal-variance t-test corroborated the iRS difference and remained significant after Holm correction (p = 0.031), though parametric inference is tentative given CA1 n = 3. iMM did not differ between regions (DG 0.534 vs CA1 0.453; U = 17, p = 1; δ = −0.13; g = 0.24). Altogether, these comparisons suggest that LFPs in CA1 are driven by repetition-suppression, whereas DG combines prediction-error and repetition-suppression contributions; due to sample size, this is only exploratory.

We also recorded LFPs in DG during a periodic oddball paradigm and compared the responses to the random oddball paradigm. Figure 6E, shows all DG LFPs (n = 13, 3 rats, 6 tracts) from channels with units showing significant CSI under both periodic and random oddball sequences. We found a significant difference in the neuronal response beginning around the onset of the deviant tone, consistent with our spike data (Fig. 6E; t-test with Holm-Bonferroni correction, p < 0.05: 36–158 ms). Additionally, we found another significant difference ~450–350 ms before the DEV stimulus onset.

These results indicate that in the hippocampus as a whole, deviant sounds produce LFP responses larger than standard sounds, and this can be attributed to an enhanced response to deviants rather than a reduced response to standards. This effect is magnified in the DG; however, it seems to be a combined influence of enhanced response to deviants and reduced response to standards when comparing to a control sequence.

Significantly higher response to deviant tones across trials over standard and control conditions

To examine whether trial position within the sequence influenced responses across different paradigms (Fig. 1C), we calculated the average spike count for each trial. Each trial consisted of a pure tone presented every second, with a total of 400 trials per paradigm for all recorded units exhibiting significant CSI (n = 20; 9 tracks in 3 animals) (Fig. 7). Since only multichannel units were analyzed, the sequences and frequencies were consistent across all recordings.

Fig. 7: Spike counts over trials for different auditory paradigms.

Each panel represents the average response at every trial of the sequence, for all the units that presented significant SSA recorded with the multichannel probe (n = 20; 3 rats). A and B correspond to the random and periodic oddball paradigms, respectively, showing responses during a deviant tone (DEV; red) or a standard tone (STD; blue). C–E illustrate the responses to the control paradigms: Many-Standards (C; dark green), Cascade Ascending (D; medium green), and Cascade Descending (E; light green). Dots indicate the average spike count at each trial, while solid lines represent linear regression fits. F Comparison of the linear regression fits for all the paradigms. G Heatmaps showing the p-values of the comparison of linear regression model estimates (intercept, β₀, left; and slope, β₁, right) between paradigms. Darker colors mean smaller p-values, as indicated by the logarithmic color bar on the right. A Holm-Bonferroni correction for multiple comparisons was applied to the p-values in each table, with statistically significant values (*p < 0.05, **p < 0.01, ***p < 0.001) highlighted in bold. The underlying data for this Figure can be found in Supplementary Data 4.

To identify general response trends, we applied a simple linear regression model (f(x) = β0 + β1x + ε), which effectively captured broad patterns in the data (Fig. 7A–F, thick lines). The model explained a meaningful portion of the variance in the response, and an ANCOVA confirmed that it performed significantly better than a constant model. Differences across paradigms were examined by comparing intercepts (β0) and slopes (β1). No significant slopes were found for STD responses, indicating a lack of repetition suppression (Table 1). Responses to the STD condition remained significantly lower than those to DEV tones across trials, as indicated by their intercept (β0) values (Table 1).

Table 1 Linear regression model output for the effect of spike counts over time

We looked for differences between the linear regression fits by constructing a comparison matrix (Fig. 7G), which displays the significance of pairwise paradigm comparisons for estimated intercepts (β₀, left) and slopes (β₁, right). None of the slopes significantly differed from one another or from the null hypothesis (Fig. 7G, Table 1), indicating no adaptation and suggesting that time (1 s/trial) did not significantly affect the response.

The intercepts for deviant tones in the random oddball paradigm (DEV-R) were significantly higher than those for the random standard tones (STD-R) (p = 0.0021, t-test with Holm-Bonferroni correction) and the many-standard paradigm (MSC), as well as both cascade control paradigms (CASC-ASC, CASC-DES) (p < 0.001). Similarly, the intercepts for deviant tones in the periodic oddball paradigm (DEV-P) were significantly higher than those for periodic standard tones (STD-P) (p = 0.0024), as well as higher than those for STD-R, MSC, CASC-ASC, and CASC-DES (p < 0.001; Fig. 7G). None of the control responses had intercepts significantly different from STD-R. However, the MSC intercept (β₀ = 2.2546 ± 0.19047, p < 0.001) was significantly lower than that of STD-P. There were no significant differences between the intercepts of ODD-R and ODD-P or between STD-R and STD-P.

We also used a Wilcoxon signed-rank test to compare the responses elicited by the MSC and CASC conditions, finding no significant differences between them. Since our results in this section indicate no significant difference between the controls, we chose to use the many-standards-evoked responses as the control (CTR) for analyses.

Discussion

We recorded single- and multi-unit activity and LFPs from CA1 and DG to examine auditory novelty responses. Our main findings are as follows: (1) A distinct subpopulation of hippocampal neurons responded to auditory stimuli, exhibiting significantly stronger responses to deviant tones compared to standard and control tones, supporting predictive coding mechanisms. (2) DG neurons showed shorter response latencies and higher mismatch indices than CA1 neurons, suggesting locally distinct mechanisms for encoding prediction error. (3) Single/multiunit population analyses indicated that mismatch responses in both CA1 and DG were primarily driven by prediction error rather than repetition suppression, whereas LFP analyses showed that iPE and iRS contributed distinctly across space and time (repetition suppression-biased patterns in CA1 with small n, mixed PE/RS contributions in DG). (4) Spike-time analyses revealed that units with stronger responses to deviants already exhibited suppression to standard stimuli (Fig. 7). (5) At both the neuronal and population LFP levels, early responses to randomly presented deviants are enhanced relative to repeated periodic deviants, consistent with prediction error signaling. In contrast, at the LFP level, late responses are stronger for periodic deviants than for randomly presented ones, suggesting an additional role in signaling the precision of predictions.

Together with previous reports^{8,21,26,27,29,31,44}, our findings demonstrate that the hippocampus contributes to predictive auditory processing and novelty detection^18,39,45.

Animal studies have documented hippocampal auditory responses using ERP and LFP recordings^46,47,48. However, single-cell studies remain elusive^{33,34,35,49,50,51} and anesthesia often attenuates responses. In line with these observations, we detected tone-evoked activity in only approximately 20% of units.

As in humans, most prior animal studies on MMN relied on LFPs. For example, mismatch responses have been observed in both CA1 and DG regions in rats^31,44. In mice, early LFP peaks around 30–50 ms post-stimulus have been reported⁴⁸, although analysis in that study was limited to the first 225 ms. In our study, LFP mismatch responses reflected contributions from both repetition suppression and prediction error, and exhibited clear habituation patterns²¹, in contrast to unit-level activity, which did not. This suggests that adaptation occurs mainly at the network level^52,53. Our recordings also revealed robust deviance-related peaks at 65 ms, 226 ms, and a pronounced late component at 580 ms. These latency differences may reflect variability in stimulus complexity, anesthetic protocols (e.g., ketamine vs. urethane), or recording locations.

Auditory information reaches the hippocampus via multiple pathways. One route relays signals through the AC via the classical (canonical) ascending auditory pathway^{54,55,56,57,58}. A second route involves the non-canonical pathway, transmitting input more directly through the medial septum and reticular formation^{39,59,60,61,62}. While the AC pathway is associated with longer-latency responses, the non-canonical route provides shorter-latency input. As we discuss further in the next section, our findings suggest that auditory responses in the hippocampus are predominantly shaped by inputs likely originating from the AC, i.e., following the canonical auditory pathway via the entorhinal cortex.

In the lemniscal AC, neuronal responses to repeated tones typically diminish by half after about seven repetitions. In contrast, in the non-lemniscal AC⁴¹, this reduction occurs after just two repetitions, as well as in both the medial prefrontal cortex⁶³ and hippocampus (current study), it is evident after a single repetition. This rapid habituation observed in our recordings is consistent with previous human studies reporting a swift decline in hippocampal activity in response to repeated stimuli^39,64,65. Indeed, our adaptation time-course analyses do not reveal a progressive suppression pattern in the hippocampus over time (Fig. 7A–F; see also Fig. 8A). Instead, responses to deviant tones consistently exceed those to standard tones, suggesting that the capacity for stimulus discrimination may arise upstream of the hippocampus, likely in the entorhinal cortex⁶⁰, auditory cortex¹⁴, or thalamus¹⁶. Although the hippocampus receives substantial input from lemniscal pathways, we found that prediction error indices in the DG were comparable to those in non-lemniscal AC regions (Fig. 8B), likely reflecting shared contextual sensitivity. This similarity suggests that non-lemniscal-like computations either emerge within hippocampal circuits or arrive via converging multimodal inputs. Prediction error levels in DG exceeded those in lemniscal AC, which primarily encodes low-level stimulus features, and were lower than in PFC, where predictive processing likely reflects the highest-order integrative functions. Consistent with this interpretation, we did not observe neurons with a clear frequency sensitivity, as occurs with purely auditory neurons. Units lacked frequency selectivity yet showed deviance sensitivity. This supports the view that hippocampal auditory codes prioritize contextual relations and expectation violations over spectral tuning^9,18,45.

Fig. 8: Comparisons between AC, mPFC, and hippocampal responses.

A Average responses for the first 10 STD trials (mean ± SEM) in the lemniscal AC (L-AC, green, dotted line), nonlemniscal AC (nL-AC, orange, dotted line), mPFC (gray, dotted line), DG (red, solid trace), and CA1 (blue, solid trace). Error bars indicate ± SEM. Open circles indicate the trial at which the STD falls below 50% relative to the first trial. Arrowheads on the left represent the minimum response to STD during the sequence, as determined by the steady-state (SS) parameter of a three-parameter power-law fit for AC and PFC, while for CA1 (n = 21; 6 rats) and DG (n = 22; 5 rats), it shows the lowest STD response observed across all trials. B Median iPE (orange) and iRS (cyan) values for each AC, PFC or hippocampus subdivision recorded, referenced against the baseline set by the CTR. Here, iPE is plotted as positive in the upward direction, while iRS is plotted as positive in the downward direction (see Fig. 1D). AC and PFC data originates from Parras et al. (2017) and Casado-Román et al. (2020), respectively. Asterisks indicate statistical significance of each index compared to a zero median (n.s., nonsignificant; *p < 0.05; **p < 0.01; ***p < 0.001; t-test with Holm-Bonferroni correction). The underlying data for this Figure can be found in Supplementary Data 4.

Earlier models posited that hippocampal mismatch responses rely entirely on upstream activity from AC and are recruited only when deviant stimuli are salient enough to trigger attentional mechanisms. In this framework, the AC can detect even subtle differences, such as tones near behavioral thresholds⁶⁶, whereas the hippocampus is recruited only when the deviant stimulus is prominent enough to disrupt ongoing processing. This view mirrors the MMN–P3a sequence observed in humans, where the full response (particularly the P3a component) is elicited only under conditions of high stimulus salience^67,68.

Although the MMN is primarily generated in auditory and frontal cortices⁶⁷, the hippocampus can modulate MMN-related activity through its connections with the entorhinal cortex and the trisynaptic circuit^58,69,70. Oddball paradigms also elicit the P300 component, which consists of two subcomponents, P3a and P3b, each associated with distinct cognitive processes such as attention, memory updating, and context evaluation^71,72,73.

Our observed peak latencies (~430 ms in CA1, ~580 ms in DG) in LFP and the late neuronal responses observed in CA1 and DG (250–350 ms range) are more in line with P3b dynamics than aligning with MMN. The same can be said for the onset latencies, with the CA1 deviant response starting around ~340 ms and the DG response at ~315 ms. These findings likely reflect hippocampal contributions to memory updating and contextual processing^20,30,38,74.

Additional studies have shown that hippocampal involvement in novelty detection depends not only on stimulus salience but also on prior learning and the continuous monitoring of temporal sequences^34,75. Recent theoretical models propose that the hippocampus plays a central role in updating internal models of the environment, linking deviance detection to the encoding of contextual representations³⁸ and expected variability⁷⁶. Within this framework, the periodic oddball involves low expected uncertainty (low entropy, predictable deviant timing), whereas the random oddball involves high expected uncertainty (trial-wise unpredictability)^76,77. Consistent with these accounts, periodic deviants evoked stronger late LFP components and earlier spiking, particularly in DG, around deviant onset (Figs. 4C, 6E), suggesting predictive responses that exploit learned temporal structure, while random deviants elicited responses dominated by surprise (prediction error). Note that the periodic effect includes a decrease during stimulus presentation in DG (Fig. 4C), consistent with a modulatory influence.

We interpret these anticipatory signals as evidence that the hippocampus encodes predictions, not merely mismatches. This interpretation is supported by findings that hippocampal representations shift from signaling prediction errors to representing predicted stimuli as regularities become established through learning¹⁸. In unpredictable contexts, such as the random oddball paradigm, the hippocampus emphasizes unexpected inputs. With repeated exposure to structured sequences, it increasingly reflects expected events. Our results suggest that even under anesthesia, hippocampal circuits internalize temporal structure and transition into a predictive mode. Thus, the periodic oddball paradigm may function as a minimal learning context that engages generative processes in the hippocampus, supporting its broader role in hierarchical inference and predictive coding. While urethane anesthesia limits direct extrapolation to awake behavior, our findings still offer insight into hippocampal deviance processing under stable and controlled physiological conditions. Previous studies have shown that auditory change detection in the hippocampus persists under anesthesia^35,78,79, though response magnitude and timing may differ from those in awake states. P300-like components have also been observed under anesthesia^29,80. One limitation of our study is the exclusive use of pure-tone oddball stimuli. Although the hippocampus responds to both simple and complex sounds, its encoding specificity can vary depending on stimulus type and context³⁹. It is generally more responsive to ecologically or behaviorally salient sounds, such as speech, vocalizations, emotionally charged stimuli, or learned cues^34,81,82,83. Additionally, hippocampal engagement is shaped by prior experience and task relevance^{84,85,86,87,88}. In our paradigm, the rats were not pre-exposed to the auditory stimuli, which may have limited the involvement of contextual memory processes. Finally, because CA1 and DG units were drawn from only partially overlapping animal sets, between-subfield effects could reflect animal variability to some extent.

Differences between single/multi-unit and LFP results may reflect the functional diversity of hippocampal neurons. Distinct cell types have varied anatomical and physiological traits that influence auditory responsiveness^{33,34,39,84,89,90}. Inhibitory interneurons often fire in sync with theta oscillations^32,81,91, and respond to acoustically meaningless sounds, as seen in GABAergic CA1 boutons receiving septal input⁹². Pyramidal neurons, by contrast, exhibit burst firing with less phase locking. While our study could not identify cell types, such functional differences may underline the observed disparities between spiking and LFP signals.

In conclusion, our findings suggest that hippocampal neurons are involved in both prediction error signaling and predictive processes, operating as part of a distributed network that includes both cortical and subcortical regions⁸. This supports the view that the hippocampus plays an active role in predictive coding, consistent with hierarchical models of predictive processing, in which the hippocampus, together with prefrontal regions³⁷, is positioned at a higher level (Fig. 8B) within the predictive hierarchy.

Methods

Statistics and reproducibility

For all unit analyses, each recorded unit or multi-unit was treated as an independent measurement, while for LFP analyses, each channel was treated as an independent measurement. Animals themselves were not treated as replicates for statistical testing; however, all experiments included multiple animals, and sample sizes (n) for each analysis are reported together with the number of animals contributing to those samples. Unit counts, channel counts, and animal contributions were extracted directly from the dataset acquired in 27 urethane-anesthetized rats. Across all experiments, we obtained 824 units (138 single units, 686 multi-units), of which 177 (27 rats) met the criterion for auditory responsiveness. From these, 43 (9 rats) neurons exhibited significant contextual modulation (CSI-significant) under the oddball paradigm.

For LFP analyses, we included 268 channels across 9 probe insertions in 3 animals, with subfield-specific analyses based on 3 CA1 channels, 2 tracts in 2 animals, and 13 DG channels, 6 tracts in 3 animals.

All offline analyses were performed using MATLAB with custom analysis scripts. Statistical comparisons used standard parametric (two-sample and paired t-tests, Welch’s t-tests for unequal variances, and one-way ANOVA/ANCOVA) and non-parametric tests (Wilcoxon sign-rank tests, Mann–Whitney U tests, and Kolmogorov–Smirnov tests for normality), selected according to distributional properties of the data. Multiple-comparison correction was performed using Holm–Bonferroni procedures (and Fisher’s combined probability when comparing PSTH time courses). Significance threshold was set at α = 0.05 (two-sided). Confidence intervals to 95% were also calculated when applicable. Effect sizes (Cliff’s δ, Hedges’ g) were reported for comparisons between CA1 and DG predictive coding indices.

Auditory-responsive neurons were observed in every recorded animal, demonstrating reproducibility across biological replicates. CSI-significant units were found across multiple animals in both CA1 and DG. LFP mismatch effects were reproducible across 9 multichannel recordings from 3 animals. Whenever results depended on smaller subsamples (e.g., CA1 LFP channels), these limitations are acknowledged in the manuscript’s Discussion.

Surgical procedures

We conducted experiments on 27 female Long-Evans rats, with body weights ranging from 200 to 350 g. The rats were anesthetized using urethane (1.9 g/kg, administered intraperitoneally). To maintain a stable level of deep anesthesia, additional doses of urethane (~0.5 g/kg, intraperitoneally) were given if corneal or pedal reflexes were observed. We selected urethane for its capacity to maintain balanced neural activity, offering a moderate effect on both inhibitory and excitatory synapses⁹³. Female rats were used to ensure stable body weight, improving dosing accuracy and physiological stability, and to maintain continuity with prior work; therefore, sex comparisons were not possible. Our aim was a general characterization of hippocampal predictive coding rather than a sex-comparative analysis, and future studies should include male cohorts to assess potential sex-specific effects.

We confirmed normal hearing via auditory brainstem responses (ABR), which we recorded using subcutaneous needle electrodes connected to an RZ6 Multi I/O Processor (Tucker-Davis Technologies, TDT) and analyzed with BioSig software (TDT). Auditory stimuli consisted of 0.1 ms clicks, presented at a rate of 21 per second, delivered to the right ear in 10 dB increments, from 10 to 90 dB SPL, using a close-field speaker. We administered 0.1 mg/kg atropine sulfate to the rats every 10 hours (subcutaneous), 0.25 mg/kg dexamethasone (intramuscular), and 5–10 ml of glucosaline solution (subcutaneous) to reduce bronchial secretions, brain edema, and prevent dehydration, respectively. The animals were artificially ventilated through a tracheal cannula with monitored expiratory [CO2] levels and were positioned in a stereotaxic frame with hollow specula to enable direct sound delivery to the ears. Body temperature was maintained at approximately 37 °C using a homeothermic blanket system (Cibertec, Spain). For surgical access, an incision was made along the scalp midline, and the periosteum was retracted to expose bregma. We performed a craniotomy above the left hippocampus, approximately 3 × 4.5 mm in size, and the dura was carefully removed.

Data acquisition

We recorded unit and multiunit activity to look for evidence of predictive coding signals under acoustic oddball stimulation in CA1 and DG, of the urethane-anesthetized rat. We conducted experiments in an electrically shielded and sound-attenuating chamber. Recording tracts were orthogonal to the brain surface of the left hippocampus: ~4–6.3 mm rostral to bregma, ~2.5 mm lateral to the midline and ~0.2–4.5 mm dorsoventrally. Therefore, we recorded in CA1 and DG, as shown in the histology picture shown in Fig. 1B. We performed extracellular neurophysiological recordings using both glass-coated tungsten microelectrodes (1.6–2.6 MΩ impedance at 1 kHz) and 32-channel Cambridge probes (H4). We used a piezoelectric micromanipulator (Sensapex) to advance and measure the penetration depth. We visualized the electrophysiological recordings of tungsten electrodes online using custom software programmed with the OpenEx suite (TDT) and MATLAB (MathWorks), and stored the data for offline analysis. For multichannel recording, we used custom software programmed in Synapse (TDT) and MATLAB. For tungsten electrodes, analog signals were digitized with an RZ6 Multi I/O Processor, a RA16PA Medusa Preamplifier, and a ZC16 headstage (TDT) at 97 kHz sampling rate and amplified 251x. We applied a band-pass filter between 0.5 and 4.5 kHz to the neurophysiological signals using a second-order Butterworth filter. We digitized multichannel recording signals using two RZ6 Multi I/O Processors (TDT), RA16PA Medusa Preamplifiers, a miniDBF adapter, ZC64 headstage cable, and a ZCA-NN64 adapter connected to an H4 multichannel probe (NeuroTech, Cambridge, UK). Data were digitized at a sampling rate of 25 kHz and band-pass filtered between 0.3 and 5 kHz using a second-order Butterworth filter.

Sound stimulation and recording protocol

The sound stimuli were generated using the RZ6 Multi I/O Processor (TDT) and custom software programmed with OpenEx Suite or Synapse (TDT) for multichannel recordings, as well as MATLAB. Sounds were presented monaurally in a close-field condition to the ear contralateral to the left hippocampus, through a custom-made speaker. We calibrated the speaker using a ¼-inch condenser microphone (model 4136, Brüel & Kjær) and a dynamic signal analyzer (Photon + , Brüel & Kjær) to ensure a flat response up to 73 ± 1 dB SPL between 0.5 and 44 kHz, and the second and third signal harmonics were at least 40 dB lower than the fundamental at the loudest output level.

When using tungsten electrodes to search for evoked auditory responses from the hippocampus (24 rats), we presented stochastic trains of white noise bursts and sinusoidal pure tones of 75 ms duration with 5 ms rise-fall ramps, varying presentation rate and intensity to avoid possible stimulus-specific effects that could suppress evoked responses.

Once auditory responses were confirmed, we used only pure tones (75 ms duration, 5 ms rise/fall ramps) for all experimental stimulation protocols. All stimulation sequences ran at 1 stimulus per second. First, the frequency response area (FRA) of the neuron was computed by randomly presenting pure tones of various frequency and intensity combinations, that ranged from 1 to 44 kHz (in 4–6 frequency steps/octave) and from 0 to 70 dBs (10 dB steps), with 1–4 repetitions per tone, similarly to our previous studies in the auditory system^41,94,95,96. However, as in our previous work on the PFC⁶³, we could not determine clear receptive fields in the FRAs of the hippocampus, so we chose the frequencies and intensity for our test sequences based on our observations during manual search, trying to maximize the auditory-evoked response when possible.

For each unit, we selected 10 equally spaced tones to generate 3 no-repetition sequences (i.e., the many-standards, cascade ascending, and cascade descending), and pairs of consecutive frequencies (within those 10 tones) to generate oddball sequences. All sequences were 400-stimuli long, and were presented always in the same order: cascade ascending, cascade descending, many-standard, oddball ascending and oddball descending (Fig. 1C), called ascending oddball since the deviant tone has a higher frequency than the standard; and descending oddball, since the frequency which was the standard in the ascending oddball (lower frequency) is now the deviant tone, and the higher frequency is the standard. An oddball sequence consisted of a repetitive tone (STD, 90% probability), occasionally replaced by a different tone (DEV, 10% probability) in a pseudorandom manner. The first 10 stimuli of the sequence set the STD, and a minimum of 3 STD tones always preceded each DEV. Oddball sequences were either ascending or descending, depending on whether the DEV tone had a higher or lower frequency than the STD tone, respectively (Fig. 1C). In 8 rats, we also presented the periodic variation of both oddballs at the end of all the paradigms mentioned above. The periodic oddball consisted of groups of 9 standard tones followed by 1 deviant tone, repeated overtime as a frozen token of stimuli, keeping the probability of appearance the same (Fig. 4B).

On the other hand, when using multichannel probes (9 tracks in 3 rats) the white noise searching and FRA protocols were omitted. We proceeded directly to insert the electrode and record the activity as we presented the auditory paradigms, with 20 seconds of silence between paradigms. All the experiments performed with multichannel probes used pure tones at 70 dB and set frequencies for the oddball (5280 Hz and 7470 Hz) and controls, which included those two frequencies and another 8 frequencies equally spaced.

One limitation of the mismatch measurements obtained using the oddball paradigm is that the effects of high-order processes like genuine deviance detection or prediction error (PE) signaling cannot be distinguished from lower-order spectral-processing effects, such as SSA^97,98, an effect in which some neurons exhibit a lower response to the repetitive, standard stimuli and a significantly higher response to the deviant sound. The so-called ‘no-repetition’ controls allow for assessing the relative contribution of both higher- and lower-order processes to the overall mismatch response⁴⁰. These controls of the auditory oddball paradigm are tone sequences that must meet 3 criteria: (1) to feature the same tone of interest with the same presentation probability as that of the DEV; (2) to induce an equivalent state of refractoriness by presenting the same rate of stimulus per second (which excludes the DEV alone from being considered a proper CTR); and (3) present no recurrent repetition of any individual stimulus, specially the tone of interest, thus ensuring that no SSA is induced during the CTR⁹⁹.

Hence, we can assess the portion of the mismatch response (DEV – STD) that can be attributed to the effects of spectral repetition yielded during the STD train, such as SSA^100,101, by comparing the auditory-evoked responses to DEV and to CTR. When the auditory-evoked response is similar or higher during CTR than in DEV, then the mismatch response can be fully accounted for by repetition suppression, and no higher-order process of deviance detection or PE signaling can be deduced (i.e.: DEV ≤ CTR; Fig. 1D). Otherwise, a stronger response to DEV than to CTR unveils a component of the mismatch response that can only be explained by a genuine process of deviance detection or PE signaling (i.e.: DEV > CTR; Fig. 1D).

To distinguish frequency-specific effects from genuine deviance detection or predictive processing, we used two no-repetition control sequences for our oddball paradigms: the many-standards and cascaded sequences (Fig. 1C). The many-standards sequence presents the tone of interest within a randomized set of tones, each appearing with the same probability as the deviant stimulus in the oddball paradigm¹⁰². In contrast, the cascade sequence arranges tones in a structured pattern, either ascending or descending in frequency. While the stimulus of interest follows a regular pattern, unlike the DEV, it does not rely on repetition-based regularity, which is susceptible to SSA as seen with the standard stimulus.

Histological verification

At the end of the experiments performed using tungsten electrodes, we induced electrolytic lesions through the recording electrode (10 μA, 10 seconds). Animals were afterwards euthanized with a lethal dose of urethane, decapitated, and the brains immediately immersed in a mixture of 4% formaldehyde in 0.1 M PB. After fixation, tissue was cryoprotected in 30% sucrose and sectioned in the coronal plane at 40-μm thickness on a freezing microtome. We stained slices with 0.1% cresyl violet to facilitate identification of cytoarchitectural boundaries (Fig. 1B). We conducted a histological assessment of the electrolytic lesions in the hippocampal subfields, processing the data blindly to each animal’s history. We assigned multiunit and single-unit locations to their corresponding areas using a rat brain atlas, based on histological verification and the stereotaxic coordinates of the recording tracts in all three axes¹⁰³. For multichannel recordings, we identified electrode-induced damage in the cortex through histology, allowing us to approximate unit locations using stereotaxic coordinates.

Data analysis

Offline data analyses were performed with MATLAB functions, the Statistics and Machine Learning toolbox, and custom-made MATLAB scripts. We first processed the tungsten electrode recordings using a principal component analysis algorithm (PCA)¹⁰⁴, obtaining more isolated single and multi-units that responded to sound from each recording. Computing PSTHs with a bin size of 25 ms, we measured unit responses to each tested tone and condition (DEV, STD, and CTR). In the case of the STD, we used the response to the STD right before a deviant tone, to have a comparable number of trial repetitions. The corresponding control would be the response to the deviant frequency used in the oddball sequence, but presented in the non-repetition sequences (e.g., Figs. 2–4: unit PSTHs, DEV/STD averages).

Multichannel offline data analyses were also performed with MATLAB functions, the Statistics and Machine Learning toolbox, and custom-made MATLAB scripts¹⁰⁵. First, we spike-sorted the data using Kilosort4 in Python^106,107 and then visually curated it using Phy, also in Python. After this, all analyses ran in parallel to each other when comparing PCA and Kilosort4-sorted units.

We chose a baseline activity window of 125 ms, which was located from 100 ms to 225 ms after stimulus onset, 25 ms before the analysis window (250 to 650 ms). This window was chosen since it is the earliest post-onset interval that showed low amplitude, a mostly flat response with no DEV–STD significant differences. Although baselines are typically pre-stimulus, in our data, the pre-onset period was not ideal. Responses were long-latency and sustained, increasing the risk that slow (very long latency) activity would leak into a pre-stimulus baseline. We defined auditory-responsive neurons as those units exhibiting a mean activity plus 2 standard deviations higher than the mean activity in the baseline activity window (e.g., Fig. 3A). To analyze the auditory-responsive pool we excluded CSI-significant units (e.g., Fig. 5).

The time of the peak response in the PSTH was determined using the bin center where the maximum peak was found, while the latency of each response was determined by the first peak to be above 1 standard deviation plus the mean of the baseline activity, after the baseline activity window. In addition to peak latency, we estimated the onset latency using a 50-ms moving window applied to PSTHs (25-ms bins). For each unit and condition (DEV, STD, and DEV-STD). Onset latency was defined as the first time point at which the 50-ms window of spike counts exceeded half of the maximum response, after baseline subtraction across the entire window; this criterion minimizes false onset latency estimation due to spontaneous activity. Onset latency was computed separately for CA1 and DG units and summarized as mean ± SEM. Group differences were assessed using Welch’s t-tests (unequal variances) and Mann–Whitney U tests (e.g., Fig. 3: latency comparisons).

To compare the differences between the responses to the periodic and random oddball paradigms, only the multichannel recording data were used. A t-test with a Holm-Bonferroni correction, for a false discovery rate of 0.1, was used to compare the random and periodic responses, and to compare the normalized spike counts among each other (e.g., Fig. 4D, E). For the significant difference window comparison in Fig. 4D, we quantified spike counts in the 25 to 50 ms window relative to DEV onset (Fig. 4C). The bar charts in Fig. 4E used the standard analysis window.

To compare across different units, we normalized the auditory-evoked responses to each tone of interest in 3 testing conditions as follows:

$${Normalized\; DEV}={DEV}/N$$

$${Normalized\; STD}={STD}/N$$

$${Normalized\; CTR}={CTR}/N$$

where

$$N=\,\sqrt{{{DEV}}^{2}+{{STD}}^{2}+{{CTR}}^{2}}$$

is the Euclidean norm of the vector defined by the DEV, STD, and CTR responses. Thereby, normalized responses are the coordinates of a 3D unit vector defined by the normalized DEV, normalized STD, and normalized CTR responses that range between 0 and 1. This normalized vector has an identical direction to the original vector defined by the non-normalized data and equal proportions among the three response measurements (e.g., Figs. 3–4A: normalized PSTHs, Fig. 4C–E: normalized PSTHs, normalized counts, Fig. 5: SI/CSI/iMM/iPE/iRS are obtained from normalized data, Fig. 6A–C: normalized amplitudes in bar graphs, which afterwards is used to calculate iMM/iPE/iRS (Fig. 6D) and Fig. 8: Normalized spike counts and indices). To enable direct comparison between random and periodic evoked responses, all panels in Fig. 4 were normalized using the normalization factor from the random oddball condition.

In order to quantify and compare SSA levels between CA1 and DG, we computed the frequency-specific SSA index for each stimulus, SI(f₁) and SI(f₂), and the CSI for every recording site, in the usual way^100,108:

$${SI}\left( \, {f}_{i}\right)=\frac{{DEV}\left( \, {f}_{i}\right)-{STD}\left( \, {f}_{i}\right)}{{DEV}\left( \, {f}_{i}\right)+{STD}\left( \, {f}_{i}\right)}{;i}={{\mathrm{1,2}}}$$

$${CSI}\left( \, {f}_{i}\right)=\frac{\sum {DEV}\left( \, {f}_{i}\right)-\sum {STD}\left( \, {f}_{i}\right)}{\sum {DEV}\left( \, {f}_{i}\right)+\sum {STD}\left( \, {f}_{i}\right)}{;i}={{\mathrm{1,2}}}$$

Where ${DEV}\left({f}_{i}\right)$, ${STD}\left({f}_{i}\right)$ are spike counts in response to frequency f_i when it was a deviant and standard, respectively. The CSI was calculated only for recordings with significant auditory responses to at least one frequency in the oddball paradigm (either as deviant or as standard, Fig. 5A). To determine if a unit was CSI-significant, we assessed whether its CSI value was statistically significant. We did this by calculating 1000 CSI values using bootstrapping and checking whether the range of generated CSI values remained consistently positive or negative. If the range retained the same sign as the original CSI value, the unit’s CSI index was considered significant, identifying it as a CSI-significant neuron (Fig. 1G: red LFP traces, Fig. 2: All examples are CSI significant, Figs. 3B–F, 4, 5: darker colors are CSI-significant units, Fig. 7 only shows CSI-significant spikes, as well as the hippocampus data in Fig. 8).

To quantify and facilitate the interpretation of the oddball paradigm controls, we calculated the indices of neuronal mismatch (iMM, computing the overall mismatch response), repetition suppression (iRS, accounting for lower-order frequency-specific effects), and prediction error (iPE, unveiling higher-order deviance detection or PE signaling activity) with the normalized spike counts as:

$${iMM}={Normalized\; DEV}-{Normalized\; STD}$$

$${iRS}={Normalized\; CTR}-{Normalized\; STD}$$

$${iPE}={Normalized\; DEV}-{Normalized\; CTR}$$

Index values ranged between -1 and 1, where

$${iMM}={iRS}-{iPE}$$

This was used in Fig. 5B (unit indices), Fig. 6D (LFP indices), and Fig. 8B (cross-area indices).

For the LFP signal analysis, only the multichannel recording data were used. We filtered the raw recording using a 4th-order Butterworth bandpass filter that allows frequencies between 0.1 Hz and 30 Hz¹⁰⁹. Then we aligned the recorded wave to the onset of the stimulus for every trial, and computed the mean LFP for every recording site and stimulus condition (DEV, STD, CTR; e.g., Fig. 1G-H: LFP traces and time-amplitude plot, Fig. 6A and first panel of Fig. 6D, where only channels with an amplitude above −0.07 mV were included). Finally, grand-averages were computed for all conditions, for CA1 and DG, taking into account only channels where neurons with a significant CSI index were recorded (e.g., Fig. 6B–D: CA1 and DG analysis, and Fig. 6E: periodic vs random LFP). The analysis window to calculate the amplitudes and indices in the LFP was also from 250 ms to 650 ms.

Our data set was normally distributed, which we verified using the Kolmogorov-Smirnov test, therefore, we were able to mostly use a t-tests throughout the study with a Holm-Bonferroni to control the family-wise error rate at α = 0.05, for most of our analysis (spike counts, normalized responses, indices, and response latencies; e.g., Fig. 3A–D, Figs. 4, 5, Fig. 6A–C). The only exception was the comparison between DEV and STD responses in CA1 and DG, where we used a t-test in combination with Fisher’s correction for combined probability across multiple comparisons (e.g., Fig. 3E, F). As well as to check for significance of our median values in Fig. 5, where we used a two-sided sign test. Given the small and unequal LFP samples (CA1 = 3; DG = 13), we compared CA1 vs DG indices (iMM, iPE, iRS) using two-sided Mann–Whitney U tests, with Holm–Bonferroni correction across indices (α = 0.05). As a sensitivity analysis, we also ran Welch’s t-tests (Holm-adjusted). We summarize medians/interquartile ranges (IQRs) and report Cliff’s δ and Hedges’ g to convey effect size and direction. Results are interpreted cautiously due to the imbalanced CA1 sample.

To analyze the responses over time of the auditory-evoked responses, we measured the DEV, STD, and CTR responses as average spike counts for every trial number within the sequence, for all recorded units exhibiting significant CSI (n = 20; 9 tracks in 3 animals). Since we only analyzed multichannel units, sequences and frequencies remained consistent across recordings⁶³. We included all the standard tones, not just the last standard before a deviant event as previously, as well as the responses to all the frequencies in the control paradigms (Fig. 7A-E). We applied a simple linear regression model in MATLAB (f(x) = β0 + β1x + ε) (Fig. 7F). To look at the differences between the linear regression fits, we constructed a comparison matrix, which displays the significance of pairwise paradigm comparisons for estimated intercepts (β₀, left) and slopes (β₁, right), a t-test with Holm-Bonferroni correction was used. To determine whether a linear model outperformed a constant model, we performed an ANCOVA (Fig. 7G, H).

We also used a Wilcoxon signed-rank test to compare the responses elicited by the MSC and CASC conditions; for this, we calculated the average firing rates for the controls for each trial in the sequence. To ensure consistency, we grouped the trials into sets of 10 and calculated the mean spike count for each group, resulting in 40 measurements for each control condition. We then computed the difference in spike counts between them for these 40 values and tested for statistical significance.

Ethics statement

All methodological procedures were approved by the Bioethics Committee for Animal Care of the University of Salamanca (USAL-ID-574) and performed in compliance with the standards of the European Convention ETS 123, the European Union Directive 2010/63/EU, and the Spanish Royal Decree 53/2013 for the use of animals in scientific research.

The methods, encompassing surgical procedures, electrophysiological recordings, stimulus design, and preprocessing steps up to but not including the statistical analyses, are based on and largely consistent with those described in Parras et al. (2017) and Casado-Román et al. (2020).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.