Clinically feasible liver tumour cell size measurement through histology-informed in vivo diffusion MRI

Abstract

Background

Innovative diffusion Magnetic Resonance Imaging (MRI) models enable the non-invasive measurement of cancer biological properties in vivo. However, while cancers frequently spread to the liver, models tailored for liver application and easy to deploy in the clinic are still sought. We fill this gap by delivering a practical, clinically-viable framework for liver tumour diffusion imaging, informing its design through histology.

Methods:

We compare MRI and histological data from mice and cancer patients, namely: MRI and hemaotxylin-eosin (HE) stains from N = 7 fixed mouse livers; MRI of N = 38 patients suffering from liver solid tumours, N = 18 of whom with HE biopsies. We study five diffusion models, ranking them according to a total MRI-histology correlation score. Afterwards, we test metrics from the top-ranking model on our cohort, assessing their sensitivity to cell proliferation (Ki-67 staining, N = 10), evaluating their association with tumour volume (N = 140 tumours), and comparing them across primary cancer types.

Results:

We select a dMRI signal model of restricted intra-cellular diffusion with negligible extra-cellular contributions, which maximises radiological-histological correlations (total score: 0.625). The model provides cell size and density estimates that i) correlate with histology (e.g., for cell size: r = 0.44, p = 0.029), ii) are associated to Ki-67 cell proliferation (for MRI cell density: r = 0.80, p = 0.006) and tumour volume (r = 0.40, p < 10^–5 for tumour volume regression), and iii) that distinguish melanoma (N = 8) from colorectal cancer (N = 13) (p = 0.011 for intra-cellular fraction).

Conclusions:

Our biologically meaningful approach may complement standard-of-care radiology, and become a new tool for enhanced cancer characterisation in precision oncology.

Plain language summary

Magnetic Resonance Imaging (MRI) is an imaging tool used frequently to detect and monitor malignant tumours. Notably, the latest MRI technology enables physicians to measure not only the size of a tumour, but even properties related to the cells it contains. This information, like number or size of cells can help oncologists to choose the best treatment. Obtaining this information using this imaging tool in tumors that have spread to the liver, remained challenging. Here we present an MRI method developed specifically to capture the biology of liver tumour cells. We base it on mathematical models that use information gathered from microscopy images – known as histology, where individual cells are visible – to guide the analysis of the scan. We show that the method quantifies tumour cell size and density from a simple, clinically feasible MRI scan and propose this technique for oncological applications.

Introduction

The clinical use of Magnetic Resonance Imaging (MRI) in cancer is based on revealing the presence of tumours within an area of interest, and on measuring their size. Nonetheless, MRI also offers the possibility of obtaining estimates of biological properties within each pixel making up the tumour image. This approach, known as quantitative MRI (qMRI)¹, involves the acquisition of multiple MRI contrasts, which are then analysed jointly with a mathetmatical model. qMRI provides promising metrics, which could become quantitative biomarkers complementing the qualitative assessment by the expert radiologist². Among existing qMRI approaches, diffusion MRI (dMRI) sensitises the MRI signal to water diffusion in biological tissues^1,3,4. Since the patterns of diffusion are influenced by the microenvironment where diffusion takes place (e.g., by obstacles such as cell membranes), dMRI ultimately enables the per-voxel estimation of properties related to the size and density of cells^5,6,7, bridging the gap between radiology and histology.

dMRI has shown promise in multiple areas, including brain⁵, spinal cord⁸, prostate⁶, breast⁹, or liver imaging^10,11. The liver is a frequent site for cancer metastasisation¹², and liver tumours are common targets for treatment response assessment in oncology. However, current image-based response criteria such as RECIST¹³ have limitations, in that they rely on MRI or computed tomography merely to measure tumour size, without accounting for changes under therapy at the cellular level. Novel dMRI metrics could instead enable the non-invasive characterisation of cancer microenvironments, shedding light on the composition of tumours that cannot be biopsied. The new readouts could also provide information on tumour heterogeneity, relevant to fight treatment resistance^14,15, and better stratify patients for personalised treatment planning, reducing sample sizes in clinical trials and ultimately improving patient outcomes¹⁶.

In practice, the estimation of the biological properties through dMRI is made possible by mathematical models, which are used to link the observed image contrasts to the biological properties themselves^17,18,19,20. However, despite their promise, advanced liver dMRI models are relegated almost exclusively to research contexts, and seldom used in real-world clinical settings. This is due to two main reasons: i) to the high number of dMRI images (and hence long scan time) required to support the fitting of such models, and ii) to the requirement for specialised dMRI acquisitions²¹, beyond those made available by manufacturers in the scanner console.

We aim to fill this clinical-research gap by delivering a practical liver dMRI framework that is truly feasible in hospital settings, i.e., on 1.5 T or 3 T systems, with scan time that does not exceed 15 min, and using vendor-provided dMRI acquisitions. With this objective in mind, we embraced the latest “histology-informed” dMRI development paradigm, which is based on informing signal model design²² with co-localised histology. The framework has shown promise in delivering dMRI approaches with unprecedented fidelity to cellular architecture, enhancing the specificity or medical imaging towards the underlying tissue biology^23,24,25.

Following preliminary abstract dissemination²⁶, in this article we compared candidate, state-of-the-art approaches using a rich data set of dMRI scans and hematoxylin and eosin (HE)-stained images, from excised mouse livers and patients’ liver biopsies. We used these unique data to select the approach maximising the correlation of radiological and histological estimates of metrics such as cell size, corroborating results with computer simulations. To our knowledge, this is the first time that the approach has been used on a rich data set of dMRI scans of liver tumours in patients in vivo, featuring multiple types of malignancies. The proposed approach is based on a model of restricted, intra-cellular (IC) diffusion with negligible extra-cellular (EC) signal contributions, which is fitted to highly diffusion-weighted (DW) images. The model provides histologically-meaningful estimates of cell size and density, which are also shown to be associated to cell proliferation within liver tumours, as well as to the tumour size. These results suggest that our dMRI framework may provide histologically-relevant descriptors of tumour characteristics. These may complement standard-of-care readouts in research and clinical practice, equipping oncologists with new tools for precision oncology in hospital settings.

Methods

dMRI models

Common biophysical body dMRI signal models^{6,17,18,27,28,29} describe the signal as arising from three, non-exchanging proton pools: vascular water; restricted, intra-cellular water; hindered, extra-cellular, extra-vascular water. The dMRI signal for a PGSE measurement at b-value b, gradient duration/separation δ/ Δ, and echo time TE is

$$s={s}_{0}\left({f}_{V}{e}^{-\frac{{TE}}{T{2}_{V}}}{a}_{V}+\left(1-{f}_{V}\right)\left({f}_{I}{e}^{-\frac{{TE}}{T{2}_{I}}}{a}_{I}+\left(1-{f}_{I}\right){e}^{-\frac{{TE}}{T{2}_{E}}}{a}_{E}\right)\right).$$

(1)

Above, ${s}_{0}$ is the apparent proton density, ${f}_{V}$ is the voxel vascular signal fraction, ${f}_{I}$ is the tissue intra-cellular signal fraction, $T{2}_{V}$/$T{2}_{I}$/$T{2}_{E}$ and ${a}_{V}$/${a}_{I}$/${a}_{E}$ are compartment-wise T2 and diffusion-weighting factors. ${a}_{V}$ captures intra-voxel incoherent motion (IVIM) effects³⁰. In vivo, the IVIM vascular ADC ranges approximately³¹ in [15; 60] µm² ms^–1. For this reason, for b > 100  s/mm², the vascular signal vanishes (${a}_{V}\approx 0$), and Eq. (1) reduces to¹⁷

$$s={s}_{0}\left(1-{f}_{V}\right)\left({f}_{I}{e}^{-\frac{{TE}}{T{2}_{I}}}{a}_{I}+\left(1-{f}_{I}\right){e}^{-\frac{{TE}}{T{2}_{E}}}{a}_{E}\right)$$

(2)

A common model for ${a}_{I}$ in Eq. (2) is that of restricted diffusion within spheres of diameter L^17,18:

$${a}_{I}={e}^{-b{AD}{C}_{I}\left({{{\rm{\delta }}}},\Delta ,{D}_{0,I},L\right)}$$

(3)

where

$$ {AD}{C}_{I} = \frac{2}{{D}_{0,I}{\delta }^{2}\left(\Delta -\delta /3\right)}{\sum}_{m=1}^{\infty }\frac{{\alpha }_{m}^{-4}}{{\alpha }_{m}^{2}{R}^{2}-2} \\ \left(2\delta -\frac{2+{e}^{-{\alpha }_{m}^{2}{D}_{0,I}\left(\Delta -\delta \right)}-2{e}^{-{\alpha }_{m}^{2}{D}_{0,I}\delta }-2{e}^{-{\alpha }_{m}^{2}{D}_{0,I}\Delta }+{e}^{-{\alpha }_{m}^{2}{D}_{0,I}\left(\Delta +\delta \right)}}{{\alpha }_{m}^{2}{D}_{0,I}}\right)$$

(4)

is the Gaussian phase distribution approximation of the intra-cellular ADC³². Above, ${\alpha }_{m}$ is the m-th root of ${\alpha }_{m}R{J}_{\frac{3}{2}}^{{\prime} }\left({\alpha }_{m}R\right)-\frac{1}{2}{J}_{\frac{3}{2}}\left({\alpha }_{m}R\right)=0$, ${J}_{\frac{3}{2}}\left(x\right)$ is the Bessel function of the first kind and order 3/2, and ${J}_{\frac{3}{2}}^{{\prime} }\left(x\right)$ its first-order derivative (${J}_{\frac{3}{2}}^{{\prime} }\left(x\right)=\frac{d}{{dx}}{J}_{\frac{3}{2}}\left(x\right)$). ${AD}{C}_{I}$ depends on the intrinsic cytosol diffusivity ${D}_{0,I}$ and on the cell size $L=2R$ (R: radius; L: diameter). Noting that dMRI-derived L represents a volume-weighted mean cell size statistics^7,33, we will refer to it as volume-weighted cell size (${vCS}$).

Conversely, the extra-cellular, extra-vascular signal may be described in terms of hindered diffusion in a tortuous space^17,28,34:

$${a}_{E}\left(b,\Delta \right)={e}^{-{bAD}{C}_{E}\left(\Delta ,{D}_{E,\infty },\beta \right)}$$

(5)

with

$${AD}{C}_{E}\left(\Delta ,{D}_{E,\infty },\beta \right)={D}_{E,\infty }+\frac{\beta }{\Delta }$$

(6)

In Eq. (6), ${D}_{E,\infty }$ is the asymptotic²⁸ ${AD}{C}_{E}$ for Δ→∞.

The 5 implementations of the two-compartment model

We investigated 5 implementations of Eq. (2), divided into two families. The first family includes models that do not make assumptions on which of ${AD}{C}_{I}$/${AD}{C}_{E}$ is higher:

i. Diff-in-exTD: the most general model, relying on the full expression of ${AD}{C}_{E}$ in Eq. (6);

ii. Diff-in-ex: a simpler implementation of Diff-in-exTD that neglects extra-cellular diffusion time dependence (TD) (β = 0 in Eq. (6)).

In the second family of models, we constrain ${AD}{C}_{E} > {AD}{C}_{I}$. This family includes

• i. Diff-in-exTDFast: equivalent to Diff-in-exTD, with the lower bound for ${D}_{E,\infty }$ ensuring ${AD}{C}_{E} > {AD}{C}_{I}$ for any L.

• ii. Diff-in-exFast: equivalent to Diff-in-ex, but again ensuring that ${AD}{C}_{E} > {AD}{C}_{I}$ for any L.

• iii. Diff-in: a model where the extra-cellular signal is negligible compared to the intra-cellular one, due to ${AD}{C}_{E}$ being much larger than ${AD}{C}_{I}$, so that Eq. (2) simplifies to

$${{{\rm{s}}}}={s}_{0}\left(1-{f}_{V}\right){f}_{I}{e}^{-\frac{{TE}}{T{2}_{I}}}{a}_{I}\left(b,{{{\rm{\delta }}}},\Delta ,{D}_{0,I},L\right)$$

(7)

In all models we used $T{2}_{I}\approx T{2}_{E}\doteq T{2}_{T}$, given the challenge of resolving accurately multiple T2 constants^18,35.

Fitting

We fitted the 5 models using custom-written Python routines, based on objective function minimisation initialised by a grid search. The objective function was ${f}_{{obj}}=-{{\mathrm{ln}}}\left(\lambda \right)$, where λ is the offset-Gaussian likelihood³⁶. Fitting provides estimates of ${vCS}$ and voxel IC signal fraction

$$F=\left(1-{f}_{V}\right){f}_{I}$$

(8)

We also combined ${vCS}$ and F into a cell density per unit volume¹⁸

$${CD}=\frac{F}{{vC}{S}^{3}}$$

(9)

Mouse data acquisition

Animals

We obtained data from 7 fixed livers of NOD.Cg-Prkdc^scid IL2rg^tm1WjI/SzJ mice. These mice develop various liver pathologies when implanted with patient-derived tumour samples. They are routinely used in patient-derived xenograft studies, and represent an ideal setting to validate the performances of new MRI methods for liver imaging. All experimental protocols were approved and monitored by the Vall d’Hebron Institute of Research Animal Experimentation Ethics Committee (CEEA; registration number 68/20) in accordance with relevant local and EU regulations. Animals were housed at the specific pathogen-free barrier area of the Vall d’Hebron Institute of Oncology following established institutional procedures. A study protocol was defined internally at institutional level, with no registration in external platforms.

We studied six livers from mice implanted with cells derived from biopsies of prostate cancer patients, as part of an ongoing study, plus an additional liver from a mouse without any implantation. We implanted one tumour biopsy core with growth factor-enriched Matrigel (Corning) subcutaneously in the flank of each mice under isoflurane inhalant anaesthesia (3−4% for induction and 1–3% for maintenance). Mice were all males, and they were implanted when 6 weeks old. Author I.C.S. was aware of the status of the mice (implanted vs not-implanted). We derived tissue from the following biopsies: iliac bone metastasis biopsy (metastatic castration-resistant prostate cancer, presenting with bone metastasis and Gleason score 3 + 4 adenocarcinoma); prostate biopsy (patient with metastatic hormone-sensitive prostate cancer, presenting with bone metastasis and Gleason score 5 + 4 adenocarcinoma); two liver biopsies (patient with metastatic castration-resistant prostate cancer, presenting with bone and visceral metastasis and Gleason score 4 + 4 acinar adenocarcinoma; patient with metastatic hormone-sensitive prostate cancer, presenting with bone and liver metastasis and Gleason score 4 + 4 adenocarcinoma). After implantation, we measured tumour size using calipers and monitored mouse weight weekly, sacrificing animals by cervical dislocation under general anaesthesia (isoflurane inhalant, 3–4%) when tumour volume exceeded 2000 mm³, to reduce distress. No adverse events were observed in the N = 7 animals used in this study. We collected the livers, fixed them overnight in formalin, and transferred them to phosphate-buffered saline (PBS) solution.

MRI

We scanned livers on a 9.4 T Bruker Avance system at room temperature. Livers were tightened with sewing thread to a histology cassette and placed into a Falcon^® tube, filled with PBS solution. A 1-channel birdcage coil was used (excitation/reception). The protocol included a T2-weighted fast spin echo sequence (resolution: 144 μm × 144 μm × 2.216  mm) and PGSE dMRI (Supplementary Fig. S27; TR = 2700  ms; resolution: 386 μm × 386 μm; matrix size: 86 × 86; 4 slices, 2.216 mm thick, NEX = 1). The protocol featured: δ = 10  ms, ∆ = {15, 30} ms, 10 linearly spaced b-values for each ∆ (minimum/maximum nominal b: 0/2800 s/mm²). DW images corresponding to ∆ = 15  ms were acquired at TE = {31, 45, 65} ms, and images corresponding to ∆ = 30 ms were acquired at  TE = {45, 65} ms. We i) denoised dMRI scans with the Marchenko–Pastur Principal Component Analysis (MP-PCA) technique³⁷ (Python code; kernel: 7 × 7 × 3), ii) mitigated Gibbs ringing (MrTrix3 local sub-voxel shift method³⁸), and iii) corrected temporal signal drifts by assessing signal changes in a PBS solution region, accounting for TE changes (PBS T2: 500 ms).

Finally, we fitted the Diff-in-exTD, Diff-in-exTDFast, Diff-in-ex, Diff-in-exFast and Diff-in models voxel-by voxel (tissue parameter bounds: [0; 1] for ${f}_{I}$; [0.8; 2.6] μm² ms^–1 for ${D}_{0,I}$; [8; 40] µm for vCS; [0.8; 2.6] μm² ms^–1 for ${D}_{E,\infty }$ in models Diff-in-ex and Diff-in-exTD and [1.75; 2.6] μm² ms^–1 in models Diff-in-exFast and Diff-in-exTDFast; [0; 10] μm² for β in models Diff-in-ex-TD and Diff-in-exTDFast). For fitting, we fixed ${f}_{V}$ and $T{2}_{T}$ to values obtained through a a two-pool vascular-tissue model³⁹ (fitting bounds: [0; 1] for ${f}_{V}$; [5; 80] ms for $T{2}_{T}$). Fitting was performed i) on all images with b > 1000  s/mm² (suppressing vascular signals, referred to as fitting on whole image set); ii) on b > 1000  s/mm² images (high b-value fitting). In our ex vivo data, the vascular signal captures PBS solution contamination (PBS ADC: roughly 2.4 μm² ms^–1). For this reason, we adopted a b-value threshold of 1000 s/mm² to achieve acceptable PBS signal suppression. We used instead a minimum b-value of 1800 s/mm² for high b-value fitting (minimising extra-cellular contributions), given the reduction in intrinsic tissue diffusivity expected ex vivo.

For comparison, we computed ADC and apparent diffusion excess kurtosis K by fitting

$$s={s}_{0}{e}^{-{bADC}+\frac{1}{6}K{\left({bADC}\right)}^{2}}$$

(10)

to DW images acquired at TE = 45 ms, Δ = 30 ms, with in-house Python code.

Histology

After MRI, samples underwent histology. We cut two 4 μm-thick histological sections at known position, stained them with HE, and digitised them (Hamamatsu C9600-12 slide scanner; 0.227 μm resolution). An experienced pathologist (S.S.) inspected images qualitatively. We then processed them with the automatic cell detection tool of QuPath⁴⁰, obtaining per-cell area A and diameter $l=\sqrt{\frac{4}{{{{\rm{\pi }}}}}A}$. Afterwards, we split images into 386 μm × 386 μm patches (matching the MRI resolution), computing patch-wise histological volume-weighted cell size ${vC}{S}_{{histo}}$, intra-cellular area fraction ${F}_{{histo}}$ and cell density per unit area $C{D}_{{histo}}$³³. ${vC}{S}_{{histo}}$, defined as

$${vC}{S}_{{histo}}={\left(\frac{ < {l}^{7} > }{ < {l}^{3} > }\right)}^{\frac{1}{4}}$$

(11)

is a more accurate counterpart of dMRI cell size than the arithmetic mean^7,33 ${aC}{S}_{{histo}}= < l >$. We accounted for biases coming from: i) estimating the size of 3D objects from 2D views (bias 1), ii) tissue shrinkage (bias 2), by rescaling ${vC}{S}_{{histo}}$ and $C{D}_{{histo}}$. The final ${vC}{S}_{{histo}}$ estimate was 1.4616 times larger than the value obtained from direct image processing (1.4616 = 1.2732 × 1.148; 1.2732, derived from the theory of spherical caps, accounts for bias 1; 1.148 accounts for bias 2, and corresponds to a plausible shrinkage of 12.9% following dehydration, clearing and paraffin embedding⁴¹). The final $C{D}_{{histo}}$ estimate was 1.318 times smaller than the value derived from direct image processing, since 1 mm² of shrunk tissue corresponds to 1.148 × 1.148 mm² = 1.318 mm² of unprocessed tissue (plausible shrinkage 12.9%⁴¹). Lastly, we co-registered histological maps to MRI³³ using DiPy⁴².

Human data acquisition

Cohort

We obtained data from patients suffering from advanced solid tumours, recruited for an ongoing imaging study approved by the Vall d’Hebron University Hospital (VHUH) Ethics committee (PR(AG)29/2020). Patients provided informed written consent to participate in the imaging study. We included 38 patients with liver malignancies, either primary or metastatic, being screened as potentially eligible candidates for various phase I clinical trials at the VHUH. Patients were scanned with either a 1.5 T or 3 T system. Approximately one week after MRI, a biopsy from one of the imaged liver tumours was obtained from 18 patients. The histological material was stained for HE, and in 10 cases also through Ki67 IHC, demonstrating cell proliferation. The eligibility criteria to enter this imaging study were: to have liver malignancies of known origin, previously confirmed on a Computer Tomography scan (diameter >10 mm); to meet all standard institutional requirements for having an MRI scan. In those cases where a biopsy was also collected, all standard institutional, requirements for having a biopsy had also to be met.

MRI

We imaged patients at the level of the abdomen. We scanned 11 patients on a 1.5 T Siemens Avanto scanner using the vendor 18-channel body coil for detection, and 27 patients on a 3 T GE SIGNA Pioneer scanner, using the vendor 48-channel torso coil for signal reception, with 32 channels enabled for detection. The 1.5 T system was located at the Vall d’Hebron Hospital radiology department, whereas the 3 T at the CETIR Clinic of Barcelona. MRI scans were acquired between October 2020 and June 2023. No software or hardware upgrades were made to the MRI systems during the acquisition of the data. Note that in this study we do not employ any clinical outcome measure related to patient treatment or to the participation in clinical trials.

In the 1.5 T Siemens system, the protocol included a T2-weighted fast spin echo scan (resolution: 1.4 × 1.4 × 5 mm³; 32 slices; TR = 4500 ms; TE = 82 ms; echo train length: 29; NEX = 8; GRAPPA = 2) and fat-suppressed DW TRSE (Supplementary Fig. S27) EPI (dMRI scan time: 16 min). It featured: resolution: 1.9 × 1.9 × 6 mm³; 32 slices; TR = 7900 ms; bandwidth 1430 Hz/pixel; averaging of 3 orthogonal diffusion directions ×2 signal averages (effective NEX = 6); GRAPPA factor of 2; 6/8 partial Fourier imaging. The dMRI protocol consisted of b = {0, 50, 100, 400, 900, 1200, 1600} s/mm², each for TE = {93, 105, 120} ms. One additional image (b = 0 s/mm²; TE = 93 ms) was acquired with reversed phase encoding polarity. The gradient timings (Supplementary Fig. S27) were: δ₁ = 8.9 ms, δ₂ = 17.6 ms, δ₃ = 20.4 ms, δ₄ = 6.0 ms, ∆_1,2 = 17.4 ms and ∆_1,4 = 63.9 ms when TE = 93 ms; δ₁ = 13.2 ms, δ₂ = 19.3 ms, δ₃ = 24.8 ms, δ₄ = 7.7 ms, ∆_1,2 = 21.7 ms and ∆_1,4 = 74.2 ms when TE = 105 ms; δ₁ = 18.9 ms, δ₂ = 21.0 ms, δ₃ = 30.5 ms, δ₄ = 9.5 ms, ∆_1,2 = 27.5 ms and ∆_1,4 = 87.5 ms when TE = 120 ms. The b-value is

$$b =\, {{{{\rm{\gamma }}}}}^{2}{G}^{2}\left({{{{\rm{\delta }}}}}_{1}^{2}\left({\Delta }_{1,2}-{{{{\rm{\delta }}}}}_{1}\right)+\frac{2}{3}{\left({{{{\rm{\delta }}}}}_{1}+{{{{\rm{\delta }}}}}_{2}\right)}^{3} \right.\\ \left.+ {\left({{{{\rm{\delta }}}}}_{1}+{{{{\rm{\delta }}}}}_{2}-{{{{\rm{\delta }}}}}_{3}\right)}^{2}\left({\Delta }_{1,4}-{\Delta }_{1,2}-{{{{\rm{\delta }}}}}_{2}-{{{{\rm{\delta }}}}}_{3}\right)\right)$$

(12)

Converely, the protocol implemented on the 3 T GE scanner included a respiratory-gated T2-weighted fast spin echo scan (resolution: 1.4 × 1.4 × 6 mm³; 32 slices; TR = 4615  ms; TE = 52.86  ms; echo train length: 16) and respiratory-gated, fat-suppressed PGSE (Supplementary Fig. S27) EPI (dMRI scan time: 16  minutes). It featured: resolution: 2.4 × 2.4 × 6 mm³; 32 slices; TR = 6000 ms; bandwidth 1953 Hz/pixel; averaging of 3 orthogonal diffusion directions ×2 signal averages (effective NEX = 6); ASSET factor of 2. The dMRI protocol consisted of b = {0, 50, 100, 400, 900, 1200, 1500} s/mm², each for TE = {75, 90, 105} ms. The gradient timings (Supplementary Fig. S27) were: gradient duration δ = {0.0, 3.9, 5.2, 9.2, 15.0, 18.2, 21.0} ms for TE = 75 ms, δ = {0.0, 3.9, 5.2, 9.2, 13.0, 15.8, 18.5} ms for TE = 90 ms and 105 ms; gradient separation ∆ = {0.0, 27.8, 29.0, 33.0, 28.7, 31.8, 34.7} ms for TE = 75 ms and ∆ = {0.0, 27.8, 29.0, 33.0, 37.0, 39.6, 42.3} ms for TE = 90 ms and TE = 105 ms.

dMRI post-processing consisted of slice-wise Python MP-PCA denoising (kernel: 5 × 5)³⁷; MRTrix3 Gibbs unringing³⁸; motion correction via affine co-registration⁴³; FSL distortion correction⁴⁴ (1.5 T data only). An experienced radiologists (R.P.L.) segmented tumours on the T2-w scan, enabling per-patient tumour volume computation. Afterwards, we warped the tumour mask to dMRI using ANTs⁴⁵ non-linear co-registration. Two researchers independently reviewed the co-registered masks, and manually edited them to correct for registration inaccuracies (F.G. and K.B.). Lastly, we fitted the 5 dMRI models, fixing again ${f}_{V}$ and $T{2}_{T}$ to previously computed values³⁹ (fitting bounds: [0; 1] for ${f}_{V}$; [20; 140] ms for $T{2}_{T}$; [0; 1] for ${f}_{I}$; [0.8; 3.0] μm² ms^–1 for ${D}_{0,I}$; [8; 40] µm for vCS; [0.8; 3.0] μm² ms^–1 for ${D}_{E,\infty }$ in models Diff-in-ex and Diff-in-exTD, and [1.75; 3.0] μm² ms^–1 in models Diff-in-exFast and Diff-in-exTDFast; [0; 10] μm² for β in models Diff-in-ex-TD and Diff-in-exTDFast).

We fitted the 5 dMRI models i) on images acquired at a b-value b > 100 s/mm², to suppress vascular signals (fitting to the whole image set); ii) to b > 900 s/mm² images, to also minimize extra-cellular contributions (high b-value fitting). For scans performed on the 1.5 T Siemens system: i) we used Δ_1,2 + δ₂ in place of Δ in Eq. (6) (Supplementary Fig. S27), ii) we replaced Eq. (4) with a numerical implementation of restricted diffusion within spheres, based on Radial Basis Function interpolation of synthetic signals generated for DW-TRSE with Monte Carlo simulations⁴⁶.

For both scanners, we also computed ADC and excess kurtosis K by fitting Eq. (10) on b > 100 s/mm² images (shortest TE), with in-house Python code.

Histology

We performed ultrasound-guided biopsies of one liver tumour at the Barcelona Vall d’Hebron University Hospital (Spain). Biopsies were obtained approximately one week after dMRI. In two patients, the biopsy was obtained after receiving immunotherapy as part of a phase I trial. In those two cases, an additional dMRI scan was also acquired after starting treatment, immediately before the biopsy. The biological material underwent standard processing, HE staining and Ki67 IHC, and final digitalisation on a Hamamatsu C9600-12 slide scanner (resolution: 0.454 μm). An experienced pathologist (S.S.) assessed the images and drew a region-of-interest (ROI) outlining tumour tissue and excluding non-tumour meterial. In parallel, an experienced radiologist (R.P.L.) inspected ultrasound and MR images, outlining the biopsied tumour on the latter. We processed HE data with QuPath and computed per-biopsy ${vC}{S}_{{histo}}$, ${F}_{{histo}}$ and $C{D}_{{histo}}$ as previously described. Additionally, we also computed the fraction of tumour labelled for Ki67 (referred to as ${F}_{{Ki}67}$) with in-house routines, in those cases where Ki67 IHC was available (IHC images acquired with the same Hamamatsu scanner used for HE). ${vC}{S}_{{histo}}$ and $C{D}_{{histo}}$ were rescaled to account for tissue shrinkage. ${vC}{S}_{{histo}}$ was multiplied by 1.503, where 1.503 = 1.1806 × 1.2732 accounts for two scaling factors, namely: i) 1.2732 accounts for cell size underestimation due to 2D sectioning, ii) 1.1806 accounts for a plausible tissue shrinkage of 15.3% following fixation, dehydration, clearing and paraffin embedding⁴¹. The final $C{D}_{{histo}}$ estimate was instead 1.3938 times smaller than the value derived from direct image processing, since 1 mm² of shrunk tissue corresponds to 1.1806 × 1.1806 mm² = 1.3938 mm² of unprocessed tissue for a shrinkage factor of 15.3%⁴¹.

Analyses

dMRI model selection

We carried out model selection independently for each of the two fitting strategies. The MRI-histology Total Correlation Score (TCS) selects the model providing the highest Pearson’s correlation between ${vC}{S}_{{MRI}}$ and ${vC}{S}_{{histo}}$, and between ${F}_{{MRI}}$ and ${F}_{{histo}}$. It is defined as

$${{{\rm{TCS}}}}=r\left({vC}{S}_{{MRI}},{vC}{S}_{{histo}}\right)+r\left({F}_{{MRI}},{F}_{{histo}}\right)$$

(13)

where $r\left({vC}{S}_{{MRI}},{vC}{S}_{{histo}}\right)$ and $r\left({F}_{{MRI}},{F}_{{histo}}\right)$ are the correlation coefficients of ${vC}{S}_{{MRI}}$ and ${F}_{{MRI}}$ with histological ${vC}{S}_{{histo}}$ and ${F}_{{histo}}$. The correlation between $C{D}_{{MRI}}$ and $C{D}_{{histo}}$ was not included in Eq. (13) since $C{D}_{{MRI}}$ is determined analytically from ${vC}{S}_{{MRI}}$ and ${F}_{{MRI}}$. For TCS computation, we pooled together mouse and human data (N = 25, including the two cases who had their biopsy collected after starting treatment, namely immunotherapy).

We remark that the main objective of the study is to use histological information to inform MRI signal model design, through MRI-histology correlation analyses. A sample size of N = 25 provides approximately 50% power to detect a Pearson’s correlation of |r| = 0.4 (moderate correlation) at a significance level α = 0.05. Our study size enables the detection of even moderate correlation at a conservative significance level, and was considered appropriate to inform MRI signal modelling. Nonetheless, we also point out that our sample size increases the risk of Type II vs Type I errors, given the statistical power of 50%. In practical terms, this implies that a true correlation of |r| = 0.4 is roughly 10 times more likely to be missed (false negative) than a false correlation of |r| = 0.4 detected (false positive).

We also performed model selection using a Histology Fidelity Criterion (HFC), and popular Bayesian Information Criterion (BIC)^36,47. HFC rewards the models providing the best accuracy in the numerical estimation of histological cell size and intra-cellular fraction estimation, i.e., minimising

$${HFC}=\frac{\left|{vC}{S}_{{MRI}}-{vC}{S}_{{histo}}\right|}{{vC}{S}_{{histo}}}+\frac{\left|{F}_{{MRI}}-{F}_{{histo}}\right|}{{F}_{{histo}}}$$

(14)

Information on $C{D}_{{MRI}}$ and $C{D}_{{histo}}$ was not included in Eq. (14) since $C{D}_{{MRI}}$ is not a degree of freedom of the dMRI models (it is determined analytically from ${vC}{S}_{{MRI}}$ and ${F}_{{MRI}}$). BIC selects the model providing the best goodness of fit, penalising complexity, by minimising

$${BIC}=P{{\mathrm{ln}}}\left(N\right)-{{\mathrm{ln}}}\left({{{\rm{\lambda }}}}\right)$$

(15)

λ is the maximised likelihood, and P/N are the number of model parameters/signal measurements. We performed BIC selection voxel-wise, followed by majority voting across voxels.

Analysis of the fitting residuals

For each voxel, fitting strategy and dMRI model, we calculated the fitting residuals as ${s}_{{fit}}-{s}_{{measured}}$, where ${s}_{{measured}}$ is the measured dMRI signal and ${s}_{{fit}}$ the signal predicted by the model at the corresponding b-values/diffusion time. Measured signals were normalised according to Eq. (7), removing relaxation effects due to changes in TE, and signal predictions were bounded between 0 and 1 (dMRI signal decay with respect to the b = 0 signal). For each b-value, diffusion time and fitting strategy, we visualised distributions across all voxels (median and interquartile range), and also scattered ${s}_{{fit}}-{s}_{{measured}}$ against ${s}_{{measured}}$.

Simulated dMRI model selection

We validated results from MRI and histology data through computer simulations. For this experiment, we synthesised signals for each of the three dMRI protocols considered in the study (ex vivo PGSE; in vivo PGSE; in vivo TRSE), fitted the 5 candidate dMRI models, and performed model selection using TCS, HFC and BIC. dMRI signals were synthesised through Monte Carlo simulations, which we performed using code from the freely available MCDC simulator⁴⁶ (https://github.com/jonhrafe/MCDC_Simulator_public). We seeded walkers in a substrate made of spherical cells of identical diameter^6,17,20,21 (Supplementary Fig. S17), controlling the intra-sphere fraction F by adding gaps of increasing size in-between abutting spheres, packed in an ideal cubic lattice. We probed four F values (0.197, 0.323, 0.406, 0.523) and four sphere diameters ${vCS}$ for each F (8, 16, 22 and 30 µm). We varied intra-/extra-sphere diffusivities (10 × 10 values; [0.8; 2.6] µm² ms^–1 for the ex vivo protocol and [0.8; 3.0] µm² ms^–1 for in vivo protocols), for a total of 1600 synthetic voxels. Signals for each synthetic voxel, featuring a unique combination of IC/EC diffusivities ${D}_{0,I}$/${D}_{0,E}$, cell diameter ${vCS}$ and IC fraction F, were generated for 3 levels of trans-cell water permeability, namely: k = 10 µm  s^–1 (low permeability); k = 25 µm  s^–1 (intermediate permeability); k = 50 µm  s^–1 (high permeability)¹⁹. We corrupted synthetic signals with Rician noise (b = 0 signal-to-noise ratio: 30), and performed model selection according to TCS, HFC and BIC.

To gauge an understanding of the diffusion times for which modelling trans-membrane water exchange becomes relevant, we also studied the random walks of spins seeded in the IC space, and derived their corresponding instantaneous apparent diffusion coefficients ${{ADC}}_{I}\left(t\right)=\frac{\left\langle \Delta {x}^{2}\left(t\right)+\Delta {y}^{2}\left(t\right)+\Delta {z}^{2}(t)\right\rangle }{6t}$ as a function of time t, given spin positions ${{{\bf{p}}}}\left(t\right)=(x\left(t\right),y\left(t\right),z(t))$, and having defined $\Delta x\left(t\right)=x\left(t\right)-x(0)$, $\Delta y\left(t\right)=y\left(t\right)-y(0)$ and $\Delta z\left(t\right)=z\left(t\right)-z(0)$, where ${{{\bf{p}}}}\left(0\right)$ is the initial spin position.

dMRI-histology correlation

We computed mean and standard deviation of all metrics i) within the mouse liver samples, ii) within a mask containing all liver tumours in patients, iii) within the biopsied patients’ tumours. We pooled together metrics from mice and patients to calculate Pearson’s correlation coefficients r, as described above. ADC was normalised to the ADC of the PBS solutions in mice and to the free water diffusivity in patients (3.0 μm² ms^–1 at 37 °C), given the difference in temperature. The correlation analysis aims to test whether MRI metrics ${F}_{{MRI}}$, ${{vCS}}_{{MRI}}$ and ${{CD}}_{{MRI}}$ are capable of detecting and replicating the contrasts seen across tumours/samples in ${F}_{{histo}}$, ${{vCS}}_{{histo}}$ and ${{CD}}_{{histo}}$, which originate from a variety of histopathological processes, e.g., necrosis, fibrosis, oedema, or presence of active cancer.

Additionally, we also fitted linear regression models for dMRI metrics ${F}_{{MRI}}$, ${{vCS}}_{{MRI}}$ and ${{CD}}_{{MRI}}$ from the selected dMRI approach. These test the specificity of these metrics towards their direct histological counterparts metrics ${F}_{{histo}}$, ${{vCS}}_{{histo}}$ and ${{CD}}_{{histo}}$. Models were:

$$\left\{\begin{array}{c}{{vCS}}_{{MRI}}={\beta }_{0}+{\beta }_{1}{{vCS}}_{{histo}}+{\beta }_{1}{F}_{{histo}}\hfill\\ {F}_{{MRI}}={\beta }_{0}+{\beta }_{1}{F}_{{histo}}+{\beta }_{2}{{vCS}}_{{histo}}\hfill\\ {{CD}}_{{MRI}}={\beta }_{0}+{\beta }_{1}{{CD}}_{{histo}}+{\beta }_{2}{F}_{{histo}}+{\beta }_{3}{{vCS}}_{{histo}}\end{array}\right.$$

(16)

The models allow us to test whether: (i) the association between ${{vCS}}_{{MRI}}$ and ${{vCS}}_{{histo}}$ is confounded by ${F}_{{histo}}$; (ii) the association between ${F}_{{MRI}}$ and ${F}_{{histo}}$ is confounded by ${{vCS}}_{{histo}}$; (iii) the association between ${{CD}}_{{MRI}}$ and ${{CD}}_{{histo}}$ is confounded by either ${F}_{{histo}}$ or ${{vCS}}_{{histo}}$. Metrics were standardised as z-scores before regression, to ensure comparability of the β coefficients. Fitting was performed in python with statsmodels⁴⁸ (https://www.statsmodels.org).

Association with immunohistochemical markers of cell proliferation

We assessed the association between ${F}_{{Ki}67}$, an IHC index assessing the fraction of biopsied tissue stained for Ki67 and demonstrating cell proliferation, with dMRI and HE-derived histological properties. For this purpose, we calculated the Pearson’s correlation coefficient between ${F}_{{Ki}67}$ and all dMRI and HE-derived metrics. We excluded two cases whose biopsies were obtained after having started receiving immunotherapy as part of a phase I trial (so N = 10).

Association with liver tumour phenotype

Finally, we tested whether metrics from the proposed dMRI approach contribute to explaining the macroscopic tumour phenotype. To this end, we studied the association between dMRI metrics and tumour volume, and compared their values, alongside histological metrics and patients’ age, between CRC and melanoma liver metastases through t-tests. Both tumour volume assessment and CRC-melanoma comparison were performed also for histological metrics, excluding two cases who had entered an immunotherapy phase I trial, and whose biopsy was obtained after receiving treatment (HE and MRI metrics excluded).

Regarding the tumour volume assessment, we computed Pearson’s correlation coefficients between mean values of dMRI metrics within each individual liver tumour and the tumour volume (N = 140 liver tumours from 38 patients; 137 metastases, 3 primary cancers). Moreover, we performed experiments in which we attempted to predict liver tumour volume given per-tumour mean values of dMRI metrics. Following a standard 5-fold cross validation design, we split the set of tumours into training and test sets. Afterwards, we used the training set to fit linear statistical models of the form

$${\log }_{10}\left({TV}\right)={\beta }_{0}+{\sum}_{n=1}^{3} {\sum}_{k=n-1}^{n}{\beta }_{k,n}{x}^{k}{y}^{3-n}$$

(17)

Above, TV is the tumour volume in mm³, modelled as a 3^rd order polynomial function of x and y, which is linear in the (unknown) β coefficients of the polynomial terms. x and y in Eq. (16) represent in turn different pairs of dMRI metrics, as for example DKI ADC and K, or pairs of metrics from the Diff-in model (we tested explicitly ${vC}{S}_{{MRI}}$ and ${F}_{{MRI}}$; ${D}_{0,I}$ and ${F}_{{MRI}}$; and ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$). Afterwards, we deployed the trained statistical models on the test data, calculating the Pearon’s correlation coefficient between ground truth and predicted ${\log }_{10}\left({TV}\right)$ values, pooling together predictions from all 5 cross-validation folds. Note that the log₁₀ of the volume was studied instead of the volume itself, since the latter spans almost 4 orders of magnitude in our data set, and is therefore difficult to handle numerically.

Regarding the CRC-melanoma comparison instead, we harmonised dMRI metrics across scanners with a custom-written ComBat⁴⁹ implementation, rescaling metrics obtained on the 1.5 T system to the 3 T range. This was done before performing the CRC-melanoma comparions to account for the fact that CRC scanned almost entirely with just one MRI system.

Statistics and reproducibility

The following statistical analyses were performed. (i) Evaluation of correlations between MRI and histology data. This test was based on a sample size of N = 25 paired MRI-histological data points with a significance level of 0.05 (two-sided Pearson’s correlation). P-values were unadjusted for multiple comparisons. Additional correlations models were also fitted accounting for the confounding effect that other MRI metrics can have in the correlation between each MRI index and its direct histological pair. These were based on linear regression models on the same sample. P-values were also unadjusted for multiple comparisons. (ii) Evaluation of correlations between synthetic MRI signals and simulated histological properties. This test was based on a sample size of N = 1600 synthetic tissue environments with a significance level of 0.05 (two-sided Pearson’s correlation). P-values were unadjusted for multiple comparisons. (iii) Evaluation of the correlation between MRI metrics and histological Ki-67 stains, visualising cell proliferation. This test was based on a sample size of N = 10 paired MRI-histology data points with a significance level of 0.05 (two-sided Pearson’s correlation). P-values were unadjusted for multiple comparisons. (iv) Tumour volume prediction from mean tumour-wise MRI metrics. This analysis was based on the analysis of N = 140 tumours from N = 38 patients. Tumour volume was predicted through logistic regression in 5-fold cross-validation. Predicted and ground truth tumour volumes were correlated through two-sided Pearson’s correlation tests (sample size N = 140). P-values were unadjusted for multiple comparisons. (v) MRI and histological metric comparison between CRC and melanoma cases. This analysis relied on a cohort of N = 13 CRC and N = 8 melanoma cases for MRI metrics; N = 6 CRC and N = 4 melanoma cases for histological HE metrics; N = 4 CRC and N = 2 melanoma cases for Ki-67 immunostain fraction. The between-group comparison was based on two-sided t-tests. P-values were unadjusted for multiple comparisons. No imputation methods were used in any of the analyses above in case of missing data (sample sizes already report the exact number of data points available).

We carried out all our analyses in python 3.12.2 (Anaconda distribution), using the following third-party packages: scipy version 1.13.1; pandas version 2.2.2; numpy version 1.26.4; matplotlib version 3.9.2; seaborn version 0.13.2; scikit-learn version 1.5.2; statsmodels version 0.14.4. The python scripts written to perform the analyses reported in the main manuscript have been included as supplementary data. Supplementary Data S6 performs MRI-histology correlation analysis and model selection (analysis (i) above); Supplementary Data S7 relates MRI metrics to Ki-67 cell proliferation immunostains (analysis (iii) above); Supplementary Data S8 evaluates the association with tumour volume (analysis (iv) above); Supplementary Data S9 compares MRI and histology metrics across CRC and melanoma groups (analysis (v) above).

Ethics

All experimental protocols in animals and PDX generation were approved and monitored by the Vall d’Hebron Institute of Research Animal Experimentation Ethics Committee (CEEA; registration number 68/20 and 70/20) in accordance with relevant local and EU regulations. The imaging study and sampe collection from cancer patients for histopathology as well as PDX generation were approved by the Vall d’Hebron University Hospital Ethics committee (PR(AG)29/2020, PR(AG)5248), Barcelona, Spain. Patients provided informed written consent to participate in the PDX study and in the imaging study.

Results

Overview: mouse and human data for histology-informed dMRI signal modelling

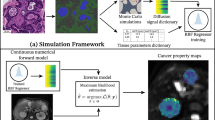
We designed and demonstrated our dMRI approach using data obtained from fixed mouse livers (mouse data) and from cancer patients in vivo (human data) (Fig. 1). Mouse data consist of pulsed gradient spin echo (PGSE) DW MRI scans of seven fixed mouse livers, performed ex vivo on a 9.4 T Bruker system. It also includes whole-organ HE-stained sections, obtained at known radiographic position. We obtained livers of mice sacrificed as part of ongoing xenograft model development studies in prostate cancer. Six had been implanted with biopsies of prostate cancer patients, while one had not had any implantation. While the livers from the implanted mice did not grow any tumours, they feature a variety of pathologies, with three unique histopathological phenotypes (Supplementary Fig. S1). The liver from the mouse with no implantation features normal liver structures, and we will refer to it as Control. Of the six implanted cases, two also show normal liver tissue, with normal representation of all hepatic structures. We will refer to these cases as Pat_NA1 and Pat_NA2 (patient biopsy implantation, but normal appearing). Another case exhibits generalised necrosis and diffuse acute and chronic inflammation surrounding necrotic areas, with presence of occluded thrombotic vessels. This specimen will be identified as Pat_nec (patient biopsy implantation, with necrosis). Finally, three specimens feature an immature, lymphoproliferative process, with various degrees of infiltration of small, lymphoid, atypical cells with abundant mitosis, which infiltrate portal vessels and sinusoidal capillaries, but without producing tumours. These will be referred to as Pat_inf1 to Pat_inf3 (patient biopsy implantation, with lymphoid cell infiltration).

Fig. 1: Illustration of the liver MRI and histology data used in the study.

Our data set consisted of preclinical mouse data and clinical human data. The mouse data encompass dMRI scans of seven fixed livers from mice (six implanted with tissue from biopsies of patients suffering from prostate cancer (PC); one without any implantation). We scanned the livers ex vivo on a 9.4 T system, and obtained HE histological sections at known position. The clinical data include in vivo liver dMRI scans performed on 38 patients suffering from advanced liver tumours. Scans were performed on clinical 1.5 T and 3 T MRI systems, and a HE-stained biopsy from one of the images tumours was collected after MRI in 18 cases. In 10 out of these 18, Ki67 immunohistochemsitry (IHC), demonstrating cell proliferation, was available beyond routine HE. In the figure, PC stands for prostate cancer; HCC for hepatocellular carcinoma; IHC for immunohistochemsitry.

We obtained human data on cancer patients suffering from advanced solid tumours, participating in an imaging study at the Barcelona Vall d’Hebron Institute of Oncology (VHIO, Spain), before being enrolled in a number of clinical trials. We included data from 38 patients with liver malignancies (mean/standard deviation (SD) of age: 61.88/11.90 years; median/inter-quartile range (IQR) of age: 62.8/14.7 years; 19 male, 19 female), of which 3 suffered from primary hepatocellular carcinoma (HCC), while 35 had liver metastases from different primary cancers (10 colon, 8 melanoma, 4 breast, 4 gastric, 3 rectal, 2 ovarian, 1 renal, 1 endometrial, 1 ureteral, 1 thyroidal). dMRI was based on diffusion-weighted (DW) echo planar imaging (EPI). We also obtained digitised HE-stained biopsies from one of imaged liver tumours approximately one week after MRI in 18 cases (mean/SD of age: 61.1/12.0 years; median/IQR of age: 62.1/14.4 years; 8 male, 10 female). Of these 18 patients, 2 suffered from primary HCC, while 16 had liver metastases (5 from colon cancer, 4 from melanoma, 3 from rectal cancer, 2 from ovarian cancer, 1 from breast and endometrial cancer). In 10 cases, Ki67 imunnohistochemsitry (IHC), demonstrating cell proliferation, was also available beyond routine HE stains.

Overview: dMRI signal models for cell size and density measurement

We studied five biophysical dMRI models, grouped into two families (Fig. 2A). All models describe the dMRI signal as originating from a combination of IC and EC contributions^6,17,20, making different assumptions. The first family, which is more general, includes:

• 1. Diff-in-exTD: a model accounting for restricted IC diffusion within spherical cells⁶, and hindered diffusion in the EC space, with diffusion time dependence³⁴ in both IC and EC signals⁵⁰. The diffusion time quantifies the time during which water molecules can sense cellular barriers, before the MR signal is measured.

• 2. Diff-in-ex: similar to model Diff-in-exTD, but neglecting diffusion time dependence in the EC space. Popular body dMRI techniques such as IMPULSED¹⁷ or VERDICT¹⁸ are essentially implementations of this model.

Fig. 2: Description of the dMRI signal models and study overview.

A Top: cartoon illustrating the two families of dMRI models considered in this study, consisting of 1) models with no assumption of which of intra/extra-cellular ADC is higher, and 2) models where the extra-cellular ADC is hypothesised to be higher than the intra-cellular ADC. B Bottom: study overview. We analysed dMRI data from fixed mouse livers and from cancer patients imaged in vivo to derive estimates of intra-cellular fraction and of cell size. In parallel, we processed histological material from the same tissues (whole-liver sections for the preclinical mouse data; biopsies from one of the imaged tumours for the clinical data), and derived the histological counterparts of such dMRI metrics. We compared dMRI and histological cell size and intra-cellular fraction to select the dMRI model featuring the best fidelity to histology. In Fig. 2, pictures from Servier Medical Art have been used. Image(s) provided by Servier Medical Art (https://smart.servier.com), licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Conversely, the second family explicitly assumes that the EC apparent diffusion coefficient (ADC) is higher in the EC than in the IC space, i.e., that ${AD}{C}_{E} > {AD}{C}_{I}$, and assumption used in certain body dMRI techniques⁵¹. This family includes:

• i. Diff-in-exTDFast: equivalent to Diff-in-exTD, but ensuring that ${AD}{C}_{E} > {AD}{C}_{I}$.

• ii. Diff-in-exFast: equivalent to Diff-in-ex, but ensuring that ${AD}{C}_{E} > {AD}{C}_{I}$.

• iii. Diff-in: a model where it is hypothesised that the EC extra-cellular signal is negligible with respect to the IC one due to its much larger ADC.

All models enable the estimation of volume-weighted mean cell size (CS) (${vC}{S}_{{MRI}}$, expressed in µm) and IC signal fraction (${F}_{{MRI}}$, dimensionless). These can be combined into an apparent cell density per unit volume ($C{D}_{{MRI}}={F}_{{MRI}}/{vC}{S}_{{MRI}}^{3}$, expressed in cell/mm³)¹⁸. All models were fitted twice: to the complete set of images, or to highly diffusion-weighted (DW) images only (i.e., to high b-values), to minimse signal contributions from the EC space. For comparison, we also considered routine ADC (in µm²/ms) and apparent diffusion excess kurtosis K (dimensionless) from diffusion kurtosis imaging (DKI)⁵², since these are popular dMRI indices sensitive to cancer cellularity and easy to compute from short acquisitions^18,53.

We processed HE-stained histological data with automatic cell detection⁴⁰ to derive histological counterparts of the dMRI metric. The two were compared to inform the design of a dMRI signal model maximising radiological-histological correlations (Fig. 2B). The histological metrics were: histological volume-weighted mean cell size (${vC}{S}_{{histo}}$, in µm), histological intra-cellular area fraction (${F}_{{histo}}$, dimensionless), and histological cell density per unit area ($C{D}_{{histo}}$, in cell/mm²). In patients for which Ki-67 ICH was available, the fraction of histological material stained for Ki-67 within the biopsy was also computed through custom routines (metric ${F}_{{Ki}67}$).

Supplementary Data S1 contains a CSV file with the MRI and histology data used for model selection, while Supplementary Data S2 contains a CSV file with MRI and histology data for model selection based on high b-value images only. Supplementary Data S3 contains a CSV file with MRI and histology metrics for each individual tumour. Additionally, Supplementary Data S4 and Supplementary Data S5 contain a CSV file with cohort information and the histological and mean MRI metrics across all tumour voxels (inter-scanner harmonisation performed in Supplementary Data S5).

A model of restricted intra-cellular diffusion with negligible extra-cellular contributions maximises radiological-histological correlations

We compared dMRI models through an MRI-Histology Total Correlation Score (TCS). TCS measures the overall correlation between histological and radiological readouts of cell size and intra-cellular fraction, and is obtained by summing Pearson’s correlation coefficients between MRI and histological cell size and IC fraction (i.e., ${vC}{S}_{{MRI}}$ and ${vC}{S}_{{histo}}$, and ${F}_{{MRI}}$ and ${F}_{{histo}}$). Negative correlations are penalised, since the model providing the highest TCS should be preferred. TCS values unequivocally suggest that models where the IC ADC is constrained to be smaller than the EC ADC provide higher correlations with histology. Among all dMRI implementations, fitting a model of IC restricted diffusion with negigilble EC signal contributions to highly DW images (referred to as model Diff-in) provides the highest TCS values, and hence the highest correlation to histological readouts (Fig. 3). Figure 3A summarises the different dMRI models, while Fig. 3B, C reports actual TCS values. In the figure, models where ${AD}{C}_{E} > {AD}{C}_{I}$, shown in violet shades, provide consistently higher TCS values than models that do not make such an assumption (orange shades), with the highest TCS observed for model Diff-in fitted to highly DW images.

Fig. 3: Biophysical dMRI signal model selection based on the MRI-histology Total Correlation Score (TCS).

A Panel summarising the salient differences between the biophysical dMRI models compared in this study. Models can be divided in two families, i.e.: i) models where it is hypothesised that the extra-cellular ADC is higher than the intra-cellular ADC, and ii) models with no hypothesis on which, between intra-/extra-cellular ADC is higher. Violet shades are used for the first family (models Diff-in, Diff-in-exFast and Diff-in-exTDFast), while orange shades for the second family (models Diff-in-ex and Diff-in-exTD). B Values of TCS for all models, as obtained by fitting them on the whole set of images featuring negligible vascular signal contribution (b > 1000 s/mm² in the fixed mouse livers; b > 100 s/mm² in vivo). C TCS values for all models when these are fitted only on high b-value images (b > 1800 s/mm² in the fixed mouse livers; b > 900 s/mm² in vivo). TCS was computed using a sample size of N = 25 MRI-histology data points. In this figure, pictures from Servier Medical Art have been used. Image(s) provided by Servier Medical Art (https://smart.servier.com), licensed under CC BY 4.0 (https://creativecommons.org/licenses/by/4.0/).

Additional model selection criteria used to compare dMRI models confirm findings from TCS-based model selection. The additional criteria were: an Histology Fidelity Criterion (HFC), measuring the sum of absolute errors in $F$ and ${vCS}$ estimation via dMRI, compared to histology; and the Bayesian Information Criterion (BIC)⁴⁷. BIC is a common criterion for dMRI model selection^36,54: it quantifies the model fitting quality, penalising model complexity. Note that model performance increases as both HFC and BIC decrease. Supplementary Fig. S2 reports the number of times, in percentage terms, that a model provides the lowest HFC and BIC across our N = 25 MRI-histology cases. TCS ranking is confiremd: models hypothesising ${AD}{C}_{E} > {AD}{C}_{I}$ are selected more frequently than models that do not do, according to HFC. The model Diff-in is the most selected model according to both BIC and HFC (Supplementary Fig. S3B; fitting to high b-value images). Supplementary Fig. S3 splits HFC and BIC rankings depending on the MRI scanner. In all cases, models with ${AD}{C}_{E} > {AD}{C}_{I}$ (Diff-in, Diff-in-exFast, Diff-in-exFastTD) are selected more frequently than models Diff-in-ex and Diff-in-ex-TD. When fitting is performed only on high b-value images, Diff-in is the most selected model according to both BIC and HFC.

Supplemetnary Figs. S4–S10 show examples of signal model fitting to dMRI measurements obtained from exemplificatory voxels. Supplementary Figs. S4–S6 refer to ex vivo mouse data (examples of voxels from the three main histological phenotypes); Supplementary Figs. S7–S10 refer instead to in vivo cancer patient (active tumour, necrosis, and other tumour regions-of-interest, from both 3 T and 1.5 T systems). On visual inspection, all models capture the main trends of the signal as a function of the b-value and of the diffusion time, e.g., low diffusion attenuation in highly cellular areas; high diffusion attenuation in necrosis; increasing dMRI signal for increasing diffusion time.

The analysis of fitting residuals reveals differences among dMRI models

We also studied fitting residuals as a function of the acquisition parameters, as patterns in the distribution of the residual can provide insight onto the features of the signal that are best – or worst – estimated by a model. Supplementary Figs. S11–S13 show median and interquartile of residual (i.e., signal predicted by a dMRI model, minus the measured signal) distributions as a function of the b-value and of the diffusion time, for both fitting strategies (Supplementary Fig. S11: distributions across ex vivo mouse tissue voxels; Supplementary Fig. S12: distributions across in vivo cancer patients voxels, 3 T scans; Supplementary Fig. S13: distributions across in vivo cancer patients voxels, 1.5 T scans). In general, all models tend to overestimate the signal at longer diffusion times, compared to shorter diffusion times acquired at the same b-value. This is potentially compatible with the fact that as the diffusion time increases, the measured signal becomes more sensitivie to IC/EC water exchange – a biological phenomenon not considered by our models, and leading to an increase in apparent diffusivities (and hence, to stronger signal decay) compared to ideal diffusion restriction¹⁹. The underestimation of the signal is more apparent for models that assume faster EC diffusion, i.e., Diff-in, Diff-in-exFast and Diff-in-exTDFast, compared to the models that do not make assumptions on which is faster between IC and EC diffusion.

These trends are confirmed by voxel-wise scatter plots in Supplementary Figs. S14–S16, in which residuals are scattered against the corresponding measured dMRI signals (Supplementary Fig. S14: ex vivo mouse tissue voxels; Supplementary Fig. S15: in vivo cancer patients voxels, 3 T scans; Supplementary Fig. S16: in vivo cancer patients voxels, 1.5 T scans). Another important aspects revelead by all plots in Supplementary Figs. S11–S16 is that, for a given dMRI measurement (i.e., fixed b and diffusion time), residuals are smaller when fitting is performed only on high b-value images, rather than on all images. This finding remarks that simplified analytical models with 3-5 parameters, as those considered here, may not always capture the full complexity of the dMRI signal over large acquisition spaces due to anaccounted biological processes, as water exchange and intra-compartmental relaxation.

Computer simulations give insight into histology-informed model selection

We related the model selection performed on mouse and human dMRI data to computer simulations of diffusion in virtual substrates made of packed spheres, representing cells, a common tissue representation in body dMRI^{6,17,19,20,21} (Supplementary Fig. S17). Simulations consisted in: i) synthesing dMRI signals for the three acquisition protocols used in this study, through Monte Carlo simulations; ii) fitting all candidate models to the synthetic dMRI signals; iii) selecting the best approach according to the TCS (correlation ground truth-estimated parameters), HFC (accuracy in parameter estimation) and BIC (quality of signal fit, penalising model complexity) criteria introduced above. Our signal synthesis explicitly accounted for IC/EC water exchange (3 membrane permeability levels, i.e., low, intermediate and high), and probed a wide range of IC fractions, cell sizes and IC/EC diffusivities.

In our synthetic data, TCS confirms that model Diff-in fitted to highly DW images provides the best overall performances in terms of correlation between ground truth and estimated CS and IC fraction, when trans-membrane permeability is low (Supplementary Table S1). In this scenario, neglecting EC signal contribution at high b provides a compact signal representation that captures salient contrasts in terms of CS and IC fraction. Nontheless, Supplementary Table S1 also shows that the performances of such a model degrade as permeability levels grow. As IC/EC water exchange increases, the IC and EC signals become more and more intermixed, and models that account explicitly for EC diffusion provide increasingly better performances. Rankings based on HFC (Supplementary Table S2) show that while Diff-in excels in ground truth-estimated parameter correlations, it is outperformed by other models in terms of accuracy of the estimation, regardless of the permeability level. This finding suggests that while a simplified signal representations such as Diff-in suffices to capture CS and IC fraction contrasts, it may provide biased microstructural estimates, due to accounted diffusion processes. Finally, BIC-based rankings (Supplementary Table S3) show that Diff-in, despite being a simplified signal representations that by design neglects signal contributions from specific water pools (i.e., EC), suffices to capture salient patterns of the dMRI signal. According to BIC, Diff-in provides excellent goodness of fit, as it systematically ranks first for almost all protocols and all fitting strategies.

To more clearly visualise how trans-membrane water exchange affects diffusion, and hence dMRI signal modelling, we plotted the instantaneous diffusion coefficient for spins seeded inside cells (${{ADC}}_{I}(t)$) for different CS, intrinsic diffusivities and cell permeability levels (Supplementary Fig. S18). The figure shows that IC/EC water exchange affects the temporal profile of ${{ADC}}_{I}(t)$, as compared to curves obtained for impermeable cells. For example, in presence of membrane permeability, ${{ADC}}_{I}(t)$ is in general higher than when obtained for impermeable cells, for any t. Moreover, it does not exhibit the characteristic decreasing behaviour approaching ${{ADC}}_{I}\to 0$ typical of restricted diffusion: while firstly it decreases sharply, due to the restricting effect of cell membranes, it then increases with time, as more and more spins leave the cells and explore the EC space with their random walks. However, the plots also show that exchange-induced deviations of ${{ADC}}_{I}$ from the ideal diffusion restriction case are the strongest for diffusion times that are unlikely to be probed with clinical systems in vivo (t > 40 ms), and that they are small for large cell diameters (22–30 µm), as those that can be expected in normal liver or in certain liver tumours.

Cell size and density estimates from the proposed dMRI model correlate with histology

In view of the results obtained from the analysis of in silico, ex vivo and in vivo MRI data, our recommended liver tumour dMRI approach is the fitting of model “Diff-in” – a one-compartment model of restricted, IC diffusion within spherical cells, with negligible EC signal contributions – to high b-values images ($\gtrapprox$1800 s/mm² ex vivo, $\gtrapprox$900 s/mm² in vivo).

The model provides estimates of IC fraction, cell size and cell density that are weakly, moderately and strongly correlated to the underlying histology. Table 1 shows Pearson’s correlation between Diff-in metrics ${F}_{{MRI}}$ (intra-cellular fraction), ${vC}{S}_{{MRI}}$ (cell size index) and $C{D}_{{MRI}}$ (cell density) with their histology counterparts ${F}_{{histo}}$, ${vC}{S}_{{histo}}$ and $C{D}_{{histo}}$. We observe a weak correlation between ${F}_{{MRI}}$ and ${F}_{{histo}}$ (r = 0.19, p = 0.370), moderate between ${vC}{S}_{{MRI}}$ and ${vC}{S}_{{histo}}$ (r = 0.44, p = 0.029), and strong between $C{D}_{{MRI}}$ and $C{D}_{{histo}}$ (r = 0.70, p = 0.0001). The weak correlation between ${F}_{{MRI}}$ and ${F}_{{histo}}$ is likely due, at least in part, to the fact that ${F}_{{MRI}}$ is a signal fraction, rather than an actual volume/area fraction. This implies that ${F}_{{MRI}}$ also encodes T2/T1 differences between IC and EC signals, unlike ${F}_{{histo}}$³⁵. Moreover, ${F}_{{MRI}}$ values may have also been biased by the exchange between intra- and extra-cellular water^19,55, especially in presence of small cells¹⁹ – a phenomenon that is is not accounted for in none of the studied signal models. Finally, we emphasise that in the N = 18 human observations, dMRI metrics from an entire tumour have been compared to a small sliver of biopsied tissue. This implies that the correlation between dMRI and histology may have been underestimated, especially for the IC fraction, for example when the biopsy misses large areas of necrosis or fibrosis, which affect ${F}_{{MRI}}$ values. Supplementary Table S4 shows results from linear regression models that test the specificity of ${{vCS}}_{{MRI}}$, ${F}_{{MRI}}$ and ${{CD}}_{{MRI}}$ to their histologica counterparts ${{vCS}}_{{histo}}$, ${F}_{{histo}}$ and ${{CD}}_{{histo}}$. Results suggest that ${{vCS}}_{{histo}}$ is the main correlate of ${{vCS}}_{{MRI}}$ (even when considering the confounding effect of ${F}_{{histo}}$), that ${F}_{{histo}}$ is the main correlate of ${F}_{{MRI}}$ (even when considering the confounding effect of ${{vCS}}_{{histo}}$), and that ${{CD}}_{{histo}}$ is the main correlate of ${{CD}}_{{MRI}}$ (even when considering the confounding effect of ${{vCS}}_{{histo}}$ and ${F}_{{histo}}$). Note that collinearity among the regressors may cause β coefficients be larger than 1 even when working with z-scores (i.e., for the model featuring ${{CD}}_{{MRI}}$ as dependent variable). In general, the association between ${F}_{{histo}}$ and ${F}_{{MRI}}$ is confirmed to be weak; between ${{vCS}}_{{histo}}$ and ${{vCS}}_{{MRI}}$ to be moderate; and between ${{CD}}_{{histo}}$ and ${{CD}}_{{MRI}}$ to be strong. These results give additional confidence about the biological specificity of the proposed dMRI approach.

Table 1 Correlation between metrics from the selected biophysical dMRI approach with their direct histological counterparts

Table 1 also reports correlation coefficients for DKI ADC and kurtosis K. The correlations are in line with previous studies^56,57. For example, both ADC and K exhibit significant, moderate correlations with histological properties, i.e., a negative correlation with cell density $C{D}_{{histo}}$ for ADC, and a positive correlation with $C{D}_{{histo}}$ for K (r = –0.47 and 0.43 respectively). Significant correlations are also seen between DKI metrics and ${F}_{{histo}}$ (r = 0.40, p = 0.048 for K).

Supplementary Figs. S19, S20 show Pearson’s correlation coefficients for all possible pairs of metrics, in the form of correlation matrices. Supplementary Data S1, S2 contain all MRI/histology metric values used to generate such matrices. In general, metrics from dMRI models where ${AD}{C}_{E} > {AD}{C}_{I}$ show stronger correlations with their histological counterparts than models Diff-in-exTD and Diff-in-ex. Specifically, we observe the strongest dMRI-histology correlations for model Diff-in fitted to high b-value images. Correlations among pairs of dMRI metrics are also seen, e.g., a strong negative correlation between $C{D}_{{MRI}}$ and ${vC}{S}_{{MRI}}$ (r = –0.81 for model Diff-in fitted to high b-value images). This finding, indicating that tighter cell packings per unit volume are achieved with smaller cells, is mirrored by histological $C{D}_{{histo}}$ and ${vC}{S}_{{histo}}$ (r = –0.88 between these two), and thus appears biophysically plausible.

The proposed dMRI model reveals histologically-meaningful tumour characteristics

The proposed model Diff-in is demonstrated in 7 fixed livers of mice suffering from a variety of pathologies, as well as in a cohort of 38 patients suffering from advanced solid tumours of the liver (both primary and metastatic). Voxel-wise Diff-in parameteric maps reveal intra-tissue and inter-tissue contrasts that are histologically meaningful, being compatible with histological features observed in HE stains. These include, for example, presence of small cells in areas characterised by lymphoproliferative processes in mouse livers, or reductions in cell density in necrosis or fibrosis in human tumours.

Figure 4 shows Diff-in and histological maps in 3 mouse livers, representative of the 3 phenotypes seen in our mouse data (Control, for normal liver structures; Pat_inf1, for small cell infiltration; Pat_nec, for necrosis). Visually, we observe excellent co-localisation between MRI slices and HE sections. The histological details reveal higher cellularity in sample Pat_inf1 compared to Control, due to packing of small cells in between larger hepatocytes, or an alternation of areas with lower/higher cell density in sample Pat_nec. These qualitative trends are confirmed in the histological maps ${F}_{{histo}}$, ${vC}{S}_{{histo}}$, $C{D}_{{histo}}$, with values in physiologically plausible ranges, as for example intra-cellular fractions around 0.75 and cell sizes of the order of 20 µm^58,59. Maps ${F}_{{MRI}}$, ${vC}{S}_{{MRI}}$ and $C{D}_{{MRI}}$ replicate the contrasts seeing in their histological counterparts ${F}_{{histo}}$, ${vC}{S}_{{histo}}$ and $C{D}_{{histo}}$. Supplementary Fig. S21 shows standard DKI ADC and kurtosis excess K in the same mouse livers. Visual trends highlight that the higher cell density of sample Pat_inf1 translates to remarkably reduced ADC and increased K compared to the Control. Lastly, Supplementary Fig. S22, S23 show additional dMRI metrics, including metrics from model Diff-in-exFast (i.e., the one providing the higher TCS when fitting is performed to the whole dMR image set). The figures highlight that overall, spatial trends seen in maps from the selected model Diff-in agree with those seen in Diff-in-exFast, but metrics from the latter appear noisier. Metrics ${D}_{0,I}$ and ${D}_{E,\infty }$ show limited between-sample contrast, and are difficult to validate histologically. Supplementary Table S5 report per-sample mean and standard deviation of all MRI and histology metrics in mice (see also Supplementary Data S1, S2). ${F}_{{MRI}}$ slightly underestimates ${F}_{{histo}}$, while ${vC}{S}_{{MRI}}$ slightly overestimates ${vC}{S}_{{histo}}$. We speculate that the discrepancies may be due, at least in part, to unaccounted factors such as variability in intrinsic cell shape/cytosol diffusivity³³ or water exchange¹⁹, and by the difficulty of relating accurately 2D histology to 3D MRI⁶⁰.

Fig. 4: Maps from the selected dMRI model Diff-in with their histological counterparts in the fixed mouse livers scanned at 9.4 T ex vivo.

The figure reports MRI and histology data for 3 specimens, representative of the 3 microstructural phenotypes observed in our ex vivo data set, namely: normal liver structures (Control case); a proliferative process, characterized by infiltration of small cells (Pat_inf1 case); necrosis and inflammation (Pat_nec case). For all specimens, the following is shown. A Top left: a high-resolution T2-w anatomical scan is shown next to the corresponding HE section, with histological details. B Bottom left: histological maps warped to the dMRI space (intra-cellular patch area fraction ${F}_{{histo}}$; volume-weighted mean cell size index ${vC}{S}_{{histo}}$; cell density per unit patch area $C{D}_{{histo}}$). C Bottom right: dMRI maps ${F}_{{MRI}}$, ${{{\rm{vC}}}}{S}_{{MRI}}$ and ${{{\rm{C}}}}{D}_{{MRI}}$ from the selected dMRI signal model (model Diff-in, fitted to high b-value images, i.e., b > 1800 s/mm²).

Figure 5 shows ${F}_{{MRI}}$, ${vC}{S}_{{MRI}}$ and $C{D}_{{MRI}}$ maps in patients, alongside biopsies. Supplementary Table S6 reports salient demographic, MRI and histology information of the cohort. Histopathological assessments highlight the variety of characteristics that can coexist within advanced solid tumours, e.g.: areas of fibrosis; localised areas of tightly packed cancer cells, sourrounded by stromal fibres; necrosis. dMRI ${F}_{{MRI}}$, ${vC}{S}_{{MRI}}$ and $C{D}_{{MRI}}$ show contrasts that are plausible with such histopathological features. For example, in a breast cancer liver metastasis in Fig. 5, we observe a core of low intra-cellular fraction ${F}_{{MRI}}$ and low cell density $C{D}_{{MRI}}$, compatible with necrosis. In a HCC case instead, we see areas of high ${F}_{{MRI}}$ and high $C{D}_{{MRI}}$, sourrounded by lower ${F}_{{MRI}}$ and lower $C{D}_{{MRI}}$, potentially indicating the alternation of high cell densities with fibrotic tissue. Supplementary Fig. S24 shows routine dMRI ${ADC}$ and K in the same tumours. These show plausible contrasts given the known tumour histology, e.g., a core of high ${ADC}$ and low K are seen in the necrotic core of the breast cancer tumour. Supplementary Fig. S25 shows ${F}_{{MRI}}$, ${vC}{S}_{{MRI}}$ and $C{D}_{{MRI}}$ from model Diff-in-exFast. Image contrasts match visually those seen in Diff-in metrics (the proposed approach), although Diff-in-exFast metrics appear noisier on visual inspection. Supplementary Fig. S26 shows intra-cellular cytosol diffusivity ${D}_{0,I}$ asymptotic ${AD}{C}_{E}$ (${D}_{E,\infty }$). Their speckled appearance suggests that these metrics are difficult to measure accurately in vivo^17,61.

Fig. 5: Examples of maps from the proposed dMRI model Diff-in in liver tumours of patients scanned at 1.5 T and 3 T in vivo, with co-localised biopsies.

MRI maps are shown in a biopsied liver tumour in two patients for each MRI scanner, arranged along rows. A Examples of slices from the high-resolution anatomical T2-w image and from a high b-value image, with biopsied tumour outlined. B Maps from the selected model (Diff-in, fitted to high b-value images b > 900 s/mm²). From left to right: intra-cellular signal fraction ${{{{\rm{F}}}}}_{{{{\rm{MRI}}}}}$; volume-weighted mean cell size index ${{{\rm{vC}}}}{S}_{{MRI}}$; cell density per unit volume ${{{\rm{C}}}}{D}_{{MRI}}$. C Histological details from the HE-stained biopsy. For the 1.5 T Siemens scanner (first and second rows from top) we report: patient 6 (primary hepatocellular carcinoma) and patient 3 (liver metastases from ovarian cancer). For the 3 T GE scanner (third and fourth rows from top) we report: patient 24 (primary hepatocellular carcinoma (HCC)) and patient 30 (liver metastases from breast cancer).

Metrics from the proposed dMRI model correlate with cell proliferation in liver tumours

We tested the potential utility of the proposed model for non-invasive liver tumour phenotyping. To this end, we studied associations between dMRI metrics an cell proliferation within patients’ biopsied liver tumours, quantified through Ki67 immunohistochemistry (IHC). The maing finding of this analysis is that dMRI cell size (${{vCS}}_{{MRI}}$) and density (${{CD}}_{{MRI}}$) are respectively negatively and positively associated to the fraction of Ki67 staining (${F}_{{Ki}67}$). This results, confirmed by histological cell size and density (${{vCS}}_{{histo}}$ and ${{CD}}_{{histo}}$), suggests that tumours featuring high cell proliferation are made, on average, by smaller and more densely packed cells, compared to tumours with lower proliferation. Figure 6 visualises the association between ${F}_{{Ki}67}$ and MRI histological cell size and density through scatter plots, reporting Pearons’s correlation coefficients. There is a strong, positive correlation between $C{D}_{{MRI}}$ and ${F}_{{Ki}67}$ (r = 0.80, p = 0.006), which is confirmed by a positive correlation between $C{D}_{{histo}}$ and ${F}_{{Ki}67}$ (r = 0.66, p = 0.038). Regarding cell size, there is a moderate, negative correlation between ${{vCS}}_{{MRI}}$ and ${F}_{{Ki}67}$ (r = –0.53, p = 0.111). This correlation, albeit not statistically significant owing to the small sample size (N = 10), is in the same direction of the correlation observed between histological ${{vCS}}_{{histo}}$ and ${F}_{{Ki}67}$ (r = –0.68, p = 0.031). Concerning other MRI metrics, weaker correlations are seen between DKI indices and ${F}_{{Ki}67}$ (r = 0.17, p = 0.633 between ${ADC}$ and ${F}_{{Ki}67}$; r = 012, p = 0.744 between $K$ and ${F}_{{Ki}67}$), or between ${F}_{{MRI}}$ and ${D}_{0,I}$ from the proposed dMRI model and ${F}_{{Ki}67}$ (r = –0.35, p = 0.319 between ${F}_{{MRI}}$ and ${F}_{{Ki}67}$; r = 0.07, p = 0.857 between ${D}_{0,I}$ and ${F}_{{Ki}67}$).

Fig. 6: Association between dMRI metrics and cell proliferation within the biopsied tumours in patients.

Top row: scatter plots and Pearson’s correlation coefficients between ${F}_{{Ki}67}$ (strength of the IHC stain demonstrating proliferation within the biopsied tumour, here expressed in percentage terms) and indices of cell size and density from both MRI and HE histology (sample size: N = 10). From left to right, A scatter plot and correlation between ${{vCS}}_{{MRI}}$ and ${F}_{{Ki}67}$; B between ${{vCS}}_{{histo}}$ and ${F}_{{Ki}67}$; C between ${{CD}}_{{MRI}}$ and ${F}_{{Ki}67}$; D between ${{CD}}_{{histo}}$ and ${F}_{{Ki}67}$. In the scatter plots, p-values were obtained from a two-sided Pearson’s correlation test, and are unadjusted for multiple comparisons. E Middle row: example of HE and Ki67 stains from a slowly-proliferating tumour (primary hepatocellular carcinoma, ${F}_{{Ki}67}$ of 0.8%). F Bottom row: example of HE and Ki67 stains from a fast-proliferating tumour (ovarian cancer liver metastasis, ${F}_{{Ki}67}$ of 19.7%), with a summary of salient MRI and histological metrics. MRI maps of the two patients are shown in Figs. 5 and 7 (both patients were scanned on the 1.5 T system). In (E) and (F), length bars are reported (2 mm for the HE and IHC tissue biopsies; 40  µm for the zoomed details visualising cells).

Figure 6 also visualises examples of biopsies from two liver tumours, featuring respectively strong and weak Ki67 staining for cell proliferation. These are: a metastatic ovarian cancer (Fig. 6F), whose ${F}_{{Ki}67}$ is of 0.197, and a primary HCC (Fig. 6E), which features a ${F}_{{Ki}67}$ of 0.008. The former tumour, with stronger Ki67 immunostain, is characterised by smaller and more densely packed cells than the latter, as suggested by both MRI and histology (for histology: ${{vCS}}_{{histo}}$ of 23.41 µm against 27.50 µm, and ${{CD}}_{{histo}}$ of 5.24‧10³ cell/mm² against 2.44‧10³ cell/mm²; for MRI: ${{vCS}}_{{MRI}}$ of 25.15 µm against 29.39 µm, and ${{CD}}_{{MRI}}$ of 2.08 ‧ 10⁵ cell/mm³ against 0.58 ‧ 10⁵ cell/mm³).

Metrics from the proposed dMRI model are associated with macroscopic tumour characteristics

We investigated whether the microscopic composition of each individual liver tumour assessed through dMRI can explain its macroscopic phenotype, e.g., salient characteristics such as its volume. For this analysis, we studied correlations between tumour-wise dMRI indices and the corresponding tumour volume, using data from N = 140 liver tumours from the 38 patients. We also performed cross-validation experiments in which we predicted liver tumour volume through statistical models that used dMRI metrics as predictors. The main finding of this analysis is that Diff-in metrics are significantly correlated with tumour volume, as is the case, for example, for MRI-derived cell size ${{vCS}}_{{MRI}}$. Statistical models that rely on cell size ${{vCS}}_{{MRI}}$ as a regressor enable meaningful predictions of tumour volumes, which are significantly correlated with ground truth values, and outperforming predictions from statistical models based on DKI metrics.

Figure 7A reports Pearson’s correlation coefficients between tumour volume and dMRI metrics from both Diff-in and DKI dMRI. The strongest, statistically significant associations are seen for Diff-in metrics ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$ (r = –0.305, p = 2.50‧10^–4 and r = 0.256, p = 2.26‧10^–3 respectively), while no significant associations are seen for DKI ADC (r = –0.092, p = 0.277) and kurtosis K (r = –0.035, p = 0.680). Figure 7B shows an example of two tumours, one larger (a primary hepatocellular carcinoma, with a volume of circa 431‧10³ mm³) and one considerably smaller (an ovarian cancer liver metastasis, with a volume of circa 21‧10³ mm³) (same tumours shown in Fig. 6). Histology shows that the former contains, on average, larger cells than the latter, a contrast that is detected by dMRI ${{vCS}}_{{MRI}}$. Figure 7C–F reports scatter plots of different pairs of dMRI metrics coloured by tumour volume, visualising the latter as a bi-dimensional function of the diffusion metrics. Trends are seen in the colouring of the plots, e.g., in panel 7F, where the dependence of tumour volume on ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$ is visualised (Fig. 7F). In Fig. 7F, the tumour volume does not appear to be monotonic in the (${D}_{0,I}$, ${{vCS}}_{{MRI}}$) plane, as it peaks for (${D}_{0,I}$, ${{vCS}}_{{MRI}}$) around (1.8 µm²/ms; 28 µm). Finally, Fig. 7G–J shows results from the 5-fold cross-validation experiments, by scattering ground truth and predicted tumour volume values for different statistical models. The highest correlation between ground truth and predicted volumes is obtained for a model where ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$ are used as predictors, i.e., a moderate but significant Pearson’s r = 0.396 (p = 1.26‧10^–6; range of r across the 5 folds of (0.146; 0.524)). This surpsasses values obtained when other dMRI metrics are used, e.g., DKI ADC and kurtosis K (r = 0.244, p = 3.68‧10^–3; range of r across the 5 folds of (0.226; 0.403)). Supplementary Data S3 reports all liver tumour values used for these analyses.

Fig. 7: Association between dMRI metrics and liver tumour volume in patients.

A Pearson’s correlation coefficients between liver tumour volume and per-tumour mean values of Diff-in and DKI metrics. B Examples of large and small tumours from a primary hepatocellular carcinoma (large) and a metastatic ovarian cancer (small), with corresponding ${{vCS}}_{{MRI}}$ dMRI metric of cell size and HE histology. C–E Visualisation of tumour volume as a bi-dimensional function of different pairs of dMRI metrics, namely: DKI ADC and K in (C); Diff-in ${D}_{0,I}$ and ${F}_{{MRI}}$ in (D); Diff-in ${{vCS}}_{{MRI}}$ and ${F}_{{MRI}}$ in (E); Diff-in ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$ in (F). G–J prediction of tumour volume based on different pairs of input dMRI, in 5-fold cross validation experiments. These were: DKI ADC and K in (G); Diff-in ${D}_{0,I}$ and ${F}_{{MRI}}$ in (H); Diff-in ${{vCS}}_{{MRI}}$ and ${F}_{{MRI}}$ in (I); Diff-in ${D}_{0,I}$ and ${{vCS}}_{{MRI}}$ in (J). In panels (G)–(J), scatter plots of ground truth tumour volumes against predicted tumour volumes are obtained by pooling together predictions from all 5 cross-validation folds. The figures also report the Pearson’s correlation coefficient between ground truth and predicted tumour volume values, with the linear regression line in grey. The line visualises the fitting relating ground truth and predicted tumour volumes through a linear relationship (x_predicted = a + b x_ground-truth). The line visualises slope/off-set of the fit, which was performed on the sample made of predictions and ground truth volumes for all N = 140 tumours from 38 patients included in this experiment. The grey interval around the regression line represents the 95% confidence interval over 1000 boostrap repetitions of the tumour volume regression. The p-values refer to a two-sided Pearson’s correlation test between ground truth and predicted tumour volumes (in logarithmic scale), and are unadjusted for multiple comparisons. The range for the correlation coefficient is obtained across cross-validation folds. Note that in these experiments, the log₁₀ of the tumour volume was studied, since the tumour volume spans several orders of magnitude and is therefore challenging to handle numerically. The results shown in this figure are based on a sample size of N = 140 tumours from 38 patients.

The proposed dMRI model distinguishes colorectal cancer from melanoma liver metastases

Lastly, we tested whether the proposed dMRI approach may complement standard diffusion metrics, such as ADC, to aid the interpretation of between-tumour differences. For this purpose, we compared the composition of liver metastases from colorectal cancer (CRC) and melanoma, the two most frequent primary cancers in our cohort. We tested for differences in dMRI metrics between the two groups, verifying results with histology. These two cancers feature distinct cellular composition: while CRC metastases are characterised by the presence of large luminal spaces, melanoma metastases consist of tightly packed malignant melanocytes (Fig. 8A, B)^62,63. The proposed Diff-in model provides estimates of IC fraction ${F}_{{MRI}}$ that are significantly larger in melanoma than in CRC metastases (p = 0.011, N = 21; Fig. 8A, B, K), a finding that is consistent with the presence of EC water trapped within CRC luminal spaces. This result is confirmed by the histological IC fraction ${F}_{{histo}}$, which is also lower in CRC than in melanoma (p = 0.034, N = 12; Fig. 8A, B, E). More standard diffusion indices also detect differences between the two cancer types: DKI ${ADC}$ is higher in CRC than in melanoma metastases (p = 0.038, N = 21; Fig. 8A, B, I), also consistent with presence of free diffusion in the lumina. No statistically significant differences between CRC and melanoma were detected for any other metric, including patient’s age.

Fig. 8: Differences in dMRI and histological metrics between liver metastases from melanoma and colorectal cancer (CRC).

Visualisation of illustrative parametric maps in a liver metastasis from melanoma and CRC, and differences between the two groups across dMRI and histological metrics. Differences are assessed through two-sided t-tests, and p-values are reported as unadjusted for multiple comparisons. A data from a melanoma liver metastasis (from left to right: DW image, ADC map and ${F}_{{MRI}}$ map from dMRI; HE histology, with quantitative IC fraction ${F}_{{histo}}$). B Same data as in (A), but for a colon cancer liver metastasis. C Age differences between the CRC and melanoma groups (N = 13 CRC; N = 8 melanoma). D Tumour volume differences (N = 13 CRC; N = 8 melanoma). E Histological IC fraction ${F}_{{histo}}$ differences (N = 8 CRC; N = 4 melanoma). F Histological cell size ${{vCS}}_{{histo}}$ differences (N = 6 CRC; N = 4 melanoma). G Histological cell density ${{CD}}_{{histo}}$ differences (N = 6 CRC; N = 4 melanoma). H Histological Ki67 staining fraction ${F}_{{Ki}67}$ differences (N = 4 CRC; N = 2 melanoma). I DKI ADC differences (N = 13 CRC; N = 8 melanoma). J DKI kurtosis K differences (N = 13 CRC; N = 8 melanoma). K Diff-in model IC fraction ${F}_{{MRI}}$ differences (N = 13 CRC; N = 8 melanoma). L Diff-in model cell size ${{vCS}}_{{MRI}}$ differences (N = 13 CRC; N = 8 melanoma). M Diff-in model cell density ${{CD}}_{{MRI}}$ differences (N = 13 CRC; N = 8 melanoma). N Diff-in model IC diffusivity ${D}_{0,I}$ differences (N = 13 CRC; N = 8 melanoma).

Discussion

The latest liver dMRI models aim to disentangle IC and EC water contributions to the total signal^6,17,20,21. This powerful approach enables the estimation of innovative tissue property maps, but its clinical deployment is hampered by the high number of unknown tissue parameters to estimate, which requires impractically long dMRI acquisitions^17,64,65. With this challenge in mind, this paper delivers a practical implementation of a two-compartment dMRI signal model, tailored for liver imaging, and truly feasible in the clinic. Through histology-informed model selection, we design a compact framework consisting of fitting a model of restricted IC diffusion to highly DW images, with negligible EC signal contributions. This provides cell size and density estimates that correlate with histology, and which may provide additional information to standard-of-care imaging for non-invasive tumour phenotyping.

To find the optimal dMRI signal implementation, we analysed co-localised dMRI and histology data (N = 25) from fixed mouse livers and from human tumours of the liver. We compared 5 signal models, each fitted according to two distinct strategies, and ranked them for their ability to estimate histological IC fraction and cell size (the uknown tissue parameters in the dMRI signal models). Rankings unequivocally suggest the highest radiological-histological agreement is obtained by fitting a model of restricted diffusion within spherical cells, with negligible EC signal contributions – a model here referred to as Diff-in –, to images acquired with b-values higher than ~900  s/mm² in vivo and 1800 s/mm² ex vivo. Interestingly, our central result, points towards the use of simpler models of diffusion if these are deployed in appropriate measurement regimes, is consistent with recent estimates of the EC liver ADC, as high as 2.5 µm²/ms¹⁷. Such a high ${AD}{C}_{E}$ implies that the EC signal would decay to roughly 5% or less of its non-DW value even for b-values of 1200  s/mm² (exp(–b ADC_E) ≈ 0.05 for b = 1.2 ms/µm² and ADC_E = 2.5 µm² ms^–1), justifying the hypothesis of negligible EC signal contributions^7,29,61. Nevertheless, we also point out that our main modelling result should be interpreted with care, since some unaccounted biological processes may also contribute to explaining the performances of the simplified Diff-in model (one-pool model of restricted intra-cellular diffusion). Notably, none of the tested signal models accounts for water exchange across cell membranes, a these are assumed to be perfectly impermeable. It is therefore possible that the good performances of the Diff-in model, or, more generally, of models featuring faster EC diffusion may be, at least in part, a consequence of non-negligible membrane permeability, and hence a manifestation of fast IC/EC water exchange.

To corroborate dMRI model selection on ex vivo and in vivo MRI, we performed model selection on simulated dMRI data. These were generated using virtual cellular models made of packed spherical cells, exhibiting a variety of packing densities, IC/EC diffusivities, and cell membrane permeabilities. Results from simulations essentially confirm rankings from ex vivo and in vivo imaging in presence of low cell permeability, as model Diff-in fitted to high b-value images provides among the best performance in terms of ground truth-parameter estimate correlation (high ranking in TCS). However, as permeability increases, the performances of Diff-in degrade, and models that account explicitly for EC signals (Diff-in-ex and Diff-in-exTD), without imposing constraints of IC vs EC diffusion, provide better performances – a finding that is in line with the lower biases in signal estimation of these models seen on actual ex vivo and in vivo dMRI measurements. Despite the degradation in performances measured by TCS and HFC as exchange increases, the model Diff-in is still capable of delivering acceptable signal fitting quality for all permeability levels in silico, as demonstrated by the fact that it ranks high on BIC (recall that BIC essentially corrects fitting mean squared errors, penalising model complexity). Nonetheless, while ranking high on BIC, the simulated HFC model selection also reveals that Diff-in is outperformed by other models in terms of accuracy of the parameter estimation. This result is consistent with the fact that the estimation of dMRI parameters can be biased by unaccounted biological processes, as, in this case, residual EC signals at high b as well as water exchange. All in all, these finding confirm that Diff-in, while being a simplified dMRI signal representation that is more prone to biases than more complex models, is a compact and potentially useful representation for liver tumour imaging when deployed in appropriate measurement regimes. These should feature negligible EC signal contributions from sufficiently high b-values, and slow IC/EC water exchange with respect to the measurement diffusion times.

Our proposed dMRI modelling approach provides metrics that visualise tissue heterogeneity over a wide field of view, beyond what can be routinely sampled in the clinic with biopsies. Diff-in metrics point, for example, to areas of high cell densities in some of the fixed mouse livers, or areas of necrosis within the core of large tumours in patients in vivo – facts that are all confirmed by histology. Notably, spatial trends from the dMRI model Diff-in agree with metrics from other candidates dMRI signal implementation, e.g., Diff-in-exFast, the model selected when fitting is performed on the whole image data set (Supplementary Figs. S22, S25). On the one hand, this gives confidence on the robustness of our signal modelling routines. On the other hand, the noisier appearance of metrics Diff-in-exFast compared to Diff-in is consistent with ill-posedness of complex dMRI models, when they include several unknowns to estimate⁶¹.

We investigated the potential clinical utility of the proposed Diff-in dMRI approach by testing whether its metrics can serve as non-invasive biomarkers of biologically relevant processes in cancer. For this, we conducted three analyses, namely: i) we studied the association between Diff-in metrics and cell proliferation; ii) we investigated the relationship between Diff-in metrics and macroscopic tumour characteristics, as their volume; iii) we tested whether Diff-in metrics reveal between-tumour differences that are histologically meaningful. Regarding the comparison with Ki67 immunostains demonstrating cell proliferation, we found that dMRI cell size and density are sensitive to Ki67 stains of cell proliferation, being respectively moderately and strongly correlated with the staining fraction ${F}_{{Ki}67}$. This finding, confirmed by histological cell size and density from HE-stained biopsies, may indicate that tumours featuring higher proliferation levels contain smaller and more densely packed cells. This is in line with previous in vitro measurements, as those obtained, for example, in colon carciomas⁶⁶, in which the time required for malignant cell populations to double in number was shorter for small cells with large nuclei, compared to larger cells but with small nuclei. The main takeaway of this analysis is that cell morphology assessment through our dMRI model may offer sensitivity to key biological processes of cancer biology, as cell proliferation⁶⁷, which are directly linked to clinical outcomes. The reported association between in vivo cell size measurements and Ki67 proliferation is, to the best of our knowledge, a novel finding. However, we acknowledge that its exact biological implications deserve additional elucidation in larger cohorts, given the small size of our data sample.

Regarding the analysis on tumour volume instead, our key result is that metrics from the proposed Diff-in approach are associated to tumour volume, albeit only moderately, in a data set of N = 140 liver tumours. This fact allowed us to develop simple regression models capable of predicting tumour volume given characteristic per-tumour dMRI metric values. The best prediction was obtained using cell size ${{vCS}}_{{MRI}}$ and cell diffusivity ${D}_{0,I}$ – statistical properties of the tumour cell ensemble – as regressors (correlation r = 0.396, p = 1.26‧10^–6 between ground truth and tumour volume predictions), surpassing correlations obtained with DKI ADC and K, which only provides r = 0.244, p = 3.68‧10^–3.

Taken as a whole, these findings may suggest that biological properties directly related to the morphology of cancer cells may contribute to explaining, at least in part, the macroscopic phenotype of individual tumours, as for example their size. Therefore, our proposed dMRI approach may offer value to complement standard-of-care radiological assessments, which focus on macroscopic tumour descriptors, providing information that is more closely related to the tumour biology. Nevertheless, we acknowledge again that further validation in larger cohorts is required to confirm these findings, since we were not able to validate the dependence of tumour volume on dMRI metrics histologically, given the limited size of the histological data sample (Supplementary Table S7). Future work will focus on studying areas of active tumour, since necrosis – common in the large tumours contained in our advanced patients’ cohort – may confound in part the associations, being CS values from both automatic histology processing and dMRI less reliable in highly necrotic areas (see, for example, Fig. 5).

As a final demonstration of the potential utility of our approach, we compared Diff-in dMRI metrics across melanoma and CRC liver metastases, being these the two most frequent cancers in our advanced cohort. The analysis showed that the Diff-in model pins down the exact microstructural property underlying the higher ${ADC}$ seen in CRC, i.e., the lower IC fraction, being ${F}_{{MRI}}$ higher in CRC than in mealona, in agreement with ${F}_{{histo}}$. This finding points once again towards the higher biological specificity of the proposed approach against standard dMRI techniques such as DKI: these, while sensitive to tissue cellulear properties, provide surrogate markers that are more difficult to interpret, and that pool several tissue properties into one number⁶⁵.

In our data, ${ADC}$ and K do offer value beyond standard-of-care tumour size assessment for cancer characterisation, for example correlating significantly with cancer cellularity and cell size, a fact that agrees with known literature^57,65, and revealing inter-tumour differences, as discussed above for CRC and melanoma. However, we point out that histology-informed, biophysical dMRI techniques as the one proposed in this article attempt to provide truly quantitative indices, with a direct biological interpretation, and thus overcome the issues related to the interpretaibility and biological specificity of DKI. Contrarily to our proposed metrics, ADC and K are semi-quantitative and protocol-dependent, and their numerical value can change as function of factors as the dMRI sequence effective diffusion time^65,68. This may be one of the reason contributing, for example, to the disappointing association between DKI metrics and Ki67 cell proliferation, a fact that confirming the need for developing novel dMRI approaches with high biological specificity for liver tumour imaging – one of the key objectives of this work.

We would like to acknowledge the following potential limitations. Firstly, our sample size is relatively small. This paper provides a first demonstration of the potential utility of metrics from a practical liver dMRI model, e.g., as markers of cell proliferation or of other biological phenomena that drive tumour phenotypes. Nonetheless, while works proposing related dMRI techniques relied on similar^21,35 (if not even smaller^17,18) sample sizes, we acknowledge that our exploratory findings require further confirmation in larger cohorts. Confirmation from larger samples is needed to ensure the generalisability of the proposed “Diff-in” approach, as well as to rule out additional confounding effects. The limited statistical power of our study (sample of N = 25 MRI-histology acquisitions) implies that additional data from different MRI manufacturers and scanner models are required to better characterise the effect of diffusion time. These could enable us to test, for example, whether the same model selection results would be obtained with shorter diffusion times through oscillating gradient diffusion encoding in vivo^17,69, or had different malignancies been included in the in vivo data set. These could have included, for example, lymphomas, being this a class of malignancies that involve the liver and in which malignant lymphocites infiltrate the liver parenchyma⁷⁰. Lymphocites are much smaller compared to hepatic cells^17,19. As a consequence, the dMRI signal from the former is more likely to be sensitive to IC/EC water exchange than the latter, potentially requiring more complex dMRI signal models than those used here, as discussed in more detail below. Similarly, additional data from other animals, beyond mice, would be needed to confirm the generalisbility of the proposed dMRI findings across species.

Secondly, we point out that results from any dMRI-histology comparison should always be taken with care. Here we related dMRI metrics obtained in vivo to histological indices from biopsies. While we were able to identify the tumours from which the biopsies were taken, we could not identify exactly the tumour area that was biopsied. This implies that a biopsy may not be fully representative of the characteristics of an entire tumour, so that the true extent of the associations between dMRI and histology may have been underestimated. Also, histology has its own limitations per se, since it provides readouts that may not be fully accurate (a fact that may explain, for example, the discrepancy in HFC rankings seen when comparying in silico and actucal in vivo/ex vivo dMRI experiments). For example, routine HE histology is an inherently 2D technique, unlike 3D MRI. Moreover, it is affected by artifacts (e.g., due to dehydration, paraffin embedding, imperfect staining, cutting, etc⁴¹), and the automatic processing of large fields-of-view requires trading off between sensitivity and specificity. We took steps to mitigate these issues, e.g., by accounting for biases due to tissue shrinkage. Nonetheless, our histology-derived estimates of cell properties are likely biased versions of the true figures, and are also subject to sampling biases compared to full 3D volumetric imaging in MRI. While it is well known that acquiring high-quality, co-localised dMRI and histology data is challenging, especially when dMRI scans are acquired in vivo in humans (e.g., prior to tumour excision), future studies are required to confirm the findings presented in this article, and ensure its generalisability across MRI manufactures, scanner models, dMRI encoding schemens, as well as tumour types.

We would also like to acknowledge that the proposed dMRI approach neglects other potentially relevant microstructural properties, such as water exchange between intra-/extra-cellular spaces^19,55, presence of cell size/cytosolic diffusivity distributions^33,69, or intra-compartmental T2 or T1³⁵. On the one hand, ignoring these properties may have biased the estimation of ${F}_{{MRI}}$ and ${vC}{S}_{{MRI}}$^19,55. ${F}_{{MRI}}$, for example, is known to be underestimated when cell permeability is neglected^19,55, and is also confounded by TE changes across imaging sessions or across images from the same session acquired at varying TE⁷¹. This latter aspects makes ${F}_{{MRI}}$ inherently protocol-dependent, potentially hindering the adoption of the metric as a quantitative biomarker. On the other hand, these properties, overlooked in our modelling framework, may be relevant markers of cellular stress per se. In future, we plan to incorporate these properties in our models, while ensuring the clinical feasibility of the dMRI protocols required to fit them. Incorporating IC/EC water exchange modelling and intra-compartmental relaxation effect may be especially relevant to increase the disappointing MRI-histology correlations observed for the IC fraction F for all dMRI models and fitting strategies, being the metric known to be biased by both permeability and relaxation effects^19,55,71.

Conclusions

To conclude, this study delivers a practical liver dMRI signal model consisting of restricted diffusion within spherical cells, with negligible EC signals, which should be fitted to b-values higher than, approximately, 900 s/mm² in vivo. This model offers estimates of cell size and density that are correlated to the underlying histology, and which may provide complementary information to routine standard-of-care imaging, as for example for the characterisation of cell proliferation, or for non-invasive tumour phenotyping in vivo. The proposed approach is appropriate in regimes where IC/EC water exchange is slow compared to the measurement diffusion time, as for example to image liver tumours containing predominantly large cells, e.g., 20–30 µm in diameter for diffusion times not exceeding 40 ms. In applications where high cell permeability is expected, as, for example, to image tumours rich in small cells, as lymphocites¹⁹ (e.g., in immunotherapy or in lymphomas), care would be needed in interpreting metrics from the proposed model, due to potential biases coming from unaccounted IC/EC water exchange, and non-negligible EC signals.

Supplementary information

This article includes Supplementary Figs. S1–S27, Supplementary Tables S1–S7, and Supplementary Data S1–S9. Supplementary Data S1: CSV file with MRI and histology data for model selection. Supplementary Data S2: CSV file with MRI and histology data for model selection based on high b-value images only. Supplementary Data S3: CSV file with MRI and histology metrics for each individual tumour. Supplementary Data S4: CSV file with cohort information, histological and mean MRI metrics across all tumour voxels. Supplementary Data S5: CSV file with cohort information, histological and mean ComBat-harmonised MRI metrics across all tumour voxels. Supplementary Data S6: zipped folder containing the code generating Table 1 and Fig. 3. Supplementary Data S7: zipped folder containing the code generating Fig. 6. Supplementary Data S8: zipped folder containing the code generating Fig. 7. Supplementary Data S9: zipped folder containing the code generating Fig. 8.