Evaluating PSA dynamics for predicting androgen deprivation failure with a patient specific prostate cancer model

Abstract

Prostate cancer is the second leading cause of cancer-related death among American men, with a new diagnosis made every 2 min in the United States. Advanced cases are commonly treated with androgen deprivation therapy (ADT). Despite its effectiveness, treatment failure remains inevitable for many patients, necessitating better predictive tools for clinical management of disease. This study presents a data-driven mathematical modeling approach that integrates patient-specific prostate-specific antigen (PSA) time-course data with experimentally measured PSA expression rates to improve the prediction of ADT failure. Our findings suggest that post-nadir PSA dynamics, rather than initial decline, hold greater prognostic value and can inform PSA monitoring schedules. By employing virtual clones of individual patients, our model integrates routinely collected PSA measurements to dynamically predict ADT failure probabilities at future clinic visits. If implemented in clinical practice, this personalized framework could empower oncologists to make proactive, informed treatment decisions and guide timely interventions.

Introduction

Recent statistics from the American Cancer Society highlight alarming trends in prostate cancer (PCa), which ranks as the most commonly diagnosed and second-deadliest cancer among men in the United States. These data indicate a significant rise in PCa incidence, along with notable racial and economic disparities¹. Furthermore, projections from a Lancet Commission² suggest that the global number of PCa cases will more than double in the next two decades, with deaths expected to rise from 375,000 in 2020 to an estimated 700,000 by 2040. These statistics underscore a critical need for improvements in screening, early diagnosis, and better prediction of recurrence post-treatment.

PCa is a complex disease characterized by cancer cells that express high levels of the androgen receptor gene, which encodes the androgen receptor and drives hormone dependency in early-stage PCa³. Consequently, androgen deprivation therapy (ADT) or hormone therapy has been a primary management strategy for PCa for over 80 years⁴. However, in its advanced stages, PCa cells often display amplification and/or mutation of the androgen receptor, leading to treatment failure and recurrence^4,5.

PCa cells secrete prostate-specific antigen (PSA), a serine protease that is transcriptionally activated by the androgen receptor⁵. Serum PSA levels, commonly elevated in men with PCa, serve as the primary biomarker for detecting and diagnosing the disease. However, serum PSA correlates poorly with tumor burden due to delays between tumor growth and PSA⁶, posing a challenge for physicians in accurately assessing the response of patients to therapy⁷. Despite these limitations, the simplicity of measuring serum PSA continues to support its use as a prognostic tool for treatment response and metastasis development.

Given the challenges of directly correlating PSA levels with tumor size, we develop a data-driven mathematical modeling approach to better understand what information can be reliably gleaned about individual patients from minimal PSA time-course data. Our model approach helps clarify the limitations and potential of PSA data in predicting the response of an individual patient’s tumor to ADT. Additionally, our approach investigates the optimal timing and frequency of PSA measurements to maximize their prognostic utility. We also forecast ADT failure and patient-specific, progression-free survival (PFS) times, enabling oncologists to proactively plan alternative treatment strategies. Importantly, we extend our findings to a diverse patient cohort, identifying tumor-specific characteristics that have a significant impact on PFS times. This key finding underscores the broader applicability and potential of our model in clinical oncology.

Indeed, a wealth of mathematical models of PCa growth and control have been proposed, spanning the spectrum from purely theoretical investigations to data-driven approaches with clinical applications. Many of these models focus on optimizing hormone-based treatment schedules and estimating the time of treatment failure; for a review, see ref. ⁸. Of note, Brady et al.⁹ employ a mathematical model calibrated and validated with longitudinal PSA data from individual patients to simulate and predict the dynamics of PCa stem and non-stem cells during intermittent ADT. Their analyses reveal dynamics associated with treatment resistance and suggest ways in which PSA dynamics can be utilized to personalize therapy and prolong the time to progression. A significant recent study¹⁰, published after the review conducted in⁸, presented a new evolutionary perspective on mathematical methods for predicting treatment failure using PSA and androgen data from a clinical trial of intermittent ADT. They proposed two new biomarkers with high predictive accuracies for ADT resistance. Taking a more theoretical approach, Phan et al.¹¹ apply three distinct models as case studies to examine the identifiability and uncertainty of model parameters. They discovered that PSA time-course data generally fail to uniquely determine model parameters, with even identifiable parameters showing significant uncertainties.

The work presented here adds unique value to the current literature in several ways. First, although some previous studies have explored model identifiability, they have yet to take the next logical step of applying this information toward enhancing model predictions. Moreover, while many modeling studies use individual PSA profiles to forecast treatment failure timelines, we take a novel approach by combining patient-specific PSA time-course data with experimentally measured PSA expression data. This integration enables the generation of realistic virtual patient clones, allowing us to predict tumor volume fold change (TVFC) and PSA levels at the time of ADT failure. We then extend our investigations to a more diverse virtual cohort to uncover broad ADT failure trends and quantify which parameters are drivers of PFS. Our innovative application of the model to evaluate the impact of PSA measurement timing on ADT failure demonstrates its ability to integrate seamlessly with routine clinical workflows, providing dynamic predictions of ADT failure probability for upcoming patient appointments.

Results

PSA expression data

Figure 1 shows the PSA levels per cell for an androgen-sensitive (LNCaP) and castration-resistant (CR) (C4-2B) cell line for various concentrations of a synthetic androgen (R1881) that approximates concentrations of dihydrotestosterone (DHT) in vivo. These data are used to estimate the rates of PSA expression per cell under androgen-rich and androgen-deprived conditions for androgen-sensitive (ρ_n) and CR (ρ_m) cells (see Eq. 3). Ranges within one standard deviation for values of ρ_n and ρ_m are summarized in Table 1. We note that the PSA expression data for 0nM concentration of R1881 was ignored in these calculations because this would mimic perfect androgen deprivation, which is unlikely to be achieved in practice.

Fig. 1: Impact of the synthetic androgen R1881 on prostate-specific antigen (PSA) production of prostate cancer cell lines.

Prostate cancer cells C4-2B (a) and LNCaP (b) were treated in triplicates with R1881 at a final concentration of 0, 0.1, 1, and 10 nM. Forty-eight hours after treatment with R1881, conditioned media was harvested and measured for PSA by ELISA, and the cells were harvested and counted. Data shows the means ± SEM, * denotes p value < 0.05 versus LNCaP 0.1 nM.

Table 1 Range of PSA expression per cell for castration-resistant (M) and androgen-dependent (N) cells

We used the 0.1 and 1 nM doses of R1881 to estimate the range of values for α = ρ_m/ρ_n and derived virtual clones of our six patients as described in the Methods. These doses represent biologically realistic levels of androgens under ADT conditions.

Simple model accurately predicts PSA dynamics across diverse patient profiles

We fit the four model parameters to patient-specific PSA time-course data and perform profile-likelihood analysis (see “Methods” section “Parameter profile-likelihood analysis”) to determine 95% confidence intervals (CIs) for each parameter for each patient. Results for a representative patient (UM10001) are shown in Fig. 2, and the results for all other patients can be found in the supplementary information (Supplementary Figs. S1–S5). Figure 2b–e plots the negative log-likelihood (NLL) as a function of the fold change in each profiled parameter. The horizontal line in Fig. 2b–e is the 95% CI threshold, and the parabola is the profile-likelihood curve of the parameter on the x-axis. Taken together, these results show that all model parameters are identifiable from PSA data.

Fig. 2: Parameter estimation and identifiability.

a Best fit (blue curve) of model parameters (${\mu }_{n}^{on},{\mu }_{m}^{on},{\rho }_{n},$ and ρ_m) to PSA serum time-course data for patient UM10001 (red asterisks). The data point associated with ADT failure is circled. b–e Twice the negative log-likelihood (NLL) is plotted as a function of the fold change in each profiled parameter. Horizontal dashed black lines denote profile-likelihood 95% confidence bounds for each parameter.

We also performed principal component analysis (PCA) to understand the relationships and identify inherent correlations between the four parameters that define the six patients in our clinical cohort. We found that tumor growth rates do not primarily distinguish patients in this cohort, with net PSA expression rates (r_N and r_M) being the dominant factors (see Supplementary Fig. S6).

PSA fold change is a poor predictor of tumor burden

Figure 3 shows the mean and standard deviation of the predicted TVFC (see Eq. 6) from the start of ADT to clinically determined progression to castration resistance. These values are plotted against the PSA fold change over the same period for the virtual clones of six clinical patients. Notably, small PSA fold change values can correspond to either large or small tumor volumes, highlighting the limitations of PSA fold change as a reliable indicator of tumor response to ADT.

Fig. 3: PSA fold change is not consistently correlated with tumor burden.

A plot of the relationship between PSA fold change (PFC) and predicted tumor volume fold change (TVFC, mean and standard deviation) over the period from the start of ADT to the clinically determined progression to castration resistance across virtual clones of six clinical patients.

Although PSA fold change is an unreliable biomarker for ADT-driven tumor volume dynamics, our mathematical model, informed by patient-specific PSA time-course data and experimentally measured PSA expression, predicts—and quantifies the uncertainty in—TVFC measured from the start of ADT to the onset of castration resistance for individual patients. As can be seen from Fig. 3 (vertical axis), there is significant variability in tumor volume responses to therapy at the level of an individual patient. For instance, patient UM10001’s average tumor volume at ADT failure is more than 100% larger than at treatment initiation, whereas UM10003 and UM10099 exhibit substantial tumor reductions despite treatment failure. Since PSA alone fails to capture these diverse tumor responses, model-based analysis is essential for accurately assessing treatment impact, providing a more meaningful measure of tumor progression than PSA readouts alone (see also Supplementary Fig. S7).

Progression-free survival analysis of a heterogeneous population

To complement the earlier results derived from the virtual clones of six patients with clinical data, we conducted a PFS analysis on a more diverse population beyond the limited clinical dataset. Specifically, we generated a heterogeneous virtual cohort of 6000 patients, as detailed in “Methods” section “Virtual patients,” and predicted tumor growth and PSA dynamics for each individual in the cohort. Figure 4a shows the PFS curve, representing the fraction of the virtual cohort remaining progression-free over time, while the accompanying table indicates how many patients remained therapy-failure-free at each time point. Our analysis reveals that nearly 50% of patients experience therapy failure within the first year, while less than 20% remain progression-free after 3 years.

Fig. 4: Progression-free survival and distribution of ADT failure times in a heterogeneous virtual patient cohort.

a The progression-free survival (PFS) curve showing the fraction of the virtual patient cohort remaining progression-free over time. The accompanying table shows the number of patients for whom therapy had not failed at each time point. b Distribution of ADT failure times across the cohort, highlighting the variability in patient responses. Vertical black lines represent the six patients in the clinical dataset.

Figure 4b further supports these findings by illustrating the distribution of ADT failure times across the cohort. Most patients fail treatment within 3 years, and only a small subset exhibits limited disease progression beyond 6 years. Our findings emphasize the variability in treatment responses within a heterogeneous virtual population and demonstrate the utility of our approach in identifying rare outcomes, such as patients who benefit substantially from therapy by experiencing very late treatment failure.

Figure 5a shows the parameter distributions for the 6000 virtual patients in our heterogeneous cohort, revealing three natural clusters (low, medium, high) for each of the four tumor growth parameters. This observation led us to investigate differences in PFS among these parameter-based groups. To ensure balanced group sizes and avoid dealing with propensity score matching, we selected a subset of 3000 patients—1000 patients each in the low, medium, and high ranges.

Fig. 5: Tumor-specific characteristics mediate therapy failure in virtual patient cohorts.

a Distributions of the four tumor growth and PSA expression parameters characterizing the heterogeneous virtual patient cohort, showing natural clustering into groups with low, medium, and high parameter values. Vertical back lines indicate maximum likelihood parameter values for the six patients in the clinical dataset. b–e Progression-free survival curves for virtual patients stratified by low, medium, and high ranges of each parameter. The accompanying table shows the number of patients for whom therapy had not failed at each time point.

Figure 5b–e compares PFS across these clusters. Notably, r_M (net PSA expression at the start of ADT) and ${\mu }_{M}^{on}$ (net growth rate under ADT) of the CR cells strongly influence PFS, as evidenced by the distinct responses in Fig. 5d, e. Low values of r_M and ${\mu }_{M}^{on}$ yield median PFS times of 1.5 and 6.4 years, respectively, whereas high values reduce PFS to 0.34 and 0.67 years, underscoring the dominant effect of ${\mu }_{M}^{on}$ on disease progression. Because r_M encodes the initial population of CR cells (Eq. 3), these results suggest that although this initial cell burden matters, CR cell growth rate is far more critical.

In contrast, the corresponding androgen-dependent (AD) cell parameters exert minimal impact on patient outcomes (Fig. 5b, c). This finding implies that early PSA declines following ADT have limited prognostic value beyond confirming that most of the tumor is AD.

ADT-induced initial decline in PSA has limited predictive value for ADT failure timing

The above results suggest that ADT-induced decreases in PSA levels may not reliably predict therapy failure times. To explore this further, we focus on virtual clones of patients in our clinical dataset. For each patient, we examine how the number and timing of PSA measurements taken prior to the serum PSA nadir affect the model’s predictions of time to ADT failure.

Using the orthogonal design strategy outlined in the section “Orthogonal design,” we introduced up to three theoretical PSA measurements between the start of ADT and the PSA nadir for each patient. We also sequentially added clinical PSA measurements taken after the nadir. Incorporating additional post-nadir PSA measurements mimics how the predictive model evolves alongside a patient’s clinical management. With each clinic visit and additional PSA data, uncertainty in parameter estimates decreases, and consequently, the model’s accuracy in forecasting ADT failure improves. This process is visualized in short movies (see Data Availability statement), which show how successive post-nadir PSA measurements refine the predicted failure times by reducing the uncertainty in the selection of a patient’s virtual clones.

Figure 6 presents screenshots of these movies for two randomly selected patients, UM10001 (top row) and UM10035 (bottom row). Each panel for a given patient corresponds to a row in the orthogonal design Table 4 and displays the PSA time courses and the predicted versus actual ADT failure times for each patient clone. In each panel, the yellow dashed line marks the earliest time of ADT failure among all clones of the patient, while the PSA time courses for individual clones are shaded yellow from the point of their respective ADT failures. Serum PSA at the actual time of clinical progression is marked by two concentric circles. The panels correspond to distinct experimental protocols outlined in the orthogonal design trial table, with “known” PSA data shown as black asterisks and “future” PSA data as red asterisks. The selected snapshots illustrate instances where the predicted ADT failure time remained unchanged despite incorporating additional post-nadir PSA measurements (red asterisks). Similar screenshots for all other patients are available in the Supplementary Information (Supplementary Figs. S9–S12).

Fig. 6: Limited predictive power of pre-nadir PSA decline.

a Patient UM10001 and b patient UM10035. The four panels correspond to the rows in the orthogonal design trial table (Table 4). Dark gray asterisks represent the “known” data points used to inform model parameters. Red asterisks indicate “unknown” data points that have not yet been incorporated into the model. The last gray asterisk represents the present time. The gray asterisk within a single circle denotes the clinically measured PSA nadir, and the red asterisk within two concentric circles marks the time of clinical failure. The yellow vertical dotted line represents the earliest predicted ADT failure time. The yellow shaded area indicates the 95% confidence interval during the period when treatment failure is predicted. The light gray shaded area represents the 95% confidence interval before therapy meets the failure criterion.

For all patients, the prediction of ADT failure time is unaffected by the number of measurements taken before the PSA nadir. These findings suggest that pre-nadir PSA measurements have minimal influence on the accuracy of ADT failure time predictions.

Capturing PSA levels post-nadir enables accurate predictions of time to ADT failure

We now examine how the number and timing of PSA measurements taken after the PSA reaches its nadir influence the model’s predictions of time to ADT failure for patients in the clinical dataset.

Using the orthogonal design strategy outlined in the section “Orthogonal design,” we introduced up to six theoretical PSA measurements, equally spaced between the PSA nadir and the final clinical PSA measurement for each patient. Clinical PSA measurements before the nadir were left unchanged. As in the previous subsection, we sequentially added theoretical post-nadir measurements to mimic how the predictive model evolves alongside a patient’s clinical management. ADT failure times were computed for each clone and each patient. As before, the model’s accuracy in forecasting ADT failure improved with each additional PSA data point collected during the theoretical clinic visits. The process is visualized in short movies (see “Data availability” statement).

Figure 7 presents screenshots from these movies for a randomly selected patient (UM10003). As before, each panel corresponds to the indicated row number in the orthogonal design table (Table 3) and displays PSA time courses and the predicted time of ADT failure for each patient clone. Our model also predicts the probability that the patient will be determined to have progressed to ADT failure at each future clinical visit, with these probabilities displayed directly below the planned visit times in each panel. These probabilities are calculated as the percentage of virtual clones that will fail treatment at each respective visit. Similar screenshots for all other patients are available in the Supplementary Information (Supplementary Figs. S13–S17).

Fig. 7: Predictive power of post-nadir PSA increase.

Patient UM10003. The eight panels correspond to the indicated row numbers in the orthogonal design trial table (Table 3). Dark gray asterisks represent the “known” data points used to inform model parameters. Red asterisks indicate “unknown” data points that have not yet been incorporated into the model. The last gray asterisk represents the present time. The gray asterisk within a single circle denotes the clinically measured PSA nadir, and the red asterisk within two concentric circles marks the time of clinical failure. The yellow vertical dotted line represents the earliest predicted ADT failure time. The yellow shaded area indicates the 95% confidence interval during the period when treatment failure is predicted. The light gray shaded area represents the 95% confidence interval before therapy meets the failure criterion. Bar plots below each panel indicate probability that the patient will be determined to have progressed to ADT failure at each future clinical visit.

Taking Panel 1 in Fig. 7 as an illustrative example, we see that with five PSA measurements post-nadir, the model predicts with 100% confidence that the patient will fail ADT by the next visit, aligning closely with the actual failure time (two concentric circles). Similarly, the other panels demonstrate that the model can maintain high confidence in predicting treatment failure even with fewer post-nadir PSA measurements. For instance, in Panel 2, with just a single PSA measurement post-nadir, the model predicts with 100% confidence that the patient will fail ADT at the second scheduled clinic visit from the present time. This prediction would provide the treating clinician with ample notice of likely disease progression. In general, highly probable predicted ADT failure times align closely with actual failure times, with slight discrepancies arising from the fact that the model uses theoretical PSA measurement times rather than the exact timing of patient visits.

These results are qualitatively consistent across all patients in the study, suggesting that our simple model is representative of actual patients and possesses good predictive value.

Discussion

This study presents a data-driven mathematical modeling approach that integrates patient-specific PSA time-course data with experimentally measured PSA expression to predict tumor volume dynamics and ADT failure times in PCa patients. This approach is particularly crucial given the projected global rise in PCa incidence² and the well-documented limitations of relying solely on PSA profiles for prognosis^6,12,13. By bridging these gaps in current clinical practice, our model provides a basis for more individualized patient care and a deeper understanding of disease progression.

Our findings indicate that inter-patient variability in serum PSA dynamics is driven primarily by differences in PSA expression rates at the onset of treatment, rather than by tumor growth rates under androgen deprivation. This aligns with earlier work⁶, which demonstrated that variability in PSA production rates can lead to significant differences in serum PSA levels among patients with similar tumor burdens. Some mathematical models of ADT have incorporated distinct PSA expression rates for different cancer cell types^10,14, whereas others have assumed uniform expression rates^9,15, potentially overlooking clinically relevant inter-patient differences. Consistent with recent findings¹⁶, our results suggest that failing to account for PSA production variability may lead to an overestimation of its prognostic value. Furthermore, we show that PSA fold change during treatment is an unreliable surrogate for tumor burden, underscoring the need for complementary biomarkers or modeling approaches to improve treatment evaluation and decision-making.

Through a virtual patient cohort analysis, we identified substantial variability in TVFC at the time of ADT failure: some patients failed at smaller tumor burdens than they had at treatment initiation, whereas others progressed with larger tumors. This broad range of outcomes is consistent with clinical findings in ref. ¹⁷, which showed that prostate volumes in patients undergoing ADT could decrease by up to 28% or increase by as much as 38%. We have previously demonstrated⁷ that changes in serum PSA levels, including treatment-induced declines, can also correlate with both tumor growth and shrinkage. This can be due to delays in PSA production, intratumoral heterogeneity, tumor vascular morphology, and other biological factors^6,18,19. Consequently, PSA alone may not reliably capture true disease status.

Clinical evidence further supports the prognostic value of tumor volume, with studies showing that tumor size at radical prostatectomy and tumor-to-prostate volume ratios predict postoperative recurrence²⁰, while whole-body tumor volume estimates derived via PET imaging are significant predictors of overall survival in advanced disease²¹. These findings suggest that incorporating tumor volume measurements into our model—alongside PSA dynamics—could enhance its predictive power, resulting in a more comprehensive framework for oncologists to interpret PSA trends and anticipate treatment outcomes.

The virtual patient cohort analysis also yielded population-level insights into PFS under ADT. PFS varied widely, primarily driven by the growth rate of CR cells and, to a lesser extent, their initial abundance at therapy onset. Our framework also identified “rare” subpopulations with exceptionally long PFS, underscoring its potential to guide more personalized treatment. Notably, the median PFS in our full virtual cohort was around 1 year—shorter than the 2–3 years reported clinically²². However, sub-cohorts with medium-to-low CR cell proliferation rates or low PSA expression at ADT onset had median survival times of at least 2 years. This discrepancy suggests that the real-world population likely skews toward these more favorable parameter ranges, whereas our full virtual cohort—derived from a limited set of six clinical patients—overrepresents more aggressive disease characteristics. As we incorporate additional patient data, we expect these population-level estimates to align more closely with observed clinical outcomes.

Our analysis of PSA measurement timing highlights a critical insight: that the initial PSA decline after ADT offers limited prognostic value, allowing clinicians to avoid intensive monitoring during this phase. Instead, measurements taken shortly after the nadir are far more predictive of future ADT failure, highlighting the importance of post-nadir dynamics. Moreover, our model seamlessly integrates into clinical workflows: as PSA data become available during routine check-ups, it dynamically estimates the probability of ADT failure by the next visit. This real-time forecasting capability enables oncologists to anticipate treatment outcomes and plan interventions proactively, ultimately improving patient care and decision-making.

A major strength of our computational framework lies in its ability to forecast the likelihood of ADT failure in real time, before patients return to the clinic. To keep computations efficient and maintain high confidence in parameter estimates, we made several simplifying assumptions. For instance, we treated the tumor as comprising only two populations—AD and CR cells—despite the well-known genetic and epigenetic heterogeneity of human PCa. Given the challenges of inferring numerous subclones from PSA data alone, these two populations were used to represent an “average phenotype.”

We also assumed constant PSA expression rates throughout treatment and immediate suppression of androgen levels by ADT. In clinical settings, PSA production is more variable, and ADT effects can be gradual. Adjusting these assumptions in future studies is straightforward and could further refine our model. Finally, because our work focuses on continuous therapy, we neglected intercellular competition: under continuous ADT, CR cells eventually outgrow AD cells. Should we explore adaptive therapy protocols, competition dynamics would likely become more important and warrant reintroduction into the model²³.

Overall, this study advances our understanding of PSA dynamics by integrating patient-specific PSA profiles with experimentally measured PSA expression rates. Unlike prior approaches, it offers novel insights into tumor burden and PFS, reinforcing the utility of patient-specific modeling for precision oncology. Future work will expand the model’s capabilities by including additional biomarkers (e.g., genetic or molecular data) and validating its predictive power in prospective clinical trials. By filling key gaps in monitoring and decision-making strategies, our findings underscore the potential of mathematical models to enhance prognostic accuracy, guide timely interventions, and ultimately improve patient outcomes.

Methods

Model development

We develop a mathematical model for PCa growth, with cancer cells assumed to grow exponentially when untreated. We further assume the presence of a small population of CR cells in the treatment-naive tumor, with the majority of the tumor mass comprising AD cells. Under this assumption, the model equations for AD and CR cells prior to treatment are:

$$\begin{array}{rcl}\frac{dN}{dt}\,=\,{\alpha }_{n}^{\,\text{off}}N-{\delta }_{n}^{\text{off}\,}N\,=\,{\mu }_{n}^{\,\text{off}\,}N\qquad &\Rightarrow &N(t)\,=\,{N}_{D}\,{e}^{{\mu }_{n}^{{\rm{off}}}(t-{t}_{D})},\\ \frac{dM}{dt}\,=\,{\alpha }_{m}^{\,\text{off}}M-{\delta }_{m}^{\text{off}\,}M\,=\,{\mu }_{m}^{\,\text{off}\,}M\qquad &\Rightarrow &M(t)\,=\,{M}_{D}\,{e}^{{\mu }_{m}^{{\rm{off}}}(t-{t}_{D})}.\end{array}$$

(1)

Here, N(t) and M(t) are the numbers of AD and CR cells at time t. The above equations are valid for t_D ≤ t ≤ t_X where t_D is the time of diagnosis and t_X is the time at which treatment, in the form of ADT, is initiated. The proliferation and death rates for each cell type under androgen-rich conditions are ${\alpha }_{i}^{\,\text{off}\,}$ and ${\delta }_{i}^{\,\text{off}\,}$, i = n, m, with ${\mu }_{i}^{\,\text{off}}={\alpha }_{i}^{{\rm{off}}}-{\delta }_{i}^{\text{off}\,} > 0$ representing their net growth rates. N_D and M_D represent the initial populations of AD and CR cells, respectively, at time t_D.

The model equations for AD and CR cells, after ADT is initiated, are:

$$\begin{array}{rcl}\frac{dN}{dt}\,=\,{\alpha }_{n}^{\,\text{on}}N-{\delta }_{n}^{\text{on}\,}N\,=\,{\mu }_{n}^{\,\text{on}\,}N\qquad &\Rightarrow &N(t)\,=\,{N}_{X}\,{e}^{{\mu }_{n}^{{\rm{on}}}(t-{t}_{X})},\\ \frac{dM}{dt}\,=\,{\alpha }_{m}^{\,\text{on}}M-{\delta }_{m}^{\text{on}\,}M\,=\,{\mu }_{m}^{\,\text{on}\,}M\qquad &\Rightarrow &M(t)\,=\,{M}_{X}\,{e}^{{\mu }_{m}^{{\rm{on}}}(t-{t}_{X})}.\end{array}$$

(2)

The above equations are valid for t≥t_X. The proliferation and death rates for each cell type under ADT are ${\alpha }_{i}^{\,\text{on}\,}$ and ${\delta }_{i}^{\,\text{on}\,}$, i = n, m, with ${\mu }_{i}^{\,\text{on}}={\alpha }_{i}^{{\rm{on}}}-{\delta }_{i}^{\text{on}\,}$ representing their net growth rates. Under therapy, we will expect ${\mu }_{n}^{\,\text{on}\,} < 0$ and ${\mu }_{m}^{\,\text{on}\,} > 0$. N_X and M_X represent the initial populations of AD and CR cells, respectively, at the start of therapy. Note that N_X and M_X can be determined from Eq. (1) as follows: ${N}_{X}={N}_{D}{e}^{{\mu }_{n}^{{\rm{off}}}({t}_{X}-{t}_{D})}$ and ${M}_{X}={M}_{D}{e}^{{\mu }_{m}^{{\rm{off}}}({t}_{X}-{t}_{D})}$.

For simplicity, serum PSA concentration is assumed to be a linear combination of the N and M cells:

$$P(t)\,=\,{\rho }_{n}N(t)+{\rho }_{m}M(t)\,=\,{r}_{n}{e}^{{\mu }_{n}^{{\rm{on}}}(t-{t}_{X})}\,+\,{r}_{m}{e}^{{\mu }_{m}^{{\rm{on}}}(t-{t}_{X})}.$$

(3)

where ρ_n and ρ_m are the PSA production rates per AD and CR cell, respectively, and r_n = ρ_nN_X and r_m = ρ_mM_X.

We note that the off-treatment model Eq. (1) is included here only for completeness. Because our analysis focuses exclusively on continuous ADT administration, the off-treatment parameters ${\mu }_{n}^{\,\text{off}\,}$ and ${\mu }_{m}^{\,\text{off}\,}$ do not influence the results presented, and are consequently not estimated.

Finally, in this modeling framework, we do not explicitly include competition between AD and AR cells (as in ref. ²³), since such competition terms typically represent the fitness cost of resistance and would be relevant in intermittent treatment scenarios (e.g., adaptive therapy). Here, our analysis focuses exclusively on continuous ADT, where these competition dynamics are less pertinent.

Experimental data

PCa cell lines LNCaP and C4-2B were used as they are androgen-responsive and androgen-independent cell lines²⁴, respectively, to reflect these aspects of PCa. The cells were plated in triplicates in 12-well plates (Corning, Corning, NY) at an initial cell density of 3 × 10⁵ cells per 1 mL in each well. On the following day, cells were treated with a 1 μM stock solution of the synthetic androgen R1881 (Millipore Sigma, Burlington, MA) to a final concentration of 0, 0.1, 1, or 10 nM. Forty-eight hours after treatment with R1881, conditioned media and cells were harvested. Cells were quantified using a Countess II automated cell counter (Life Technologies, Carlsbad, CA). PSA was measured in the conditioned media (in duplicates) using the Human Kallikrein 3/PSA Quantikine ELISA Kit (R&D Systems, Minneapolis, MN) per the manufacturer’s directions. The PSA values were compared as ng/mL (the original result from the ELISA) and ng/cell (ELISA result divided by the cell count at the time of harvest). Statistical significance was determined using one-way ANOVA and Fisher’s Least Significant Difference for post-hoc analysis.

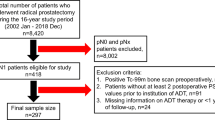
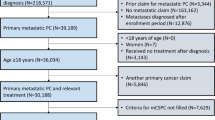
Clinical data

Patients were selected from a Human Subjects Internal Review Board-approved de-identified internal retrospective database of genomically sequenced PCa patients with metastatic disease. The patients were screened for having initiated ADT and if they had increasing PSA values at least a week apart. Clinical characteristics of patients included in this study are summarized in Table 2. This study involves analysis of pre-existing de-identified patient data, and no new data collection from human subjects was conducted specifically for this work.

Table 2 Clinical characteristics of patients

Parameter profile-likelihood analysis

To determine the practical identifiability of our model parameters given each set of patient data, we use the profile-likelihood method described in refs. ^25,26. Practical identifiability examines how real-world data affects our ability to uniquely estimate model parameters and is a means to quantify uncertainty in parameter estimates. Briefly, this approach “profiles” a single parameter by holding it fixed across a range of values, and estimating all remaining parameters for each fixed value of the parameter of interest. The likelihood profile for the fixed parameter is generated by identifying the maximum value of the likelihood function (or the lowest value of the sum of squares if employing least squares, which is equivalent to the NLL) for each specific parameter value.

We also use the likelihood profiles to calculate likelihood-based 95% CIs for each parameter. Specifically, the 95% confidence region for the ith parameter is defined as the set encompassing all permissible values for this parameter, as outlined below:

$$\left\{{\theta }_{i}\left\vert \right.\,2(LL({\theta }_{i}^{* })-LL({\theta }_{i})) < {\Delta }_{0.95}\right\}\qquad \,{\text{with}}\,\qquad {\Delta }_{0.95}={\chi }^{2}(0.95,df).$$

(4)

Here, LL is the log-likelihood function, ${\theta }_{i}^{* }$ is the best-fit value of the model parameter θ_i, the threshold Δ_0.95 is the 0.95 quantile of the χ²-distribution, and df is the total degrees of freedom, that is, the number of model parameters. Specifically, we assume that as we profile a parameter, twice the difference in log-likelihood is a chi-squared distribution. For more details on how to compute these likelihood-based CIs, we refer the reader to ref. ²⁷. In our case, these CIs are computed with df = 4 and assuming the error in PSA measurement data follows the standard normal distribution with zero mean and standard deviation σ = 8% of the measured value, as reported in ref. ²⁸.

Virtual patients

In our computational framework, each “virtual” patient undergoing ADT is determined by four positive parameters: $-{\mu }_{n}^{\,\text{on}\,}$, the (negative) net rate of AD cell growth under ADT; ${\mu }_{m}^{\,\text{on}\,}$, the net rate of CR cell growth under ADT; r_n, the net level of PSA expression by AD cells at the start of ADT; and r_m, the net level of PSA expression by CR cells at the start of ADT.

Virtual clones or digital twins²⁹ of each of our six patients are constructed by considering all possible combinations of the model parameters ${\mu }_{n}^{\,\text{on}\,}$, ${\mu }_{m}^{\,\text{on}\,}$, r_n and r_m, that lie within their respective 95% likelihood-based CIs, as determined from fitting to PSA time-course data. In addition, we define α(=ρ_m/ρ_n) as the relative rate of PSA expression by CR versus AD cells, and use it as a fifth parameter for our virtual patient. α is sampled uniformly from its mean plus or minus one standard deviation, and is estimated from PSA expression data as described in the section “PSA expression data.” Thus, each virtual patient is represented by a vector of sampled values for these five parameters.

To create a more representative and diverse set of virtual patients, reflecting a broader real-world population beyond the initial six individuals, we independently sample the likelihood-informed parameter ranges for each of the four model parameters (${\rho }_{n},{\rho }_{m},{\mu }_{n}^{on},{\mu }_{m}^{on}$). Specifically, we sample these parameters one thousand times from their respective distributions for each patient, resulting in six thousand values for each parameter. We then employ Latin Hypercube Sampling to randomly group these parameter values, creating a matrix 6000 × 4, each row of which represents a virtual patient.

Criteria for ADT failure

Following clinical protocols^30,31, a virtual patient in our simulations fails ADT when all three criteria are met:

• a. The current PSA level is 25% higher than that at the nadir.

• b. The current PSA level is 2 units (ng/mL) higher than that at nadir.

• c. There have been at least two consecutive increases in the PSA measurement.

Principal component analysis

We take individual patient parameters ${\mu }_{n}^{\,\text{on}\,}$, ${\mu }_{m}^{\,\text{on}\,}$, r_n and r_m as variables for the PCA. Given that these parameters vary in units and magnitudes, we standardize each variable by subtracting its mean and dividing by its standard deviation. This z-score normalization ensures that each parameter contributes equally to the analysis, thereby avoiding any bias due to scale differences.

$${z}_{ij}=\frac{{\theta }_{ij}-{\bar{\theta }}_{j}}{{\sigma }_{j}},$$

(5)

where θ_ij is the ith value of the parameter θ_j, and ${\bar{\theta }}_{j}$ and σ_j are the mean and standard deviation of parameter θ_j across all patients. The PCA was implemented using the PCAfun function in MATLAB, which uses singular value decomposition to calculate the principal components.

Tumor volume fold change

We calculate the TVFC from the start of ADT (at time t = t_X) to the clinical determination of progression to castration resistance (at time t = t_C) for each virtual patient clone as follows.

$$\begin{array}{ll}TVFC=\frac{\#\,{\text{of}}\,{\text{tumor}}\,{\text{cells}}\,{\text{at}}\,{\text{castration}}\,{\text{resistance}}}{\#\,{\text{of}}\,{\text{tumor}}\,{\text{cells}}\,{\text{at}}\,{\text{start}}\,{\text{of}}\,{\text{ADT}}}\,\\ \qquad\quad\,\,=\frac{{N}_{X}{e}^{{\mu }_{N}^{on}({t}_{C}-{t}_{X})}\,+\,{M}_{X}{e}^{{\mu }_{M}^{on}({t}_{C}-{t}_{X})}}{{N}_{X}\,+\,{M}_{X}}\\\qquad\quad\,\, =\frac{\alpha \,{r}_{n}{e}^{{\mu }_{N}^{on}({t}_{C}-{t}_{X})}\,+\,{r}_{m}{e}^{{\mu }_{M}^{on}({t}_{C}-{t}_{X})}}{\alpha \,{r}_{n}\,+\,{r}_{m}},\end{array}$$

(6)

where α = ρ_M/ρ_N is the ratio of PSA expression rates by CR and AD cells as determined in the section “PSA expression data.”

Orthogonal design

We used an orthogonal design study³² to assess the impact of increasing the number of clinical PSA measurements prior to its nadir on our model’s ability to predict the time to androgen ablation failure for a given patient. We also used an orthogonal design study to predict times of ADT failure for each virtual patient based on equally spaced PSA measurements made after its nadir.

Orthogonal design is an experimental methodology employed in various fields, including operations research and healthcare³³, to structure experiments such that the effects of different factors can be independently estimated without confounding. This approach emphasizes providing maximum information with a minimal number of experiments.

To evaluate the impact of post-nadir PSA measurements on the model’s ability to predict the time to androgen ablation failure, we assumed six equally spaced possible measurement times post-PSA nadir and prior to clinical failure for each virtual patient (pos1 through pos6), resulting in the design Table 3 (six effects with two levels: 1 indicating a PSA measurement was taken and 0 indicating a PSA measurement was not taken). With the orthogonal study design, we need to test only 8 out of the 63 possible PSA measurement schedules, significantly reducing the computational burden, given that each patient in our study has 1000 digital twins, whose PSA measurements are simulated in this manner. Clinical PSA measurements at these theoretical time points were approximated using the best-fit parameters from Eq. (3) for each patient.

Table 3 Orthogonal design for post-nadir measurements

To evaluate the impact of capturing the initial decline in PSA following ADT, that is, early pre-nadir PSA measurements on the model’s ability to predict the time to androgen ablation failure, we assumed three possible measurement times pre-PSA nadir for each virtual patient (pos1 through pos3), resulting in the design Table 4 (three effects with two levels: 1 indicating a PSA measurement was taken and 0 indicating a PSA measurement was not taken). The time intervals between these measurements were patient-specific, with each time step representing an equivalent reduction in PSA levels. To ensure consistency when comparing patients, the clinically measured data points strictly between PSA at ADT onset and PSA nadir were removed from this analysis.

Table 4 Orthogonal design for pre-nadir measurements