Quantitative evaluation of thermal runaway in lithium-ion batteries under critical heating conditions to enhance safety

Abstract

Thermal stability in lithium-ion batteries is crucial for ensuring safety in energy storage systems and electric vehicles, where thermal runaway poses significant risks due to localized heating and the uncontrolled propagation of exothermic reactions. This study investigates the thermal dynamics in lithium-ion batteries under various critical heating conditions using a three-dimensional finite volume model. The research examines the effects of heating power, heating positions, and cell spacing on thermal runaway propagation patterns, focusing on both single-cell and multi-cell battery pack configurations. Analysis revealed that the direction of heat flow plays a significant role in thermal behavior, with side heating leading to faster runaway and central heating initially delaying initiation before accelerating at specific thresholds. Key findings indicate that lithium iron fluoride cathode materials exhibit superior thermal stability compared to nickel-manganese-cobalt-aluminum oxide types, and increasing cell spacing reduces the severity and timing of thermal runaway. A comparative evaluation of heating scenarios—side, central, and vertical—highlighted vertical 20 mm heating as the safest option. Moreover, the study details the heat release dynamics of different chemical processes: the negative solvent contributed the most significant heat generation (1.78 kW), while the solid electrolyte interphase layer produced the lowest (0.133 kW). Non-linear impacts of heating power were also observed, with a 7 kW/m² configuration producing higher peak temperatures than 10 kW/m² and resulting in an 18% reduction in thermal initiation time. These results improve the understanding of thermal runaway under varying conditions and provide insights for designing safer lithium-ion battery systems, with implications for thermal management in automotive, aerospace, and energy storage applications.

Introduction

While fossil energies remain the primary source of energy globally, their extensive use poses significant challenges, including environmental degradation, greenhouse gas emissions, and depletion of finite resources. These issues not only threaten ecological balance but also undermine the long-term sustainability of energy systems^1,2. LIBs (lithium-ion batteries) offer superior energy density and efficiency, making them ideal for EVs (electric vehicles) by providing longer driving ranges and quicker charging times^3,4. Lithium-ion batteries face challenges such as the risk of thermal runaway (TR), where excessive heat buildup can lead to uncontrollable reactions, potentially causing fires or explosions^5,6. Thermal runaway is a chain reaction in lithium-ion batteries where excessive heat triggers uncontrolled chemical processes, potentially leading to fires, explosions, and system failures^7,8. Thermal runaway begins when a lithium-ion battery experiences internal or external heating beyond safe limits, often caused by overcharging, physical damage, or internal short circuits^9,10. This leads to a cycle of heat buildup that triggers chemical reactions, releasing more heat and gases, eventually resulting in venting, fire, or explosion^11,12. Thermal runaway is characterized by rapid temperature rise, excessive heat generation, gas venting, increased battery pressure, and its likelihood is influenced by the SOC (State of Charge), which rapidly decreases during the event but plays a role in the initial risk level^13,14.

One of the main limitations of LIBs from the perspective of thermal runaway is the risk of uncontrollable chain reactions due to excessive heat, which can lead to fires, explosions, and system damage^15,16. The thermal energy generated can lead to the decomposition of battery materials and release of flammable gases¹⁷. To reduce the impacts of thermal runaway in LIBs, measures such as advanced cooling mechanisms, thermal barriers, and the development of non-flammable electrolytes can be adopted^18,19. Furthermore, efficient cell organization within battery modules improves heat management and minimizes the risk of thermal propagation between cells^20,21.

Many studies focus on improving the energy capacity and density of batteries, but these developments can also raise the risk of thermal runaway caused by the battery’s increased energy content^22,23. Gao et al.²⁴ reported that the Gallium-doped α-MnO₂ nanowires could enhance stability, conductivity, and ion diffusion, improving capacity and cycle durability. The potential for lithium-ion batteries to fire presents a substantial risk to numerous applications, particularly in the transportation sectors. Analysis of government safety data by USA TODAY indicates that there have been a minimum of nine occurrences of fires caused by lithium-ion batteries aboard aircraft or in cargo intended for aircraft since 2005²⁵. A battery pack, consisting of numerous LIBs, poses the possibility of one cell failure causing the ignition of other cells, resulting in widespread explosions²⁶. Chen et al.²⁷ conducted a study on the thermal runaway behavior of cylindrical 21,700-LIBs. They reported that fully charged cells exhibited aggressive fire behavior and highlighted the difficulty of comprehending the spread of TR (thermal runaway) among cell groups purely based on experimental studies.

In recent times, a significant number of benchmark experimental studies have been carried out to examine the spread of thermal runaway in battery packs^28,29,30,31. Wang et al.³² employed custom thermal testing apparatus to carry out research on polymer lithium-ion battery cells including diverse cathode materials. Their research revealed that the composition of the cathode, the speed at which it is heated, and the surrounding temperature have a substantial influence on the thermal and gas emissions produced by the packs. Cao et al.³³ reported that the Cross-linked K₂Ti₄O₉ nanoribbons enable stable, high-capacity, and long-lasting performance as additive-free anodes for lithium-ion batteries. In³⁴, the impact of cell size and the placement of short-circuits on heat retention in LIBs was investigated using experimental methods. A subsequent investigation³⁵ further examined the heat production of the battery, ascribing it to electrochemical reactions, convective heat transfer, and ohmic heating. The study indicated that variables such as thermal conductivity, electrode thickness and materials, and discharge rate were pivotal in determining the amount of heat generated by the battery.

Yue et al.³⁶ evaluated the TR characteristics and hazards of different types of 18,650 batteries (i.e., sodium-ion and lithium-ion) under various cathode materials. In the presence of natural convection, an NTM battery that was fully charged had the potential to ignite without external influence when the storage temperature surpasses 169.6 °C. Zou et al.³⁷ conducted an empirical analysis on the TR-propagation situation of the LIB module in situations where insulation materials were not utilized and with a variety of insulation materials. Mao et al.³⁸ investigated the utilization of varying thicknesses of aerogel felts and yttria-stabilized zirconia ceramic plates (5%) in creating a 3-mm-wide composite material aimed at inhibiting TR-propagation of LIBs. The most effective layout was determined to be a combination of 1 mm-aerogel felt and 2 mm-zirconia ceramic. Meng et al.¹¹ conducted a study on the thermal properties and fire responses of LIBs exposed to varying charging rates and without charging preconditioning across different incident heat fluxes through the utilization of a cone calorimeter.

Recent studies have explored TR behaviors in LIBs and methods to improve safety. Zhou et al.³⁹ found medium overcharged 18,650-type NCM523 batteries produced larger flame areas compared to high and low-level overcharging. Lai et al.⁴⁰ analyzed TR-propagation in nickel-rich and silicon-carbon electrodes, proposing a scalable model for larger systems. Lin et al.⁴¹ showed semi-solid electrolyte LIBs had slower temperature rise and higher gas production but demonstrated better safety at 100% SOC. Xu et al.⁷ reported no TR in Li(Ni0.6Co0.2Mn0.2)O₂ modules with SOC below 25% in confined spaces. Peng et al.²⁹ revealed surfactant-generated foam effectively reduced TR severity. Ping et al.⁴² showed liquid nitrogen effectively stopped TR-propagation in confined spaces but not semi-confined spaces. Xie et al.⁴³ identified human factors as a major cause of fires in LIB warehouses, while Li et al.⁴⁴ observed increased transport risks from self-heating after four hours. These findings enhance understanding of TR mechanisms and safety strategies across diverse LIB applications.

In⁴⁵, a thermal-electrochemical approach was employed to evaluate the TR characteristics of distinct LIBs types. Their suggestion was that implementing targeted cooling solutions could have a substantial impact on the thermal characteristics of the batteries, hence aiding in the TR prevention or reduction. In⁴⁶, a theoretical model to analyze thermal abuse in battery packs was developed. Feng et al.⁴⁷ provided a comprehensive analysis of thermal failure, which can be divided into distinct phases: separator melting, disintegration of the SEI coating, reaction at the anode, interaction between the electrolyte and cathode, and the occurrence of extensive internal short circuit. In⁴⁸, the TR-propagation in both longitudinal and transverse directions was investigated. They observed that the longitudinal propagation was slower because it had the reduced heat transfer area and an extended transfer route. Moreover, the rate of propagation was higher in the direction of the positive pole as compared to the opposite way. The literature^49,50 also examined the utilization of PCMs (phase change materials) to store heat in battery cells and maintain acceptable operational temperatures, provided that they were utilized in appropriate quantities and melting points. Nevertheless, the use of PCMs for battery heat management was typically impracticable due to their limited heat absorption capabilities. Therefore, it is advisable to choose a combined thermal management approach that incorporates active cooling methods (e.g., forced/natural air or water cooling) as reported by references^51,52.

Sheng et al.⁵³ developed an innovative cooling plate to regulate temperature distribution in LIBs, finding that flow rate increases significantly reduce cell temperature rise, while channel width minimally affects temperature distribution but impacts power consumption. Additionally, they designed a cooling jacket for a 21,700 cell, conducting numerical and dimensionless analyses to evaluate its thermal performance, supported by test bench validation⁵⁴. Reference⁵⁵ proposed a method to assess heat generation in large-format LIBs under high and low temperatures, aiding battery thermal design. Reference⁵⁶ explored the anisotropic thermal conductivity of LIBs, offering insights on in-plane vs. cross-plane conductivity through experimental validation. Sheng et al.⁵⁷ further identified gaps in thermal behavior characterization for aluminum-air batteries. Lastly, Reference⁵⁸ presented a heat generation measurement method for cylindrical LIBs, showing that lower temperatures and higher discharge rates increase heat generation.

Thermal runaway in lithium-ion batteries represents a critical safety concern, especially in applications such as electric vehicles and large-scale energy storage systems. The inherent instability of these batteries under certain conditions particularly localized heating or internal short circuits, can lead to catastrophic failure if not properly managed. Extensive research has been conducted on the mechanisms of TR, with a focus on factors such as material decomposition, internal short circuits, and electrolyte reactions. Several studies have addressed the importance of the heating position and cell spacing in thermal propagation within battery modules. However, despite the growing body of literature, there remain significant gaps in understanding how specific heating conditions and spatial configurations influence TR dynamics in real-world battery packs. In particular, the impact of different heating intensities and positions on the dissipation of heat and temperature gradients across both individual cells and multi-cell configurations has not been sufficiently explored. Furthermore, the role of flow direction and its influence on thermal propagation patterns has not been adequately quantified, nor has the effect of cell spacing been studied in a non-linear manner.

To address these gaps, this study presents a numerical analysis of an isolated cell, examining different critical heating locations and power settings. Furthermore, a thorough examination of TR in a 3 × 3 battery pack is conducted using a multi-scale/multi-dimensional model, with modifications made to characteristics such as the position of cell heating and the spacing between cells within the pack. This enhanced focus on the localized and systematic impacts of heating conditions allows us to draw significant conclusions regarding the operational safety and risk management of lithium-ion battery systems. By elucidating the complex dynamics of thermal runaway and identifying key factors influencing its propagation, this work contributes significantly to the field of process safety and risk engineering. The findings not only aid in the prevention of hazardous conditions that could lead to severe accidents but also enhance the design and operational safety strategies for energy storage systems. This study thus serves as a foundational piece for future research aimed at mitigating risks associated with lithium-ion batteries in both automotive and grid-scale applications. The novelty of this work lies in its detailed examination of heating position effects, identification of flow direction as a critical factor in heat dissipation, and the non-linear analysis of cell spacing on TR timing. This research offers a new perspective on thermal management strategies, enabling more robust and safer battery pack designs. Therefore, the main contributions of the present article are summarized as:

• A three-dimensional, multi-scale finite volume model was developed to investigate the effects of heating location, power density, and cell spacing on thermal runaway in both single-cell and module-level configurations.

• A comprehensive spatial analysis revealed how flow direction and heat dissipation paths affect the severity and propagation of thermal runaway, identifying vertical heating as the safest configuration.

• A quantitative ranking of heat generation from distinct chemical reactions—especially identifying negative solvent reactions as dominant contributors—was presented to guide safer battery design.

Methodology

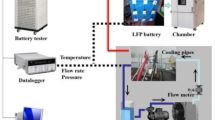
The impacts of critical situations on both the cell and module are being investigated using a three-dimensional numerical model, implemented with the ANSYS FLUENT solver, which employs a finite volume method. This study specifically examines the 21,700 LIB-cell, which is comprised of several layers, including the separator, negative/positive electrodes, and collectors made of both copper and aluminum. In order to reduce the computing requirements, the jelly roll, which initially consists of a mixture with a fine structure, has been represented as a 3D solid structure that is uniform throughout^45,59,60. In this section, the thermal/electrochemical model of the battery is developed.

• Thermal model

The main method by which heat is transferred in the cell is through thermal conduction, as explained in Eq. (1). Conduction is the primary mechanism for internal heat flow in the modes of heat transfer, which include conduction, convection, and radiation^61,62.

$$\left\{ \begin{gathered} Q_{tot} + \nabla .\left( {k\nabla T} \right) = \rho .C_{P} \frac{\partial T}{{\partial t}} \hfill \\ Q_{tot} = \sum\limits_{t} {Q_{t} } \hfill \\ \end{gathered} \right.$$

(1)

Here t: anode, cathode, electrolyte, separator, SEI, and binder.

The equations that describe the energy interactions between the cell and its environment, as well as between the cell and the heater, are denoted by Eqs. (2):

$$\left\{ \begin{gathered} Q + k\frac{\partial T}{{\partial m}} = 0 \hfill \\ \varepsilon \sigma .\left( {T_{a}^{4} - T^{4} } \right) + h.\left( {T_{a} - T} \right) + k\frac{\partial T}{{\partial m}} = 0 \hfill \\ \end{gathered} \right.$$

(2)

In this context, the symbol ρ represents the density of a substance, $h$ represents the convective coefficient. Further, $T$, $C_{P}$, and $k$ represent the temperature, heat capacity, and thermal conductivity, correspondingly. Moreover, $Q_{tot}$, $\varepsilon$, and $\sigma$ refer to the overall heat released at TR, emissivity of the cell’s surface, and Stefan-Boltzmann constant, correspondingly.

• Electrochemical model

The SEI-layer is essential in ensuring the appropriate operation of the LIB by serving as a protective shield that inhibits additional interactions between the electrolyte and the electrode material. The SEI-layer can undergo decomposition as a result of elevated temperatures, excessive charging or discharging, or repeated battery cycling, potentially leading to the creation of a novel stratum that exhibits decreased stability and heightened reactivity. This enhances the probability of interactions between the electrode materials and the electrolyte^21,63. In this regard, the rate of decomposition follows the Arrhenius formula⁶⁴:

$$A_{SEI} .c_{SEI} .\exp \, \left( {\frac{{E_{a,SEI} }}{RT}} \right) + \frac{{dC_{SEI} }}{dt} = 0$$

(3)

The equation that relates the heat emitted during the decomposition of SEI ($Q_{SEI}$) to its decomposition kinetics is stated by:

$$Q_{SEI} = - \frac{{dc_{SEI} }}{dt} \times H_{SEI} .W_{SEI}$$

(4)

Here $E_{a,SEI}$ represents the activation energy, $c_{SEI}$ denotes the dimensionless lithium concentration in the SEI-layer, $R$ represents the universal gas constant, $A_{SEI}$ refers to the frequency factor, $W_{SEI}$ indicates the SEI content in the jelly roll, and $H_{SEI}$ represents the heat produced at decomposition process.

According to the breakdown of the SEI layer, a reaction occurs between the anode and electrolyte. This leads to the activation of the safety vent, which allows oxygen to enter the cell, as described in Eq. (5)⁶⁵:

$$A_{anode} .c_{anode} .n.\exp \, \left( {\frac{{E_{a,anode} }}{RT}} \right).\exp \, \left( { - \frac{{c_{SEI} }}{{c_{SEI,ref} }}} \right) + \frac{{dc_{anode} }}{dt} = 0$$

(5)

The amount of heat released per unit volume at the decomposition of the anode is measured using Eq. (6):

$$Q_{anode} = - \frac{{dc_{anode} }}{dt} \times H_{anode} .W_{anode}$$

(6)

here $c_{anode}$ denotes the dimensionless lithium concentration in the carbon compound, $A_{anode}$ represents the frequency factor, $E_{a,anode}$ stands for the activation energy post-thermal onset, $H_{anode}$ denotes the emitted heat (per unit mass), and $W_{anode}$ represents the specific lithium content in the jelly roll.

The separator is essential for maintaining a barrier between the cathode and anode, ensuring that direct contact is avoided, and facilitating the movement of lithium ions via the electrolyte. High temperatures can cause the separator to melt, increasing the danger of direct contact between the cathode and anode, which can result in internal short circuits¹². An internal short circuit, as described by the Arrhenius formula, converts electrical energy into thermal energy through a single-step chemical process, as shown in Eq. (7):

$$\left\{ \begin{gathered} A_{separator} .T_{ISC} .SOC.\exp \, \left( {\frac{{E_{a,separator} }}{RT}} \right) + \frac{dSOC}{{dt}} = 0 \hfill \\ Q_{separator} = - \frac{dSOC}{{dt}} \times \frac{3600 \times V \times \eta \times C}{{V_{cell} }} \hfill \\ \end{gathered} \right.$$

(7)

The parameters in these equations consist of $\eta$ (efficiency factor), $V$ (cell voltage), $V_{cell}$ (all cells volume), $SOC$ (state of charge ranging from 0 to 1), and $T_{ISC}$ (internal short circuit temperature threshold).

The cathode’s exothermic reaction is expressed by Eq. (8):

$$\left\{ \begin{gathered} A_{cathode} .\alpha_{cathode} .\exp \, \left( {\frac{{E_{a,separator} }}{RT}} \right).\left( {1 - \alpha_{cathode} } \right) + \frac{{d\alpha_{cathode} }}{dt} = 0 \hfill \\ Q_{cathode} = \frac{{d\alpha_{cathode} }}{dt} \times H_{cathode} \times W_{cathode} \hfill \\ \end{gathered} \right.$$

(8)

The emitted thermal power (per unit mass) in this reaction is determined using factors such as $A_{cathode}$ (frequency factor), $\alpha_{cathode}$ (degree of conversion), $W_{cathode}$ (specific cathode content in the jelly roll), and $H_{cathode}$ (emitted heat at the cathode reaction).

Electrolyte decomposition refers to the process of breaking down electrolytes into their constituent elements or ions through the application of an electric current. The electrolyte in lithium-ion batteries is predominantly comprised of a lithium salt that is dissolved in an organic solvent. This component is susceptible to deterioration when subjected to overcharging or prolonged usage, resulting in the generation of heat and gasses⁶⁶. The electrolyte can break down via many mechanisms (e.g., hydrolysis, thermal degradation, and oxidative decomposition). Further, the electrolyte’s related breakdown reaction is detailed in Eq. (9):

$$\left\{ \begin{gathered} A_{electrolyte} .c_{electrolyte} .\exp \, \left( {\frac{{E_{a,electrolyte} }}{RT}} \right) + \frac{{dc_{electrolyte} }}{dt} = 0 \hfill \\ Q_{electrolyte} = - \frac{{dc_{electrolyte} }}{dt} \times H_{electrolyte} \times W_{electrolyte} \hfill \\ \end{gathered} \right.$$

(9)

Binder reaction refers to a chemical process involving the formation of a binder, which is a substance used to hold together particles or materials in a cohesive manner. The binder is crucial for preserving the integrity of the electrode structure by securely binding the active components and conductive additives, thereby assuring structural strength. Once the temperature surpasses 260 °C, the binder initiates decomposition, resulting in the release of heat as indicated in Eq. (10) ^67,68:

$$\left\{ \begin{gathered} A_{Binder} .c_{Binder} .\exp \, \left( {\frac{{E_{a,Binder} }}{RT}} \right) + \frac{{dc_{Binder} }}{dt} = 0 \hfill \\ Q_{Binder} = - \frac{{dc_{Binder} }}{dt} \times H_{Binder} \times W_{Binder} \hfill \\ \end{gathered} \right.$$

(10)

The parameters that determine this reaction are $A_{Binder}$, which represents the frequency factor; $c_{Binder}$, a dimensionless measure of the quantity of the binder; $E_{a,Binder}$, the activation energy of the binder under thermal stress; $W_{Binder}$, the specific content of binder within the jelly roll; and $H_{Binder}$, the released heat at the binder decomposition.

Numerical method

The assessment includes the analysis of both an individual cell and a module using numerical methods. Table 1 provides a comprehensive summary of the specific thermodynamic and kinematic parameters. Figure 1 illustrates the geometric characteristics of the individual cell, which has a diameter of 21 mm and a height of 70 mm. Further, Fig. 2 depicts a 3 × 3 LIB array that is parallelly connected to a copper bus bar. The bus bar is positioned at two separate heating locations. The battery pack has a fixed length of 72 mm, but its width changes depending on the spacing between cells. Table 2 provides a comprehensive list of the different heating settings utilized in the investigation, and also presents the precise characteristics and properties of the cathode materials that were employed. Note that, for the LNCMC (Lithium Nickel Manganese Cobalt Aluminum Oxide Cell) and LIFC types (Lithium Iron Fluoride Cell), the models provided (based on the manufacturer) were Panasonic LNCMC (Tesla Battery Models) and Iron Fluoride Cathode Development (under Argonne National Laboratory).

Table 1 A comprehensive summary of the specific thermodynamic and kinematic parameters, adopted from⁴⁵.

Figure 1

The geometric characteristics of the individual cell.

Figure 2

A 3 × 3 LIB array that is parallelly connected to a copper bus bar.

Table 2 A comprehensive list of the different heating settings utilized in the investigation and the precise characteristics and properties of the cathode materials that were employed^72,73,74.

The simulation parameters incorporate a pressure-based solver with a dynamic scenario, and the multi-scale/multi-dimensional model is enabled to accommodate voltage fluctuations that correlate to variations in SOC. The thermal abuse model incorporates a four-formula kinetic approach within the cell. The material characteristics are obtained from⁶⁹. All boundaries, except for the heating positions, experience mixed conditions consisting of convection and radiation. Radiative heat transfer is crucial at elevated temperatures due to its significant impact. The free stream temperature and the external radiation temperature were both set to 25 °C to represent a thermally neutral ambient environment, in the absence of additional radiative sources. This is a standard assumption in battery thermal modeling to simulate laboratory-scale or controlled operating conditions. Further, the thermal conductivity and external emissivity are specified as 10.26 W/m²K and 0.72, correspondingly. The external emissivity was set to 0.72, which is a typical value for battery casing materials such as aluminum or other metals commonly used in battery packs. This value reflects the high heat dissipation capability of the casing in thermal runaway scenarios, contributing significantly to radiative heat transfer. Further, the thermal conductivity of the external casing was set at 10.26 W/ m²K, corresponding to the typical conductivity of aluminum, which is widely used in battery pack enclosures. This high thermal conductivity ensures efficient heat conduction away from the cell during thermal runaway, thus influencing the propagation patterns observed in the simulation.

The SIMPLE method was utilized for pressure–velocity coupling, while a second-order upwind technique was implemented for the momentum, energy, and pressure formulas to improve the correctness of the outcomes. Further, the battery pack was set up in such a way that one side functions as the entrance for the flow with a velocity of 0.35 m/s, while the opposite side serves as the outlet for the flow with zero gauge pressure⁷⁰. The battery pack’s four outer walls are subjected to mixed convection conditions. The system of coupling pressure and velocity was defined by being associated under a Courant number of 0.66⁷¹.

To ensure the credibility of transitioning from a single-cell to a module-level model, the same thermophysical properties, boundary conditions, and solver settings were consistently applied across both simulations. The module-level model expands the computational domain to a 3 × 3 LIB-cell array (as shown in Fig. 2), while preserving the core modeling approach of the single-cell setup. Each cell within the module maintains identical internal structure, chemical reaction mechanisms, and material properties. The inter-cell spacing was varied systematically, and busbars were introduced to mimic electrical and thermal connectivity. Flow conditions were defined to simulate realistic cooling scenarios, with an inlet velocity of 0.35 m/s and outlet at zero gauge pressure. The mixed convection-radiation boundary condition used for the single cell was retained for the full pack. Local mesh refinement was also applied near inter-cell gaps to ensure accurate resolution of thermal propagation. This modeling consistency supports the feasibility and reliability of extending the single-cell framework to a module-scale thermal analysis.

Results and discussion

Model verification

Figure 3 depicts the comparison between experimental data and numerical simulations for a cathode material of LNCMC type, which is subjected to heating by a polyimide electro-thermal film with a power output of 32.5 W⁴⁵. A tetrahedral mesh with varying cell lengths (1, 1.5, and 2 mm) was created, and temperature characteristics were examined. The experimental results showed that the medium mesh (1.5 mm cell length) had the best alignment. However, the deflection exhibited a maximum error of 8.72%, primarily due to assuming a homogenous structure rather than a jelly roll one⁴⁵. Note that, in the context of this study, the term alignment refers to the spatial arrangement and orientation of the heating positions in relation to the cells within the battery pack. Proper alignment is critical as it affects the flow direction of heat and the propagation of TR throughout the pack. By aligning heating elements in different configurations (such as vertical or central), we can observe distinct patterns of heat dissipation and TR progression, allowing for more accurate predictions of failure points and the optimization of safety measures. The maximum temperature and the temperature at which TR begins closely corresponded to the experimental results. The modeling of this article was also validated with the data and results reported in reference²⁵, which indicates its acceptability. In addition, compared to reference²⁵, improved observations were obtained, which are discussed in the results section. Although a separate grid consistency section was not included, the mesh sensitivity was assessed through this comparison. The 1.5 mm mesh was chosen for its balance between computational cost and accuracy, ensuring stable and reliable outcomes for the complex simulations of thermal runaway in both single-cell and multi-cell configurations.

Figure 3

The comparison between experimental data and numerical simulations for a cathode material of LNCMC type.

It should be noted that Fig. 3 presents model validation under moderate heating conditions (32.5 W from a polyimide electro-thermal film), which represent a low-risk thermal scenario. The mesh and boundary conditions were optimized for validation accuracy. However, in the next sub-section, more critical thermal abuse conditions were simulated using significantly higher heat fluxes to analyze full-scale thermal runaway progression. These elevated temperatures are the result of cumulative internal exothermic reactions and are in agreement with values reported in experimental TR studies involving oxygen release and solvent reactions. While the underlying model assumptions and boundary settings remain consistent across all simulations, the differences in heating power and scenario intensity explain the variation in peak temperatures. The model validation not only demonstrates strong agreement with experimental data but also confirms the reliability of the proposed simulation framework for predicting thermal behavior in both single and multi-cell configurations—laying the foundation for the novel analyses in subsequent sections.

Single cell results

In order to prevent TR, it is essential to create cathode materials that demonstrate enhanced thermal stability. To do this, one must either implement a new design that has higher melting points and lower reactivity, or improve existing cathode designs by adding materials like nickel to enhance thermal resistance. The thermal stability is directly influenced by factors such as internal heat generation, separator features, heat dissipation during different reactions, as well as peak and ambient temperatures. This study provides valuable information on several factors that affect thermal durability.

The TR behavior is greatly influenced by variations in cathode materials, which have a major impact on both the timing and temperature of the event, as reported in⁴⁵. Figure 4-A depicts the temperature distribution of a cell undergoing thermal failure. The analysis was conducted by subjecting the cell to various heat powers ranging from 1.5 to 7 kW/m², under the cathode material being LNCMC. The selection of these particular heating powers is based on the conclusions drawn from previous literature⁴⁵. The temperatures at which thermal runaway was initiated were measured at 35.68 °C, 36.53 °C, 41.8 °C, and 37.21 °C for heat powers of 1.5, 3, 5, and 7 kW/m², respectively. The cell reached its greatest temperatures at different power densities: 945.62 °C at 1.5 kW/m², 947.03 °C at 3 kW/m², 945.28 °C at 5 kW/m², and 948.22 °C at 7 kW/m². Further, raising the heating power by twice resulted in a reduction of 5.85 min in the time it took for thermal runaway to occur. Additionally, raising the heating power by an extra 25% led to a further decrease in the failure time by 0.39 min. The heating process escalated to a level of 7 kW/m², resulting in thermal runaway within a time span of 0.72 min.

Figure 4

Temperature distribution: (A) the temperature distribution of a cell undergoing thermal failure, (B) the temperature distribution of a cell using LIFC as the cathode material, (C) the temperature distribution showing the extent of thermal damage to a LIB under various heat powers, and (D) the temperature distribution that demonstrate thermal harm to the cell when heated in a longitudinal manner along a 20 mm strip starting from the bottom, under changes in heat power.

Figure 4B displays the temperature distribution of a cell using LIFC as the cathode material. When subjected to a heat intensity of 1.5 kW/m², this cell experienced TR after 13.2 min, which is 10.97 min later than the case subjected to a heat intensity of 3 kW/m². The LIFC cathode achieved a maximum temperature that was roughly 24% lower than the LNCMC kind. Upon examining the cooling patterns, there was an absence of any discernible alteration in the cooling curve as the heating output was raised. The thermal failure time difference between 3 and 5 kW/m² was 0.66 min, whereas the difference among 5 and 7 kW/m² was 0.43 min, indicating a 57.6% reduction in the time step compared to the preceding enhancement. Further, the temperatures at which the triggering occurred ranged from 44.4 to 37.65 °C, as the heat power increased from 1.5 to 7 kW/m². The highest temperatures reached for various heat increments were 636.16, 632.56, 633.46, and 637.96 °C, correspondingly.

Figure 4C illustrates the temperature distribution showing the extent of thermal damage to a LIB under various heat powers: 1.5, 3, 5, and 7 kW/m². The convective heat transfer coefficient in this case is 10.26 W/m² K. When subjected to bottom heating, LNCMC type cathode materials have a longer thermal failure time compared to LIFC and LNCMC types. The temperatures at which the peak failures occurred were 714.45 °C for an incident heat flux of 3 kW/m², 710.86 °C for 5 kW/m², and 705.46 °C for 7 kW/m². These failures happened at times corresponding to 9.65th min, 5.29th min, and 3.3th min, respectively. The instances of thermal failure were seen at 9.18 th min, 4.79th min, and 3.23th min, correspondingly. Further, the initial boost in heat flow worsened the TR, causing a drop in duration (4.41 min). This was followed by a further increase, which accelerated the temperature increase to a degree above the melting point of the separator, taking an additional 1.63 min.

The uneven distribution of heat within a lithium-ion battery pack, caused by many connections and varied connection techniques, leads to the absorption of heat at different sites in varying quantities. The heat outflow from the cell can be described as follows⁴⁵:

$$Q_{out} = \varepsilon \times \sigma \times \left( {T_{surface}^{4} - T_{a}^{4} } \right) + S \times h \times \left( {T_{surface} - T_{a} } \right)$$

(11)

here ($S$) indicates the area through which heat is dissipated, and ($T_{surface}$) denotes the average surface temperature of the cell. Figure 4-D depicts the temperature distribution that demonstrate thermal harm to the cell when heated in a longitudinal manner along a 20 mm strip starting from the bottom, under changes in heat power. As demonstrated, the cell, exposed to a heat flux of 5 kW/m², had TR at 44.86 °C, due to six consecutive chemical processes that caused the peak temperature to rise to 720.76 °C. A decrease of 50% in heating power compared to the preceding situation resulted in a delay of 3.3 min in TR. Under a heating power of 1.5 kW/m², the cell experienced heating triggering after roughly 8.14 min, resulting in a TR temperature of ~ 42 °C. The temperatures of the thermal triggering climbed from 41.3 to 44.9 °C as the heating power rose from 1.5 to 4 kW/m².

When the cell was subjected to varying heating powers (1.5, 2, and 4 kW/m²) at its center, the 1.5 kW/m² setting did not trigger thermal runaway for a duration of 23.75 min, indicating that this position is relatively safer (see Fig. 5A). The experiment conducted at a power density of 2 kW/m² failed after 15.55 min, as the temperature reached a peak value surpassing 789.16 °C. Increasing the heating power by a factor of two changed the temperature at which thermal triggering occurred from 48.46 °C to 45.76 °C and interrupted the previously observed consistent increase in temperature at a rate of 2 kW/m². The power increase resulted in an 11.4-min decrease in the duration until failure, going from the 2 kW/m² level to 4 kW/m².

Figure 5

Temperature distribution: (A) the temperature distribution when the cell was subjected to varying heating powers at its center, (B) the temperature profiles of a LIB-cell when subjected to different power levels across a 10 mm wide longitudinal strip, and (C) he temperature distribution when comparing the bottom and vertical heating locations.

Figure 5-B exhibits the temperature profiles of a LIB-cell when subjected to different power levels (2.5, 4, and 6 kW/m²) across a 10 mm wide longitudinal strip. Decreasing the width of the heating strip by 60% resulted in a 2.37 min extension of the thermal runaway duration at a heat flux of 4 kW/m². At 11.3 min, the thermal runaway was initiated by the 2.5 kW/m² setting, resulting in a peak temperature of 715.36 °C. At this particular amount of power, the separator started to undergo the process of melting at a temperature of 45.31 °C, while the electrolyte began to decompose at ~ 100.66 °C. Moreover, increasing the heat power by a factor of two resulted in a decrease in the failure time by 9.05 min.

When comparing the bottom and vertical heating locations, as depicted in Fig. 5C, the power of 5.5 kW/m² at the bottom ceased at 3.23 min, whereas the vertical position ceased at around 12.63 min, showing a lesser degree of severity in vertical heating. The highest temperatures reached by the cells were 774.8 °C, 771.2 °C, and 776.6 °C, corresponding to heating powers of 7.5, 5.5, and 9.5 kW/m², respectively. The duration taken to attain these highest temperatures from the TR’s initial trigger was 0.27, 0.3, and 0.25 min, respectively. A 2 kW/m² increase in heating power led to a 41.28% decrease in the time required for thermal triggering. Subsequent increases in heating power resulted in a 29.76% reduction.

Implementing techniques like employing thermal insulating substances, boosting contact resistance, and upgrading monitoring systems for battery thermal management can significantly reduce the occurrence of thermal failures by identifying areas prone to overheating. Figure 6 illustrates the LIB’s TR when exposed to a power of 4.5 kW/m² under diverse different locations. The bottom end under 20 mm (width) is the most vulnerable position to thermal runaway, but the vertical-20 mm position did not initiate TR within the initial 15.83 min. The time of thermal runaway propagation and the maximum temperature reached are critical factors in ensuring the safety design. The temperature reached consistent thermal levels across different locations, with the exception of the central 20 mm. The safety order, determined by the time to failure, for the developed assessment was as: bottom-10 mm < center-20 mm < bottom-10 mm < bottom-end < vertical-20 mm. Further, the center-20 mm heating has a maximum temperature that surpasses other positions by 54–63 °C. With the exception of the vertical scenario, the TR durations for all other situations varied between 1.58 and 4.75 min, indicating the significant intensity of heating in those regions.

Figure 6

The LIB’s TR when exposed to a power of 4.5 kW/m² under diverse different locations.

Figure 7 depicts the sequential process of TR in a LIB-cell at three distinct heating levels. Thermal runaway is initiated from the bottom position, causing a wave to propagate towards the opposite end. The central position produces two heat waves that propagate towards the positive and negative poles, respectively. A hotspot emerges at the central surface and spreads horizontally in the vertical position, displaying distinct patterns compared to those observed in the center and bottom locations. The highest temperature recorded in each instance exceeds 789.16 °C. As the heat wave recedes, the highest temperatures in the affected areas are noted to decrease. Figure 7A depicts the increase in temperature above the melting point of the separator, indicating the beginning of thermal runaway. Figure 7B depicts the internal-short circuits’ initiation and the degradation of electrolyte.

Figure 7

The sequential process of TR in a LIB-cell at three distinct heating levels.

Figures 7C, D illustrate the point at which thermal runaway reaches its maximum with the rapid breakdown of the anode, cathode, and binder caused by exposure to oxygen in the atmosphere, following the release of pressure from the cell. Figure 7E marks the end of the TR phase, in which both electrodes have fully decomposed. The initiation of the cell’s cooling process is brought about by a combination of radiation and convection. The data on heat transfer levels indicate that the bottom location exhibits the maximum rate as a result of heating at the positive pole, whilst the vertical location demonstrates the minimum rate. This section reveals critical nonlinear effects of heating intensity on thermal runaway onset and propagation, and introduces, for the first time, a comparative safety evaluation of multiple heating positions, establishing new design insights for targeted cell-level protection.

Battery pack results

Cell spacing denotes the separation distance among electrodes within a LIB-cell, and it is an important factor to consider for ensuring safety in the design of battery packs. The spacing between components of the battery has a significant effect on both its safety and mechanical strength. Achieving the desired spacing involves careful planning, taking into account several aspects such as the width of the electrodes, the amount of material being used, and the characteristics of the separator. Figure 8A depicts the TR characteristics of a LIB-cell in a battery array consisting of nine cells arranged in a 3 × 3 configuration. The spacing between the cells is 1, 3, 5, and 7 mm. An aluminum heater of 20 mm in width was used to heat the lower end of a central cell. Cell breakdown was discovered at a spacing of 1 mm, occurring around 5.14 min and reaching a peak temperature of roughly 789.16 °C. By widening the spacing to 3 mm, the larger gap facilitated more efficient convection, resulting in a delay in the occurrence of thermal runaway. The cell experienced a failure after 6.96 min, with the temperature slightly above 744.16 °C. Increasing the distance to 5 mm resulted in a 0.79 min reduction in delay, accompanied by a 27 °C temperature decrease. By increasing the spacing to 7 mm, the time to TR was reduced by an additional 0.55 min. The results suggest that there is a decline in the occurrence of thermal runaway as the distance beyond 3 mm is enlarged.

Figure 8

(A) Thermal runaway (TR) characteristics of the central heated cell (Cell-#34) in a 3 × 3 LIB module under different cell spacing conditions (1, 3, 5, and 7 mm). The temperature curves represent the core temperature at the geometric center of Cell-#34, extracted via a fixed thermal probe and (B) Thermal failure behavior of a side cell in the 3 × 3 configuration, showing core temperature variation under the same spacing conditions. The results highlight the impact of cell spacing on TR onset and peak temperature.

Figure 8-B illustrates a cell’s thermal failure phenomenon in a 3 × 3 LIB configuration with varying spacings: 1, 3, 5, and 7 mm. For this instance, a lateral cell located in the 3rd column and row is subjected to heating using an aluminum heater that had 20 mm (width) and a density of 6 kW/m². In this case, TR was initiated after roughly 7.83 min when the distance between objects was 1 mm. The occurrence of a 3 mm gap took place at around 7.12 min, with an initial temperature of around 49.36 °C. The peak temperature reached around 789.16 °C with a spacing of 5 mm, occurring at approximately 6.65 min. At a 7 mm separation, the peak temperature reached comparable levels, and the thermal runaway occurred at 5.46 min. As the distance between objects rose, the time it took for thermal runaway to occur reduced, although not consistently. This phenomenon stems from a localized variation in heating power and material properties, which caused an irregular temperature rise.

In Fig. 8, the temperature curves correspond to the center-point temperature of Cell-#34, which is the cell directly subjected to bottom-side heating. The values were extracted from a fixed probe placed at the geometric center of the cell. This approach allows us to evaluate the influence of cell spacing on the local thermal behavior and the onset of thermal runaway. The variation in peak temperature and failure time reflects the thermal propagation effects within the module.

Heating a single row of cells within a module above the temperature of the remaining cells usually results in the formation of temperature variances, which cause unequal thermal stress across the pack. This first results in physical harm and hastened deterioration of cells. Over a period of time, the gradual build-up of heat can initiate a process called TR, as reported in⁷⁵. Figure 9-A illustrates the sequential TR pattern observed in a 3 × 3 LIB with a 1 mm gap and a power of 6 kW/m². The cells in the last row had earlier failure than those in the initial row, due to the change in air flow direction from the initial row to the final row. The cells in the last row experienced a failure after around 4.75 min. As a result, the cells next to the heated cell in the 1st row experienced TR. The cells exhibited varying maximum temperatures, with later failing cells attaining higher temperatures. Following the TR occurrence, cell-#34, which experienced TR earlier, had a slower cooling rate in comparison to cell-13, which was affected later but cooled down more rapidly. Both cell-#15 and cell-#23 experienced thermal runaway at around 5.14 min, with peak temperatures reached within a span of roughly ~ 0.16 min.

Figure 9

(A) The sequential TR pattern observed in a 3 × 3 battery pack with a 1 mm gap and a power of 6 kW/m², (B) the TR process of multiple cells in a 3 × 3 LIB pack, with three various row cells spaced 3 mm apart and subjected to 6 kW/m², (C) the temperature distribution of various cells in relation to varied rows during their experience of TR, and (D) the thermal abuse scenario at different locations within a pack subjected to a heat flux of 6 kW/m² with a cell separation of 7 mm.

Figure 9B illustrates the TR process of multiple cells, with 3 various row cells spaced 4 mm apart and subjected to 6 kW/m². The thermal failure duration for the 3 cells varies at 7.12–7.6 min. As the cell spacing doubles (from 1 to 3 mm), the time difference among the TR of the first and last cells is approximately 0.19 min. The cooling time for the cells to reach ambient temperature exceeds 8.31 min. Figure 9C illustrates the temperature distribution of various cells in relation to varied rows during their experience of TR. The cells below were subjected to TR when the side cell was exposed to 6 kW/m². Further, cell-32 experienced TR earlier than cell-#15 and cell-#23, reaching a peak temperature of 798.16 °C at ~ 6.52 min. Moreover, cell-#23 underwent TR, reaching a highest temperature of 796.36 °C at about 6.72 min, 0.2 min after the failure of cell-#23. Additionally, cell-#15 experienced thermal failure, reaching a highest temperature of 789.16 °C after a time delay of 0.08 min following the failure of cell-#23. The whole pack experienced TR within 0.4–0.48 min after the initial TR trigger in a cell.

Figure 9D illustrates the thermal abuse scenario at different locations within a pack subjected to a heat flux of 6 kW/m² with a cell separation of 7 mm. Accordingly, the thermal propagation duration among cell-#34 and cell-#23 was found to be 0.24 min for a 7 mm gap, 0.16 min for a 5 mm gap, less than 0.16 min for a 3 mm gap, and 0.4 min for a 1 mm gap. In comparison to the 1 mm gap, there was a variation in the fire propagation from cell-#34 to cell-#23 rather than cell-#34 to cell-#15. The thermal onset temperatures were 46.57 °C for cell-#15, 48.25 °C K for cell-#34, and 46.12 °C for cell-#23 at time steps of 6.32, 5.81, and 6.03 min, correspondingly. The peak temperatures reached were similar to those observed in previous spacings, indicating that the maximum temperature is minimally influenced by the cell separation.

Figure 10A illustrates the TR occurrence in a 3 × 3 LIB under a 1 mm gap between cells. The analysis was conducted for duration of 15.83 min. According to this study, cell-#34 reached a peak 771.16 °C earlier than the other cells, indicating that it underwent thermal abuse conditions sooner. The temperatures at which thermal runaway was initiated in the three cells differed slightly, under cell-#23 experiencing TR under a slightly lower temperature compared to cell-#15 and cell-#34. Within a time frame of 6.33 min, the temperature distribution for the three cells exhibited a significant degree of overlap, indicating comparable alterations in temperature and rates of heat loss. Cell-#23 had TR at ~ 7.52 min, with its core temperature reaching 789.16 °C. On the other hand, cell-#15 had a more significant effect, surpassing this temperature and reaching roughly 807.2 °C at 7.83 min. The TR transition from the third row to the first row occurred within approximately 0.7–0.8 min, as the rows were traversed at the given flow velocity.

Figure 10

(A) The TR occurrence in a 3 × 3 LIB under a 1 mm gap between cells, (B) the TR initiation in a pack consisting of a 3 × 3 arrangement of cells, (C) the TR occurrence in a LIB pack consisting of 9 cells connected in parallel, and (D) the performance of a series arrangement of 9 cells when subjected to a heat flux of 6 kW/m².

Figure 10B illustrates the TR initiation in a pack consisting of a 3 × 3 arrangement of cells. This occurs when the pack is exposed to 6 kW/m² and under 3 mm (heater width) located at the base of one of the cells on the side. Cell-#34 experienced TR at ~ 6.5 min, with 51.2 °C. It displayed a slower rate of cooling compared to cell-#15 and cell-#23. Further, cell-#34, cell-#23, and cell-#15 all attained peak temperatures of 789.16 °C. However, cell-#23 reached its peak temperature 0.31 min before cell-#15. The TR timing varied between 6.5 and 7.12 min for the three cells. At a flow velocity of 0.35 m/s, variations in cell spacing had a minor impact on peak temperatures but had a significant effect on the cooling patterns, resulting in faster cooling in setups with larger cell spacing. Figure 10C depicts the TR occurrence in a LIB pack consisting of 9 cells connected in parallel. A power of 6 kW/m² is applied over a 5 mm width at the base of the third-row cell. The TR happened slightly earlier in comparison to a similar configuration with a 1 mm gap between cells. Cell-#34 was the first to fail in this configuration, which emphasizes the crucial significance of coolant flow direction in battery pack design. The maximum temperatures recorded in the cells were 780.2 °C for cell-#34 and 789.16 °C for cell-#15. These results demonstrate that increasing the spacing between cells has a notable effect on the cooling efficiency. Specifically, cell-#15 exhibited a noticeable decrease in temperature after 7.12 min, indicating a faster cooling rate compared to previous observations made with narrower spacing.

Figure 10D examines the performance of a series arrangement of 9 cells when subjected to a heat flux of 6 kW/m². The analysis primarily focuses on the behavior of the central cell. The cell located in the initial row experienced the final impact of the fire, occurring around 5.49 min after the incident, attaining a maximum 786.5 °C. The cell located at the final row is subjected to the effects of a fire at 4.98 min, resulting in 789.16 °C. When comparing cell-#15 at 7 and 5 mm intervals, there was a reduction of 1.1 min in reaction time. However, the time it took for the fire to spread from the third to the first row remained consistent at approximately 0.63 min, regardless of the spacing. Uneven temperature profiles were seen in the cooling patterns, with cell-#15 experiencing more rapid cooling at larger spacings ranging from 1 to 7 mm.

Figure 11 illustrates the development of TR in a pack measuring 3 × 3, at various time intervals. Thermal physics investigation showed that when the temperature reaches a threshold level of 9.5 kW/m², the separator becomes unstable and starts to melt. This leads to interactions between lithium ions and electrons, causing an internal short circuit. The event was first seen at 5.4 min and quickly resulted in a sudden increase in temperature within a few seconds. A heat wave originated at the lower end of cell-#34 and spread upwards, encompassing 86.4% of the cell after 5.49 min. It then proceeded to impact the neighboring cell-#33 with a circular heat front. After 5.6 min, cell-#34 was completely degraded, causing fast heat to spread to nearby cells. Within a span of 6.16 min, the complete battery pack experienced thermal runaway, leading to deterioration in both its structural and electrical stability. This issue might potentially pose significant safety risks, particularly in applications such as electric automobiles.

Figure 11

The development of TR in a pack measuring 3 × 3 at various time intervals.

Figure 12 analyzes the TR characteristics in different rows of a 3 × 3 LIB under varying heating powers of 6 and 9 kW/m². The analysis reveals that cells exposed to 9 kW/m² saw a much faster failure rate. Specifically, row-#1 collapsed at approximately 5.38 min, whereas at 6 kW/m², it collapsed at 6.97 min. The temperature reached its peak at 793.66 °C. Curiously, the maximum temperature achieved using the lesser heating output was somewhat 9 °C higher compared to the higher power. The time between failures in row-#2 decreased by 16.32% when the heating power was raised, resulting in a 0.95 min interval. Similarly, row-#3 displayed a similar pattern of decreased delay. Based on observations of cooling patterns, it was shown that cells exposed to 6 kW/m² cooled at a faster rate compared to cells exposed to a higher power setting. Figure 13 illustrates the occurrence of thermal abuse, specifically when the center cell was subjected to heat from a ring-shaped aluminum strip that is 8 mm wide. LIFC, renowned for its exceptional stability as a cathode material, attained a maximum 744.2 °C. The TR sequence begins with column-#3, subsequently followed by columns-#2 and #1. The thermal failure lasted for a total of about 3.16 min. Column-#3 failed ~ 1.9 min before column-#2, and there was a 1.27 min delay before column-#1 failed. This pattern suggests that the process of heat transfer during thermal runaway is non-uniform and is affected by several factors. The centrally placed Column-#2 saw improved convection, resulting in lower peak temperatures compared to the surrounding columns. During the cooling phase, column 1 exhibited a higher rate of heat dissipation compared to column-#3, which experienced convection for a longer duration. As a result, column-#3 cooled down between 159.2 °C and 204.1 °C within a time span of 15.83 min. Note that, the irregularities were due to the non-uniformity in heat dissipation caused by uneven cell spacing and differences in the thermal conductivity of adjacent cells.

Figure 12

The TR characteristics in different rows of a 3 × 3 LIB under varying heating powers of 6 and 9 kW/m².

Figure 13

The occurrence of thermal abuse, specifically when the center cell was subjected to heat from a ring-shaped aluminum strip that is 8 mm wide.

Figure 14 provides a comprehensive breakdown of the heat emitted during thermal runaway in a cell that contains LNCMC material. It specifically highlights the contributions made by five distinct chemical reactions. At the peak of the thermal runaway, the total heat output reached 4.46 kW. This was measured by multiplying the heat source strength by the cell volume. The high heat production lasted for around 0.4 min. The rate of heat release initially increased significantly as the separator melted, triggering a series of decompositions that began with the SEI layer, followed by the electrolyte, and ultimately culminated in the maximum heat release during the breakdown of the negative solvent, surpassing the intensity of other reactions. Figure 15 depicts the proportions of the electrolyte, positive and negative electrodes, and SEI-layer during thermal abuse. The SEI-layer underwent melting when the fraction reached 0.165 after around 5.86 min. This caused the safety vents to open, allowing oxygen to enter. The oxygen then reacted with the cell materials, leading to an increase in temperatures. The succeeding series of events, including the contact between the electrolyte and oxygen, the disintegration of the positive electrode, and the reaction of the negative electrode, occurred rapidly and resulted in a significant explosion. Figure 16 illustrates the amount of heat that is generated under various chemical processes inside a LIB-cell after the TR occurrence. The negative solvent reaction produced the highest level of heat, followed by the internal-short circuit. Conversely, the SEI-layer disintegration emitted far lower amounts of heat. The measured numbers indicated that the negative solvent reaction released 1.78 kW of energy, the internal short circuit generated 1.04 kW, the positive solvent decomposition produced 0.43 kW, and the electrolyte breakdown resulted in just 0.133 kW. These findings demonstrate a notable difference in the amount of heat generated by each reaction.

Figure 14

Heat generation curve of the LIB cell during thermal runaway. The primary peak (~ 6.3 min) corresponds to the initial exothermic reactions including SEI-layer breakdown and separator melting. A smaller secondary rise (~ 6.5 to 6.6 min) is observed due to delayed reactions involving oxygen ingress, leading to intensified anode-oxygen and solvent-based reactions. This two-stage heat release reflects the cascading nature of TR and aligns with the sequence of decomposition events.

Figure 15

The proportions of the electrolyte, positive and negative electrodes, and SEI-layer during thermal abuse.

Figure 16

The amount of heat that is generated under various chemical processes inside a LIB-cell after the TR occurrence.

The appearance of a second heat generation peak in Fig. 14 signifies a critical stage in the thermal runaway process. This peak is triggered by the release of oxygen following safety vent rupture, which enables highly exothermic reactions between the anode and oxygen, as well as the aggressive decomposition of the electrolyte and the negative solvent. These reactions occur subsequent to the initial SEI breakdown and separator melting, forming a characteristic two-peak thermal profile commonly observed in TR events. Note that, heating from different positions within a battery pack does indeed exist and can lead to varying outcomes in terms of thermal runaway propagation, as demonstrated both experimentally and through simulations in previous studies. The differences in results arise because lithium-ion batteries are complex systems where heat distribution, dissipation, and accumulation vary depending on the heating source’s location. The internal structure of a battery—comprising layers of electrodes, separators, and electrolytes—creates uneven heat flow paths. Therefore, heating from the side, center, or at specific points of the battery affects the propagation of thermal runaway differently due to variations in thermal conductivity and the physical layout of these components.

In this study, the findings align with this understanding, showing that side heating results in faster TR initiation and propagation, particularly as cell spacing increases, while central heating initially delays TR up to a specific threshold before decreasing. This observation reflects how different thermal flow paths and localized hotspots develop based on the heating position, which can significantly influence battery safety. This phenomenon has been validated in both experimental setups and numerical models, where uneven heating in real-world applications (such as due to electrical shorts, external impacts, or faulty cooling systems) often leads to localized overheating. For example, side heating may mimic conditions where a battery is exposed to external heat sources (e.g., from a neighboring overheated cell), while central heating may resemble internal short circuits or localized manufacturing defects.

Finally, while it is well-known that an increase in heating power typically shortens the time to thermal runaway, the innovation in this study lies in the detailed quantitative analysis of how specific variations in heating power, position, and cell spacing influence thermal runaway propagation, particularly in a multi-cell battery pack configuration. This study goes beyond simply confirming that higher heating power accelerates TR by providing new insights into:

• (i) Non-linear Impact of Heating Power: The study reveals that the highest temperature achieved under 7 kW/m² was slightly higher than that under 10 kW/m², a counterintuitive result that is not commonly observed. Furthermore, it was found that while the time to peak heating power decreases by 18%, this relationship does not follow a straightforward linear pattern across all tested configurations. This highlights the complex interaction between heating conditions and thermal dynamics, which has not been fully explored in previous literature.

• (ii) Effects of Heating Position and Cell Spacing: A novel aspect of this study is the investigation of how variations in heating position and cell spacing affect TR propagation. It was observed that side heating led to shorter timeframes with increasing cell spacing, while central heating initially increased the TR timing up to 4 mm before decreasing. This nuanced understanding of the spatial impact of heating provides valuable guidance for improving battery safety design, particularly for large-scale battery packs used in electric vehicles and grid storage.

• (iii) Chemical Heat Release Dynamics: The study ranks the heat release rates of various chemical processes involved in TR, specifically identifying that the negative solvent contributes the highest rate of heat generation, while the SEI-layer has the lowest. This detailed ranking of chemical heat sources is not commonly addressed in previous studies and offers a new perspective on how different components contribute to TR progression, allowing for targeted safety enhancements. The analysis of the 3 × 3 module introduces a novel spatially-resolved understanding of how cell spacing, flow direction, and heating configuration interact—marking a significant advancement in predictive modeling for battery pack safety design.

Conclusions

This study presented a detailed three-dimensional, multi-scale/multi-physics numerical model to investigate the TR behavior in lithium-ion batteries. The analysis considered the effects of various heating positions and cell spacing in both single-cell and 3 × 3 battery module configurations. The results demonstrate that flow direction, heating location, and inter-cell spacing are critical parameters that influence the onset, propagation, and severity of TR. The negative solvent was identified as the dominant contributor to internal heat generation, while the SEI-layer exhibited the lowest thermal contribution. The following specific findings were derived from the simulations:

• (i) Among cathode configurations, LNCMC material with vertical 8 mm heating showed the most stable TR behavior and delayed failure.

• (ii) Central heating (20 mm) at 4.5 kW/m² resulted in the highest peak temperature, highlighting its risk in densely packed modules.

• (iii) TR timing demonstrated non-linear sensitivity to spacing: side heating accelerated TR with wider spacing, while center heating showed an initial delay at 3 mm spacing before declining.

• (iv) The ranking of heat generation sources confirmed that the negative solvent reaction produced the highest heat, and the SEI-layer the least.

• (v) A counterintuitive result revealed that 6 kW/m² heating led to a marginally higher peak temperature than 9 kW/m², but with a 16.32% shorter time to reach maximum heating power.

This work offers several novel contributions:

• It establishes a bridge between single-cell and module-level modeling under consistent boundary and material assumptions, enhancing the reliability of system-level TR prediction.

• It provides a chemical-level decomposition of TR heat sources, enabling precise identification of dominant contributors in critical failure phases.

• It introduces a spatially-resolved analysis of heating configurations, which supports the development of safer thermal management strategies and battery pack architectures.

Overall, the insights gained from this study contribute directly to battery safety engineering, especially in electric vehicles and high-density energy storage systems, offering guidance for safer battery design and deployment under thermal abuse scenarios.