A computational model that integrates unrestricted callus growth, mechanobiology, and angiogenesis can predict bone healing in rodents

Abstract

We present a computational model that integrates mechanobiological regulations, angiogenesis simulations and models natural callus development to simulate bone fracture healing in rodents. The model inputs include atomic force microscopy values and micro-computed tomography on the first-day post osteotomy, which, combined with detailed finite element modeling, enables scrutinizing mechanical and biological interactions in early bone healing and throughout the healing process. The model detailed mesenchymal stem cell migration patterns, which are essential for tissue transformation and vascularization during healing, indicating the vital role of blood supply in the healing process. The model predicted bone healing in rodents (n = 48) over 21 days, matching daily tissue development with histological evidence. The developed computational model successfully predicts tissue formation rates and stiffness, reflecting physiological callus growth, and offers a method to simulate the healing process, potentially extending to humans in the future.

Introduction

Key factors in bone repair depend on the healing tissue’s local mechanical environment. A study by Isaksson et al.¹ examined computational mechanobiology in bone healing, revealing variables such as strain, pressure, stability, and fluid velocity play essential roles in tissue development during bone repair. However, the complete understanding of the transduction of these mechanical factors to cellular stimuli is still incomplete².

Subsequent investigations have demonstrated that bone regeneration can be modeled during fracture healing and osteochondral defect repair using mechanoregulation (MR) algorithms based on computing strain and/or fluid flow within the regenerating tissue^3,4. Prendergast et al.³ utilized a biphasic finite element model, based on the work of Sabelle et al.⁵, to understand how varying mechanical stimuli influence differentiation, suggesting that a spectrum of mechanical forces corresponds to the formation of fibrous tissue, cartilage, and bone. Claes et al.⁴ also employed finite element (FE) modeling alongside histological data to illustrate the interplay between mechanical strain, hydrostatic pressure, and cell differentiation in tissue development during bone healing².

Giorgi et al.⁶ suggested that in silico bone mechanobiology has generally taken a reductive approach in attempting to answer discrete biological research questions, with research in the field broadly separated into two streams: (1) mechanoregulation algorithms to predict mechanobiological changes to bone tissue and (2) models to investigate cell mechanobiology. Mechanobiological models have been used to investigate the role of various mechanical and biological factors on bone healing. Despite significant progress, the earliest phases of healing, characterized by inflammatory response and early callus formation, are frequently overlooked. However, Ghiasi et al.⁷ developed a finite element model to assess the impact of various initial phase parameters, such as stem cell migration and the properties of granulation tissue, on the healing outcome. More recently, Yang et al.⁸ introduced a computational model that continuously simulates all four phases of bone healing, focusing on the impact of initial fracture conditions, mechanical loading, and vascular growth rate. The initial geometry and tissue properties of the healing tissue at the fracture site significantly impact the progression of fracture healing, with computational models demonstrating that unfavorable initial conditions and mechanical loading have non-linear effects that can disproportionately influence healing outcomes, potentially leading to delayed healing or non-union.

Incorporating biological factors into finite element simulation models has marked a pivotal shift in the field. These models integrate roles for different cell types, growth factors, and blood vessel development, enriching traditional approaches^1,9. The importance of angiogenesis, which begins early in the healing trajectory^10,11, is particularly underscored as it significantly boosts blood supply, oxygen, nutrient delivery, and waste removal^10,12,13. However, high levels of tissue strain can adversely affect angiogenesis and new vessel formation^12,13, which underscores the necessity of a comprehensive understanding of these interrelationships.

Due to their healing processes akin to humans, sheep have been used to test and improve computer model predictions^4,8,14,15. Rats are also favored in studies for their size, manageability, and translatability of their healing processes to human clinical practice^16,17,18,19. Whether different animals follow comparable mechanobiological rules during tissue regeneration and bone healing remains unknown. Researchers have shown slower healing in large animals compared to small animals²⁰. Checa et al.²¹ investigated whether differences observed in in vivo dynamics of bone healing between smaller animals, such as rats, and larger ones, such as sheep, are merely due to size differences or distinct mechanobiological responses^16,21. They discussed the differences between sheep and rats in mechanobiological modeling and suggested that the ossification process in sheep occurs under higher levels of mechanical stimulation than in rats. Therefore, the same mechanobiological model cannot precisely predict the bone healing process for both species²¹.

In the initial stages of healing, characterizing soft tissues as poroelastic materials has become widely accepted, as it more accurately reflects the biological dynamics at fracture sites¹. The poroelastic model delineates different tissue types as the solid phase and interstitial fluid as the fluid phase. The site fills with soft tissue post-fracture, challenging conventional mechanical testing to measure tissue stiffness. Consequently, indentation testing is a superior technique for evaluating the nascent tissue’s rigidity in the early phases of healing. Additionally, histological evaluation, especially with Movat’s Pentachrome staining, facilitates the visual identification and quantification of diverse tissue types during the healing process, offering an inclusive perspective on tissue regeneration and its efficacy^16,22.

This study introduces an innovative mechanobiological model for rodent bone fracture healing, crafted from species-specific experimental data to emulate the various phases of bone healing. We harnessed micro-computed tomography (µCT), atomic force microscopy (AFM)-based nanoindentation, and histological assessment to measure the mechanical and biological elements involved in the initial healing phase. This allowed for the quantification of callus development, evaluation of material characteristics, and observation of the timing and locality of cellular responses, which influence the formation of distinct tissue types.

Expanding on prior models that deployed mechanoregulatory algorithms for tissue differentiation, our model integrates physiological nuances of callus growth. Moving from conventional constraints to a pre-established callus area^7,21,23, our approach initiates a void opposite the plate fixation. This strategy, inspired by Lipphaus et al.’s work²⁴ on callus growth, allows the emergent tissue to expand and differentiate organically, reflecting the inherent bone healing processes. Our model diverges from earlier research, primarily dealing with secondary bone healing through external fixators. It is meticulously crafted to simulate healing under plate fixation conditions, enhancing the thoroughness of the healing assessment. The model advances our comprehension of how various fixation methods impact bone regeneration and augments the precision of predictions for primary and secondary bone healing outcomes. Additionally, it considers oxygen levels in blood vessels, a crucial determinant of tissue production rates¹³. Drawing upon Grivas et al.’s research²⁵, we’ve derived rules that correlate mechanical stress with oxygen concentration, thereby adjusting tissue transformation rates that affect tissue formation and cellular density in healing elements.

We hypothesize that integrating updated mechanobiological standards, refining tissue formation rates, and incorporating angiogenesis simulation based on real-world observations can bolster our model’s accuracy in forecasting bone healing stages in rats—a capability not possible with models predicated on sheep data. Our model endeavors to emulate natural physiological processes more closely by representing bone healing in an unfixed, organic environment, thus bridging the divide between computational models and actual biological processes and enhancing the model’s practical relevance and application.

Methods

Animal model

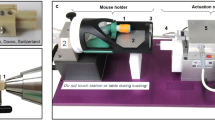
The Institutional Animal Care and Use Committee (IACUC) at Beth Israel Deaconess Medical Center approved the experimental study protocol with the findings reported in accordance with ARRIVE guidelines. All experiments were performed in accordance with relevant guidelines and regulations. A 2 mm transverse osteotomy was performed using a Gigli saw (RISystem AG, Landquart, Switzerland) on the right femur of 48 healthy 13-week-old (skeletally mature) rats distributed equally between males and females (Charles River Laboratories, Inc., Boston, MA, USA). Eight rats were sacrificed per day on days 1, 2, 3, 7, 14, and 21 post-surgery and anesthetized with CO2 inhalation in a sealed chamber with secondary means of euthanasia confirmation (cardiac puncture). Isoflurane was used for anesthesia at 5% concentration with 2 L oxygen/min for induction and 2.5% with 2 L oxygen/min for maintenance. Following anesthesia, the right leg and the area between the shoulders were shaved and disinfected with a povidone-iodine scrub. Before the skin incision, a sustained-release buprenorphine analgesia was administered at a dose of 1.2 mg/kg. An anterolateral approach was performed for the skin incision with blunt, soft tissue separation along the femur laterally. The intermuscular plane between the vastus lateralis and the biceps femoris muscles was separated. After exposing and disrupting the periosteum of the femur, an eight-hole PEEK plate (20 × 3 × 5 mm with a 2 mm notch) was secured to the right femur using two supracondylar and two subtrochanteric bicortical screws (Special Designs, LaVernia, TX, USA). After clearing the defect of reaming debris with sterile saline, the skin was closed with clips. Twenty-four rats (i.e., four per day) were used for AFM-based nanoindentation, and the remaining animals were used for µCT imaging and histology (Fig. 1A).

Fig. 1

(A) Overview of the animal model and experimental setup for the study. (B) AFM analysis of fracture site tissues in the animals post-osteotomy, representing tissue sampling from the fracture site’s central, intermediate, and outer regions borders at various follow-up times. Tissues were preserved in PBS for biomechanical property examination.

Atomic force microscopy (AFM) based nanoindentation

This study utilized AFM-based nanoindentation to examine the biomechanical properties of tissue formed at fracture sites post-osteotomy at various follow-up times. Researchers have previously utilized this technique to identify nanoscale heterogeneity in the elastic modulus values of callus during bone healing^26,27. Four rats were euthanized at each time point, and the tissues from the fracture sites were collected and maintained in PBS to ensure hydration throughout the experiment. These tissues were categorized into three distinct regions (central, intermediate, and outer) for detailed analysis (Fig. 1B). Three distinct regions were selected by excising the entire healing tissue from the fracture gap and dividing it into three concentric sections centered on the fracture site. These sections correspond to an inner region with a radius of $\:{r}_{inner}$ = 1.7 ± 0.2 mm, an intermediate region with a radius of $\:{r}_{intermediate}$ = 2.3 ± 0.2 mm, and an outer region with a radius of $\:{r}_{outer}$ = 2.9 ± 0.2 mm.

A conical-tip AFM probe featuring a tip height of 15 μm and a tip radius under 20 nm was employed to test each region nine times across three randomly selected locations. The AFM probe had two types of cantilevers: a soft one with a length of 130 μm and stiffness of 0.6 N/m for testing tissues harvested on days 1 through 7 and a stiffer one with a length of 90 μm and stiffness of 2 N/m for tissues from days 14 and 21. During each indentation test, force and indentation depth data were collected to calculate the tissue’s reduced elastic modulus ($\:{\text{E}}_{\text{r}}$) using the Oliver–Pharr method (Eq. 1).

$$\:{\text{E}}_{\text{r}}=\frac{\text{E}}{1-{\text{v}}^{2}}=\:\frac{\sqrt{{\uppi\:}}\text{S}}{2\sqrt{\text{A}}}$$

(1)

$$\:{\text{E}}_{\text{r}}=\:\frac{{\uppi\:}\text{S}}{4\:\text{d}\text{tan}\left(\frac{{\uptheta\:}}{2}\right)}$$

(2)

This calculation incorporated the tissue’s Young’s modulus (E), Poisson’s ratio (v), the experimentally measured unloading stiffness (S), and the projected contact area (A), with the unloading stiffness determined at 95% of the maximum indentation depth. The assumption was that the AFM tip remained rigid compared to the tissues, allowing for an accurate assessment of the tissues’ biomechanical properties based on the indentation depth (d) and probe tip cone angle (θ). The reduced elastic modulus can be presented as the following (Eq. 2). After each test, the true elastic modulus was calculated based on Eq. 1 from $\:{\text{E}}_{\text{r}}\:$values.

Micro-computed tomography and histology

For each specimen, the entire fractured femur was immediately harvested post-euthanasia and fixed in formalin. Then, the fixed fractured femur was imaged with a micro-computed tomography (µCT) system (Scanco AG µCT40, Brüttisellen, Switzerland) to scan the fracture site and the bone shaft between the two implant screws. The voxel size was 30 × 30 × 30 μm, where every axial CT image contained 731 × 652 voxels, resulting in an in-plane field of view (FOV) of 21.93 × 19.56 mm. After µCT imaging, the same samples were subjected to decalcification in preparation for histological analysis. The area of interest, which included the healing callus and the bone shaft located between the first pair of implant screws, was excised, embedded into paraffin blocks, and subsequently sectioned along the sagittal plane to produce slides for microscopic examination.

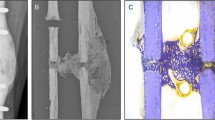
Two staining techniques, Hematoxylin-Eosin (H&E) and Movat’s Pentachrome, were used to visualize different tissue types at fracture sites over time. The H&E staining, as a conventional method, highlighted the general tissue architecture and facilitated a clearer interpretation of Movat’s Pentachrome-stained slides. Through Movat’s Pentachrome staining, detailed differentiation of tissue types was achieved, with bone being colored yellow-orange, cartilage green and blue-green, fibrous and granulation tissues blue and red-blue, and hematoma solid red. Histomorphometric analysis on Movat’s Pentachrome-stained slides enabled quantitative assessment of tissue healing progression, detailing tissue expression dynamics during fracture repair. We quantified each tissue type by measuring and normalizing the surface area of identified regions on microscopic slides relative to the total tissue surface area formed by corresponding post-surgery days.

Finite element modeling

The mechanobiological regulation presented by Prendergast et al. ³ was modified based on the work of Checa et al.²¹ to move the bars of tissue differentiation type under applied mechanical loads toward rat species from sheep, which was previously mentioned and discussed. Our study elaborates on this idea through an animal experiment that compared the temporal changes in normalized material properties of the callus region to those of intact bone up to 21 days post-surgery. It reveals that tissue heals faster based on physiologic differences between rat and sheep femurs. Based on the work of Sapotnick et al.²⁸, abrupt changes in tissue differentiation should be smoothed to mimic better the biological regulations in the fracture site. This has been done by scholars before^7,8,29. As shown in Fig. 2A1, A2, we modified the ranges based on mechanical stimulus using Eq. 3 as a function of octahedral shear strain and fluid flow. This modification was based on the expected range elastic modulus of healed tissue seen in rats from day 21 post-fracture, but the core of the MR algorithm stayed intact.

$${\text{S}} = {\text{~}}\frac{{{\text{E}}_{{{\text{oct}}}} }}{3} + {\text{~}}\frac{{{\text{F}} \cdot {\text{V}}}}{{2.4}}$$

(3)

In this formula, shear strain ($\:{E}_{oct})$ is in percentage, and fluid velocity (FV) is in µm/s calculated for each element at each iteration. Compared to the older threshold for the MR modeling used in larger animals, the criteria for tissue production based on octahedral shear strain and fluid flow decreased, speeding up tissue growth in rats (Fig. 2A1). By calculating the mechanical stimulus for each element, the algorithm can identify which tissue region will form based on the defined thresholds (Fig. 2A1). The formation rate is then determined using the mathematical functions plotted in Fig. 2A2.

The rat femoral shaft was modeled as a hollow cylinder with a transverse cut perpendicular to the cylindrical axis. A full biphasic finite-element analysis of the bone was developed using linear poroelastic material properties similar to the model presented by Lacroix & Prendergast³⁰ and developed by Ghiasi et al.⁷. This simplified 2D model of the rat right femur was constructed in version 23, software (Dassault Systèmes Simulia Corp, Vélizy-Villacoublay, France, https://www.3ds.com/products-services/simulia/products/abaqus/). At the same time, measurements were extracted from µCT scans of the rats’ femur Supplementary Fig. 1 and simplified to a 2D version to mimic the same overall geometry to eliminate the computational cost at this level (Fig. 2C1). For this model, a 2 mm interfragmentary gap size with a void area (width = 3×gap) containing the fracture gap along with the whole opposite side of the plate was chosen, and material properties of the inner region of the AFM region-based nanoindentation at day one was assigned to it as baseline. The model used 8-node biquadratic, reduced integration pore pressure elements. The mesh size was refined at the fracture site and the surrounding region (Fig. 2C2). A mesh convergence study was conducted to eliminate any mesh dependency in the results, and distinct mesh sizes were chosen for cortical bone, marrow, fractured region, and plate, which caused the targeted fracture region to have 15,108 biquadratic elements. Material properties of the bone and the bone marrow were defined based on previous rat studies presented in Table 1, along with the plate material used^21,25,31,32.

Table 1 Material properties of healing tissues, bone, screws, and plate used in the computational model.

The bone healing process was simulated for 21 iterations (days), with results obtained each day using an iterative process controlled by a Python code. Loading conditions were imposed based on the forces and moments a rat gait study indicated³³. We applied 50% of the loading estimated by the gait analysis to account for the impact of bone fracture on the rats’ application of stresses on their fractured femur. Therefore, a 14.7 N compression force was applied and was determined to equal the 50th percentile of rat normal walking loading. Wehner et al.³³, in the gait analysis experiment, found that the shear force on the mid-femur was much smaller (~ 0.6 to 0.9 × body weight) compared to the compression forces (6 to 7 × body weight) and thus negligible compared to the strain induced by compression forces. Also, we didn’t include the bending moments, which significantly act in the sagittal plane and are out of the plane for 2D analysis. Boundary conditions were applied at the bottom and left borders where screws are in contact with the plate, as shown in Fig. 2C3. The distal femur was fixed, and the plate cannot have lateral movement as it is bounded in physiologic configuration by muscles and surrounding tissues. Screws are designed and implemented to tightly grip between the plate and the cortical shaft, which has been implemented by fixing the screw intersection points in the model and simulated as a rigid beam function that is fixed at one end(plate-side) (Fig. 2C3) and their movement is limited, this causes the model better to predict the behavior of screws in the in-vivo configuration as they hold and transfer force to the plate. In this model, screws made of stainless steel were selected and designed to function on each side, treated as beams that are fixed to the plate side. This setup connects the nodes between the cortical bone and the plate along their axis. The choice of stainless steel for the screws was based on the plate fixation surgical procedure in the determined protocol while modeling them as fixed beams enhanced the simulation’s accuracy by replicating the mechanical support provided in real-life surgical scenarios. Fluid velocity and octahedral shear strain were calculated for each element using a biphasic analysis in ABAQUS. Through a separate finite element-based diffusion analysis, cell migration was simulated for every iteration to determine the spatial and temporal cell distribution using Fick’s first law (Eq. 4), where c is the cell density, D is the diffusion coefficient of cell migration, $\:{P}_{i},\:{A}_{i}\:$ are cell-specific proliferation and apoptosis rate, and t represents time. In this equation, $\:i$ = 1, 2, 3, 4, represents mesenchymal stem cells, fibroblasts, chondrocytes, and osteoblasts, respectively. The last term in Eq. 4 represents the changes by differentiation of each cell type to others.

$$\frac{{\partial c_{i} }}{{\partial t}} = D~\nabla ^{2} c_{i} + P_{i} \cdot c_{i} - A_{i} \cdot c_{i} ~ + ~~\Delta c_{i}$$

(4)

$$\begin{gathered} \Delta c_{{fb}} = F_{1} \cdot c_{{MSC}} - ~F_{5} \cdot c_{{fb~}} ,\,~\Delta c_{{cc}} = ~F_{2} \cdot c_{{MSC}} + F_{5} \cdot c_{{fb}} - ~F_{6} \cdot c_{{cc}} ~, \hfill \\ \Delta c_{{im_{{ob}} }} = F_{3} \cdot c_{{MSC}} + ~F_{6} \cdot c_{{cc}} - ~F_{7} \cdot c_{{im_{{ob}} }} ,\,\Delta c_{{m_{{ob}} }} = ~F_{4} \cdot c_{{MSC}} + F_{7} \cdot c_{{im\_ob}} \hfill \\ \end{gathered}$$

(5)

$$F_{i} = ~s_{i} \cdot f_{i} \left( {v~} \right)~~~~~i = 1,\,2,\,3,\,4~$$

(6)

In Eq. 5,$\:{F}_{1},\:{F}_{2},\:{F}_{3},{F}_{4}$ are rates of fibrogenic, chondrogenic, and osteogenic (mature and immature) differentiation from MSC, respectively and $\:{F}_{5},\:{F}_{6},\:{F}_{7}\:$are constant rates of osteogenic differentiation of fibroblast, chondrocytes, and osteoblasts respectively. Figure 2A3 shows the reaction diagram of Eq. 5 depicting the rates of conversions between cell types.$\:{F}_{1},\:{F}_{2},\:{F}_{3},{F}_{4}\:$are defined as Eq. 5, which comes from the regulatory rules of mechanical stimulus formation rates ($\:{s}_{i})$ in Fig. 2A2, and angiogenesis, modeled through the blood regulation function$\:{f}_{i}\left(v\:\right)$as illustrated in Fig. 2B. The$\:{s}_{i}$values represent the mechanical stimulus formation rates. These rates are calculated based on the mechanical stimulus S from Eq. 3. The mechanical stimulus influences the differentiation rates of MSCs into specific cell types, which subsequently form tissues (Fig. 2A2). Therefore, while the differentiation occurs at the cellular level, it results in tissue formation, reflected in the material properties updates in the model. The blood regulation function$\:{f}_{i}\left(v\:\right)$is computed using a set of mathematical formulas (Eqs. 7 and 8), which link the level of blood supply (v) to tissue differentiation rates. Specifically, $\:{f}_{2}$is used to calculate the chondrogenic differentiation rate ($\:{F}_{2})$which will be used along with the$\:{\:s}_{2}$value from mechanical stimulus representing red graph in Fig. 2A2, while ($\:{f}_{i=\text{1,3},4})$is used to calculate fibrogenic and osteogenic(immature and mature) differentiation rates using alongside with pink, green, and blue plots in Fig. 2A2. The rationale behind blood regulation functions and their differences is based on the varying vascular requirements of different tissues, which will be explained further in “Vascularization and MSC migration” Section.

$$f_{2} \left( v \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {v < 0.2} \hfill \\ {\frac{1}{{1 + e^{{60 \cdot \left( {v - 0.3} \right)}} }}} \hfill & {0.2 < v < 0.4} \hfill \\ 0 \hfill & {v > 0.4} \hfill \\ \end{array} } \right.$$

(7)

$$f_{{i = {\text{1,3}},4}} \left( v \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {v < 0.6} \hfill \\ {\frac{{ - 1}}{{1 + e^{{60 \cdot \left( {v - 0.7} \right)}} }} + 1} \hfill & {0.6 < v < 0.8} \hfill \\ 1 \hfill & {v > 0.8} \hfill \\ \end{array} } \right.$$

(8)

The cell diffusion coefficient was considered based on previous FE models, which were chosen in the range of 0.1 to 0.6 mm²/day for this study and changed for each element based on the cellular differentiation of the specified element in that day (For instance if the majority of cells in the element is differentiating to cartilage from granulation tissue the diffusion coefficient for the following days for the cells in this element would become third of initial value to take into account lower cell migration rates for chondrocytes. Table 2 presents the constant rates for all tissue types chosen based on ranges mentioned in previous work or assumed (like cellular diffusivity rate) based on the range used previously in the literature^7,21,31. The differentiation rates in this table represent the constant rate of osteogenic differentiation of fibroblasts, chondrocytes, and immature osteoblasts to mature ones. The diffusion model assumes MSC proliferation and migration occur from high to low-density areas, originating mainly from bone marrow and the periosteal surface of the cortical bone^{30,31,34,35,36}. Previously, researchers reported that the concentration of MSCs in the border of marrow and osteotomy was between 10 and 30% of the total region in mice^25,34. In this simulation method, elements begin with an initial void ratio that can be filled by moving particles and solutes. Initially, stem cells fill 30% of the available space at the marrow-callus intersection elements (horizontal blue-brown border in Fig. 2D). For the periosteum layer (vertical grey-brown border in Fig. 2D), located at the bone-void intersection near the osteotomy, the fill rate was set to 60%, decreasing linearly to 10% as it extends toward the distal part of the bone, further from the fracture site. This reflects the natural biological gradient of response to injury (Fig. 2D, left panel). During surgery, screws fix the plate to the bone, penetrating the femur and disrupting the periosteum around the insertion sites, where cellular activities, including MSC presence, are altered. We modified the boundary condition to model this by removing boundary cells at the screw-bone interface. This disrupts uniform diffusion as cells migrate toward low-concentration regions near the screws, slowing normal migration toward the fracture site²⁵. Also, the no-flux boundary has been chosen for the cortical bone and outer layer of the void region, so cell migration is only possible toward the healing fracture site.

Table 2 Dynamics of cellular processes in fracture healing.

In each section of the forming callus, differentiation was processed at the cellular level from initial mesenchymal stem cells. Then, differentiated cells synthesized new extra-cellular matrixes that were influenced by local mechanical conditions and MSC concentrations (Fig. 2D). The tissue combination contributes to updating material properties in each element. By assuming the linear rule of mixtures and an additional rule that the sum of cell concentrations in each element is equal to 1, we averaged the properties of elementwise newly formed tissue with those from the previous nine iterations in the same element to continuously update material characteristics, which were then applied in subsequent FE analyses to model tissue behavior under stress⁷ (Eq. 6) more accurately. Daily, we quantified granulation, cartilaginous, and bony callus elements based on their local elastic modulus quantified locally as the elements updated their material properties, which fell within predefined ranges reflecting typical values for each tissue type and transition phases between tissues. This classification system allowed us to map out and compare the distribution of tissue volumes within a specific observation window against histological samples. This method gave us a detailed and dynamic understanding of tissue development during the healing process. $\:{C}_{i}$in the equation is the concentration of various cellular types in the element.

$$\begin{aligned} At\,each\,element\,at\,time = & t:E_{t} = ~\sum\limits_{{i = 1}}^{4} {C_{i} } \cdot E_{i} ,~\sum\limits_{{i = 1}}^{4} {C_{i} } = 1 \\ E_{{element\_final}} = & ~\frac{{\sum\nolimits_{{t = t - 9}}^{t} {E_{t} } }}{{10}} \\ \end{aligned}$$

(9)

Vascularization and MSC migration

Vascularization during healing was modeled with a continuous variable, vessel density (v), as a representative of blood supply, which regulates the oxygen level of cells based on Burke and Kelly’s model³⁵. In this framework, angiogenesis is conceptualized as a diffusion process that begins on the first day of healing and continues throughout, governed by a strain-dependent diffusion coefficient. This method allows for a dynamic simulation of blood vessel growth in response to the mechanical environment (Fig. 2D). The scale for vessel density is set from 0 to 1, where 0 indicates a complete absence of blood supply and 1 indicates optimal blood supply conditions. This range provides a quantifiable measure of vascularization^13,35.

$$\:\frac{\partial\:v}{\partial\:t}={D}_{v}\:{\nabla\:}^{2}v$$

(10)

$$\:{D}_{v}=f\left(\epsilon\:\right)=\:\left\{\begin{array}{c}{D}_{{v}_{0}}\:\:\:\:\:when\:\epsilon\:\le\:{\:\epsilon\:}_{angiogenesis}\\\:0\:\:\:\:\:\:\:\:\:\:when\:\epsilon\:>{\:\epsilon\:}_{angiogenesis}\end{array}\right.$$

(11)

$\:{D}_{v}$ represents the free angiogenic diffusion coefficient, while ε denotes the deviatoric strain in this set of equations. Furthermore, $\:{\:\epsilon\:}_{angiogenesis}$is the threshold for deviatoric strain beyond which angiogenesis is inhibited, with this threshold lying in the 6–9% range according to prior research on strain-induced blood supply during fracture healing^11,13,31.

Inspired by the work of Simon et al.³⁸, blood perfusion was used as a variable to simulate interactions between vascularization and the tissue differentiation process. This approach was designed to describe the extent of local blood concentration, supplying cells with essential oxygen and nutrients and facilitating the removal of metabolic waste. To further regulate tissue differentiation, two functions were defined for relatively low and high blood concentration at each element (Eqs. 7 and 8). This scalar variable ranged from 0% (no concentration) to 100% (optimal for bone formation), inspired by the fuzzy logic method and fuzzification algorithm. Endochondral ossification is the process of bone tissue forming gradually by cartilage, which requires adequate blood supply, but intramembranous ossification is the direct formation of bone from mesenchymal stem cells without cartilage precursor. This process can occur in areas with relatively low vascularity. In the endochondral ossification, areas with low blood perfusion would act in favor of cartilage formation (Eq. 7), and areas with medium and high blood concentration would act in favor of immature and mature bone formation (Eq. 8). Based on blood vessel concentration and tissue requirements, the algorithm checks the blood supply for each element. If supply is below a certain level, it favors cartilage formation using$\:\:{f}_{2}\left(v\:\right)$. Conversely, if blood supply exceeds the adequate level, it promotes osteogenesis and bone formation, accelerating the process via$\:{f}_{i=\text{1,3},4}\left(v\:\right)$(Fig. 2B). These functions act as cell differentiation rate adjustments that can control the speed of ossification based on blood supply (Eq. 6).

These sets of mathematical functions inspired by the work of Ganadhiepan¹³ were used for this rat model to correlate different stimulus and vessel density levels to tissue differentiation rates (Fig. 2B). Blood perfusion below 40% counts as low, promoting cartilage formation. Additionally, there is a direct correlation between blood vessel density and oxygen level^13,25,31.

Our model refined the representation of blood vessel dynamics in the bone marrow and around the fracture site to align more closely with the early stages of bone fracture healing. The disruption of blood vessels supplying the bone and periosteum during a fracture leads to the formation of a hematoma at the fracture site, which is rich in hematopoietic cells³⁹. A rapid surge in blood flow following surgery leads to an initial increase in blood vessel density. Subsequently, vessels progressively grow towards the fracture site, facilitating the delivery of essential nutrients and cells crucial for healing. As healing progresses, the number of blood vessels in the callus area stabilizes and reaches a steady state. This has been achieved by gradually decreasing the angiogenesis boundary level at the marrow and proximal fracture periosteum, which controls the steady state level of blood concentration in the diffusion process. This adjustment in our model allows for a more accurate simulation of the natural progression of bone fracture healing, capturing the dynamic changes in blood vessel density that are vital for supporting tissue repair and regeneration.

Fig. 2

(A1) Mechanobiological regulation by Prendergast et al.³. (A2) Modified (smoothed) mechanobiological regulation criteria for tissue differentiation in rats. (A3) Reaction diagram showing the rates of differentiation between MSCs, fibroblasts, chondrocytes, and osteoblasts, labeled with corresponding rate constants F_i=1,0.7. (B) Blood regulation functions (f_i=1,3,4, f₂) showing the dependencies of cell differentiation rates to blood vessel density. (C1) 2D Finite element model of rat femur for biomechanical analysis modeled femoral shaft as a hollow cylinder with specifications derived from µCT scans post-surgery. (C2) highlights the refined mesh around the fracture site and mesh convergence analysis for each region separately. (C3) Force and boundary conditions contain mechanical (axial load and fixed screws) and physiological (cell concentrations) used for separate phases of the simulation. (D) Schematic representation of the algorithm used for cell differentiation influenced by angiogenesis and mechanical stimulus. A closer look into simulation of tissue differentiation and vascularization in healing callus: this demonstrates the dynamic development of bone, cartilage, and fibrous tissue within the callus influenced by mechanical conditions and MSC concentration, alongside an angiogenesis model reflecting blood vessel growth regulated by strain-dependent diffusion, mirroring the oxygen supply to cells during the healing process based on work of Ganadhiepan¹³.

Following the progression of the simulation and its three phases outlined above, we used specific rates to model the differentiation of MSCs into fibrogenic, chondrogenic, and osteogenic pathways, which are essential for tissue repair and growth. Adjustments to these rates were made daily in the simulation based on mechanical stimuli, MSC concentration, and blood vessel density in each area. Each day, we evaluated healing progress by integrating the day’s changes with the current state of repair. This iterative approach continuously updated tissue states based on cell diffusion, differentiation, proliferation, and apoptosis at specified rates. The resultant cell numbers were then transformed into different tissue types. By applying a linear rule of mixture daily, we determined the material properties of the tissue at that stage. Below is a schematic of the MR algorithm used to update tissue conditions (Fig. 3).

Fig. 3

Schematic of the MSC differentiation algorithm in fracture healing simulation. This illustrates the iterative process used to update tissue types and material properties daily, based on MSC differentiation rates into fibrogenic, chondrogenic, and osteogenic cells, influenced by mechanical stimuli, cell concentration, and vascularization, guiding tissue repair and growth in the rat model.

Statistical analysis

For validation, the AFM-based nanoindentation results from the desired time points were evaluated and compared to the results of the same regions from the FE model by fitting a 4th -order parabolic function to both plots and then calculating the root-mean-square error (RMSE) of these functions compared at each time point. Our study analyzed stiffness changes in samples post-surgery using AFM data across three regions (central, intermediate, and outer) at six time points. A Shapiro-Wilk normality test was conducted to assess the normality of the data. Depending on the normality results, the Friedman non-parametric or Kruskal-Wallis test was utilized to analyze the effect of time points and region on material updates. Post-hoc multiple comparison was performed and adjusted using Dunn’s correction. Simple linear regression analysis was employed to compare AFM data with FE simulation results up to 21 days post-surgery in each specific region and to compare their respective regression slopes.

A descriptive analysis was performed to evaluate the precision and predictive capability of the computational model compared to histology. Two datasets were assessed at the same specific region on a given day. First, we looked at the proportion of different tissue types within the entire histological area relative to the total tissue volume in a particular slice. Then, we compared this to the proportion of FE elements designated for the corresponding tissue material relative to the total number of elements assigned that day. Each region’s average and standard deviation were calculated by performing a descriptive analysis. All statistical analyses were performed using GraphPad Prism (Version 10, GraphPad Software, San Diego, California, USA, https://www.graphpad.com/scientific-software/prism). Two-tailed p-values less than 0.05 were considered significant.

Results

Experimental findings

The average elastic modulus of tissues in three predefined regions (central, intermediate, and outer) of the fracture site was measured using AFM-based nanoindentation at nine random locations for each rat. Figure 4 shows the stiffness of the formed tissues over time from days 1–21. The mean values for the elastic modulus in the central region increased from 46 to 217 kPa within the initial 14 days, culminating at 853 kPa by day 21. In the intermediate region, the elastic modulus ranged from 72 to 305 kPa during the first three days, progressing incrementally to 4.27 MPa by the 21st day. Likewise, the outer region demonstrated a progressive stiffening across the 21 days, with its modulus ranging from 235 kPa to 13.33 MPa.

Fig. 4

Temporal stiffness progression in fracture site regions from AFM Data, displaying the stiffness of tissues within central, intermediate, and outer regions over 21 days, based on AFM measurements at nine random locations per animal.

Region of analysis had a significant effect on elastic modulus on days 2, 3, 14, and 21 (p-values < 0.01), with notable variations between the central and outer regions on same time points (p-values: 0.014, 0.014, 0.01, and 0.01, respectively). Additionally, we performed post-hoc analysis for different time points at each specific region. Significant differences were observed within the central region of the callus upon comparing data from days 1, 2, and 7 with day 21 (p-values: 0.003, 0.012, and 0.040, respectively). Furthermore, significant distinctions were detected in the intermediate region beneath the cortical bone when examining data from days 1, 2, and 7 compared to day 21 (p-values: 0.003, 0.006, and 0.019, respectively). Similarly, significant differences were evident in the outer region across various time points. Specifically, comparisons between days 1 and 14, 1 and 21, 2 and 21, 7 and 14, and 7 and 21 exhibited significant differences (p-values: 0.032, 0.004, 0.028, 0.045, and 0.006, respectively).

Histology slides revealed two main findings: the progression trend and differentiation of each tissue type in the fracture site via the timeline and the amount of each transformed tissue in the stained window normalized to the sum of the total tissue area. Figure 5 displays histology images of one representative sample with H&E staining (A) and Movat’s pentachrome (B) through the defined time points post-fracture. Initially, the center of the fracture was occupied by a hematoma, with granulation tissue forming around it by the first-day post-operation. By the third day, the hematoma was largely replaced by granulation tissue. By the seventh day, cartilage began to appear at the outer edges, while granulation tissue continued to fill the central and intermediate areas. On day fourteen, cartilage patches were visible in both the outer and intermediate areas, and a small amount of new bone started to form at the outer edge, as well as some regions between cortical bone stems. As we get closer to the twenty-first day, the fracture site features a mix of granulation tissue, cartilage, and new bone, illustrating the progressive stages of healing over time. The formed tissue cells have been identified during the timeline and shown in Fig. 5C, D.

Fig. 5

Histological analysis of tissue progression and differentiation post-fracture for one representative sample at each timepoint between days (1–21). This represents histology slides at various time points post-fracture using H&E staining (A) and (B) Movat’s Pentachrome staining with higher magnification views of cartilage and new bone outlined in blue and orange, respectively. The images illustrate the tissue progression and differentiation trend within the fracture site. The images illustrate the progression and differentiation of tissue within the fracture site. Parts (C) and (D) provide detailed, zoomed-in views of specific regions on days 14 and 21, highlighting chondrocytes and osteoblasts within the fracture window, respectively.

Figure 6 shows the quantification of tissue volumes after a fracture, tracking the normalized volume of hematoma, granulation tissue, cartilage, and newly formed bone over 21 days. These quantitative insights are detailed in Table 3 and align with the histological observations in Fig. 5, illustrating the dynamic nature of bone healing. Initially, the fracture site is predominantly hematoma (75% on day 1), which reduces to 0.5% by day 21. Granulation tissue emerges on day 2, increasing from 28 to 85% by day seven and then decreasing to 60% by day 21. Cartilage appears around day 7, peaks at 23% by day 14, and reduces to 19% by day 21, aiding bone formation. Notably, immature bony callus formation is initiated around day 14, accounting for 20% of the total tissue observed in histological slides by day 21 post-fracture.

Fig. 6

Analysis of tissue volume formation post-fracture, presenting daily tissue formation volumes within a designated region up to day 21 post-surgery, as quantified from the histological study.

Table 3 Daily quantification of tissue volume post-fracture in designated region for histology.

Finite element analysis

We utilized a computational model from µCT scans to simulate bone fracture healing in rat femurs over 21 days. This model allowed us to closely monitor key outcomes and the predictability of our findings against experimental data. FE results showed a gradual decrease in mechanical stimuli (S) from day 1 to day 21 post-surgical osteotomy because, as healing progresses and tissue differentiates into higher mechanical properties, the overall element-wise strain and fluid velocity under the same loading conditions become less. Initial estimation following surgery showed octahedral shear strain between 3.7% and 2.06% in the mid and outer regions of the cortical cross-section, which reduced to 2.94% and 1.64% in those same areas by the 21st day. Fluid flow rates were decreased but not as much and were between 30 and 60 μm/s (Supplementary Table 2).

The simulation results in Fig. 7A demonstrate that the material properties of tissues surrounding the fracture site undergo continuous updates from day one, with particularly noticeable changes occurring in and around the cortical bones on the side opposite to the plate, where callus formation begins. Moreover, a closer examination of the area beneath the plate, as illustrated in Fig. 7B, reveals that tissue development jumps to higher ranges but at a slower pace. By day 21, it achieves a stiffness range of 10–40 MPa, indicating early signs of hard callus formation. As seen in the notch region beneath the plate, the material properties are not symmetrically updated, indicating differences in mechanical stimulus. This result comes from the slightly different distribution of shear strain and fluid velocity in the area (Supplementary Fig. 2). Unlike an idealized scenario with equal and opposite forces at the top and bottom of the bone, the physiological load applied to the hip creates a more complex, uneven strain distribution. While the reaction forces are present, the strain on the top and bottom of the plate is not identical due to natural variations in loading and the plate’s influence on stress transfer.

MSC migration and vasculature

The results from the FE diffusion phase provide details on the behavior of MSCs in the context of fracture healing. Initially, MSCs migrate from areas of high concentration at the borders, dispersing evenly across the fracture site. This migration is pivotal for guiding the tissue transformation process, as it increases the cell concentration within each element encountered by the MSCs. Figure 7.C illustrates a distinct pattern of cell migration toward the outer void areas of the fracture site. By approximately day seven post-fracture, there’s an accumulation of cells beneath the plate area. The simulation further reveals that from day 1, the concentration of cells begins to rise around the border, initiating migration towards the central and further regions of the fracture site. Between days 7 and 14, the cell concentration reaches a saturation point (value around 1) within the fracture site. Beyond this point, although MSCs continue to migrate and circulate within the region, their distribution throughout the site diminishes their role as key regulatory agents, rendering them less critical to the model’s outcomes.

In a separate analysis, the diffusion process simulated vasculature (vessel density) and, subsequently, oxygen supplies. Vasculature indicates blood supply along the healing process (Fig. 7D). Each element of the fracture site has a unique vessel density value through healing, and as seen in this figure, the new blood vessels grow from existing ones. The callus will build a blood vessel network as healing progresses by day seven post-fracture, and then vessel formation plateaus and is uniformly distributed in the callus area. Similar to MSC migration, vasculature development occurs in high vessel density zones (mostly from mid-section under marrow and bone, which is the origin of vascularization) to low vessel density zones. By days 14 to 21, vascularization stabilizes, returning to the normal levels observed within healthy vessels, which typically feature around a 20% oxygen supply. This pattern highlights the critical role of vascularization and oxygenation in supporting and regulating the healing process over time. We ensured our model’s reliability and accuracy using tissue prediction and material update trends. We compared normalized tissue production volume by time with histology and elastic modulus evaluation with in vivo AFM results.

Fig. 7

Evolution of material properties in fracture healing from FE simulation. Rows a and b showcase the progressive changes in tissue stiffness (E), especially around the cortical bones and beneath the plate, leading to hard callus formation with stiffness of 10–40 MPa by day 21, highlighting the model’s ability to capture the dynamic nature of bone healing. Row c shows MSCs Migration and Concentration in Fracture Healing Simulation. Row c demonstrates MSCs migration from high concentration areas towards the outer regions of the fracture site, with significant cell accumulation noted beneath the plate by day 7. It highlights the dynamic distribution of MSCs critical for tissue transformation, reaching saturation around days 7 to 14, and the diminishing impact of further MSC distribution on the healing process beyond this point. Lastly, Row d shows FE Simulation of Vascularization in Fracture Healing. Illustrates vessel density changes and oxygen supply via diffusion, showing blood vessel network development in the callus by day seven and gradual stabilization of vascularization to normal levels by days 14 to 21, highlighting the importance of vascular growth and oxygenation in the healing process.

Tissue prediction and material update trends

Our initial analysis focused on the pattern of tissue development and changes in material properties over time, as depicted in Fig. 7A. These trends closely matched our expectations based on histological evidence and previous research, indicating a consistent daily progression of healing^21,40. This shows the same trend in the ossification and tissue differentiation by time, which we elaborated under histology results (Fig. 5).

Normalized tissue volume measurement

We quantified the volume of tissue formed each day post-fracture within a designated region, analogous to those examined in histological studies. The simulation results in Fig. 8 demonstrate an agreement in both the timing and quantity of tissue formation with those observed in histological analyses (Fig. 6). This comparison suggests that our model accurately captures the crucial phases of early to mid-stage bone fracture healing. Figures 6 and 8 show the quantity of each tissue type formed every day after surgery until day 21 from histology and model simulation. The results indicated a high amount of hematoma formed around days 1 and 2 after surgery and decreased afterward. Granulation tissue forms from day two and reaches its highest concentration around days 11–13. After day 14, cartilage started to be seen in the site and increased continuously to 45% around day 21, also confirmed by histology results. New bony tissue started forming in the process of endochondral ossification from cartilage around day 14 and increased by 7% since its concentration is highly related to cartilage concentration. We expect intramembranous ossification and primary bone healing around and under the plate region, facing relatively less strain. Still, it is unlikely for this bony tissue to mostly be related to this process as primary healing is slower than secondary healing. Its contribution is predicted to be less than 10% of the site chosen for screening.

Fig. 8

(A) Temporal analysis of tissue volume formation post-fracture. Presents daily tissue formation volumes within a designated region up to day 21 post-surgery, as quantified from model simulations. The result demonstrates the model’s ability to replicate hematoma formation and transformation of tissue types together as the healing progresses. Comparing it to histological data from Fig. 7 highlights the correlation in timing and quantity of hematoma, granulation tissue, cartilage, and new osteogenesis. (B) The spatial and temporal tissue formation and differentiation trend in the model after fracture specified to match the coloring in part A.

Elastic modulus evaluation

Through daily assessments of the elastic modulus of individual cells post-fracture, we approximated the tissue stiffness within three distinct regions of the fracture site, aligning with areas examined in AFM-based nanoindentation results. This process has been done by considering each element in the fracture area as equal to mesh size = 0.1 mm, which led us to count the elements and choose predefined sets of elements for each specific region from the center of fracture with thickness equal to gap size (2 mm) as the AFM was performed on extracted tissue from fracture gap. By averaging these estimations over 21 days, we achieved a granular comparison of tissue stiffness among the central, intermediate, and outer regions, as depicted in Fig. 9A–C. We applied two sets of fourth-order polynomial equations to elastic modulus data vs. time to understand the model’s validity to our simulation outcomes and the experimental data (Supplementary Fig. 3). This allowed us to quantitatively gauge the model’s precision by analyzing the root mean square error (RMSE) for the early days of bone healing. The RMSE values for the central, intermediate, and outer regions during the initial stage of healing (days 2 to 7) were 0.025, 0.15, and 0.39, respectively, indicating a high degree of alignment with experimental findings. As we proceeded further away from the initial day, the RMSE increased to a higher level (1–3), and the model prediction was not as accurate as the early days but still within the standard deviation range when compared to 4 data points at days 14 and 21. More information, including the fit functions and plot, can be found in Supplementary Fig. 3. An examination of Fig. 9A–C comparing the simulation predictions of the regions’ elastic modulus with AFM-based nanoindentation measurements revealed that the predictions generally fell within the range of experimental test cases and were closely aligned with the average values and showed that the MR model was more adept at forecasting outcomes in the intermediate region of the healing site, compared to the central and outer regions. Notably, inconsistencies became apparent, particularly around day 14 of the healing process, indicating inaccuracies in the model’s predictions for these areas. However, the results converged closer to in vivo as we reached day 21. The statistical outcomes, including the average and standard deviation from the experimental AFM-based nanoindentation data and FE analysis, are presented in Table 4. Figure 9D–F highlights this comparison but with the previous sheep-derived MR model. This indicated that the simulation predicts an order of magnitude higher elastic modulus and is inconsistent with the AFM-based nanoindentation results. We also compared the slope from the linear regression analyses of FE and AFM-based nanoindentation data across different regions. This comparison was made for the current rat FE analysis and a previously established model derived from sheep data. The results indicated that the differences in slopes between AFM and the rat-derived FE data within the central (F = 3.12, p = 0.085), intermediate (F = 0.13, p = 0.72), and outer regions (F = 0.14, p = 0.71) were not statistically significant. Conversely, comparing the slopes derived from the previously established sheep FE model and the AFM-based nanoindentation data revealed a significantly different slope. In the central (F = 86.82), intermediate (F = 911.00), and outer regions (F = 275.70), significant differences were observed, with all p-values being less than 0.001. The quality of each linear regression fit, as assessed by the coefficient of determination (R²), is detailed in Supplementary Table 1.

Fig. 9

Elastic modulus comparison across fracture site regions over 21 days. The first row shows the current model, and the second row shows the common MR model using sheep data, illustrating the variation in tissue stiffness within the fracture site’s central, intermediate, and outer regions based on daily assessments and AFM-based nanoindentation tests. Figures (A–C), and (D–F) compare current and previous MR simulation predictions of elastic modulus with AFM experimental data, respectively, highlighting this model’s accuracy in early bone healing stages and demonstrating its particularly effective prediction in the intermediate region.

Table 4 Statistical comparison of experimental AFM data and FE analysis results.

Discussion

We used a well-established mechanoregulatory model presented by Lacroix & Prendergast³⁰. Over the years, this model has undergone numerous modifications by various scholars, with the majority of these adjustments being validated through in-vivo experiments conducted on sheep. With the idea of differences between sheep and rodents mentioned by Checa et al.²¹ in the bone fracture healing process, we developed a modified version of the MR model, which can computationally predict different stages of bone healing before remodeling. It is important to highlight that during the development of our model, the initial value and the range of the elastic modulus for each region were utilized as the foundational parameter. Subsequently, the in-vivo data gathered from animal studies validated the model and assessed its predictive capabilities with trend and tissue formation volume comparisons. This model seeks to improve accuracy by incorporating various critical factors identified in the literature as essential to fracture healing. These enhancements include adjustments to the rates and regulatory mechanisms of the mechanobiological process. Notably, we have improved the representation of mesenchymal stem cells (MSCs) by adjusting their concentration at the borders and enabling more dynamic diffusion across the healing timeline through variable diffusivity tailored to each tissue type. Additionally, we introduced a third phase of simulation focusing on the vasculature, acknowledging its significant contribution to the healing process and recognizing it as one of the most important factors in tissue differentiation and transformation^21,31,34. The combination of mesenchymal stem cell contribution and vessel density, which represents the blood oxygen level locally, is possible through a series of mathematical functions, and it would help the healing process become more dynamic. Finally, we tested our FE model’s and simulation approach’s validity by comparing our findings to preliminary in vivo observations in a rat plate fracture model over 21 days.

In our model, vasculature is modeled as a diffusion approach, representing the process of forming blood clots and increasing blood flow in the early days after fracture. As the histology model shows, it also represents decreasing this blood gradually to a normal level as healing progresses. When used as a representative of oxygen concentration (assuming that vascularization directly impacts oxygen level), this method has been proven to help tissue differentiation during this process. Lu et al.⁴¹ examined the effects of oxygen tension on fracture healing and tested the ability of hyperoxia to rescue healing defects in a mouse model of ischemic fracture healing. The influx of inflammatory cells to the fracture site, stem cell differentiation, tissue vascularization, and fracture healing were analyzed. The oxygen level in the later stages of the healing site has been chosen from the same work to be around normoxia. As detailed in the “Methods” Section, stabilizing blood vessel numbers in the callus area is a crucial part of the healing process. This stabilization is achieved by gradually reducing the angiogenesis boundary at the marrow and proximal fracture periosteum, which regulates blood concentration levels. Delays in this process can prolong healing and increase blood supply to the area, leading to excessive granulation tissue formation and delayed chondrogenesis. This, in turn, results in later bone formation, a less rigid callus, and a need for a larger callus to ensure stability. Physiologically, this scenario could mirror conditions where vascularization is excessive or poorly regulated, potentially leading to hypertrophic non-unions or delayed healing often observed in clinical settings with compromised angiogenesis. Conversely, a quicker transition to stable blood vessel density promotes cartilage formation, enhances callus stability, and accelerates osteogenesis and overall healing. It is important to note that these outcomes assume an intact immune response and fulfillment of other healing requirements, with changes occurring specifically in blood supply and angiogenesis during the healing process.

By initiating our model with material properties derived from first-day AFM-based nanoindentation measurements at various locations around the osteotomy site, we tested the model’s predictability using in-vivo data. This approach allowed us to conduct a more accurate verification than solely relying on pre-established material properties from existing literature, despite the consistency in scale between our data and prior research^21,40. Comparing our findings to those reported by Leong et al.²⁷, who conducted nanoindentation on rat femur fracture callus, we find that our range of indentation moduli aligns closely with their results. They reported indentation moduli for granulation tissue, chondroid tissue, and woven bone ranging from 0.61 to 1.27 MPa, 1.39 to 4.42 MPa, and 26.92 to 1010 MPa, respectively, with median values of 0.99 MPa, 2.89 MPa, and 132 MPa. Our model’s results fall within the same order of magnitude for granulation and cartilage, indicating a comparable mechanical environment within the healing callus. A slight difference was observed in the woven bone at day 21, with our values around their minimum report. This discrepancy could be due to delayed healing from our open fracture surgery compared to their closed fracture and nail fixation method and the different measurement time points (day 21 vs. day 35). Additionally, our data underwent a predictability check and performance comparison with in-vivo results (AFM and histology) in 5-time points from day 2–21, reinforcing the reliability of our findings.

The model shows and mimics the blood vessel formation after fracture and attracts nutrients and cells to the site. This process would affect the cell concentration and tissue differentiation daily from MSCs and at each element via a set of mathematical rules from previous studies^13,31. The model shows an accumulation of MSCs around the plate, which could be due to its proximity to the MSC source (bone marrow and periosteum). Additionally, the daily concentration of cells is influenced by the time and distance from borders from which the cells migrate. Enough MSC and low strain due to structure stability start the process of primary bone healing in this region. However, since the fluid velocity is lower at this location as the deformation and, subsequently, pressure is higher in the outer edge of the cortical bone, the bony tissue would not form instantly, and this process takes more time to complete. Usually, in plate fixation under the implant, there is a region where low interfragmentary movement (IFM), in case of a small fracture gap, would show intramembranous ossification, and bony tissue starts to be seen without cartilage formation in the fracture site⁴². Although this was not seen vividly in the histology, as the staining section was not perpendicular to the plate, capturing this phenomenon from our FE model is promising since it is based on the body’s physiological process. Achieving this was facilitated by the model’s incorporation of a strain threshold within the targeted region, which is critical for osteogenesis in the initial phase following a fracture. The presence of an implant plate plays a crucial role in mitigating shock impacts, thereby stabilizing the region and enabling the commencement of bone tissue development. Nonetheless, the progression of this tissue formation occurs at a moderated rate, influenced by the concentration of MSC and the extent of vascularization, which collectively dictate the pace of the bone healing process.

Our understanding of fracture treatment and healing has significantly changed in recent decades. Now, there is an acknowledgment that both mechanics and biology play critical roles in the treatment process. While precise reduction and absolute stable fixation are not always necessary, maintaining enough rigidity with controlled interfragmentary movement (IFM) to support function without compromising biological integrity is essential. Surgeons can create absolute or relative stability depending on the fracture type and the surgical objective. Rigid fixation with absolute stability is typically used for peri-articular fractures to achieve perfect anatomical reduction, involving very minimal interfragmentary motion (less than 0.15 mm), strains under 5%, and hydrostatic pressure below 0.15 MPa, facilitating contact or gap healing (0.2 mm to 0.5 mm). Alternatively, surgeons may choose relative stability for an optimal biological healing environment, allowing 0.2–1 mm of motion, which usually results in healing via periosteal callus formation. This understanding has prompted a reconsideration of using overly stiff metal plates^43,44. Using very stiff plates might stop the bone from moving as it naturally would, which could slow down or even stop the healing process. So, it’s better to use plates that allow a little movement, supporting the body’s natural healing. By choosing the right type of stabilization—whether it’s very rigid or allows some movement—we can help fractures heal better, keeping the natural healing process in mind^17,44,45,46. It is worth noting that although the strain range in this study might seem high (2–4%) compared to rigid plate fixation, our experimental design incorporated a less rigid plate with a strategic gap at the fracture site, and the fracture size in this model was also a critical defect in rat femur (2 mm) which contributes to this high strain and will help us investigate the threshold for successful fracture healing. This gap allows bone growth towards the plate and facilitates increased IFM, pivotal for enhancing bone fracture healing.

As can be seen from histology slides (H&E and Pentachrome), as the healing process advances, there are variations in tissue differentiation and the pace of change. The relative location of the tissue in the fracture site and certain crucial time-related factors influence these variations. Notably, during the initial days post-surgery (1–3), factors such as angiogenesis and cell migration play a more important role in the healing process. In our observations, the healing process at the fracture site demonstrated a complex and dynamic progression over three weeks. Initially, on the seventh-day post-fracture, the early signs of soft callus were marked by cartilage formation along the outer borders of the fracture site. At the same time, the central and intermediate regions were predominantly filled with granulation tissue. This granulation tissue plays a crucial role in the healing process, providing a scaffold for new tissue growth and facilitating the migration of cells necessary for tissue repair.

As we moved into the second week, specifically by the fourteenth day, cartilage became more widespread, extending from the outer regions to the intermediate zones of the fracture site. This period also marked the initiation of new osteogenesis, not only along the outer edges but also in selected areas between the cortical bone stems, as it is unique to rodents and was reported before by Miller et al.⁴⁰. This new osteogenesis at the intermediate stages of healing signifies the transition from a soft callus phase, predominantly composed of cartilage, to the onset of a hard callus phase where mineralization begins to solidify the newly formed bone. By the twenty-first day, the fracture site exhibited a comprehensive and integrated mix of granulation tissue, cartilage, and newly formed bone. This composition reflects the culmination of the healing process, showcasing the body’s ability to repair and regenerate bone tissue through a sequential and organized progression. The presence of these various tissues illustrates the stages of bone healing, from the initial inflammatory response to the formation of a hard callus and eventual bone remodeling.

Historically, fracture healing models have often neglected the initial healing phase and overlooked the critical role of angiogenesis and related parameters, significantly influencing the healing outcome. In recent years, there has been a growing emphasis on incorporating biological processes into modeling, recognizing that while the mechanical aspects are largely understood, there is a pressing need for more detailed simplifications within each biological pathway. This approach is vital for effectively merging them with mechanobiology simulation models. Such advancements promise to yield more cohesive and meaningful models, potentially transforming their applicability on a clinical scale in the future.

In our current model, we have tried to integrate the key elements of the first three stages of healing before the remodeling phase into a computational framework. This integration aims to assess the model’s efficacy on an in-vivo scale. Unlike relevant computational studies, we did not model the involved tissues in the fracture site as a homogeneous material, as heterogeneity was seen in the early days of healing in AFM-based nanoindentation and histology. Furthermore, we did not assume a fixed callus size during and after the initial healing phase. it is clinically observed that callus forms and grows during the first few days after fracture, and it stops growing at some point. It desorbs at later stages to reform the cortical bone borders, so it should fluently change its geometry to have a better and more accurate result^47,48,49. In this study, we assumed that mechanical factors and MSC migration can predict callus growth during the process, which needs further investigation to assess, but by comparing model results to the in-vivo study, it showed a good correlation in most days post-fracture in both AFM and histology by linear regression analysis, with a slight diversity around day 14 for central and outer region which can be because of limited number of samples and our limitations in simulating the true biological process. Furthermore, histological data indicates high cartilage levels at day 7, which only appears around day 14 in the model. This suggests that while the MR model has strengths in capturing the distinctions of tissue differentiation in certain zones, it may require further refinement to enhance its predictive accuracy across all regions of a bone fracture site, especially at critical junctures in the healing timeline. Moreover, the evidence of foreseeing hard callus formation under the plate without cartilaginous tissue formation points towards the dynamic and progressive nature of bone healing, emphasizing the critical role of spatial and temporal changes in tissue properties for better model prediction.

One of the inherent limitations of our study is the modest sample size, comprising only four in-vivo samples per day over a relatively narrow window of 21 days, with six distinct time points. This restricted sampling range does not fully capture the broad spectrum of physiological transformations that occur in bone during the post-fracture healing period. Moreover, the research employed an established method of open-surgery osteotomy in its animal model. While not novel, this technique has been previously applied to rats to investigate the critical fracture gap associated with an increased risk of nonunion⁵⁰. A notable consequence of open surgery is removing blood clots and disrupting the marrow border, which can hinder the secondary bone healing process. This was evident in the histological slide observations. Future studies could address this issue by comparing the result with a developed animal model based on a closed fracture approach. Such comparison can give clinicians insights into the fundamental differences between closed and open fracture healing time courses and can be validated by patient-specific CT scan models.

“Additionally, the 2D model used in this study introduces some limitations, particularly in capturing the periosteal continuity around the screw, which may exaggerate the delay in mesenchymal stem cell migration. Future work will aim to develop a 3D model that more accurately represents the geometry of the bone and screws. This approach will better capture periosteal effects on cell migration dynamics and, combined with integrating more physiological factors in callus growth and resorption, enhance the model’s accuracy in mimicking the body’s healing process.” This study can be a foundation for further study on a more dynamic callus modeling and its effect on healing outcomes. For future direction, more physiological factors should be involved in the callus growth and resorption and animal study to better modify the model for further accuracy in mimicking the actual process in the body. Another assumption that has been used widely among researchers in this field was assuming the MSC migration to be governed by general diffusion and the effect of fluid flow as mechanical stimuli for this migration^7,13,51, but we have modified this model to change the diffusion for each tissue cell every day through the process as they have a different rate of migration and resistance to flow in the body because of their texture and microenvironment of extracellular matrix. Also, this study suggests a notable gap in our understanding regarding the application and effectiveness of region-specific MR models, suggesting a vital area of study that could significantly advance our knowledge and capabilities in predicting and managing bone healing processes.

Conclusion

In this study, we have introduced a computational model that simulates bone fracture healing in rats using mechanobiological regulations and angiogenesis simulation, and we are considering a natural space for callus development. Through a temporal experimental approach involving Atomic Force Microscopy, microcomputed tomography, and histological analysis alongside a refined finite element modeling technique, mechanical and biological processes during the initial phase of bone healing have been closely examined to challenge the common knowledge about physiologic trend happening in bone fracture. A novel aspect of this model is the ability to predict tissue formation rates and incorporate callus growth’s physiological aspects, which offers a more natural healing simulation. This model can better predict the healing outcomes in rats by adjusting tissue differentiation thresholds and simulating MSC migration and angiogenesis. This advancement is helpful since there is a gap in the literature, where mechanobiological responses of different animal models, particularly rats compared to larger animals like sheep, have been underexplored. The experimental results, followed by the computational simulation, highlight the significant changes in tissue properties and cell migration patterns over time. Moreover, incorporating angiogenesis alongside physiological response to mechanical and biological factors has enhanced the model’s accuracy, providing deeper insights into the early to mid-stage bone fracture healing process. Despite the promising outcomes, we acknowledge the limitations of our study, including the sample size and the scope of physiological factors considered. The reliance on open-surgery osteotomy in our animal model presents another constraint, potentially affecting the natural healing process. Future direction for this research would focus on expanding the model to include a broader range of physiological factors influencing callus growth and resorption and developing animal models that better capture the real-life fractures with more samples at each time point. Such advancements could refine the model’s accuracy and applicability, allowing enhanced clinical interventions to treat bone fractures.