A UAV path planning algorithm for bridge construction safety inspection in complex terrain

Abstract

In response to the challenge of rapid unmanned aerial vehicles (UAV) path planning for bridge construction in complex terrain, this paper presents an enhanced snake optimization (CSGLSO) UAV three-dimensional path planning algorithm. Initially, this study enhances the stochasticity strategy for generating initial populations within the Snake Optimization (SO) algorithm employing the Piecewise Chaotic Mapping technique, thereby obliterating transient periodic traits and fostering equilibrium in the solution space of the SO algorithm’s progenies. Subsequently, integrating the Subtraction-Average-Based Optimizer algorithm mitigates the issue of convergence speed within the SO algorithm confronting high-dimensional complex functions. Ultimately, employing adaptive t-distribution and lens imaging reverse learning facilitates the evasion of local optima within the current position by the SO algorithm, thus augmenting its exploratory prowess. To ascertain the efficacy of the enhanced algorithm, 14 standard test function convergence comparison experiments were conducted, as well as three-dimensional path planning simulation experiments under multi-scenario conditions of bridge construction by UAV. Experimental findings reveal that relative to SO, Hybrid Snake Optimizer Algorithm, Improved Salp Swarm Algorithm, and Exploratory Cuckoo Search, CSGLSO manifests shorter and more streamlined trajectories, accelerated convergence rates, and elevated optimization precision. Thereby, UAVs are empowered to execute path-planning endeavors expeditiously and precisely within intricate environments.

Introduction

The realm of bridge construction spans expansive territories, navigates intricate landscapes, and contends with formidable natural elements, brimming with myriad safety perils and environmental hazards within its vicinity¹. Manual inspection is currently the predominant inspection modality deployed across bridge construction sites². Nevertheless, this method grapples with constraints in terms of coverage, time expenditure, and efficacy. Certain sections remain beyond the purview of manual inspection owing to terrain complexities and environmental exigencies. Concurrently, with the evolution of UAV technology^3,4,5, there is a burgeoning interest in harnessing UAV technology to ensure safety in bridge construction inspections. In contrast to conventional manual inspection methods, UAVs can swiftly and securely survey entire construction sites. Manual inspections entail elevated safety jeopardy within intricate settings like high-altitude terrain, mountainous expanses, waterway traverses, and bustling urban locales. Therefore, the integration of UAV technology into bridge construction has emerged as a prevailing trend^6,7,8. Optimizing UAV path planning algorithms holds substantial engineering value in improving autonomy, real-time responsiveness, and operational robustness.

Currently, UAVs rely primarily on battery power. However, the limited capacity of these batteries restricts the duration of missions that can be executed. Within this context, the quest for energy-efficient, expansive, collision-averse trajectories emerges as a pivotal hurdle in UAV trajectory plotting^9,10. The problem of UAV 3D path planning can be regarded as a typical complex multi-constraint global optimization problem. This is to say that the optimal flight path between the starting point and the end point is to be found under the comprehensive consideration of the mission requirements and UAV performance constraints^11,12,13.

Predominantly employed path planning methodologies encompass Classical star algorithms and Metaheuristics^14,15. Classical star algorithms delineate into graph-centric, sampling-oriented, and optimization-driven variants, contingent upon their intrinsic attributes and domain-specific applications. Exemplars of graph-based algorithms encompass A*¹⁶ and Dijkstra¹⁷, At the same time, sampling-based methodologies feature rapidly exploring random trees (RRT)¹⁸ probabilistic roadmaps (PRM)¹⁹, and optimization-driven approaches incorporate simulated annealing algorithm²⁰ and artificial potential field method²¹. Metaheuristic algorithms draw inspiration from the synergistic behaviors exhibited by diverse biological populations in nature, exemplified by Particle Swarm Optimization²², Ant Colony Optimization (ACO)²³, and Artificial Fish Swarm Algorithm (AFSA)²⁴. Classical star algorithms are conceptually straightforward and versatile, yet they entail heightened computational intricacy, susceptibility to initial conditions, and substantial requisites for memory and computational resources^25,26,27. Conversely, while metaheuristic algorithms exhibit simplicity and robustness, they exhibit sluggish convergence rates and susceptibility to local optima entrapment^28,29,30,31.

For the classical star algorithm, Diao et al.³² introduced an enhanced Artificial Potential Field Rapidly Exploring Random Tree (APF-IRRT*) path planning algorithm explicitly tailored for disaster relief UAV missions. This algorithm leverages adaptive step size and dynamic search range within the RRT* framework, synergizing it with the APF algorithm to achieve refined trajectory smoothing during optimization. The algorithm effectively addresses the issues of slow convergence speed and an unsmooth path in UAV path planning, and achieves satisfactory performance in both offline static and online dynamic environment path planning. Wang et al.³³ devised an enhanced three-dimensional environmental path planning algorithm root-ed in A*, termed the Adaptive Bidirectional A* algorithm. This algorithm dynamically adjusts to three-dimensional environmental variables and employs bidirectional ex-ploration to ascertain the optimal path. Relative to its predecessor, the new algorithm substantially reduces planning duration, slashing it by 91.2%. To address the issue of stagnant UAV path planning and the resulting slow search speeds, Sun et al.³⁴ introduced a hybrid UAV route planning algorithm that amalgamates the Ant Colony Algorithm with the Intelligent Water Drops Algorithm. The symbiotic relationship between the IWD and ant colony algorithms facilitates mutual information exchange to optimize pathway configuration.

For the metaheuristic algorithm, Xiong et al.³⁵ introduced a hybrid UAV three-dimensional path planning approach denoted as HISOS-SCPSO, refining the Improved Symbiotic Organisms Search (ISOS) and Sine Cosine Particle Swarm Optimization (SCPSO) algorithms. The proposed solution effectively addresses the limitations of path planning algorithms, which are known to exhibit reduced accuracy and instability in complex three-dimensional environments. To resolve the issue of a reduction in the number of feasible solutions that arise due to the presence of constraints in complex environments, Chai et al.³⁶ delineated a Multi-Strategy Fusion Differential Evolution Algorithm (MSFDE) amalgamating diverse population tactics, innovative adaptive approaches, and interactive mutation strategies to harmonize exploration and exploitation competencies. Population segmentation comprises three index subpopulations and one reward subpopulation to preserve diversity; the teaching–learning-based optimization (TLBO) method is integrated with adaptive measures for regulating the F and CR parameters; and interactive mutation strategies facilitate intergenerational information exchange, bolstering population diversity. The three-dimensional space-based path planning problem for autonomous navigation of UAVs in complex space has been effectively solved. Luo et al.³⁷ advocated an enhanced Butterfly Optimization Algorithm integrated with Tent Chaotic Mapping (BOA-TSAR) for autonomous UAV three-dimensional path planning. Tent chaotic mapping enhances solution space equilibrium during initial population generation. Furthermore, in addressing high-dimensional complex functions, BOA’s convergence rate and precision are bolstered via adaptive weighting, simulated annealing, and global adaptive mutation techniques. Zhang et al.³⁸ introduced an enhanced variant of the AFSA algorithm, termed IAFSA, distinguished by its global search prowess and rapid convergence characteristics. It effectively mitigates the challenges associated with population distribution discrepancies and the inclination towards local optimization, issues that remain unresolved in extant AFSA iterations.

Despite advancements in the aforementioned improved algorithms, they continue to face dual challenges in complex UAV application scenarios: On one hand, while classical algorithms (e.g., A*, RRT*) accelerate convergence through bidirectional search or potential field optimization, their reliance on fixed-rule mechanisms or sampling strategies renders them less adaptable to abrupt changes in the solution space due to dynamic obstacle distribution. On the other hand, while meta-heuristic algorithms (e.g., PSO, ACO) exhibit strong global search capabilities, issues such as population diversity decay and an imbalance between exploitation and exploration can exacerbate path redundancy and energy consumption. Particularly when UAVs navigate urban canyons, dense forests, or sudden threats, the algorithm is susceptible to “path deadlock” caused by local optima, posing a severe risk to mission safety. Overcoming the intrinsic limitations of traditional algorithmic frameworks and developing hybrid intelligent algorithms that integrate rapid response capabilities with global optimization remains a pressing challenge in autonomous UAV navigation.

To tackle these challenges, this study introduces the CSGLSO algorithm, an improved SO³⁹-based UAV path planning approach. The acronym “CSGLSO” is constructed as follows: "C" originates from the Chaos mapping strategy, "S" from the Subtraction-Average-Based Optimizer, "G" from the Fusion Subtraction Averaging Fuser algorithm, and "L" from the Lens Imaging Reverse Learning Strategies. It is innovative in three ways:

• 1. Enhancing Initial Solution Equilibration: The population initialization strategy is reconfigured using piecewise chaotic mapping to mitigate the distribution clustering effect induced by the short-period sequences of the traditional SO algorithm, thereby improving the coverage of initial paths within the 3D solution space;

• 2. Breakthrough in High-Dimensional Convergence Efficiency: The SABO⁴⁰ leverages its differential evolution mechanism and gradient-oriented properties to minimize the number of path search iterations in complex terrains;

• 3. Enhancing Local Optimal Escape Capability: An adaptive t-distribution variation and lens imaging reverse learning strategy are introduced to improve the algorithm’s global optimal hit rate under obstacle interference by dynamically adjusting the perturbation intensity and reverse search range.

The SO algorithm

The SO algorithm demonstrates remarkable adaptability. It draws inspiration from snake mating habits. Snakes adjust their activities based on environmental conditions, focusing on mating in cold environments with ample food and foraging in other situations. This adaptability is mirrored in the search process, which is bifurcated into two phases: the exploration phase and the exploitation phase.

Throughout the exploration phase, snakes’ behavior is predominantly shaped by environmental factors like temperature and food availability. During this period, snakes primarily forage for sustenance within the immediate surroundings.

Throughout the exploitation phase, the primary objective is to enhance overall efficiency at a global scale. Snakes prioritize approaching food sources in conditions of ample food but elevated temperatures. Conversely, mating behavior ensues in environments with plentiful food and cold temperatures. There are two distinct modes during mating: combat mode and mating mode. In combat mode, males fiercely compete to mate with the most desirable females. In mating mode, snakes pair up for mating, and the mating frequency is strongly influenced by food availability. If mating occurs within the search area, females may lay eggs, leading to the birth of new snakes. These offspring replace the weakest members of the snake population.

Adaptation formula:

$${f}_{i}=fobj({X}_{i})$$

(1)

The notation ${f}_{i}$ represents the fitness of the ith snake individual, $fobj$ denotes the objective function, and ${X}_{i}$ denotes the position of the i-th individual snake. In this algorithm, the solution is represented by the position of each snake, denoted as ${X}_{i}$. The fitness value ${f}_{i}$ of this position is calculated using the objective function $fobj({X}_{i})$. This fitness value serves as a measure of the quality of the position. A smaller fitness value indicates a better solution.

Initialization:

$${X}_{i}={X}_{min}+rand\times \left({X}_{max}-{X}_{min}\right)$$

(2)

Within the equation, while ${X}_{min}$ and ${X}_{max}$ are the lower and upper bounds of the search space, respectively.

Following the initialization of the snake population, they are randomly dispersed throughout the search space and subsequently evenly partitioned into two cohorts: females and males.

$${N}_{m}=\frac{N}{2}$$

(3)

$${N}_{f}=N-{N}_{m}$$

(4)

Within the equation, N denotes the total population size, while ${N}_{m}$ and ${N}_{f}$ signify the count of male and female snakes, respectively.

Defining temperature and food quantity:

$$Temp=exp\left(\frac{-t}{T}\right)$$

(5)

$$Q={c}_{1}\times exp\left(\frac{t-T}{T}\right)$$

(6)

Within the equation, t denotes the current iteration number, while T represents the maximum iteration count. Q represents the food quantity, and ${c}_{1}$ is a constant set to 0.5.

Exploration stage

If Q falls below the Threshold (0.25), snake individuals opt to randomly select positions for foraging, update the position of the solution.

Update formula for the position of the male snakes:

$${X}_{i,m}\left(t+1\right)={X}_{rand,m}\left(t\right)\pm {c}_{2}\times {A}_{m}\times \left(\left({X}_{max}-{X}_{min}\right)\times rand+{X}_{min}\right)$$

(7)

Update formula for the position of the female snakes:

$${X}_{i,f}\left(t+1\right)={X}_{rand,f}\left(t\right)\pm {c}_{2}\times {A}_{f}\times \left(\left({X}_{max}-{X}_{min}\right)\times rand+{X}_{min}\right)$$

(8)

$${A}_{m}=exp\left(\frac{-{f}_{rand,m}}{{f}_{i,m}}\right)$$

(9)

$${A}_{f}=exp\left(\frac{-{f}_{rand,f}}{{f}_{i,f}}\right)$$

(10)

In this equation, ${X}_{i,m}$ and ${X}_{i,f}$ denote the positions of the i-th male or female individual, correspondingly. ${X}_{rand,m}$ and ${X}_{rand,f}$ are randomly selected male or female positions, respectively. ${A}_{m}$ and ${A}_{f}$ signify the foraging abilities of males and females, respectively. ${c}_{2}$ is a constant set to 0.05, and rand is a random number within the range [0,1]. ${f}_{rand,m}$ and ${f}_{rand,f}$ are the fitness values in randomly selected male or female individuals, respectively. ${f}_{i,m}$ and ${f}_{i,f}$ indicate the fitness values of the i-th individual position among males and females, respectively.

Exploitation stage

If Q surpasses the Threshold (0.25) while the temperature exceeds the Threshold (0.6), snakes concentrate on seeking out food sources. The position of the solution will move towards the direction of the best individual position, with the update formula given by:

$${X}_{i,j}\left(t+1\right)={X}_{food}\pm {c}_{3}\times Temp\times rand\times \left({X}_{food}-{X}_{i,j}\left(t\right)\right)$$

(11)

Within the equation, ${X}_{i,j}$ denotes the position of the snake individual, ${X}_{food}$ denotes the optimal individual location, and ${c}_{3}$ = 0.05.

If Q exceeds the Threshold (0.25) while the temperature falls below the Threshold (0.6), snakes engage in combat mode or mating mode. The positions of the male and female snakes will be updated through their interactions with each other.

Combat mode:

$${X}_{i,m}\left(t+1\right)={X}_{i,m}\left(t\right)+{c}_{3}\times FM\times rand\times \left(Q\times {X}_{best,f}-{X}_{i,m}\left(t\right)\right)$$

(12)

$${X}_{i,f}\left(t+1\right)={X}_{i,f}\left(t\right)+{c}_{3}\times FF\times rand\times \left(Q\times {X}_{best,m}-{X}_{i,f}\left(t\right)\right)$$

(13)

$$FM=exp\left(\frac{-{f}_{best,f}}{{f}_{i}}\right)$$

(14)

$$FF=exp\left(\frac{-{f}_{best,m}}{{f}_{i}}\right)$$

(15)

Within the equation, ${X}_{best,m}$ and ${X}_{best,f}$ denote the optimal position among males or females individuals, while FM and FF signify the mating capabilities of males or females. ${f}_{best,m}$ and ${f}_{best,f}$ denote the optimal fitness value in a male or female individual, respectively.

Mating mode:

$${X}_{i,m}\left(t+1\right)={X}_{i,m}\left(t\right)+{c}_{3}\times {M}_{m}\times rand\times \left(Q\times {X}_{i,f}\left(t\right)-{X}_{i,m}\left(t\right)\right)$$

(16)

$${X}_{i,f}\left(t+1\right)={X}_{i,f}\left(t\right)+{c}_{3}\times {M}_{f}\times rand\times \left(Q\times {X}_{i,m}\left(t\right)-{X}_{i,f}\left(t\right)\right)$$

(17)

$${M}_{m}=exp\left(\frac{-{f}_{i,f}}{{f}_{i,m}}\right)$$

(18)

$${M}_{f}=exp\left(\frac{-{f}_{i,m}}{{f}_{i,f}}\right)$$

(19)

In the formula, ${f}_{i,m}$ represents the fitness value of the male individual, and ${f}_{i,f}$ represents the fitness value of the female individual.

The decision to trigger the update mechanism is determined by randomly selecting an integer within the interval [1,2]. When the random value is equal to 1, the spawning and hatching mechanism is activated, leading to the random generation of new snake positions, which replace the individuals with the lowest fitness in the population.

$${X}_{worst,m}={X}_{min}+rand\times \left({X}_{max}-{X}_{min}\right)$$

(20)

$${X}_{worst,f}={X}_{min}+rand\times \left({X}_{max}-{X}_{min}\right)$$

(21)

In the formula, ${X}_{worst,m}$ and ${X}_{worst,f}$ represent the positions of the worst male and female individuals, respectively.

The updated individual positions are designated as ${X}_{new,m}$ for males or ${X}_{new,f}$ for females. It is essential to ensure that the positions of the solutions remain within the search space. If the value of any dimension exceeds the established boundaries, it will be constrained to fall within those limits.

The fitness of the updated individual is calculated as follows:

$${f}_{i,m}=fobj({X}_{new,m})$$

(22)

$${f}_{i,f}=fobj({X}_{new,f})$$

(23)

The solution ${X}_{i}$ is a multidimensional vector that represents the position of the snake within the search space, with its fitness calculated through the objective function. The algorithm progressively optimizes the positions of these solutions through multiple iterative stages, ultimately converging on the global optimal solution to the problem.

Improved SO algorithm

Piecewise chaos mapping strategy

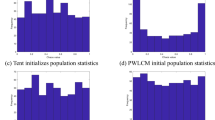
Chaos mapping presents an exceedingly efficient approach to augmenting the diversity of initial positions within the SO algorithm. The infusion of chaotic elements engenders heightened randomness throughout the search trajectory, thereby enhancing traversal across the solution space and facilitating the discovery of optimal solutions. Moreover, the stochastic and non-linear attributes inherent in chaos mapping facilitate the evasion of local optima and enable the exploration of a broader solution spectrum. While chaos mapping demonstrates remarkable proficiency in global exploration, it concurrently expedites convergence to the optimal solution during the local search phase.

Piecewise Chaos Mapping employs piecewise functions to characterize the overarching function. It partitions the domain of the global function into numerous subintervals and formulates function expressions tailored to each subinterval. Consequently, the dynamics of the global function are thoroughly captured through the amalgamation of these piecewise functions across the subintervals. Furthermore, the random numbers generated within the [0,1] range by Piecewise Chaos Mapping demonstrate notable uniformity, amplifying the diversity of initial positions within the SO algorithm. Consequently, this paper advocates adopting Piecewise Chaos Mapping to tackle optimization challenges more effectively.

$$x\left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {\frac{x\left( t \right)}{p},} \hfill & {0 \le x\left( t \right) < p} \hfill \\ {\frac{x\left( t \right) - p}{{0.5 - p}},} \hfill & {p \le x\left( t \right) < 0.5} \hfill \\ {\frac{1 - p - x\left( t \right)}{{0.5 - p}},} \hfill & {0.5 \le x\left( t \right) < 1 - p} \hfill \\ {\frac{1 - x\left( t \right)}{p},} \hfill & {1 - p \le x\left( t \right) < 1} \hfill \\ \end{array} } \right.$$

(24)

In the aforementioned equation, $p$ represents a mapping function with values within the range [0,1], and $x\left(t\right)$ denotes a time variable with values within the range [0,1].

By integrating Eq. (2) with Piecewise Chaos Mapping, the initial positions of the snake population can be acquired as follows:

$$X_{i} = \left\{ {\begin{array}{*{20}l} {X_{min} + \frac{x\left( t \right)}{p} \times \left( {X_{max} - X_{min} } \right),} \hfill & {0 \le x\left( t \right) < p} \hfill \\ {X_{min} + \frac{x\left( t \right) - p}{{0.5 - p}} \times \left( {X_{max} - X_{min} } \right),} \hfill & {p \le x\left( t \right) < 0.5} \hfill \\ {X_{min} + \frac{1 - p - x\left( t \right)}{{0.5 - p}} \times \left( {X_{max} - X_{min} } \right),} \hfill & {0.5 \le x\left( t \right) < 1 - p} \hfill \\ {X_{min} + \frac{1 - x\left( t \right)}{p} \times \left( {X_{max} - X_{min} } \right),} \hfill & {1 - p \le x\left( t \right) < 1} \hfill \\ \end{array} } \right.$$

(25)

Integration of the SABO algorithm

The Subtraction-Average-Based Optimizer algorithm offers simplicity in implementation, devoid of intricate mathematical derivations or parameter adjustments. Throughout its execution, it autonomously adjusts particle positions and updates search directions contingent on the objective function’s state. This adaptability expedites convergence to the optimal solution, circumventing entrapment in local optima arising from disparate updating methods in early versus late stages. Notably, the SO algorithm manifests exceedingly sluggish optimization velocity in the initial stages, indicative of deficiencies in its position-updating mechanism during exploration, impeding prompt food discovery. Consequently, this paper integrates the Subtraction-Average-Based Optimizer algorithm to supplant the exploration phase’s position updating formula.

$${X}_{i}^{new}={X}_{i}+\overrightarrow{{r}_{i}}*\frac{1}{N}\sum_{j=1}^{N}\left({X}_{i}-v{X}_{j}\right),i=\text{1,2},\dots ,{N}_{n}$$

(26)

where ${N}_{n}$ signifies the total number of particles, and ${r}_{i}$ is a vector that is normally distributed in the interval [0,1]. The "-$v$" operation represents a novel computational concept of the Subtraction-Average-Based Optimizer, denoted as the v-subtraction between search agent B and search agent A. By amalgamating Eq. (26) with the position updating formula of the Subtraction-Average-Based Optimizer, Eqs. (7) and (8) undergoes the following transformation:

$${X}_{i,m}\left(t+1\right)={X}_{i,m}\left(t\right)+\overrightarrow{{r}_{i}}*\frac{1}{{N}_{m}}\sum_{j=1}^{{N}_{m}}\left({X}_{i,m}-v{X}_{j,m}\right)$$

(27)

$${X}_{i,f}\left(t+1\right)={X}_{i,f}\left(t\right)+\overrightarrow{{r}_{i}}*\frac{1}{{N}_{f}}\sum_{j=1}^{{N}_{f}}\left({X}_{i,f}-v{X}_{j,f}\right)$$

(28)

where $v$ is a random integer between 1 and 3.

This paper employs the Lens Imaging Reverse Learning Strategy to generate reverse individuals in the population and calculates their fitness values. If the fitness value of a reverse individual is superior to that of the original individual, a replacement is made.

Lens imaging reverse learning strategy

Integrating the reverse learning strategy into the SO algorithm can expedite convergence to the optimal solution. The fundamental concept behind lens imaging reverse learning involves leveraging the principles of convex lens imaging to generate a mirrored position based on the current coordinates, thereby broadening the search scope. This approach facilitates escape from local optima and augments population diversity, thereby bolstering the algorithm’s exploratory prowess. By amalgamating the optical imaging principle with the SO algorithm, lens imaging reverse learning efficaciously steers the algorithm towards the more efficient exploration of the solution space, thereby hastening convergence towards the global optimum. The formula for implementing the lens imaging reverse learning principle within the SO algorithm is delineated as follows:

$${x}_{j}^{*}=\frac{ub+lb}{2}+\frac{ub+lb}{2k}-\frac{{x}_{j}}{k}$$

(29)

$$k={\left(1+\sqrt{\frac{t}{T}} \right)}^{10}$$

(30)

Within the equation, ${x}_{j}^{*}$ denotes the reverse solution of ${x}_{j}$, with $k$ representing the scaling factor.

Adaptive t-distribution strategy

The adaptive t-distribution is a probability distribution whose degrees of freedom vary with the number of iterations of the algorithm. As the iterations progress, the distribution gradually approximates a Gaussian distribution, enhancing the algorithm’s convergence rate. In optimization algorithms, the adaptive t-distribution perturbs the positions of individuals within the population, thereby augmenting the algorithm’s exploratory capability. Initially, owing to higher degrees of freedom, it fosters global exploration; subsequently, as degrees of freedom diminish, it fosters local exploration. The algorithm iterates continuously, computing the t-distribution based on current fitness and iteration number, perturbing the population’s positions, and incorporating individuals with higher fitness into the population. In this study, the adaptive t-distribution is introduced during the phase wherein snakes concentrate on approaching food, mitigating the risk of local optima. The updated position update formula is delineated as follows:

$$freen=exp\left(4{\left(\frac{t}{T}\right)}^{2}\right)$$

(31)

$${X}_{i,m}\left(t+1\right)={X}_{best,m}+trnd\left(freen\right)\times {X}_{best,m}$$

(32)

$${X}_{i,f}\left(t+1\right)={X}_{best,f}+trnd\left(freen\right)\times {X}_{best,f}$$

(33)

Within the equation, ${X}_{best,m}$ and ${X}_{best,f}$ denote the best individuals among males or females, respectively. "$freen$" signifies the degrees of freedom parameter of the t-distribution, while "$trnd\left(freen\right)$" generates a t-distributed random number.

Improved CSGLSO algorithm flow

Algorithm 1 presents the pseudocode of the enhanced CSGLSO algorithm:

Algorithm 1

The CSGLSO algorithmic

The flowchart of the CSGLSO algorithm is shown in Fig. 1.

Fig. 1

Flowchart of CSGLSO algorithm.

Computational complexity of CSGLSO

N represents the population size, T denotes the maximum number of iterations, and dim specifies the problem dimension.

During the population initialization phase, each individual generates dim random numbers, resulting in a total complexity of ${\text{O}}\left( {{\text{N }} \times \left( {{\text{dim }} + { 1}} \right)} \right) \approx {\text{O}}\left( {{\text{N }} \times {\text{ dim}}} \right)$.

The computational complexity of male and female grouping is O(N).

The computational complexity of updating the male population during the exploration phase is O(N_m × N_m × dim) ≈ O((N/2)² × dim) = O(N²/4 × dim), which simplifies to O(N² × dim).

The computational complexity of updating the female population is identical to that of the male population, maintaining the same double-loop structure and complexity of O(N² × dim).

During the development phase, the computational complexity of food searching for snakes is O(N × dim).

The computational complexity of combat mode is O(N × dim), whereas entering mating mode results in a lower complexity.

For both male and female populations, each individual traverses dim dimensions with a complexity of O(N × dim).

Each individual evaluates the objective function (fobj) once, leading to a total complexity of O(N).

The computational cost of finding the minimum value in both male and female populations is O(N).

Overall computational complexity analysis:

Initialization Phase: O(N × dim).

Per iteration:

In the worst-case scenario, if the algorithm enters the exploration phase, the main double-loop component incurs a complexity of O(N² × dim), while all other parts are O(N × dim) or lower, leading to an overall single-iteration complexity of O(N² × dim).

In the best-case scenario, if the algorithm enters the development phase, the single-iteration complexity primarily remains O(N × dim).

Total Iterations: T

Worst-Case Complexity (Exploration Phase in Each Iteration): O(T × N² × dim).

Best-Case Complexity (Exploitation Phase in Each Iteration): O(T × N × dim).

In summary, the computational complexity of the CSGLSO algorithm ranges from O(T × N × dim) to O(T × N² × dim), surpassing the computational complexity of the SO algorithm, which at O(T × N × dim).

Algorithm performance testing and analysis

Test functions and experimental environment

The experiments detailed in this study were carried out within a testing environment featuring an Intel(R) Core(TM) i5-8300H CPU, 2.30 GHz, and 16 GB memory, operating on Windows 10 (64-bit). All implementations were developed using MATLAB R2022b. Fourteen benchmark test functions were meticulously selected for experimentation, with their respective formulas, dimensions, search ranges, and optimal values outlined in Table 1. Among these functions, ${f}_{1}$ to ${f}_{5}$ represent unimodal benchmark tests designed to assess the algorithm’s convergence speed and local search efficacy; ${f}_{6}$ to ${f}_{12}$ constitute basic multimodal benchmark functions, while ${f}_{13}$ to ${f}_{14}$ represent extended multimodal benchmark functions, aimed at evaluating the algorithm’s balance between convergence, local, and global search capabilities.

Table 1 Benchmark functions.

Algorithm comparison experiment

To assess the efficacy of the CSGLSO algorithm thoroughly, we conducted comparative analyses against a suite of optimization methodologies including the original SO algorithm, HSOA⁴¹, ISSA⁴², ECS⁴³, across the designated test functions. The pseudo-code for each comparison algorithm is shown in Algorithm 2–5, respectively, and the corresponding algorithmic flowchart is displayed in Figs. 2, 3, 4 and 5. In this experiment, the population size for all algorithms is set to 50, with a maximum of 500 iterations. To ensure a fair performance comparison, multiple simulation experiments are conducted to determine the optimal parameter configurations for each algorithm. The detailed parameter settings are presented in Table 2. To mitigate experimental variability and bolster the robustness of our findings, we conducted 30 independent runs of each algorithm on the 14 benchmark test functions. The objective of the optimization algorithms, aimed at minimizing the function, is represented by the optimal fitness value, encompassing metrics such as minimum (Min), average (Avg) and rank of average (RANK) values, as elaborated in Table 3. In instances of tied ranks, the average value is considered. A visual depiction of the function evaluation results is provided through the box plot in Fig. 6, where the horizontal axis delineates different algorithms, and the vertical axis denotes optimization accuracy. Additionally, the convergence curves of various algorithms on selected functions are portrayed in Fig. 7, with the horizontal axis representing the number of iterations and the vertical axis indicating optimization accuracy. It’s worth noting that for optimization problems such as ${f}_{9}$, ${f}_{11}$ and ${f}_{14}$ which exhibit relative simplicity, the improved CSGLSO algorithm converges at an accelerated pace, rendering its convergence curve challenging to effectively display.

Fig. 2

Flowchart of SO algorithm.

Fig. 3

Flowchart of HSOA algorithm.

Fig. 4

Flowchart of HSOA algorithm.

Fig. 5

Flowchart of ECS algorithm.

Table 2 Parameter settings for each algorithm.

Table 3 Comparison results of 5 algorithms based on standardized test functions.

Fig. 6

Function box diagram.

Fig. 7

Convergence curve of the function.

Algorithm 2

The SO algorithm

Algorithm 3

The HSOA algorithm

Algorithm 4

The Improved Salp Swarm Algorithm (ISSA)

Algorithm 5

The Exploratory Cuckoo Search (ECS)

Analyzing the experimental results presented in Table 3, Figs. 6 and 7 reveals that the CSGLSO algorithm demonstrates substantial performance advantages across various test functions, particularly in terms of global optimization capability, convergence speed, and stability. A detailed analysis of the experimental results from various test functions is presented below:

On the benchmark test functions ${f}_{1}$ to ${f}_{4}$, the CSGLSO algorithm not only consistently achieves the global optimal solution but also exhibits the fastest convergence speed, demonstrating high robustness in its optimization process. In contrast, while the ISSA and ECS algorithms can also achieve global optimality on these functions, their optimization searches exhibit lower stability and fail to consistently guarantee a globally optimal solution in every experiment. The SO algorithm, however, demonstrates poor stability, characterized by large confidence intervals, indicating high volatility and a lack of reliability in its optimization results.

The ISSA and ECS algorithms outperform the CSGLSO, SO, and HSOA algorithms in terms of optimization stability, convergence speed, and optimal values on the ${f}_{5}$ and ${f}_{6}$ benchmark functions. However, the CSGLSO algorithm surpasses the other four algorithms in terms of stability, convergence speed, and optimal values on the ${f}_{7}$ benchmark function. On the ${f}_{8}$ benchmark function, the ISSA and ECS algorithms are prone to falling into local optima and perform worse than the CSGLSO, SO, and HSOA algorithms. Among them, the CSGLSO and SO algorithms exhibit the best performance in terms of stability, convergence speed, and optimality. These results indicate that the CSGLSO algorithm possesses superior global search capability.

The CSGLSO, ISSA, and ECS algorithms achieve the global optimum on the ${f}_{9}$, ${f}_{10}$, and ${f}_{11}$ benchmark functions, demonstrating high optimization stability and rapid convergence. However, on the ${f}_{9}$ and ${f}_{11}$ benchmark functions, the convergence rate is excessively high, making it difficult to effectively illustrate the convergence curve. On the ${f}_{12}$ and ${f}_{13}$ benchmark functions, the ISSA, ECS, CSGLSO, and HSOA algorithms exhibit similar performance in terms of stability and optimization values. However, the ISSA and ECS algorithms achieve slightly faster convergence. Notably, the HSOA algorithm exhibits a large confidence interval, indicating greater volatility and reduced stability in its optimization results.

On the ${f}_{14}$ benchmark test function, all five algorithms attain global optimality. However, the ISSA and ECS algorithms exhibit poor stability in locating the optimum and display large confidence intervals, suggesting potential unreliability in practical applications. In contrast, the CSGLSO algorithm maintains a smaller confidence interval while preserving its global optimization capability, further confirming its reliability in practical applications.

In summary, the enhanced CSGLSO algorithm achieves an average ranking of 2.0 across all tested functions, securing the top position overall. Overall, the CSGLSO algorithm demonstrates strong performance in convergence accuracy, convergence speed, and global optimization capability, with a high ability to escape local optima. Its stable performance across various test functions confirms its broad applicability and robustness in solving complex optimization problems. Additionally, the well-balanced trade-off between convergence speed and stability in the CSGLSO algorithm enhances its potential for practical engineering applications. Future research should further investigate the performance of the CSGLSO algorithm on large-scale and high-dimensional problems, as well as its integration with and enhancement through other advanced optimization techniques.

Wilcoxon rank-sum test

To statistically compare the performance of the CSGLSO algorithm with the algorithms discussed in sections "Algorithm comparison experiment" for solving the CEC2005 standard test functions ${f}_{1}$ to ${f}_{14}$, this study conducted a non-parametric test using the Wilcoxon rank-sum (WRS) test for the eleven algorithms. The significance level was set to 5%. A P-value of less than 0.05 indicates a significant difference between the two algorithms. Conversely, if the P-value is greater than 0.05, it implies that the performance of the two algorithms is essentially similar, with no significant difference observed. The calculated P-values are presented in Table 5. In this table, a " + " denotes a significant performance difference favoring the CSGLSO algorithm over the comparison algorithm, while a "-" indicates a significant performance difference where the CSGLSO algorithm performs worse than the comparison algorithm. " = " denotes no significant difference between the two algorithms. “NaN” signifies the identical experimental sample data, rendering the algorithm performances comparable.

Analyzing the Wilcoxon rank sum test results in Table 4 reveals that the CSGLSO algorithm demonstrates significant performance advantages over the SO and HSOA algorithms across most tested functions. Specifically, in the majority of cases, the P-value for comparisons between the CSGLSO algorithm and the competing algorithms is less than 0.05, indicating that the CSGLSO algorithm consistently outperforms the SO and HSOA algorithms. These results indicate that the enhanced CSGLSO algorithm exhibits statistically significant superiority. While the performance differences between the CSGLSO algorithm and the competing algorithms are not statistically significant for certain individual test functions, the overall improvement of the CSGLSO algorithm is substantiated by statistical validation.

Table 4 Statistical results based on Wilcoxon rank−sum test (CSGLSO vs. SO, HSOA, ISSA, ECS).

A deeper analysis of the comparative results between the CSGLSO algorithm and the ISSA and ECS algorithms reveals significant differences in the ${f}_{1}$~${f}_{4}$, ${f}_{7}$, ${f}_{8}$, and ${f}_{14}$ test functions, with the CSGLSO algorithm demonstrating markedly superior performance over the latter two. This outcome substantiates the CSGLSO algorithm’s comprehensive effectiveness in addressing complex optimization problems, including unimodal and multimodal landscapes, non-smooth functions, higher-order terms, noise interference, and variable coupling. Its advantages are primarily manifested in its global search capability, convergence speed, robustness, and strong adaptability to complex optimization challenges. However, the CSGLSO algorithm exhibits notably weaker performance than the ISSA and ECS algorithms on the ${f}_{5}$ test function, suggesting that the latter two may hold greater advantages in optimization problems characterized by strong nonlinearities, nonconvexity, and pronounced variable coupling. Furthermore, the performance differences among the CSGLSO, ISSA, and ECS algorithms on the ${f}_{6}$ and ${f}_{9}$~${f}_{13}$ test functions are not statistically significant, indicating comparable performance across these functions.

In summary, the results of the Wilcoxon rank sum test clearly demonstrate that the improved CSGLSO algorithm exhibits significant performance advantages across most benchmark functions. Its superiority is not only evident in comparisons with the SO and HSOA algorithms but is also partially validated against the ISSA and ECS algorithms. While the CSGLSO algorithm may exhibit comparable or slightly weaker performance on certain individual test functions, it overall achieves notable improvements in global optimization capability, convergence speed, and stability. These findings further substantiate the potential and reliability of the CSGLSO algorithm in practical applications, providing both theoretical foundations and experimental validation for its broader deployment in solving complex optimization problems.

Simulation experiments and analysis

This optimization problem seeks to determine the shortest, safest, and most energy-efficient flight trajectory within complex environments, such as bridge construction, enabling the UAV to efficiently navigate from the starting point to the destination. The optimization process must adhere to constraints on radial distance, pitch angle, heading angle, flight altitude, and minimum safety distance, while simultaneously integrating considerations such as path length, hazardous area avoidance, altitude regulation, and trajectory smoothness. A feasible candidate solution comprises a sequence of discrete path points (x, y, z, $\psi$, $\varphi$), which define the UAV’s spatial position and orientation in three-dimensional space, thereby ensuring both feasibility and optimality of the trajectory (As shown in Fig. 8). By refining the snake optimization algorithm and incorporating adaptive t-distribution variation, a lens imaging inverse learning strategy, and a fusion subtraction averaging fuser algorithm, the convergence rate is enhanced, and path quality is improved, thereby meeting the stringent requirements for rapid and safe navigation in complex construction environments.

Fig. 8

Optimization Problem Illustration.

UAV path planning constraints

UAV path planning encompasses delineating its aerial trajectory within a predefined airspace, predicated upon constraints and objective functions. Concurrently conforming to aviation control stipulations and upholding air traffic safety, the algorithm computes the optimal flight pathway to reach the designated destination expediently. Within this study, hazards encountered at bridge construction locales are simplistically characterized as cylindrical entities.

In order to guarantee the safe and efficient completion of the flight mission in the complex environment, this paper defines the radial distance, pitch angle, heading angle, flight altitude, and minimum safe distance of the UAV. The following is a detailed account of the specific information pertaining to the UAV path planning constraints.

Radial distance constraints

The radial distance (r) denotes the linear distance from the UAV’s current position to the subsequent path node. Enforcing constraints on the radial distance guarantees that the UAV adheres closely to the predetermined trajectory during flight, thereby preserving the stability of the flight path, as illustrated by:

$$0<r<\frac{2\times L}{d}$$

(34)

Within Eq. (34), L symbolizes the distance spanning from the initial point to the terminal destination, while d denotes the count of path nodes.

Pitch constraints

The pitch angle ($\psi$) denotes the inclination of the UAV’s fuselage relative to the horizontal plane, serving to characterize the UAV’s orientation in the vertical axis. Imposing limitations on the pitch angle guarantees flight stability and fluidity by regulating altitude fluctuations throughout the flight trajectory.

$$-\theta <\psi <\theta$$

(35)

Within Eq. (35), $\theta$ represents the restricted angle range.

Heading angle constraints

The heading angle ($\varphi$) is gauged horizontally relative to the ground plane, indicating the UAV’s orientation with respect to the earth’s surface. Limiting the heading angle ensures the UAV adheres to the intended direction throughout the flight, guiding it along the predetermined route and averting deviations from the desired trajectory.

$${\varphi }_{0}=atan2\left({y}_{d}-{y}_{s},{x}_{d}-{x}_{s}\right)$$

(36)

$${\varphi }_{max}={\varphi }_{0}+\theta$$

(37)

$${\varphi }_{min}={\varphi }_{0}-\theta$$

(38)

where (${x}_{s},{y}_{s}$) denotes the coordinates of the starting point, and $({x}_{d},{y}_{d}$) signifies the coordinates of the destination point.

Flight altitude constraints

Taking into account factors including UAV operational safety, inspection efficacy, and pertinent regulations and standards, limitations are enforced on the UAV’s flight altitude (h), delineated by maximum (${h}_{max}$) and minimum ((${h}_{min}$) thresholds.

$${h}_{min}<h<{h}_{max}$$

(39)

Minimum safe distance constraints

The minimum safety distance (${d}_{k}$) denotes the requisite separation distance mandated between the UAV and potential hazards throughout the flight operation to uphold aerial safety. Imposing constraints on the minimum safety distance aids in averting collisions and safeguarding the UAV’s preplanned flight trajectory from damage.

$${d}_{k}>{R}_{k}+D$$

(40)

In Eq. (40), ${R}_{k}$ symbolizes the radius of the threat cylinder, while D denotes the diameter of the UAV. Let ${C}_{k}$ represent the center of the threat cylinder, S denote the hazardous area, and ${P}_{i,j}{\prime}$ and ${P}_{i,j+1}{\prime}$ be the endpoints of the specified road segment $\Vert \overrightarrow{{P}_{i,j}{P}_{i,j+1}}\Vert$ in the top-down view, as illustrated in Fig. 9.

Fig. 9

Threat costing model.

Path cost function

Environmental modeling

The mathematical path planning model employed in this paper primarily simulates UAVs executing safety inspection assignments at bridge construction sites. The mountainous terrain model sourced from reference⁴⁴ is utilized to replicate the UAV’s aerial environment. The threats present at the construction site of the bridge are symbolized by cylinders, as illustrated in Fig. 10.

Fig. 10

Threat area simulation map.

Path length cost

In order to facilitate the efficient completion of safety inspection duties by the UAV, meticulous planning of an optimal pathway is imperative. Assuming the path nodes in the search map are designated as ${P}_{ij}=\left({x}_{ij},{y}_{ij},{z}_{ij}\right)$, the Euclidean distance between consecutive nodes is computed as the path length in this study. Hence, the cost function for path length can be computed as follows:

$${F}_{1}\left({X}_{i}\right)=\sum_{j=1}^{n-1}\Vert \overrightarrow{{P}_{ij}{P}_{i,j+1}}\Vert$$

(41)

Within the equation, n symbolizes the count of path nodes, with ${x}_{i}$ denoting the list of each individual path node.

Hazardous area cost

The associated cost of a given path segment $\Vert \overrightarrow{{P}_{ij}{P}_{i,j+1}}\Vert$ is directly correlated with its distance (${d}_{k}$) from the center ${C}_{k}$. The cost function for the hazardous area is expressed as follows:

$$T_{k} \left( {\overrightarrow {{P_{ij} P_{i,j + 1} }} } \right) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {if\;{ }d_{k} > S + D + R_{k} } \hfill \\ {\left( {S + D + R_{k} } \right) - d_{k} ,} \hfill & {if{ }\;D + R_{k} < d_{k} \le S + D + R_{k} } \hfill \\ {\infty ,} \hfill & {if{ }\;d_{k} \le D + R_{k} } \hfill \\ \end{array} } \right.$$

(42)

$$F_{2} \left( {X_{i} } \right) = \mathop \sum \limits_{j = 1}^{n - 1} \mathop \sum \limits_{k = 1}^{k} T_{k} \left( {\overrightarrow {{P_{ij} P_{i,j + 1} }} } \right)$$

(43)

In this equation, S signifies the distance to the hazardous zone, which can be adjusted based on the precision of UAV positioning. ${d}_{k}$ denotes the distance from the path segment $\Vert \overrightarrow{{P}_{ij}{P}_{i,j+1}}\Vert$ to the center ${C}_{k}$ of the threat cylinder, as depicted in Fig. 9.

Flight altitude cost

In the realm of UAV flight, accounting for the direct correlation between target image scale variation and flight altitude, juxtaposed with the inverse relationship between threat risk and flight altitude, the cost associated with flight altitude along the path is computed as follows:

$$H_{ij} = \left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}l} {\left| {h_{ij} - \frac{{\left( {h_{max} + h_{min} } \right)}}{2}} \right|} \hfill \\ {\infty ,} \hfill \\ \end{array} ,} & {\begin{array}{*{20}l} {if{ }h_{min} \le h_{ij} \le h_{max} } \hfill \\ {otherwise} \hfill \\ \end{array} } \\ \end{array} } \right.$$

(44)

$${F}_{3}\left({X}_{i}\right)=\sum_{j=1}^{n}{H}_{ij}$$

(45)

In this equation, ${h}_{ij}$ denotes the altitude relative to the ground.

Path smoothing cost

To uphold path stability and efficiency during UAV mission execution, it is advantageous to mitigate abrupt turns and sudden deviations in the trajectory. Thus, the cost function for path smoothing is formulated as follows:

$$\overrightarrow {{P_{ij}^{\prime } P_{i,j + 1}^{\prime } }} = \vec{k} \times \left( {\overrightarrow {{P_{i,j} P_{i,j + 1} }} \times \vec{k}} \right)$$

(46)

$$\varphi_{ij} = arctan\left( {\frac{{\overrightarrow {{P_{ij}^{\prime } P_{i,j + 1}^{\prime } }} \times \overrightarrow {{P_{ij + 1}^{\prime } P_{i,j + 2}^{\prime } }} }}{{\overrightarrow {{P_{ij}^{\prime } P_{i,j + 1}^{\prime } }} \cdot \overrightarrow {{P_{ij + 1}^{\prime } P_{i,j + 2}^{\prime } }} }}} \right)$$

(47)

$$\psi_{ij} = arctan\left( {\frac{{z_{i,j + 1} + z_{ij} }}{{\overrightarrow {{P_{ij}^{\prime } P_{i,j + 1}^{\prime } }} }}} \right)$$

(48)

$${F}_{4}\left({X}_{i}\right)={a}_{1}\sum_{j=1}^{n-2}{\varphi }_{ij}+{a}_{2}\sum_{j=1}^{n-1}\left|{\psi }_{ij}-{\psi }_{i,j-1}\right|$$

(49)

Within the equation, ${\varphi }_{ij}$ signifies the heading angle, ${\psi }_{ij}$ represents the pitch angle, $\overrightarrow{k}$ denotes the unit vector along the z-axis, and $\overrightarrow{{P}_{ij}{\prime}{P}_{i,j+1}{\prime}}$ depicts the projection of $\overrightarrow{{P}_{ij}{P}_{i,j+1}}$ onto the Oxy plane, as shown in Fig. 11. Additionally, ${a}_{1}$ and ${a}_{2}$ serve as penalty coefficients for the heading and pitch angles, respectively.

Fig. 11

Calculation of corner climb angle.

Total consideration

Considering the UAV’s path length, danger zone, flight altitude, and path smoothing, the comprehensive cost function for the path ${X}_{i}$ is expressed as follows:

$$F\left({X}_{i}\right)=\sum_{k=1}^{4}{b}_{k}{F}_{k}\left({X}_{i}\right)$$

(50)

Within the equation, ${F}_{1}\left({X}_{i}\right)$ through ${F}_{4}\left({X}_{i}\right)$ denote the expenses linked to path length, danger zone, flight altitude, and path smoothing, correspondingly. Meanwhile, ${b}_{k}$ signifies the weighting coefficients assigned to each cost component.

Simulation and Analysis of three-dimensional UAV Path Planning

Three-dimensional path planning simulations were conducted using MatlabR2022b, featuring three scenarios: a trumpet-shaped interchange, a mountainous elevated bridge, and a non-interwoven interchange, depicted in Fig. 12a–f. Each scenario underwent simulation experiments. Hazard information for each scenario is detailed in Table 5, with a radius of 30 indicating bridge pillars and a radius of 50 representing large machinery like cranes. The path planning outcomes of the CSGLSO algorithm in these scenarios were juxtaposed against those of the SO, HSOA, ISSA, and ECS algorithms to gauge the viability and efficacy of the CSGLSO algorithm.

Fig. 12

Simulation scene. (a) Toll Roads in Indonesia. (b) China’s G70 Fuyin Expressway. (c) Baltimore Beltway, Maryland. (d) Simulation scenario of a trumpet-shaped overpass. (e) Mountain viaduct simulation scenario. (f) Simulation scenarios for non-intertwined overpasses.

Table 5 Hazardous source information.

The UAV’s flight space spans 1045m × 879m × 400m, featuring an initial point at coordinates (160, 60, 50) and a target point at (900, 720, 99). The population size is standardized at 50, undergoing 500 iterations, with altitude constraints set between 50 and 99, and an angular limitation defined by $\theta =\pi /4$. The weight coefficients are b = [5, 1, 10, 1].

Through an in-depth analysis of simulation experiments conducted in the flared overpass scenario, this study evaluates the path planning performance of the CSGLSO algorithm in comparison with the SO, HSOA, ISSA, and ECS algorithms. As illustrated in the 3D trajectory map (Fig. 13a) and the top-view trajectory representation (Fig. 13b), the paths generated by the SO, HSOA, ISSA, and ECS algorithms exhibit pronounced zigzagging patterns. This suboptimal trajectory characteristic directly increases path cost, indicating the inefficacy of these algorithms in complex path planning scenarios. In contrast, the CSGLSO algorithm demonstrates markedly superior performance in trajectory optimization.

Fig. 13

Trumpet-shaped overpass scene. (a) Flight three-dimensional track map. (b) Top view of flight path. (c) Convergence graphs of the five algorithms. (d) Total cost box diagram.

A detailed examination of the convergence curves in Fig. 13c and the total cost box plots in Fig. 13d indicates that the CSGLSO algorithm achieves markedly superior performance across multiple evaluation metrics compared to the other algorithms. Specifically, the CSGLSO algorithm demonstrates enhanced global optimization capabilities and achieves the fastest convergence rate. Moreover, the algorithm’s performance is more tightly clustered within the 95% confidence interval, providing empirical evidence of its superior stability and robustness. These advantages primarily stem from the integration of adaptive t-distribution variation and the lens imaging inverse learning strategy within the CSGLSO algorithm. This design enhances its ability to effectively circumvent local optima in complex environments while ensuring rapid convergence.

Figure 14 presents a comparative analysis of the path planning results obtained using the CSGLSO algorithm and the SO, HSOA, ISSA, and ECS algorithms in a mountainous viaduct scenario. This analysis encompasses path planning performance, convergence trends, and total cost distributions. The 3D path planning results in Fig. 14a and the top-down view in Fig. 14b clearly illustrate that the CSGLSO algorithm outperforms the compared algorithms, exhibiting superior smoothness and overall effectiveness. Specifically, the CSGLSO algorithm produces paths with reduced curvature and shorter overall length while effectively minimizing unnecessary deviations. This indicates its enhanced adaptability and optimization potential in complex terrain environments.

Fig. 14

Mountain viaduct scene. (a) Flight three-dimensional track map. (b) Top view of flight path. (c) Convergence graphs of the five algorithms. (d) Total cost box diagram.

Analyzing the convergence characteristics, the convergence curves in Fig. 14c demonstrate that the CSGLSO algorithm converges at a faster rate during iterations and attains stability within fewer iterations. In contrast, the SO, HSOA, ISSA, and ECS algorithms exhibit slower convergence and a higher tendency to become trapped in local optima. Furthermore, the total cost box plot in Fig. 14d reveals that the cost distribution of the CSGLSO algorithm across 30 independent trials is more concentrated, with a narrower 95% confidence interval. This suggests that the CSGLSO algorithm exhibits enhanced stability and robustness.

Figure 15a–d presents the path planning results, convergence curves, and total cost box plots for the five algorithms in the non-interleaved overpass scenario. The experimental results indicate significant performance variations among the different algorithms. Based on the path planning results, the SO and HSOA algorithms exhibit poor convergence. This phenomenon occurs because the diversity of population solutions diminishes as iterations progress, limiting the algorithm’s ability to effectively explore unknown regions in the search space, thereby leading to premature convergence to local optima. Although the ISSA and ECS algorithms demonstrate some search capability in the initial stage, their large 95% confidence intervals and poor optimization result stability indicate insufficient robustness in complex scenarios.

Fig. 15

Non-intertwined overpasses scene. (a) Flight three-dimensional track map. (b) Top view of flight path. (c) Convergence graphs of the five algorithms. (d) Total cost box diagram.

In contrast, the CSGLSO algorithm demonstrates outstanding performance in the non-interleaved overpass scenario. Its path planning results surpass those of other algorithms in terms of smoothness, efficiency, and stability. The convergence curve reveals that the CSGLSO algorithm converges rapidly while preserving high population diversity, thereby mitigating the risk of premature convergence to local optima. Furthermore, the 95% confidence interval range in its total cost box plots is significantly narrower, further substantiating the algorithm’s superior stability and robustness.

As evident from the comparison of the average runtime across 30 experiments conducted in the three simulated environments (Table 6), the enhanced CSGLSO algorithm exhibits a longer path search time relative to the SO algorithm. Specifically, the CSGLSO algorithm requires approximately 2 additional seconds to complete the search compared to the SO algorithm in the mountainous viaduct and non-interleaved overpass scenarios, whereas in the flared overpass scenario, the increase in runtime is merely 0.2 s. This discrepancy may arise from the CSGLSO algorithm’s ability to reduce search time to some extent by optimizing the search space or decreasing the number of iterations in complex scenarios. In contrast, the ISSA and ECS algorithms require less computational time than the SO algorithm, whereas the HSOA algorithm exhibits higher computational cost. These findings suggest that further refinements are required to balance the CSGLSO algorithm’s optimization efficiency and computational cost.

Table 6 Comparison of average time for 30 experiments in three simulation environments.

By synthesizing the path planning results across the three aforementioned scenarios, it can be concluded that the SO, HSOA, ISSA, and ECS algorithms exhibit slightly inferior performance compared to the CSGLSO algorithm in terms of path planning effectiveness. Nevertheless, despite the superior performance of the CSGLSO algorithm, its prolonged computational time remains a critical limitation that requires further optimization.

Conclusions and future works

This paper presents an enhanced Snake Optimization Algorithm (CSGLSO) designed to address the challenge of rapid 3D path planning for UAVs in bridge construction over complex terrain. By integrating the Piecewise Chaotic Mapping strategy, the Fusion Subtraction Averaging strategy, the Adaptive t-Distribution strategy, and the Lens Imaging Inverse Learning strategy, CSGLSO achieves notable enhancements in population diversity, global optimization capability, and convergence speed. Experimental results demonstrate that CSGLSO surpasses competing algorithms (SO, HSOA, ISSA, and ECS) across 14 standard test functions and three bridge construction scenarios, including flared overpasses, mountainous viaducts, and non-intertwined overpasses. Notably, it excels in global optimization capability, convergence speed, and stability. CSGLSO achieves an average ranking of 2.0 and secures the highest overall position, highlighting its broad applicability and robustness in complex optimization tasks.

Despite demonstrating strong performance across multiple test functions and simulation scenarios, the CSGLSO algorithm has certain limitations. First, the CSGLSO algorithm may underperform compared to the ISSA and ECS algorithms when addressing optimization problems characterized by strong nonlinearity, nonconvexity, and tightly coupled variables. Second, the path search time of the CSGLSO algorithm increases compared to the SO algorithm, which indicates that its balance between the efficiency of the search and the time consuming still needs to be further optimized.

The CSGLSO algorithm offers several key advantages:

• 1. Superior global optimization capability: By incorporating multiple enhancement strategies, the CSGLSO algorithm effectively mitigates the risk of local optima and demonstrates exceptional global search performance.

• 2. Rapid convergence: Across most test functions and simulation scenarios, the CSGLSO algorithm achieves significantly faster convergence than the competing algorithms.

• 3. High stability: The algorithm exhibits a narrow confidence interval, signifying its strong reliability and robustness in real-world applications.

However, the CSGLSO algorithm has certain limitations:

• 1. Higher computational cost: In complex scenarios, the algorithm exhibits increased path search time compared to the SO algorithm, potentially impacting its feasibility for real-time applications.

• 2. Limited adaptability to complex optimization problems: The CSGLSO algorithm may exhibit inferior performance compared to the ISSA and ECS algorithms when addressing highly nonlinear and nonconvex optimization tasks.

In practical bridge construction, UAV path planning encompasses both technical and managerial challenges. For instance, determining optimal UAV deployment strategies in real-world construction environments, ensuring seamless coordination between UAVs and other construction equipment, and addressing unforeseen environmental changes (e.g., adverse weather conditions). While the CSGLSO algorithm offers an efficient technical solution for UAV path planning, its practical implementation must be aligned with the specific requirements of construction management to further refine UAV deployment and scheduling strategies.

This study conducts a comprehensive performance analysis of the CSGLSO algorithm across 14 standard test functions and three simulation scenarios, benchmarking it against the SO, HSOA, ISSA, and ECS algorithms. Experimental results demonstrate that the CSGLSO algorithm surpasses the comparison algorithms in global optimization capability, convergence speed, and stability, particularly in path planning tasks within complex terrains. However, the algorithm’s performance in highly nonlinear problems requires further enhancement, and its prolonged path search time necessitates additional optimization.

Future research directions may focus on the following key areas:

• 1. Enhancing algorithmic efficiency: Investigate strategies to reduce the path search time of the CSGLSO algorithm and improve its performance in real-time applications.

• 2. Expanding application domains: Apply the CSGLSO algorithm to large-scale, high-dimensional optimization problems to assess its effectiveness across diverse scenarios.

• 3. Validation in real-world construction: Evaluate UAV path planning in actual bridge construction environments, integrating construction management needs to optimize the algorithm’s practical implementation.

• 4. Adaptability to dynamic environments: Investigate the algorithm’s robustness in dynamic conditions, such as weather variations and sudden obstacles, to enhance its practical reliability.