Revealing excitation-inhibition imbalance in Alzheimer’s disease using multiscale neural model inversion of resting-state functional MRI

Abstract

Background

Alzheimer’s disease (AD) is a serious neurodegenerative disorder without a clear understanding of pathophysiology. Recent experimental data have suggested neuronal excitation-inhibition (E-I) imbalance as an essential element of AD pathology, but E-I imbalance has not been systematically mapped out for either local or large-scale neuronal circuits in AD, precluding precise targeting of E-I imbalance in AD treatment.

Method

In this work, we apply a Multiscale Neural Model Inversion (MNMI) framework to the resting-state functional MRI data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) to identify brain regions with disrupted E-I balance in a large network during AD progression.

Results

We observe that both intra-regional and inter-regional E-I balance is progressively disrupted from cognitively normal individuals, to mild cognitive impairment (MCI) and to AD. Also, we find that local inhibitory connections are more significantly impaired than excitatory ones and the strengths of most connections are reduced in MCI and AD, leading to gradual decoupling of neural populations. Moreover, we reveal a core AD network comprised mainly of limbic and cingulate regions. These brain regions exhibit consistent E-I alterations across MCI and AD, and thus may represent important AD biomarkers and therapeutic targets. Lastly, the E-I balance of multiple brain regions in the core AD network is found to be significantly correlated with the cognitive test score.

Conclusions

Our study constitutes an important attempt to delineate E-I imbalance in large-scale neuronal circuits during AD progression, which may facilitate the development of new treatment paradigms to restore physiological E-I balance in AD.

Plain language summary

The cells within the brain, neurons, communicate using excitatory and inhibitory activity. The Excitation-inhibition (E-I) balance is a measure of the contribution of excitatory and inhibitory communication. Alzheimer’s disease (AD) is a brain disorder in which memory, thinking and reasoning are disrupted. The E-I balance is found to be disrupted in people with AD. We applied a computational model to brain imaging data and found that E-I balance is progressively disrupted during AD progression. E-I balance could potentially be used to identify people with AD. Also, treatments could be developed that improve the E-I balance, possibly improving symptoms for people with AD.

Introduction

Alzheimer’s disease (AD) is neurodegenerative disorder characterized by progressive and irreversible cognitive decline^1,2,3. It is the leading cause of dementia affecting more than 47 million people worldwide and this number is expected to increase to 131 million by 2050⁴. The healthcare cost for patients with AD and other dementias is enormous and is estimated to be 236 billion in the US for 2016 alone and predicted to quadruple by 2050⁵. Despite decades of extensive research, a clear understanding of the etiology and pathophysiology of AD remains elusive. Current treatments are only symptomatic without slowing down the progression of the disease⁶. The lack of effective treatment highlights the paramount importance of identifying new pathophysiological and therapeutic targets⁷.

Excitation-inhibition (E-I) balance, referred to as the relative contributions of excitatory and inhibitory synaptic inputs⁸, represents a promising pathophysiological and therapeutic target for AD. First, disrupted E-I balance may underlie the key pathophysiological mechanism of AD. One of the pathological hallmarks of AD is the accumulation of amyloid-β (Aβ) peptides in the brain that occurs long before clinical disease onset^9,10. During this long extended preclinical stage, soluble Aβ oligomers and amyloid plaques disrupt neuronal circuit activity and function by altering synaptic transmission and E-I balance leading to cognitive malfunction^11,12,13. In particular, high Aβ levels elicit epileptiform discharges and non-convulsive seizures in both hippocampal and neocortical networks of human amyloid precursor protein (hAPP) transgenic mice¹⁴, which closely relates to the increased incidence of epileptic seizures in AD patients¹⁵. Second, E-I disruption is not only the consequence of Aβ deposit, but also a driver of the amyloid pathology. Experimental data indicate that Aβ release is regulated by neuronal activity^16,17 and driven by increased metabolism^18,19. Also, Aβ accumulation is associated with enhanced neural activity in task-related regions during memory encoding²⁰ and reduction of neural hyperactivity decreases Aβ aggregation as well as axonal dystrophy and synaptic loss²¹. Lastly, restoration of E-I balance has been shown to rescue circuit dysfunction and ameliorate cognitive impairments in both AD mouse models^21,22,23 and humans with early AD²⁴, suggesting a direct link between E-I imbalance and cognitive malfunction. Taken together, these findings emphasize the significance of identifying E-I imbalance in AD, particularly in the initial disease stage for early diagnosis and intervention.

Neurofibrillary tangles (NFT) of hyperphosphorylated tau are another major pathological hallmark of AD²⁵. Studies show that tau bidirectionally modulates neuronal excitability. On one hand, tau increases the excitability of frontal cortical principal cells²⁶ and contributes to Aβ toxicity via strengthening glutamate synapses^27,28. On the other hand, tau suppresses neural activity and dominates Aβ-dependent neuronal hyperactivity^29,30, leading to reduced E-I ratio. Our study aims to delineate regional E-I imbalance primarily caused by Aβ and tau accumulation during AD progression.

Functional magnetic resonance imaging (fMRI) is a core noninvasive method to measure brain activity using the blood-oxygen-level-dependent (BOLD) contrast technique and can be classified into task-based fMRI and resting-state fMRI^31,32. While task-based fMRI is utilized to examine neural response to specific experimental input, resting-state fMRI is adopted to investigate the functional architecture of the brain in the absence of specific task^32,33. Functional MRI has been widely used to study functional network alterations in AD^34,35,36. These studies have revealed both abnormal brain network activation/deactivation and dysfunctional connectivity patterns in AD involving the default mode (DMN), salience, executive control and limbic networks^{37,38,39,40,41,42,43,44,45}. However, conventional fMRI cannot distinguish E and I activity because fMRI signal increases regardless of selective E or I activation^46,47,48. This is not surprising, as activation of inhibitory neurons also consumes energy and triggers subsequent vascular signaling cascades that drive functional hyperemia^47,48,49. Moreover, most current analytic approaches for fMRI, including graph theory, seed-based approaches, and independent component analysis^50,51,52 do not allow for determination of causal relationships between regions, nor do they provide insight into the dynamic meso-scale neuronal relationships that underpin BOLD signal variations, thus unable to identify E-I imbalance at circuit levels.

Generative modeling, by comparison, builds on biologically plausible models of neural interactions^53,54,55,56 and thus can, in principle, resolve excitatory versus inhibitory neuronal activity. Using a computational framework termed “The Virtual Brain (TVB)”, Zimmerman et al.⁵⁷ estimated personalized local excitation and inhibition parameters as well as global coupling strength based on resting-state fMRI (rs-fMRI) data from healthy individuals and patients with amnestic MCI (aMCI) and AD. They demonstrated that the model parameters required to accurately simulate empirical functional connectivity (FC) significantly correlate with cognitive performance, which surpasses the predictive capability of empirical connectomes. van Nifterick et al.⁵⁸ proposed a large-scale brain network model to link AD-mediated neuronal hyperactivity to large-scale oscillatory slowing observed from magnetoencephalography (MEG) data in human early-stage AD patients. They modified relevant model parameters to simulate six literature-based cellular conditions of AD and found that neuronal hyperactivity can indeed result in oscillatory slowing, supporting the hypothesis that E-I imbalance underlies whole-brain network dysfunction in prodromal AD. Multiscale computational models have also been developed to directly link Aβ and/or tau burdens informed by positron emission tomography (PET) to regional E-I imbalance and abnormal brain dynamics. Stefanovski et al.⁵⁹ constructed personalized virtual brains in the TVB to connect excessive Aβ with local hyperexcitation and found AD groups showed slower oscillation frequencies in simulated local field potentials and electroencephalogram (EEG) compared to MCI and healthy subjects. Patow et al.⁶⁰ used whole-brain modeling techniques to discern the impact of Aβ and tau on regional dynamics, demonstrating a clear dominance of Aβ over tau on brain dynamics in the earlier AD stages (i.e., MCI) and a dominance of tau over Aβ in more advanced disease stages. Nevertheless, all these previous studies focused on cellular/network simulation or AD differentiation rather than E-I estimation. In addition, these models either used structural connectivity (SC) from Diffusion Tensor Imaging (DTI) as a proxy for synaptic efficiency, assumed the same local kinetic parameters for all regions, presumed E-I imbalance for high Aβ/tau accumulation, or estimated only one global scaling coefficient for all long-range inter-regional connections, which cannot infer region-specific E-I imbalance in AD.

To overcome the aforementioned limitations of existing modeling studies, we applied a recently developed computational framework termed Multiscale Neural Model Inversion (MNMI)^61,62 to the rs-fMRI data obtained from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) database to identify region-specific E-I imbalance in AD. The salient features of MNMI include using a biologically plausible neural mass model to describe network dynamics, estimating both intra-regional and inter-regional effective connectivity (EC)^53,63, and constraining EC estimation with structural information. Specifically, MNMI estimates within-region (local) recurrent excitation and inhibition coupling weights as well as inter-regional connection strengths at single subject level based on rs-fMRI, thus enabling the inference of region-specific E-I balance. We focused our analysis on four functional networks (DMN, salience, executive control and limbic networks) due to their critical role and significant disruption in AD pathophysiology^{37,38,39,40,41,42,43,44,45}. Results indicate that MNMI is able to identify altered regional E-I balance in MCI and AD which concentrates on the limbic and cingulate regions, deteriorates with disease progression, and correlates with cognitive performance. This computational study offers mechanistic insights into the alteration of E-I balance during AD progression and the findings have the potential to contribute to the development of novel diagnostic techniques and treatment approaches by enabling the detection and modulation of E-I imbalance in AD.

Methods

Overview of the analysis pipeline

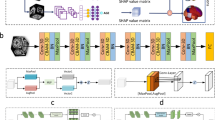
The overall analysis pipeline is shown in Fig. 1a. We use rs-fMRI data from the ADNI database (ADNI-GO and ADNI-2) and DTI data from the Human Connectome Project (HCP) database (as DTI data is not available for every ADNI-GO/2 subject). The ADNI dataset consists of 48 normal control (NC), 48 MCI and 48 AD subjects (Supplementary Table S1), while the HCP dataset includes 100 unrelated subjects⁶⁴. After preprocessing, functional connectivity matrices are calculated for the ADNI subjects and structural connectivity matrices are computed for the HCP subjects. Using FC and SC, MNMI estimates both intra-regional and inter-regional connection strengths for each individual ADNI subject and regional E-I balance is derived based on estimated connection strengths. We then perform statistical analysis to identify disrupted connectivity and impaired regional E-I balance in MCI and AD. Lastly, we examine the association between regional E-I balance and cognitive performance represented by the Mini-Mental State Examination (MMSE) or Clinical Dementia Rating (CDR) score.

Fig. 1: Overview of the analysis pipeline and the MNMI framework.

a Overview of the analysis pipeline. We use resting-state functional MRI (rs-fMRI) data from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) and diffusion tensor imaging (DTI) data from the Human Connectome Project (HCP). After preprocessing, functional connectivity (FC) matrices are calculated for the ADNI subjects and structural connectivity (SC) matrices are computed for the HCP subjects. Using FC and SC, MNMI estimates both intra-regional and inter-regional connection strengths for each individual ADNI subject and regional excitation-inhibition (E-I) balance is derived based on the estimated connection strengths. We then perform statistical analysis to identify disrupted connectivity and impaired E-I balance in MCI and AD. Lastly, we examine the association between regional E-I balance and cognitive performance represented by the Mini-Mental State Examination (MMSE) or the Clinical Dementia Rating (CDR) score. b Overview of the MNMI framework. The neural activity (x) is described by a neural mass network model containing multiple brain regions (R1, R2, etc.). Each region consists of one excitatory (E) and one inhibitory (I) neural population coupled with reciprocal connections. The excitatory neural population excites itself (W_EE) and the inhibitory neural population (W_EI), while receiving feedback inhibition from the latter (W_IE). Inter-regional connection strength (W₁₂, W₂₁, W₁₃, etc.) is constrained by structural connectivity from diffusion MRI. The neural activity (x) is converted to the corresponding blood-oxygen-level-dependent (BOLD) signal (y) via a hemodynamic response function and simulated FC is computed. The model parameters are optimized to minimize the difference between simulated FC and empirical FC calculated based on rs-fMRI.

The MNMI framework

The schematic diagram of the MNMI framework is depicted in Fig. 1b. The neural activity (x) is generated by a neural mass network model consisting of multiple brain regions (R1, R2, etc.). Each region contains one excitatory (E) and one inhibitory (I) neural population coupled with reciprocal connections and receives spontaneous input (u). Different brain regions are connected via long-range fibers whose baseline strengths are determined by SC from diffusion MRI; the weak inter-regional connections are removed to avoid over-parameterization and superficial links⁶². The neural activity (x) is converted to simulated BOLD signal (y) via convolution with a hemodynamic response function (HRF)⁶⁵. Simulated FC is then computed from simulated BOLD signals and empirical FC is calculated from empirical rs-fMRI BOLD time series. Genetic algorithm, a biologically inspired method for solving optimization problems based on natural selection⁶⁶, is applied to estimate both intra-regional recurrent excitation (W_EE) and inhibition (W_IE) weights and inter-regional connection strengths (W₁₂, W₂₁, etc.) as well as the spontaneous input (u), by minimizing the difference between simulated FC and empirical FC. We construct a large network model with 46 regions of interest (ROIs) selected from the DMN, salience, executive control and limbic/subcortical networks (Supplementary Table S2), and set the baseline SC matrix as the average of 100 HCP subjects.

Subjects and dataset

The rs-fMRI data were obtained from the ADNI database⁶⁷ (http://adni.loni.usc.edu/). The ADNI is a longitudinal, multi-center, observational study aimed to validate biomarkers for AD clinical trials. A total of 144 subjects with CDR and MMSE scores were selected from the ADNI-Go and ADNI-2 studies (Supplementary Table S1), including 48 NC (26/22 males/females, age: 73.4 ± 6.5 years, CDR-sum of boxes (CDR-SB): 0.03 ± 0.12, MMSE: 29.1 ± 1.2), 48 MCI (31/17 males/females, age: 73.9 ± 10 years, CDR-SB: 1.1 ± 0.9, MMSE: 28.1 ± 1.7) and 48 AD subjects (27/21 males/females, age: 73.5 ± 8.5 years, CDR-SB: 4.3 ± 1.3, MMSE: 23.1 ± 2.5). All subjects are matched in terms of age (p = 0.94, one-way analysis of variance (ANOVA)) and gender (p = 0.55, one-way ANOVA). All rs-fMRI was scanned by the Phillips Medical Systems using one standard protocol and the subjects were instructed to keep their eyes open during the entire scan⁶⁷. All imaging parameters were checked by a quality control team to ensure the correct sequence was used. The gap between MMSE/CDR evaluation and fMRI acquisition is 24.4 ± 40.9 days for NC, 26.0 ± 59.7 days for MCI, and 29.1 ± 32.6 days for AD. The ADNI inclusion of NC, MCI and AD subjects depends on cognitive assessments and subjective memory concerns⁶⁸. NC subjects have MMSE scores between 24 and 30 inclusive, CDR global scores of zero and memory box scores of zero. The inclusion criteria of MCI include a MMSE score between 24 and 30 inclusive, a CDR global score of 0.5, a memory box score of at least 0.5, and subjective memory concerns. For AD participants, they express subjective memory concerns and have MMSE scores between 20 and 24 inclusive with CDR global scores of 0.5 or 1.0. MCI subjects can be further classified into three different subtypes: reverted MCI (rMCI), stable MCI (sMCI) and progressive MCI (pMCI), depending on the actual disease progression⁶⁹. The rMCI subjects revert to cognitive normalcy after 6 or more months, the sMCI subjects maintain stable for at least 36 months, while pMCI subjects transition to AD after 6 or more months. Based on this criterion, we classified 6 rMCI, 23 sMCI, and 6 pMCI. The remaining 13 MCI subjects had only baseline scans or follow-up visits less than 36 months (no reversal to normalcy or transition to AD during this period), thus unable to be classified as one of the subtypes. We used the baseline rs-fMRI scans only of the 144 subjects in this study.

The DTI data were obtained from 100 unrelated subjects (46/54 males/females, mean age: 29.1 ± 3.7 years) from the WU-Minn HCP young healthy adults, 1200 subjects release⁶⁴ (https://www.humanconnectome.org/). Both the ADNI and HCP studies were approved by the Institutional Review Boards (IRB) of all of the participating institutions and informed written consent was obtained from all participants at each site. Both datasets are publicly available and access to the data requires account registration and acceptance of the Data Use Agreement. Since this study did not involve actual data collection, no IRB approval was required.

Image preprocessing

Data quality control was implemented in ADNI to ensure consistency across imaging centers in terms of the scanner, imaging protocol, and signal-to-noise ratio⁷⁰. The fMRI data (7 min, 140 volumes) were preprocessed using AFNI⁷¹ according to a well-accepted pipeline⁷², which includes first ten volumes removal, head motion correction, normalization, nuisance signals regression, detrend and bandpass filtering (0.01 to 0.08 Hz). Nuisance regressors include the head motion parameters (the “Friston-24” model), the mean BOLD signal of the white matter, and the cerebrospinal fluid. To minimize artifacts due to excessive motion, the subjects with an average frame displacement (FD)⁷³ greater than 0.5 mm were removed. Finally, fMRI data were smoothed with 6 mm full width at half maximum (FWHM) Gaussian kernel and then nonlinearly registered to the Montreal Neurological Institutes (MNI) space. The diffusion MRI data were preprocessed using the HCP protocol⁷⁴.

Functional and structural connectivity

Regional averaged BOLD rs-fMRI time series were extracted using the Desikan-Killiany (DK) atlas⁷⁵ with 84 ROIs. To reduce computational burden, avoid overfitting, and focus on the networks that are most affected in AD⁷⁶, we selected 46 ROIs from the DMN, salience, executive control (i.e., frontoparietal control) and limbic networks (Supplementary Table S2) based on Yeo’s seven network definition⁷⁷ and computed the individual FC matrix using Pearson’s correlation. Structural connectivity is computed using probabilistic tractography based on the diffusion MRI data from HCP. To compute SC, we conducted whole-brain tractography using asymmetry spectrum imaging (ASI) fiber tracking which fits a mixture of asymmetric fiber orientation distribution functions (AFODFs) to the diffusion signal^78,79. White matter streamlines are generated by successively following local directions determined from the AFODFs. The output streamlines are cropped at the gray/white-matter interface with a search distance of 2 mm, where the DK atlas is applied to obtain 84 × 84 SC matrix. The reduced SC matrix with 46 ROIs is extracted from the full SC matrix and averaged among the 100 subjects followed by normalization so the SC is bounded between 0 and 1. Finally, we selected the strongest 10% SC connections for network modeling and the weaker connections were removed^62,80.

Neural mass model and hemodynamic response

We employed computational neuronal modeling to capture the neural interactions and dynamics in the AD network. Regional brain dynamics are simulated by a neural mass model using the biologically motivated nonlinear Wilson-Cowan oscillator⁸¹ due to its simplified yet powerful description of neural network dynamics and proved validity in modeling a wide range of neuroscience phenomena^82,83,84. The population-level activity of the jth region is governed by the following equations^62,85:

$${\tau }_{e}\frac{d{E}_{j}(t)}{{dt}}=-{E}_{j}\left(t\right)+S\left({\sum}_{k}{W}_{{kj}}{C}_{{kj}}{E}_{k}(t)+{W}_{{EE}}^{j}{E}_{j}(t)-{W}_{{IE}}^{j}{I}_{j}\left(t\right)+u+\varepsilon \left(t\right)\right)$$

(1)

$${\tau }_{i}\frac{d{I}_{j}(t)}{{dt}}=-{I}_{j}\left(t\right)+S\left({W}_{{EI}}^{j}{E}_{j}\left(t\right)+\varepsilon (t)\right)$$

(2)

where E_j and I_j are the mean firing rates of excitatory and inhibitory neural populations in brain region j, τ_e and τ_i are the excitatory and inhibitory time constants (20 ms⁸⁶), and ${W}_{{EE}}^{j},{W}_{{IE}}^{j}{{{\rm{and}}}}{W}_{{EI}}^{j}$ are the local coupling strengths (i.e., recurrent excitation, recurrent inhibition and excitatory to inhibitory weight). The variable u is a constant spontaneous input representing baseline excitation (assumed to be identical for all regions) and ε(t) is random additive noise following a normal distribution^87,88. The long-range connectivity strength from region k to region j is represented by W_kj which is scaled by empirical SC (C_kj), and the nonlinear response function S is a sigmoid function $S=1/(1+{e}^{-(\frac{x-\mu }{\sigma })})$ (µ = 1.0; σ = 0.25)⁸⁵.

To increase computational efficiency, we replace the hemodynamic state equations in the original MNMI model⁶² with the canonical HRF and compute the hemodynamic response as the convolution of regional neural activity and the HRF kernel⁶⁵:

$$h\left(t\right)=\frac{{t}^{{\alpha }_{1}-1}{{\beta }_{1}}^{{\alpha }_{1}}{e}^{-{\beta }_{1}t}}{\Gamma ({\alpha }_{1})}-c\frac{{t}^{{\alpha }_{2}-1}{{\beta }_{2}}^{{\alpha }_{2}}{e}^{-{\beta }_{2}t}}{\Gamma ({\alpha }_{2})}$$

(3)

where t indicates time, α₁ = 6, α₂ = 16, β₁ = β₂ = 1, c = 1/6, and Γ represents the gamma function. The regional neural activity is calculated as the weighted sum of excitatory and inhibitory neural activity (${x}_{j}=\frac{2}{3}{E}_{j}+\frac{1}{3}{I}_{j}$); the respective weighting is taken from a previous thalamo-cortical neural mass model of hemodynamic activity⁸⁹ based on the dynamical behavior of globally coupled heterogeneous neural networks of excitatory and inhibitory neurons⁹⁰.

Estimation of model parameters

Both local (intra-regional) and long-range (inter-regional) connection strengths in the model are estimated. For the local parameters, we estimate both recurrent excitation (W_EE) and recurrent inhibition (W_IE) weights in each ROI, resulting in 92 local parameters. The E→I coupling weight (W_EI) is assumed to be constant⁶² as the effect of W_EI could be accommodated by change in W_IE. To avoid over-parameterization and false positive connections due to DTI noise⁹¹, we estimate the strongest 10% inter-regional connections (N = 212) and remove the remaining weaker connections. In addition, the spontaneous input (u) is estimated, which results in a total of 305 free parameters for estimation.

We use genetic algorithm (implemented by the ga function in MATLAB global optimization toolbox) to estimate the model parameters. Genetic algorithm (GA) is a biologically inspired method for solving both constrained and unconstrained optimization problems based on the biological process of natural selection⁶⁶. It can solve a variety of optimization problems that are not suited for standard optimization algorithms, including problems with discontinuous, non-differentiable, stochastic or highly nonlinear objective functions. GA repeatedly modifies a population of individual solutions. At each step, it selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. In addition to elite children (individuals with the best fitness values), GA produces mutation children by making random changes to a single parent and crossover children by combining the vector entries of a pair of parents. Unlike regular optimization algorithms, GA does not stop at local minimum, thus could evolve toward a global optimum over successive generations. We use the default hyperparameters in MATLAB with a crossover fraction of 0.8, an elite count of 10 and a population size of 200. To achieve balanced excitation and inhibition in the network, the estimated parameters are bounded within certain ranges⁶²: W_EE and ${W}_{{IE}}$∈[2,4]$,{W}_{{ki}}$∈$[-{{\mathrm{2,2}}}]$, and $u\in [{{\mathrm{0.2,0.4}}}]$. GA maximizes the Pearson’s correlation between the simulated and empirical FC matrices with the functional tolerance set to be 1e−3 and the maximal number of generations set to be 128.

Numerical integration

The differential equations of the neural mass model are simulated using the 4th order Runge-Kutta (RK) scheme with an integration step of 10 ms; a shorter integration step has no significant effect on the results reported. We simulate the network for a total of 200 s, and the first 20 s of the BOLD activity is discarded to remove transient effects. The remaining 180 s time series are downsampled to 0.33 Hz to have the same temporal resolution as the empirical BOLD signal (TR = 3 s). The model along with the optimization procedure are coded in MATLAB (R2021a) and run in parallel with 24 cores in a high-performance UNC Linux computing cluster operating with Red Hat Enterprise Linux 7. The GA converges within 128 generations for all the subjects and the computing time (for each individual subject) typically ranges from 30 to 72 h, with a few subjects going up to 100 h.

Metrics for E-I balance

Regional E-I balance is quantified by either E-I difference (sum of incoming excitatory EC − sum of incoming inhibitory EC) or E/I ratio (the ratio of the sum of incoming excitatory EC to the sum of incoming inhibitory EC). We define three metrics of regional E-I balance: (1) intra-regional E-I balance; (2) inter-regional E-I balance; and (3) total E-I balance. The intra-regional E-I balance is calculated as the difference (or ratio) between recurrent excitation and recurrent inhibition strength, while inter-regional E-I balance is computed as the difference between the sum of incoming excitatory inter-regional EC and the sum of incoming inhibitory inter-regional EC. We do not compute inter-regional E/I ratio because some regions receive excitatory or inhibitory EC only, as observed experimentally in macaque cerebral cortex⁹². The total E-I balance is calculated as the difference (or ratio) between total excitation level (recurrent excitation strength + all incoming excitatory inter-regional EC) and total inhibition level (recurrent inhibition strength + all incoming inhibitory inter-regional EC) to a particular region.

Statistics and reproducibility

Model parameters are estimated for each subject and compared between NC and MCI, NC and AD, and MCI and AD. We use two-sample and two-sided t-tests⁹³, the most applied statistical test under the condition of normal distribution, to compare local and inter-regional connection strengths as well as intra-regional, inter-regional and total E-I balance. Multiple comparisons are corrected either by controlling the family-wise error rate (FWER; Bonferroni adjustment), the false discovery rate (FDR)⁹⁴, or Network-based Statistics (NBS)⁹⁵, all at a significance level of p < 0.05. The Bonferroni method is one of the most used methods to control FWER, but it is too conservative and can have a high false negative rate⁹⁶. By comparison, the FDR method is less conservative and has greater power than the Bonferroni correction, but the probability of type I error is larger than FWER. Lastly, NBS is a method to control FWER in the weak sense when mass univariate testing is performed at every connection comprising a graph⁹⁵. It can provide substantially greater power than FDR or FWER if the connections associated with the effect of interest are connected to form a structure. Consequently, we use Bonferroni adjustment and FDR to correct node-based comparisons (i.e., 46 regional (local) connection strengths or E-I balance) and NBS to correct edge-based comparisons (i.e., 212 inter-regional connections). This is because the number of inter-regional connections is much larger than intra-regional connections, making it difficult to identify significant connections that survive FWER or FDR correction. We report both p values and the Cohen’s d effect size which is determined by calculating the mean difference between the two compared groups, and then dividing the result by the pooled standard deviation⁹⁷. All data analysis is performed with MATLAB (R2021a) and is reproducible using the code linked below in “Code availability”.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results

MNMI performance

The performance of MNMI is illustrated in Supplementary Fig. S1. The average fitness value (i.e., Pearson’s correlation between simulated and empirical FC) was 0.6 ± 0.08 for NC, 0.61 ± 0.07 for MCI, and 0.62 ± 0.08 for AD, respectively, consistent with previous modeling studies^88,98. Both the simulated neural activity and simulated BOLD signals displayed rhythmic fluctuations (Supplementary Fig. 1a, b). The oscillation frequency of the neural activity was about 7–10 Hz, consistent with α oscillations during relaxed wakefulness⁹⁹. The frequency of the BOLD signals ranged between 0.01 and 0.05 Hz, in line with experimental observations¹⁰⁰. The group-averaged empirical FC and simulated FC (for all NC subjects) are displayed in Supplementary Fig. S1c, d respectively, where the pattern of the simulated FC closely matched that of the empirical FC (with a correlation coefficient 0.83). Consistently, the empirical and simulated FC showed similar graph theoretical properties (binarized with a proportional threshold of 0.5; calculated using the Brain Connectivity Toolbox¹⁰¹), including global efficiency (empirical: 0.63, simulated: 0.68), mean local efficiency (empirical: 0.80, simulated: 0.75), mean clustering coefficient (empirical: 0.73, simulated: 0.68) and shortest path length (empirical: 0.5, simulated: 0.5).

Recurrent inhibition exhibits more significant and stable impairments in MCI/AD than recurrent excitation

We first examined whether intra-regional (local) E-I balance is altered in MCI and AD. Comparison of the recurrent excitation weights (W_EE in Fig. 1b) within 46 ROIs is shown in Fig. 2a for NC and MCI, Fig. 2b for NC and AD, and Fig. 2c for MCI and AD, respectively. For the NC-MCI comparison, three regions (right inferior parietal cortex (R.IPC), left rostral anterior cingulate cortex (L.rACC) and right caudal anterior cingulate cortex (R.cACC)) showed marginal decrease in MCI (R.IPC: p = 0.044; L.rACC: p = 0.013; R.cACC: p = 0.031, uncorrected), and three regions (right entorhinal cortex (R.ETC), left pallidum (L.PAL) and right nucleus accumbens (R.ACB)) showed marginal increase in MCI (R.ETC: p = 0.04; L.PAL: p = 0.003; R.ACB: p = 0.017, uncorrected) (Fig. 2a). For NC-AD comparison, R.ACB showed significant increase in AD compared to NC (t = −3.67, p = 0.019, Bonferroni corrected, Cohen’s d: −0.75; Fig. 2b), which was the only region that showed consistent and significant excitation change across both MCI and AD. Also, five regions displayed marginal change in AD (p < 0.05, uncorrected), including left caudal middle frontal cortex (L.cMFC, p = 0.041), R.PAL (p = 0.009), left hippocampus (L.HPC, p = 0.043) and left amygdala (L.AMY, p = 0.018) with decreased excitation, and left posterior cingulate cortex (L.PCC, p = 0.016) with increased excitation (Fig. 2b). Regarding MCI-AD comparison, only the region of R.AMY showed marginal decrease in AD (p = 0.006, uncorrected; Fig. 2c). This suggests that as a prodromal stage of AD, MCI has similar recurrent excitation level as AD, though AD shows more significant impairments in certain brain regions (i.e., R.ACB) when compared with NC.

Fig. 2: Impaired local recurrent excitation in MCI and AD.

Boxplot comparison of recurrent excitation weight between a NC and MCI, b NC and AD, and c MCI and AD for all 46 regions (n = 48 for each independent sample). One star (*) indicates uncorrected significance (p < 0.05), double stars (**) indicate corrected significance by FDR (p < 0.05), and triple stars (***) denote corrected significance by the Bonferroni method (p < 0.05). For the boxplots, the central mark indicates the median, and the bottom and top edges of the box indicate the 25th and 75th percentiles, respectively. The whiskers extend to the most extreme data points not considered outliers, and the outliers are plotted individually using the “o” marker symbol (same for figures below). IPC inferior parietal cortex, rACC rostral anterior cingulate cortex, cACC caudal anterior cingulate cortex, ETC entorhinal cortex, PAL pallidum, ACB nucleus accumbens, PCC posterior cingulate cortex, cMFC caudal middle frontal cortex, HPC hippocampus, AMY amygdala, L left hemisphere, R right hemisphere, DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

Comparison of the recurrent inhibition weights (W_IE in Fig. 1b) within 46 ROIs is shown in Fig. 3a for NC and MCI, Fig. 3b for NC and AD, and Fig. 3c for MCI and AD, respectively. Both MCI and AD showed significant difference in recurrent inhibition compared with NC. In MCI, recurrent inhibition in L.cMFC was significantly decreased (t = 4.06, p = 0.005, Bonferroni corrected, Cohen’s d: 0.83; Fig. 3a). In addition, four regions (right superior parietal cortex (R.SPC), right inferior temporal cortex (R.ITC), L.PAL and R.ACB) showed marginal decrease (R.SPC: p = 0.029; R.ITC: p = 0.038; L.PAL: p = 0.01; R.ACB: p = 0.013, uncorrected), while one region (left superior frontal cortex (L.SFC)) showed marginal increase in MCI (p = 0.041, uncorrected). In AD, the change in recurrent inhibition was much more pronounced than MCI in that the difference in seven regions survived multiple comparison correction (Fig. 3b). Specifically, the recurrent inhibition in the right isthmus cingulate cortex (R.ICC) (t = 2.76, p = 0.045, FDR corrected, Cohen’s d: 0.56), L.cMFC (t = 3.22, p = 0.013, FDR corrected, Cohen’s d: 0.66), R.SPC (t = 3.23, p = 0.013, FDR corrected, Cohen’s d: 0.66), R.ITC (t = 4.14, p = 0.004, Bonferroni corrected, Cohen’s d: 0.84) and L.PAL (t = 3.64, p = 0.02, Bonferroni corrected, Cohen’s d: 0.74) was significantly reduced, while that in R.cACC (t = −3.59, p = 0.024, Bonferroni corrected, Cohen’s d: −0.73) and L.HPC (t = −3.42, p = 0.043, Bonferroni corrected, Cohen’s d: −0.70) was significantly increased in AD compared with NC. Moreover, three regions (left precuneus (L.PCU), R.rACC and L.PCC) showed marginal decrease (L.PCU: p = 0.025; R.rACC: p = 0.043; L.PCC: p = 0.041, uncorrected) and one region (L.SFC) showed marginal increase in AD (p = 0.041, uncorrected). Notably, five ROIs showed stable change across MCI and AD including L.SFC, L.cMFC, R.SPC, R.ITC and L.PAL (compare Fig. 3b with Fig. 3a). Importantly, the difference in R.SPC, R.ITC and L.PAL was only marginal in MCI, but was robust to correction for multiple comparisons in AD, suggesting greater disruption of inhibitory interactions in AD than in MCI. Despite greater impairments in AD than MCI, the difference between MCI and AD was only marginally significant in three ROIs including L.cACC, R.cACC, and R.ACB (L.cACC: p = 0.042; R.cACC: p = 0.023; R.ACB: p = 0.041, uncorrected) (Fig. 3c). Again, this suggests that the changes in recurrent excitation and inhibition become more subtle from MCI to AD, compared with the changes from NC to MCI or AD.

Fig. 3: Impaired local recurrent inhibition in MCI and AD.

Boxplot comparison of recurrent inhibition weight between a NC and MCI, b NC and AD, and c MCI and AD for all 46 regions (n = 48 for each independent sample). One star (*) indicates uncorrected significance (p < 0.05), double stars (**) indicate corrected significance by FDR (p < 0.05), and triple stars (***) denote corrected significance by the Bonferroni method (p < 0.05). SFC superior frontal cortex, cMFC caudal middle frontal cortex, SPC superior parietal cortex, ITC inferior temporal cortex, PAL pallidum, ACB nucleus accumbens, ICC isthmus cingulate cortex, PCU precuneus, rACC rostral anterior cingulate cortex, PCC posterior cingulate cortex, cACC caudal anterior cingulate cortex, HPC hippocampus, L left hemisphere, R right hemisphere, DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

To visualize the alterations in recurrent excitation and inhibition better, we listed the significant changes in MCI and AD (from NC) in Table 1 where an up arrow indicates a significant increase while a down arrow indicates a significant decrease. Marginal significance without correction, FDR correction and Bonferroni correction are marked by one star, two stars and three stars, respectively. Several observations can be made. First, more regions showed significant difference in AD than MCI. This is to be expected as AD represents a more severe disease stage than MCI. Second, the strength of the majority of connections (69%) was decreased in MCI/AD compared to NC. This is consistent with the widespread decrease in FC during the progression of AD^34,35,36. Third, if a region exhibited impairments in both recurrent excitation and inhibition, their directions of change were opposite to each other thus strengthening E-I imbalance, except for the executive control network where recurrent excitation and recurrent inhibition changed in the same direction. This indicates the existence of compensatory mechanisms in the executive control network to maintain similar E-I balance in the presence of AD pathology due to the critical role of this network in cognitive function^102,103,104. Lastly, recurrent inhibition was more significantly disrupted by MCI/AD than recurrent excitation, in agreement with the emerging viewpoint of interneuron dysfunction in network impairments^12,105,106. The consistent impairment of recurrent inhibition across MCI and AD also suggests that inhibitory connections are more stable biomarkers of AD than excitatory connections.

Table 1 Alteration in recurrent excitation and inhibition strength in MCI and AD (compared with NC)

We next examined network-averaged recurrent excitation and inhibition changes in MCI and AD (Supplementary Fig. S2). It is noted that the only significant difference that passed multiple comparison correction lay in the executive control network where the recurrent inhibition strength in AD was significantly lower than NC (t = 3.04, p = 0.028, FDR corrected, Cohen’s d: 0.62; Supplementary Fig. S2b). In addition, the recurrent excitation strength showed a marginal decrease from NC to AD in the executive control network (p = 0.028, uncorrected; Supplementary Fig. S2a), while the recurrent inhibition strength displayed a marginal decrease from NC to MCI in the executive control network (p = 0.011, uncorrected) and from NC to AD in the DMN (p = 0.021, uncorrected), and a marginal increase from NC to AD in the salience network (p = 0.014, uncorrected) (Supplementary Fig. S2b). Thus, similar to the regional comparison, on the network level, impairments in recurrent excitation and inhibition become more notable in AD than MCI. The decrease in both recurrent excitation and inhibition in the executive control network may compensate for the loss of each other, thus maintaining a relatively stable E-I balance.

Intra-regional E-I balance is progressively impaired from NC to MCI and to AD

The alterations in recurrent excitation and inhibition strengths resulted in intra-regional E-I imbalance in MCI and AD as shown in Fig. 4. The intra-regional (local) E-I balance was quantified as the E-I difference (i.e., recurrent excitation strength − recurrent inhibition strength; similar results were obtained for E/I ratio), which measured the level of net excitation. In MCI, the E-I balance was significantly elevated in L.PAL (t = −4.06, p = 0.005, Bonferroni corrected, Cohen’s d: −0.83) and R.ACB (t = −3.39, p = 0.048, Bonferroni corrected, Cohen’s d: −0.69), the two regions in the limbic network, when compared with NC (Fig. 4a). In addition, three regions showed a marginal decrease in E-I balance, including L.rACC, R.cACC and L.HPC (L.rACC: p = 0.034; R.cACC: p = 0.01; L.HPC: p = 0.016, uncorrected), while one region (R.ITC) displayed a marginal increase in E-I balance (p = 0.007, uncorrected). In AD, five regions showed consistent E-I impairments as MCI, including R.cACC, R.ITC. L.PAL, L.HPC and R.ACB (Fig. 4b). Notably, the E-I alteration in R.cACC and L.HPC became more robustly significant in AD than MCI, surviving multiple comparison correction (R.cACC: t = 3.08, p = 0.031, FDR corrected, Cohen’s d: 0.63; L.HPC: t = 3.91, p = 0.008, Bonferroni corrected, Cohen’s d: 0.80). The change in R.ITC was marginal as MCI (p = 0.009, uncorrected) and the changes in L.PAL and R.ACB maintained significant as MCI (L.PAL: t = −3.64, p = 0.021, Bonferroni corrected, Cohen’s d: −0.74; R.ACB: t = −2.95, p = 0.037, FDR corrected, Cohen’s d: −0.60). In addition to the five stable regions, intra-regional E-I balance in L.PCU, L.PCC, left putamen (L.PUT) and L.AMY was also impaired in AD, with a significant increase in L.PCC (t = −3.12, p = 0.031, FDR corrected, Cohen’s d: −0.64), a marginal increase in L.PCU (p = 0.013, uncorrected), and a marginal decrease in L.PUT and L.AMY (L.PUT: p = 0.036; L.AMY: p = 0.038, uncorrected). In contrast to the marked E-I balance changes from NC to MCI/AD, the changes from MCI to AD were much less pronounced with only three ROIs showing uncorrected significance (R.ICC: p = 0.024; R.SFC: p = 0.009; L.PUT: p = 0.049, uncorrected; Fig. 4c). Overall, intra-regional E-I imbalance in MCI and AD was highly consistent and concentrated on the limbic network (Fig. 4a, b).

Fig. 4: Disrupted intra-regional excitation-inhibition (E-I) balance in MCI and AD.

Boxplot comparison of local E-I difference (recurrent excitation − recurrent inhibition) between a NC and MCI, b NC and AD, and c MCI and AD for all 46 regions (n = 48 for each independent sample). One star (*) indicates uncorrected significance (p < 0.05), double stars (**) indicate corrected significance by FDR (p < 0.05), and triple stars (***) denote corrected significance by the Bonferroni method (p < 0.05). rACC rostral anterior cingulate cortex, cACC caudal anterior cingulate cortex, ITC inferior temporal cortex, PAL pallidum, HPC hippocampus, ACB nucleus accumbens, PCU precuneus, PCC posterior cingulate cortex, PUT putamen, AMY amygdala, ICC isthmus cingulate cortex, SFC superior frontal cortex, L left hemisphere, R right hemisphere, DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

To visualize the progressive changes in E-I balance from NC to MCI and to AD, we fit a linear model to the local E-I difference of all NC, MCI and AD subjects and found the model significance of six brain regions passed the correction for multiple comparisons including L.PCC (r = 0.26, p = 0.024, FDR corrected), R.cACC (r = −0.26, p = 0.024, FDR corrected), R.ITC (r = 0.23, p = 0.048, FDR corrected), L.PAL (r = 0.31, p = 0.007, Bonferroni corrected), L.HPC (r = −0.31, p = 0.006, Bonferroni corrected), and R.ACB (r = 0.24, p = 0.036, FDR corrected) (Supplementary Fig. S3). Specifically, the E-I difference of L.PCC, R.ITC, L.PAL and R.ACB was progressively increased from NC to MCI and to AD, while the E-I difference of R.cACC and L.HPC was progressively decreased from NC to MCI and to AD (Supplementary Fig. S3). Thus, different brain regions could exhibit different profiles of E-I balance change over the course of AD development and increased excitation dominated decreased excitation for intra-regional E-I balance change. Notably, the brain regions that survived multiple comparison correction for the linear model are consistent with those regions showing stable and significant E-I impairments across MCI and AD, except for L.PCC which displayed significant change in AD only (Fig. 4a, b). Linear fitting of intra-regional E-I balance for the homologous regions from the opposite hemisphere (i.e., R.PCC, L.cACC, L.ITC, R.PAL, R.HPC and L.ACB) is shown in Supplementary Fig. S4 where no regions showed significant change in E-I balance over AD advancement, suggesting that bilateral regions may have different E-I changes in MCI and AD.

Inter-regional connection strengths are predominantly reduced in MCI and AD

In addition to intra-regional recurrent connections, inter-regional excitatory and inhibitory connections were also disrupted in MCI and AD. The color-coded average inter-regional EC (W_ij in Fig. 1b) for NC, MCI and AD are shown in Fig. 5a–c, respectively (the white area indicates removed weak connections). We observed that the EC patterns were similar for NC, MCI and AD where there were more excitatory (positive) connections than inhibitory (negative) connections. As regions of the same network (or cortical networks) connected stronger than regions of two different networks (or cortical-limbic networks), we observed a modular or diagonal structure for EC, consistent with a previous EC study¹⁰⁷. The marginally significant EC connections in MCI (compared with NC) are indicated by the blue edges in Fig. 5d (p < 0.05, uncorrected), where they were broadly distributed among the four networks. The significant EC connections in AD (compared with NC) are shown in Fig. 5e where the blue edges indicate uncorrected significant connections (p < 0.05, uncorrected) and the red edges denote significant connections (p = 0.009) corrected by NBS. Of note, the corrected significant connections (red edges) involved mostly the executive control and limbic networks. Multiple marginally significant connections also existed between MCI and AD comparison (p < 0.05, uncorrected; Fig. 5f), which mostly involved the DMN and executive control network. It should be noted that the overlap of significant connections among the three-way comparison (NC-MCI, NC-AD and MCI-AD) was low. To visualize the EC changes better, we compared the significant inter-regional EC (corrected and uncorrected) between NC and MCI in Fig. 6a, between NC and AD in Fig. 6b, and between MCI and AD in Fig. 6c. As indicated by the EC difference in the bottom panels, most of the connection strengths were reduced in MCI and AD compared with NC (Fig. 6a, b), indicating weaker interactions between regions in MCI and AD. The corrected significant connections in AD (p = 0.009, corrected by NBS) included R.SPC → R.PUT, right caudate (R.CA) → right thalamus (R.THAL), R.SFC → R.PAL, R.PAL → R.PUT, right rostral middle frontal cortex (R.rMFC) → R.PUT, R.CA → R.rMFC, and R.PUT → R.PAL (Fig. 6b). Interestingly, for MCI-AD comparison, the EC of most of the marginally significant connections (p < 0.05, uncorrected) was increased in AD compared with MCI (Fig. 6c). This suggests that progression of AD may involve different sets of inter-regional connections that are differentially disrupted.

Fig. 5: Altered inter-regional effective connectivity (EC) in MCI and AD.

Average inter-regional EC for a NC, b MCI, and c AD. The white area indicates removed weak connections. d Significant EC connections in MCI when compared with NC. e Significant EC connections in AD when compared with NC. f Significant EC connections in AD when compared with MCI. For d–f, green edges indicate insignificant connections, blue edges indicate uncorrected significant connections (p < 0.05, uncorrected), and red edges indicate significant connections corrected by Network-based Statistics (NBS; p < 0.05). DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

Fig. 6: Significant inter-regional connections for group pairwise comparison.

Significant inter-regional effective connectivity (EC) for a NC and MCI comparison, b NC and AD comparison, and c MCI and AD comparison (n = 48 for each independent sample). For each subplot, the top panel shows the boxplot of inter-regional EC while the bottom panel plots the EC mean difference between the two compared groups. One star (*) indicates uncorrected significance (p < 0.05), and double stars (**) indicate corrected significance by NBS (p < 0.05). ICC isthmus cingulate cortex, PCU precuneus, rMFC rostral middle frontal cortex, CA caudate, PAL pallidum, PUT putamen, MTC middle temporal cortex, SMG supramarginal gyrus, PCC posterior cingulate cortex, SFC superior frontal cortex, IPC inferior parietal cortex, ITC inferior temporal cortex, cACC caudal anterior cingulate cortex, SPC superior parietal cortex, IN insula, THAL thalamus, cMFC caudal middle frontal cortex, ETC entorhinal cortex, HPC hippocampus, STC superior temporal cortex, L left hemisphere, R right hemisphere.

The average intra- and inter-network EC (summation of all excitatory and inhibitory inter-regional EC within or between networks divided by the number of connections) is shown in Supplementary Fig. S5. We observed that the EC from the executive control network to the salience network was marginally decreased in MCI when compared with NC (p = 0.015, uncorrected, Supplementary Fig. S5a, b). In AD, the EC from the DMN to the limbic network was significantly reduced compared to NC (t = 2.95, p = 0.049, FDR corrected, Cohen’s d: 0.60) and the EC from the executive control network to the limbic network was marginally decreased (p = 0.029, uncorrected) (Supplementary Fig. S5a, c), suggesting cortical-limbic decoupling. Moreover, the EC from the limbic network to the executive control network was marginally decreased from MCI to AD (p = 0.011, uncorrected, Supplementary Fig. S5b, c). Overall, the excitatory interactions between networks are considerably decreased in MCI and AD when compared with NC, consistent with the predominantly reduced inter-regional EC during AD progression (Fig. 6).

Inter-regional E-I balance is progressively disrupted from NC to MCI and to AD

To evaluate the inter-regional E-I balance change in MCI and AD, we computed the inter-regional E-I difference (i.e., difference between the sum of all positive incoming EC and the absolute sum of all negative incoming EC) to a particular ROI (Fig. 7). The E-I change from NC to MCI is shown in Fig. 7a where seven regions showed marginally impaired inter-regional E-I balance (p < 0.05, uncorrected). A majority of the seven ROIs showed decreased excitation, including L.PCU (p = 0.034), right insula (R.IN, p = 0.022), R.ITC (p = 0.012), R.PUT (p = 0.018) and R.PAL (p = 0.005), and only two ROIs (R.cMFC (p = 0.02) and L.THAL (p = 0.049)) exhibited increased excitation. In AD, three stable regions showed reduced excitation as MCI, including R.ITC, R.PUT and R.PAL, all belonging to the limbic network (Fig. 7b). In particular, the significant changes in R.PUT (t = 3.62, p = 0.022, Bonferroni corrected, Cohen’s d: 0.74) and R.PAL (t = 3.14, p = 0.0497, FDR corrected, Cohen’s d: 0.64) were able to survive correction for multiple comparisons, again indicating more severe E-I disruption in AD than MCI. The change in R.ITC was marginal (p = 0.026, uncorrected). Moreover, the excitation of L.HPC was marginally reduced (p = 0.012, uncorrected), while that of R.PCC was marginally elevated in AD (p = 0.025, uncorrected). Comparison of the E-I difference between MCI and AD indicated that four brain regions had marginal E-I balance changes (p < 0.05, uncorrected, Fig. 7c). Specifically, the E-I difference of L.IN (p = 0.023), L.rMFC (p = 0.044), and L.THAL (p = 0.043) was marginally reduced while that of R.PCC (p = 0.005) was marginally increased. We then fit a linear model to the E-I difference and found that the net excitation of R.PUT and R.PAL, the two regions with consistent E-I impairment in MCI and AD and that passed multiple comparison correction in AD (Fig. 7a, b), reduced significantly from NC to MCI and to AD (R.PUT: r = −0.3, p = 0.015, Bonferroni corrected; R.PAL: r = −0.26, p = 0.037, FDR corrected; Supplementary Fig. S6). Thus, different from the mixed intra-regional E-I balance change (Supplementary Fig. S3), inter-regional E-I balance decreases progressively over the course of AD development, consistent with the majority of reduced inter-regional EC in both MCI and AD (Fig. 6). Linear fitting of inter-regional E-I balance for the homologous regions from the opposite hemisphere (i.e., L.PUT and L.PAL) is shown in Supplementary Fig. S7 where L.PUT showed marginal decrease in E-I balance over AD progression (r = −0.17, p = 0.04, uncorrected) with no significant change for L.PAL.

Fig. 7: Disrupted inter-regional excitation-inhibition (E-I) balance in MCI and AD.

Boxplot comparison of inter-regional E-I difference between a NC and MCI, b NC and AD, and c MCI and AD for all 46 regions (n = 48 for each independent sample). One star (*) indicates uncorrected significance (p < 0.05), double stars (**) indicate corrected significance by FDR (p < 0.05), and triple stars (***) denote corrected significance by the Bonferroni method (p < 0.05). PCU precuneus, IN insula, cMFC caudal middle frontal cortex, ITC inferior temporal cortex, THAL thalamus, PUT putamen, PAL pallidum, PCC posterior cingulate cortex, HPC hippocampus, rMFC rostral middle frontal cortex, L left hemisphere, R right hemisphere, DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

Disrupted overall E-I balance in the limbic network persists over MCI and AD

The above analysis indicates that both intra-regional and inter-regional E-I balance is impaired in MCI and AD. As the overall neural excitability depends on both intra-regional and inter-regional input drive, we computed the overall E-I balance as the difference between total excitation (recurrent excitation + all incoming excitatory inter-regional EC) and total inhibition (recurrent inhibition + all incoming inhibitory inter-regional EC) for all ROIs. We found that the overall E-I balance was altered in a number of regions in MCI and AD and most of the regions were located in the limbic network (Fig. 8). Specifically, in MCI, the E-I difference of R.PAL was significantly decreased (t = 3.31, p = 0.030, FDR corrected, Cohen’s d: 0.68), while that of R.ACB was significantly increased (t = −3.39, p = 0.048, Bonferroni corrected, Cohen’s d: −0.69) (Fig. 8a). Additionally, the E-I difference of R.IN, R.PUT, and L.HPC was marginally decreased (R.IN: p = 0.027; R.PUT: p = 0.015; L.HPC: p = 0.04, uncorrected), while that of R.cMFC was marginally increased in MCI (p = 0.01, uncorrected). In AD, the alterations in overall E-I balance remained consistent for R.PUT, R.PAL, L.HPC and R.ACB, all four regions from the limbic network, and with more pronounced difference (compare Fig. 8b with 8a). In addition to R.PAL (t = 3.35, p = 0.018, FDR corrected, Cohen’s d: 0.68) and R.ACB (t = −2.95, p = 0.046, FDR corrected, Cohen’s d: −0.60), the E-I balance changes in R.PUT and L.HPC were able to pass multiple comparison correction in AD (R.PUT: t = 3.80, p = 0.012, Bonferroni corrected, Cohen’s d: 0.78; L.HPC: t = 3.71, p = 0.016, Bonferroni corrected, Cohen’s d: 0.76; Fig. 8b). Besides, the overall E-I difference of L.PUT was marginally reduced (p = 0.023, uncorrected), while that of L.PCC and R.PCC was marginally increased in AD (L.PCC: p = 0.015; R.PCC: p = 0.022, uncorrected; Fig. 8b).

Fig. 8: Disrupted overall excitation-inhibition (E-I) balance in MCI and AD.

Boxplot comparison of total E-I difference between a NC and MCI, b NC and AD, and c MCI and AD for all 46 regions (n = 48 for each independent sample). One star (*) indicates uncorrected significance (p < 0.05), double stars (**) indicate corrected significance by FDR (p < 0.05), and triple stars (***) denote corrected significance by the Bonferroni method (p < 0.05). IN insula, cMFC caudal middle frontal cortex, PUT putamen, PAL pallidum, HPC hippocampus, ACB nucleus accumbens, PCC posterior cingulate cortex, ICC isthmus cingulate cortex, L left hemisphere, R right hemisphere, DMN default mode network, SAL salience network, EXE executive control network, LIM limbic network.

Comparison of the overall E-I balance between MCI and AD revealed that four regions exhibited marginal differences, including L.ICC, L.PCC, R.PCC and L.IN (Fig. 8c). Specifically, the E-I differences of L.ICC, L.PCC and R.PCC were marginally increased (L.ICC: p = 0.031; L.PCC: p = 0.033; R.PCC: p = 0.003, uncorrected), while that of L.IN was marginally reduced from MCI to AD (p = 0.008, uncorrected). Of note, the E-I differences in L.PCC and R.PCC were consistent with the marginal increase from NC to AD (compare Fig. 8c with Fig. 8b), with no significant change from NC to MCI (Fig. 8a). This suggests that E-I disruption in PCC may be specific to the disease progression from MCI to AD and an elevation in PCC excitability may signal the transition from MCI to AD. In contrast, significant E-I alterations in the limbic network (R.PUT, R.PAL, L.HPC and R.ACB) were observed in both NC-MCI and NC-AD comparisons (Fig. 8a, b), but not in MCI-AD comparison (Fig. 8c). This indicates that E-I impairments in the limbic network are specific to NC to MCI progression and could serve as early biomarkers for AD.

The potential differential roles of PCC and limbic network in AD progression remained consistent when the inhibitory neural time constant was reduced from 20 ms to 10 ms (Supplementary Fig. S8) or when the respective weighting of the excitatory and inhibitory neural activity to the BOLD signal changed from 2:1 to 1:1 (Supplementary Fig. S9). Specifically, significant difference was observed in the limbic regions for NC-MCI and NC-AD comparisons, while such difference was found in the PCC regions for NC-AD and MCI-AD comparisons. It also generally accords with the Braak staging where the HPC and other limbic regions (e.g., ITC) are affected by the tau neurofibrillary tangles earlier than the association cortex¹⁰⁸. Lastly, the MCI subjects selected in this study included reverted MCI (rMCI), stable MCI (sMCI), and progressive MCI (pMCI) (see “Methods”). The progressive disrupted nature of E-I imbalance during AD advancement could also be evidenced by the E-I difference among rMCI, sMCI and pMCI (Supplementary Fig. S10). Specifically, the E-I difference concentrated on the ACC and MFC regions where there was marginal difference in three regions between rMCI and sMCI (L.cACC: p = 0.017; R.cMFC: p = 0.013; L.rMFC: p = 0.027, uncorrected), and significant difference in R.cACC between rMCI and pMCI (t = 7.46, p = 0.001, Bonferroni corrected, Cohen’s d: 4.31), and between sMCI and pMCI (t = 4.85; p = 0.002, Bonferroni corrected, Cohen’s d: 2.22). Consistently, the E-I balance of most regions decreased from rMCI to sMCI, and to pMCI (but note the small number of subjects for rMCI and pMCI, see “Methods”).

Consistent with the stable E-I alterations across MCI and AD, linear model analysis revealed that the same four brain regions in the limbic network that exhibited significant E-I impairments in MCI and AD (i.e., R.PUT, R.PAL, L.HPC and R.ACB; Fig. 8a, b), showed progressive E-I imbalance from NC to MCI and to AD (Supplementary Fig. S11). Specially, the overall E-I difference in R.PUT, R.PAL and L.HPC was progressively reduced (R.PUT: r = −0.31, p = 0.007; R.PAL: r = −0.28, p = 0.027; L.HPC: r = −0.30, p = 0.01, all Bonferroni corrected; Supplementary Fig. S11a–c), while that of R.ACB was progressively increased from NC to MCI and to AD (r = 0.24, p = 0.045, FDR corrected; Supplementary Fig. S11d). Linear fitting of total E-I balance for the homologous regions from the opposite hemisphere (i.e., L.PUT, L.PAL, R.HPC, and L.ACB) is shown in Supplementary Fig. S12 where L.PUT showed marginal decrease in E-I balance (r = −0.20, p = 0.02, uncorrected) over AD advancement with no significant change for other bilateral regions. Lastly, we examined the change of spontaneous input during AD progression. There was no difference in the spontaneous input between NC and MCI, while the spontaneous input was significantly decreased in AD, when compared with NC (t = 2.21, p = 0.044, FDR corrected, Cohen’s d: 0.45) or MCI (t = 2.24, p = 0.044, FDR corrected, Cohen’s d: 0.46; Supplementary Fig. S13). This again suggests that the excitatory drive to the network is reduced in the AD stage, consistent with overall reduction in regional E-I balance (Fig. 8).

Regional E-I balance is associated with cognitive performance

To evaluate the behavioral relevance of E-I imbalance in AD progression, we examined the association between regional E-I balance and MMSE or CDR score (we used sum of boxes score for CDR) (Fig. 9). The correlation analysis was performed for both total regional E-I difference and total regional E/I ratio. We first computed the Pearson’s correlation between regional E-I difference and individual MMSE score for all 46 ROIs and the correlation that passed FDR or Bonferroni correction (p < 0.05) is reported in Fig. 9a–d. We found that the E-I difference in L.IN (r = 0.25, p = 0.04, FDR corrected), L.PUT (r = 0.24, p = 0.045, FDR corrected), R.PUT (r = 0.25, p = 0.04, FDR corrected), and L.HPC (r = 0.31, p = 0.007, Bonferroni corrected) was positively correlated with the MMSE score, suggesting that lower overall excitation level in these regions was associated with lower MMSE scores in MCI/AD. If the total E-I balance was assessed as E/I ratio, significant positive correlation with the MMSE score was retained in L.HPC only (r = 0.29, p = 0.017, Bonferroni corrected; Supplementary Fig. S14). We next performed correlation analysis between regional E-I balance and individual CDR score and found largely consistent results. Specifically, for total regional E-I difference, R.PCC showed positive correlation with the CDR score (r = 0.25, p = 0.03, FDR corrected), while R.PUT (r = −0.32, p = 0.003, Bonferroni corrected), R.PAL (r = −0.27, p = 0.019, FDR corrected), and L.HPC (r = −0.35, p = 0.0009, Bonferroni corrected) displayed negative correlation with the CDR score (Fig. 9e–h). Since MCI and AD subjects are associated with lower MMSE but higher CDR scores, the negative correlation with CDR is consistent with the positive correlation with MMSE for R.PUT and L.HPC. Also, the positive correlation with CDR in R.PCC suggests that higher excitation in this region is associated with cognitive impairment in MCI/AD. If the total regional E-I balance was assessed as E/I ratio, all the four regions maintained a significant correlation with the CDR score, with the addition of L.IN showing a negative correlation with CDR (r = −0.23, p = 0.046, FDR corrected) (Supplementary Fig. S15). It should be noted that E-I balance showed a stronger correlation with CDR than MMSE as evidenced by smaller p values and more regions with a significant correlation with CDR (when E-I balance was assessed as E/I ratio) (compare Fig. 9e–h with Fig. 9a–d, and Supplementary Fig. S15 with Fig. S14). Also, the left HPC exhibited the most robust and significant association with the MMSE/CDR score. Taken together, regional E-I imbalance is a meaningful physiological substrate for cognitive impairment.

Fig. 9: Correlation between regional excitation-inhibition (E-I) balance and cognitive measurement.

Scatter plots between total E-I difference and Mini-Mental State Examination (MMSE) score for a Left insula (L.IN), b Left putamen (L.PUT), c right putamen (R.PUT), and d Left hippocampus (L.HPC). Scatter plots between total E-I difference and Clinical Dementia Rating (CDR) score for e Right posterior cingulate cortex (R.PCC), f Right putamen (R.PUT), g Right pallidum (R.PAL), and h Left hippocampus (L.HPC). The Pearson’s correlation coefficient (r) and the associated corrected p value are displayed for each region. One star (*) indicates corrected significance by FDR (p < 0.05), and double stars (**) denote corrected significance by the Bonferroni method (p < 0.05).

Discussion

Converging evidence suggests that E-I imbalance is a critical regulator of AD pathology^{11,12,13,109,110,111} and may represent a core element that underpins a “central feature” of AD by integrating pathophysiological findings from multi-levels of analysis (cell-circuit-network)¹¹². Identifying pathological E-I balance during the progression of AD thus constitutes an important first step to developing new diagnostic techniques that use E-I imbalance as a biomarker and new treatment paradigms that aim to restore physiological E-I balance. Our study provides both a novel framework to estimate pathological E-I balance and important insights into the systematic features and circuit mechanisms of E-I alterations during the progression of AD.

Due to the inability of conventional fMRI to resolve excitatory versus inhibitory neural activities^46,47,48, a fMRI-based computational framework that could accurately estimate E-I imbalance during AD progression is urgently needed. As the two major generative modeling frameworks for fMRI, Dynamic Causal Modeling (DCM)^53,113,114 and Biophysical Network Model (BNM)^{87,115,116,117,118} either apply a bilinear approximation to describe neuronal dynamics with one state per region (DCM) or uses structural connectivity as a proxy for inter-regional connection strength (BNM). Although the extended two-state DCM incorporates two neuronal populations for each region¹¹⁹, the neuronal model is still inherently linear, which may not capture the long-term pattern of brain spatio-temporal dynamics⁹⁸. In addition, two-state DCM enforces the recurrent E → E connections to be negative and the inter-regional connections to be positive, which does not accord with the biological realism. For a comprehensive review of generative modeling frameworks for fMRI, readers are referred to Li and Yap⁵⁶. In this study, we applied a recently developed MNMI framework^61,62 to an ADNI dataset to identify disrupted E-I balance in a large network during AD progression. Results show that MNMI is capable of identifying impaired excitatory and inhibitory connections in MCI and AD, which can be harnessed to infer E-I imbalance at a mesoscale circuit level. The accuracy and reliability of MNMI are supported by the following observations: (1) E-I balance is more significantly impaired in AD than MCI, consistent with the more advanced disease stage of AD; (2) The brain regions that exhibit the most consistent and robust E-I alterations in MCI and AD (e.g., HCP and ACC) concur with their critical roles in AD pathophysiology (see below); and (3) E-I imbalance in multiple brain regions is found to be significantly correlated with cognitive impairments in MCI/AD, indicating that MNMI-derived E-I alterations are behaviorally meaningful and relevant. Thus, MNMI provides a promising new tool to identify E-I imbalance in AD based on rs-fMRI.

One important hallmark of AD pathology is the progressive disruption of synaptic transmission^120,121. Consistently, we demonstrated that both excitatory and inhibitory interactions are substantially altered during the advancement of AD and such alterations exhibit systematic features. First, excitatory and inhibitory connections are progressively disrupted during AD progression. For both intra-regional and inter-regional neural interactions, more connections are impaired in AD than MCI (when compared with NC) and the degree of impairments also becomes more significant in AD. As a result, the E-I balance is progressively impaired, which is confirmed by linear model analysis. Second, AD pathology differentially alters excitatory and inhibitory connections. Compared with recurrent excitatory connections, more recurrent inhibitory connections are impaired and to a greater extent, in agreement with the emerging viewpoint of GABAergic dysfunction in AD^12,105,106. Importantly, alterations of inhibitory connections exhibit a more stable pattern than excitatory connections as consistent impairments are observed across MCI and AD. Lastly, AD progression is associated with a general decoupling of excitatory and inhibitory interactions. Although the strength of excitatory and inhibitory connections could either increase or decrease in MCI/AD, a reduction of connection strength dominates for both intra-regional and inter-regional connections, consistent with the “synaptic dismantling” theory of AD¹²². The heterogenous but decrease-dominated alterations in excitatory and inhibitory coupling strengths also concord with the observed bidirectional changes but widespread decrease in functional connectivity in MCI and AD^34,35,36. Of note, it has been reported in MEG studies that MCI is associated with hyperconnectivity mostly over anterior brain regions and hypoconnectivity mostly over posterior areas¹²³. Consistently, we found that for the marginally significant inter-regional connections in MCI (Fig. 6a), a majority of them were reduced if they connected two posterior areas (e.g., L.SPC-L.IPC), while most of the connections were increased if they involved an anterior region (e.g., R.CA-R.cMFC). As a result, inter-regional E-I balance increased in anterior regions (e.g., R.cMFC) and decreased in posterior areas (e.g., L.PCU and R.ITC) (Fig. 7a).

One important finding of this study is that we observed heterogenous, region-specific alteration of E-I balance. Depending on the specific modulation of excitatory and inhibitory connections, E-I balance can either increase or decrease for different brain regions, though due to the predominant decrease of excitatory interactions, most of the regions exhibit reduced overall E-I balance during AD progression (Fig. 8 and Supplementary Fig. S11). Our findings are consistent with the experimental data that show hyperactive neurons coexist with hypoactive neurons in an AD mouse model¹²⁴ and MCI and AD are associated with both regional hyperactivation and hypoactivation in human^40,125. We further revealed that increase of E-I balance is mostly due to a decrease of inhibitory connection strength, in agreement with experimental findings that neuronal hyperactivity is a result of decreased synaptic inhibition¹²⁴. Of note, studies have revealed that alteration of E-I balance depends on the stage of AD progression, where the HPC shows hyperactivity in early-stage aMCI, but reduced activity in late aMCI and AD^38,39,40. By comparison, our modeling results indicate that alterations in E-I balance remain consistent across MCI and AD for the same region and the (left) HCP exhibits reduced E-I balance throughout. This may be due to the fact that elevated excitation in HPC is a temporal event in the early aMCI stage, similar to the transient increase of FC in the DMN and salience networks at the very mild AD phase¹²⁶. Lastly, intra-regional E-I balance is more robustly impaired than inter-regional E-I balance during AD progression. This is evidenced by more regions having more significant intra-regional E-I disruptions than inter-regional E-I impairments in MCI and AD (compare Fig. 4 with Fig. 7). Such a finding suggests the importance of measuring and modulating intra-regional E-I imbalance for AD diagnosis and treatment, which requires generative modeling and EC analysis because conventional FC analysis cannot detect intra-regional E-I imbalance.

Despite the heterogeneous and distributed changes in E-I interactions, we observed consistent patterns of E-I disruptions in a set of brain regions including the HPC, pallidum, putamen, nucleus accumbens, ITC, ACC, and PCC. These brain regions are consistently impaired across MCI and AD for intra-regional E-I balance, inter-regional E-I balance and/or overall E-I balance. Such a core network highlights the paramount importance of the limbic/subcortical regions and cingulate areas in AD pathophysiology. The involvement of HPC, the core region in the medial temporal lobe, is consistent with the vast majority of literature about the central role of this critical structure in AD^{14,24,38,39,40,127}. The reduction of E-I balance in HPC due to increased inhibition is also consistent with the experimental findings that high GABA content in reactive astrocytes of the dentate gyrus was discovered in brain samples from human AD patients as well as an AD mouse model resulting in increased tonic inhibition and memory deficit¹²⁸. The stable participation of the basal ganglia including the pallidum, putamen and nucleus accumbens in E-I disruption is somewhat unexpected as these subcortical structures are primarily involved in motor control¹²⁹, though now we know they also play an important role in reward and reinforcement, executive functions and behaviors, and emotions¹³⁰. Indeed, recent MRI studies have consistently revealed substantial volume reduction in the basal ganglia of Alzheimer’s patients, including the putamen and caudate nucleus^131,132,133. The striatum, consisting of the putamen, nucleus accumbens and caudate nucleus, is particularly susceptible to AD degeneration since both Aβ plaques and NFT of hyperphosphorylated tau are found in striatal regions¹³⁴, suggesting that the basal ganglia could be an important pathophysiological target in AD.

The ITC plays a critical role in visual perception, object recognition, and semantic memory processing^135,136,137. Functional deficits in these cognitive processes have been well documented in patients with MCI and AD^{138,139,140,141}. It was observed that inferior temporal tau is associated with daily functional impairment in AD¹⁴². Disruption of E-I balance in ITC is consistent with the significant synaptic loss in this region in individuals with aMCI¹⁴³, which may underlie early AD symptomatology. Lastly, the anterior cingulate cortex (ACC) plays a vital role in multiple cognitive processes including executive function, memory and emotion^144,145,146. It is one of the earliest affected areas by Aβ accumulation^147,148 and exhibits disrupted FC in MCI and AD^149,150. It has been demonstrated that Aβ alters E-I balance in ACC through inhibiting presynaptic GABA-release from fast-spiking interneurons onto pyramidal cells¹⁵¹.

In addition to the above core AD network regions, the PCC, one of the central nodes in the DMN, shows increased E-I balance in AD that is significantly correlated with cognitive impairment as measured by the CDR score (Fig. 9e). As the main connectivity hub of the DMN, the PCC is involved in high-order cognitive functions such as emotion, arousal, self-consciousness, memory, and visuospatial processing^152,153,154. It is one of the most salient areas of tau deposition and neuroinflammation¹⁵⁵. Recent studies have indicated that involvement of the PCC is significant for the development of AD¹⁵⁶. Increased excitation in PCC is consistent with task-induced deactivation deficits in DMN, a robust functional impairment in MCI and AD^37,41,157. Overall, the core network is consistent with the cortical/subcortical hubs implicated in AD including the middle/inferior temporal cortex, PCC, cingulate cortex, and basal ganglia^158,159.

The MNMI model has made multiple specific and testable predictions regarding E-I imbalance during AD progression, which could be tested in future investigations. One important prediction is that in addition to the hippocampus, the basal ganglia and ACC may serve as early AD E-I biomarkers and important therapeutic targets. To validate E-I imbalance in these brain regions, one could perform vitro receptor autoradiographical analysis or immunohistochemistry of human brain tissues to compute excitatory-to-inhibitory receptor density or glutamate/GABA content in postmortem AD patients and compare them with normal controls^128,160. Also, pharmacological or modulatory interventions (such as deep brain stimulation) that specifically restore physiological E-I balance in these brain regions may be particularly beneficial for AD treatment. Second, the model predicts that inhibitory synapses are more severely impaired than excitatory synapses in MCI/AD. This model prediction will be supported if therapeutic treatments that specifically target inhibitory synapses provide a better clinical outcome than those targeting excitatory synapses. Third, the model predicts that local intra-regional connections may be more stable and robust biomarkers than long-range inter-regional connections. Consequently, machine learning-based MCI/AD identification that uses intra-regional connection strengths as features should perform better than those using inter-regional connection features. Lastly, as a general validation for the computational framework, we could apply MNMI to the rs-fMRI data collected from AD animal models to predict regional E-I imbalance that can be validated using in-vivo electrophysiological or optical measurements^161,162.

An in-depth comparison of MNMI with DCM and BNM, the two major generative modeling frameworks for fMRI, can be found in our previous publications^56,62. In brief, MNMI attempts to combine the biological realism of BNM with the estimability of DCM to estimate both intra-regional and inter-regional connectivity for individual subjects based on rs-fMRI. It should be noted that recent developments in BNM have enabled the inference of more physiologically based connection parameters in a more efficient manner. Wang et al.⁸⁸ inverted a large-scale dynamic circuit model of human cerebral cortex and revealed a cortical hierarchy in the resting human brain. Specifically, the authors estimated region-specific recurrent excitation strength and external input as well as a global scaling factor and noise amplitude for a dynamic mean filed model (MFM) using the expectation-maximization algorithm. In a subsequent study¹⁶³, researchers from the same group extended the MFM to parameterize region-specific recurrent excitation, external input and noise amplitude as linear combinations of group-level T1w/T2w myelin maps and the first principal gradient of FC. Using an optimization procedure termed Covariance Matrix Adaptation Evolution Strategy (CMA-ES), five thousand candidate parameter sets were generated from a training dataset where the top ten candidate parameter sets were selected based on the model fit in a validation dataset and evaluated in a test dataset. It was shown that parameterizing local circuit properties with both anatomical and functional gradients generated more realistic static and dynamic resting-state FC. The main differences between MNMI and MFM (or parameterized MFM) are that MNMI models intra-regional recurrent inhibition in addition to recurrent excitation, estimates individual inter-regional connection strength (instead of a global scaling factor), applies to individual FC (instead of group-averaged FC) and uses less sophisticated optimization procedure. More recently, a more sophisticated large-scale BNM was developed by Schirner et al.¹⁶⁴ that incorporated both local recurrent inhibition and long-range feedforward inhibition (in addition to local recurrent excitation and long-range feedforward excitation). Using a standard gradient descent schema, both long-range feedforward excitation and feedforward inhibition strengths were estimated at individual subject level to fit FC, but local recurrent excitation and inhibition weights were not explicitly estimated, though the recurrent inhibition strength was modulated by feedback inhibition control to achieve stable firing rates in the network. Thus, MNMI differs from the model of Schirner et al.¹⁶⁴ in term of the neural mass model (Wilson-Cowan vs. dynamical mean field model), local parameter estimation/modulation (estimation of recurrent excitation/inhibition vs. feedback inhibition control), inter-regional connectivity (combined excitatory/inhibitory connection vs. separate feedforward excitation and inhibition), as well as the optimization scheme (genetic algorithm vs. gradient descent). Lastly, efforts have been made to infer not only region- and subject-specific parameters, but also the neural mass model representing the regional dynamics based on structural connectivity and parcellated rs-fMRI. Sip et al.¹⁶⁵ introduced a data-driven approach to estimate both the unknown generative dynamical system and the parameters varying across regions and subjects. Since this approach does not rely on the specific form of the regional dynamics, the proposed framework could potentially lead to a new generation of more expressive, data-driven network models of large-scale brain dynamics. Thus, MNMI is conceptually different from the framework of Sip et al.¹⁶⁵ as MNMI assumes a fixed neural mass model.

One notable limitation of the current study is that we used DTI data from HCP subjects (as DTI data is not available for every ADNI-GO/2 subject) to calculate SC, following the practice of a previous MNMI study⁶². Nevertheless, the impact of this limitation should be minimal since MNMI uses the average SC (from 100 HCP subjects) as a common base to constrain EC estimation (i.e., the EC is scaled by the SC which is the same for all subjects; Eq. (1)). This average SC could mitigate the individual differences between HCP and ADNI subjects. Also, the optimization of each individual EC parameter (W_kj in Eq. (1)) can compensate for the potential SC difference between HCP and ADNI subjects. In addition, to remove false positive SC links and avoid over-parameterization, we estimated only 10% of the strongest inter-regional connections based on SC. We did not estimate more than 10% since it will substantially increase the number of free parameters in this large network which would reduce the estimation accuracy due to potential overfitting. Future improvements of MNMI may allow for the estimation of more EC parameters in a large-scale network. Moreover, for computational efficiency, MNMI assumes a fixed canonical HRF function for all individuals and regions as other fMRI-based EC models such as regression DCM⁸⁰ and MINDy⁹⁸. However, existing studies have suggested variability in HRF across individuals and regions^166,167, which could substantially confound within-subject connectivity estimates and between-subjects connectivity group differences¹⁶⁸. It was reported that significant HRF variability in the DMN resulted in an error of about 15% in FC estimates¹⁶⁹, and accurate EC estimates from fMRI were possible if the spurious interactions due to HRF variability were minimized using explicit or implicit deconvolution of the hemodynamic effects in fMRI time series¹⁷⁰. Though a recent dynamic fMRI model with fixed HRF reported robust EC estimation in the presence of spatially heterogenous hemodynamic response⁹⁸, we will consider the temporal and dispersion derivatives of the HRF⁶⁵ in future improvement of MNMI. Lastly, our definition of NC, MCI and AD diagnosis labels followed the conventional ADNI practice which depended on cognitive assessments and subjective memory concerns. It should be noted that more advanced AD classification systems have been proposed that make use of biological biomarkers (e.g., PET-Aβ/tau)¹⁷¹. We will fully integrate these biological biomarkers into our future investigation of the complex interplay among Aβ/tau, E-I imbalance and cognitive impairments.

In conclusion, using a multiscale neural model inversion framework, we identify disrupted regional E-I balance as well as impaired excitatory and inhibitory neural interactions during AD progression. We observe that E-I balance is progressively disrupted from NC to MCI and to AD and alteration of E-I balance varies from region to region. Also, we find that inhibitory connections are more significantly impaired than excitatory connections and the strength of most connections reduces in MCI and AD, leading to gradual decoupling of neural populations. Moreover, we reveal that a core AD network comprised mainly of limbic and cingulate regions exhibits consistent and stable E-I alterations across MCI and AD, which may represent early AD biomarkers and important therapeutic targets to restore physiological E-I balance. Furthermore, we find that alterations in regional E-I balance are behaviorally relevant by showing a significant correlation with the cognitive measurement.