Introduction

Cell cultures are widely used in biomedical research and play an important role in different research fields, such as biochemistry, cell and molecular biology, pharmacology, just to name a few. Analysis of cell cultures often uses qualitative models to interpret cell behaviour and/or intracellular molecular pathways. Dynamic microscopy and quantitative data analysis have been used to obtain parameters descriptive of specific aspects of cell morphology and functionality and to understand how the behaviour of a cell population changes over time or reacts to perturbations1,2,3,4,5. Quantitative models and simulations have often provided the opportunity to test hypotheses, make predictions trying to fill gaps in knowledge, set up experimental procedures or evaluate conditions that would be difficult to obtain with in vitro cell cultures6. In silico simulations, by integrating information from various sources, help bridge the gap between concepts, models and experimental data and may provide a better view of cell behaviour7. In recent years, they have been used to analyse problems in population genetics8, to study neuronal activity9,10,11, to investigate cell dynamics in the colonic crypt12,13 or to model liver regeneration14,15, among others. Understanding the effects of biological perturbations can suggest ways to intervene and reestablish proper cell function in diseases such as cancer or in autoimmune disorders16,17,18,19,20,21.

Tools and procedures aimed to simulate cell behaviour range from cell mass simulation, where a generic cell represents the behaviour of a whole population22,23,24, to tools where cells are represented by one or more lattice elements, among which a relevant example is CompuCell3D25,26 which uses Glazier-Graner-Hogeweg (GGH) models based on Cellular Potts Method (CPM) to simulate cell behaviour and dynamics at single-cell resolution in the context of cell organisation into tissues. CompuCell3D has been used to variously describe cell growth, division, differentiation, death, motion and contact with neighbouring cells27,28,29. Its combination with a C++ library for two-dimensional CPM led to the development of a comprehensive simulation environment, the Tissue Simulation Toolkit30,31, which has been widely used for the implementation of in silico models for studying cell migration and morphology in different tissue contexts32,33,34,35. More recently, simulation systems have been shifting towards models based on cell agents where mass, volume and morphology behave according to rules, thus allowing additional flexibility as each cell can depend on its neighbours and the surrounding environment. Among these, CellSys is a modular software tool for off-lattice simulation of cell growth and organisation in multi-cellular systems where each cell is modelled by an isotropic, elastic and adhesive sphere capable of migration, growth and division36. PhysiCell is another open source agent-based simulator able to handle many interacting cells in dynamic tissue microenvironments. It was originally developed for studying cancer cells and includes a standard library of customisable sub-models for cell volume changes, cycle progression, apoptosis and necrosis, cell-cell interaction and motility37,38. Some simulation tools rely on MaBoSS to enable probabilistic simulations of cellular networks, where molecules are boolean variables24,39. UPMaBoSS40 produces dynamic populations of interacting cells, associating cell fate decision, division and death, while PhysiBoSS simulates spherical cells that can grow/shrink, divide, move, die while interacting with their environment or other cells41,42.

Some simulations only model specific aspects of cell behaviour, such as cell fate decisions related to proliferation, death or differentiation. Fouliard et al.43 for example, represent the evolution of cultured stem cells by modelling a heterogeneous cell population, in which cell cycle alternates between a quiescence phase and a proliferation phase: local growth medium composition influences the transition probability between cycle phases and cell differentiation43. Similarly, Altinok et al.44 used a simple cell cycle model, where cells switch between phases, divide into daughter cells or exit cycle because of death, to study how cell cycle dynamics is affected by factors as phase duration, population size and initial conditions44. A purely mechanical approach was used by Taylor et al.45 to integrate cell motion and cell-cell interaction in 2-dimensional cultures. Simulated cells move by combining random and persistent components while interactions are introduced as steric repulsion and/or as cell-cell attraction by transient links between cells45. Movement paths may also be produced within CelltrackR by combining a range of movement features, although no support is included for interactions between cells or reaction to other stimuli46.

In this work, a novel simulation system and tool, SimulCell, is proposed, based on cell agents which integrate movement, growth and other features to produce synthetic cell populations which can closely reproduce the behaviour of experimental ones. Here, simulated cell agents control growth, survival and replication as well as cell cycle transitions, considering volume changes and external stimuli, such as local cell confluence and the presence of growth factors or other drugs in the medium. Movement simulation builds on a previously developed motion model, representing the movement of experimental cell populations in terms of random, persistence and bias components47, and adds the ability to modify movement according to cell-cell repulsion, attractant molecules, cell health and metabolism, attachment state and cell cycle. The system is accessible through a web application which allows to run simulations and evaluate results in numerical and graphic format.

Results

Growth, proliferation and survival of single cell agents in simulated populations

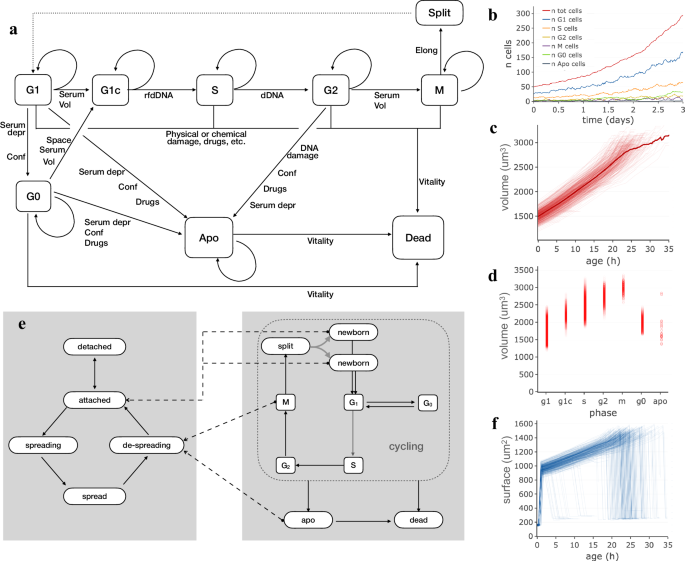
Cell proliferation is possibly the most visible feature of a growing cell population and, during every experiment, cells grow, die or progress in the cell cycle until they eventually reach mitosis, split and give rise to daughter cells. In an attempt to produce synthetic cell populations composed of independent cell agents interacting with each other, a simple but flexible procedure was setup, in which cell cycle transitions and mitosis depend on a combination of factors which take into account volumetric growth, extracellular signalling and DNA replication. The developed procedure uses a Markov chain approach to model cell cycle progression as a succession of states, broadly related to cycle phases, where cells move from one state to the next according to probabilities which depend on several internal or external factors (Fig. 1a). In the model, during G1 phase cells may pass a checkpoint and move to a G1c state where cells are committed to S phase in dependence of current volume and extracellular signalling provided by serum or other factors. Similarly, G2-M phase transition depends on a combination of current cell volume and serum type and concentration. Entering S phase depends on genomic DNA being ready for duplication (rfdDNA), while complete DNA duplication is needed to move to G2 phase. During M phase, nucleus breakdown and cell elongation result into cell duplication. In addition to the “main loop” phases, G1 cells can temporarily exit the cycle by entering G0 and optionally reenter it by moving into G1c, influenced by cell volume, local cell crowding and/or serum type and concentration. When cells are highly confluent or low serum concentration persists, they have a higher probability to undergo apoptosis which then leads to decrease in vitality and death. Cell death may also be the result of cell damage by physical events, like a scratch, or drug addition to the medium. Damaged cells can recover from damage or undergo death according to the damage level. Volumetric cell growth is simulated by an exponential model in which, during each time interval (Δt), cell volume increases according to

$${V}_{t}={V}_{c}\cdot{e}^{\alpha \Delta t}$$
(1)

where, Vc is the current volume and α is the growth rate, which in turn depends on cell type and cycle phase and varies over time and among cells, which may grow faster or slower than the population average. The described procedure works effectively with time intervals ranging between a few minutes and a few hours, according to the need. An example population, simulated with this model and followed for 3 days at 20 min time interval, is shown in Fig. 1b–d. The number of cells (Fig. 1b) exponentially increases over time, with an average replication time of about 24 h and a small portion of cells undergoing apoptosis and death. The accuracy of the replication time obtained by simulating cell cycle in this way was tested by comparing requested versus calculated replication time (average cell age at mitosis) in a panel of simulated populations (Supplementary Table 1): for all of them, the two values turned out to be always very close, even with a broad range of replication times (20–32 h); the apparent duplication time of the same populations is also coherent with the expectations as it is necessarily larger due to the fraction of cells which die or spend time in G0 before undergoing apoptosis.

Fig. 1: Simulation of cell cycle progression, survival and proliferation.
figure 1

Markov models used in simulating cell attachment and proliferation and cell population produced through them. a Schema of states and transitions used to simulate phase changes and cell replication. b Growth of a simulated population with average duplication time of 24 h in which cells are duplicated according to the Markov chain based cell cycle model; the different lines report the number of cells in the different cycle phases over time. c Cell volume plotted as a function of cell age. Each line corresponds to one of the simulated cells in the population. The thicker curve represents the average volume. d Cell volume values in different cycle phases; circles correspond to individual cells at a given time. e The succession of states used to model attachment and spreading to the plate substratum. Dashed arrows indicate phase changes in the cell cycle which produce forced changes in attachment state. f Cell surface plotted, separately for each cell, as a function of cell age.

Full size image

Cell cycle phase composition, as should be expected, reflects phase durations and is maintained over time: most cells (50–60%) are in G1, 20–30% of cells are in S phase, while smaller fractions of cells are in the other phases (Fig. 1b). Cell volume, plotted as a function of age separately for each cell (Fig. 1c), shows an overall increase pattern although, within the same population, curves differ for different cells as internal state and external factors play a role in generating variability between cells. Cell volume changes during the cell cycle (Fig. 1d), progressively increasing from G1 to M phase. Cell numbers and volumes, calculated according to this model, are coherent with known doubling times and not far from growth patterns experimentally observed in different cell cycle phases48,49,50,51,52.

Cells growing on a culture dish change shape and attachment status following interactions with the substrate and in relation to phase changes. To represent the association between these processes, a second Markov chain was introduced and connected to the above described cell cycle model (Fig. 1e). Basically, a detached cell is modelled as freely fluctuating into the medium and has a variable probability, depending on substratum and cell type features, of making a first stable contact with the plate thus becoming attached. Similarly, an attached cell has a given probability of starting a spreading process, thus becoming spreading, i.e. a state in which it reshapes by progressively flattening its volume and increasing its surface, until it becomes fully spread. Some phase changes in the cell cycle produce changes in attachment state, represented in Fig. 1e by dashed lines connecting, for example, M phase or apoptosis (apo) state with the de-spreading state. These attachment states can influence cell behaviour by acting on growth rates and motility and may be used as hints when graphically representing cells. In Fig. 1f, cell surface, plotted as a function of age for each cell of the previously described population, is shown to rapidly increase in the first few hours, as a result of cell spreading; after that, surface increases following volume increase and finally decreases, rapidly when cells undergo mitosis or more slowly when de-spreading during apoptosis.

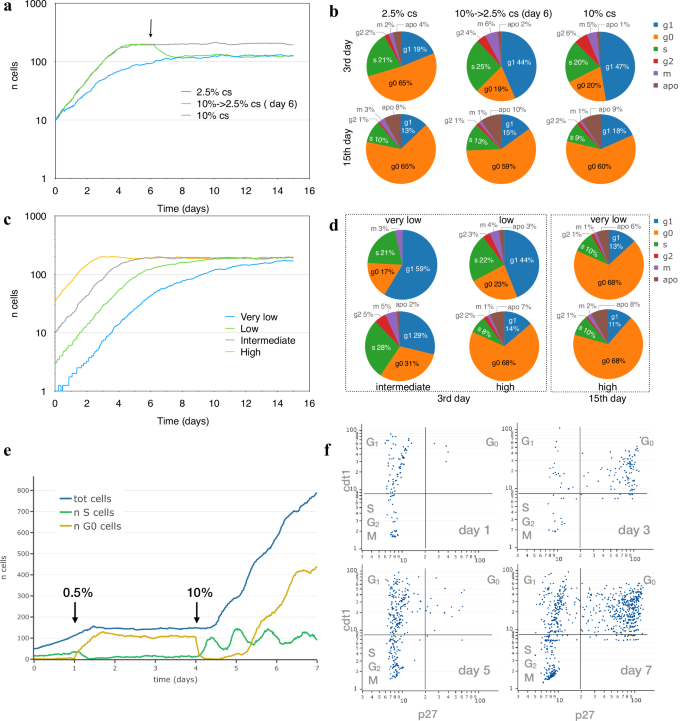
In Fig. 2a, two populations of NIH3T3-like simulated cells were followed for 15 days while growing at serum concentrations of either 10% or 2.5% calf serum together with a third one first growing at 10% and later at 2.5%, after a serum step down on the sixth day. The simulated populations show different growth rates for the two serum concentrations, and stop growing at different cell densities when the cultures arrive at confluence and cell numbers become stable; these patterns are very similar to those observed a long time ago in experimental cultures53; see Supplementary Fig. 1 for a graphic comparison. Consistently, the distribution of cells in the different cell cycle phases changes with time: on the 3rd day (exponential growth), about half cells are in G1 phase at 10% cs, but only 20% of cells are in G0; the G0 fraction is much higher (52%) in cells growing at 2.5% cs (Fig. 2b). This difference becomes much smaller when populations reach confluence and cell numbers stop increasing: under these conditions, cell cycle phase composition is very similar for the three analysed populations (15th day). These fractions are very close to those observed under similar conditions in experimental cell populations54,55,56,57; for cells exponentially growing at 10% serum, for example, Kues et al. report 67–73% cells in G0/G1 and 9–16% in S phase. In Fig. 2c, d simulated NIH3T3-like cells, seeded at four different densities, were “grown” for 15 days at 5% cs. During the earlier days, the observed percentage of G0 cells varies and progressively increases as cell numbers go up, but when, later in the experiment, the stationary phase is reached, most cells (~70%) are in G0 phase and cell numbers become independent of the initial seeding density (Fig. 2c, d).

Fig. 2: Analyses of cell populations simulated by the cell cycle progression model.
figure 2

a Growth curve, expressed as number of cells per 0.58 mm2, obtained for two simulated NIH3T3 populations followed for 15 days while growing at 10% (grey) and 2.5% (blue) calf serum, and for a third population (green) initially kept at 10 calf serum and moved to 2.5% on the sixth day (arrow). b Cell fractions in the different cycle phases on the 3rd day (exponential growth) and on the 15th day (stationary state). c Growth curve, expressed as number of cells per 0.58 mm2, for four simulated NIH3T3 populations seeded at four different densities (1, 4, 10, 50 per 0.58 mm2) and followed for 15 days while growing at 5% calf serum (grey). d Percentage of cells in the different cycle phases on the 3rd and 15th day. e Growth arrest of simulated population induced by serum starvation and rescue by serum re-addition. NIH3T3-like cells were simulated while growing under 10% FBS and, at day 1, starved by moving them to 0.5% FBS; on day 4 serum was restored to 10% and cells were followed for 3 more days. Total number of cells (blue line) and the number of cells in S (green line) and G0 (yellow line) phase are shown in the plot. f Snapshots of the simulated population in (e) at day 1, 3, 5 and 7 are reported by plotting each cell according to cdt1 and p27 concentration.

Full size image

Cells simulated in this way respond to different levels of serum by modifying their growth rate and progression through the cell cycle; their behaviour under more extreme conditions was tested to see whether they react by temporary or permanently arresting cell cycle progression. In Fig. 2e, NIH3T3-like cells were simulated initially as growing under 10% FBS and then as starved by reducing FBS to 0.5%; results show that while cells are kept at 10% FBS, they exponentially grow over time but, when starved by stepping down FBS to 0.5%, cells slow down until they stop increasing in number as a large fraction (79–85%) of cells enter G0 phase, a fraction very close to the 78–80% observed in experimental populations under similar conditions47. Cell rescue from starvation, by again raising FBS to 10%, causes cells to enter S phase and synchronously restart growth and proliferation until they reach confluence and slow down again. In order to monitor cell cycle modifications, the accumulation of two reporter proteins, cdt1 and p27, frequently used as markers for G1 and G0, respectively, was also simulated by relating their synthesis to intracellular state and propensity to phase changes. In Fig. 2f, where each simulated cell is positioned in the plot according to the concentration of the two proteins on the indicated day, for each of the different serum levels the results are consistent with curves in Fig. 2e and very similar to those reported in the literature for the same cell type under similar conditions55,56. Cells “grown” under 10% FBS (day1) mostly have low p27 levels, following a pattern typical of cycling cells, while cells kept in low serum mostly show high levels of both cdt1 and p27, a pattern typical of G0 phase (day3). Cells rescued by raising serum back to 10% gradually reenter cell cycle as confirmed by the reduced p27 levels (day5) which again go up on the 7th day when they start reaching confluence. Supplementary Figure 2 represents the same plots, using colour to highlight the phase of every single cell: in the vast majority of cases, the quantity of p27/cdt1 matches the cell cycle phase.

Cell motion paths generated in silico accurately reproduce experimental cells moving on a culture surface

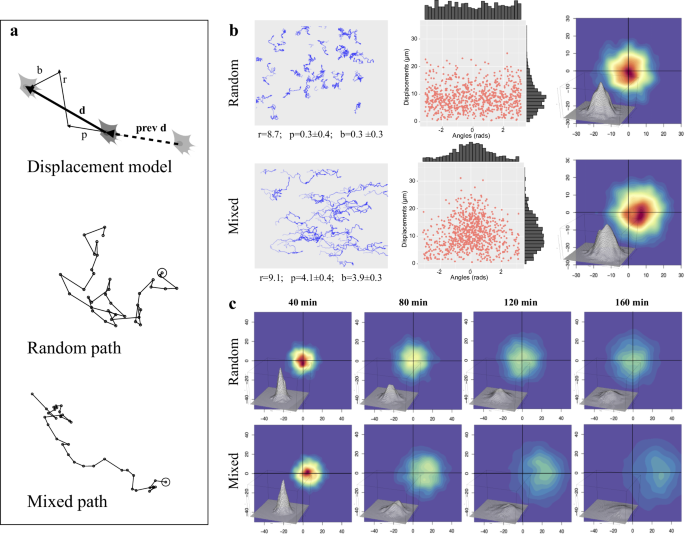
Simulation of cell movement was setup by taking advantage of a previously published motion model, which describes movement of experimental cell populations as the combination of three vectors: a random, a persistence and a directional bias component47. The procedure, reported in Fig. 3a and in the Methods section, uses random, bias and/or persistence vectors to produce migration paths corresponding to completely diffusive, persistent or directionally biased movements, in various combinations. For each time interval, final cell displacement (d) is simulated by combining a random vector (r) with a persistence one (p), characterised by a user defined module and the same direction as the previous cell displacement (prev d), and a user defined external bias vector (b). While the combination of purely random displacement steps produces a relatively tortuous “Random path”, the “Mixed path” generated by more complex movement types is also characterised by directional persistence and/or bias along a given angle. The paths followed by two simulated populations, respectively characterised by “Random” and “Mixed” movement, are reported in the left column of Fig. 3b; in both cases, individual paths are different from each other and reproduce the variability typically observed in experimental cell cultures. Purely random paths, analysed according to the three-component model, show a 8.7 µm random module while persistence and bias ones are very close to zero; displacement lengths (centre column) show a long-tailed distribution peaking around the random module, with randomly distributed directions. Density distribution of displacement endpoints, plotted as starting from the origin (right column), shows the highest frequencies (indicated by warmer colours) around the origin and uniformly enlarges in all directions. Mixed movement, simulated by adding a persistence and a bias vector, produced more linear paths, directed towards the bias angle (0°), with estimated persistence and bias modules of about 4 µm. Accordingly, displacement directions are clustered around the bias angle while modules are higher than in random paths although still showing a long-tailed distribution. Cell displacements are strongly shifted in the direction of the bias vector but remain symmetrically distributed around the x axis. When simulated cell displacements are followed over time (Fig. 3c), their distribution progressively enlarge in all directions with time, maintaining the highest frequencies around the origin for random movements, and shifting it towards the bias direction for mixed population.

Fig. 3: Simulation of cell migration and analysis of simulated cell paths.
figure 3

a Simulation of single cell displacement and full paths. The top schema shows the construction of a cell displacement (d), produced by combining a random vector (r) with a persistence one (p), characterised by a user defined module and the same direction as the previous cell displacement (prev d), and an external bias vector (b) along user defined direction. The lower two schemas report examples of a purely “Random” path and a “Mixed” one, in which directional persistence and bias have been added. b Paths and displacements produced by simulating two cell populations characterised by “Random” (top row) or “Mixed” (bottom row) movement. For each simulated population, the paths followed by each cell are reported in the left column, with, below each graph, the values of random, persistence and bias modules obtained by analysing them by using the three-component model47; an opacity gradient is used to mark the passing of time while drawing cell paths. In the middle column, displacement modules are reported as a function of direction, with their distributions reported as histograms along the two axes. The right column reports, for each cell population, cell displacements as two-dimensional kernel density distribution of shifts from previous positions using a colour code (warm to cold colours correspond to higher to lower density regions); a tridimensional representation of the same data is also included. c For each cells population, the same two-dimensional kernel density distribution is reported using shifts corresponding to four different time intervals, 40, 80, 120, 160 min.

Full size image

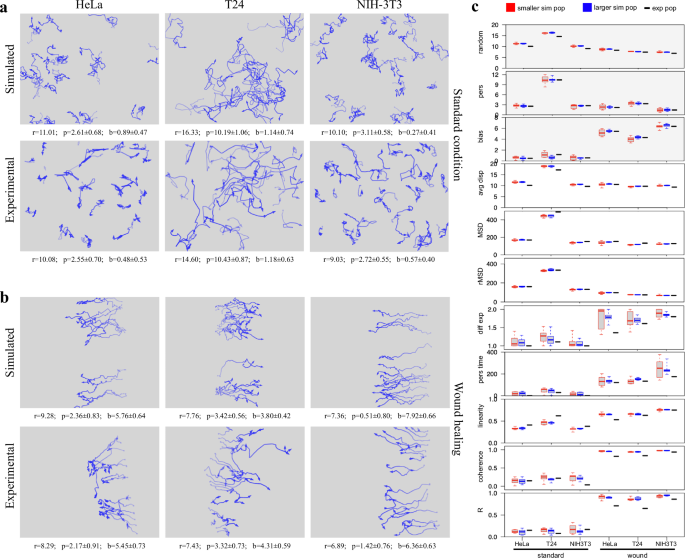
In order to test the ability of the described procedure to reproduce the behavior of experimental cell populations observed in time-lapse experiments, the three-component model was used to calculate, from a panel of experimental cell cultures, random, persistence, and directional components to be used to generate movement in simulated populations. The panel includes a number of human tumour-derived cell lines (HeLa, T24, MDA-MB-231, PC3, A2058, A375, Calu and wm115) as well as two lines from murine embryonal fibroblasts, NIH-3T3 and NIH-Ras, the latter over-expressing a constitutively active variant of Ras, also known to be present in T24 cells. All lines were cultured and analysed while exponentially growing under standard conditions; for HeLa, T24 and NIH-3T3 lines, motion parameters were also determined while cells were moving in wound healing assay for 12 h after scratching the cell layer (Supplementary Table 2). Random, persistence and bias modules from experimental HeLa, T24 and NIH-3T3 populations were used to simulate motion behaviour of a small population of the same size as the experimental one, as well as a standard 50 cell population (Table 1). The results show very similar values for random, bias and persistence components for all populations of the same group and are well separated from those of the other groups (Supplementary Figure 3). Interestingly, simulated populations are very close to experimental ones also for additional movement parameters, not used to generate the simulated populations, such as average displacement module, final MSD and rMSD (random Mean Squared Displacement). In addition, simulations were also able to match the superdiffusive motion parameter α, consistently close to those obtained from the experimental populations and also higher when cells move responding to wound stimulus. In this case, persistence time, linearity and coherence as well as circular statistics R parameter also show correspondingly higher values. Paths generated by simulating standard populations also appear very similar to those originally observed in the experimental cultures (Fig. 4a). In addition, simulations reproduce many features of the experimental populations and maintain the differences between cell lines, with tortuous paths for HeLa, more linear and persistent ones for T24 and intermediate features for NIH-3T3 cells. Cells simulated while moving towards the wound produced directionally biased movements, similar both in appearance and as estimated parameters (Fig. 4b). Finally, in Fig. 4c, the variability of different simulated populations, generated from the same configuration parameters, was tested by producing, for each experimental population, ten simulated ones with the same number of starting cells and ten more with 50 starting cells each. For each of eleven parameters measured in both experimental and simulated populations, the distributions of values obtained from each group of simulated populations are displayed as box and whiskers plot alongside the corresponding values obtained from the experimental populations. The obtained distributions were rather tight for all tested parameters, even in populations characterised by lower cell numbers, and values from experimental cultures mostly fall within, or are very close to them. More variable values were only observed for diffusion coefficient and persistence time: also in this case the larger distributions observed in small populations become tighter when larger numbers of starting cells are used. It is worth noting that only three of the eleven parameters were used to configure the simulated populations (grey-background plots). Although not related to movement, replication time was also determined for the same populations with results reported in Supplementary Fig. 4: also in this case, the obtained distributions were rather tight and values from experimental cultures fall well within them.

Fig. 4: Simulations based on the movement model effectively reproduce cell paths observed in experimental cultures.
figure 4

For HeLa, T24 and NIH-3T3 populations, x–y coordinates registered during experimental time-lapse acquisitions and simulation experiments were used to draw paths followed by each cell, both under standard culture conditions (a) and during wound healing experiments (b); an opacity gradient is used to mark the passing of time while drawing cell paths. The calculated random (r), persistence (p) and bias (b) modules were reported under each graph. c For both standard and wound conditions, 10 populations were simulated starting either with the same number of cells as in the corresponding experimental one (red boxes) or with a standard number of 50 cells (blue boxes): for each movement parameter, a plot reports the distribution of its values among the simulated populations compared with the value obtained from the corresponding experimental one (black dashes). A grey background in the plot indicates parameters used to configure the features of the simulated cell populations.

Full size image
Table 1 Similarity between simulated and experimental cell populations goes beyond the parameters used to configure the simulations
Full size table

From reproducing cell subpopulations to predicting conditional cell behaviour on a culture plate

Unlike the previous simulations, where populations or subpopulations are homogenous and cell-to-cell differences mostly derive from apparently random individual variability, the behaviour of different cells growing on a culture dish is more likely not homogenous and changes according to intracellular state and/or local external conditions, thus giving rise to a potentially large number of different subpopulations within the same culture. To reproduce this cell-by-cell variability, the above-described motion model was extended to include the ability to modify speed, directionality, and other features according to the presence of an attractant, repulsion from neighboring cells, attachment state, and cell cycle phase. The method for generating movement was therefore modified to take into account the many factors able to modify movement, while calculating the displacement of each individual cell (Fig. 5a). Basically, random (rand), persistence (pers) and bias (bias) modules, obtained from an experimental population, were respectively assumed to be the result of the following expressions:

$${rand}=r\cdot{d}_{{tot}}$$
(2)
$${pers}=p\cdot{d}_{{tot}}$$
(3)
$${bias}=b\cdot{d}_{{tot}}$$
(4)

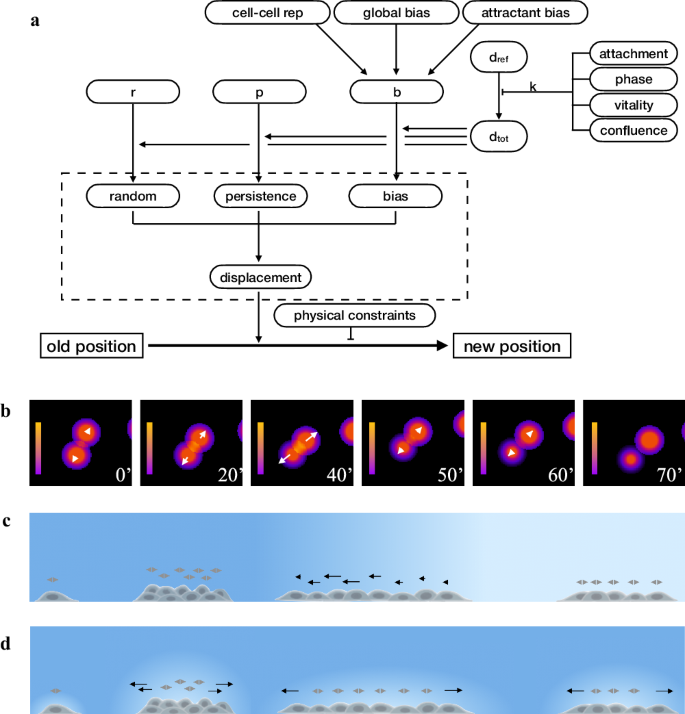
where r, p, b, whose sum is equal to one, correspond to the fraction respectively used by random, persistence and bias components of dtot, i.e. the “maximum potential displacement” of a given cell type, travelling under a given condition. The average dtot value observed in the experimental population is in turn assumed to derive from a reference value, dref, through a coefficient k, representing the cumulative effect of cell confluence, limited nutrients or growth factor availability, or other inhibitors of cell movement. When generating movement with the extended motion model, for each simulated cell, dtot is re-calculated by multiplying dref for a k value depending on various factors including cell cycle phase, attachment state, level of vitality and local confluence. Similarly, b is modified by taking into account the effect of factors able to influence the final bias vector, such as global bias, repulsion from neighbouring cells or bias due to the presence of an attractant gradient. Re-calculated r, p, b and dtot are now used to obtain the new random, persistence and bias modules, which, combined according to the three component model, give the final displacement. Finally, cell position is modified using the obtained displacement and optionally taking into account the presence on the culture surface of physical borders or other constraints which slow down or completely block cell movement.

Fig. 5: Schematic representation of the movement model.
figure 5

a The extended motion model used in the simulator builds on the original three component model, contained in the dashed box, to simulate the influence of internal and external factors on cell movement. dtot is the maximum displacement for a defined time interval and is derived from dref, assumed to be the maximum potential displacement obtained for the same cell type under an “optimal” set of conditions; r, p and b indicate how much of dtot is necessary to produce the corresponding random, persistent and bias components. By modifying these parameters, a wide range of factors can influence cell displacement and its final position; examples are cell cycle phase, attachment state, level of vitality and of local confluence, the presence of physical constraints and “local” bias, like repulsion from neighbouring cell or attraction due to the presence of an attractant gradient in the plate. b Cell-cell repulsion gradient represented as colour shades corresponding to cell influence on the surrounding environment. For each cell, the repulsion vector is reported as a white arrow along the straight line between two neighbouring cells and whose module depends on gradient. The time interval between the first three images was 20’ intervals, while the others were taken at 10’ interval. c Effect of a relatively sharp attractant gradient on cell movement. For each cell, the bias vector is reported as an arrow whose module depends on the difference in attractant level over a distance corresponding to the size of the cell body. d Effect of dynamic self-generated local gradients on cell movement. The bias vector is reported as an arrow with a module which, as in c, depends on attractants level, which, in this case, is locally modified by the presence of cells able to degrade the attractant molecule in its immediately vicinity: higher cell concentration produces greater gradient than sparse cells. In both panels, a more intense blue indicates higher attractant level.

Full size image

As with the extended motion model it is relatively easy to compose the effects of different factors simultaneously affecting the movement of every single cell, support was added for short range cell–cell repulsion and locally variable gradients of attractant molecules.

Cell-cell repulsion was determined by identifying, for a given cell, the neighbouring cells within a given distance and by calculating, for each of them, a repulsion vector along the straight line between the two cells with a module depending on distance, cell speed and sensibility to repulsion by other cells (Fig. 5b).

Similarly, to simulate the effect of gradients of attractant molecules, another bias vector is determined from the difference in attractant level between front and back of a given cell. This vector works very nicely for short and/or sharp gradients able to produce concentration differences at distances comparable to the size of a cell body (Fig. 5c). Support for shallow gradients was introduced by considering the effect of dynamic self-generated local gradients as those previously described in literature58,59, which assume that a shallow or even completely flat gradient is locally reinforced by the ability of cells to degrade the attractant molecule in their immediately vicinity (Fig. 5d). Such local gradients have been shown by different authors to be more robust, to work across greater distances and to be better suited to represent the effect of the local environment than purely passive cell responses60,61,62,63,64,65,66.

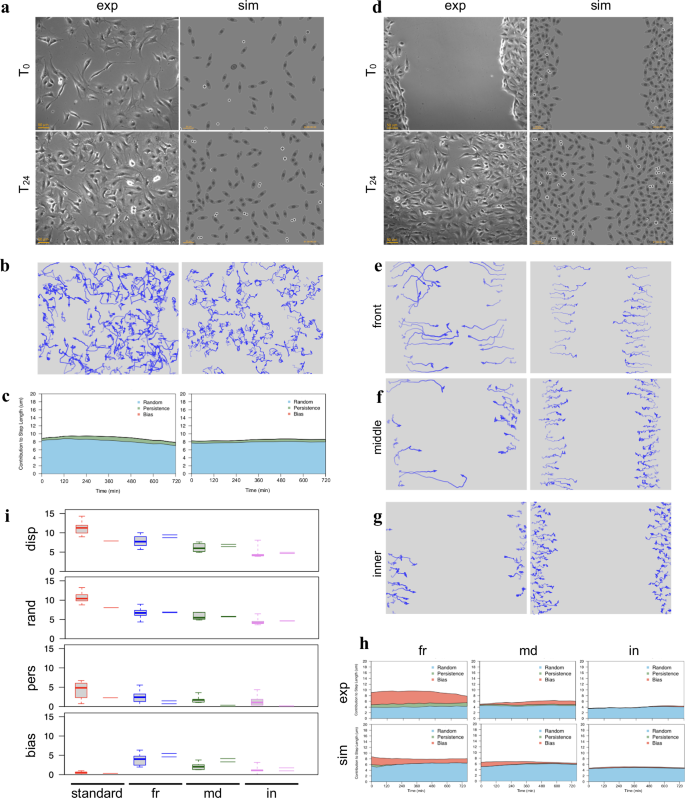
The extended motion model can effectively generate, as shown in Fig. 6, the variety of different cell subpopulations typical of wound healing experiments, starting from the parameters determined from an experimental NIH-3T3 culture exponentially growing under standard conditions and moving in absence of any directional bias. As shown in Fig. 6a, the original experimental culture (left panels) was analysed to obtain the “base parameters” r, p, b and dref, which were then used to produce a similarly numbered population of simulated cells (right panels) which, “growing” under the same conditions, reach a comparable number of cells in 24 h and, at the same time, move along similar paths (Fig. 6b). The contributions to displacement of the three components, evaluated over time (see Methods), show a pattern similar to the experimental population, with an average displacement mostly made of a random component, with a smaller persistence and no bias (Fig. 6c). In Fig. 6d, the same “base parameters” were used to simulate a wound healing experiment where cells are grown at high density, to make them initially produce an highly confluent “layer” which is then subjected to a scratch. While “growing” at high density, dtot values are reduced by lower nutrient availability or specific cellular states: for example, cells move slower when in G0 or during apoptosis. After the scratch, cells by themselves tend to move towards the free space by diffusion reinforced by cell-cell repulsion. The “attraction” by the wound was simulated by adding two further components, both simulated using dynamic self-generated local gradients, which reflect the effect of free space and the attraction by cell debris produced in the wound area soon after the scratch. The first uses a flat long-lived attractant uniformly present in the plate to represent the effect of different serum factors; the second, with a relatively short half-life, simulates the effects of molecules released by scratch damaged cells67,68,69,70,71,72,73. The two gradients produce two bias vectors which, combined with others, such as that introduced by cell to cell repulsion, result in a final bias, different for each cell. The resulting behaviour is much more complex than in the starting population and leads to wound closure (Fig. 6d, right panels) with timing and patterns very similar to those of an experimental NIH-3T3 population observed under the same conditions (Fig. 6d, left panels). Simulated cell paths show a progressive decrease in length and linearity as the distance from wound front increases (Fig. 6e–g) and front (fr), middle (md) and inner (in) subpopulations, separately analysed produce results which closely resemble those from experimental cultures. The contributions to displacement of the three components, evaluated over time, also show patterns close to those of experimental populations, with longer displacements for front populations mostly due to higher bias, much lower displacement and bias values for internal cells with intermediate values for middle cells (Fig. 6h). When movement parameters obtained from the analysis of the simulated populations are compared to a larger number of experimental populations in the same conditions, total displacement as well as random, persistence and bias components are within or very close to the range of experimental values (Fig. 6i).

Fig. 6: Simulation of NIH3T3-like cells moving under wound healing experiments.
figure 6

Movement parameters obtained from the experimental cell population, kept under standard conditions, of panels (a-c) were used to produce synthetic populations moving in a wound healing experiment in panels (d–h). a Phase contrast images taken at 24 hour distance of cells exponentially growing under standard culture conditions and in absence of any directional bias (left side images), compared to a simulated cell culture “grown” under the same conditions and rendered at the same times using a phase-contrast inspired symbolic representation (right side images). b Movement paths of experimental and simulated cells during the 24 h period, drawn by using an opacity gradient to mark the passing of time. c Contributions to cell displacement of random (blue), persistence (green) and bias (red) evaluated for experimental and simulated cells by analysing, at each time point, overlapping 12-h windows. d A wound healing simulation, where the cell population uses parameters from the experimental population of panel (a), is compared to a wound healing experiment featuring an independent experimental population. For both simulated and experimental populations the images are organised as in panel (a). e–g Movement paths for experimental and simulated sub-populations corresponding to cells located after the wound at the front (e), middle (f) or back (g), drawn, as in (b), by using an opacity gradient to mark the passing of time. h Average contributions to cell displacement of random (blue), persistence (green) and bias (red) evaluated over time, by separately analysing overlapping 12-h windows for experimental and simulated cells located at the front (fr), middle (md) and back (in). i Distribution of displacement, random, persistence and bias values obtained for experimental cells from 5 populations under standard culture conditions (red boxes), 16 populations at the wound front (blue boxes) and 6 intermediate (green boxes) and internal populations (violet boxes). The corresponding values from the simulated populations are reported as dashes.

Full size image

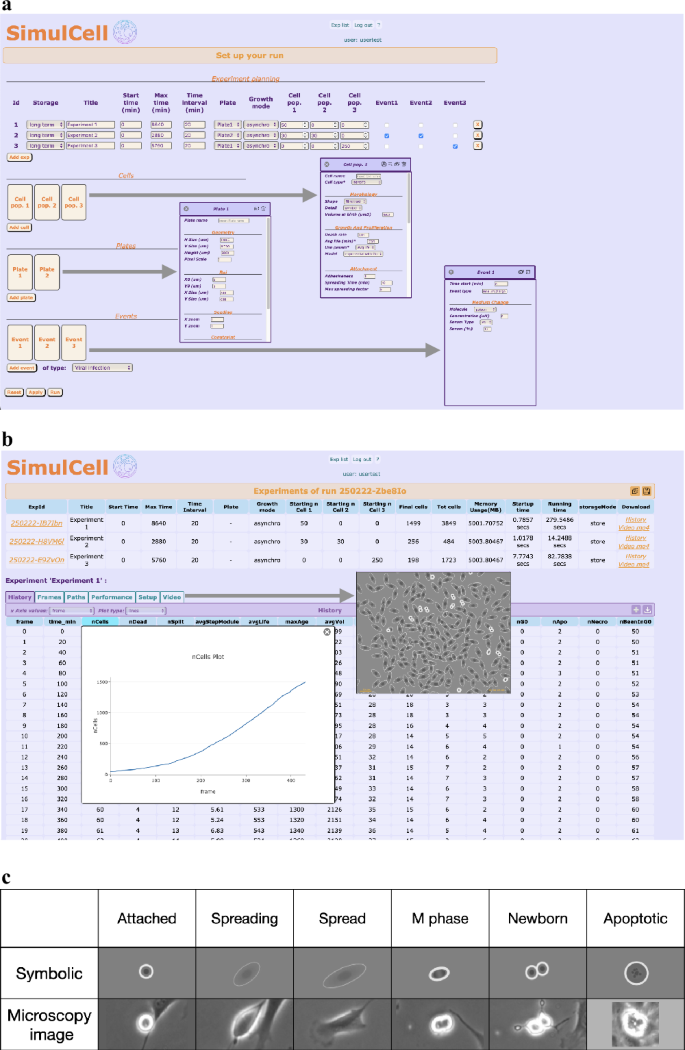
Setting up and executing simulations within SimulCell web application

The described models and procedures can be used together to produce simulated populations within SimulCell, a web application designed to setup and run simulation experiments and to quickly analyse the results. Input data can be manipulated using standard dialog boxes, organised in sections containing experiment, plate, cell and event parameters (Fig. 7a). During the calculation, the application provides support for monitoring the process, by showing images of the simulated cultures and plots reporting number of cells or other data. After the calculation, the result page displays major parameters and statistics organised in different tables: History, containing summary results for each time point, Path and Frame, where data are respectively organised by cell and time interval, in addition to Setup and Performance, containing the major simulation parameters used to setup the experiment and run duration and other performance indicators. Still within SimulCell, many different plots can be generated to visualise data as custom graphs designed to highlight specific data features (Fig. 7b) and images and videos are used to display cell behaviour and morphology during the simulated experiment. Within SimulCell, as also in images shown in Fig. 6, cell visualisation uses a “symbolic” representation, where cells are simple geometric shapes, which change depending on cell type, status and condition. Cell body is represented by a circle or an ellipse whose size conveys information about volume, degree of spreading and cell polarisation. Images use a grey level colour set, reminiscent of phase contrast microscopy, to let the user recognise cell growth, attachment status, nuclear duplication and division in a familiar way; some examples are reported in Fig. 7c.

Fig. 7: SimulCell web application.
figure 7

a The setup page is used to define a multi-experiment run using the available plates, cells and events and gives access to all parameters needed to run a simulation through dialog sections customised for plate, cell and event. b The result page gives access to the simulation results using customised tables and plots and showing videos to display cell behaviour. c Simulated “symbolic” representations of cell morphology compared to phase contrast images of experimental NIH3T3 cells under similar conditions: cells are visualised as oval shapes, whose size and elongation depend on cell features as well as simulated volume and degree of spreading; as for their experimental counterpart, border colour is dimmer in fully spread cells and becomes thicker and clearer when cells de-spread during nuclear duplication and division or apoptosis.

Full size image

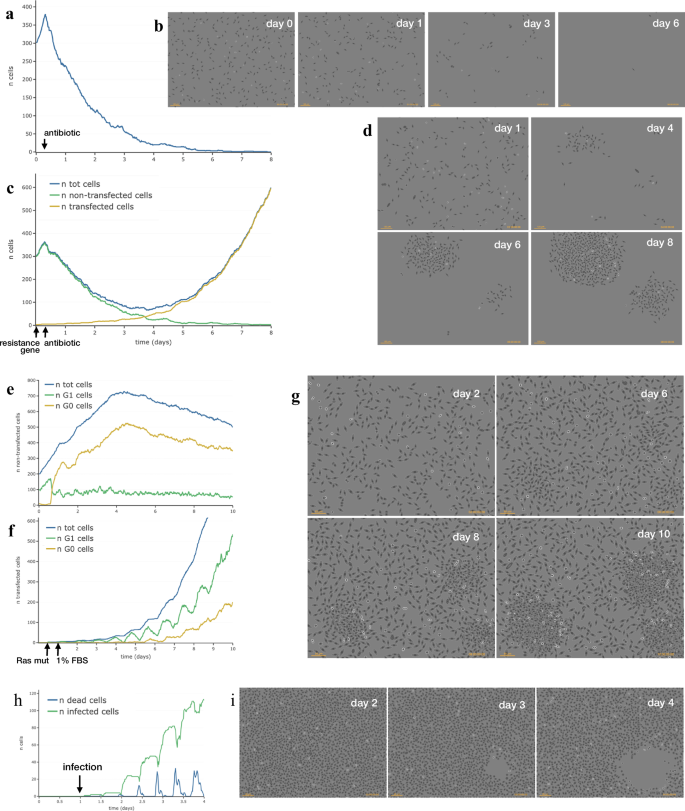
Figure 8 shows some simulations executed within SimulCell, which highlight how cell behaviour is affected by the specific conditions defined while setting up the experiment and each individual cell agent integrates different aspects of cell behaviour and reacts to local environment changes produced by other cells or resulting from external physical or chemical events.

Fig. 8: Experiment examples performed within SimulCell.
figure 8

a Number of simulated NIH3T3-like cells while responding to an antibiotic added to the medium at time 6 h and followed for 8 days. b Phase-contrast like images of the same population on days 0, 1, 3 and 6. c Production of antibiotic-resistant clones by DNA transfection. After transfection with an antibiotic resistance gene at time 0, the number of total simulated NIH3T3-like cells (blue line), non-transfected (green line) and transfected cells (yellow line) is reported over time while cells respond to an antibiotic added to the medium at time 6 h. d Phase contrast like images of the same population on days 1, 4, 6 and 8. e–g Production of foci by overgrowth after transformation by exogenous DNA. The total number of cells (blue line) and the number of cells in S (green line) and G0 (yellow line) phase after transfection with constitutively activated Ras gene at time 12 h and serum step down to 1% FBS ate time 24 h is reported for non transfected (e) and transfected cells (f). g Phase contrast like images of the same population on days 2, 6, 8 and 10. h Number of dead (blue line) and infected (green line) simulated VeroE6 cells after infection with a lytic virus (9 h replication time). i Phase contrast like images of the same population on days 2, 3 and 4.

Full size image

In the example reported in Fig. 8a, b, the vitality of each cell is differently affected by an antibiotic drug added to the medium and simulated cells respond by progressively dying until they completely disappear over time. When the same cells are “transfected” with an antibiotic resistance gene, some acquire the new gene (Fig. 8c, yellow line), become resistant to the antibiotic and grow and proliferate in its presence, producing resistant clones (Fig. 8c, d) (Supplementary Movie1).

In Fig. 8e–g, simulated NIH3T3-like cells were modified by acquiring a constitutively active Ras gene by transfection and later moved to 1% FBS (Supplementary Movie2). Under these conditions, cells keep growing although at a lower rate because of reduced serum stimulation and, after a few days, some cells, having acquired the mutated Ras gene, accelerate growth and produce clonal foci which after a while start overcoming the surrounding cells (Fig. 8g and Supplementary Fig. 5). The plots show that in low serum non-transfected cells slow down their growth and enter G0 phase, unlike the few transformed cells which actively proliferate and in a few days start a fast exponential growth and become the predominant cell population concomitantly with the appearance of foci in the culture.

Finally Fig. 8h, i, shows the effect of infecting simulated cells with a lytic virus (Supplementary Movie3). Here, cell agents were configured with parameters from VeroE6 cells and virus infection was assumed to lead to cell lysis in about 9 h and to release new infective virus particles in the surrounding area. The results show that 24 h after infection (day 2) the layer is still confluent, but that starting from day 3, a lysis plaque becomes visible and enlarges over time following the few replication cycles corresponding to the sequential waves of infection caused by subsequent local releases of new virus particles.

Discussion

Modelling the enormously variable behaviour of a population of eukaryotic cells is an inherently difficult task, given the inevitable differences between single individual cells. In many cases, the simple observation of cell populations of different sizes allows to define a “collective” behaviour, usually relatively easy to analyse and even predict once a number of environmental parameters have been established. But in a real cell population, the “collective” behaviour derives from the combination of many independent individual cells, each of them behaving according to its own microenvironment and following basic rules defined by physics and chemistry: an approach completely based on this principle could, if at all conceivable, completely define all cell features and activities. Although such a detailed approach appears to be well beyond our current abilities, different aspects of cell behaviour, such as cell proliferation and movement, have been the target, in recent years, of a search for parameters and models able to describe them in good detail from the phenomenological point of view2,5,74,75. Such models have been used as a base to generate, by in silico simulation, new populations which, to a given extent, can resemble experimental ones and may be challenged for testing hypotheses6,26,30,37. Observing the behaviour of such simulated cultures may turn out to be particularly useful when the experimental system is complex, components and parameters increase in number and the outcome is consequently more difficult to predict analytically.

The agent-based simulation system proposed in this work goes along these lines, simulating single cells which, interacting with each other and with their environment, individually contribute to generate a simulated cell population which can accurately reproduce movement and many other features observed in experimental cell cultures. Movement simulation builds on a previously developed motion model47, which was here further extended to add the necessary flexibility: within the system, the cells, defined by “base” parameters obtained from the analysis of a given population, react to environmental changes, by modifying the “base” parameters taking into account their own intracellular state and local external conditions. This approach gives rise to a potentially large number of different cells and/or subpopulations within the same culture. Cells simulated in this way, can, all at the same time, feel cell-to-cell repulsion, choose their direction reacting to the presence of attractant molecules and modify movement according to cell metabolism, attachment state and cell cycle phase; while doing that, the same cells control growth, survival and replication, as well as cell cycle transitions, also in relation to local cell confluence and presence of nutrients or drugs in the medium. In this way, cell-to-cell differences derive from random individual variability but are also due to a non-random differential behaviour, which reflects intracellular state and/or local external conditions and can give rise to different subpopulations within the same culture.

Simulation planning and execution takes advantage of a web application, SimulCell (http://simulcell.ceinge.unina.it/), which provides a standard setup, but where most parameters may be modified and a large number of cell functions and features can be easily graduated or simply turned on/off. SimulCell was designed to be an environment where models for movement, growth and proliferation are already available, and can be used to test the behaviour of cultured cells by users who can access parameters for different cell types and easily modify them. It provides a small collection of basic parameters, corresponding to a set of experimental cell types and/or populations, and can be used to modify most parameters defining cell behaviour, culture plate specifications, medium components, geometry of the acquisition area. Events occurring during the simulation are also set up through the interface, including changes in serum type and level, addition or removal of physical borders, mechanical injuries, addition of attractant molecules or drugs; in the same way, even simple acquisitions of exogenous genes or a basic “viral” infection procedure can be used in experiment planning. Being available as a freely accessible web application, SimulCell requires no installation or package dependence and can run, maintaining performance, independently from the available computer hardware or operating systems. These features possibly contribute to make cell simulation more easily accessible by users with no programming experience than other currently available simulation tools. In this sense SimulCell, unlike other frameworks for building models such as CompuCell3D and PhysiCell, does not require users to write their own code or build and manage more or less complex XML models, although a large number of parameters may still be modified and different combinations may be easily tested, stored and replayed; in this sense, the system may turn out to be usable when testing hypotheses or trying to answer questions of the “What if…?” type. SimulCell is also a potentially useful demonstration tool for academic courses, where it should be relatively easy to set up typical experimental situations involving standard cell cultures to test cell response in different conditions and to try experimental setups difficult or impossible to reproduce in a wet-lab practical lesson. The use of SimulCell within an educational context could be particularly indicated as, being a web tool, its performance is relatively independent from the browser or the computer hardware available to the user: of course, when long tables or large movies are produced, better hardware and a faster browser can result in a more pleasant experience.

Although the system is effective at simulating motion and proliferative behaviour, its use is necessarily restricted by the planned aspects of cell behaviour. For example, the 2D nature of the current model does not account for complex 3D interactions between cells and with the extracellular matrix, a feature which would obviously help while working with tissue-like structures. In addition, in its present form the system only keeps track of a few protein molecules: more molecular simulations would certainly help create more control points for internal signalling or external factors. However, the modular architecture makes it relatively easy to extend, thus opening up future perspectives. A welcome addition, for example, would be a better definition of cell morphology, which could be of help in both simulation and result visualisation phases. Similarly, interfacing with an external molecular simulation tool would add support for a larger number of simulated molecules, a useful feature when investigating physiological or pathological situations involving regulatory molecules and signalling pathways76,77,78,79.

Methods

Cell culture

Cells were propagated in Dulbecco’s Modified Eagle’s Medium (DMEM) supplemented with L-Glutamine (2 mM), 10% foetal bovine serum (FBS), penicillin (10 U/ml) and streptomycin (10 ng/ml) and maintained at 37 °C and 5% CO2. Cells were transferred by detaching them in trypsin/EDTA (trypsin 0.05% and 0.53 mM EDTA) and collecting them with a complete culture medium. After centrifugation at 1200 rpm for 5 min, pellets were suspended in fresh medium, properly diluted, and plated again.

The cell lines used for time-lapse acquisitions include murine fibroblasts NIH-3T380 and NIH-Ras produced by transfecting RasV12 into NIH-3T381, and human immortalised cell lines HeLa from cervical cancer82, T24 from bladder carcinoma83 MDA-MB-231 from breast cancer84, A2058, A375 and wm115 cells from melanoma85,86,87 and PC3 and Calu cells from prostatic and lung adenocarcinoma, respectively88,89.

To investigate random movement ability, 25000 cells/well were seeded in 12 well plates and maintained in complete medium at 37°C and 5% CO2. After 16–18 h, the plate was placed in the incubator chamber of the microscope. For wound healing assays, cells were seeded in confluent monolayers by plating 250000 cell/well in 12 well plates in complete medium; 24 h after plating the cell layer was scratched with a sterile pipette tip.

Data acquisition

Phase contrast images (objective 10x) of different samples have been acquired at 10 min interval for 24 h or more by using a Zeiss Cell Observer system, composed by an inverted microscope (Axiovert 200 M), an incubator chamber that maintains the temperature at 37°C and CO2 partial pressure of 5%, and a digital camera (Axiocam H/R or Hamamatsu Orca Flash). A motorised stage was used to permit prolonged automatic acquisitions at different positions. For this work, digital frames were typically acquired as 16 bit images of 650×514 pixels. The pixel scale of the acquired images is 0.767 pixel/µm, obtained by acquiring with the same system an image of a Burker chamber with known measures.

Cell displacement was tracked by using a semi-automated procedure available within MotoCell90. The tracking procedure allows to collect cell positions (in terms of x/y coordinates) at different times (frames) to construct for each cell a path characterised by an origin (start, newborn, found, gone in) and a destiny (split, dead, lost, gone out). The registered data are stored in a text file that can be read by MotoCell to perform the quantitative analysis.

Mathematical and statistical analyses

Mathematical and statistical analyses were carried out within the R environment. The function kde2d (MASS package) has been used to compute the two-dimensional density distribution of cell positions (x and y coordinates), graphically represented by using the image and persp functions (graphics package), for 2D and 3D representations, respectively. In addition, stats package from the basic configuration as well as the external package ggplot2 have been used to produce most graphics. Curve fitting has been done by using nls (non-linear least squared) function.

Determination of movement parameters

The random, persistence and bias components of analysed cell movements were evaluated using the model and procedure described in Toscano et al. (2022)47. Diffusive behaviour was evaluated by collecting mean squared displacements (MSD) corresponding to progressively increased time intervals and by fitting the function \({MSD}=k\cdot{t}^{\alpha }\) to the data, using weights proportional to the number of averaged squared displacements. Persistence analysis was carried out by fitting the model initially proposed by Fürth et al. in 192091and described by Alt et al. in 199092, where the relation between MSD and time (t) is given by the following equation:

$${MSD}=2{S}^{2} \cdot{P}\cdot\left[t-{P}\cdot\left(1-{e}^{\frac{-t}{P}}\right)\right]$$
(5)

where S is the root mean squared speed and P is the directional persistence time, i.e. the time in which cell movement tends to persist in the same direction.

Linearity was calculated as the ratio of net displacement (i.e. the distance between the starting and end point) to path length. For a given population, linearity is the average of linearity values independently calculated for each cell. The coherence parameter of a population was measured as the ratio between the length of the resulting vector, obtained by composing the displacement vectors for each cell path and the sum of the single net displacement vector lengths. Circular statistics analysis was used to evaluate the distribution of cell displacement directions. The displacement vectors were combined without taking into account vector modules to obtain a resulting vector having its origin in the centre of a circle with unit radius. Its direction is defined as the average angle, whereas its length is named linear dispersion coefficient (R), which is descriptive of the dispersion of the angles around the average. R value ranges between 0 and 1: values close to 0 indicate a uniform angle distribution with no directional bias; larger values are obtained when displacement angles are clustered around a given direction, reaching 1 in the special case of all identical angles.

The average scalar contribution of random, persistence and bias components to displacement length were calculated by averaging, for a given time window, the projections of each of the corresponding vectors onto the displacement direction.

Calculation of cell cycle state transitions

Cell cycle state progression was simulated by using Markov chains, where each cell moves from one state to the next by using probabilities calculated by combining the effects of number of factors able to influence the transition. At each time point, the probability (prob) of moving to a different status in a given time (probTime) is adapted to the simulation time interval (timeInt) according to the following formula:

$${pro}{b}_{{timeInt}}=1-\left({(1-{prob})}^{\frac{{timeInt}}{{probTime}}}\right)$$
(6)

The effect (eff) of each enhancing or limiting factor affecting the transition is reported within the 0–1 interval by using the logistic function:

$${eff}=\frac{1}{1+{e}^{k({X}_{c}-{X}_{{ref}})}}$$
(7)

where Xc in the current value of the parameter which influences the transition, Xref is the mean of logistic function and is the value at which there is a 50% probability to go the next state and k is the logistic growth rate or steepness of the curve.

Generation of cell displacement from movement parameters

Cell movement is simulated by using three parameters corresponding to the length of random, persistence and bias components: during each time interval, a ten step random walk is calculated to generate a vector of variable direction and module which is optionally combined with a persistence and a bias vector. The three components may be provided by the user, but more often are the result of the evaluation of experimental paths according to the method and procedure described in Toscano et al. (2022)47. In alternative, the two-level approach described in the Results section was used to obtain movement parameters starting from the “base parameters” (r, p, b and dtot). This last method allows to adapt experimentally determined parameters to culture conditions other than those used to acquire them and, at the same time, is used to modify them for each individual cell, taking into account local medium changes or other factors affecting cell movement. In addition, the global bias represented by b value, is combined with additional bias vectors due to repulsion from neighbouring cells and/or the presence of an attractant gradient. Modified b value, together with r and p values, are then rescaled to bring their sum back to 1 and used to obtain the new random, persistence and bias components to be used to calculate the final displacement. Support for short range cell-cell repulsion is introduced as an additional bias: for each cell, the neighbouring cells within a given radius are identified and, for each of them, a repulsion vector is calculated along the straight line between the two cells and with a module depending on distance, cell speed and sensibility to repulsion by other cells. Another additional bias is used to support local attractant gradients determined as difference in attractant level between cell front and back. These levels are optionally adjusted to produce a dynamic self-generated local gradient to simulate cells able to degrade attractants.

SimulCell development

SimulCell has been built by using the PHP programming language and using an object oriented approach which allowed the development of a strongly modular program. A schematic representation of the architecture of the simulation system in terms of objects and data flow is reported in Supplementary Figure 6. The execution of a simulation run is started by an expRunner object using parameters obtained from one or more expSetup objects, originally setup by the user through the SimulCell graphical interface or other means. For each expSetup, the expRunner creates one experiment object, responsible for time management and for processing simulation data, recorded at each time interval using a movie object. An experiment creates a plate object, which works as a “dynamic” container of cells and represents the ever changing environment in which they live, move and proliferate. A plate has properties like geometry, surface and medium, whose components are updated at each step and can influence cell behaviour. According to the input parameters defined by the user, different cell objects are added to the plate, each of them set up starting from a parameter library derived from the analysis of experimental cell populations (some are reported in Supplementary Table 2) and modified according to user choices contained in the expSetup. The cell object contains the current state of the cell and provides most functionality in terms of functions, responsible for implementing the models defining cell behaviour. Cells use a plate-owned cellGrid to manage and calculate cell-cell and cell-device distances and interactions. A general event class is used to contain the basic features of any event and is further extended to produce specific events: update, mediumChange, moleculeAddition, gradientAddition, contraintRemoval, scratchOnPlate, transfection, viralInfection, are examples of currently available events.

In its present form, SimulCell runs as a web application in an apache2-PHP environment and benefits to some extent from multi core processing. Examples of execution times obtained from a 12-core M1 processor are reported in Supplementary Table 3. Simulation of a 100 cell starting population for 5 days produces a final population of over 1600 cells in less than 3 min. Execution time per cell increases linearly with simulation time; similarly, it linearly increases with the number of starting cells, with an average of 0.04-0.06 seconds per cell per day, corresponding to over 1400-1900 cell updates per second of simulation.

Representation of cell morphology

Within SimulCell, the generated simulations produce, in addition to text based outputs which report the results as tables or plots, a dynamic graphical representation of cells that can be used to build image stacks and mp4 movies. Here cells are represented by using a “symbolic” representation where cells use simple geometric shapes which change depending on cell type, status and condition. Cell body is represented by either a circle whose radius depends on cell volume and degree of spreading or an ellipse which, in addition, has a variable level of elongation to indicate cell polarisation along one axis. Images use grey level colour sets, reminiscent of phase contrast microscopy, where changes in shape, border colour, cell opacity and contents are used as visual hints to help the user better recognise cell growth, attachment status, nuclear duplication and division.