Quadratic interpolation optimization-based 2DoF-PID controller design for highly nonlinear continuous stirred-tank heater process

Abstract

Temperature control in continuous stirred tank heater (CSTH) systems is essential for ensuring energy efficiency, safety, and product quality in industrial processes. However, the nonlinear dynamics and external disturbances make conventional proportional-integral-derivative (PID) control inadequate for reliable operation. This study presents a novel two-degrees-of-freedom PID (2DoF-PID) controller optimized using the quadratic interpolation optimization (QIO) algorithm to enhance CSTH temperature regulation. The QIO-based approach allows independent tuning for setpoint tracking and disturbance rejection, overcoming the limitations of classical PID controllers. Extensive nonlinear time-domain simulations, reference tracking, and disturbance rejection tests demonstrate the superior performance of the proposed controller in terms of reduced overshoot, faster settling time, and minimal steady-state error. Furthermore, comparative evaluations with traditional tuning methods (Murrill and Rovira) and several state-of-the-art metaheuristic optimizers (DE, PSO, FLA, MGO) validate the effectiveness and robustness of the QIO-optimized strategy. This work introduces a pioneering application of the QIO algorithm in industrial temperature control, offering a scalable and cost-efficient solution for complex nonlinear systems.

Introduction

Industrial process control requires stable control of processes with time-varying operating conditions and complex dynamics. Continuous stirred-tank heaters (CSTH) are an important process control system in this respect, ensuring precise control of temperature and liquid level in industrial processes. CSTH systems are used in a variety of industries such as the chemical, energy and pharmaceutical industries to improve product quality, energy efficiency and process safety. In such systems, liquid constantly flows in and out of a tank and mixing and heating processes are carried out simultaneously. The main objective of CSTH systems is to achieve optimum process performance by stable control of the temperature and liquid level in the tank. However, nonlinear dynamics, strong coupling, time delays and instantaneous disturbances make the control of CSTH systems a very difficult problem. Rojas et al. and Alfaro and Vilanova have shown how complex the control of these systems is and that advanced control strategies are needed to overcome these problems^1,2.

CSTH systems consist of a number of elements such as a tank, a heat exchanger, an agitator, control valves and sensors to effectively control flow rates, temperature gradients and power variables^1,2. The liquid level and temperature profile of the tank should be maintained by a synergy between these units. In particular, temperature is one of the most sensitive parameters when it comes to improving energy efficiency and product quality.

CSTH processes are difficult to control because they are non-linear and multivariable. The dynamic behavior of the system is complicated by non-linear interactions between variables such as temperature and level. In addition, a time delay in the mixing and heating process can slow down the response time of the system and degrade the control performance. The influence of disturbances on the system, such as the instantaneous inlet flow rate or temperature, can lead to transient behavior and deterioration of system stability. Therefore, the control means used for CSTH systems must enable fast and stable control and take these extended dynamics into account.

Studies on the control of CSTH systems have focused on the modeling, simulation and implementation of various control techniques. In this context, the CSTH simulation model proposed by Thornhill et al. has been widely used for teaching and application purposes in process control and has formed the basis for numerous subsequent studies³. Sehgal and Acharya mainly focused on the design and performance of conventional PI controllers in CSTH control⁴. Standard PI controllers were found to be inadequate in the existing studies to handle the complexity arising from the nonlinear behavior of CSTH systems.

These shortcomings have highlighted the need for better control methods for CSTH systems. Sharma and Kumar emphasized better control methods for controlling nonlinear systems by comparing the performance of a brain emotional learning based intelligent controller (BELBIC) with that of a PI controller⁵. Similarly, Li and Jiang applied the CSTH model to process control and showed that such systems have high learning and application capability⁶.

In recent years, great interest has been aroused in new approaches for CSTH systems. Gao et al. proposed a data-driven predictive control approach that can be generalized to real-time systems and demonstrated its potential as a versatile solution for dynamic industrial processes⁷. Mahmood and Nawaf also investigated the use of PID cascade controllers in CSTH processes and found that they make a useful contribution to improving transient response and system stability⁸. Balaji and Kadirvelu developed adaptive PID controllers using reinforcement learning based designs that were applied in uncertain and dynamic environments⁹.

Although many advances have been made, PID controllers have been a standard for industrial process control for decades due to their simplicity and versatility. However, conventional PID controllers are generally unable to handle the complexity of nonlinear systems^10,11. The classical structure of PID controllers, which operate with one degree of freedom (1DoF), cannot be simultaneously optimized for setpoint tracking (servo control) and disturbance rejection (closed-loop control)¹².

To avoid these limitations, a PID controller with two degrees of freedom (2DoF-PID) was proposed. Compared to conventional PID controllers, 2DoF-PID controllers offer greater design freedom and enable better control performance². While conventional PID controllers try to sacrifice setpoint tracking and disturbance rejection by a single parameter, 2DoF-PID controllers offer the possibility to optimize these functions separately. This individual optimization option leads to a more precise and reliable control response, especially in non-linear systems with varying operating conditions. However, the applicability of 2DoF-PID controllers depends heavily on the correct setting of the controller parameters.

The use of 2DoF-PID controllers in a wide range of applications is well documented in the literature. Ghosh et al. used 2DoF-PID controllers effectively in magnetic levitation systems¹³, while Sahu et al. used them with a learning-based optimization algorithm for automatic generation control in power systems¹⁴. Roy et al. applied 2DoF-PID controllers to demonstrate their effectiveness in physio-therapeutic applications, particularly in elbow rehabilitation¹⁵. Yuan et al. described their application to biomolecular systems using DNA chain substitution reactions¹⁶. Dong et al. recently improved the performance of an engraving machine system by embedding a 2DoF-PID controller in a Kalman filter¹⁷.

In addition to advanced control strategies, hybrid optimization techniques have emerged as an important research area for the control of nonlinear CSTH systems. Dhanasekar and Vijayachitra have presented an integrated method for modeling and controlling nonlinear systems and highlighted the value of integrating various optimization methods¹⁸. In addition, Wu et al. have demonstrated the effectiveness of adaptive predictive subspace control methods in coping with the complexity of CSTH systems with complicated dynamics¹⁹.

These studies are consistent with metaheuristic algorithms that have been used extensively in the optimization of nonlinear systems. Metaheuristic-based CSTH controller designs are not yet found in the literature. The aim of this study is to close this gap. Metaheuristic algorithms are robust algorithms that optimize based on mathematical and natural phenomena to find global solutions. Several studies have been published in the literature addressing the effectiveness of such algorithms for optimizing controller parameters and obtaining global solutions to complex problems^{20,21,22,23,24}. For example, Storn and Price introduced the differential evolution (DE) algorithm and presented an effective and simple method for global optimization in continuous spaces²⁵. Wang et al. comprehensively investigated the performance of the PSO algorithm in nonlinear systems²⁶. Ghasemi et al. recently presented the flood algorithm (FLA) as a powerful metaheuristic optimization method for engineering optimization²⁷. In addition, Abdollahzadeh et al. proposed the mountain gazelle optimizer (MGO) in the literature as a new nature-inspired algorithm for solving global optimization problems²⁸. In comparison to the metaheuristic approaches documented in the literature, this paper presents the quadratic interpolation optimization (QIO) algorithm²⁹, which attracts attention and offers advantages in this context due to its mathematical basis.

In this study, the QIO algorithm²⁹ is proposed as an optimization method for the controller parameters. The QIO algorithm is a versatile and efficient method for optimizing nonlinear systems that use quadratic interpolation polynomials to determine the global minima of the objective function. Its architecture consists of various exploration and exploitation stages that improve the accuracy and stability of the algorithm by preventing it from getting trapped in local minima³⁰. Moreover, the optimization speed of the QIO algorithm enables efficient adaptation to the dynamic nature of systems to achieve improved energy efficiency and overall performance improvement of control systems.

The main objective of this work is to design a QIO-based 2DoF-PID controller for effective temperature control in nonlinear CSTH systems. This is achieved through physical and dynamic modeling of the CSTH system, design of the controller based on MATLAB/Simulink environment and rigorous performance evaluation with stringent testing. The proposed technique addresses the challenge posed by the nonlinear dynamics of such systems and develops a revolutionary solution to improve energy efficiency and process quality. This study also provides a robust theoretical and practical approach to improve the performance of industrial process control systems. To summarize, this work makes the following original contributions:

• For the first time, a QIO-based 2DoF-PID controller is developed in this study, and its application in a nonlinear multivariable system CSTH is also presented for the first time in this study.

• Although metaheuristic methods such as PSO, DE, FLA and MGO are widely used in the literature, this work shows that QIO, which is mathematically based, provides faster, more stable and more reliable results due to its improved optimization performance.

• To overcome the limitations of conventional PID controllers, a 2DoF-PID is optimized using the QIO algorithm to provide a much more flexible, sensitive and robust control mechanism against setpoint tracking and disturbances.

• The proposed QIO-based 2DoF-PID control strategy not only provides a theoretical contribution to industrial temperature control processes but is also an innovative solution that can be directly implemented through improved energy efficiency and enhanced process quality.

Overview of quadratic interpolation optimization

Quadratic interpolation is a well-established technique for curve fitting, often employed to locate the minimum of a function over a specified interval. The method constructs a quadratic interpolation polynomial $L(x)$ to approximate the function $f(x)$ and identify its minimizer. Determining the minimizer of $L(x)$ yields an estimate of the minimum point of $f(x)$²⁹. The fundamental quadratic interpolation formulation can be stated as follows:

$$L\left( x \right) = \alpha^{2} + \beta x + \delta ; \alpha ,\beta ,\delta \in R$$

(1)

Here α, β, γ are uncertain coefficients. In this case, assume that $f(x)$ has three points: ${P}_{i}\left({x}_{i},f\left({x}_{i}\right)\right)$, ${P}_{j}({x}_{j},f({x}_{j}))$ and ${P}_{k}({x}_{k},f({x}_{k}))$. For the interpolation conditions $a\le {x}_{i}<{x}_{j}<{x}_{k}\le b$, $f(x)$ is equal to $L(x)$ at the interpolation points. In this case, ${x}_{i}, {x}_{j} ve {x}_{k}$ are expressed as follows.

$$\begin{array}{*{20}c} {L\left( {x_{i} } \right) = \alpha x_{i}^{2} + \beta x_{i} + \delta = f\left( {x_{i} } \right) } \\ {L\left( {x_{j} } \right) = \alpha x_{j}^{2} + \beta x_{j} + \delta = f\left( {x_{j} } \right)} \\ {L\left( {x_{k} } \right) = \alpha x_{k}^{2} + \beta x_{k} + \delta = f\left( {x_{k} } \right)} \\ \end{array}$$

(2)

To find the minimum of $L(x)$, the derivative of Eq. (1) is taken and set to 0 (zero). The minimizer ${x}^{*}$ is expressed as in Eq. (3):

$$x^{*} = - \frac{\beta }{2\alpha }$$

(3)

Then $\alpha$ and $\beta$ are found by solving Eqs. (4) – (5).

$$\alpha = \frac{{\left( {x_{j} - x_{k} } \right)f\left( {x_{i} } \right) + \left( {x_{k} - x_{i} } \right)f\left( {x_{j} } \right) + \left( {x_{i} - x_{j} } \right)f\left( {x_{k} } \right)}}{{\left( {x_{j} - x_{k} } \right)\left( {x_{k} - x_{i} } \right)\left( {x_{i} - x_{j} } \right)}}$$

(4)

$$\beta = - \frac{{\left( {x_{j}^{2} - x_{k}^{2} } \right)f\left( {x_{i} } \right) + \left( {x_{k}^{2} - x_{i}^{2} } \right)f\left( {x_{j} } \right) + \left( {x_{i}^{2} - x_{j}^{2} } \right)f\left( {x_{k} } \right)}}{{\left( {x_{j} - x_{k} } \right)\left( {x_{k} - x_{i} } \right)\left( {x_{i} - x_{j} } \right)}}$$

(5)

In this case, the substitution of $\alpha$ and $\beta$ in Eqs. (4), (5) into Eq. (3) yields Eq. (6):

$$x^{*} = - \frac{{\left( {x_{j}^{2} - x_{k}^{2} } \right)f\left( {x_{i} } \right) + \left( {x_{k}^{2} - x_{i}^{2} } \right)f\left( {x_{j} } \right) + \left( {x_{i}^{2} - x_{j}^{2} } \right)f\left( {x_{k} } \right)}}{{2. \left[ {\left( {x_{j} - x_{k} } \right)f\left( {x_{i} } \right) + \left( {x_{k} - x_{i} } \right)f\left( {x_{j} } \right) + \left( {x_{i} - x_{j} } \right)f\left( {x_{k} } \right)} \right]}}$$

(6)

After all these steps, you can obtain the second-order interpolation polynomial $L(x)$ as follows:

$$L\left( x \right) = \frac{{\left( {x - x_{j} } \right)\left( {x - x_{k} } \right)}}{{\left( {x_{i} - x_{j} } \right)\left( {x_{i} - x_{k} } \right)}}f\left( {x_{i} } \right) + \frac{{\left( {x - x_{i} } \right)\left( {x - x_{k} } \right)}}{{\left( {x_{j} - x_{i} } \right)\left( {x_{j} - x_{k} } \right)}}f\left( {x_{j} } \right) + \frac{{\left( {x - x_{i} } \right)\left( {x - x_{j} } \right)}}{{\left( {x_{k} - x_{i} } \right)\left( {x_{k} - x_{j} } \right)}}f\left( {x_{k} } \right)$$

(7)

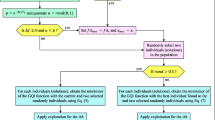
The exploration phase of the QIO algorithm aims to discover new regions in the search space. This helps the algorithm to avoid premature convergence and to avoid getting stuck in local minima. This process is performed in three steps: Point selection ${x}_{i},{x}_{j},{x}_{k}$, cubadic interpolation (${x}_{j}^{*}$, the best predicted point for the solution) and position update. The mathematical expression for the update in the exploration phase is as in Eqs. (8) and (9):

$$\begin{gathered} v_{i} \left( {t + 1} \right) = x_{{i,rand1,rand2}}^{*} \left( t \right) + w_{1} *\left( {x_{{rand3}} \left( t \right) - x_{{i,rand1,rand2}}^{*} \left( t \right)} \right) \hfill \\ + round\left( {0.5*\left( {0.05 + r_{1} } \right)} \right)*\log \frac{{r_{2} }}{{r_{3} }} \hfill \\ \end{gathered}$$

(8)

$$x_{i,rand1,rand2}^{*} \left( t \right) = GQI\left( {x_{i} \left( t \right),x_{rand1} \left( t \right),x_{rand2} \left( t \right),f\left( {x_{i} \left( t \right)} \right),f\left( {x_{rand1} \left( t \right)} \right),f\left( {x_{rand2} \left( t \right)} \right)} \right)$$

(9)

Here ${x}_{i,rand1,rand2}^{*}\left(t\right)$ is the minimizer determined using the generalized quadratic interpolation (GQI) method for the current individual and two randomly selected individuals. ${w}_{1}$​, ${r}_{1}$​, ${r}_{2}$ and ${r}_{3}$ are control parameters that set the balance between search (exploration) and deeper inspection (exploitation). In the exploitation phase of the QIO algorithm, the algorithm focuses on improving the best available solutions. The updated position in the exploitation phase is calculated as in Eqs. (10) and (11).

$$v_{i} \left( {t + 1} \right) = x_{best,rand1,rand2}^{*} \left( t \right) + w_{2 } . \left( {x_{best} \left( t \right) - round\left( {1 + rand} \right)} \right) .\left( {\frac{Ub - Lb}{{Ub^{rD - } Lb^{rD} }} } \right). x_{i}^{rD}$$

(10)

$$\begin{gathered} x_{{best,rand1,rand2}}^{*} \left( t \right) = GQI(x_{{best}} \left( t \right),x_{{rand1}} \left( t \right),x_{{rand2}} \left( t \right) \hfill \\ ,f\left( {x_{{best}} \left( t \right)} \right),f\left( {x_{{rand1}} \left( t \right)} \right),f\left( {x_{{rand2}} \left( t \right)} \right) \hfill \\ \end{gathered}$$

(11)

$$W_{2} = 3 \cdot \left( {\frac{1 - t}{T}} \right)$$

(12)

Once the exploration and exploitation has been performed, the position of each individual is updated according to the calculated minimizers. In this context, the following Eq. (13) is used.

$$x_{i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}c} {x_{i} \left( t \right);f\left( {x_{i} \left( t \right)} \right) \le f\left( {v_{i} \left( {t + 1} \right)} \right)} \\ {v_{i} \left( {t + 1} \right);f\left( {x_{i} \left( t \right)} \right) > f\left( {v_{i} \left( {t + 1} \right)} \right)} \\ \end{array} } \right.$$

(13)

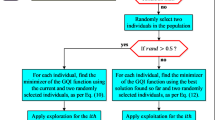
According to the QIO flow diagram in Fig. 1, the process steps are as follows: In the first step, the control parameters of the QIO algorithm are set and then the initial population is created. The fitness value of each individual in the population is calculated. The individual with the lowest fitness value is determined as, x-best. If the stop condition is met, the best solution is saved and the process is terminated. If not, the next step is taken. Two individuals are randomly selected from the population. If a random number is greater than 0.5, the minimizer of the GQI function is found using the best solution and two random individuals (Eqs. (8) and (9)). Otherwise, the corresponding exploration (Eq. (11)) or exploitation (Eq. (10)) is performed for each individual. In the last phase, the i-th individual is updated using Eq. (13).

Fig. 1

Flowchart of QIO algorithm.

Modeling of continuous stirred-tank heater

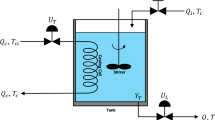
CSTH is a common task in industrial processes, as illustrated in Fig. 2. Inside the tank, a heat exchanger is used to warm the fluid; its flow is regulated by a valve with input ${U}_{t}$​. The fluid enters the heat exchanger at temperature ${T}_{ci}$ and exits at temperature ${T}_{co}$​, while its average temperature is ${T}_{ca}$​. The tank’s volume can vary due to an inlet flow ${Q}_{i}$, at temperature ${T}_{i}$​, and an outlet flow $Q$, at temperature $T$. The outlet flow is controlled by a valve with input ${U}_{L}$. To minimize heat loss, the tank is surrounded by a jacket. Following Alfaro and Vilanova², one possible model of this process can be described by the following set of algebraic-differential equations.

Fig. 2

Simplified diagram of a continuously stirred tank heater to be controlled.

Tank mass balance

$$A\frac{dH\left( t \right)}{{dt}} = Q_{i} \left( t \right) - Q\left( t \right){ }$$

(14)

Here, ${\varvec{A}}$ is the tank’s cross-sectional area, and $H(t)$ represents the fluid level in the tank.

Tank energy balance

$$\rho C_{p} AH\left( t \right)\frac{dT\left( t \right)}{{dt}} = \rho C_{p} Q_{i} \left( t \right)\left( {T_{i} \left( t \right) - T\left( t \right)} \right) + W\left( t \right)$$

(15)

where ${C}_{p}$ is the fluid’s specific heat capacity, and $W\left(t\right)$ is the rate of heat transfer from the heat exchanger to the fluid in the tank.

Heat exchanger energy balance

$$\rho C_{p} V_{c} \frac{{dT_{ca} \left( t \right)}}{dt} = \rho_{c} C_{pc} Q_{c} \left( t \right)\left( {T_{ci} \left( t \right) - T_{co} \left( t \right)} \right) - W\left( t \right)$$

(16)

where ${\rho }_{c}$ is the density of the heating fluid, ${C}_{pc}$ is its specific heat capacity, and ${V}_{c}$ is the volume of the heat exchanger.

Heat transfer between heat exchanger and tank

$$W\left( t \right) = UA_{c} \left( {T_{ca} \left( t \right) - T\left( t \right)} \right)$$

(17)

where $U$ is the overall heat-transfer coefficient and ${A}_{c}$ is the heat-exchanger area. The average temperature inside the heat exchanger, ${T}_{ca}\left(t\right)$, is related to ${T}_{co}\left(t\right)$ and ${T}_{ci}\left(t\right)$ as

$$T_{ca} \left( t \right) = \frac{{T_{ci} \left( t \right) + T_{co} \left( t \right) }}{2}$$

(18)

Alfaro and Vilanova² also propose models for the transmitters and valves:

Level transmitter

A capacitive electronic transmitter with first-order dynamics:

$$K_{L} H\left( t \right) = T_{L} \frac{{dY_{L} \left( t \right)}}{dt} + Y_{L} \left( t \right)$$

(19)

where ${T}_{L}$ is the transmitter’s time constant, ${Y}_{L}(t)$ is the level signal, and ${K}_{L}$ is the transmitter gain.

Temperature transmitter

An $A{P}_{t100}RTD$ electronic sensor is placed in a thermowell at the tank outlet. It usually exhibits second-order dynamics:

$$T_{T}^{2} \frac{{d^{2} Y_{T} \left( t \right)}}{{dt^{2} }} + 2T_{T} \frac{{dY_{T} \left( t \right)}}{dt} + Y_{T} \left( t \right) = K_{T} T\left( t \right)$$

(20)

where ${T}_{T}$ is the sensor’s time constant and ${K}_{T}$​ is its gain.

Level control valve

A ball valve with an electropneumatic actuator and near-quadratic flow characteristics. The relationship between outlet flow $Q(t)$ and the input ${U}_{L}(t)$ is described by two equations:

$$T_{vL} \frac{{dX_{L} \left( t \right)}}{dt} + X_{L} \left( t \right) = K_{xL} U_{L} \left( t \right)$$

(21)

$$Q\left( t \right) = K_{vL} X_{L}^{2} \left( t \right)\sqrt {\rho gH\left( t \right)}$$

(22)

where ${T}_{vL}$ is the valve’s time constant, ${K}_{xL}$ is the stem constant, ${K}_{vL}$ is the flow coefficient, $\rho$ is the fluid density, $g$ is gravitational acceleration, and ${X}_{L}\left(t\right)$ is the normalized stem travel.

Temperature control valve

Another ball valve with an electropneumatic actuator but with an equal-percentage inherent flow characteristic:

$$T_{vT} \frac{{dX_{T} \left( t \right)}}{dt} + X_{T} \left( t \right) = K_{xT} U_{T} \left( t \right)$$

(23)

$$Q_{c} \left( t \right) = K_{vT} R_{vT}^{{\left( {X_{T} \left( t \right) - 1} \right)}} \sqrt {P_{cp} - \left( {R_{c} Q_{c}^{2} \left( t \right) + P_{cr} } \right)}$$

(24)

where ${T}_{vT}$ is the valve’s time constant, ${K}_{xT}$ is the stem constant, ${K}_{vT}$ is the flow coefficient, ${R}_{vT}^{({X}_{T}\left(t\right)-1)}$ is the valve range factor, ${P}_{cp}$ is the heating fluid pump discharge pressure, ${P}_{cr}$ is the return pressure, and ${X}_{T}\left(t\right)$ is the normalized stem travel.

Based on this model, the controlled variables are ${Y}_{L}(t)$, representing the tank level, and ${Y}_{T}(t)$, representing the tank outlet temperature. The manipulated variables are ${U}_{L}(t)$, which directly influences $Q$, and ${U}_{T}(t)$, which directly affects ${Q}_{c}$. The inlet flow ${Q}_{i}(t)$, the inlet temperature ${T}_{i}$, and the heat exchanger inlet temperature ${T}_{ci}$ are considered disturbances. The system’s state variables include $H(t)$, ${T}_{T}(t)$, ${T}_{co}$, ${Y}_{L}(t)$, ${Y}_{T}$, ${X}_{L}(t)$, and ${X}_{T}(t)$. Altogether, this formulation yields a seventh-order nonlinear system for a two-input, two-output industrial process. The model parameters are presented in Table 1. This table contains the most important parameters for the CSTH process and is taken from Refs.^1,2. It contains critical technical parameters related to the tank and the heat exchanger system, such as density, heat capacity, pressure and temperature. The parameters listed in this table were used in this study. The detailed specification of such parameters plays an important role in the modeling and control design of CSTH systems.

Table 1 The parameters of the CSTH process.

Novel control method for CSTH process

Two-degrees-of-freedom (2DoF-PID) control scheme

In control systems in general, and in process control applications in particular feedback control or closed-loop control is the control structure used to solve most control problems that arise. The feedback control structure has been used for a long time, but if we limit ourselves to the field of industrial process control, the history of the application of PID control with proportional, integral and derivative components begins in 1940 with the introduction of the Taylor Fullscope 100 pneumatic PID controller². This was the first controller equipped with buttons and calibrated dials for three responses.². The simple trinomial original PID control algorithm has evolved over time into four or five 2DoF-PID implementations. Equation (25) gives the mathematical expression of the realistic 2DoF-PID controller.

$$U\left( s \right) = K_{p} \left( {\beta \times R\left( s \right) - Y\left( s \right) + \frac{1}{{T_{i} s}}\left[ {R\left( s \right) - Y\left( s \right)} \right] + \frac{{T_{d} s}}{{\alpha T_{d} s + 1}}\left[ {\gamma \times R\left( s \right) - Y\left( s \right)} \right]} \right)$$

(25)

• ${K}_{p}$: Proportional gain.

• ${T}_{i}$: Integral time constant.

• ${T}_{d}$: Derivative time constant.

• $\beta$: Reference weighting parameter (improves set-point tracking).

• $\gamma$: Weighting parameter for the derivative action (improves disturbance rejection).

• $\alpha$: Parameter that modifies the behavior of the derivative term for robustness.

With conventional PID controllers, the response to setpoint changes often at odds with disturbance rejection. 2DoF-PID, $\beta$ parameters can solve this problem by allowing a more accurate adaptation to the reference signal. The $\gamma$ parameter makes the system more robust to input disturbances. This is crucial to prevent external disturbances from negatively impacting the control performance, especially in industrial applications. Figure 3 shows the block diagram of the realistic 2DoF-PID controller used in this study. Reference signal $R\left(s\right)$ is the target value to be monitored by the system. This is the signal β and γ parameters to provide a more flexible control structure. Output signal $Y\left(s\right)$ is a real-time measurement of the controlled variable. Errors are detected by comparing the output with the reference signal. The error signal $E\left(S\right)=R\left(s\right)-Y\left(s\right)$ difference is the signal with which the controller attempts to reduce the difference between the setpoint and actual value.

Fig. 3

Block diagram of realistic 2DoF-PID controller for industrial application.

Objective function

The objective function Zwe-Lee Gaing (ZLG)³¹ is used in this study to minimize the performance criteria of dynamic behavior such as maximum overshoot, steady-state error, settling time and rise time. Setpoint change $t=100$ seconds and was increased from 76 to 81%. This function measures how well the system responds to this change, taking into account several performance metrics.

$$ZLG = \left( {1 - e^{ - \xi } } \right)\left( {\frac{{N_{os} + N_{se} }}{100}} \right) + e^{ - \xi } \left( {N_{st} - N_{rt} } \right)$$

(26)

where ${N}_{os}$ is the normalized percent overshoot, ${N}_{se}$ denotes the normalized percent steady-state error, ${N}_{st}$ represents the normalized settling time ($\pm 2\%$ tolerance band), and ${N}_{rt}$ is the normalized rise time. It is important to note that tuning a 2DoF-PID controller inherently involves trade-offs among competing performance objectives such as fast response, low overshoot, minimal steady-state error, and robust disturbance rejection. These trade-offs are explicitly addressed in the $ZLG$ objective function via the weight parameter ($\xi$), which balances accuracy (overshoot and steady-state error) with speed (settling and rise times). A higher $\xi$ value emphasizes precision and stability, while a lower $\xi$ prioritizes rapid system response. In this study, $\xi$ was taken as 1. The QIO algorithm systematically explores this trade-off landscape to identify controller parameters that offer an optimal compromise tailored to the nonlinear dynamics of the CSTH process. This ensures that neither transient nor steady-state performance is disproportionately sacrificed.

Integration of QIO algorithm

Figure 4 shows the block diagram of the QIO-based 2DoF-PID controller for the CSTH process. The setpoint in the block diagram is the target control value of the system. ${U}_{T}$ is the output of the 2DoF-PID controller, which generates the required control signal by comparing the setpoint with the output signal received from the system. This signal is forwarded to the CSTH system. The tank then controls variables such as temperature and flow rate. The system has non-linear dynamics here; therefore, precise controller design is crucial. The output signal ${Y}_{T}$ is evaluated by metrics such as overshoot (${N}_{os}$), steady-state error (${N}_{se}$), settling time (${N}_{st}$) and rise time ${(N}_{rt}$). This output signal is fed back to the controller via feedback in order to minimize the error. These metrics are analyzed with the $ZLG$ objective function. The QIO algorithm then optimizes the controller parameters (${K}_{p}$, ${T}_{i}$, ${T}_{d}$, $\alpha$ , $\beta$, $\gamma$) to achieve the best performance. These parameters are continuously updated to minimize the performance metrics.

Fig. 4

Block diagram of QIO-based 2DoF-PID controller design for CSTH process.

While the proposed controller design does not explicitly impose numerical constraints on the control signal during the optimization process, practical limitations are inherently considered through the nonlinear CSTH model, which includes actuator dynamics such as valve response time and gain. These system components naturally restrict the amplitude and rate of change of the control signal. Furthermore, the use of performance metrics like overshoot, rise time, and settling time in the ZLG objective function discourages aggressive control actions, indirectly promoting energy-efficient and smooth control behavior. For real-time implementations, these implicit constraints can be further extended with saturation blocks to ensure safe and feasible actuator commands.

Results and discussion

In order to evaluate the effectiveness of the proposed QIO-based 2DoF-PID controller design and provide a comprehensive comparison, DE-, PSO-, FLA- and MGO-based 2DoF-PID controllers are also implemented for benchmarking. These algorithms were selected based on their time efficiency, solution accuracy and widespread use in literature. FLA and MGO are recent metaheuristic algorithms that perform well on nonlinear and complex optimization problems. These algorithms provide an efficient solution by optimizing the trade-off between exploitation and exploration using randomization and exploration mechanisms. Therefore, they are used as suitable benchmark candidates to evaluate the performance of a new algorithm, QIO. PSO and DE have long been used in the field of optimization and are characterized in particular by their simplicity, robustness and applicability to various technical problems. The adjustable parameters of PSO such as inertia weight ($w$), cognitive (${c}_{1}$) and social coefficients (${c}_{2}$) and the adjustable parameters of DE such as scaling factor and crossover probability have contributed to the widespread use of these algorithms in the literature. The inclusion of these algorithms provides a solid basis for comparing the performance of QIO with existing and proven methods.

Table 2 shows that QIO is defined by the population size (${N}_{pop}$) and the number of iterations (${iter}_{max}$), which shows that it does not require parameter setting. This shows that QIO simplifies the optimization process and makes the algorithm more adaptable. Especially for systems that require precise optimization, such as temperature control, the simplicity of QIO provides a stable and fast solution while reducing computational costs. While the parameter settings required by other algorithms (e.g. the crossover probability in PSO or DE) increase complexity, QIO does not have these limitations.

Table 2 Control parameters of QIO and other algorithms.

Statistical test

Table 3 shows the statistical metrics of the algorithms in the $ZLG$ objective function optimization. Each algorithm was run 30 times with fixed parameters (population size and maximum number of iterations). This test procedure ensures a fair comparison of the algorithms and enables a statistical evaluation of the differences in performance.

Table 3 Statistical metrics of QIO and other algorithms.

The analysis of the performance of the proposed method, QIO, shows the lowest mean (54.2382) and standard deviation (1.1033), indicating that QIO has superior performance in terms of both precision and consistency. The narrow range between the minimum and maximum values (approx. 4) shows that the algorithm is very stable in the optimized solution space. This shows the effectiveness of QIO in minimizing the $ZLG$ objective function. DE has a higher mean (61.0975) and a higher standard deviation (1.7772) compared to QIO. This indicates that the results of the algorithm vary over a larger range (approx. 5) and are less consistent. The high maximum value (65.8938) shows that DE can perform poorly at times. However, the low minimum value (57.9184) also shows that the algorithm can deliver good results in some cases. The mean (60.0273) and standard deviation (1.3342) of PSO are worse than QIO, but better than DE. This shows that PSO provides more stable results than DE, but lags behind QIO in overall performance. The difference between the minimum and maximum values (approx. 6) also shows that PSO occupies a middle position in terms of consistency. FLA showed the third best performance after QIO with a mean (58.5222) and a standard deviation (1.4717). The minimum value (56.2536) shows that the algorithm is able to produce effective solutions, but the maximum value (61.8177) is higher, indicating that it can produce inconsistent results in some cases. The mean (56.8670) and standard deviation (1.2076) of MGO are close to FLA but lower than QIO. The difference between the minimum and maximum values (approx 5) shows that MGO outperforms PSO and DE in terms of consistency, but lags behind QIO.

Change of objective function

Figure 5 shows the evolution of QIO and other algorithms in the process of minimizing the $ZLG$ objective function. According to the results in Table 4, the QIO algorithm has shown superior performance by exhibiting a balanced structure in optimizing the controller parameters. The parameters ${K}_{p}$, ${T}_{i}$, ${T}_{d}$, $\alpha$, $\beta$, and $\gamma$ determined by QIO provide both fast and stable system response, thus offering a suitable solution for the dynamic requirements of the nonlinear CSTH system. Particularly low $\alpha$ and $\beta$ values increased the stability of the controller and enabled fast tracking of the reference signal. Compared to the other algorithms, the parameter choices of DE and PSO were more unbalanced, resulting in longer settling times and fluctuating system behavior. Although FLA and MGO achieved similar results to QIO in certain parameters, they lagged behind in overall performance.

Fig. 5

Evolution of $ZLG$ objective functions for QIO and other algorithms.

Table 4 Optimized 2DoF-PID controller parameters obtained by QIO and other algorithms.

Nonlinear time-domain simulations

The setpoint in the system, $t=100$ seconds, was also increased from 76 to 81%. Figure 6 and Fig. 7 show the responses of closed-loop systems controlled with 2DoF-PID. Figure 6 shows the overall response, while Fig. 7 shows an enlarged version in which the differences can be seen more clearly. When the time response characteristics given in Table 5 and the closed loop responses in Fig. 6 and Fig. 7 are evaluated together, it can be clearly seen that the 2DoF-PID controller optimized by the QIO algorithm performs best. QIO has the lowest overshoot rate of 1.6480% and reaches the temperature setpoint fastest and with minimal oscillations, avoiding unnecessary fluctuations in the system. The lowest value for the steady-state error (1.8415E-04%) shows that the system reaches the reference point with high accuracy. In addition, with the shortest settling time of 202.3821 s and the fastest rise time of 59.3230 s, QIO ensures that the system stabilises in the shortest possible time. In contrast, the PSO and DE algorithms have the highest overshoot rates (1.9740% and 1.8781%), the longest settling times (296.9894 s and 244.6652 s), and the highest steady-state errors (0.0122% and 0.0115%) and delay the stabilization of the system due to more fluctuations and a delayed response, as shown in Fig. 7. Although FLA and MGO have higher overshoot rates compared to QIO, they gave better results than PSO and DE. In general, the 2DoF-PID controller optimized by the QIO algorithm shows superior control performance as it is much faster, more stable and with lower error compared to the other algorithms.

Fig. 6

Closed-loop response of 2DoF-PID controlled systems tuned by QIO and other algorithms.

Fig. 7

Magnified version of closed-loop response of 2DoF-PID controlled systems.

Table 5 Comparison of time response characteristics of 2DoF-PID controlled systems.

Evaluation of performance with commonly used error-based cost functions

The metrics integral of absolute error (IAE), integral of squared error (ISE), integral of time-weighted absolute error (ITAE) and integral of time-weighted squared error (ITSE) are error-based measures that comprehensively evaluate the performance of a controller. IAE measures the magnitude of the error by taking the time integral of the absolute value of the error, while ISE takes the squared error, penalizing larger errors more heavily and evaluating the sensitivity of the system to drift. ITAE analyzes how the impact of an error changes over time by multiplying the absolute value of the error by time, while ITSE multiplies the square of the error by time to more strongly measure the impact of large and long-lasting errors on the system^32,33. These metrics show that at low values, the controller effectively minimizes both the error magnitude and time-dependent effects and provides fast, stable system response. These metrics defined by Eqs. (27) – (30) are used to evaluate the control performance of the algorithms in terms of accuracy, stability and response speed using the error function ($e(t)$) over the total simulation time (${t}_{f}=1000$ s).

$$F_{IAE} = \mathop \smallint \limits_{0}^{{t_{f} }} \left| {e\left( t \right)} \right|dt$$

(27)

$$F_{ISE} = \mathop \smallint \limits_{0}^{{t_{f} }} e^{2} \left( t \right)dt$$

(28)

$$F_{ITAE} = \mathop \smallint \limits_{0}^{{t_{f} }} t\left| {e\left( t \right)} \right|dt$$

(29)

$$F_{ITSE} = \mathop \smallint \limits_{0}^{{t_{f} }} te^{2} \left( t \right)dt$$

(30)

According to the results in Table 6, QIO has the lowest values in all error metrics. This shows that the controller performs well in minimizing the error size and time-dependent error effects. query

DE and PSO have higher error values compared to QIO. In particular, the larger values for the and metrics show that these algorithms do not minimize the time-dependent error effects well enough. FLA and MGO perform worse than QIO, but achieve better results than DE and PSO. In particular, MGO performs similarly well to FLA for the error size metrics.

Table 6 Comparison of error-based performance indicators.

Comparison with traditional control methods

The results obtained with QIO are compared with the traditional methods of Murrill¹ and Rovira¹, which are widely used in literature. The controller parameters obtained via those methods are ${K}_{p}=5.87$, ${T}_{i}=65.02$, ${T}_{d}=23.21$, $\alpha =0.1$, $\beta =1$ and $\gamma =0$ for Murrill tuning method and ${K}_{p}=4.34$, ${T}_{i}=120.81$, ${T}_{d}=18.48$, $\alpha =0.1$, $\beta =1$ and $\gamma =0$ for Rovira tuning method. Figure 8 shows the closed- loop responses of these methods. In addition, the time response characteristics and the error-based performance indicators are shown in Tables 7 and 8.

Fig. 8

Closed-loop response of 2DoF-PID controlled systems tuned by QIO, Murrill and Rovira methods.

Table 7 Comparison of time response characteristics of 2DoF-PID controlled systems.

Table 8 Comparison of error-based performance indicators.

Table 7 compares the time response of 2DoF-PID controllers tuned with the QIO, Murrill and Rovira methods. The QIO method provides the fastest and most stable control of the system with the lowest overshoot rate (1.6480%), the lowest steady-state error (1.8415E-04), the shortest settling time (202.3821 s) and the fastest rise time (59.3230 s). The Murrill method, on the other hand, has the highest overshoot rate of 33.4273% and the longest settling time of 511.4720 s, which leads to an overreaction of the system and a late stabilization. The Rovira method has a longer settling time compared to QIO (327.2199 s) and is one of the slowest responding algorithms, especially in terms of rise time (82.1821s).

Table 8 compares the error-based performance indicators (IAE, ISE, ITAE, ITSE) of the different tuning methods. For all error measurements, QIO has the lowest values and provides the best control performance. In particular, the values for ${F}_{IAE}$ (299.9501), ${F}_{ISE}$ (1.1158E + 03), ${F}_{ITAE}$(4.2743E + 04) and ${F}_{ITSE}$ (1.4021E + 05) show that QIO minimises the error level and provides the most precise control. In contrast, the Murrill method has the highest error values and resulted in larger deviations of the system. The Rovira method has higher error values than QIO, especially in terms of ${F}_{ITAE}$(6.4121E + 04) and ${F}_{ITSE}$ (2.1879E + 05), indicating that the system stabilises later and with more errors.

Setpoint tracking performance of QIO-based 2DoF-PID controller

Figure 9 shows the closed-loop response of the QIO-based 2DoF-PID controller under variable setpoint conditions. The controller adapts quickly and stably to setpoints between 72 and 78%. In particular, the settling time for each setpoint change was kept short and the system reached the target value with minimum overshoot and low steady-state error. Figure 9 successfully demonstrates both the dynamic and steady-stable responses performance of the controller and clearly shows the effectiveness and adaptability of QIO in nonlinear systems.

Fig. 9

Closed-loop response of QIO-based 2DoF-PID controlled system under varying setpoint conditions.

Disturbance rejection performance of QIO-based 2DoF-PID controller

The QIO-based 2DoF-PID controller showed stable performance in the face of sudden and large disturbance signals. Figure 10 shows the disturbance signals used in the system controlled by the QIO-based 2DoF-PID controller. Three different disturbance inputs are analyzed:

• ${Q}_{i}({m}^{3}/s)$: Sudden change in the input flow rate. The disturbance signal represents a reduction in flow rate around 1400 s.

• ${T}_{i}(^\circ C)$: The change in inlet temperature shows a sudden increase at 2200 s.

• ${T}_{ci}(^\circ C)$: The change in target temperature is reflected as a decrease t 700 s.

Fig. 10

Disturbance signals.

Figure 11 shows the disturbance rejection behavior of the QIO-based 2DoF-PID controller with these disturbance signals. The tank temperature sensor (in percent) is continuously adjusted to the setpoint by the controller. The controller responded quickly to each disturbance and then returned to the setpoint with minimum steady-state error.

Fig. 11

Disturbance rejection behavior of QIO-based 2DoF-PID controlled system.

Conclusion and prospects for future research

In this paper, the control performance of a 2DoF-PID controller using the QIO algorithm for nonlinear CSTH temperature control was systematically investigated. The balanced exploration and utilisation mechanism of the QIO algorithm quickly and efficiently learns the nonlinear system dynamics and shows excellent control performance. Compared to the conventional tuning methods (Murrill and Rovira), the QIO-based controller showed significantly better performance with a low overshoot rate, fast settling time and a minimum steady-state error of zero. In addition, comparisons with certain well-known meta-heuristic algorithms such as DE, PSO, FLA and MGO showed that QIO performed better on all dynamic and error-based performance criteria. The QIO-based 2DoF-PID controller responds quickly to any change in the setpoint, achieves system stability and has satisfactory disturbance rejection against any external disturbance. In addition, the success of the parameter optimization algorithm has led to benefits in precise control and energy efficiency. These results prove that the QIO algorithm can be an implementable solution even for complex processes such as CSTH and other industrial systems with nonlinear characteristics. Although the proposed controller has only been validated through simulation, it is important to emphasize that the CSTH model employed in this study is highly detailed and reflects the complex nonlinear behavior typically observed in real industrial processes. The model includes realistic actuator dynamics, sensor characteristics, and multiple disturbances, offering a high-fidelity approximation of practical CSTH systems. Implementing real-time experiments, while ideal, involves substantial hardware infrastructure, rigorous safety protocols, and extended testing phases, which are beyond the current scope. Nevertheless, the rigorous nonlinear simulations under varying operating conditions (complemented by statistical performance evaluations and benchmark comparisons) provide strong evidence of the controller’s feasibility and reliability. As such, the conducted simulations serve as a robust preliminary validation step prior to physical implementation.

Despite the promising results, several limitations of the proposed method should be acknowledged. First, the effectiveness of the QIO-based 2DoF-PID controller is dependent on the accuracy of the CSTH model used during optimization; real-world discrepancies may reduce its performance. Second, the controller parameters are optimized offline and do not adapt in real time to process variations or unmodeled dynamics. Third, while QIO is computationally efficient for single–input–single–output systems like CSTH, applying it to larger-scale multivariable systems could increase computational complexity. Lastly, the presented results are based on simulations only; future work should include hardware-in-the-loop testing or real-time implementations to validate the controller’s robustness and practicality in real industrial environments. To address the aforementioned limitations and further advance the proposed methodology, several avenues for future research can be considered. First, developing adaptive or self-tuning versions of the QIO-based 2DoF-PID controller that can dynamically adjust parameters in real time will improve robustness against model uncertainties and time-varying dynamics. Second, the integration of hybrid optimization schemes, combining QIO with fast local search techniques or machine learning methods, may accelerate convergence and enhance control precision, particularly for large-scale and highly nonlinear systems. Third, the extension of the QIO framework to handle multi-input multi-output (MIMO) systems and constrained control problems would broaden its applicability to more complex industrial scenarios. Moreover, implementing robust control design techniques that explicitly account for modeling uncertainties and external disturbances would improve reliability under practical conditions. Finally, hardware-in-the-loop simulations and experimental validation using real CSTH setups or pilot plants will be essential to verify the algorithm’s effectiveness under real-world conditions and to assess its implementation feasibility on embedded platforms.