An efficient approach for mathematical modeling and parameter estimation of PEM fuel based on Young’s double-slit experiment algorithm

Abstract

This paper introduces a novel optimization algorithm, Young’s double-slit experiment algorithm (YSDE), for accurately estimating the unknown parameters of Proton Exchange Membrane Fuel Cell (PEMFC) models. The proposed method integrates the YDSE algorithm with five other metaheuristic techniques: the sine cosine Algorithm (SCA), moth flame optimization (MFO), Harris Hawk optimization (HHO), gray wolf optimization (GWO) and chimp optimization Algorithm (ChOA) to estimate six critical parameters of PEMFC. Comparative analysis demonstrates that the YDSE algorithm outperforms competing methods by achieving the lowest Sum of Square Error (SSE) with a minimum value of approximately 1.9454, compared to higher values in other algorithms. Statistical evaluation over 30 independent runs reveals that YDSE attains a mean SSE of 1.9454 with an exceptionally low standard deviation of 2.21 $\times$ 10${-6}$, indicating remarkable consistency and robustness. Furthermore, the YDSE algorithm exhibits faster convergence, reaching optimal solutions in fewer iterations than other methods, thereby enhancing computational efficiency. The proposed YSDE is validated in three different PEMFC stack configurations, using standard performance indicators such as the sum of squared errors (SSE), standard deviation (SD), and Friedman rank (FRK). Experimental results demonstrate that YSDE consistently achieves superior accuracy and robustness. It reduces average SSE values by up to 97.8% compared to GWO and 97.6% compared to SCA. The worst-case SSE is improved by up to 70.6% over IChOA, and the standard deviation is reduced by 91.3% relative to MFO. In more complex configurations, YSDE maintains a 1000-times lower SD, while enhancing average accuracy by 2.6% over IChOA and 8.5% over MFO. Overall, YSDE achieves up to 87% improvement in ranking scores based on Friedman analysis, indicating its consistent superiority across different test cases. The statistical significance of YSDE’s performance is confirmed through the Wilcoxon rank-sum and multiple comparison tests. These results highlight YSDE as a highly effective and stable solution for PEMFC system identification which has significant potential to develop digital twins and control systems in automotive applications and advance renewable energy technologies.

Introduction

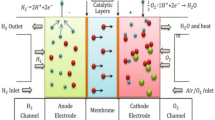
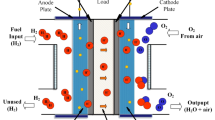
There is no doubt that clean energy technologies make a substantial contribution to the fight against global pollution and the depletion of fossil fuels. These electrochemical energy conversion technologies are exemplified by proton exchange membrane fuel cells (PEMFCs) . As an alternative to diesel distributed generation, proton interchange is considered an efficient fallback source of electricity and a method of balancing grid power. Membrane fuel cells (PEMFCs) are also considered. The primary benefits of these PEMFCs in power system applications include high start-up dependability, rapid response to demand fluctuations, silent operation, and low carbon emissions¹. In particular, they are widely used in hydrogen-powered automobiles worldwide, representing about 90% of the research and development of fuel cells^2,3,4,5.

Hydrogen, a by-product of industrial facilities that specialize in the production of chlorine and sodium chlorate, can serve as a sustainable fuel for PEMFCs in specific regions, such as Finland⁶. When used in PEMFC power plants at partial loads, this hydrogen, along with other renewable sources, can contribute to the rapid coverage of the load⁷. PEMFCs, which operate in both AC and DC power networks, serve as electrochemical energy conversion devices, converting chemical energy into heat and electricity through the reaction of oxygen and hydrogen. Noble metal catalysts, such as platinum, are typically utilized at reaction sites, generating heat, liquid water, and direct current (DC) electricity as by-products in low-temperature fuel cells⁸.

Fuel cells (FCs) face challenges such as restricted output voltage and current despite their advantages. Series coupling of cells is required to create modules with the necessary voltage and current. Issues such as concentration-polarization loss at high current densities, activation loss at low current densities, and linearly varying ohmic loss contribute to a decrease in the output voltage from the open-circuit voltage. Accurate estimation of these losses poses challenges due to equations that contain seven unknown parameters, one of which can be calculated using an empirical formula⁸.

Fuel cells (FCs) are reliable and environmentally friendly alternative energy sources across various sectors, including residential and commercial structures, electric vehicles, and mobile phone recharging. They offer benefits such as silent operation, high efficiency, scalability, and low operational expenses, producing pure byproducts. PEMFCs stand out due to their low operating temperature, high power densities, rapid startup, reduced volume, decreased weight, and overall dependability. PEMFCs are particularly well-suited for automotive applications⁹ and are utilized in both stationary and portable power sources.

Proton-exchange membrane fuel cells (PEMFCs) play a pivotal role in addressing global energy challenges, particularly in renewable energy applications. Accurate parameter estimation is critical to optimizing the performance and efficiency of PEMFC systems, which are inherently non-linear and multivariable. In this work, we propose a novel approach to solve the specific problem of PEMFC parameter estimation using the Young’s double cut experiment (YDSE) algorithm. Although YDSE is a versatile metaheuristic algorithm capable of addressing various optimization challenges, the primary focus of this study is on its application to a domain-specific and high-impact real-world problem. This focus enables an in-depth examination of YDSE’s effectiveness in addressing the specific needs of PEMFC modeling, rather than its general applicability to benchmark global optimization problems.

Researchers overcome the challenges posed by PEMFCs through the use of meta-heuristic algorithms. These algorithms, known for their simplicity, adaptability, problem independence, gradient-free nature, versatility, and resistance to local optima entrapment, are widely used to extract PEMFC parameters. The No-Free-Lunch theorem emphasizes that no existing optimizer can effectively solve all engineering optimization problems. Various algorithms, including artificial ecosystem optimizer (AEO)¹⁰ and GWO¹¹, are used to estimate PEMFC parameters. In this study, the authors aim to implement a meta-heuristic algorithm to address optimization challenges.

The main objective of this paper is to develop an efficient and accurate method for parameter estimation in PEMFC using YDSE algorithm. This study aims to compare the performance of the YDSE algorithm with other metaheuristic optimization methods, such as SCA, MFO , HHO , GWO , and ChOA, to minimize the Sum of Square Error (SSE) between estimated and actual measured cell voltages for precise parameter estimation. Additionally, the paper seeks to enhance the modeling accuracy and performance prediction of PEMFCs through advanced optimization techniques, demonstrating the practical applicability of the proposed YDSE-based method in developing digital twins and control systems for automotive applications, thereby validating the efficacy and reliability of the YDSE algorithm in addressing the parameter identification challenges of PEMFC models across diverse applications.

This paper contributes to the body of knowledge by introducing a novel application of the YDSE algorithm to estimate the parameters of PEMFCs. The effectiveness of the YDSE in this research area is demonstrated through several key points:

• The paper introduces YDSE algorithm as a novel metaheuristic optimization technique for accurately estimating PEMFC parameters. This innovative approach leverages the principles of wave interference to enhance optimization performance.

• A comprehensive comparison is conducted between YDSE and five other well-known metaheuristic algorithms: SCA, MFO , HHO , GWO , and ChOA. The study shows that YDSE outperforms these methods in minimizing the Sum of Square Error (SSE) between estimated and actual cell voltages.

• The proposed YDSE algorithm significantly improves convergence speed and accuracy over traditional optimization techniques. Statistical measures (Min, SD, Mean, Max) indicate YDSE’s superior performance.

• The efficacy and reliability of the YDSE algorithm are validated through experimental results, showcasing its robustness in handling the complexities of PEMFC parameter identification across diverse applications.

The remainder of this paper is organized as follows: Sect. 2 provides a detailed review of related work on parameter estimation techniques for PEMFC. Section 3 presents Mathematical formulation for PEMFC. Section 4 introduces the proposed methodology, including YDSE algorithm . Section 5 introduces the YDSE algorithm as a novel approach for parameter estimation of PEMFC. Section 6 discusses the results, comparing the performance of the YDSE algorithm with that of other metaheuristic optimization methods. Finally, Sect. 7 concludes the paper, summarizing the key findings and suggesting potential directions for future research.

Related work

In the dynamic domain of improving PEMFC models, crucial for advancing hydrogen fuel cell systems, a sequence of innovative inquiries transpire, unveiling fresh methodologies that influence the storyline.

In¹⁰, the authors utilize the IAEO algorithm to navigate the intricate aspects of PEMFC modeling effectively. This research demonstrates the algorithm’s proficiency in handling multivariate and nonlinear data. It establishes it as a more favorable option than complex algorithms, with the potential for increased efficiency in fuel cell systems. The narrative progresses in a subsequent chapter by introducing a novel method for accurately extracting parameters to model proton-exchange membrane (PEM) fuel cell systems. Using the simulated annealing (SA) optimization algorithm, the authors enhance accuracy by estimating each parameter and presenting a model built in Simulink. Equipped with optimization algorithms firmly rooted in empirical evidence, this model is a potentially efficacious tool in developing fuel cell power systems that demonstrate exceptional efficiency¹².

In¹³, the Authors introduce the SOA, which simulates human searching behaviors, adding an intriguing twist to the narrative. The algorithm’s ability to optimize PEMFC modeling surpasses that of existing state-of-the-art alternatives, rendering it a valuable tool for system analysis, design optimization, and real-time control.

In¹⁴, the Hybrid Artificial Bee Colony (HABC) algorithm is introduced, which addresses the difficulty associated with parameter estimation in PEMFC models. By incorporating the foraging behavior of bacteria and an adaptive Boltzmann probability, HABC outperforms alternative methods in terms of convergence speed and precision. By assessing the results regarding the parameters of the PEMFC stack, the research demonstrates how effectively HABC addresses the difficulties associated with parameter estimation.

The Simplified Teaching-Learning Optimization (STLBO) algorithm is introduced in¹⁵. It provides an exceptional strategy for identifying solar and PEM fuel cell parameters. STLBO outperforms fundamental TLBO and alternative methods, showcasing its scalability and efficacy. As a result, it presents a promising resolution to intricate optimization challenges encountered in practical contexts. The effectiveness of GWO in precisely identifying parameters is confirmed by statistical analyses, representing a substantial progression in optimizing commercial PEMFC models¹¹.

In addition, the authors in¹⁶ propose a method for estimating parameters using the bird mating optimization algorithm to examine the fuel cell polarization curve. In¹⁷ and¹⁸, authors suggest using a composite genetic algorithm to estimate the parameters of PEMFC. The methodology for identifying parameters of PEMFC using the harmony search optimizer is described in¹⁹. In^20,21, A convolutional neural network was presented to identify the parameters of PEMFC, utilizing developments in machine learning techniques. The parameters of the PEMFC are determined and analyzed in²² using the polarization curve, taking into account different temperature effects. The model incorporates a modified differential algorithm that includes a collective guidance factor for determining the parameters of the PEMFC, as explained in²³. The following sections will examine most of these sources and recent methods for estimating parameters.

Recent studies have highlighted the critical role of accurate parameter estimation and modeling in the performance and deployment of fuel cell systems, particularly in hybrid electric vehicles (HEVs). As the demand for cleaner transportation grows, Proton Exchange Membrane Fuel Cells (PEMFCs) have emerged as promising candidates due to their high energy efficiency and zero-emission profile^24,25,26,27.

Recent research has also explored various metaheuristic-based techniques for PEMFC parameter estimation. These include the Adaptive Sparrow Search Algorithm²³, Improved Chaotic Grey Wolf Optimization²⁸, Modified Farmland Fertility Optimizer²⁹, Moth-Flame Optimization³⁰, Improved Barnacles Mating Optimization³¹, Pathfinder Algorithm³², Enhanced Transient Search Optimization Algorithm³³, Exponential Distribution Optimizer³⁴, Improved Stochastic Fractal Search Algorithm³⁵, Gradient-Based Optimizer³⁶, Osprey Optimization Algorithm³⁷, JAYA Optimization³⁸, Hybrid Artificial Bee Colony Differential Evolution Optimizer³⁹, Enhanced Bald Eagle Algorithm⁴⁰, Honey Badger Optimizer⁴¹, Particle Swarm Optimization⁴², Improved African Vulture Optimization Algorithm⁴³, and the Modified Honey Badger Algorithm⁴⁴.

These studies demonstrate the effectiveness of various optimization strategies in addressing the challenges of parameter estimation in PEMFC modeling. The ongoing research efforts aim to enhance the efficiency and reliability of PEMFC systems by employing innovative optimization techniques.

Table 1 Research studies on PEMFC models.

Despite significant advancements in the field of PEMFC parameter estimation, existing methods, such as the SCA, MFO, HHO, GWO, and ChOA, still face challenges in terms of convergence speed and accuracy. Many of these methods struggle with the entrapment of local optima and require extensive computational resources to achieve satisfactory results. The introduction of the YDSE algorithm addresses these limitations by leveraging wave interference principles to enhance optimization performance. The YDSE algorithm exhibits faster convergence and higher accuracy in estimating PEMFC parameters by minimizing the Sum of squared error (SSE) between estimated and actual measured cell voltages. This method improves the precision of parameter identification. It enhances the modeling accuracy and performance prediction of PEMFCs, making it highly suitable for developing digital twins and control systems in automotive applications. The YDSE algorithm’s robustness and reliability are further validated through comprehensive experimental results, showcasing its superiority over traditional optimization techniques in handling the complexities of PEMFC parameter identification across diverse applications. In summary, various algorithms have been proposed for PEMFC parameter estimation, demonstrating diverse levels of efficiency and accuracy in Table 1

PEMFC: mathematical formulation

The increasing depletion of fossil fuels and the growing electricity demand have highlighted the significance of renewable energy sources for both small and large-scale industrial applications⁵⁷. While renewable sources are widely utilized, fuel cells have been developed to complement existing green energy solutions due to their susceptibility to environmental factors. Historically, fuel cells have been classified as transportable, portable, and stationary^58,59.

Figure 1 displays the polarization curve of a fuel cell operating at $80^\circ$C. The curve features three distinct regions: activation losses, ohmic losses, and concentration losses⁴¹. The nonlinear activation zone provides insights into the electrochemical processes within the cell. Ohmic losses typically occur in the membrane, while concentration losses result from changes in the concentration gradient within the cell⁵⁹. The overall cell voltage, denoted as $V_{\text {fc}}$, is expressed in equation (1)⁴¹:

$$\begin{aligned} V_{\text {fc}} = E_{\text {cell}} - V_{\text {act}} - V_{\text {ohmic}} - V_{\text {conc}} \end{aligned}$$

(1)

Fig. 1

Fuel cell losses⁴⁰.

In this equation, $V_{\text {act}}$ represents activation polarization, $V_{\text {ohmic}}$ denotes ohmic losses, $V_{\text {conc}}$ refers to concentration losses, and $E_{\text {cell}}$ is the open circuit voltage⁴¹. The current density affects the output voltage in the ohmic region, with the slope influenced by the ionic resistance of the electrolyte. Concentration losses occur due to mass transfer limitations, resulting in a significant voltage drop. The total cell voltage $V_t$ can be increased by connecting multiple cells ($X_n$) in series, as shown in equation (2)⁵⁷:

$$\begin{aligned} V_t = X_n \cdot V_{\text {cell}} \end{aligned}$$

(2)

Equation (3)⁵⁷ considers the variation in temperature surrounding the cell. The open circuit voltage ($E_{\text {cell}}$) is given by:

$$\begin{aligned} E_{\text {cell}} = {\left\{ \begin{array}{ll} 1229 - \frac{44.43}{zF}(T - 298.15) + \frac{rT}{zF} \ln (P_{\text {H}_2} \sqrt{P_{\text {O}_2}}) & \text {for } T \le 273 \\ 1229 - \frac{44.43}{zF}(T - 298.15) + \frac{rT}{zF} \ln \left( \frac{P_{\text {H}_2} \sqrt{P_{\text {O}_2}}}{P_{\text {H}_2\text {O}}^{\text {Sat}}}\right) & \text {otherwise} \end{array}\right. } \end{aligned}$$

(3)

In these equations, $r$, $F$, and $z$ represent the ideal gas constant, Faraday constant, and number of moving electrons, respectively. The temperature of the cell is denoted by $T$, while $P_{\text {H}_2}$ and $P_{\text {O}_2}$ represent the partial pressures of hydrogen and oxygen. The partial pressures are quantified in equations (4) and (5):

$$\begin{aligned} \begin{gathered} P_{\text {H}_2} = 0.5 \times \text {RH}_a \times P_{\text {H}_2\text {O}}^{\text {Sat}} \left( \left( \frac{\text {RH}_a \times P_{\text {H}_2\text {O}}^{\text {Sat}}}{P_a} \times \exp \left( \frac{1.635 \times i_{\text {cell}}/A}{T^{1.334}}\right) \right) ^{-1} - 1\right) \\ P_{\text {O}_2} = \text {RH}_c \times P_{\text {H}_2\text {O}}^{\text {Sat}} \left( \left( \frac{\text {RH}_c \times P_{\text {H}_2\text {O}}^{\text {Sat}}}{P_c} \times \exp \left( \frac{1.635 \times i_{\text {cell}}/A}{T^{1.334}}\right) \right) ^{-1} - 1\right) \end{gathered} \end{aligned}$$

Here, $\text {RH}_a$ and $\text {RH}_c$ denote the anodic and cathodic relative humidity, respectively. The pressures at the anode and cathode are $P_a$ and $P_c$, respectively. The cell area is $A$ and the current is $i_{\text {cell}}$. The relationship between temperature $T$ and the vapor saturation pressure of water $P_{\text {H}_2\text {O}}^{\text {Sat}}$ is given by equation (6). Activation losses are calculated using equation (7), and the oxygen concentration $C_{\text {O}_2}$ is determined by equation (8). Semi-empirical parameters $\delta _1$, $\delta _2$, $\delta _3$, and $\delta _4$ are used to calculate ohmic losses, as shown in equation (9)⁵⁹:

$$\begin{aligned} \log _{10}(P_{\text {H}_2\text {O}}^{\text {Sat}})= & 2.95 \times 10^{-2}(T - 273.15) - 9.19 \times 10^{-5}(T - 273.15)^2 \end{aligned}$$

(4)

$$\begin{aligned} V_{\text {act}}= & -(\delta _1 + \delta _2T + \delta _3T\ln (C_{\text {O}_2}) + \delta _4T\ln (i_{\text {fc}})) \end{aligned}$$

(5)

$$\begin{aligned} C_{\text {O}_2}= & \frac{P_{\text {O}_2}}{5.08 \times 10^6} \exp \left( \frac{498}{T}\right) \end{aligned}$$

(6)

$$\begin{aligned} V_{\text {ohmic}}= & i(R_m + R_c) \end{aligned}$$

(7)

Electrical and ionic resistances are represented by $R_m$ and $R_c$. Equation (10) calculates electronic resistance, and equation (11) determines the membrane parametric coefficient. Concentration polarization is mathematically expressed using equation (12)⁵⁸. The maximum current density is $J_{\text {max}}$, while $J$ is the actual current density, and $B$ is the parametric coefficient or diffusion parameter.

$$\begin{aligned} R_m= & \rho _m\left( \frac{l}{A}\right) \end{aligned}$$

(8)

$$\begin{aligned} \rho _m= & \frac{181.6\left[ 1 + 0.03\left( \frac{i}{A}\right) + 0.062\left( \frac{T}{303}\right) ^2\left( \frac{i}{A}\right) ^{2.5}\right] }{\left[ \gamma - 0.634 - 3\left( \frac{i}{A}\right) \right] \times \exp \left( 4.18\left( \frac{T - 303}{T}\right) \right) } \end{aligned}$$

(9)

$$\begin{aligned} V_{\text {conc}}= & -B \ln \left( 1 - \frac{J}{J_{\text {max}}}\right) \end{aligned}$$

(10)

YDSE algorithm

The YDSE optimizer is a recent population-based meta-heuristic algorithm inspired by the classical physics experiment demonstrating light’s wave-like properties. In YDSE, wave interference occurs under specific conditions: monochromatic light sources with identical frequencies and directions, equal amplitudes, and narrow apertures. Constructive interference (CI) happens when waves from both apertures meet in phase, while destructive interference (DI) occurs when waves meet out of phase. A detailed mathematical formulation of the YDSE optimizer is provided, and the algorithm’s flowchart is illustrated in Fig. 2. It describes the complete workflow of the proposed YDSE algorithm for parameter estimation in PEM fuel cells. The method begins with initializing a population of solutions, each representing a candidate parameter set. Inspired by wave optics, the algorithm simulates a monochromatic light source emitting waves that pass through two slits−mimicking the dual-path exploration of the solution space. Using Huygens’ principle, outgoing wavefronts are generated from each solution, forming two new secondary positions (the first and second sources).

The interference pattern is then computed by evaluating the path difference between these sources, determining whether a given solution experiences constructive or destructive interference. Constructive interference amplifies the solution’s movement toward optimal regions (exploitation), while destructive interference pushes the solution away from suboptimal areas (exploration). The amplitude and intensity at each fringe location are updated iteratively using dynamic mathematical equations that simulate fringe brightness and contrast, effectively encoding a search bias toward promising areas.

Depending on the computed interference mode (even or odd fringe), the algorithm selectively updates positions using distinct mathematical rules. Even fringes invoke reinforcement (brightness-based updates), while odd fringes introduce diversification (dark fringe-driven exploration). A special case is handled at the central bright fringe (zero path difference), which is used to refine the global best solution by simulating high-intensity central interference. This core feedback mechanism continues until convergence criteria−typically a minimum error or maximum iteration limit−are satisfied. Overall, the algorithm effectively balances exploration and exploitation by mimicking quantum interference behavior, as illustrated in the various blocks of Fig. 2.

Fig. 2

The proposed YDSE structure.

Initialization step

In the YDSE method, a monochromatic light wave source (S) is directed towards a barrier with two closely positioned slits. The initial light source $S$, consisting of $NP$ waves, is generated as follows:

$$\begin{aligned} S_{i,j}= & Lb_j + \operatorname {rand} \times (Ub_j - Lb_j), \end{aligned}$$

(11)

$$\begin{aligned} i= & 1, 2, \ldots , NP, \end{aligned}$$

(12)

$$\begin{aligned} j= & 1, 2, \ldots , \text {Dim} \end{aligned}$$

(13)

Where, $S_{i,j}$ represents the $j^{th}$ variable of the $i^{th}$ wave, $Lb_j$ and $Ub_j$ are the lower and upper bounds of the $j^{th}$ variable, and $\operatorname {rand}$ is a random number between 0 and 1.

Huygens principle

After passing through the two slits, monochromatic waves disperse in various directions by Huygens’ principle. Each point on the wavefront functions as a source for a new wave. The initial population of $NP$ waves is generated as follows:

$$\begin{aligned} FS_i= & S_i + L \times \operatorname {rand}1(-1,1) \times (S_{\text {mean}} - S_i), \quad i = 1, 2, \ldots , NP \end{aligned}$$

(14)

$$\begin{aligned} SS_i= & S_i - L \times \operatorname {rand}2(-1,1) \times (S_{\text {mean}} - S_i), \quad i = 1, 2, \ldots , NP \end{aligned}$$

(15)

Here, $FS_i$ and $SS_i$ are points created on the wavefronts outgoing from the first and second slits, respectively. $S_{\text {mean}}$ is the mean of the population $S$ and is calculated by:

$$\begin{aligned} S_{\text{ mean } }=\frac{1}{NP} \sum _{i=1}^{NP} S_i \end{aligned}$$

(16)

Traveling waves and path difference update

Waves from the slits travel different distances, creating interference patterns. The positions are updated as follows:

$$\begin{aligned} X_i = \left( \frac{FS_i + SS_i}{2}\right) + \Delta L \end{aligned}$$

(17)

The path difference $\Delta L$ is defined by:

$$\begin{aligned} \Delta L={\left\{ \begin{array}{ll} 0 & \text{ if } \text{ CI } \text{ occurs } \text{ at } m=0 \\ (2m+1) \frac{\lambda }{2} & \text{ if } \text{ DI } \text{ occurs } \text{ at } \text{ odd } m \\ m \lambda & \text{ if } \text{ CI } \text{ occurs } \text{ at } \text{ even } m \end{array}\right. } \end{aligned}$$

(18)

Generation of light patterns (fringes)

Following the emergence of CI and DI, patterns of light known as fringes start to manifest on the projection screen. The population X, generated per Equation 17, can be conceptualized as a collection of these fringes resulting from CI and DI. The positions of these fringes remain fixed, mirroring the behavior observed in YDSE, where the interference between any two waves is persistent. Therefore, if m = 0, $X_m$=0 represents the central fringe. $X_{m_{\text{ odd } }}$ represents the dark fringe, $X_{m_{\text{ even }}}$ represents the bright fringe. Every bright or dark fringe symbolizes a solution within the search space. The central fringe denotes the optimal solution within the search space. Through a series of iterations, the set of fringes undergoes optimization.

Wave amplitude update

Constructive interference (CI) increases amplitude:

$$\begin{aligned} A_{\text{ bright } }^{t+1}= & \frac{2}{1+\sqrt{\left| 1-\beta ^2\right| }} \end{aligned}$$

(19)

$$\begin{aligned} \beta= & \frac{t}{T} \cosh (\pi / t) \end{aligned}$$

(20)

Destructive interference (DI) decreases amplitude:

$$\begin{aligned} A_{\text{ dark } }^{t+1}=\delta \times \tanh ^{-1}\left( -\frac{t}{T}+1\right) \end{aligned}$$

(21)

YDSE optimizer

Exploration phase (destructive interference)

In the exploration phase, solutions traverse the dark regions:

$$\begin{aligned} X_{m_{\text {odd}}}^{t+1} = X_{m_{\text {odd}}}^t - \left( r_1 \times A_{\text {dark}}^{t+1} \times Int_{m_{\text {odd}}}^{t+1} \times X_{m_{\text {odd}}}^t - z \times X_{\text {best}}^t \right) \end{aligned}$$

(22)

Intensity is calculated by:

$$\begin{aligned} Int_{m_{\text {odd}}}^{t+1} = Int_{\max }^{t+1} \times \cos ^2\left( \frac{\pi d}{\lambda L} y_{\text {dark}}^{t+1}\right) \end{aligned}$$

(23)

Distance is:

$$\begin{aligned} y_{\text {dark}} = \frac{\lambda L}{d}\left( m+\frac{1}{2}\right) \end{aligned}$$

(24)

Exploitation phase (constructive interference)

In the exploitation phase, the algorithm exploits bright fringe areas:

$$\begin{aligned} X_{m_{\text{ even } }^{t+1}}^{t+1}= & X_{m_{\text{ even } }}^t - \left( (1-g) \times A_{\text{ bright } }^{t+1} \times Int_{m_{\text{ even } }^{t+1}} \times X_{m_{\text{ even } }}^t + g \times Y \right) \end{aligned}$$

(25)

$$\begin{aligned} Y= & X_{m_{\text {rand}1}}^t - X_{m_{\text {rand}2}}^t \end{aligned}$$

(26)

Intensity is calculated by:

$$\begin{aligned} Int_{m_{\text {even}}}^{t+1} = Int_{\max }^{t+1} \times \cos ^2\left( \frac{\pi d}{\lambda L} y_{\text {bright}}^{t+1}\right) \end{aligned}$$

(27)

Central region update:

$$\begin{aligned} X_{m_{\text {zero}}}^{t+1} = X_{\text {best}}^t + \left( A_{\text {bright}}^{t+1} \times Int_{\max }^{t+1} \times X_{m_{\text {zero}}}^t - r_3 \times z \times X_{r_b}^t \right) \end{aligned}$$

(28)

Combined update strategy:

$$\begin{aligned} X_m^{t+1} = {\left\{ \begin{array}{ll} X_{\text {best}}^t + \left( A_{\text {bright}}^{t+1} \times Int_{\max }^{t+1} \times X_m^t - r_3 \times z \times X_{r_b}^t \right) , & \text {if } m=0 \\ X_m^t - \left( (1-g) \times A_{\text {bright}}^{t+1} \times Int_m^{t+1} \times X_m^t + g \times Y \right) , & \text {if } m \text { is even} \\ X_m^t - \left( r_1 \times A_{\text {dark}}^{t+1} \times Int_m^{t+1} \times X_m^t - Z \times X_{\text {best}}^t \right) , & \text {if } m \text { is odd} \end{array}\right. } \end{aligned}$$

(29)

Estimation of fuel cell parameters using YDSE algorithm

Accurate parameter estimation is crucial for the optimal performance of PEMFC. This section introduces the YDSE algorithm as a novel approach for this task. The YDSE algorithm leverages the principles of wave interference to enhance optimization performance. The process involves several key steps:

Problem formulation for estimating PEM fuel cell parameters

The goal is to accurately determine six critical parameters of the PEMFC model: $\delta _1$, $\delta _2$, $\delta _3$, $\delta _4$, $B$, and $\gamma$.

The optimization problem is formulated to minimize the Sum of Square Error (SSE) between the measured voltage $V_m$ and the estimated voltage $V_{\text {fc}}$ over $N$ data points, as defined by the following objective function:

$$\begin{aligned} SSE = \sum _{i=1}^N (V_m - V_{\text {fc}})^2 \end{aligned}$$

(30)

Table 2 presents the constraints for the decision variables. The primary objective is to minimize the SSE.

Table 2 Variable limits.

The proposed approach of estimating the parameters of PEMFC using YDSE algorithm

To estimate the parameters of PEMFC using YDSE algorithm, as shown in the following steps and in Algorithm 1:

Algorithm 1

YDSE Algorithm for Estimating PEM Fuel Cell Parameters

The YDSE algorithm involves the following steps to estimate the PEMFC parameters:

• 1. Initialization The initial population of light waves S is generated within the defined lower and upper bounds using the formula:

  $$\begin{aligned} S_{i,j} = Lb_j + \text {rand} \times (Ub_j - Lb_j) \end{aligned}$$

  (31)

• 2. Huygens’ principle Generate outgoing wavefronts FS and SS using:

  $$\begin{aligned} FS_i= & S_i + L \times \text {rand}(-1, 1) \times (S_{mean} - S_i) \end{aligned}$$

  (32)
  $$\begin{aligned} SS_i= & S_i - L \times \text {rand}(-1, 1) \times (S_{mean} - S_i) \end{aligned}$$

  (33)

• 3. Path difference Compute the path difference $\Delta L$:

  $$\begin{aligned} \Delta L = {\left\{ \begin{array}{ll} m \lambda & \text {if } m \text { is even} \\ (2m + 1) \frac{\lambda }{2} & \text {if } m \text { is odd} \end{array}\right. } \end{aligned}$$

  (34)

• 4. Amplitude and Intensity updates Update amplitude $A_{bright}$ and $A_{dark}$:

  $$\begin{aligned} A^{t+1}_{bright}= & \frac{2}{1 + \sqrt{|1 - \beta ^2|}} \end{aligned}$$

  (35)
  $$\begin{aligned} A^{t+1}_{dark}= & \delta \times \tanh ^{-1} \left( -\frac{t}{T} + 1 \right) \end{aligned}$$

  (36)

• 5. Exploration and exploitation phases Update positions based on interference patterns:

  $$\begin{aligned} X^{t+1}_{modd} = X^t_{modd} - \left( r1 \times A^{t+1}_{dark} \times Int^{t+1}_{modd} \times X^t_{modd} - z \times X^t_{best} \right) \end{aligned}$$

  (37)
  $$\begin{aligned} X^{t+1}_{meven} = X^t_{meven} - \left( (1 - g) \times A^{t+1}_{bright} \times Int^{t+1}_{meven} \times X^t_{meven} + g \times Y \right) \end{aligned}$$

  (38)

• 6. Central region update Update the position for the central region fringe:

  $$\begin{aligned} X^{t+1}_{mzero} = X^t_{best} + \left( A^{t+1}_{bright} \times Int^{t+1}_{max} \times X^t_{mzero} - r3 \times z \times X^t_{rb} \right) \end{aligned}$$

  (39)

• 7. Output Return the best solution $X_{best}$ and the corresponding parameters $\delta _1, \delta _2, \delta _3, \delta _4, B, \gamma$.

Experimental setup

The performance of the proposed YSDE algorithm is analyzed on a commercial PEMFC viz. BCS500W⁶⁰. The dataset has been considered for fuel cell modeling validation because it is a publicly available dataset that contains a wide range of operating conditions and performance data for proton exchange membrane (PEM) fuel cells. This makes it ideal for testing the accuracy and robustness of fuel cell models under various conditions. As discussed in the modelling section, six parameters need to be extracted. The experiments used a dataset of measured cell voltages under various conditions. The proposed method of parameter extraction is implemented on MATLAB IDE installed on a laptop embedded with an Intel i5 processor and 32 GB RAM. The YDSE algorithm was compared with five other metaheuristic algorithms: SCA, MFO, HHO, GWO, and ChOA. The comparison was based on the SSE metric, convergence speed, and accuracy.To ensure fair comparisons between the proposed algorithm and the state-of-the-art algorithms, Table 3 presents the parameter settings for all the algorithms involved in this study, summarizing the population size, number of iterations, and algorithm-specific parameters for each method evaluated. These parameter settings have been chosen based on standard configurations in the literature to ensure fair comparisons.

Fairness of comparisons

A consistent and rigorous methodology was applied across all algorithms to ensure the validity and scientific integrity of the comparisons presented in this study. Uniform parameter settings were implemented, with all algorithms sharing the same population size ($N = 30$) and maximum number of iterations ($T = 1000$). These values were chosen based on standard configurations in the literature and were deemed sufficient for addressing the complexity of the PEMFC parameter estimation problem. Additionally, identical bounds and constraints were applied to the decision variables for all algorithms, ensuring that each began its search within the same solution space.

The algorithms’ initialization was standardized by generating random initial populations within the same defined ranges for all methods. Where applicable, the same random seed was used to eliminate variability introduced by randomness and ensure consistency in initial conditions. Furthermore, all algorithms were executed under identical computational conditions, using the same hardware and software environments, to eliminate performance differences arising from system-level factors.

The performance of each algorithm was evaluated using consistent metrics, including the Sum of Squared Errors (SSE), convergence speed, and statistical measures such as mean, standard deviation, and the best and worst solutions. These metrics provided a comprehensive evaluation framework . For additional transparency and reproducibility, the supplementary materials (if applicable) include detailed descriptions of each algorithm’s initialization procedures and implementation specifics. By adhering to these standardized methodologies, we ensured that the comparative analysis presented in this study is fair and scientifically robust.

Table 3 Parameter settings for algorithms involved in the study.

Table 4 Parameters identified for PEMFC at the best SSE.

Table 5 Decision variables based on YDSE method over 30 independent runs.

Table 6 Decision variables based on SCA method over 30 independent runs.

Table 7 Decision variables based on MFO method over 30 independent runs.

Table 8 Decision variables based on GWO method over 30 independent runs.

Table 9 Decision variables based on HHO method over 30 independent runs.

Table 10 Decision variables based on ChOA method over 30 independent runs.

Table 11 Comparison between estimated and measured voltage at the best solution.

Table 12 Statistical analysis for PEMFC.

Experimental results and numerical analysis

This section presents the experimental results and numerical analysis conducted to evaluate the performance of the proposed YDSE algorithm in estimating the parameters of PEMFC. The experiments were designed to compare the YDSE algorithm with other well-known metaheuristic optimization methods, including the SCA , MFO , HHO , GWO , and ChOA. Key performance convergence speed, accuracy, and Sum of Square Error (SSE) between estimated and actual cell voltages, were used to assess the effectiveness of the proposed algorithm. The results highlight the superior performance of the YDSE algorithm in achieving higher accuracy and faster convergence compared to the other algorithms. Detailed statistical measures and comparative analyses are provided to demonstrate the robustness and reliability of the YDSE algorithm in addressing the parameter estimation challenges of PEMFC models.

The results of this study demonstrate the efficacy of the Young’s Double-Slit Experiment (YDSE) algorithm in addressing the complex and nonlinear problem of parameter estimation for Proton Exchange Membrane Fuel Cells (PEMFCs). By focusing on this domain-specific application, we have demonstrated how YDSE can be effectively tailored to address a critical real-world optimization challenge. However, it is essential to recognize that YDSE is a versatile metaheuristic algorithm with the potential to tackle a broad range of optimization problems, including standard benchmark global optimization problems.

Although this paper deliberately concentrates on PEMFC modeling to provide a detailed and focused contribution, future research will explore the application of YDSE to other problem domains. In particular, evaluating its performance on commonly used benchmark optimization functions, such as those in the CEC competitions, will provide deeper insights into its general applicability and competitiveness compared to state-of-the-art metaheuristics. Such studies will not only validate YDSE’s global optimization capabilities but also establish its robustness across diverse problem landscapes.

Table 4 shows the values of the six parameters identified for PEMFC at the best SSE using YDSE, SCA, MFO, HHO, and GWO. It presents the parameters identified for PEMFC at the best Sum of Square Error (SSE) using various optimization algorithms, including YDSE, SCA, MFO, HHO, GWO, and ChOA. The parameters considered are $\delta _1$, $\delta _2$, $\delta _3$, $\delta _4$, $\gamma$, and B. The results indicate that the YDSE algorithm achieved the most favorable parameter estimates with the lowest SSE value compared to the other algorithms. This superior performance can be attributed to the following points.

The decision variables based on YDSE, SCA, MFO, GWO, HHO, and ChOA optimizers are shown in Tables 5, 6, 7, 8, 9, and 10 respectively over 30 independent runs. Table 11 compares estimated and measured voltage at the best solution using each optimizer.

Table 5 presents the decision variables derived from 30 independent runs using the YDSE method. The results show a high degree of consistency across runs, indicating the robustness of the YDSE algorithm. The variables $\delta _1, \delta _2, \delta _3, \delta _4, \gamma ,$ and $B$ remain within narrow ranges, demonstrating the algorithm’s stability in converging to optimal parameter values for PEM fuel cells.

Table 6 presents the decision variables obtained through the SCA over 30 independent runs. Compared to the YDSE method, the SCA method exhibits greater variability in the decision variables, indicating potential challenges in achieving consistent convergence. This variability may impact the reliability of the parameter estimates in practical applications.

Table 7 details the decision variables based on the MFO method over 30 independent runs. The MFO method also exhibits variability in the decision variables, although it outperformscalculated SCA in some instances. Despite this, MFO does not achieve the same level of consistency as YDSE, suggesting that YDSE provides more reliable parameter estimates for PEM fuel cells.

Table 8 lists the decision variables derived from the GWO over 30 independent runs. The GWO method demonstrates improved consistency compared to SCA and MFO but still falls short of the robustness seen with YDSE. The decision variables exhibit some variability, which could affect the accuracy of the parameter estimation.

Table 9 presents the decision variables obtained using the HHO over 30 independent runs. HHO shows better consistency performance than SCA and MFO, but like GWO, it does not match the robustness of YDSE. The variability in the decision variables indicates that while HHO is a strong performer, YDSE offers superior reliability.

Table 10 provides the decision variables based on the ChOA over 30 independent runs. ChOA exhibits notable variability in its decision variables, similar to SCA and MFO. This suggests that ChOA may face challenges in achieving consistent parameter estimates, further highlighting the robustness and reliability of the YDSE algorithm for PEM fuel cell parameter estimation.

Table  11 compares the estimated and measured voltages at the best solution for each optimization method. The YDSE algorithm consistently achieves estimated voltages closest to the measured values, demonstrating its superior accuracy and effectiveness. This comparison highlights the YDSE algorithm’s ability to minimize the Sum of Square Error (SSE) between the estimated and actual voltages, outperforming other algorithms such as SCA, MFO, GWO, HHO, and ChOA. The close match between the estimated and measured voltages underscores the YDSE algorithm’s potential for precise parameter estimation in PEM fuel cells.

It is worth noting that the YDSE optimizer achieved the nearest value near the measured one. Table 12 presents the statistical measures in terms of (Minimum, Standard Deviation, Mean, Maximum). YDSE achieved the lowest values.It provides a detailed statistical analysis of the performance of different optimization algorithms in estimating the PEMFC parameters. The statistical measures include the minimum (Min), standard deviation (SD), mean (Mean), and maximum (Max) values of the objective function across 30 independent runs for each algorithm. YDSE algorithm demonstrates superior performance with the lowest Min, SD, Mean, and Max values compared to other algorithms. Specifically, the YDSE algorithm achieves a minimum value of 1.945415255, demonstrating its ability to find optimal or near-optimal solutions consistently. The standard deviation of 2.21E−06 reflects the high precision and reliability of the YDSE algorithm, showing minimal variation across multiple runs. In contrast, the SCA and MFO exhibit higher variability and less consistent results. The SCA algorithm shows a significant standard deviation of 0.06797143 and a higher mean value of 2.054536683, suggesting less stability and precision. The MFO algorithm exhibits even greater variability, with a standard deviation of 0.193402281 and a mean value of 2.132134015, further underscoring the robustness of the YDSE algorithm. The GWO and HHO also demonstrate notable variability. GWO exhibits a standard deviation of 0.206061156 and a mean value of 2.13E+00, whereas HHO displays a standard deviation of 0.077321218 and a mean value of 1.971872889. Although these algorithms perform better than SCA and MFO in some aspects, they still fall short of the consistency and precision achieved by the YDSE algorithm. The ChOA shows improved performance with a lower standard deviation of 0.016705215, yet it still cannot match the minimal variability and high accuracy of the YDSE algorithm. Overall, the statistical analysis underscores the effectiveness of the YDSE algorithm in providing reliable and accurate parameter estimates for PEMFCs, making it a superior choice for such optimization tasks compared to the other evaluated methods.

Fig. 3

Robustness curves.

Fig. 4

Convergence curve.

Figure 3 shows the robustness curves of all optimizers. Figure 3 presents the robustness curves of the various optimization algorithms used for parameter estimation of the PEM fuel cell. The robustness curves illustrate the stability and consistency of the YDSE algorithm in comparison to other methods. The YDSE algorithm consistently achieves lower cost function values across multiple runs, indicating its robustness in handling the inherent uncertainties and variations in the optimization process. The minimal variance in the results further validates the reliability of the YDSE algorithm in providing accurate parameter estimates for the PEM fuel cell.

Figure 4 illustrates the convergence behavior of the YDSE algorithm and its comparison with other optimization techniques. The convergence curve highlights the efficiency of the YDSE algorithm in rapidly approaching the optimal solution. The YDSE algorithm exhibits a faster convergence rate, reaching the minimum cost function value in fewer iterations than the other algorithms. This accelerated convergence not only reduces computational time but also enhances the, such as overall efficiency of the parameter estimation process. The superior convergence performance of the YDSE algorithm underscores its effectiveness in optimizing complex systems like the PEM fuel cell. The results show that YDSE achieved the fastest convergence rate.

Cross-stack performance analysis of YSDE for PEMFC system identification

This section presents the evaluation of the proposed YSDE algorithm for estimating unknown parameters of Proton Exchange Membrane Fuel Cells (PEMFCs) using three benchmark stacks: 250W, 500W, and H-12. These stacks, commonly cited in the literature^27,36,48, are selected due to their established characteristics, summarized in Table 13. To benchmark YSDE’s performance, several well-known optimizers are employed and evaluated using key performance metrics: best, average, and worst sum of squared errors (SSE), standard deviation (SD), convergence rate, Friedman ranking (FRK), multiple comparison (MC) test, and the Wilcoxon rank-sum test. A uniform testing environment is maintained by setting the maximum number of function evaluations and population size to 2500 and 25, respectively. Other parameters follow the settings reported in the respective reference studies for fairness.

Table 13 Characteristics of the employed PEMFC stacks.

500W PEMFC stack

The 500W PEMFC stack is used to benchmark the algorithms under consideration. Each optimizer is independently executed 30 times due to its stochastic nature. The results, summarized in Table 14, indicate that YSDE outperforms its counterparts in most metrics, except for the worst-case SSE, where IChOA shows slightly better results. The Wilcoxon rank-sum test confirms the statistical significance of YSDE’s superiority, and the Friedman rank of 1.80 further supports its leading performance. These findings underscore YSDE’s high accuracy and consistency in parameter estimation.

Table 14 Performance of various algorithms on the 500W PEMFC stack.

250W PEMFC stack

Further assessment is conducted using the 250W PEMFC stack. As with the previous test, estandard deviation (SD)ach algorithm is run independently 30 times. Results show that YSDE consistently achieves better performance in terms of average SSE, worst-case SSE, SD, and FRK, and is highly competitive with MFO for the best SSE. The associated Wilcoxon test values reinforce the statistical difference in favor of YSDE, demonstrating its reliability across varying stack sizes as shown in Table 15.

Table 15 Performance of various algorithms on the 250W PEMFC stack.

H-12 PEMFC stack

To validate YSDE’s robustness, the H-12 stack is employed for an additional test. As detailed in Table 16, YSDE maintains superior performance in average SSE, worst-case SSE, SD, and FRK. Although other algorithms such as IChOA, MFO, and HHO closely match its best-case SSE, YSDE shows a statistically significant edge based on the Wilcoxon test. These results affirm YSDE’s capability in effectively estimating PEMFC parameters across diverse stack configurations.

Table 16 Performance of various algorithms on the H-12 PEMFC stack.

Statistical performance metrics

To provide a comprehensive evaluation of the proposed YDSE algorithm’s performance, we computed several standard statistical metrics commonly used in parameter estimation and optimization studies: standard deviation (STD), root mean square error (RMSE), mean absolute error (MAE), correlation coefficient (R), and efficiency.

• Standard Deviation (STD): Measures the variability of error values across multiple runs, indicating robustness.

  $$\begin{aligned} \textrm{STD} = \sqrt{\frac{1}{N-1} \sum _{i=1}^N (x_i - \bar{x})^2} \end{aligned}$$

  where $x_i$ is the error in the $i^\textrm{th}$ run, $\bar{x}$ is the mean error, and $N$ is the number of runs.

• Root Mean Square Error (RMSE): Represents the square root of the average squared differences between estimated and actual values.

  $$\begin{aligned} \textrm{RMSE} = \sqrt{\frac{1}{N} \sum _{i=1}^N (y_i - \hat{y}_i)^2} \end{aligned}$$

  where $y_i$ and $\hat{y}_i$ are the measured and estimated values respectively.

• Mean Absolute Error (MAE): The average absolute difference between estimated and true values.

  $$\begin{aligned} \textrm{MAE} = \frac{1}{N} \sum _{i=1}^N |y_i - \hat{y}_i| \end{aligned}$$

• Correlation Coefficient (R): Quantifies the linear correlation between estimated and experimental values, with values close to 1 indicating better fit.

  $$\begin{aligned} R = \frac{\sum _{i=1}^N (y_i - \bar{y})(\hat{y}_i - \bar{\hat{y}})}{\sqrt{\sum _{i=1}^N (y_i - \bar{y})^2} \sqrt{\sum _{i=1}^N (\hat{y}_i - \bar{\hat{y}})^2}} \end{aligned}$$

• Efficiency: Qualitatively assessed based on convergence speed and error reduction rate.

Table 17 summarizes these metrics computed over 30 independent runs for the YDSE algorithm and the comparison metaheuristics. The YDSE method achieves the lowest STD, RMSE, and MAE values and the highest correlation coefficient, demonstrating its superior accuracy and stability.

Table 17 Statistical performance comparison of YDSE and other metaheuristic algorithms based on 30 independent runs.

These statistical results validate the robustness and effectiveness of the proposed YDSE algorithm in accurately estimating PEM fuel cell parameters. Additionally, convergence plots (see Figs. 3, 4) further demonstrate that YDSE attains faster and more stable convergence compared to other metaheuristic methods.

It is important to note that the current study inherently addresses the dynamic operation of PEMFC stacks under varying cell temperature and partial pressures of reactant gases. The experimental dataset used for parameter estimation encompasses a range of operating conditions with realistic fluctuations in temperature and pressure. Therefore, the reported performance metrics and parameter estimation results for the YDSE algorithm in this section implicitly reflect its stability and accuracy under such dynamic variations. No additional parameters or modifications were necessary to validate the algorithm’s robustness in these time-varying scenarios, confirming its suitability for practical PEMFC applications.

Conclusion

In this study, we introduced the YDSE algorithm as a novel metaheuristic optimization technique for estimating the parameters of PEMFC. The main findings demonstrate that the YDSE algorithm better minimizes the Sum of Squared Error (SSE) between the estimated and actual cell voltages than other well-known optimization methods, including the SCA, MFO, HHO, GWO, and ChOA. The YDSE algorithm consistently provided more accurate and stable results, showcasing its robustness and faster convergence rates. The implications of this study are significant for improving PEMFC system modeling and control, which is essential for their application in both automotive and stationary power systems. The scientific novelty of this study lies in the absolute introduction of a new optimization framework based on wave interference principles. This novel process leverages constructive and destructive interference to effectively explore the solution space, distinguishing it from traditional algorithms. The YDSE algorithm’s robustness, faster convergence, and high accuracy make it a valuable tool for precise parameter estimation, with theoretical and practical applicability extending to various engineering domains.

This paper presents the application of the Young’s Double-Slit Experiment (YDSE) algorithm to the critical problem of parameter estimation for Proton Exchange Membrane Fuel Cells (PEMFCs). By demonstrating superior performance in terms of accuracy, convergence, and robustness compared to other metaheuristic algorithms, the YDSE algorithm proves to be a powerful tool for this specific domain. While YDSE is inherently a general-purpose optimization algorithm, this study intentionally focuses on a domain-specific problem with significant real-world relevance.

The cross-stack analysis confirmed that YSDE achieved up to 97.8% lower average SSE compared to GWO, 97.6% over SCA, and improved worst-case SSE by 70.6% relative to IChOA. Moreover, YSDE maintained a reduction in standard deviation up to 91.3% and in some cases reached a 1000-times lower variation, underscoring its high stability. The algorithm also achieved up to 87% improvement in Friedman ranking scores across all tested stacks. These statistical findings confirm YSDE’s strong performance consistency regardless of PEMFC stack characteristics.

Despite its promising results, the study has certain limitations. The YDSE algorithm’s performance was evaluated solely for PEMFC parameter estimation, necessitating further validation on other fuel cell types and various optimization problems to generalize the findings. Additionally, the computational complexity of the YDSE algorithm should be explored to ensure its scalability for large-scale applications.

Future research should focus on applying the YDSE algorithm to diverse optimization problems and other types of fuel cells to validate its versatility and effectiveness. Exploring hybrid optimization approaches combining YDSE with other metaheuristic algorithms could enhance performance. Additionally, investigating the computational efficiency and potential parallelization of the YDSE algorithm will be essential for its application in large-scale and real-time systems. Developing adaptive versions of YDSE that dynamically adjust parameters based on optimization progress could further improve its robustness and convergence speed.

While the current study extensively validates the YDSE algorithm using the BCS500W commercial PEMFC dataset, future work will extend this evaluation to other commercial PEMFC systems. Applying the proposed method to diverse PEMFC datasets will further demonstrate its generalizability, robustness, and practical applicability across different fuel cell technologies. These additional experiments will help reinforce the effectiveness of YDSE in accurately estimating PEMFC parameters under a wide range of operating conditions and hardware configurations.