Introduction

Switched Reluctance Motors (SRMs) have become increasingly popular in industrial applications due to their robust design, simplicity, and high efficiency. However, they face challenges such as torque ripple and acoustic noise, which arise from their inherent nonlinear magnetic properties and the nature of their switching operations1,2. These issues hinder the use of SRMs in applications that require smooth torque output and precise speed control, especially under varying loads3,4.

To mitigate the issues of torque ripple and improve control accuracy, researchers have explored various control strategies for SRMs. Traditional proportional-integral-derivative (PID) controllers are widely used for their simplicity and effectiveness in maintaining stable speed control5. However, advanced controllers, such as fractional order PID (FOPID)6, fuzzy logic control (FLC)7, and fast terminal sliding mode control (FTSMC) 8, have also been implemented to handle SRM’s nonlinear behavior and provide better performance in high-torque and high-speed applications. Additionally, torque sharing functions (TSF) specifically address torque ripple by distributing torque smoothly across phases9. The versatility of these controllers, from the cascaded PID and FOPID to fuzzy-based configurations, highlights the diversity of approaches aimed at optimizing SRM control for enhanced stability and reduced ripple10,11.

Optimization algorithms play a vital role in tuning controller parameters to achieve optimal performance in SRM systems. Traditional optimization methods such as particle swarm optimization (PSO)12 and genetic algorithms (GA)6 have been successfully applied to SRM control, specifically for improving speed regulation. More recent algorithms, including ant colony optimization (ACO)13 and multiple stage ant colony optimization (MSACO)14, have focused on minimizing torque ripple and enhancing control precision. The dung beetle optimizer (DBO)12 and ant lion optimizer (ALO)15 have shown significant improvements in convergence speed and computational efficiency. Additionally, bio-inspired algorithms like the flower pollination algorithm (FPA)16 and the spotted hyena optimizer (SHO)6, as well as techniques like local unimodal sampling (LUS)6, have been utilized to tune cascaded PID controllers, demonstrating the evolution of intelligent algorithms in SRM optimization.

Several studies have sought to address the control and performance challenges of SRMs by integrating advanced optimization techniques and control strategies. Al-Amyal et al.14 utilized multiple stage ant colony optimization (MSACO) to optimize switching angles in direct instantaneous torque control, which reduced torque ripple and enhanced motor efficiency. Their method included a current detector to minimize negative torque, achieving a smoother torque profile. da Cunha Reis et al.17 explored different control techniques for SRMs by modulating excitation voltage and switching angles. They demonstrated that dynamic control parameters improved efficiency and response time while maintaining low computational costs, particularly in speed control applications. Divandari et al.18 proposed a fuzzy logic-based FTSMC, combining robustness and reduced chattering effects. Their results showed improved speed stability and faster response times compared to conventional PI controllers, making FTSMC suitable for applications with parameter uncertainties. Gengaraj et al.19 employed the FPA with a TSF to minimize torque ripple. By optimizing commutation angles, their method effectively distributed torque across motor phases, making it particularly beneficial for applications that demand smooth torque output.

Kotb et al.6 implemented LUS and the SHO to tune cascaded PID controllers for SRMs. Their results showed that the SHO-based cascaded PID controller reduced torque ripple more effectively than the FOPID controller, providing enhanced speed response across varying load conditions. Rajendran and Karthik20 compared PI and FLCs, finding that while PI controllers ensured reliable speed control, FLCs were better suited for handling SRM’s nonlinear dynamics and torque control. Jabari and Rad12 applied the DBO and ALO to optimize PID and FOPID controllers, which led to reduced torque ripple and improved speed control. Their study highlighted the benefits of bio-inspired optimization methods in refining SRM performance. The literature review summary is provided in Table 1.

Table 1 Overview of utilizing controller and optimization method for SRM in the recent papers.
Full size table

To effectively controls the SRM, an optimized method for identifying the switching angles is essential for minimizing torque ripple and ensuring smooth operation22. In this study, we use a combination of proportional-integral (PI) and fractional-order proportional-integral-derivative (FOPID) controllers, integrated with the hybrid adaptive ant lion optimization (HAALO) algorithm. The HAALO algorithm dynamically adjusts the switching angles in real-time, optimizing their values based on the motor’s operating conditions to achieve better performance. The switching angles determine the timing for current switching between the motor’s phases, and their optimization is crucial for reducing torque ripple and enhancing stability. The SRM is powered by a full-bridge converter, which regulates the current delivered to the motor’s phases and ensures the appropriate voltage levels are maintained. This converter type was selected for its precision in controlling phase currents and ensuring stable operation across varying speeds and loads, which complements the performance of the proposed control method.

This paper presents the HAALO algorithm integrated with PI and FOPID controllers to improve SRM performance. The main contributions are as follows:

  1. 1.

    Fastest and optimized parameters with HAALO: HAALO continuously adjusts optimization parameters, enhancing SRM control by adapting to diverse load conditions and achieving more effective torque ripple reduction than conventional methods.

  2. 2.

    Enhanced PI and FOPID controllers: By leveraging HAALO, the PI and FOPID controllers achieve superior speed regulation and torque stability, accommodating SRM’s nonlinear characteristics and outperforming standard PI and FOPID setups.

  3. 3.

    Improved torque ripple and speed response: Simulation results show that HAALO-optimized PI and FOPID controllers provide significant torque ripple reduction and enhanced speed stability, surpassing algorithms such as PSO, PPSO, GEO, GA, ALO, and RIME-optimized PID and FOPID controllers.

  4. 4.

    Robust performance across operating conditions: The adaptive PI and FOPID controllers optimized with HAALO maintain efficient SRM control under various speeds and loads, making them suitable for dynamic industrial applications.

The paper is organized as follows: “Mathematical model of the switched reluctance motor” section addresses the modeling of the SRM, with a thorough explanation of its nonlinear characteristics. In “Optimization” section, we introduce the design and development of both the ALO and the HAALO methods. “Results of the simulation and analysis” section goes into detail on the HAALO method, emphasizing its effectiveness for parameter tuning. “Comparison in different scenarios” section presents simulation results, comparing the performance of HAALO with other commonly used controllers and meta-heuristic optimization techniques. Lastly, “Conclusions” section concludes with a summary of key insights and suggestions for future research directions.

Mathematical model of the switched reluctance motor

The mathematical model of the SRM describes the complex interaction between electrical inputs, magnetic characteristics, and mechanical outputs, enabling us to understand and control the motor’s operation. At the core of SRM modeling are three main relationships: the voltage applied across the windings, the flux linkage in response to the rotor’s position, and the resulting torque generated by electromagnetic forces.

The voltage equation for each SRM phase describes how applied voltage is divided between resistive losses and the time-dependent changes in the flux linkage. This equation can be expressed as:

$$Vin = Rs \times i + \frac{{d\lambda \left( {\theta ,i} \right)}}{dt}$$
(1)

where \(Vin\) is the phase voltage, \(Rs\) is the winding resistance, \(i\) is the phase current, and \(\lambda \left( {\theta ,i} \right)\) represents the flux linkage. This flux linkage depends on both the rotor’s angular position, \(\theta\), and the phase current, \(i\), due to the nonlinearity arising from magnetic saturation. To express the rate of change in flux linkage, the derivative can be expanded to account for both rotor position and current change over time, applying the chain rule as follows:

$$\frac{{d\lambda \left( {\theta ,i} \right)}}{dt} = \frac{\delta \lambda }{{\delta \theta }} \times \frac{d\theta }{{dt}} + \frac{\delta \lambda }{{\delta i}} \times \frac{di}{{dt}}$$
(2)

Here, \(\frac{d\theta }{{dt}} = \omega\) represents the rotor speed, connecting flux changes directly to the motion of the rotor. This expanded form is critical for dynamic simulations and SRM control, as it reflects the intertwined effects of electrical input and mechanical motion. The electromagnetic torque generated by the SRM arises from the tendency of the rotor to align with the highest magnetic field, a torque production mechanism distinct from conventional motors. This torque can be computed as \(T_{e} = i \times \frac{{\delta \lambda \left( {\theta ,i} \right)}}{\delta \theta }\), linking it to the co-energy of the system. The electromagnetic torque depends on both the current and the rate of change in inductance relative to rotor position, which varies as the rotor rotates through alignment with the stator poles. The mechanical dynamics of the SRM’s motion can be described by Newton’s second law for rotation:

$$J \times \frac{d\omega }{{dt}} + B \times \omega = T_{e} - T_{L}$$
(3)

Here, \(J\) represents the rotor’s moment of inertia, \(B\) is a friction coefficient, \(\omega\) denotes rotor speed, and \(T_{L}\) represents the load torque. This equation expresses how the net torque, a combination of electromagnetic and load torque, affects the rotor’s acceleration and speed. Together, this set of equations represents a highly nonlinear system. Another important aspect of SRM modeling is the inductance profile of each phase winding. The inductance varies as the rotor position changes, introducing nonlinearity. The flux linkage can thus be modeled as \(d\lambda \left( {\theta ,i} \right) = L\left( \theta \right) \times i\), or by using a look-up table to capture magnetic saturation effects accurately. This approach helps account for the unique inductance values encountered at different rotor positions.

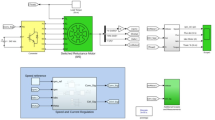
Figure 1 shows a linear profile for the per-phase inductance in an SRM motor. Figure 2 shows Inductance (linear) profile of all three phase. Table 2 presents the parameters used for SRM modeling in this study, while Fig. 3 provides an overview of the SRM and the controllers analyzed12,21.

Fig. 1
figure 1

Per-phase inductance (linear) profile.

Full size image
Fig. 2
figure 2

Inductance (linear) profile of all three phase.

Full size image
Table 2 Parameters used in case study.
Full size table
Fig. 3
figure 3

General schematic of proposed controller and SRM system.

Full size image

SRM structure and implementation controller

Converter structure

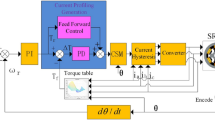
As showed in Fig. 3 proposed system uses a three-phase asymmetric bridge converter to drive the SRM. This converter consists of two switches and two diodes per phase. These two switches can be IGBTs or MOSFETs. When a phase needs to be energized, the two switches turn on, allowing current to flow from the DC power source into the motor winding. This creates a magnetic field that pulls the rotor towards the aligned position. When the switches turn off, the energy stored in the winding is released through the diodes, ensuring smooth current decay and reducing voltage spikes. This process is repeated for each phase, ensuring continuous rotation of the motor.

Identification of switching angles

The switching angles are determined based on rotor position feedback. The system uses a position sensor to detect the rotor’s current position and decide the best moment to energize and de-energize each phase. The HAALO optimization method is used to fine-tune input current in converter for improving efficiency and reducing torque ripple. Inner and outer controllers help the motor achieve better performance and smooth current regulation. This smooth current flow ensures more stable torque generation, reduces sudden variations in motor operation. Additionally, maintaining a well-regulated current improves switching transitions, reducing stress on power electronics components and enhancing the overall reliability of the system.

Control method

The system uses a cascaded control structure with two loops:

  • Outer loop: This controller compares the desired speed \(\omega_{ref}\) with the actual motor speed \(\omega_{m}\) and generates a reference current. The HAALO optimization method helps adjust the speed controller parameters for better performance.

  • Inner loop: The inner loop ensures that the motor phase currents follow the reference current generated by the speed controller. The HAALO optimization method helps adjust the current controller and hysteresis band parameters for better performance.

This cascaded control structure ensures precise speed regulation and reduced torque ripple, making the system more efficient and stable.

Optimization

Ant-lion optimization (ALO)

The ant lion optimization (ALO) algorithm is a bio-inspired metaheuristic introduced by23. It mimics the predatory behavior of antlions in nature, where antlions capture ants by trapping them in funnel-shaped sand pits. In the ALO algorithm, ants represent potential solutions, and antlions represent elite solutions guiding the search process. The algorithm alternates between exploration and exploitation, making it a powerful tool for solving complex optimization problems.

Exploration

Random walk of ants In ALO, the ants’ movements are modeled as random walks across the search space, representing the exploration phase. Each ant performs a stochastic exploration defined by the equation:

$$x_{i} \left( {t + 1} \right) = x_{i} \left( t \right) + r\left( t \right)$$
(4)

where \(x_{i} \left( t \right)\) is the position of the \(i{\text{th}}\) ant at iteration t, and r(t) is a random walk vector. Each element of r(t) is generated using a stochastic process defined by:

$$r_{j} \left( t \right) = {\text{cumulative sum of random steps}}\left( {2 \times {\text{rand}}\left( 1 \right) - 1} \right)$$
(5)

where, rand (1) generates random numbers uniformly distributed in the range [0,1]. The search space is bounded by lower and upper limits lb and ub, ensuring that ants remain within feasible regions:

$$x_{i} \left( t \right) \in \left[ {l_{b} ,u_{b} } \right]$$
(6)

The random walk of ants provides the exploration capability, allowing the algorithm to search diverse regions of the solution space.

Exploitation

Trap building by antlions As the ants explore the search space, they are influenced by antlions, which represent elite solutions guiding the ants towards better regions. During each iteration, antlions create traps, which metaphorically pull the ants towards optimal solutions. The process of trapping is modeled by narrowing the boundaries of the search space around the ants as they approach antlions, mimicking the natural hunting behavior of antlions. The elite antlions influence the ants’ movements by dynamically adjusting their search regions, encouraging exploitation of promising areas in the solution space. The algorithm incorporates a roulette wheel selection mechanism to favor fitter antlions, which further ensures that the best solutions are more likely to guide the search process.

Balance between exploration and exploitation

ALO is designed to strike a balance between exploration and exploitation. In the early stages of the algorithm, the ants are allowed to explore the search space broadly to identify potential solutions. As the iterations progress, the focus shifts toward exploitation, refining the best solutions found so far. This balance is crucial in preventing premature convergence to local optima while ensuring that the algorithm converges to the global optimum over time. The ALO algorithm continues this process until a stopping criterion, such as a maximum number of iterations, is met. The best solution found by the antlions is then reported as the global optimum.

Hybrid adaptive ant lion optimization (HAALO)

To further enhance the performance of the standard ALO algorithm, a hybrid adaptive ant lion optimization (HAALO) approach has been developed. HAALO introduces several adaptive and hybrid techniques to address limitations such as slow convergence or premature stagnation in local optima. These enhancements make the algorithm more robust, especially when dealing with highly complex and multimodal optimization problems. Figure 4 depicts flowchart of HAALO Implementation for the SRM system.

Fig. 4
figure 4

Flowchart of HAALO Implementation for the SRM System.

Full size image

Mutation-based exploration

To increase diversity and prevent the algorithm from getting trapped in local optima, HAALO introduces a mutation operator. Mutation introduces random perturbations in the ants’ positions with a probability \({P}_{mut}{:}\)

$$x_{i} \left( {t + 1} \right) = \left\{ {\begin{array}{*{20}l} {x_{i} \left( t \right) + \delta \times rand\left( n \right),} \hfill & {if rand \left( 1 \right) < P_{mut} } \hfill \\ {x_{i} \left( t \right)} \hfill & {otherwise} \hfill \\ \end{array} } \right.$$
(7)

where \(\delta\) is a small perturbation factor, and \({P}_{mut}\) is the mutation probability. The mutation ensures that the search process continues exploring new regions of the solution space, especially in later iterations when exploitation becomes dominant.

Elite preservation strategy

HAALO incorporates an elite preservation mechanism, ensuring that the best-performing solutions are retained throughout the optimization process. A fraction \(\alpha\) of the population, representing elite solutions, is preserved at each iteration:

$$n_{{{\text{elite}}}} = \left[ {\alpha \times n_{{{\text{p}}opulation}} } \right]$$
(8)

The elite solutions guide the ants during exploitation, preventing the loss of high-quality solutions due to randomness or mutation. Elite solutions are selected based on their fitness and used to refine the search in subsequent iterations.

Self-adaptive parameter control

To further enhance the performance, HAALO employs self-adaptive mechanisms for controlling parameters such as the inertia weight \(\omega_{t }\) and the exploration–exploitation balance. The inertia weight is dynamically adjusted based on the diversity of the population at each iteration t:

$$\omega_{t} = \omega_{min} + \left( {\omega_{max} - \omega_{min} } \right) \times \frac{D\left( t \right)}{{D_{max} }}$$
(9)

where \(D\left( t \right)\) is the diversity of the population at iteration t, and \(D_{max}\) is the maximum diversity observed. The diversity is calculated as:

$$D\left( t \right) = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} x_{i} \left( t \right) - x_{mean} \left( t \right)$$
(10)

where \(x_{mean} \left( t \right)\) is the mean position of all ants at iteration t. By dynamically adjusting parameters, HAALO ensures that the balance between exploration and exploitation is maintained throughout the optimization process.

Convergence and final solution

HAALO converges to the optimal solution by combining adaptive exploration and exploitation techniques. The algorithm terminates when the maximum number of iterations \(T_{max}\) is reached, and the best solution found is returned as the global optimum:

$$x^{*} = argmin f\left( {x_{i} \left( {T_{max} } \right)} \right)$$
(11)

The final solution is \(x^{*}\) the best antlion’s position. Table 3 shows the pseudocode table for HAALO optimization method:

Table 3 Pseudocode for proposed optimization method (HAALO).
Full size table

Performance analysis of the proposed algorithm on CEC-2022 test suite

This section validates the enhanced optimization capabilities of the HAALO algorithm through rigorous experimentation. The evaluation begins with tests conducted on the latest CEC-2022 benchmark functions, recognized for their complexity and diversity in representing real-world optimization challenges. These benchmarks ensure that the algorithm’s performance is assessed against standard and widely accepted criteria. Following this, the algorithm is applied to the proposed SRM problem, focusing on objectives such as torque ripple minimization, speed regulation, and adaptability under dynamic load conditions. Detailed results from both the benchmark and application-specific experiments are presented in the subsequent subsections, highlighting the algorithm’s robustness and superiority compared to other optimization methods.

Simulation and benchmarking setup

To rigorously evaluate the effectiveness of the proposed HAALO algorithm, its performance was benchmarked against a comprehensive suite of state-of-the-art metaheuristic optimization methods. The evaluated methods included particle swarm optimization (PSO), progressive particle swarm optimization (PPSO), genetic algorithm (GA), ant lion optimizer (ALO), RIME optimizer, golden eagle optimizer (GEO), multiple stage ant colony optimization (MSACO), dung beetle optimizer (DBO), flower pollination algorithm (FPA), spotted hyena optimizer (SHO), and local unimodal sampling (LUS). These algorithms were selected for their prominence in optimization research and their diverse operational mechanisms, providing a robust and comprehensive comparative framework. The evaluation utilized the CEC-2022 benchmark functions, with 30 independent runs conducted for each algorithm. A maximum of 500 iterations and a population size of 20 were maintained across all experiments to ensure uniformity and reliability in the results. The CEC 2022 benchmarks, featuring 10- and 20-dimensional hyper-spaces, were chosen for their ability to replicate real-world optimization challenges, offering a rigorous testbed for assessing algorithmic performance. All parameter settings for the compared algorithms were initialized based on their recommended default values to provide an ideal environment for performance demonstration. This systematic approach ensured fairness and enabled a detailed analysis of HAALO’s capabilities relative to other advanced optimization techniques, highlighting its potential to excel in complex optimization scenarios.

Statistical results

The proposed HAALO algorithm was evaluated using the CEC 2022 test suite, which features 10- and 20-dimensional search spaces. This suite comprises 12 distinct functions, categorized into unimodal, multimodal, hybrid, and composition functions, providing a diverse set of optimization challenges24. Further details about these functions can be found in24. Tables 4 and 5 respectively provide the comparative statistical results of 10 and 20 dimensional CEC 2022 benchmark functions. Besides, the comparative results of the Wilcoxon’s signed rank test are provided in Tables 6 and 7. The presented results within those tables confirm the superiority of the proposed HAALO in terms of exploration and exploitation.

Table 4 Comparative statistical results on CEC-2022 test suite (Dimension = 10).
Full size table
Table 5 Comparative statistical results on CEC-2022 test suite (Dimension = 20).
Full size table
Table 6 Wilcoxon’s signed rank test on CEC-2022 test suite (Dimension = 10).
Full size table
Table 7 Wilcoxon’s signed rank test on CEC 2022 test suite (Dimension = 20).
Full size table

Objective function definition

The objective function (OF) is a measure used by the designer to evaluate the dynamic response of the system. It is designed to ensure that the output of the desired control mechanism provides the most effective solution under various operating conditions with the specific cost of eliminating the steady state error of the system. The objective function is defined as Eq. (12) 12,21:

$$OF_{min} = \mathop \smallint \limits_{0}^{{t_{sim} }} \left( {\Delta c} \right)^{2} + \left( {\Delta s} \right)^{2} dt$$
(12)

Here, \(t_{sim }\) represents the simulation time in seconds. \(\Delta c\) and \(\Delta s\) refer to the current error and speed error, respectively. The OF is constrained by the range of the controller coefficients, which sets the boundaries of the search space for the optimization problem, as outlined in Table 8.

Table 8 Range of gains in proposed and other controllers.
Full size table

Results of the simulation and analysis

In this section, we implement the proposed PI and FOPID controllers based on the HAALO algorithm to perform control functions within the SRM, as previously discussed in “Optimization” section. The closed-loop system is modeled in MATLAB 2023a using Simulink. Through 100 iterations with 20 particles, the HAALO algorithm has identified the optimal controller coefficients. The simulation duration is set to 10 s. Fractional-order (FO) operators are modeled using the FOMCON plugin in MATLAB, with a frequency range of [0.001, 1000] and an approximation order of 5. Testing with higher-order approximations showed minimal change in results. The HAALO optimization algorithm was run independently in 20 trials, with Table 9 summarizing the best, worst, and average OF values achieved across different controllers. Figure 5 provides a comparative analysis using boxplots for seven algorithms HAALO, PSO, PPSO, ALO, GEO, RIME, and GA based on their effectiveness in minimizing the objective function. The boxplot in Fig. 5 indicates that even the lowest-performing result from the HAALO algorithm outperforms the highest results of the other six algorithms, highlighting the clear performance advantage of the proposed HAALO algorithm. Figure 6 depicts the best results of the OF by running the proposed HAALO, ALO, PSO, RIME, PPSO, GEO and GA algorithms.

Table 9 Values of the OF following 20 rounds of optimization algorithms using various controllers.
Full size table
Fig. 5
figure 5

Boxplot schematic for HAALO optimization and other metaheuristic algorithms.

Full size image
Fig. 6
figure 6

The best results of the OF by running the proposed HAALO, ALO, PSO, RIME, PPSO, GEO and GA algorithms.

Full size image

The HAALO algorithm has undergone sufficient iterations, confirming its convergence to the optimal solution. To evaluate the efficiency of the proposed controller, we utilize the HAALO technique for optimization. Figure 5 illustrates the outcomes from this optimized implementation, showing that the lowest OF values were achieved after 100 iterations, highlighting the controller’s enhanced performance. The HAALO optimization was also independently executed across 20 trials, with Table 9 presenting the best, worst, and average OF values obtained with different controllers.

Table 10 provides the optimal controller parameter values derived from the best results achieved by the HAALO algorithm. To enable a thorough numerical comparison, we calculated and reported the time-domain evaluation indices for each scenario. These indices include the integral of square error (ISE), integral of time-weighted square error (ITSE), integral of absolute error (IAE), and integral of time-weighted absolute error (ITAE). The equations for these indices are provided in Eqs. (13) to (16).

$$ISE = \mathop \smallint \limits_{0}^{x} e^{2} \left( t \right)dt$$
(13)
$$ITSE = \mathop \smallint \limits_{0}^{x} t.e^{2} \left( t \right)dt$$
(14)
$$IAE = \mathop \smallint \limits_{0}^{x} \left| {e\left( t \right)} \right|dt$$
(15)
$$ITAE = \mathop \smallint \limits_{0}^{x} t.\left| {e\left( t \right)} \right|dt$$
(16)

where, x is simulation time in s, and e(t) is an error signal between speed and current in SRM.

Table 10 Optimum gains of proposed and other controllers.
Full size table

Comparison in different scenarios

Scenario 1: no load applied SRM

In this scenario, the motor operates without an external load, and we observe its output speed, torque, and current by setting the reference speed to 2000 r.p.m. Figures 7 and 8 display the motor’s speed response under no-load conditions for the SRM. Here, the PI controller with the proposed optimization method is compared against the traditional PID controller, showing superior results. Notably, the HAALO-based PI and FOPID controllers achieve the most accurate speed tracking. In addition, for better clarity, Figs. 9, 10 provide a magnified comparison of the proposed method with the two best responses for speed in the SRM.

Fig. 7
figure 7

Time response of speed for PI-HAALO and other controllers in scenario 1.

Full size image
Fig. 8
figure 8

Time response of speed for FOPID-HAALO and other controllers in scenario 1.

Full size image
Fig. 9
figure 9

Time response of speed for PI-HAALO and two best controllers in scenario 1.

Full size image
Fig. 10
figure 10

Time response of speed for FOPID-HAALO and two best controllers in scenario 1.

Full size image

Table 11 outlines the transient response characteristics, demonstrating that the proposed optimization method achieves faster response times than other meta-heuristic algorithms. Additionally, Figs. 11 and 12 reveal that the HAALO-based PI and FOPID controllers produce the lowest torque ripple at the reference speed compared to other controllers. Additionally, for better clarity, Figs. 13, 14 provide a magnified comparison of the proposed method with the two best responses for torque in the SRM. Figures 15 and 16 illustrate the output current in one phase of the SRM using various controllers. Table 12 provides time-domain evaluation criteria for internal and external controllers, confirming that the proposed controller yields lower error values.

Table 11 Transient response specifications in scenario 1.
Full size table
Fig. 11
figure 11

Time response of total torque for PI-HAALO and other controllers in scenario 1.

Full size image
Fig. 12
figure 12

Time response of total torque for FOPID-HAALO and other controllers in scenario 1.

Full size image
Fig. 13
figure 13

Time response of total torque for FOPID-HAALO and two best controllers in scenario 1.

Full size image
Fig. 14
figure 14

Time response of total torque for FOPID-HAALO and two best controllers in scenario 1.

Full size image
Fig. 15
figure 15

Time response of phase current for PI-HAALO and other controllers in scenario 1.

Full size image
Fig. 16
figure 16

Time response of phase current for FOPID-HAALO and other controllers in scenario 1.

Full size image
Table 12 Time-based indicators illustrating the dynamic response of the SRM in scenario.
Full size table

Scenario1: no load with time-delay non-linearity for PI-HAALO controller

Managing systems becomes more challenging due to factors such as time delays, non-linearity from power line interference, or SRM malfunctions. In this case, it is assumed that the control system’s stimulation signal experiences a 20 ms delay on the outer controller. As shown in Fig. 17, the PI-HAALO controller outperforms others in reaching the reference speed, with other controllers following in rank. Transient response values are listed in Table 13. In addition, for better clarity, Fig. 18 provide a magnified comparison of the proposed method with the two best responses for speed in the SRM.

Fig. 17
figure 17

Time response of speed for PI-HAALO and other controllers in scenario 1 with time delay.

Full size image
Table 13 Transient response specifications in scenario 1 with time delay.
Full size table
Fig. 18
figure 18

Time response of speed for PI-HAALO and two best controllers in scenario 1 with time delay.

Full size image

Figures 19 displays the SRM torque curve, where the proposed controller demonstrates strong performance. Additionally, for better clarity, Fig. 20 provide a magnified comparison of the proposed method with the two best responses for torque in the SRM. Figure 21 shows the phase current for each controller in the SRM. Notably, it achieves a low torque ripple at the reference speed, whereas other controllers have yet to reach this speed.

Fig. 19
figure 19

Time response of total torque for PI-HAALO and other controllers in scenario 1 with time delay.

Full size image
Fig. 20
figure 20

Time response of total torque for PI-HAALO and two best controllers in scenario 1 with time delay.

Full size image
Fig. 21
figure 21

Time response of phase current for PI-HAALO and other controllers in scenario 1 with time delay.

Full size image

Scenario 2: change speed in SRM

In practical scenarios, motors often do not operate under ideal conditions. In this case, a reference speed of 3000 r.p.m is applied to the SRM to assess the performance of the optimization method and controllers under these conditions. Table 14 outlines the transient response characteristics, demonstrating that the proposed optimization method achieves faster response times than other meta-heuristic algorithms. Figures 22 and 23 display the speed response when 3000 rpm is imposed on the SRM. These figures clearly show that the proposed optimization method tracks the reference speed faster than other controllers. In addition, for better clarity, Figs. 24, 25 provide a magnified comparison of the proposed method with the two best responses for speed in the SRM.

Table 14 Transient response specifications in scenario 2.
Full size table
Fig. 22
figure 22

Time response of speed for PI-HAALO and other controllers in scenario 2.

Full size image
Fig. 23
figure 23

Time response of speed for FOPID-HAALO and other controllers in scenario 2.

Full size image
Fig. 24
figure 24

Time response of speed for PI-HAALO and two best controllers in scenario 2.

Full size image
Fig. 25
figure 25

Time response of speed for FOPID-HAALO and two best controllers in scenario 2.

Full size image

A notable advantage of the proposed controller is its stable and acceptable torque ripple at the target speed. In contrast, while other controllers fail to reach the reference speed for the SRM, they exhibit higher torque ripple compared to the PI and FOPID controllers based on the HAALO method. Figures 26, 27, 28, and 29 present a comparison of torque between the proposed controller and other controllers in the SRM. Specifically, Figs. 28 and 29 provide a magnified comparison between the proposed controller and the two best-performing controllers. Figures 30 and 31 display current characteristics of the SRM in this scenario. Table 15 provides time-domain evaluation criteria for internal and external controllers, confirming that the proposed controller yields lower error values.

Fig. 26
figure 26

Time response of total torque for PI-HAALO and other controllers in scenario 2.

Full size image
Fig. 27
figure 27

Time response of total torque for FOPID-HAALO and other controllers in scenario 2.

Full size image
Fig. 28
figure 28

Time response of total torque for PI-HAALO and two best controllers in scenario 2.

Full size image
Fig. 29
figure 29

Time response of total torque for FOPID-HAALO and two best controllers in scenario 2.

Full size image
Fig. 30
figure 30

Time response of phase current for PI-HAALO and other controllers in scenario 2.

Full size image
Fig. 31
figure 31

Time response of phase current for FOPID-HAALO and other controllers in scenario 2.

Full size image
Table 15 Time-based indicators illustrating the dynamic response of the SRM in scenario 2.
Full size table

Scenario 3: dynamic load (stepwise load decrease)

In this section, a stepwise dynamic load is applied to the SRM, starting with a load of 10 N.m from t = 2 s to t = 4 s, followed by an increased load of 30 N.m from t = 4 s to t = 10 s. Figures 32 and 33 illustrate the performance of the proposed optimization method in this scenario. As shown in Figs. 32 and 33, the proposed optimization method experiences less speed drop under loading compared to other metaheuristic algorithms. When the load is removed, it effectively tracks the reference speed. One key advantage of the proposed PI and FOPID controllers based on HAALO method is its stable torque ripple at the target speed, unlike other controllers, which not only struggle to reach the SRM’s reference speed but also show higher torque ripple than the PI and FOPID controllers based on the HAALO method. Figures 34, 35, 36, and 37 provide a comparison of torque between the proposed controller and other controllers of the SRM in this scenario. Specifically, Figs. 36 and 37 provide a magnified comparison between the proposed controller and the two best-performing controllers. Figures 38 and 39 display current characteristics of the SRM in this scenario.

Fig. 32
figure 32

Time response of speed for PI-HAALO and other controllers in scenario 3.

Full size image
Fig. 33
figure 33

Time response of speed for FOPID-HAALO and other controllers in scenario 3.

Full size image
Fig. 34
figure 34

Time response of total torque for PI-HAALO and other controllers in scenario 3.

Full size image
Fig. 35
figure 35

Time response of total torque for FOPID-HAALO and other controllers in scenario 3.

Full size image
Fig. 36
figure 36

Time response of total torque for PI-HAALO and two best controllers in scenario 3.

Full size image
Fig. 37
figure 37

Time response of total torque for FOPID-HAALO and two best controllers in scenario 3.

Full size image
Fig. 38
figure 38

Time response of phase current for PI-HAALO and other controllers in scenario 3.

Full size image
Fig. 39
figure 39

Time response of phase current for FOPID-HAALO and other controllers in scenario 3.

Full size image

Scenario 4: complicated operation

In this scenario, a challenging operation is designed for the SRM to assess how effectively the proposed optimization method and controller functions under rare and demanding conditions. This operation unfolds in three stages:

  1. 1.

    From t = 0 s to t = 2 s, there is no load on the motor, while a reference speed of 2000 r.p.m is maintained from t = 0 s to t = 3 s.

  2. 2.

    At t = 2 s, a load torque of 10 N.m is applied, lasting until t = 4 s, while the reference speed increases to 3000 r.p.m from t = 3 s to t = 10 s.

  3. 3.

    At t = 4 s, the load torque rises to 30 N.m, continuing until t = 10 s, with the reference speed held at 3000 r.p.m from t = 3 s onward.

Figures 40 and 41 demonstrate that the proposed optimization approach, combined with PI and FOPID controllers based HAALO method, achieves more adaptable performance compared to other PID and FOPID controllers, ensuring the SRM operates reliably even in abnormal conditions. Figures 42 and 43 display the SRM’s torque during this period, showing that, unlike other controllers that result in motor speeds below the reference, the optimized method enables the motor to achieve a desirable torque at the reference speed. Additionally, for better clarity, Figs. 44 and 45 provide a magnified comparison of the proposed method with the two best responses for torque in the SRM. Figures 46 and 47 illustrate the output current for one phase of the SRM under different controllers.

Fig. 40
figure 40

Time response of speed for PI-HAALO and other controllers in scenario 4.

Full size image
Fig. 41
figure 41

Time response of speed for FOPID-HAALO and other controllers in scenario 4.

Full size image
Fig. 42
figure 42

Time response of total torque for PI-HAALO and other controllers in scenario 4.

Full size image
Fig. 43
figure 43

Time response of total torque for FOPID-HAALO and other controllers in scenario 4.

Full size image
Fig. 44
figure 44

Time response of total torque for PI-HAALO and two best controllers in scenario 4.

Full size image
Fig. 45
figure 45

Time response of total torque for FOPID-HAALO and two best controllers in scenario 4.

Full size image
Fig. 46
figure 46

Time response of phase current for PI-HAALO and other controllers in scenario 4.

Full size image
Fig. 47
figure 47

Time response of phase current for FOPID-HAALO and other controllers in scenario 4.

Full size image

Conclusions

SRMs by integrating the HAALO algorithm with PI and FOPID controllers. The proposed method significantly reduces torque ripple and enhances speed regulation, offering a more adaptable and robust solution compared to traditional control methods. Simulation results confirm that HAALO-optimized controllers outperform established optimization techniques, showing faster convergence, reduced computational overhead, and superior control accuracy. While the simulation results demonstrate the effectiveness of the proposed method, there are practical limitations to consider. The real-world implementation of the HAALO-optimized controllers may be constrained by factors such as hardware limitations, real-time computational capacity, and the ability to maintain control precision under extreme operating conditions. In practice, challenges such as sensor inaccuracies, external disturbances, and system nonlinearity could affect the accuracy of switching angle optimization and the overall system performance.

Future work should focus on addressing these limitations by investigating the practical implementation of the proposed control system in real-time applications. This would involve testing the system with actual SRM hardware, exploring hardware-specific adjustments, and evaluating performance under real-world conditions. Additionally, integrating machine learning techniques for predictive control and fault detection could further enhance the adaptability of the system. The extension of the HAALO algorithm to multi-objective optimization, targeting energy efficiency and thermal management, could provide even more practical benefits for high-performance applications. Lastly, exploring hybrid optimization methods that combine HAALO with other advanced control strategies may lead to further improvements in SRM performance in industrial environments.