A bias-reduced estimator for generalized Poisson regression with application to carbon dioxide emission in Canada

Abstract

The generalized Poisson regression model (GPRM) provides a flexible framework for modeling count data, especially those exhibiting over- or underdispersion. Although the generalized Poisson maximum likelihood estimator is considered the standard method for estimating the parameters of this model, its reliability and accuracy are severely affected by the presence of multicollinearity among explanatory variables. Multicollinearity inflates the variance of parameter estimates, undermining the validity of statistical inference and ultimately leading to unstable and unreliable estimators. To mitigate these problems, this study presents the ridge estimator as a robust alternative within the GPRM framework. Several new strategies are proposed for selecting the optimal value of the ridge parameter. The statistical properties of the proposed ridge estimator were theoretically studied. Theoretical comparisons and extensive Monte Carlo simulations demonstrated a clear and significant superiority of the ridge estimator under multicollinearity conditions, confirming its robustness and efficiency. To demonstrate the scientific and practical relevance of the proposed estimator, it was applied to a real-world case study modeling carbon dioxide emissions in Canada. The results of this experimental application conclusively confirmed the simulation and theoretical comparison results, with the ridge estimator providing more stable and interpretable results than the conventional method, making it a valuable tool for researchers and decision makers in analyzing multicollinear environmental and economic data.

Introduction

The Poisson regression model (PRM) is a fundamental tool for analyzing count data, where the outcome variable consists of non-negative integers representing the frequency of events. A core assumption of the PRM is equidispersion—the equality of the mean and variance¹. However, empirical data frequently violate this assumption, displaying either overdispersion, where variance exceeds the mean, or the less common underdispersion, where variance is constrained below the mean. These patterns often emerge from unobserved heterogeneity, dependencies between events, or other latent factors, potentially leading to inefficient estimates and misleading inferences. To overcome these limitations, numerous alternative count models have been developed. These include the negative binomial regression model (NBRM), which incorporates a dispersion parameter to handle overdispersion^2,3; the geometric regression model (GERM) for underdispersed data⁴; and the Conway–Maxwell Poisson regression model (CMPRM), which offers flexibility for both types of dispersion⁵. Additional approaches include the double Poisson model (DPRM), which explicitly corrects for deviations from equidispersion⁶; the Bell regression model (BRM) for overdispersed counts; and the Poisson-inverse Gaussian model (PIGRM) for data with severe overdispersion and heavy tails⁷. Among these, the generalized Poisson regression model (GPRM) stands out for its ability to directly adjust the mean-variance relationship, effectively addressing both over- and underdispersion, making it a versatile alternative when the standard Poisson assumptions are untenable⁸.

The GPRM effectively handles both over- or underdispersed count data, making it valuable in numerous fields⁹. For example, it has been used to study child stunting in Indonesia¹⁰, neonatal mortality in Ethiopia¹¹, and COVID-19 spread in Ghana¹². The GPRM has also inspired new methods, such as a stochastic process for signed integers¹³. These applications demonstrate the model’s flexibility in addressing real-world data challenges.

The presence of multicollinearity, a high degree of intercorrelation among explanatory variables, poses a significant challenge to regression analysis. This condition detrimentally inflates the variance of parameter estimates derived from both ordinary least squares (OLS) and maximum likelihood estimation (MLE)¹⁴. The issue is particularly acute within the context of the GPRM, where MLE can produce excessively high variance in the presence of correlated predictors. To mitigate the adverse effects of multicollinearity, several techniques are commonly employed. These include variable selection methods like Lasso regression and the use of biased estimation techniques, such as Ridge regression¹⁵. Under conditions of multicollinearity, such biased estimators often outperform MLE by trading a small amount of bias for a substantial reduction in variance, thereby yielding a lower scalar mean squared error (MSE) and more reliable estimates. The ridge estimator, formulated as $\hat{\beta }_{RE} = (X^\prime X + kI)^{-1}X^\prime Y$ where $X$ is the design matrix, $Y$ the response vector, $I$ the identity matrix, and $k > 0$ the ridge parameter, can be analyzed through its spectral properties to derive its MSE. The selection of an optimal $k$ value is critical, and numerous methods have been developed for this purpose, building upon the foundational work of Hoerl and Kennard^16,17 for nonorthogonal problems. Subsequent advancements include the alternative estimators proposed by Kibria¹⁸ and further methodological elaborations by Muniz and Kibria¹⁹.

Ridge regression has been widely used in generalized linear models (GLMs), with Segerstedt²⁰ being one of the first to apply it in GLMs. This technique has since been used in various models to deal with multicollinearity. For instance, Månsson and Shukur²¹, Schaefer et al.²², Rady et al.²³, Månsson²⁴, Tharshan et al.²⁵, Almulhim et al.²⁶, Abonazel et al.²⁷, Sami et al.²⁸, Algamal et al.²⁹, Dawoud³⁰, El-Alosey et al.³¹, Akram et al.³², Shahzad et al.³³, and Ashraf et al.³⁴.

A substantial body of literature has explored the development and application of ridge estimators and other biasing parameters across a range of statistical frameworks, from classical linear regression to various count and GLMs. Despite these extensive developments, the integration of ridge regression methodology within the GPRM remains notably understudied. This research aims to address this gap by systematically evaluating the efficacy of ridge regression in ameliorating the dual challenges of multicollinearity and overdispersion within the GPRM framework and derivation and evaluation of optimal estimators for the ridge parameter $k$. The performance of the resulting ridge estimators will be rigorously compared against the conventional generalized Poisson maximum likelihood estimates (GPMLE). Theoretical comparisons and Monte Carlo simulations will be used to study the performance of the proposed estimator, and these findings will be further validated through a real-world application.

This paper is organized in the following: Section "Generalized Poisson regression model" provides the statistical formulation of the Generalized Poisson (GP) distribution and its corresponding regression model. Section "Generalized Poisson ridge regression estimator" presents the methodological framework for addressing multicollinearity within the GPRM through the application of ridge regression. The performance criteria used to evaluate the proposed estimators are defined in Sect. "The superiority of the GPRRE over the GPMLE". Section "Selection of the biasing parameters" is devoted to a discussion of the methods for selecting the optimal ridge parameter, $k$. The efficacy of the proposed methodology is then rigorously assessed via an extensive Monte Carlo simulation study in Sect. "Monte Carlo simulation". To demonstrate its practical utility, the approach is applied to empirical datasets in Sect. "Application". Finally, the principal findings, along with concluding remarks and potential avenues for future research, are summarized in Sect. "Conclusion".

Generalized Poisson regression model

The GP distribution initially introduced by Consul and Jain³⁵, which has parameters $\theta$ and $\nu$. This distribution’s probability mass function (PMF) is defined as:

$$\begin{aligned} P(Y = y; \theta , \nu ) = \frac{\theta }{y!} (\theta + \nu y)^{y-1} e^{-(\theta + \nu y)}, \end{aligned}$$

(1)

where $y = 0, 1, 2, \dots$, $\theta > 0$, and $\max (-1,-\theta /4) \le \nu \le 1$. The GP distribution was initially introduced as an approximation to the generalized negative binomial distribution. Its properties were subsequently extensively developed by Consul³⁶, whose foundational work led to it being commonly referred to as Consul’s GP distribution. The mean and variance of the distribution are given by:

$$\text {E}(Y) = \frac{\theta }{1 - \nu },$$

and

$$\quad \text {Var}(Y) = \frac{\theta }{(1 - \nu )^3}.$$

Famoye³⁷ suggested a more appropriate parametrization of the GP distribution for regression models by reparameterizing the original formulation in Eq. (1). Specifically, let $\mu = \frac{\theta }{1 - \nu }$ and $\varphi = \frac{\nu }{\theta }$. This transformation leads to the relationships $\theta = \frac{\mu }{1 + \varphi \mu }$ and $\nu = \frac{\varphi \mu }{1 + \varphi \mu }$. Under this reparameterization, the PMF for the GP distribution, denoted as $\text {GP}(\mu , \varphi )$, is given by:

$$\begin{aligned} P(Y = y ; \mu , \varphi ) = \frac{(1 + \varphi y)^{y-1}}{y!} \left( \frac{\mu }{1 + \varphi \mu } \right) ^y \exp \left( -\frac{\mu (1 + \varphi y)}{1 + \varphi \mu } \right) ,\quad \mu > 0,~ y = 0, ~1, ~2,~ \dots \end{aligned}$$

(2)

This parameterization is very good for regression since it is easy to understand and fits well with modeling frameworks. The GP distribution is great for analyzing count data because it can handle over- or underdispersion. The mean and variance of $\text {GP}(\mu , \varphi )$ are:

$${\text {E}(Y|x_i)} = \mu _i,$$

and

$$\text {Var}(Y|x_i) = \mu _i (1 + \varphi \mu _i)^2.$$

The GPRM provides a flexible extension of the standard PRM, designed to handle count data characterized by either over- or underdispersion. The model is constructed within the GLM framework. In this specification, the mean of the response variable, denoted by $\mu _i$, is connected to a linear combination of predictors through a logarithmic link function, expressed as:

$$\begin{aligned} \log \mu _i = \eta _i = {x}_i^\prime {\beta }, \end{aligned}$$

(3)

where $\mu _i$ denotes the expected count for the $i$-th observation. This mean is modeled as a function of a $p \times 1$ vector of explanatory variables, ${x}_i$, and a corresponding $p$-dimensional vector of unknown regression coefficients, ${\beta }$. The coefficients quantify the relationship between the explanatory variables and the expected value of the response variable. The MLE method is commonly used to estimate the parameters of the GPRM. In this approach, we maximize the likelihood function $L({\beta }, \varphi )$, which expresses the probability of observing the data given the model parameters. The log-likelihood function $\ell ({\beta }, \varphi )$ is given by:

$$\begin{aligned} \ell ({\beta }, \varphi ) = \sum _{i=1}^n \left[ y_i \left[ \log {(\mu _i)}- \log {(1 + \varphi \mu _i)} \right] + (y_i - 1) \log (1 + \varphi y_i) - \log (y_i!) - \frac{\mu _i (1 + \varphi y_i)}{1 + \varphi \mu _i} \right] . \end{aligned}$$

(4)

Eq.(4) represent the GPMLE for the parameters $\varphi$ (dispersion parameter) and $\beta _r$ (regression coefficients) in a GPRM:

$$\begin{aligned}&\frac{\partial \ell }{\partial \varphi } = \sum _{i=1}^n \left( \frac{-y_i \mu _i}{1 + \varphi \mu _i} + \frac{y_i (y_i - 1)}{1 + \varphi y_i} - \frac{\mu _i (y_i - \mu _i)}{(1 + \varphi \mu _i)^2} \right) = 0, \end{aligned}$$

(5)

$$\begin{aligned}&\quad \frac{\partial \ell }{\partial \beta _r} = \sum _{i=1}^n \frac{y_i - \mu _i}{\mu _i (1 + \varphi \mu _i)^2} \frac{\partial \mu _i}{\partial \beta _r} = 0. \end{aligned}$$

(6)

Since the likelihood equation for the regression coefficients, $\beta$, is nonlinear, the Iterative Weighted Least Squares (IWLS) algorithm (also known as the Fisher Scoring method) proposed by Dutang³⁸ is employed to derive the MLE. Let $\varvec{\beta }^{(s-1)}$ denote the vector of regression coefficients estimated at the $(s-1)$-th iteration. The coefficient vector is subsequently updated at the $s$-th iteration according to the following rule:

$$\begin{aligned} \beta ^{(s)} = \beta ^{(s-1)} + I^{-1}(\beta ^{(s-1)}) S(\beta ^{(s-1)}), \end{aligned}$$

(7)

where $S(\beta ^{(s-1)})$ is the score function evaluated at $\beta ^{(s-1)}$ and $I(\beta ^{(s-1)})$ is the Fisher information matrix. In the final step of the algorithm, the GPMLE for the regression coefficients, $\hat{\beta }_{\text {GPMLE}}$, is given by:

$$\begin{aligned} \hat{\beta }_{\text {GPMLE}} = A^{-1} X^\prime \hat{W} \hat{z}, \end{aligned}$$

(8)

where $A = X^\prime \hat{W} X$, $\hat{z}$ is the adjusted response vector, and $\hat{W}$ is a diagonal weight matrix with diagonal elements $\hat{w}_i$. The diagonal elements of $\hat{W}$ are $\hat{w}_i = \frac{\hat{\mu }_i}{(1 + \varphi \mu _i)^2}$, and the elements of the adjusted response vector $\hat{c}$ are $\hat{z}_i = \log (\hat{\mu }_i) + \frac{y_i - \hat{\mu }_i}{\hat{\mu }_i}.$

The asymptotic covariance matrix, matrix mean squared error (MMSE), and the MSE for GPMLE are given by:

$$\begin{aligned}&\text {Cov}(\hat{\beta }_{\text {GPMLE}}) = \left[ -E\left( \frac{\partial ^2 \ell }{\partial \beta \partial \beta ^\prime } \right) \right] = \hat{\varphi } ~Q \Lambda ^{-1}Q^\prime , \end{aligned}$$

(9)

$$\begin{aligned}&\quad \begin{aligned} \text {MMSE}(\hat{\beta }_{\text {GPMLE}}) =&\text {E}\left[ (\hat{\beta }_{\text {GPMLE}} - \beta )(\hat{\beta }_{\text {GPMLE}} - \beta )^\prime \right] \\ =&\text {Cov}(\hat{\beta }_{\text {GPMLE}}) + \left( \text {E}(\hat{\beta }_{\text {GPMLE}}) - \beta \right) \left( \text {E}(\hat{\beta }_{\text {GPMLE}}) - \beta \right) ^\prime = \hat{\varphi } ~Q \Lambda ^{-1}Q^\prime , \end{aligned} \end{aligned}$$

(10)

$$\begin{aligned}&\quad \begin{aligned} \text {MSE}(\hat{\beta }_{\text {GPMLE}}) =&\text {Tr}\left( \text {MMSE} (\hat{\beta }_{\text {GPMLE}})\right) =\hat{\varphi } \sum _{j=1}^{p} \frac{1}{\lambda _j}. \end{aligned} \end{aligned}$$

(11)

where Tr is the trace of the matrix, $\hat{\varphi }$ is the estimated dispersion parameter, the matrix $A$ is expressed as $A = Q \Lambda Q^\prime$, $\Lambda = \text {diag}(\lambda _1, \lambda _2, \dots , \lambda _{p}) = QA Q^\prime$ with $Q$ is an orthogonal matrix whose columns represent the eigenvectors of $QA Q^\prime$, and $\lambda _j$ is the jth eigenvalue of the A matrix. When the explanatory variables in the GPRM are highly correlated, the weighted cross-product matrix $A$ becomes unstable. This leads to inefficient estimates from the GPMLE, with large variances. As a result, the estimated coefficients are often too large, making them difficult to interpret.

Generalized Poisson ridge regression estimator

Segerstedt²⁰ introduced the ridge estimator for GLMs as a solution to multicollinearity, building on the foundational work of Hoerl and Kennard^16,17. When the explanatory variables in the GPRM are highly correlated, the GPMLE produces inefficient estimates characterized by a large MSE. Following the contributions of Månsson and Shukur²¹, Sami et al.²⁸, Shahzad et al.³³, and Ashraf et al.³⁴, this paper introduces a ridge estimator extended to the GPRM, referred to as the Generalized Poisson Ridge Regression Estimator (GPRRE). Its formulation is expressed as:

$$\begin{aligned} \hat{\beta }_{{k}^*} = \left( A + k^*I_p \right) ^{-1} S \hat{\beta }_{\text {GPMLE}}, \end{aligned}$$

(12)

where $k^* ( k^* > 0)$ is the ridge parameter, $I_p$ is the identity matrix, and if $k^*=0$ then the GPRRE is reduced to GPMLE.

The bias vector and variance-covariance matrix of the GPRRE are given by:

$$\begin{aligned} \begin{aligned} \text {Bias}\left( \hat{\beta }_{{k}^*} \right)&= E\left( \hat{\beta }_{{k}^*} \right) -\beta =-k^* Q \Lambda _{k^*}^{-1} \alpha , \end{aligned} \end{aligned}$$

(13)

$$\begin{aligned} \begin{aligned} \text {Cov}\left( \hat{\beta }_{{k}^*} \right)&=\text {E}\Bigg [\left( \hat{\beta }_{{k}^*}-\text {E}(\hat{\beta }_{{k}^*}) \right) \left( \hat{\beta }_{{k}^*}-\text {E}(\hat{\beta }_{{k}^*}) \right) ^\prime \Bigg ] =\hat{\varphi }~ Q\Lambda _{k^*}^{-1} \Lambda \Lambda _{k^*}^{-1} Q^\prime . \end{aligned} \end{aligned}$$

(14)

The MMSE and MSE for the GPRRE can be computed using Eqs. (13) and (14) as follows:

$$\begin{aligned} \begin{aligned} \text {MMSE}\left( \hat{\beta }_{{k}^*} \right) =&\text {E}\left( (\hat{\beta }_{{k}^*}-\beta )(\hat{\beta }_{{k}^*}-\beta )^{\prime }\right) =\text {Cov}\left( \hat{\beta }_{{k}^*} \right) +\text {Bias}\left( \hat{\beta }_{{k}^*} \right) \text {Bias}^{\prime }\left( \hat{\beta }_{{k}^*} \right) \\ =&\hat{\varphi }~ Q\Lambda ^{-1}_{k^*} \Lambda \Lambda ^{-1}_{k^*}Q^\prime + {k^*}^2Q \Lambda ^{-1}_{k^*} \mathbf {\alpha } { \mathbf {\alpha }}^\prime \Lambda ^{-1}_{k^*} Q^\prime , \end{aligned} \end{aligned}$$

(15)

$$\begin{aligned} \begin{aligned} \text {MSE}\left( \hat{\beta }_{{k}^*} \right) =&\text {Tr} \left[ \text {MMSE}\left( \hat{\beta }_{{k}^*} \right) \right] =\hat{\varphi } \sum ^{p}_{j=1}\frac{\lambda _j}{(\lambda _j+ k^* )^{2}}+{k^*}^{2}\sum ^{p}_{j=1} \frac{\alpha _j^2}{(\lambda _j + k^* )^{2}}, \end{aligned} \end{aligned}$$

(16)

where the vector $\alpha = Q^{T} \beta$, and $\Lambda _{k^*} = \text {diag}(\lambda _1 + k^*, \lambda _2 + k^*, \dots , \lambda _{p} + k^*) = Q(A + kI) Q^\prime$.

The superiority of the GPRRE over the GPMLE

To assess the superiority of the GPRRE compared to GPMLE, Hoerl and Kennard¹⁶ proposed theoretical results regarding the properties of the MSE for ridge regression estimators in the linear regression model. In this study, we demonstrate that these results are also applicable to the GPRM. Based on these theorems, we will investigate the superiority of the GPRRE over the GPMLE.

Theorem 1

The variance $D_1(k^*)$ and the squared bias $D_2(k^*)$ are continuous functions of $k^*$, where $D_1(k^*)$ is monotonically decreasing and $D_2(k^*)$ is monotonically increasing, provided that $k^* > 0$ and $\lambda _j > 0$.

Proof

Using Eq. 16, we are given the following expressions for the variance and squared bias:

$$D_1(k^*) = \hat{\varphi } \sum _{j=1}^{p} \frac{\lambda _j}{(\lambda _j + k^*)^2}, \quad D_2(k^*) = {k^*}^2 \sum _{j=1}^{p} \frac{\alpha _j^2}{(\lambda _j + k^*)^2}.$$

• 1. Monotonicity of $D_1(k^*)$: The derivative of $D_1(k^*)$ with respect to $k^*$ is:

  $$\frac{dD_1(k^*)}{dk^*} = -\hat{\varphi } \sum _{j=1}^{p} \frac{2\lambda _j}{(\lambda _j + k^*)^3},$$

  since $\lambda _j > 0$ and $k^* > 0$, we conclude that $\frac{dD_1(k^*)}{dk^*} < 0$, implying $D_1(k^*)$ is monotonically decreasing.

• 2. Monotonicity of $D_2(k^*)$: The derivative of $D_2(k^*)$ with respect to $k^*$ is:

  $$\frac{dD_2(k^*)}{dk^*} = 2k^* \sum _{j=1}^{p} \frac{\alpha _j^2}{(\lambda _j + k^*)^3} \lambda _j,$$

  since $\lambda _j > 0$ and $k^* > 0$, we have $\frac{dD_2(k^*)}{dk^*} > 0$, implying $D_2(k^*)$ is monotonically increasing.

Thus, $D_1(k^*)$ is monotonically decreasing and $D_2(k^*)$ is monotonically increasing for $k^* > 0$. $\square$

Theorem 2

For the GPRM, the GPRRE is more efficient than the GPMLE if

$$\text {MSE}(\hat{\beta }_{\text {GPMLE}})- \text {MSE}(\hat{\beta }_{k^*})> 0 \quad \text {for all} \quad k^*> 0 \quad \text {and} \quad \lambda _j > 0.$$

Proof

For $D_1(k^*)$ when $k^* = 0$, we have:

$$D_1(k^*) = \hat{\varphi } \sum _{j=1}^{p} \frac{1}{\lambda _j},$$

which equals $\text {MSE}(\hat{\beta }_{k^*})$ . The difference between $\text {MSE}(\hat{\beta }_{k^*}) ~\text {and} ~\text {MSE}(\hat{\beta }_{\text {GPMLE}})$ is:

$$\begin{aligned} \Delta&= \hat{\varphi } \sum _{j=1}^{p} \frac{1}{\lambda _j} - \left( \hat{\varphi } \sum _{j=1}^{p} \frac{\lambda _j}{(\lambda _j + k^*)^2} + \sum _{j=1}^{p} {k^*}^2 \frac{\alpha _j^2}{(\lambda _j + k^*)^2} \right) = \sum _{j=1}^{p} \frac{k^*(\hat{\varphi }k^*+2\hat{\varphi }\lambda -k^*\lambda \alpha _j^2)}{{\lambda _j}{(\lambda _j + k^*)^2}}, \end{aligned}$$

for any $k^* > 0$, then $\Delta > 0$ if and only if $\hat{\varphi }k^* + 2\hat{\varphi }\lambda - k^*\lambda \alpha _j^2 > 0$. Consequently, $\text {MSE}(\hat{\beta }_{\text {GPMLE}})-\text {MSE}(\hat{\beta }_{k^*}) > 0$ holds under the same condition, i.e., $\hat{\varphi }k^* + 2\hat{\varphi }\lambda - k^*\lambda \alpha _j^2 > 0$. $\square$

Selection of the biasing parameters

The ridge parameter ($k$) is a critical component of the ridge regression estimator, as its value directly governs the degree of shrinkage and bias introduced to stabilize the coefficient estimates. Consequently, the selection of an optimal value for this shrinkage parameter has become a central challenge in the application of the ridge methodology. This is particularly vital in the presence of multicollinearity, where high correlations among explanatory variables can severely degrade the performance of standard estimators. In response, a significant body of research has been dedicated to developing methods for estimating the optimal $k$ across diverse regression frameworks, such as those of Månsson and Shukur²¹, Schaefer et al.²², Rady et al.²³, Tharshan and Wijekoon²⁵, Algamal et al.²⁹, Akram et al.³².

The foundational work on this technique was established by^16,17, who first proposed ridge estimation to mitigate multicollinearity in linear regression models. Their approach has since been successfully generalized to a wider array of models, including the gamma regression model³² and the zero-inflated CMPRM³⁴. Within the context of the GPRM, the resulting estimator is designated as the GPRRE. For our analysis, following the works of^16,17 and²¹, we adopt the following values for $k^*$:

$$\begin{aligned} \hat{k}_{^*_1}&= \frac{\hat{\varphi }}{\sum _{j=1}^p \hat{\alpha }_{j}^2}, \end{aligned}$$

(17)

$$\begin{aligned} \hat{k}_{^*_2}&= \frac{\hat{\varphi }}{\max (\hat{\alpha }_{j}^2)}, \end{aligned}$$

(18)

$$\begin{aligned} \hat{k}_{^*_3}&= \min \left( \frac{\hat{\varphi }}{\hat{\alpha }_{j}^2}\right) . \end{aligned}$$

(19)

Following Ashraf et al.³⁴, we use the following values for $k^*$:

$$\begin{aligned} q_j&= \frac{\hat{\varphi }}{2\lambda _j \hat{\alpha }_{j}^2 + \hat{\varphi }}, \end{aligned}$$

(20)

$$\begin{aligned} \hat{k}_{^*_4}&= \text {median}(q_j), \end{aligned}$$

(21)

$$\begin{aligned} \hat{k}_{^*_5}&= \text {median}\left( \frac{\lambda _j}{1 + 2\lambda _j \hat{\alpha }_{j}^2}\right) . \end{aligned}$$

(22)

Following Shahzad et al.³³, we use the following values for $k^*$:

$$\begin{aligned} \hat{k}_{^*_6}&= \min \left( \frac{\lambda _j \hat{\varphi }}{\hat{\varphi } + \lambda _j \hat{\alpha }_{j}^2}\right) , \end{aligned}$$

(23)

$$\begin{aligned} \hat{k}_{^*_7}&= \frac{1}{\max (\hat{\alpha }_{j}^2)}. \end{aligned}$$

(24)

Following Tharshan et al.²⁵, we use the following values for $k^*$:

$$\begin{aligned} \hat{k}_{^*_8}&= \text {median}\left( \sqrt{\frac{1}{\hat{\alpha }_{j}^2}}\right) , \end{aligned}$$

(25)

$$\begin{aligned} \hat{k}_{^*_9}&= \max \left( \frac{1}{\sqrt{\frac{1}{\hat{\alpha }_{j}^2}}}\right) . \end{aligned}$$

(26)

Following Sami et al.²⁸, we use the following value for $k^*$:

$$\begin{aligned} \hat{k}_{^*_{10}}&= \min \left( \frac{1}{\sqrt{\frac{\max (\lambda _j \hat{\varphi })}{(n - p - 1)\hat{\varphi } + \max (\lambda _j)\hat{\alpha }_{j}^2}}}\right) . \end{aligned}$$

(27)

Following Amin et al.³⁹, we use the following values for $k^*$:

$$\begin{aligned} \hat{k}_j&= \frac{1}{\hat{\alpha }_{j}^2}, \end{aligned}$$

(28)

$$\begin{aligned} \hat{k}_{^*_{11}}&= \frac{p}{\sum _{j=1}^p \frac{1}{k_j}}. \end{aligned}$$

(29)

Building upon the previous works, we propose the following values for $k^*$:

$$\begin{aligned} \hat{k}_{^*_{12}}&= \frac{\hat{\varphi }}{\sum _{j=1}^p \sqrt{\frac{1}{k_j}}}, \end{aligned}$$

(30)

$$\begin{aligned} \hat{k}_{^*_{13}}&= \sum _{j=1}^p \left( pq_j\right) , \end{aligned}$$

(31)

$$\begin{aligned} \hat{k}_{^*_{14}}&= \text {median}\left( \frac{\hat{\varphi }p}{\sqrt{\frac{\hat{\varphi }}{\hat{\alpha }_{j}^2}}}\right) , \end{aligned}$$

(32)

$$\begin{aligned} \hat{k}_{^*_{15}}&= \frac{1}{p} \text {mean}\left( \frac{\lambda _j}{\hat{\varphi } + 2\lambda _j \hat{\alpha }_{j}^2}\right) . \end{aligned}$$

(33)

Monte Carlo simulation

This section presents Monte Carlo simulations to evaluate the performance of the proposed estimator, including the simulation design, results, and a comparison of relative efficiency.

Simulation design

This section describes the Monte Carlo simulation study conducted to evaluate the performance of different estimators in the GPRM under multicollinearity. The response variable (y) was generated from a GP distribution^40,41, with the mean ($\mu _i=\exp (x_i \beta )$) for $i = 1, \dots , n$, $\beta$ representing the vector of coefficients, and $x_i$ being the $i$ th row of the design matrix $X$ contains the explanatory variables. The explanatory variables were simulated using the formula^42,34:

$$\begin{aligned} x_{ij} = \sqrt{1 - \rho ^2} \, e_{ij} + \rho e_{i,p+1}, \quad i = 1, \dots , n; \quad j = 2, \dots , p, \end{aligned}$$

(34)

where $\rho$ determines the correlation between explanatory variables and $e_{ij}$ is drawn from a standard normal distribution. Multicollinearity was analyzed for $\rho$ values of 0.80, 0.85, 0.90, 0.95, and 0.99. Models were tested with 4, 7, and 10 explanatory variables. The intercept ($\beta _0$) was set to 1, and the dispersion parameter $\varphi$ was varied at 0.01, 0.5, and 1⁴¹. The slope coefficients were set such that $\sum _{j=2}^{p} \beta _j^2 = 1$, with equal values for $\beta _1, \dots , \beta _{p-1}$. Simulations were conducted for sample sizes of 50, 100, 150, 200, 300, and 400.

The simulations were implemented in the R software (R version 4.4.1). For each iteration, the estimated MSE of the estimators was calculated as follows^43,44:

$$\begin{aligned} \text {MSE}(\beta ^*) = \frac{\sum _{l=1}^{1000} (\hat{\beta }_l - \beta )^T (\hat{\beta }_l - \beta )}{1000}, \end{aligned}$$

(35)

where $\varvec{\beta }_l$ denotes the vector of estimated coefficients from the $l$-th simulation run for a specific estimator (such as the GPMLE or a GPRRE employing a particular ridge parameter). The estimator associated with the smallest MSE was deemed optimal for alleviating the effects of multicollinearity within the GPRM framework.

Table 1 Estimated MSE values for different estimators at $p=4$ and $\varphi =0.1$.

Table 2 Estimated MSE values for different estimators at $p=4$ and $\varphi =0.5$.

Table 3 Estimated MSE values for different estimators at $p=4$ and $\varphi =1$.

Table 4 Estimated MSE values for different estimators at $p=7$ and $\varphi =0.1$.

Table 5 Estimated MSE values for different estimators at $p=7$ and $\varphi =0.5$.

Table 6 Estimated MSE values for different estimators at $p=7$ and $\varphi =1$.

Table 7 Estimated MSE values for different estimators at $p=10$ and $\varphi =0.1$.

Table 8 Estimated MSE values for different estimators at $p=10$ and $\varphi =0.5$.

Table 9 Estimated MSE values for different estimators at $p=10$ and $\varphi =1$.

Simulation results

Simulation Tables 1, 2, 3, 4, 5, 6, 7, 8 and 9 provide a detailed comparison of the MSE for the GPMLE and different versions of the GPRRE under various experimental conditions. These conditions include different levels of multicollinearity ($\rho$), sample sizes ($n$), dimensions ($p$), and shrinkage parameters ($\varphi$). The tables highlight the best-performing estimator in each scenario by marking the lowest MSE values in bold. Main factors affecting simulation:

• 1. Effect of multicollinearity:

  • The degree of multicollinearity ($\rho$) emerged as the most critical factor influencing estimator performance. As expected, the MSE of the GPMLE becomes increasingly severe with higher $\rho$ values.

  • Under severe multicollinearity, the GPMLE’s MSE becomes prohibitively large, often by an order of magnitude or more compared to the best-performing GPRRE. The ridge estimators, particularly $\hat{k}^*_{13}$, $\hat{k}^*_{14}$, and $\hat{k}^*_{15}$, demonstrate remarkable robustness, maintaining stable and low MSE by effectively shrinking the coefficients and controlling variance, even when the correlation between predictors approaches 0.99.

  • While the performance gap narrows under moderate multicollinearity, the GPRRE variants still consistently achieve a lower MSE than the GPMLE. This advantage is most evident for smaller sample sizes ($n = 50, 100$), where the data provides less information to stabilize the MLE.

• 2. Effect of sample size:

  • The benefits of the ridge approach are most acute in “small n” situations, which are common in modern statistical applications.

  • For small $n = 50, 100$, the GPMLE is highly unstable. The GPRRE provides dramatic improvements in these settings, often reducing the MSE by half or more. This confirms that ridge regression is an essential tool for preventing overfitting when data is scarce.

  • As the sample size increases ($n = 300, 400$), the performance of all estimators improves, and the relative advantage of the GPRRE diminishes. This is consistent with theoretical expectations, as the GPMLE is asymptotically unbiased. However, even with $n=400$, the GPRRE often retains a slight edge, especially under high multicollinearity.

• 3. Effect of number of explanatory variables:

  • The benefits of the ridge approach are most acute in “large p” situations, which are common in modern statistical applications.

  • The challenge of estimation increases with the number of explanatory variables. The GPRRE shows a clear and growing advantage over the GPMLE as p increases from 4 to 10, effectively managing the added complexity and severe multicollinearity.

• 4. Effect of dispersion parameter:

  • The value of the dispersion parameter $\varphi$ influences the scale of the MSE but does not alter the fundamental ranking of the estimators. The relative performance of the different GPRRE variants remains consistent across values of $\varphi$. Among the fifteen evaluated ridge estimators, $\hat{k}^*_{13}$, $\hat{k}^*_{14}$, and $\hat{k}^*{15}$ consistently emerge as top performers. Their success is attributed to a more effective calibration of the shrinkage intensity, optimally balancing the introduced bias against the reduction in variance to minimize the total MSE.

The results consistently demonstrate that the proposed GPRRE outperforms the conventional GPMLE across virtually all simulated scenarios. The reduction in MSE is particularly pronounced, underscoring the efficacy of introducing a bias-variance trade-off to manage the adverse effects of multicollinearity. The GPMLE, which relies on asymptotic properties that are violated in the presence of high correlation among predictors and finite samples, exhibits significantly inflated variance. In contrast, the GPRRE successfully stabilizes the coefficient estimates, leading to a substantial decrease in MSE.

In summary, the simulation study provides robust empirical evidence that the GPRRE is a superior alternative to the traditional maximum likelihood estimator in the presence of multicollinearity. Its performance is particularly strong in finite samples, with high-dimensional data, and under severe correlation among regressors. The proposed estimators $\hat{k}^*_{13}$ and $\hat{k}^*_{14}$ are recommended as reliable choices for practitioners, as they consistently provide the most accurate and stable estimates across a wide range of challenging data conditions. This demonstrates that the GPRRE is not merely a theoretical exercise but a practical and necessary enhancement to the regression toolkit for overdispersed and multicollinear count data.

Relative efficiency

Relative Efficiency (RE) is used to compare the performance of statistical estimators by measuring their precision and reliability. This comparison relies on the MSE, which combines bias and variance, with a lower MSE indicating better performance. The formula for RE is:

$$\begin{aligned} \text {RE}(\beta _{{k^*}_i}) = \frac{\text {MSE}(\beta _{\text {GPMLE}})}{\text {MSE}(\beta _{{k^*}_i})}, \end{aligned}$$

(36)

where $\beta _{{k^*}_i}$ represents the MSE of GPRRE with each parameter. The reference estimator, $\text {MSE}(\beta _{\text {GPMLE}})$, is often used as a benchmark due to its strong asymptotic properties.

Fig. 1

Estimated MSE of the GPRRE under different parameter settings and sample sizes.

Fig. 2

Estimated MSE of the GPRRE under different parameter settings and multicollinearity level.

Fig. 3

Estimated MSE of the GPRRE under different parameter settings and number of explanatory variables.

Fig. 4

Estimated MSE of the GPRRE under different parameter settings and dispersion parameter.

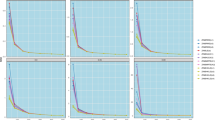
Figures 1, 2, 3 and 4 present a comprehensive evaluation of RE was conducted to rigorously assess the performance of the GPRRE under different shrinkage parameters, with RE plotted as a function of key statistical parameters: sample size ($n$), population correlation ($\rho$), the number of predictor variables ($p$), and a measure of dispersion ($\varphi$). The results demonstrate that the proposed GPRRE estimator consistently achieved the highest relative efficiency across the vast majority of the investigated scenarios. This superior performance manifests as a high RR, indicating that the GPRRE provides estimates with greater precision and stability that is, a smaller variance and reduced susceptibility to bias compared to its competitors. The empirical evidence thus robustly confirms that the GPRRE is the most efficient estimator within the defined class of models under study. This dominance was particularly pronounced when compared to the estimator denoted as $\hat{k}^*_{13}$, $\hat{k}^*_{14}$, and $\hat{k}^*_{15}$, which was consistently outperformed, often by a significant margin.

Application

This study investigates CO$_2$ emissions from plug-in hybrid electric vehicles (PHEVs) sold in Canada between 2020 and 2025. The primary dataset focuses on vehicles from this five-year period, though additional data for other years is available through Open Canada. The dataset includes 245 vehicles, with CO$_2$ emissions in grams per kilometer ($y$) as the response variable and six explanatory variables: motor power in kilowatts ($x_1$), engine size in liters ($x_2$), number of cylinders ($x_3$), city fuel consumption in liters per 100 kilometers ($x_4$), highway fuel consumption in liters per 100 kilometers ($x_5$), and combined fuel consumption in liters per 100 kilometers ($x_6$). Fuel consumption metrics are provided separately for city and highway driving, along with a combined rating (55% city and 45% highway) expressed in both liters per 100 kilometers and miles per gallon. CO$_2$ emissions are derived from combined city and highway driving data and are reported in grams per kilometer.

Initially, the fit of the data to the chosen model is carefully evaluated using commonly used criteria such as log-likelihood (LL), Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC). The best model is selected based on having the highest LL value and the lowest values for both AIC and BIC. Based on the results presented in Table 10, the GPRM model performs best in modeling this data, achieving the highest LL value and the lowest values for both AIC and BIC.

The correlation plot (Fig. 5) indicated strong correlation among the variables, suggesting the presence of multicollinearity. To assess this formally, variance inflation factors (VIFs) and the condition number (CN) were calculated. The CN, defined as the ratio of the largest to the smallest eigenvalue, was 4557.855. The computed VIF values were 1.28, 8.79, 10.38, 2873.80, 804.81, and 6496.13, which clearly demonstrate severe multicollinearity. These results confirm that the variables are highly correlated, raising concerns about the stability and reliability of subsequent regression analyses.

Fig. 5

Correlation matrix illustrating the relationships between explanatory variables in the dataset.

Table 10 Comparison of model performance for the dataset.

Table 11 Estimated MSE and coefficient of GPMLE and GPRRE for the dataset.

Table 11 compares the GPMLE and the GPRRE for a dataset with seven regression coefficients ($\beta _0$ to $\beta _6$). The coefficients are estimated using Eqs. (8) and (12), while the MSE is computed using Eqs. (11) and (16), respectively. The GPMLE yields an MSE of 29.2930, indicating poor performance likely due to multicollinearity. In contrast, the GPRRE, evaluated using 15 ridge parameters ($\hat{k}^*_1$ to $\hat{k}^*_{15}$), demonstrates significantly lower MSE values, with the best performance achieved by $\hat{k}^*_{14}$ (MSE = 1.3728). This substantial improvement highlights the effectiveness of the ridge estimator in mitigating multicollinearity by stabilizing coefficient estimates and reducing overfitting. The consistent performance of GPRRE across various ridge parameters underscores its robustness, making it a superior choice for datasets affected by multicollinearity.

Fig. 6

Estimated MSE with different values of ridge parameter.

Figure (6) compares the performance of the GPMLE and GPRRE estimators based on MSE values across a range of ridge parameters ($k^*$). The graph illustrates that GPRRE significantly outperforms GPMLE in reducing MSE, particularly as $k^*$ increases. The MSE associated with the GPRRE demonstrates a substantial reduction, achieving its minimum at higher values of the ridge parameter $k^*$. In contrast, the MSE for the Generalized Poisson Maximum Likelihood Estimator (GPMLE) remains consistently larger across the entire range of $k^*$ values. This performance improvement is attributed to the ridge estimator’s mechanism for mitigating multicollinearity, which stabilizes coefficient estimates and reduces their variance through the introduction of a penalty term contingent upon $k^*$. Furthermore, the accompanying figure delineates the bias-squared and variance components of the GPRRE, illustrating how the estimator successfully negotiates a trade-off between these two elements. Although the squared bias experiences a marginal increase, it is offset by a considerable reduction in variance, culminating in a net decrease in the overall MSE. These findings underscore the efficacy of the GPRRE in enhancing predictive performance, particularly in contexts where the data exhibit pronounced multicollinearity.

Table 12 Results confirming the necessary condition for Theorem 2.

Table 12 presents the results of the verification process for the necessary condition associated with Theorem 2 under the GPRRE. The analysis evaluates this condition across a range of proposed ridge parameters ($k^*_i$) and for each of the seven coefficients ($\lambda _1$ to $\lambda _7$). The computed values of the condition are consistently positive for all combinations of $k^*$ and $\lambda _j$, thereby confirming that the requisite condition is satisfied. This uniform positivity demonstrates the efficacy of the GPRRE in stabilizing the model and reducing estimation variance, even in the presence of significant multicollinearity. Consequently, these results underscore the capability of the GPRRE to manage complex data structures while simultaneously enhancing model performance and reliability.

Conclusion

The GPRM serves as a robust framework for analyzing count data, particularly in cases of overdispersion or underdispersion. While the GPMLE is widely employed, its efficacy is compromised in the presence of multicollinearity among explanatory variables. To mitigate this issue, this study introduces ridge estimators within the generalized GPRRE framework and explores methodologies for optimal ridge parameter selection. The theoretical properties of the ridge estimator are rigorously derived, and its performance is assessed using both MMSE and MSE criteria. A detailed Monte Carlo simulation study is conducted, examining various parametric configurations, including sample sizes, numbers of predictor variables, dispersion levels, and degrees of multicollinearity. Furthermore, the proposed estimators are applied to a real-world dataset concerning carbon dioxide emissions. The results from both the simulation study and the empirical application consistently demonstrate that the GPRRE, particularly when paired with an optimally selected ridge parameter, significantly outperforms the GPMLE in reducing MSE under conditions of severe multicollinearity, especially for parameter values $k^*_{13}$ and $k^*_{14}$. These findings underscore the GPRRE as a superior estimation technique for addressing multicollinearity in overdispersed count data. Despite the positive results of this study, it is not without limitations. The performance of the GPRRE method depends primarily on selecting the optimal value for the shrinkage parameter ($k^*$), which is highly sensitive and balances bias and variance. Furthermore, the high dimensionality of the data increases the complexity of the calculations and poses significant challenges that require further research and improvement. Additionally, the current application of this method is limited to addressing multicollinearity in the Generalized Poisson Regression Model (GPRM), which opens promising avenues for future development to address other issues, such as outliers, building upon previous research, such as the study by Dawoud et al.⁴⁵, Abonazel and Dawoud⁴⁶, Mohammad et al.⁴⁷, and Alghamdi et al.⁴⁸.