Forward-thinking frequency management in islanded marine microgrid utilizing heterogeneous source of generation and nonlinear control assisted by energy storage integration

Abstract

The increasing environmental challenges and global warming concerns have driven a shift towards renewable energy-based power generation, particularly in microgrids. However, marine microgrids face challenges in load-frequency regulation due to renewable energy intermittency, unpredictable load variations, and nonlinear system dynamics. Conventional control strategies often struggle with poor convergence, limited adaptability, and suboptimal frequency stabilization. Addressing these challenges requires an advanced control optimization technique for robust frequency regulation and system stability in dynamic marine environments. This study proposes a Chaotic Chimp-Mountain Gazelle Optimizer (CCMGO) for optimizing fractional-order proportional-integral-derivative (FOPID) controllers, enhancing load-frequency regulation in a multi-source marine microgrid. The system integrates wave energy, wind turbines, solar towers, and photovoltaic energy, along with controlled biogas turbines, micro hydro turbines, and bio-diesel engine generation. To improve frequency stability and grid flexibility, battery energy storage systems, ultra-capacitors, and electric vehicles are incorporated for dynamic compensation. The CCMGO algorithm combines the exploration strength of the mountain gazelle optimizer with solution diversity enhancements from chaotic mapping and chimp optimization algorithm, preventing premature convergence and improving control efficiency. The performance of CCMGO-optimized controllers (PID, PD–PID, FOPI–FOPID, and FOPID) is evaluated under various load conditions, including impulse, ramp, and stochastic disturbances, to test robustness and adaptability. Simulation results demonstrate that CCMGO-based FOPID controllers outperform conventional strategies, achieving lower frequency deviations, faster settling times, and enhanced transient response. These findings establish CCMGO–FOPID as a powerful tool for optimizing control performance in marine microgrids, ensuring greater resilience, stability, and energy efficiency.

Introduction

Symbol	Nomenclature	Value
KAWEC.TAWEC	AWEC gain and time constant	1,0.3 s
KWT, TWT	Gain and time constant of WTG unit	1,1.5 s
ρ, Ar, λ, β, CP, VW, Rb and Wb	Air density, blade-swept area, tip-speed ratio and blade pitch angle, power coefficient, speed of the wind, radius of blades, and turbine nominal speed of WTG	1.25 kg/m3,1735m2, − 23.5 and 3.14
KPV, TPV	Gain and time constant of PV system	1, 1.8 s
KRF, KRV, KG, KT	gain values of refocus, receiver, governor, and turbine of ST	1, 1, 1, 1
TRF, TRV, TG, TT	time constant of refocus, receiver, governor, and turbine of ST	1.33, 4, 0.08, 1 s
KMH	Participation factor of MHTG unit	0.5
TMG, TRS, TRH, THT	Governor gain, delay, reset, transient droop and delay of MHTG unit, respectively	0.2 s, 5 s, 28.75 s, 1.0 s
KBD	Participation factor of BDEG unit	0.5
KVA, TVA, KBE, TBE	Valve gain, valve actuator delay, engine gain and time constant of BDEG unit respectively	1, 0.05 s,1.0.0.5 s
KBG	Participation factor of BGTG	0.5
R1, R2, R3	Droop characteristics	2.0
TCR, TBG, XC, YC, bB, TBT	Combustion reaction delay, biogas delay, lead time, lag time, valve actuator and discharge delay of BGTG unit, respectively	0.01 s, 0.23 s, 0.6,1.0 s, 0.05, 0.2 s
KBESS, TBESS	Gain and time constant of BESS system	0.03,0.1 s
KEV, TEV	Gain and time constant of EV	1,1 s
KUC, TUC	Gain and time constant of UC	0.7,0.9 s

Basics: problem under study case

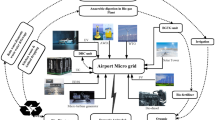
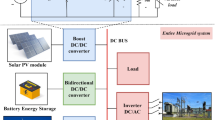
The global shift towards sustainable energy systems has placed microgrids at the forefront of modern power systems, particularly in specialized environments like marine settings. Marine microgrids, which incorporate renewable energy sources, energy storage systems, and advanced control mechanisms, are considered the future of marine power systems due to their efficiency, reliability, and reduced environmental impact. A marine microgrid consists of distributed energy resources such as AWES, WTG, PV, ST, BGTG, BDEG, MHTG and EV along with energy storage systems like BESS and UC all are integrated. These systems operate in a controlled, islanded mode to power marine vessels, offshore platforms, and remote coastal facilities. Marine microgrids, due to their independence and adaptability, are ideal for scenarios where grid connection is not possible or feasible. Microgrids are becoming more popular due to the growing demand for resilient and sustainable energy systems, especially in critical infrastructure such as marine areas. Microgrids generate power locally and can operate independently from the main grid, making them a reliable option during outages and grid instability. However, isolated microgrids can struggle to maintain a constant power frequency, especially when a large number of different generation sources are involved. Propulsion systems, auxiliary equipment, and weather conditions subject marines to significant load fluctuations, necessitating the use of LFC to ensure the stability and operational efficiency of marine microgrids. Dynamic load changes are common on marines, so LFC is required to regulate frequency stability and prevent potential equipment damage. Effective LFC prevents sudden load changes from affecting the overall system frequency, ensuring smooth operation. Moreover, the marine microgrid is increasingly integrating intermittent renewable energy sources like wind, solar, and wave energy into controlled generations such as BGTG, biodiesel, MHTG and EV as well as energy storage devices like BESS and UC. Complex Control Strategies Maintaining system stability and managing frequency under such fluctuating conditions requires optimization techniques, such as hybrid optimization techniques. Hybrid optimization strategies combine the benefits of multiple optimization techniques to fine-tune control parameters for frequency regulation. This method allows for more accurate frequency control of the system, reducing fluctuations and improving the overall performance of the microgrid. Integrating energy storage devices into this optimized control technique can solve the problem of isolated microgrids powered by heterogeneous generation in a more robust and adaptive manner. ESS are crucial as they improve LFC performance by providing power during times of high demand or absorbing excess energy. Furthermore, the distributed control and communication framework of marine microgrids mitigates the possibility of frequency instability due to communication delays, enabling localized and real-time LFC. Even under challenging marine conditions, these microgrids can maintain stability due to their inherent resilience.

Literature survey

The LFC field has grown significantly in recent years due to the increasing complexity of microgrid systems and the demand for improved stability and performance of hybrid power systems integrated with renewable energy sources. This has created a need for robust and efficient LFC systems. To address the dynamic challenges posed by renewable energy sources, time delays, and communication issues, many studies have investigated different optimization approaches, controller designs, and hybrid system architectures. Fundamentals of Microgrid Development and Installation was presented by Roosa¹. The architecture, control, and protection techniques developed by Tabatabaei et al.² were examined.

As microgrids become increasingly complex and dependent on renewable energy sources, there is a growing demand for advanced and efficient optimization techniques. This recent work focuses on bio-inspired algorithmic control mechanisms and has made significant progress towards ensuring the stability and reliability of microgrid systems under a variety of operating conditions. El-Fergany and El-Hameed³ study improving frequency controllers in dual-area hybrid microgrids using social spider optimization techniques. Their work shows how adaptive and resilient control strategies can effectively improve system performance and stability in isolated microgrids. Rajaguru and Annapoorani⁴ propose a virtual synchronous generator with superconducting magnetic energy storage using African Vulture optimization techniques. Their work shows improved performance under various load conditions and addresses the critical problem of frequency regulation in microgrids with a high share of renewable energy sources. Sobhy et al. focus on LFC to improve control of systems with various energy sources. Sobhy et al.⁵ apply the Manta foraging optimization algorithm to modern hybrid power systems. A one-hour optimization method for shared energy storage in renewable energy plants was presented by Ma et al.⁶. The approach improves frequency regulation by maximizing the use of energy storage and addresses the intermittency issue in renewable energy production. Barik and Das⁷ study demand response in a hybrid microgrid supported by bio-renewable cogeneration and optimized using a quasi-adversarial selfish herding algorithm. Their work highlights the importance of incorporating demand management into LFC planning to improve performance. The use of Grasshopper optimization techniques for reliable LFC in shipboard microgrids has been presented by Choudhary et al.⁸. Their work shows how well bio-inspired optimization techniques can handle frequency regulation in complex systems such as marine microgrids. Guha et al. ⁹ use chaotic crowd search method to compare several controllers for hybrid power systems. Their study shows that the chaotic concept based approach improves stability and accuracy and significantly improves the performance of the controller in frequency regulation. Quasi-adversarial harmonic search algorithm is used by Shankar and Mukherjee¹⁰ for an autonomous hybrid power system with emphasis on LFC. Their study shows how the harmonic search algorithm can maximize the system performance in various stressful scenarios. A multi-objective coordination formula for LFC in low inertia microgrids incorporating renewable energy sources such as solar PV, wind, fuel cells, and BESS was developed by Khalil et al.¹¹. Their work highlights the need for advanced coordination techniques to maintain the stability of microgrids powered primarily by renewable energy sources. A multi-agent soft actor-critic algorithm for LFC in isolated multi-microgrid systems was proposed by Xie et al.¹². Her work shows how distributed control and reinforcement learning can be used for frequency regulation in networked microgrids. Latif et al.¹³ addressed the control approach and presented a WCA-optimized fractional controller for a dual-area isolated microgrid using EVs in combination with wind and PV power generation systems, demonstrating improved system stability. A BOA-optimized PFOID controller for a three-area microgrid with different energy storage technologies is developed by Latif et al.¹⁴ in a related work. By using DC connection, we were able to demonstrate improved frequency management. In a system with a lagging EV aggregator, Babaei et al.¹⁵ optimized a fractional order PID controller for LFC using the Salp swarm algorithm and suggested that a fractional order controller can improve dynamic response during delays. Aftab et al.¹⁶ successfully reduced the impact of communication delays on frequency regulation by presenting an optimized cascade controller for microgrids integrated with energy storage. Shaker et al.¹⁷ emphasized adaptive nonlinear controllers for frequency regulation in multi-island microgrids, demonstrating improved stability and dynamic performance in complex grid architectures. Latif et al.¹⁸ also tackled load frequency stabilization using double-stage controllers in hybrid maritime microgrids, incorporating wind and ocean wave energy systems for enhanced performance. Further, research by Latif et al.¹⁹ introduced a time-delay and GCSC coordination strategy for dual-area interlinked microgrids, optimizing frequency stabilization through non-integer controller optimization. Latif et al.²⁰ also proposed a demand response-supported system with a dual-stage PIFOD controller, focusing on wind, tidal, and biodiesel-based two-area microgrids, showing that incorporating demand response improves system coordination. Pan and Das²¹ contributed by applying chaotic multi-objective optimization to fractional-order LFC in interconnected power systems, achieving better control under varying system dynamics. Khooban et al.²² studied a stochastic fractional controller for microgrids that enables robust frequency control, especially in uncertain environments. Recent work by Latif et al.²³ studied a modified slope integral controller for active interference suppression in marine microgrids that incorporates inertial emulation via DC connection to further improve frequency stability in dynamic marine environments. Khalil et al.²⁴ developed a unique cascade controller for islanded microgrids using the Dandelion optimizer, which improved the system stability and control accuracy. Overall, these studies demonstrate advances in LFC strategies in terms of optimization techniques, fractional order controllers, and hybrid systems, especially addressing communication limitations, time delays, and renewable energy integration issues. Khokar et al.²⁵ used a chaotic sine–cosine algorithm for microgrid LFC based on a 2D sine logistic map, which improved the system’s resistance to shocks and dynamic responses. Yıldız et al. use a fuel cell-based system to mitigate cyber-attacks, combining fractional control with cybersecurity measures. Yıldız²⁶ LFC in microgrids for renewable energy. Redox flow batteries have been developed by Elkasem et al.²⁷ and have been proposed as a means of frequency control in hybrid renewable energy grids, successfully stabilizing the system under fluctuating conditions. khooban et al.²⁸ introduced an innovative approach to LFC in shipboard microgrids, focusing on hybrid power sources and autonomous systems. Vafamand et al. further investigated this technique and addressed the issue of time delays in stabilizing LFC using an additional control loop²⁹. Khooban et al. conducted additional research to demonstrate the reliability of frequency control in mobile microgrids using a hardware-in-the-loop (HIL) implementation. This means that the system responds faster and is more adaptive³⁰. Mutarraf et al. demonstrated the potential of hybrid marine microgrids by focusing on the control of a hybrid diesel/PV/battery/ultracapacitor system³¹. To build a more effective shipboard power system, Wang et al.³² proposed a new marine hybrid power generation system with a high-voltage direct current connection. Bahrampour et al.³³ They recently made progress in optimizing LFC in shipboard microgrids by designing a fractional order controller with a direct search method. The Grasshopper optimization technique was developed by Choudhary et al.⁸ with the aim of improving the control efficiency under dynamic marine conditions by ensuring resilience and frequency control in shipboard microgrids. Abdollazadeh et al.³⁴ demonstrated the effectiveness of this approach in various engineering applications by introducing it to tackle challenging global optimization problems. Apart from this, Recent studies focus on microgrid optimization, energy management, and control strategies. Pushkarna et al.³⁵ and Pushkarna et al.³⁶ optimized DG placement and power loss minimization. Kumar et al.³⁷ enhanced power quality using DSTATCOM, while Khan et al.³⁵ reviewed microgrid energy strategies with AI and EVs. Ahmed et al.³⁸ developed a sliding mode controller for frequency regulation, and Gbadega and Sun³⁹ applied enhanced-WOA-tuned PID for load frequency control. Gbadega et al.⁴⁰ and Gbadega and Saha⁴¹ focused on optimal power management and adaptive model predictive control. Gbadega and Balogun^42,43 introduced transactive energy management for renewable microgrids, contributing to stability and efficiency improvements.

Analysis: literature work study

A literature review on Load Frequency Control (LFC) for microgrid systems highlights recent advances in the areas of optimization techniques, controller design, and command with a focus on the integration of renewable energy sources. Optimization techniques are becoming increasingly popular. These include biologically inspired algorithms such as African vulture optimization and social spider optimization, as well as more sophisticated approaches such as harmony search and quasi-adversarial selfish swarm algorithms. Controller designs include fractional order PID and FOPI–FOPID controllers, adaptive and robust control approaches, and cascaded controllers for complex architectures. The integration of renewable energy sources such as wind, solar photovoltaics, ST, and ocean wave energy has been a key focus, with strategies to address the challenges of intermittency through virtual synchronous generators and energy storage systems. Emphasis is placed on hybrid system architectures, especially in multi-area interconnected microgrids, and specialized applications such as shipboard and marine microgrids. Challenges such as time delays, communication issues, and demand response integration are addressed with a focus on cybersecurity in renewable energy microgrids. New technologies such as hardware-in-the-loop implementation, high-voltage DC interconnects, and battery energy storage systems for frequency regulation are also gaining attention. Advanced control strategies such as reinforcement learning, distributed control, and adaptive nonlinear controllers are investigated for multi-island microgrids, along with inertial emulation techniques to improve stability. To address the increasing complexity of microgrids with high renewable energy penetration and optimize system stability and performance, the study highlights the trend towards intelligent, adaptive, and resilient control systems. The analysis of literature review has been discussed in Table 1.

Table 1 Analysis of state-of-the -art literature.

Problem identification, motivation and the proposed approach

Problem identification

Ensuring stable frequency in isolated marine microgrids, especially those integrating multiple renewable energy sources such as wind, solar, and wave energy, presents significant obstacles. The inclusion of multiple renewable energy sources introduces inherent intermittency, complicating the task of load frequency control. Unpredictability of load demand caused by dynamic operating conditions such as ship propulsion systems and auxiliary equipment further exacerbates frequency regulation. Existing control algorithms often fail to effectively optimize system performance due to their inability to adapt to fluctuations and handle varying energy inputs, especially in real-time scenarios. Furthermore, standard controllers such as PID are unable to control the nonlinearities and time delays inherent in complex systems, resulting in poor stability and performance.

Motivation

Especially in the maritime sector, the transition towards greener and more sustainable energy systems is driving the demand for advanced control solutions that ensure operational efficiency and reliability. This research is motivated by the growing demand for energy-efficient and reliable offshore microgrids that can operate autonomously. The stability of such systems is crucial, especially in remote and harsh marine areas where grid connection is not practical. Furthermore, the increasing integration of renewable energy sources necessitates the development of control algorithms that can dynamically adapt to fluctuating demand conditions and mitigate the effects of energy interruptions. The ability to exploit the flexibility of modern controls combined with robust optimization techniques motivates us to develop and test new solutions that can improve the dynamic performance of marine microgrids.

Proposed approach

This study presents a hybrid CCMGO algorithm to work out the frequency deviation problem in marine microgrid systems. The proposed control method uses robust control techniques to enhance system stability under varying load conditions. The hybrid CCMGO algorithm method uses the chaos map and exploration capabilities of MGO and integrates the adaptation technique of ChOA. Unlike PSO and GA, which often suffer from premature convergence and slow adaptation in nonlinear systems, CCMGO integrates chaotic mapping, enhancing solution diversity and global search capability.

Key contribution

Rigorous simulation studies are conducted to test LFC under different operating scenarios, helping to optimize control parameters and design robust systems. Through these strategies, marine microgrids achieve high reliability and resilience, even amidst the complexities of renewable energy integration and fluctuating load demands. Therefore, the key contributions are as follows:

• a. A new marine microgrid is modelled, designed, optimized and analyzed with the inclusion of diverse generations like AWEC, WTG, PV, ST, BTGU, MTGU, BDGU, EV, BESS and UC to enhance the microgrid’s flexibility and ability to balance generation and load.

• b. The study applied CCMGO algorithm in advancement of primary frequency regulation in marine microgrid involving the concept of chaotic and CHOA algorithm for better exploration and exploitation capacity.

• c. The research study evaluates the superiority of CCMGO algorithm with the design FOPID controller subjected to PID, cascaded PD–PID and FOPI–FOPID controllers for LFC analysis in marine microgrid.

• d. Conducted extensive simulations to test effectiveness of the implemented control strategies under various load conditions, including step-ramp changes, positive and negative impulses, and random load variations.

The paper systematically explores power system modelling and control. Section “Test system modelled and investigated” details the test system components, Section “Modelling of controller: controller design and methodology” covers controller design and methodology, and Section “Problem formulation: defining LFC objective function” formulates an optimization problem to improve LFC. Section “Implemented algorithm details” introduces the chaotic chimp mountain gazelle optimization algorithm, with Section “Simulation results and analysis” presenting simulation results demonstrating its effectiveness. Sections “Limitations and constraints of this study” and “Conclusions and scopes of future work” acknowledge limitations and propose future research directions to enhance the algorithm’s application in micro-grid control.

Test system modelled and investigated

Basic description of the model

This study explores LFC performance in a marine power system model, incorporating various energy generation and storage components. The key elements include BDEG, which uses biodiesel as fuel, and BGTG and MHTG.WTG converts wind energy to electricity, governed by control equations with specific time constants. AWEG harnesses ocean wave energy, while PV converts solar radiation to electricity. Energy storage includes UC for quick discharge, BESS for medium to long-term use, and also uses the EV. A central controller manages inputs from these sources and storage devices to balance output. The proposed marine microgrid power system using a bio-renewable energy cycle is illustrated in Fig. 1. A simplified dynamic model of marine network including RESs is shown in Fig. 2. The interconnection of marine micro grid with renewable cogeneration with AGC implementation is depicted in Fig. 3. The test system is represented by a transfer function model in Fig. 4. The network model and its implementation to the marine microgrid power system are detailed in Fig. 5.

Fig. 1

Perception model of the marine network with bio-renewable energy cycle.

Fig. 2

Simplified dynamic model of marine network including RESs.

Fig. 3

Interconnection of marine renewable cogeneration with AGC implementation.

Fig. 4

Transfer function based modelled diagram of the test system under study.

Fig. 5

Network model and its implementation to the marine network.

Basic description of the model: autonomous generation

AWEC: independent power generation

A completely submerged wave energy converters, or WECS, corresponds to AWS. It generates usable electrical power using the floater’s vertical motion caused by the waves in the ocean. To convert mechanical wave energy into electrical energy, AWS is connected to a permanent magnet synchronous generator. It is possible to install this WECS at depths greater than 25 m. The AWEC’s dynamic velocity and force can be expressed as follow¹⁴.

$$ V_{W} = \frac{dx}{{dt}} $$

(1)

$$ F_{AW} = m_{ft} \frac{{dV_{W} }}{dt} + \beta_{G} V_{W} + \beta_{W} V_{W} + K_{C} x $$

(2)

The irregular sinusoidal wave force of AWEC is expressed as

$$ F_{AW} = F\sin \left( {\omega_{AW} t} \right) + \frac{F}{2}\sin \left( {2\omega_{AW} t} \right) + \frac{F}{3}\sin \left( {3\omega_{AW} t} \right) $$

(3)

The simple linear first-order transfer function of AWEC (neglecting all nonlinearities) can express as¹⁴

$$ TF_{AWEC} \left( s \right) = \frac{{K_{AWEC} }}{{1 + sT_{AWEC} }} $$

(4)

WTG: independent power generation

One of the most developed and proven RESs with the greatest potential is wind power. A wind turbine generator is the device that converts wind energy into electrical power. The extractable output power of the wind turbine generator is expressed as⁷

$$ P_{W} = 0.5\rho C_{P} A_{r} V_{W}^{3} $$

(5)

The power coefficient (C_p) of the WTG is⁷

$$ C_{p} = \left( {0.44 - 0.0167\beta } \right)\sin \left( {\frac{{\left( {\lambda - 3} \right)\pi }}{15 - 0.3\beta }} \right) - 0.0184\left( {\lambda - 3} \right)\beta $$

(6)

where $\lambda = \frac{{R_{b} W_{b} }}{{V_{W} }}$.

After simplifying, the transfer function of WTG is⁷

$$ G_{WTG} \left( s \right) = \frac{{K_{WT} }}{{1 + sT_{WT} }} $$

(7)

PV: independent power generation

Solar panels convert sunlight directly into electricity by exciting electrons in a semiconductor material. The amount of electricity generated depends on temperature and sunlight levels. To track the more power from solar panels, photovoltaic systems often use MPPT systems. The transfer function of a PV model is²⁵.

$$ TF_{PV} \left( s \right) = \frac{{K_{PV} }}{{1 + sT_{PV} }} $$

(8)

ST: Independent power generation

The solar tower, also known as the central receiver system, is surrounded by a large number of slightly curved dual-axis (horizontal and vertical) tracked heliostats. A central receiver positioned at top the tower receives solar radiation reflected by the field of heliostats, with a concentration ratio reaching up to 500–1000. At 500–850 °C, the receiver fluid—typically a stream, hot air, or molten salt—carries the heat to the stream generator, creating a superheated stream that powers the turbine–generator, which is programmed to generate electricity with a 28% efficiency. According to NREL, there are about 35 solar thermal plants in the world, with three of them having capacities greater than 20 megawatts (such as the world’s largest solar thermal plant, ISEGS, with a capacity of 377 megawatts)¹⁴.

$$ P_{i} = \eta_{H} IA $$

(9)

The net electrical power from ST is described by

$$ P_{elect} = P_{th} \eta_{rank} \eta_{W} $$

(10)

The state equation of the outlet temperature of the receiver tube can be expressed as¹⁴

$$ \left( {\rho cV} \right)\frac{{dT_{0} }}{dt} = \alpha R - F_{0} \left( {\frac{{T_{0} - T_{in} }}{L}} \right) - \gamma \left( {\frac{{T_{0} - T_{in} }}{L} - T_{a} } \right) $$

(11)

The fluid velocity (Fo) of the receiver tube can be expressed as

$$ F_{0} = \frac{{\left( {\left( {\left( {\eta_{H} A\alpha } \right)/A_{rec} } \right)I - \gamma \left( {T_{av} - T_{a} } \right)} \right)}}{{2T_{av} }} \cdot L $$

(12)

Finally, the state equation of ST receiver can be represented as

$$ \frac{{dT_{0} }}{dt} = \frac{{\left( {\left( {\eta_{H} A\alpha } \right)/A_{rec} } \right)}}{C}J - \frac{{F_{0} }}{LC}\left( {T_{0} - T_{in} } \right) - \frac{\gamma }{C}\left( {T_{av} - T_{a} } \right) $$

(13)

By linearising above we could estimate the TF model of ST considering a thermal generator¹⁴.

$$ TF_{ST} \left( s \right) = \left( {\frac{{K_{RF} }}{{1 + sT_{RF} }}} \right)\left( {\frac{{K_{RV} }}{{1 + sT_{RV} }}} \right)\left( {\frac{{K_{G} }}{{1 + sT_{G} }}} \right)\left( {\frac{{K_{T} }}{{1 + sT_{T} }}} \right) $$

(14)

Basic description of the model: controlled generation

BDEG units: controlled generation

In BDEG units, biodiesel derived from the transesterification of leftover edible oils or appropriate energy crops with qualities similar to those of diesel may be utilized in blended or pure (B100) form. Taking into account the engine and inlet valve actions, the linearized model of BDEG is estimated as follows⁷.

$$ G_{BDEG} \left( s \right) = K_{BD} \left( {\frac{{K_{VA} }}{{1 + sT_{VA} }}} \right)\left( {\frac{{K_{BE} }}{{1 + sT_{BE} }}} \right) $$

(15)

MTPG: controlled generation

A micro-turbine power generator is a compact, high-speed turbine that produces 25–200 kW of power. It’s quiet, has low emissions, and can use different fuels, making it ideal for homes and businesses. The power it generates is given by a specific formula:

$$ P_{MTPG} = P_{T} - P_{CP} $$

(16)

The linearised transfer function of MTPG is expressed as⁷

$$ TF_{MTPG} (s) = \left( {\frac{{K_{VP} }}{{1 + sT_{VP} }}} \right)\left( {\frac{{K_{FA} }}{{1 + sT_{FA} }}} \right) $$

(17)

BTGU: controlled generation

Biogas produced from biodegradable wastes and animal droppings of the community could be stored and resourcefully recycled in BGTG units for power generation. Considering the actions of biogas inlet-valve, governor, combustor, and turbine, the linearised model of BTGU is estimated as (8)⁷.

$$ G_{BGTG} \left( s \right) = \left( {\frac{{1 + sX_{c} }}{{\left( {1 + sY_{c} } \right)\left( {1 + sb_{B} } \right)}}} \right)\left( {\frac{{1 + sT_{CR} }}{{1 + sT_{BG} }}} \right)\left( {\frac{{K_{BG} }}{{1 + sT_{BT} }}} \right) $$

(18)

EV: controlled generation

The EV performance helps to mitigates any fluctuations in the system because they can function as a load when the system is in the charging mode and as a supply when it is in the discharging mode.the first order transfer function models the EVs system as⁷

$$ TF_{EV} \left( s \right) = \frac{{K_{EV} }}{{1 + sT_{EV} }} $$

(19)

UC: back-up device

Ultracapacitors store and release energy very quickly. They’re reliable, long-lasting, and work well in cold weather. The linear transfer function model of ultra capacitors is⁷

$$ TF_{UC} \left( s \right) = \frac{{K_{UC} }}{{1 + sT_{UC} }} $$

(20)

BESS: back-up device

The Battery Energy Storage System (BESS) helps keep the system’s frequency stable by either storing energy or supplying power as needed. The BEES first-order transfer function is⁹

$$ TF_{BESS} \left( s \right) = \frac{{K_{BESS} }}{{1 + sT_{BESS} }} $$

(21)

Modelling of controller: controller design and methodology

PID controller: external controller

The three controllers that are present in it are derivative, integral, and proportional. ACE is the input of the controller. It generates the necessary control signal Y(s) for the power generating system for frequency regulation based on the error signal. In order to achieve a healthier controller response during sudden load demand, a controller design with appropriate gain values is therefore essential^{22,23,24,25,26,27,28,29}. Equation presents the transfer function of the PID controller (refer Fig. 6a)⁸.

$$ G\left( s \right) = K_{p} + \frac{{K_{i} }}{s} + K_{d} s $$

(22)

Fig. 6

Implemented controller structures: (a) PID, (b) cascaded PD–PID, (c) FOPID and (d) FOPI–FOPID.

PD–PID controllers: external controller

The cascaded PD–PID control strategy is an advanced and efficient approach for controlling complex dynamic systems that require accurate and stable control over many time scales. The system has two control loops: an inner PD controller and an outer PID controller. The central PD controller manages the fast dynamics of the system, enabling quick response and improving stability by reducing oscillations. The outer PID controller controls the slower dynamics, improving long-term performance by reducing steady-state errors and improving overall accuracy. The PD–PID structure allows for independent fine-tuning of fast and slow dynamics, thus increasing flexibility and easing optimization. This hierarchical control technique is especially beneficial in applications where fast response and sustained accuracy are essential, such as engine control, temperature control, and aviation systems. Cascaded PD–PID controllers’ ability to combine fast response with high stability makes them the recommended option in scenarios where single-loop controllers are insufficient, improving performance when managing complex multivariable processes. (refer Fig. 6b)¹⁸.

$$ G\left( s \right) = \left( {K_{p1} + K_{d1} s} \right)\left( {K_{p2} + \frac{{K_{i2} }}{s} + K_{d2} s} \right) $$

(23)

Fractional order concept

The concept of fractional order calculus emerged from the theory of generalising integral order calculus to fractional order calculus. The most commonly utilised fractional order integrodifferential definitions are derived from Riemann–Liouville (RL), Grunwald–Letnikov, and Caputo formulations. The RL fractional order integration and differentiation, frequently employed by researchers, are delineated in (24)–(25)^13,14.

$$_{a} D_{t}^{\alpha } f\left( t \right) = \frac{1}{{\Gamma \left( {n - \alpha } \right)}}\frac{{d^{n} }}{{dt^{n} }}\int\limits_{a}^{t} {\left( {t - \tau } \right)}^{n - \alpha - 1} \,f\left( \tau \right)\,d\tau $$

(24)

$$_{a} D_{t}^{ - \alpha } f\left( t \right) = \frac{1}{\Gamma \left( \alpha \right)}\frac{{d^{n} }}{{dt^{n} }}\int\limits_{0}^{t} {\left( {t - \tau } \right)}^{\alpha - 1} \,f\left( \tau \right)\,d\tau $$

(25)

where $_{a} D_{t}^{\alpha }$ is the fractional driver. With an integer n and Euler’s gamma function $\Gamma$(.), the value of α will be in between (n − 1) and n.

Traditional PID controllers eliminate steady-state error through continuous integration of past errors, but this can cause overshooting and instability. The FOPID controller, a generalization of the PID, is noted for its enhanced robustness. Its fractional integral and derivative terms improve adaptability to parameter changes, uncertainties, and external disturbances, which is beneficial for systems with time delays and high nonlinearity. This results in better stability and transient response. The fractional-order integral term in FOPI and FOPID controllers offers more precise control over system memory, reducing steady-state errors and preventing excessive overshoot.

FOPID controller: external controller

The primary difference between a PID and FOPID controller is that the FOPID controller’s order is not an integer. This feature allows for additional control over the controller gain values, and when compared to traditional PID controllers, it performs better. Over the past few years, there has been a lot of discussion about the advantages of the FOPID controller over the conventional PID controller, as mentioned above. The following is FOPID controller transfer function (refer Fig. 6c).

$$ G\left( s \right) = K_{p} + \frac{{K_{i} }}{{s^{\lambda } }} + K_{d} s^{\mu } $$

(26)

FOPI–FOPID controller: external controller

FOPI and FOPID controllers extend traditional PI and PID controllers using fractional calculus principles. Unlike traditional controllers that use integer derivatives and integrals, FOPI and FOPID controllers use fractional order dynamics, which allows for greater tuning flexibility and improved control performance. The use of fractional calculus allows for non-integer ordering of integral and derivative operations, making these controllers particularly suitable for complex systems with long memory effects, such as those featuring time delays and fractional dynamics.

FOPI controllers improve upon traditional PI controllers by incorporating fractional order integral components, allowing for more precise tuning and better resilience to shocks and uncertainties. Fractional order controllers improve the capabilities of PID controllers by integrating fractional orders of integral and derivative components, resulting in more dynamic system control, improved stability margins, and better frequency response performance. These controllers are particularly beneficial in areas such as process control, robotics, and power systems where traditional controllers suffer from nonlinearities and time delays. The large number of parameters in FOPID controllers makes them more difficult to fine-tune compared to standard PID controllers, resulting in tuning and computational challenges when implementing fractional order controllers.

Techniques such as frequency response analysis and optimisation methods, including genetic algorithms and particle swarm optimisation, tackle these difficulties. FOPID controllers exhibit enhanced performance, especially in systems with intricate dynamics; yet, their implementation is computationally intensive due to fractional-order operations, complicating practical use. Nonetheless, the adaptability and superior control features of FOPI and FOPID controllers are vital for contemporary control applications, providing considerable benefits compared to conventional systems (refer Fig. 6d).

$$ G\left( s \right) = \left( {K_{p1} + \frac{{K_{i1} }}{{s^{{\lambda_{1} }} }}} \right)\left( {K_{p2} + \frac{{K_{i2} }}{{s^{{\lambda_{2} }} }} + K_{d2} s^{{\mu_{2} }} } \right) $$

(27)

Problem formulation: defining LFC objective function

Objective: defining optimization goals and objective function

The ITAE is vital in AGC, as it heavily penalizes long-term errors, encouraging quick convergence to set points, smooth responses, and grid stability. It aids in designing and fine-tuning controllers, evaluating control strategies, and guiding optimization algorithms, thus advancing AGC strategies and enhancing power system resilience and reliability. The ITAE objective function is expressed mathematically as^{8,30,31,32,33}.

$$ FOD = ITAE = J = \int\limits_{0}^{{t_{s} }} {\left\{ {\left| {\Delta f_{i} } \right| + \left| {\Delta P_{tieij} } \right|} \right\}} tdt $$

(28)

Constrained optimization: defining the boundaries of constrained

• (a) The PID controller gains function as restrictions for the model’s optimisation work, with their parameters limited as outlined in (29).

  $$ {\begin{array}{*{20}l} {K_{P}^{\min } \le K_{p} \le K_{p}^{\max } } \hfill \\ {K_{i}^{\min } \le K_{i} \le K_{i}^{\max } } \hfill \\ {K_{d}^{\min } \le K_{d} \le K_{d}^{\max } } \hfill \\ \end{array} } $$

  (29)

• (b) The limitations for the FOPID controller gains in the modelling optimisation process are delineated by the bounds stated in (30).

  $$ \begin{array}{*{20}l} {K_{P}^{\min } \le K_{p} \le K_{p}^{\max } } \hfill \\ {K_{i}^{\min } \le K_{i} \le K_{i}^{\max } } \hfill \\ {K_{d}^{\min } \le K_{d} \le K_{d}^{\max } } \hfill \\ {\lambda^{\min } \le \lambda \le \lambda^{\max } } \hfill \\ {\mu^{\min } \le \mu \le \mu^{\max } } \hfill \\ \end{array} $$

  (30)

• (c) The PD–PID controller gains serve as constraints for the model’s optimization task, with parameter bounds defined in (31).

  $$ \begin{array}{*{20}l} {K_{P1}^{\min } \le K_{p1} \le K_{p1}^{\max } } \hfill \\ {K_{d1}^{\min } \le K_{d1} \le K_{d1}^{\max } } \hfill \\ {K_{p2}^{\min } \le K_{p2} \le K_{p2}^{\max } } \hfill \\ {K_{i2}^{\min } \le K_{i2} \le K_{i2}^{\max } } \hfill \\ {K_{d2}^{\min } \le K_{d2} \le K_{d2}^{\max } } \hfill \\ \end{array} $$

  (31)

• (d) The FOPI–FOPID controller gains serve as constraints in the model’s optimization task, with parameter boundaries provided in Eq. (32).

  $$ \begin{array}{*{20}l} {K_{P1}^{\min } \le K_{p1} \le K_{p1}^{\max } } \hfill \\ {K_{i1}^{\min } \le K_{i1} \le K_{i1}^{\max } } \hfill \\ {\lambda_{1}^{\min } \le \lambda_{1} \le \lambda_{1}^{\max } } \hfill \\ {K_{P2}^{\min } \le K_{p2} \le K_{p2}^{\max } } \hfill \\ {K_{i2}^{\min } \le K_{i2} \le K_{i2}^{\max } } \hfill \\ {K_{d2}^{\min } \le K_{d2} \le K_{d2}^{\max } } \hfill \\ {\lambda_{2}^{\min } \le \lambda_{2} \le \lambda_{2}^{\max } } \hfill \\ {\mu_{2}^{\min } \le \mu_{2} \le \mu_{2}^{\max } } \hfill \\ \end{array} $$

  (32)

Measure of performance: defining performance indices

Integrating varied performance indices into AGC optimization guarantees grid stability and effective control amidst RESs unpredictability. This paper performs a comprehensive comparative analysis of IAE, ITSE, ISE, and ITAE to determine optimal control strategies that reconcile swift disturbance response, long-term error reduction, and overall system efficacy. Choosing the correct performance index is essential for optimising Automatic Generation Control in renewable energy source-dominant power systems. IAE assesses overall control accuracy, ITSE focuses on speedy stabilization, and ISE stresses reducing big deviations. Collectively, these indices enable a thorough optimisation strategy, directing AGC solutions that improve grid reliability and performance amidst RES unpredictability. In the analysed models, ITAE IAE, ITSE, and ISE values serve as performance indices, with their mathematical formulas defined in (33)–(36).

$$ ITAE = \int\limits_{0}^{{t_{s} }} {\left( {\left| {\Delta f_{i} } \right| + \left| {\Delta P_{tieij} } \right|} \right)t} \,dt $$

(33)

$$ IAE = \int\limits_{0}^{{t_{s} }} {\left( {\left| {\Delta f_{i} } \right| + \left| {\Delta P_{tieij} } \right|} \right)} \,dt $$

(34)

$$ ITSE = \int\limits_{0}^{{t_{s} }} {\left( {\left( {\Delta f_{i} } \right)^{2} + \left( {\Delta P_{tieij} } \right)^{2} } \right)t\,dt} $$

(35)

$$ ISE = \int\limits_{0}^{{t_{s} }} {\left( {\left( {\Delta f_{i} } \right)^{2} + \left( {\Delta P_{tieij} } \right)^{2} } \right)\,dt} $$

(36)

Implemented algorithm details

MGO algorithm: basic details

The MGO, a sophisticated optimisation algorithm released in 2022, draws inspiration from the social systems of mountain gazelles, encompassing maternity herds, bachelor male herds, and lone territorial males³⁴. Researchers utilised these natural behaviours to develop a mathematical model that improves optimisation. The MGO algorithm integrates gazelle traits like as territoriality, social hierarchy, migration, and swift movement. The algorithm adeptly investigates and engages within the solution space by modelling interactions among bachelor male herds, maternity herds, and the foraging movements of territorial males. This method allows MGO to effectively explore and optimise intricate issues by utilising dynamic and adaptive techniques derived from gazelle behaviour. The algorithm guarantees comprehensive investigation and utilisation of the search space, becoming it an essential instrument in optimisation.

Concept of algorithm: inspiration

The mountain gazelle is a species of gazelle that inhabits the Arabian Peninsula and adjacent areas, with a low population density despite its vast territory. Their habitat is strongly associated with the Robinia pseudoacacia tree species. During the Late Holocene, rising temperatures caused their distribution to decline, leading to their replacement by Gazella bennettii, which is adapted to a warmer climate. Mountain gazelles exhibit strong territorial behavior, keeping considerable distances between individual territories and organizing themselves into three groups: mother-calf herds, herds of young males, and solitary males. Adult males often engage in territorial disputes that are less violent than those over females, but young males use their horns more vigorously than older males. These migratory gazelles travel around 200 kms in search of food and can sprint hundreds of metres at speeds of up to 80 kms per hour.

Mathematical formulation

• (a) Territorial Solitary Males (TSM):

  Upon reaching adulthood, male gazelles establish and defend solitary territories. The optimal global position (the adult male) is updated via a mathematical model incorporating random factors and the positions of other males in bachelor herds³⁴.

  $$ TSM = male_{gazelle} - \left| {\left( {ri_{1} \times BH - ri_{2} \times X\left( t \right)} \right) \times F} \right| \times Cof_{r} $$

  (37)

• (b) Maternity Herds (MH):

  Maternity herds are essential for birthing strong male gazelles, a behavior modelled to generate robust solutions by simulating herd interactions and the impact of dominant males³⁴.

  $$ MH = \left( {BH + Cof_{1,r} } \right) + \left( {ri_{3} \times male_{gazelle} - ri_{4} \times X_{rand} } \right) \times Cof_{1,r} $$

  (38)

  here $X_{rand}$ represents a vector position of a gazelle randomly selected from the population.

  ‘ri₃’ and ‘ri₄’ integers randomly selected position.

• (c) Bachelor Male Herds (BMH):

  As young males mature, they attempt to establish their territories, leading to conflicts with established males. This is modelled to represent the competition among solutions to improve their positions³⁴.

  $$ BMH = \left( {X\left( t \right) - D} \right) + \left( {ri_{5} \times male_{gazelle} - ri_{6} \times BH} \right) \times Cof_{r} $$

  (39)

  where ‘D’ is calculated using the current positions and ‘male_gazelle’ is the best solution.

• (d) Migration to Search for Food (MSF):

  Gazelles constantly migrate in search of food, covering large distances. This behavior is modelled to enhance exploration capabilities, allowing the algorithm to search diverse areas of the solution space.

  $$ MSF = \left( {ub - lb} \right) \times r_{7} + lb $$

  (40)

  where ‘ub’ and ‘lb’ are the upper and lower bounds of the problem, and ‘r₇’ is a random number.

CHOA algorithm

Chimpanzees, highly social great apes closely related to humans, live in dynamic fission–fusion societies where group size and composition fluctuate. This social structure is mirrored in the CHOA, where independent groups explore the search space using diverse strategies, leveraging individual strengths to solve complex problems⁴⁴. Hunting occurs during exploration and exploitation. Calculate driving and pursuing prey. For driving and following prey, (41) and (42) are mathematical models.

$$ d = \left| {c.x_{prey} \left( t \right) - m.x_{chimp} \left( t \right)} \right| $$

(41)

$$ x_{chimp} \left( {t + 1} \right) = x_{prey} \left( t \right) - a.d $$

(42)

The vectors a and c are examined in accordance with Eqs. (43) and (44), respectively⁴⁴.

$$ a = 2.f.r_{1} - f $$

(43)

$$ c = 2.r_{2} $$

(44)

Driver, barrier, and chaser chimpanzees sometimes hunt, but attackers usually do. The best prey location is unknown in a search space. It is hypothesized that the first attacker, the most ideal solution, and the driver, barrier, and chaser chimpanzees have a better understanding of the possible prey’s location to mathematically describe their behaviour. Thus, the other chimpanzees’ locations are adjusted to match those of these better chimps, helping them to improve their search techniques. The relationship mentioned is represented by Eqs. (45)–(47)⁴⁴.

$$ \begin{array}{*{20}l} {d_{Attac\ker } = \left| {c_{1} x_{Attac\ker } - m_{1} x} \right|} \hfill \\ {d_{Barrier} = \left| {c_{2} x_{Barrier} - m_{2} x} \right|} \hfill \\ {d_{Chaser} = \left| {c_{3} x_{Chaser} - m_{3} x} \right|} \hfill \\ {d_{Driver} = \left| {c_{4} x_{Driver} - m_{4} x} \right|} \hfill \\ \end{array} $$

(45)

$$ \begin{array}{*{20}l} {x_{1} = x_{Attac\ker } - a_{1} \left( {d_{Attac\ker } } \right)} \hfill \\ {x_{2} = x_{Barrier} - a_{2} \left( {d_{Barrier} } \right)} \hfill \\ {x_{3} = x_{Chaser} - a_{3} \left( {d_{Chaser} } \right)} \hfill \\ {x_{4} = x_{Driver} - a_{4} \left( {d_{Driver} } \right)} \hfill \\ \end{array} $$

(46)

$$ x\left( {t + 1} \right) = \frac{{x_{1} + x_{2} + x_{3} + x_{4} }}{4} $$

(47)

In the final stage, chimps abandon their roles and become chaotic. This is modelled by a 50% chance of using chaotic movement instead of the normal updating process. This helps the algorithm escape local optima and explore new solutions. The search process involves chimps in different roles, adjusting their positions based on the estimated prey location. Parameters are adaptively tuned for faster convergence. The ‘f’ value decreases over time, encouraging exploration initially and exploitation later. The mathematical model is expressed by Eq. (48)⁴⁴.

$$ x_{chimp} (t + 1) = \left\{ \begin{gathered} x_{prey} (t){ - }a.d \ldots if\,\mu < 0.5 \hfill \\ chaotic\_value \ldots if\,\mu > 0.5 \hfill \\ \end{gathered} \right. $$

(48)

Briefly, ChOA searches begin with chimpanzees, possible solutions. These chimpanzees are randomly assigned to attackers, barricades, chasers, and drivers. Group-based “f” coefficient updates are used by each chimp. Each iteration, the attacker, barrier, chaser, and driver chimpanzees assess their prey’s position. Each potential solution modifies its prey distance based on this estimate. The “c” and “m” vectors are adaptively modified to accelerate convergence and prevent local optima. To improve exploitation and prey capture, “f” is progressively lowered from 2.5 to zero. Candidate solutions will split and explore various search space areas if |a|> 1. If the inequality is not fulfilled, potential solutions will converge on the prey.

Chaotic concept

Using a chaotic map instead of a random process has become increasingly popular in optimization. Random-based optimization approach uses disorderly motion instead of stochastic motion for unpredictability⁴⁵. Chaotic mapping enhances the optimizer’s performance by introducing a deterministic yet unpredictable search pattern, which improves exploration and prevents premature convergence to local optima. Unlike purely stochastic approaches, chaotic sequences maintain ergodicity, ensuring a more uniform search across the solution space. Random-based algorithms enable unpleasant situations or solutions with a predetermined probability. A chaos-based optimization strategy seeks order in a chaotic system to escape a local optimum. Due to its sensitivity to the initial condition and quasi-stochasticity, chaos is valuable in optimization. If the correct beginning point is picked and the search is done inside a finite sphere around it, all potential outcomes may be found. The equation for the same is shown in (49).

$$ x_{i + 1} = \alpha x_{i} \left( {1 - x_{i} } \right) $$

(49)

The value of $\alpha$ is taken as 4. The flowchart of the (refer Fig. 7).

Fig. 7

Flowchart of the proposed CCMGO algorithm.

Proposed algorithm: CCMGO

The proposed CCMGO is an advanced hybrid algorithm combining the strengths of MGO and CHOA, further enhanced by chaotic maps. CCMGO uses MGO’s simulation of mountain gazelles’ social behaviours, such as territoriality, hierarchy, and migration, to effectively explore and exploit the search space. It also employs CHOA’s hunting roles and adaptive strategies to enhance the search process and improve convergence. The integration of chaotic maps adds unpredictability, helping the algorithm escape local optima and promoting exploration and diversity. This combination aims to achieve superior performance in solving complex optimization problems, surpassing traditional algorithms in accuracy, efficiency, and robustness.

Simulation results and analysis

A marine system with renewable cogeneration is evaluated through a comparative analysis of control strategies, including PID, cascaded PD–PID, FOPID, and FOPI–FOPID controllers, designed using the CCMGO algorithm with ITAE as the performance index. These controllers are assessed based on dynamic performance, effectiveness in managing transient responses and energy storage devices, and their impact on overall performance and frequency stability across varied operational scenarios. The optimization is programmed in MATLAB/Simulink 2024a, and the system is modelled in Simulink using the FOMCON toolbox. Frequency stability is assessed under various operational conditions. and the system configuration is Intel core i5 10th generation Microsoft office. Initially, the proposed CCMGO algorithm is investigated with GA and PSO by optimizing the FOPID controller for LFC. The results now included in Table 2 of the revised manuscript demonstrate the lower ITAE and other performance values showing better frequency regulation and reduced overshoot, ensuring smoother microgrid operation. The following scenario has been considered into the study after the validation of CCMGO algorithm.

Table 2 Comparative analysis with GA and PSO.

Scenario A:	Analysing test system performance under positive impulse and negative impulse load disturbance
Scenario B:	Assess test system functioning under positive impulse load disturbance
Scenario C:	Examine the test system functioning under step ramp combination-based load disturbance
Scenario D:	Evaluate test system functioning under stochastic random load perturbation

Scenario A: Analysing test system performance under Stepwise increasing and decreasing load disturbance

The valuation arrangement reviewed here is illustrated above (see Figs. 1, 2, 3, 4, and 5). This scheme evaluates PID/cascaded PD–PID/FOPID/FOPI–FOPID controllers individually as subordinate controllers on separate bases, with the load profile shown in Fig. 6. Optimal controller attributes are determined via CCMGO using ITAE, with the best values presented in Table 3 and significant results shown in Figs. 8, 9, 10, 11, and 12. Figure 8 depicts inputs to independent power generation like wave, wind, solar radiation and PV radiation. Figure 9 shows independent power generation outputs like AWEC, WTG, ST and PV. Figure 10 details the LFC response in terms of frequency deviation, load demand, controller output, and generation load demand response. Figure 11 profiles energy storage systems like EV, BESS and UC, while Fig. 12 shows controlled power generation DEG, BTGU and MTPG. BESS provide medium- to long-term energy buffering with a relatively slower response (around 0.1 s), making them ideal for sustained energy compensation during prolonged load imbalances to maintain frequency stability. In contrast, UC, with their extremely fast response (approximately 0.9 s) and high power density, act like a first-aid measure by quickly counteracting sudden, transient frequency deviations. Additionally, EV offer flexible, dynamic storage; they can operate as either loads or energy sources with a response time of about 1 s, effectively bridging the gap between the immediate action of ultra-capacitors and the longer-term support provided by BESS, thereby creating a robust and integrated approach to frequency regulation in the microgrid.

Table 3 Optimized controller gains for the test system Scenario A.

Fig. 8

Inputs to the independent power generation (refer Scenario A): (a) Wave Condition, (b) Wind Condition, (c) Solar radiation, (d) PV radiation.

Fig. 9

Independent power generation (refer Scenario A): (a) AWEC, (b) WTG Condition, (c) ST, and (d) PV.

Fig. 10

LFC response profile (Refer Scenario A) (a) Frequency deviation, (b) Load demand, (c) Controller output and (d) Generation load demand.

Fig. 11

Profile of the energy storage system (refer Scenario A): (a) EV, (b) BESS and (c) UC.

Fig. 12

Controlled power generation (refer Scenario A): (a) DEG, (b) BTGU, and (c) MTPG.

Tables 4, 5 compare the performance of four control strategies optimized by CCMGO: CCMGO PD–PID, CCMGO PID, CCMGO FOPI–FOPID and the proposed CCMGO FOPID under Scenario 1 of a test system. Performance is assessed using indices ITAE, IAE, ITSE, and ISE, where lower values signify better control system performance. Computational time for each algorithm is also evaluated. Results show the proposed CCMGO FOPID algorithm outperforms others, achieving ITAE of 13.385, IAE of 0.003, ITSE of 0.142, and ISE of 0.293, significantly lower than other algorithms. This indicates superior performance in minimizing error and achieving faster settling times. The CCMGO FOPI- FOPID algorithm also performs competitively, particularly in ITAE 19.452 and IAE 0.017, demonstrating its effectiveness in error reduction.

Table 4 Comparative measure of performance indices for test system Scenario A.

Table 5 Study of computational time for test system Scenario A.

The proposed CCMGO FOPID algorithm proves to be the most effective optimization technique for the test system under Scenario A, excelling in error minimization and faster settling times. In terms of computational efficiency, CCMGO FOPID requires a computational time of 1752s, CCMGO FOPI–FOPID requires a computational time of 1764s, CCMGO PID requires a computational time of 1776s, and CCMGO PD–PID requires a computational time of 1788s.

Table 6 represents the Eigen value analysis for the CCMGO FOPID for Scenario 1, Scenario 2, Scenario 3 and Scenario 4. The eigenvalues confirm that all system poles lie in the left half of the complex plane, ensuring system stability under different load conditions.

Table 6 Eigen Value analysis.

In the additional discussion, CCMGO algorithm in terms of execution time, memory usage, and convergence rate is further evaluated. It is noted that the execution time of CCMGO—defined as the total time required for initialization, objective function evaluation, and iterative position updates—is comparable per iteration to that of traditional methods; however, CCMGO typically converges faster due to its hybrid structure and chaotic mapping mechanism. In terms of memory usage, while CCMGO incurs a modest increase by maintaining additional data structures (e.g., chaotic sequences) to preserve solution diversity, this overhead remains within acceptable limits for real-time microgrid applications. Finally, the convergence rate, which measures the speed at which the algorithm reduces the objective function error over iterations, is significantly enhanced in CCMGO.

Scenario B: Assess test system functioning under positive impulse load disturbance

The prior sub-section specifies that the FOPID controller is the highest-performing controller. However, in this sub-section, the PD–PID controller is optimized again using CCMGO. The optimal values of the controller’s parameters obtained through algorithms are listed in Table 7. Figure 13 depicts the system’s dynamic behavior in response to load demand changes, illustrating frequency deviation, load demand fluctuations, controller output and the generation load demand response, providing insights into control actions taken to regulate the system. Figure 14 highlights the energy storage system, showing profiles of both the EV, BESS and UC, likely revealing their charge/discharge patterns and their role in supporting the LFC system with ancillary services. Figure 15 visualizes controlled power generation from various sources, including DEG, BTGU, and MTPG. demonstrating how power output is adjusted in response to load changes and frequency deviations to maintain system stability. The effective outcomes are shown in Figs. 13, 14, and 15. Detailed examination of these figures indicates that the CCMGO-augmented subordinate controller provides improved dynamics with reduced oscillations.

Table 7 Optimized controller gains for the test system Scenario B.

Fig. 13

LFC response profile (Refer Scenario B) (a) Frequency deviation, (b) Load demand, (c) Controller output, (d) Generation load demand and (e) Controller output of PD–PID.

Fig. 14

Profile of the energy storage system (refer Scenario B): (a) EV, (b) BEES and (c) UC for a duration of 120 s.

Fig. 15

Controlled power generation (refer Scenario B): (a) DEG, (b) BTG and (c) MTPG for a duration of 120 s.

Tables 8, 9 compares the performance of three control strategies optimized by CCMGO: CCMGO F0PID, CCMGO PID, CCMGO FOPI–FOPID and the proposed CCMGO PD–PID under Scenario B. The evaluation covers performance indices (ITAE, IAE, ITSE, ISE) and computational time. Results show CCMGO PD–PID excels in ITAE 2.910 and IAE 0.003, indicating lower overall error and faster response, albeit with computational time 1376 s. The choice between CCMGO FOPI–FOPIDD and CCMGO PD–PID depends on specific application needs and the trade-off between performance and computational efficiency. CCMGO PD–PID is ideal for faster response and lower error.

Table 8 Comparative measure of performance indices for test system Scenario B.

Table 9 Study of computational time for test system Scenario B.

In terms of computational efficiency, CCMGO FOPID requires a computational time of 1389 s, which is slightly higher than that of CCMGO PD–PID 1376 s, CCMGO PID 1396 s and CCMGO FOPI–FOPID 1398 s which is less and giving the faster response compared to CCMGO PID and CCMGO FOPI–FOPID. And in this Scenario CCMGO PD–PID is giving the better results as compared to our proposed CCMGO FOPID.

Scenario C: Examine the test system functioning under step ramp combination-based load disturbance

The prior sub-section specifies that the PD–PID controller is the highest-performing controller. However, in this sub-section, the FOPID controller is optimized again using CCMGO. The optimal values of the controller’s parameters obtained through algorithms are listed in Table 10. Figure 16 depicts the system’s dynamic behavior in response to load demand changes, illustrating frequency deviation, load demand fluctuations, controller output and the generation load demand response, providing insights into control actions taken to regulate the system. Figure 17 highlights the energy storage system, showing profiles of both the EV, BESS and UC, likely revealing their charge/discharge patterns and their role in supporting the LFC system with ancillary services. Figure 18 visualizes controlled power generation from various sources, including bio-deg, BTGU, and MTPG. demonstrating how power output is adjusted in response to load changes and frequency deviations to maintain system stability. The effective outcomes are shown in Figs. 16, 17, and 18. Detailed examination of these figures indicates that the CCMGO-augmented subordinate controller provides improved dynamics with reduced oscillations.

Table 10 Optimized controller gains for the test system Scenario C.

Fig. 16

LFC response profile (Refer Scenario C) (a) Frequency deviation, (b) Load demand, (c) Controller output, and (d) Generation load demand for a duration of 120 s.

Fig. 17

Profile of the energy storage system (refer Scenario C): (a) EV, (b) BEES and (c) UC for a duration of 120 s.

Fig. 18

Controlled power generation (refer Scenario C): (a) DEG, (b) BTG and (c) MTPG for a duration of 120 s.

Tables 11, 12 compares the performance of three control strategies optimized by CCMGO: CCMGO PID, CCMGO PD–PID, CCMGO FOPI–FOPID and the proposed CCMGO FOPID under Scenario C. The evaluation covers performance indices (ITAE, IAE, ITSE, ISE) and computational time. Results show CCMGO FOPID excels in ITAE 9.099 and IAE 1.388, indicating lower overall error and faster response, in terms of computational efficiency, CCMGO FOPID requires a computational time of 1479 s, CCMGO PD–PID requires a computational time of 1484 s, CCMGO PID requires a computational time of 1488 s, and CCMGO FOPI–FOPID requires a computational time of 1496 s.

Table 11 Comparative measure of performance indices for test system Scenario C.

Table 12 Study of computational time for test system Scenario C.

Scenario D: Evaluate test system functioning under stochastic random load perturbation

However, in this sub-section, our proposed controller FOPID controller is optimized again using CCMGO. The optimal values of the controller’s parameters obtained through algorithms are listed in Table 13. Figure 19 depicts the system’s dynamic behavior in response to load demand changes, illustrating frequency deviation, load demand fluctuations, controller output and the generation load demand response, providing insights into control actions taken to regulate the system. Figure 20 highlights the energy storage system, showing profiles of both the EV, BESS and UC, likely revealing their charge/discharge patterns and their role in supporting the LFC system with ancillary services. Figure 21 visualizes controlled power generation from various sources, including bio-deg, BTGU, and MTPG. demonstrating how power output is adjusted in response to load changes and frequency deviations to maintain system stability. The effective outcomes are shown in Figs. 19, 20, and 21. Detailed examination of these figures indicates that the CCMGO-augmented subordinate controller provides improved dynamics with reduced oscillations.

Table 13 Optimized FOPID controller gains for the test system Scenario D.

Fig. 19

LFC response profile (Refer Scenario D) (a) Frequency deviation, (b) Load demand, (c) Controller output, and (d) Generation load demand.

Fig. 20

Profile of the energy storage system (refer Scenario D): (a) EV, (b) BEES and (c) UC.

Fig. 21

Controlled power generation (refer Scenario D): (a) DEG, (b) BTG and (c) MTPG.

The proposed CCMGO FOPID under Scenario D. The Tables 14, 15 evaluation covers performance indices (ITAE, IAE, ITSE, ISE) and computational time. Results show CCMGO FOPID excels in ITAE (61.701) and IAE (0.002), indicating lower overall error and faster response, albeit with higher computational time (5458 s). CCMGO FOPID is ideal for faster response and lower error.

Table 14 measure of performance indices for test system Scenario D.

Table 15 Study of computational time for test system Scenario D.

Limitations and constraints of this study

This study is based on simplified power system models under idealized conditions, with limited experimental validation and a primary focus on marine microgrids. While the proposed algorithm demonstrates strong performance in simulations, its efficacy under various system configurations, diverse operating conditions, and different optimization problems requires further exploration. Additionally, a more comprehensive comparison with other state-of-the-art optimization algorithms is needed to fully delineate its strengths and weaknesses.

Conclusions and scopes of future work

This study presents a novel control methodology that not only addresses the inherent variability of renewable energy sources but also enhances the microgrid capacity to maintain stable frequency through the coordinated use of energy storage. By leveraging the CMGO algorithm, the study significantly enhances the performance of various controllers, including PID, cascaded PD–PID, FOPID, and FOPI–FOPID controllers. Extensive simulations under different load conditions, such as step-ramp and random load variations, demonstrate the superior performance of CCMGO-optimized controllers, especially in terms of frequency stability and load management. The use of fractional-order controllers, particularly the FOPID, offers improved adaptability to system dynamics, providing more precise control and better transient responses. This research also highlights the importance of integrating energy storage devices, such as EV, BESS and UC to balance load-generation mismatches and support the stability of islanded marine microgrid. The results show that the proposed system can handle complex load scenarios effectively, outperforming traditional optimization techniques in error minimization and system reliability. Future studies will address these limitations by incorporating more complex and realistic power system models, extensive experimental validations, broader application scenarios, and rigorous comparative analyses with alternative optimization approaches.