Introduction

Throughout 2020–2022, SARS-CoV-2 induced large epidemic waves of infection internationally, with a considerable proportion of these infections requiring medical care. During peak epidemic periods, the demand for hospital beds overwhelmed the capacity of healthcare systems in many settings1,2,3. The number of beds occupied by COVID-19 cases depends upon the number of new patients admitted and the length of stay of these patients—with both quantities being products of the severity of disease and of clinical practice4,5,6,7. Forecasts of hospital occupancy can provide public health decision makers with intelligence to support decision-making.

Australia’s early COVID-19 experience differed from most other countries, with only a small proportion of the population having been infected prior to the widespread uptake of vaccination; by December 2021, over 80% of adults had been vaccinated, and less than 2% of adults had been recorded as infected amidst intensive public health measures8,9. The Omicron variant of SARS-CoV-2 emerged in November 2021, with the Omicron BA.1 lineage inducing major waves of infection across Australia and resulting in at least 17% of the population having been infected by March 202210. We limit our study to the period between March and September 2022, which was defined by two major waves of infection: a wave induced by the Omicron BA.2 lineage, which peaked in March–April 202211; and a wave induced by the Omicron BA.4 and BA.5 lineages, which peaked in late July 202212.

In this work, we describe a model for producing short-term (21-day) forecasts of hospital occupancy. We chose daily bed occupancy as a forecast target—rather than daily admissions—as occupancy more closely relates to the overall capacity of the hospital system. Furthermore, such bed occupancy counts had been collected and publicly reported for each state and territory of Australia on a daily basis since the early stages of the pandemic13. Our forecasting model takes as input an independently produced forecast of daily case incidence (specifically, an ensemble forecast consisting of four component models, each produced by a different researcher(s)14), with this incidence then transformed into ward and ICU occupancy counts through a stochastic compartmental model, with the probabilities of hospitalisation and of ICU admission informed by near-real-time data. The duration of time spent in each compartment is informed by censoring-adjusted estimates of patient length of stay15. Simulation outputs are then fit to reported occupancy counts using an Approximate Bayesian Computation approach16.

Under the specifications of the Australian National Disease Surveillance Plan for COVID-1917, we reported forecasts from our model to key national decision-making committees on a weekly basis as part of a national COVID-19 situational assessment programme14. We examine the performance of the forecasts throughout the study period (March–September 2022), both qualitatively—using visual cheques—and quantitatively—with the use of formal statistical metrics18,19,20,21. We discuss how the performance of our occupancy forecasts changes with the epidemiological context and how it depends upon the performance of the input case forecasts.

Methods

Summary

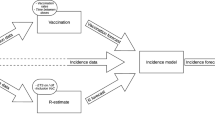
We produced forecasts of the number of COVID-19 cases in hospital ward and ICU beds (i.e. the ward and ICU occupancies) on a weekly basis using a bespoke clinical forecasting pipeline (Fig. 1a). We simulated the pathways taken by COVID-19 cases through a hospital as flow through a compartmental model (Fig. 2a). Our clinical forecasting pipeline takes in three primary inputs: an ensemble case forecast, time-varying estimates of key epidemiological parameters (the age distribution of cases, the probability of hospital admission, and the probability of ICU admission), and estimates of patient length of stay. The model outputs are fit to reported occupancy counts across a seven-day window prior to the forecast start date using Approximate Bayesian Computation (ABC)16. We reported the resultant 21-day forecasted counts of ward and ICU occupancy to public health committees on a weekly basis.

Fig. 1: Overview of the clinical forecasting pipeline.
figure 1

a The forecasting pipeline from inputs (left) through to output forecasts (right).

Full size image
Fig. 2: The compartmental model of COVID-19 clinical progression used to simulate the flow of COVID-19 patients through a hospital.
figure 2

a The compartmental model. The probability of transition between Case and Ward and between Ward and ICU was informed by time-varying age-specific estimates, all other probabilities were specified according to age-specific estimates from the multi-state length of stay analysis. The number of occupied ward beds reported by the model is the sum of the individuals in the Ward and Post-ICU ward compartments, and the number of occupied ICU beds is the number of individuals in the ICU compartment.

Full size image

Compartmental pathways model

Our compartmental model simulates the progression of severe COVID-19 disease and corresponding pathways taken through a hospital (Fig. 2a). The design of this model was informed by COVID-19 clinical progression models previously developed for the Australian health system context22,23,24. In our model, new COVID-19 cases start in the Case compartment according to their date of symptom onset (inferred where not recorded). From this compartment, some fraction of cases are admitted to hospital, according to a (time-varying) probability of case hospitalisation. Hospitalisations start in the Ward compartment, from which a patient can then develop further severe disease and be admitted to ICU, according to a (time-varying) probability of ICU admission. Patients in the ICU compartment can then move to the Post-ICU ward compartment. In addition, across each of the Ward, ICU, and Post-ICU ward compartments, we assume patients have some probability of dying or being discharged. We count the number of occupied ward beds as the number of patients in the Ward and Post-ICU ward compartments, and the number of occupied ICU beds as the number of patients in the ICU compartment.

Length of stay estimates

To simulate the flow of patients through the compartmental model, we need to specify distributional estimates of the duration of time they will spend within a compartment before a transition occurs (i.e. their length of stay), and the probabilities of each particular transition occurring (i.e. transition probabilities). We produced estimates of length of stay and transition probabilities using a multi-state survival analysis approach15. This survival analysis framework allowed us to produce estimates across our compartmental model in near-real-time while accounting for right-censoring, such that we could rapidly incorporate any changes in length of stay or transition probabilities when necessary. Changes in these quantities may have arisen as a consequence of factors such as a new variant exhibiting different clinical severity, changes in clinical practice, or vaccination. Although we did not include these factors as covariates in the survival model, their net effect on length of stay statistics during the study period was captured by producing our length of stay estimates over only recently admitted patients. We estimated length of stay and transition probabilities using hospital data from the state of New South Wales (see ref. 15, Supplementary Methods). We were not able to produce similar estimates for the other states and territories of Australia as the requisite line-listed hospital stay data were not accessible to us or did not exist. The delay distribution for Case to Ward was informed by estimates (not described here) from the FluCAN sentinel hospital surveillance network study25, as appropriate data were not available to estimate this delay in the New South Wales dataset (Supplementary Methods), noting that this delay only affects the relative timing of the occupancy time series. The transition probabilities from the multi-state survival model were used across all transitions in the compartmental model except for the Case to Ward and the Ward to ICU transitions. The transition probabilities for these two transitions were estimated as time-varying (described later), given their substantial impact upon the net occupancy counts. The length of stay and transition probability estimates were provided to the simulation model as bootstrapped samples of gamma distribution shape and scale parameters and multinomial probabilities of transition.

Case incidence

In our compartmental model (Fig. 2a), cases of COVID-19 begin in the Case compartment. As such, we must inform the model with the number of new cases entering this compartment each day: we achieve this through use of a time series of historically reported case incidence concatenated with a trajectory of forecasted case incidence.

We received time series of historical case incidence indexed by date of symptom onset from an external model26. This external model performs imputation of symptom onset dates where they have not been recorded in the data, with the final time series being the count of cases with a (reported or imputed) onset date on each given date. Because this external model did not perform multiple imputation of the symptom onset date, we added noise to capture uncertainty in the case counts via sampling from a negative binomial distribution with a mean of the historical case count and a dispersion of k = 25. This uncertainty was expected to assist the subsequent inference stage by increasing the prior predictive uncertainty. A dispersion value of 25 was selected through visual inspection such that the expected variability in incidence by symptom onset date was captured (noting that the subsequent inference stage was able to further refine this uncertainty where necessary, e.g. rejecting samples where the uncertainty in case incidence was too great or too small).

Our method is agnostic to the case forecasting approach used as input, thus allowing us to couple it with any independently produced forecast of case incidence. Here we used outputs from an ensemble forecast of case incidence, which varied in model composition during the study period (methodologies and summary outputs for the ensemble forecast are publicly available14). A total of four different models were used at various stages: two mechanistic compartmental models, one mechanistic branching process model, and a non-mechanistic time series model (see in refs. 14,27,28 for details). Models within the ensemble received ongoing development across the study period in response to changes in our understanding of the epidemiology and biology of the virus14.

Estimation of time-varying parameters

We specified three parameters in the compartmental model of clinical progression as time-varying. For each forecast, we produced estimates stratified by age group a and varying with time t of: the probability of a case being within a certain age group, page(a, t); the probability of a case being hospitalised, phosp(a, t); and the probability of a hospitalised case being admitted to ICU, pICU(a, t). These parameters were chosen to capture phenomena such as changes in case age distribution, changes in case ascertainment, differences in variant virulence and outbreaks of the disease within populations subgroups. We defined age groups as 10-year groups from age 0 to 80, followed by a final age group comprising individuals of age 80 and above (i.e. 0–9, 10–19, ..., 80+).

The time-varying parameters were estimated using case data from the National Notifiable Disease Surveillance System (NNDSS), which collates information on COVID-19 cases across the eight state and territories of Australia. For each case in this dataset, we extracted the date of case notification, the recorded symptom onset date, the age of the case, and whether or not the case had been admitted to hospital or ICU. Where symptom onset date was not available, we assumed it to be one day prior to the date of notification (where this was the median delay observed in the data).

For each of the three time-varying parameters, we constructed estimates using a one-week moving-window average, with estimates for time t including all cases with a symptom onset date within the period (t − 7, t]. To capture uncertainty in these time-varying parameters, estimates were produced using bootstrapping (sampling with replacement) from the line-listed data. A total of 50 bootstrapped samples were produced, with each sample consisting of three parameter time series (each stratified by nine age groups for a total of 27 time series). At the simulation and inference stage, each simulation received a single such sample as input, such that correlation between the 27 time series was preserved. We calculated the first parameter page(a, t), which defines the multinomial age distribution of cases over time, as the proportion of cases within each age group for an estimation window:

$${p}_{{{\rm{age}}}}(a,t)=\frac{\mathop{\sum }_{\tau = t-6}^{t}{n}_{a}(t)}{\mathop{\sum }_{\tau = t-6}^{t}{\sum }_{i}{n}_{i}(\tau )},$$
(1)

where na(τ) is the number of cases in age group a with symptom onset at time τ. To calculate the probability of a case being hospitalised and the probability of a hospitalised case being admitted to ICU, we produced estimates with adjustment for right-truncation. Here, right-truncation was present as we used near-real-time epidemiological data and indexed our estimates by date of symptom onset. The most recent symptom onset dates in our estimates thus included cases that would eventually be (but had not yet been) hospitalised (and similarly for cases admitted to hospital, but not yet admitted to ICU). Had we not accounted for this right-truncation, we would have consistently underestimated the probabilities of hospitalisation and ICU admission for the most recent dates. We describe the maximum-likelihood estimation of the hospitalisation and ICU admission parameters in the Supplementary Methods.

If in a given reporting week we identified a jurisdiction as having unreliable data on hospitalised cases (most often, missing data on cases admitted to hospital or ICU due to data entry delays), we replaced the local estimates with estimates produced from pooled data across all other (reliable) jurisdictions. Changes made in this regard during the study period are listed in the Supplementary Methods.

Simulation and inference

To simulate a single trajectory of ward and ICU occupancy, we sampled: a trajectory of case incidence from the ensemble; a sample of the bootstrapped time-varying parameters (each comprising three time series across nine age groups); and a sample from the bootstrapped length of stay and transition probability estimates. Using these inputs, we performed simulations across the compartmental model (Fig. 2a) independently across each age group and then summed across all age groups to produce total ward and ICU counts for each day. The compartmental model simulates the pathways of patients through the hospital at the population scale with an efficient agent-based approach; we provide details on this algorithm in the Supplementary Methods.

To ensure that trajectories simulated from the clinical pathways model aligned with reported occupancy counts, we introduce a simple rejection-sampling approximate Bayesian method, rejecting trajectories that did not match the true reported occupancy counts within a relative tolerance ϵ across a one-week calibration window. For each simulation with a simulated ward occupancy count \(\hat{W}(t)\) and simulated ICU occupancy count \(\hat{I}(t)\), simulations were rejected where either:

$$\left\vert W(t)-\hat{W}(t)\right\vert > \max (\epsilon W(t),10)\,{{\mbox{or}}}\,\left\vert I(t)-\hat{I}(t)\right\vert > \max (2\epsilon I(t),10),$$
(2)

where W(t) and I(t) were the true reported occupancy counts for each date t in the fitting window, with these counts retrieved from the covid19data.com.au project13. We selected ϵ using a simple stepped threshold algorithm, initialising ϵ at a small value, and continued to sample simulations until 1000 trajectories had been accepted by the model. If 1000 trajectories were not accepted by the time that 100, 000 simulations had been performed (i.e. 100 rejections per target number of output trajectories), we increased ϵ in sequence from [0.1, 0.2, 0.3, 0.5, 1, 10] and restarted the sampling procedure. This behaviour was chosen to achieve a good degree of predictive performance while ensuring that reporting deadlines were met (typically less than 24 h from receipt of ensemble forecasts and relevant hospital data), even where the model was otherwise unlikely to capture hospital occupancy at tighter degrees of tolerance.

We fit simulation outputs over a calibration window defined as the seven days following the start of the 28-day case forecast. This was chosen such that the most up-to-date occupancy data could be used in fitting (typically data as of, or a day prior to, the date clinical forecasts were produced). We could fit the clinical forecast over occupancy data points which were seven days in the future relative to the start of the case forecast for two reasons: the case forecasts were indexed by date of symptom onset and began at the date where a majority (>90%) of cases had experienced symptom onset, adding a delay of 2–3 days; and case forecasts were affected by reporting delays of 3–4 days (whereas occupancy data was not lagged). We did not fit over a larger window as the seven-day window was expected to be sufficient for our purposes, and the computational requirements of model fitting would increase exponentially with a larger window. The forecasts we reported on a weekly basis and examine here are the model outputs across the 21 days following this seven-day fitting window.

We introduced two additional parameters to improve the ability of the model to fit to the reported occupancy counts. These parameters increased variance in the magnitude of the output ward and ICU occupancy count trajectories, reducing the probability of a substantial mismatch between these trajectories and the reported occupancy counts. The first parameter added was H, a modifier on the probability of hospitalisation acting linearly across logit-transformed values:

$${p}_{\,{\mbox{h}}}^{* }={{\mbox{logit}}}^{-1}({{\mbox{logit}}}({p}_{{{\rm{h}}}})+H),H \sim N(0,{\sigma }_{{\mbox{hosp}}\,}^{2}).$$
(3)

The second parameter added was L, which modified the shape of the length of stay distributions across the transitions out of Case, Ward, and Post-ICU Ward, acting linearly across log-transformed values:

$${{\mbox{shape}}}_{i}^{* }={{\mbox{exp}}}({{\mbox{log}}}({{\mbox{shape}}}_{i})+L),L \sim N(0,{\sigma }_{{\mbox{los}}}^{2}).$$
(4)

The values of H and L were sampled from normal distribution priors with means of zero and standard deviations of \({\sigma }_{\,{\mbox{hosp}}\,}^{2}=0.8\) and \({\sigma }_{\,{\mbox{los}}\,}^{2}=0.5\) respectively. We specified these values to reduce the computational time required while ensuring the output model trajectories had good coverage over the reported occupancy counts. These parameters were changed for some jurisdictions during the study period; see the Supplementary Methods for details.

To illustrate the effect of the H and L parameters, we simulated model outputs for an example forecast with and without these parameters set to zero (Supplementary Methods). This demonstrates that output trajectories without the effect of H and L may already align with the reported occupancy counts, but where this does not occur, they enable the recent reported occupancy counts to be well captured by the fitted model outputs (Supplementary Methods).

Performance evaluation

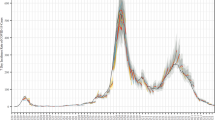
We consider the performance of our forecasts produced between March and September 2022. We produced plots for the visual assessment of forecast performance (Fig. 3a, b and Supplementary Figs. 9–24) which depict all forecasts across the study period with the same presentation of uncertainty as was used in official reporting of the forecasts (with pointwise credible intervals ranging from 20% through to 90% by steps of 10%, and reported occupancy counts overlaid).

Fig. 3: Forecasts of ward and ICU occupancy for the state of New South Wales produced between March and September 2022.
figure 3

a Forecasts of ward occupancy. b Forecasts of ICU occupancy. Credible intervals from 20% through to 90% in 10% increments are displayed in progressively lighter shading. Reported occupancy counts are overlaid. As we produced our forecasts on a weekly basis and each forecast spans three weeks, forecasts are plotted interleaved across three rows; reported occupancy counts are repeated across each row. Forecast start dates are displayed as vertical dashed lines. Note that forecast start date was dependent upon that of the case forecast, and this varied slightly over time (see forecasts 5, 9, 12, and 19). The second week for each forecast (days 8–14) has background shaded in light blue. An identifier for each forecast, 1 through 21, is displayed above each forecast start, and a ^ is displayed where the upper credible intervals of a forecast exceed the y-axis limits. Forecasts for other states and territories are provided in the Supplementary Materials.

Full size image

To evaluate the overall performance of our forecasts, we calculated continuous ranked probability scores (CRPS) across log-transformed counts of occupancy. The CRPS measures the distributional accuracy of a set of forecasts against the eventual observations18. The CRPS is a proper scoring rule: in the limit, where a forecast reports the true probabilities of the underlying process, it will receive the greatest score. We calculated CRPS over log-transformed counts (specifically, \({x}^{* }={\log }_{e}(x+1)\)) rather than over raw counts, as this has been argued to be more meaningful given the exponential nature of epidemic growth19. This transformation also allows us to interpret the resultant CRPS values as a relative error19, enabling comparison of the forecast performance between different settings. We also calculated skill scores of our forecasting model in comparison to a naive random walk model (Supplementary Methods), with results presented in Supplementary Figs. 7 and 8.

We calculated forecast bias to examine where the overall performance of our forecast was reduced due to consistent overprediction or underprediction20 (Fig. 5a–h). Forecast bias (as opposed to, for example, estimator bias29) ranges between  −1 and 1, with a bias greater than zero indicating overprediction and less than zero indicating underprediction. Bias values of approximately zero are ideal, indicating a forecast that overpredicts as often as it underpredicts (or vice versa).

We produced plots demonstrating the association between the performance of our ward and ICU occupancy forecasts and the underlying case forecasts used as input. Specifically, we compared the case forecast performance calculated using CRPS to the bias of the ward occupancy forecasts (Fig. 6a–h) and ICU occupancy forecasts (Supplementary Fig. 5), and the bias of the case forecasts to that of the ward occupancy forecasts (Supplementary Fig. 6). These values were calculated across the whole horizon of the respective forecasts; it should be noted that such comparisons are inherently limited due to the lag between onset of symptoms and admission to hospital, i.e. the performance of the case forecast at the 28 day horizon would be expected to be of lesser influence given these cases are less likely to be hospitalised within the time-frame of our simulation.

We produced probability integral transform (PIT) plots to evaluate the calibration of the forecast (Supplementary Fig. 3). Calibration refers to the concordance between the distribution of our forecasts and the eventual distribution of observations21; for example, in a well calibrated forecast, each decile across the distribution of all forecast predictions should contain ~10% of the eventual observations. Where overlapping intervals contained the eventual observation (typically due to small integer counts, e.g. in smaller population size jurisdictions), we have counted each overlapping interval as containing the observation, with these down-weighted such that any given observation only contributed a total count of one.

Version control repositories are available on GitHub for the simulation and inference steps (http://github.com/ruarai/curvemush), the forecasting pipeline (http://github.com/ruarai/clinical_forecasts), and performance evaluation and manuscript figure plotting code (http://github.com/ruarai/clinical_forecasting_paper). Analysis was performed in the R statistical computing environment (version 4.3.2)30. The forecasting pipeline was implemented using the targets package31, with tidyverse packages used for data manipulation32, pracma for numerical solutions of the maximum-likelihood estimates33, and Rcpp for interfacing with the stochastic simulation C++ code. Forecasting performance was evaluated using the fabletools, tsibble, and distributional packages34,35,36.

Ethics

The study was undertaken as urgent public health action to support Australia’s COVID-19 pandemic response. The study used data from the Australian National Notifiable Disease Surveillance System (NNDSS) provided to the Australian Government Department of Health and Aged Care under the National Health Security Agreement for the purposes of national communicable disease surveillance. Non-identifiable data from the NNDSS were supplied to the investigator team for the purposes of provision of epidemiological advice to government; data were securely managed to ensure patient privacy and to ensure the study’s compliance with the National Health and Medical Research Council’s Ethical Considerations in Quality Assurance and Evaluation Activities. Contractual obligations established strict data protection protocols agreed between the University of Melbourne and sub-contractors and the Australian Government Department of Health and Aged Care, with oversight and approval for use in supporting Australia’s pandemic response and for publication provided by the data custodians represented by the Communicable Diseases Network of Australia. The use of these data for these purposes, including publication, was agreed by the Department of Health with the Communicable Diseases Network of Australia. Ethical approval for this study was also provided by The University of Melbourne’s Human Research Ethics Committee (2024-26949-50575-3). Further, as part of this ethics approval, the University of Melbourne’s Human Research Ethics Committee provided waiver of consent for the use of the case data, as it was believed to be impracticable to contact each individual included in this routinely collected surveillance data and that there was no likely reason that individuals would not consent if asked.

The study used routinely collected patient administration data from the New South Wales (NSW) Patient Flow Portal (PFP). De-identified PFP data were securely managed to ensure patient privacy and to ensure the study’s compliance with the National Health and Medical Research Council’s Ethical Considerations in Quality Assurance and Evaluation Activities. These data were provided for use in this study to support public health response under the governance of Health Protection NSW. The NSW Public Health Act (2010) allows for such release of data to identify and monitor risk factors for diseases and conditions that have a substantial adverse impact on the population and to improve service delivery. Following review, the NSW Ministry of Health determined that this study met that threshold and therefore provided approval for the study to proceed. Approval for publication was provided by the NSW Ministry of Health.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Results

Visual performance assessments

We examined the qualitative performance of our ward and ICU forecasts through visual assessment using the state of New South Wales as a case study (Fig. 3a, b, respectively). Forecasts 1–3 captured both ward and ICU counts (with observed data falling within the 60% intervals across the 15–21 day horizon) during the early growth phase of Omicron BA.2 in late March and early April 2022. The peak in ward occupancy induced by Omicron BA.2 in late April fell within the central density (50% interval) across the 15–21 day horizons of forecasts produced 2–3 weeks prior to the peak (forecasts 4, 5). Forecasts of the declining phase of the BA.2 epidemic exhibited varied performance. The first forecast in mid-April (forecast 6) underpredicted ward occupancy, though not ICU occupancy. This was followed by two forecasts (forecasts 7, 8) which captured ward occupancy better than forecast 6, although forecast 8 predicted ICU occupancy with insufficient uncertainty (i.e. overconfidence), with observations falling outside of the 80% interval for the majority of time points across the forecast horizon. The subsequent forecast produced in early May (forecast 9) incorrectly predicted that ward and ICU occupancy counts would resurge rather than continue to very slowly decline.

New South Wales forecasts produced during the inter-epidemic period between the BA.2 and BA.4/5 waves in late May and early June consistently underpredicted ward occupancy and marginally underpredicted ICU occupancy (forecasts 11–14). We continued to predict declines in occupancy, with the early growth phase of the BA.4/5 wave not captured in our predictions until late June (forecast 15), almost a month after occupancy had begun to stabilise and then slowly increase. Similar to the BA.2 peak, early forecasts captured the magnitude of the BA.4/5 peak in ward occupancy in mid-July, with observations across days 15–21 of the forecast horizon lying within the 40% interval and the 80% interval for forecast 17 and 18, respectively. However, these forecasts failed to predict the timing of the peak, instead predicting that ward occupancy would continue to increase into August. Our forecasts only correctly predicted reductions in the occupancy counts once counts had already begun to stabilise in late July (forecasts 19–21), though these still marginally overpredicted ward occupancy counts.

Further plots for the visual assessment of forecast performance for all other jurisdictions are available in the supplementary materials (Supplementary Figs. 9–24).

Quantitative performance

Measured forecast performance varied over the duration of the study period and across Australia’s eight states and territories (Fig. 4a–d). Measuring performance aggregated by forecast horizon (Fig. 4a) shows that the performance of the ward occupancy forecasts generally degraded the further into the future predictions were made (such a reduction in forecasting performance as the time horizon increases is common to many domains18). Ward occupancy performance for the Northern Territory was particularly unstable across all days of the horizon (Fig. 4a). The drop in forecast performance as forecast horizon increased was less visible for the ICU forecasts (Fig. 4c), likely reflecting the reduced scale of variation in the ICU time series, where the effect of changes in epidemic activity were less visible.

Fig. 4: Summary performance of the ward and ICU forecasts across the study period (March to September 2022) measured using CRPS across log-transformed counts.
figure 4

ACT is the Australian Capital Territory, NSW is New South Wales, NT is the Northern Territory, QLD is Queensland, SA is South Australia, TAS is Tasmania, VIC is Victoria, and WA is Western Australia. a, c Forecast performance for ward (top) and ICU (bottom) by forecast horizon. Median performance (in white) and intervals for 50%, 75%, 90%, and 95% density (in purple or green) are displayed. Note the differing x-axis scale across the ward and ICU forecast plots. b, d Summary forecast performance for ward (top) and ICU (bottom) across all forecasting dates. Frequency for each state is displayed as a histogram (in black), and density underneath (in purple or green), with median overlaid (white and black points). States have been ordered according to median forecast performance. Note the differing x-axis scale across the ward and ICU forecast plots. Due to the limited x-axis scales, 14 points are omitted from the histogram for ward for the Northern Territory and 1 point for ICU for Tasmania.

Full size image

Median ward occupancy forecast performance averaged across all horizons was best in New South Wales (Fig. 4b), possibly reflecting our use of hospital length of stay estimates derived from New South Wales data rather than local estimates (as the requisite data for other states and territories were not accessible or did not exist). ICU occupancy forecast performance was best in Victoria, followed by New South Wales. The states and territories with smaller populations (Tasmania, the Australian Capital Territory and the Northern Territory) tended to have worse performance for both ward and ICU occupancy forecasts, possibly due to a greater impact of individual-level variation in length of stay where admission counts were low (Supplementary Figs. 9, 10, 13, 14, 19, 20). Although South Australia had a (marginally) worse median ward occupancy forecast CRPS than New South Wales (Fig. 4b), examining performance across the 15–21 day horizon (Fig. 4a), the CRPS for South Australia exhibited a greater consistency in performance.

Examining changes in performance of the ward occupancy forecast over the duration of the study period (Fig. 5a–h), we note associations between forecast performance and the epidemiological context, with ward occupancy forecasts often biased downwards during pre-epidemic peak phases, and biased upwards during the post-epidemic peak phases. Results for ICU occupancy forecast performance over time (Supplementary Fig. 4) show similar trends, though here variation in length of stay at the individual-scale likely has a greater influence on performance, given the low (<50) counts for occupancy across most jurisdictions over the study period.

Fig. 5: Three week (days 15–21) horizon performance of the ward forecasts for the forecasts produced between March and September 2022.
figure 5

a–h The forecast performance over time across the eight states and territories of Australia. Light blue shading indicates alternating forecast weeks. The true ward occupancy count is displayed at the top of each panel, with vertical dashed lines indicating dates of visually distinct peaks and troughs (dotted and dashed lines, respectively) in the time series. The CRPS and bias of the forecast are displayed below, reflecting the performance of forecasted counts for that date within the 15–21 day forecast horizon. Upwards bias is displayed in magenta and downwards bias in blue. The CRPS is calculated over log-transformed counts. Optimal forecasting performance is achieved where these values are nearest to zero.

Full size image

We examined how the performance of the ensemble case forecast used as input to our model affected the performance of our ward and ICU forecasts. Averaged across the horizon of each of the forecasts, the mean ward forecast CRPS tended to be lower than that of the corresponding case forecast (Fig. 6a–h). This is expected given that the case forecast is a forecast of incidence, whereas our forecasts are of occupancy (i.e. prevalence), and as such exhibit greater autocorrelation and hence predictability. Comparing the ICU forecast performance to that of the case forecast (Supplementary Fig. 5) yields broadly similar results, although ICU performance in the Australian Capital Territory notably underperforms in comparison to the case forecasts. Bias in the case forecasts tended to be reflected in the ward occupancy forecasts (Supplementary Fig. 6), although this effect is less clear in jurisdictions with smaller populations, such as the Northern Territory (which has a population of approximately 250,000, compared to 8.1 million for New South Wales or 6.5 million for Victoria).

Fig. 6: Performance of the ward occupancy forecasts (y-axis) in comparison to the corresponding ensemble case forecast used as input (x-axis).
figure 6

a–h Comparison of forecast performance between the case forecasts and the ward occupancy forecasts. Performance is measured using CRPS over log-transformed counts. Each dot represents performance measured over a 28-day case incidence ensemble forecast and performance measured over a corresponding 21-day occupancy forecast.

Full size image

In our probability integral transform plots (Supplementary Fig. 3), we observe that forecast calibration varies from good (with the transformed distribution approximately uniform) to poor (with the transformed distribution far from uniform) between states and across the ward and ICU forecasts. Calibration was best for the ward forecasts in South Australia and best for the ICU forecasts in New South Wales. A few forecasts were overconfident, with Northern Territory, Queensland, and Tasmanian ward forecasts and Queensland ICU forecasts having a substantial proportion of observations occurring in the bottom- or top-most intervals. A similar pattern can be observed for the New South Wales ward occupancy forecasts, with a large proportion of observations falling in the top-most interval; this was likely a consequence of a string of underpredicting forecasts from late May through to early July (Fig. 3a, b, forecasts 11–14). The ICU forecasts for South Australia and Victoria had excessive levels of uncertainty, with few observations falling in the outer intervals.

We inspected the relative performance of our model compared to a naive random walk forecasting model (Supplementary Fig. 7). We find that we outperformed the naive model for most states and territories for both ward and ICU occupancy across the forecasting horizon. However, across the 2–3 week horizon, the naive model outperforms our forecasts for ward occupancy in New South Wales, the Australian Capital Territory, and Western Australia, and for ICU occupancy in Western Australia. These results suggest that there may be differences in the inherent difficulty of forecasting occupancy between the different states and territories. For predictions at a very short time horizon (less than 3 days ahead), our model was consistently worse on average than the naive model, likely reflective of our fitting procedure, where we allowed for trajectories to have some degree of error around the recent observed counts. We observe substantial heterogeneity in skill scores between forecasts across the study period (Supplementary Fig. 8). In New South Wales, two forecasts had skill scores of less than negative three, and in Western Australia, three forecasts had skill scores of less than negative three. These poorly performing forecasts likely had a substantial influence on our overall ward forecasting skill scores for these states. Notably, forecasts for ICU occupancy in Victoria outperformed the naive forecasting model across all forecasts produced.

Discussion

We have presented a clinical forecasting model for forecasting the number of patients with COVID-19 in ward and ICU beds. The model simulates the progression of patients through a compartmental model of hospital pathways, with simulations informed by near-real-time epidemiological data and fit to reported bed occupancy counts using Approximate Bayesian Computation. We have evaluated the performance of our forecasting methodology as it was applied and reported to public health decision-makers in the Australian context between March and September 2022 (although forecast outputs were produced between December 2021 and March 2022, we do not consider them in this study as the model received intensive development throughout that period). Our use of an independently produced case forecast as input to the clinical model has allowed us to take advantage of diverse case forecasting methodologies, and we have shown how the performance of our clinical forecasts can be evaluated in terms of the input case forecast performance.

Our results show that forecasting performance was variable over the study period and dependent upon the epidemiological context. The 15–21 day performance of the ward forecasts was poorest across most jurisdictions during the transition from Omicron BA.2 dominance to Omicron BA.4/5 dominance between May and July 2022 (Fig. 5a–h). This reduced performance can be observed in New South Wales from late May until early June (Fig. 3a, forecasts 11–14); by late June (forecast 15), a BA.4/5 transmission advantage was included in the mechanistic case forecasting models14, increasing median predicted occupancy counts but also the uncertainty across these predictions. Forecasting the burden of infectious disease during such variant transition events has previously been noted to be challenging, primarily due to the difficulty in rapidly ascertaining any differences in the biological properties of a new variant and incorporating these into models37,38. These differences could include a change in the virulence of the pathogen, leading to changes in length of stay, probability of hospital admission, or probability of ICU admission. However, in the absence of evidence for a difference in virulence between the Omicron BA.2 and BA.4/5 variants39, it is most likely that improving our clinical forecasts during this period would have required adjustments to the underlying case incidence forecasts.

Accurate prediction near epidemic peaks has previously been recognised to be a particularly difficult problem, both in the context of case incidence forecasts40,41,42 and hospital burden forecasts43,44. In our results, forecasting performance around epidemic peaks varied. Prior to peaks (in the epidemic growth phase), our forecasts generally performed well, although they tended to be biased downwards (Fig. 5a–h). Examining forecasts with start dates in the weeks prior to epidemic peaks (Supplementary Figs. 8 and 9–24), we see that occupancy count at the peak was generally well captured by forecasts produced one or two weeks prior to the point of peak occupancy. Forecasts that were produced three weeks prior to the peak performed comparatively worse, with most predicting that occupancy would continue to grow beyond what eventuated to be the peak. However, at this three-week horizon, forecasts typically had wide credible intervals, which appropriately conveyed the uncertainty of our predictions. During these peak periods, the performance of the forecasts was likely strongly influenced by the underlying case forecast performance. However, it is also possible that proactive changes in clinical practice could have led to reductions in length of stay or hospital admission rates around peak periods5. Such reductions in these key epidemiological parameters could only be captured in our model once they were realised in the data used for estimation. If reductions in length of stay or hospital admission rates occurred across the forecasting horizon, our forecasts would over-predict occupancy.

Previously published forecasting models for COVID-19 clinical burden can be broadly categorised into two groups: statistical models and mechanistic models. Statistical models produce predictions of clinical burden by learning patterns in the observed data, and may take as input only the target time series data45,46,47,48, or may consider regression against other observations such as mobility or historical case incidence47,48,49,50. In contrast, mechanistic forecasting models of clinical burden consider the flow of individuals through an explicitly described model of disease progression and clinical care pathways. Such mechanistic models may capture the entry of individuals into the healthcare system through an embedded model of infection dynamics23,51,52,53,54 or through statistical predictions of the entry process50,55,56. Statistical models may perform as well (or better) than mechanistic models in some situations; however, one notable advantage of the mechanistic modelling approach is in allowing for the effect of changes in epidemiological parameters to be predicted and explained (e.g. a reduction in patient length of stay)57.

Our work is distinguished from similar mechanistic clinical burden forecasting models through its use of an independently produced forecast of case incidence as input. This decoupling of the clinical progression model from the case forecasting models allows for greater separation of concerns since the development of each model can occur independently58. A potential disadvantage of this modular approach is that clinical observations cannot be used to inform the underlying forecasts of infection dynamics, as each model is fit to data separately. Figure 6a–h demonstrate that the quality of our occupancy forecasts depends upon the performance of the input case incidence forecasts (a similar result has been previously reported for a model of hospital admissions47), implying that our use of an ensemble case forecast as input has been advantageous for the performance of our occupancy forecasts, given ensembles have repeatedly been shown to improve case forecasting performance43,47,48,59,60.

Our clinical forecasting model is designed to receive outputs from forecasts of case incidence as a (large) sample of trajectories. However, it has been more common for forecast outputs to be summarised using prediction intervals, which quantify the probability of outcomes falling within certain ranges. Examples of this have included the collaborative ensemble forecasts reported by the US and European COVID-19 forecast hubs43,61. These prediction intervals are incompatible with our methodology as they obscure the underlying autocorrelation in the case incidence time series—if we were to sample from such intervals across each day of the forecast, uncertainty in the cumulative case count would be underestimated. We recommend that collaborative ensemble forecasts of infectious disease report outputs as trajectories where possible, so as to enable the appropriate propagation of uncertainty in further applications (such as that presented here).

Infectious disease forecasting models often exhibit reduced performance when predicting in low count contexts45,51. In our work, we produced forecasts across low counts of both ward and ICU occupancy, typically during inter-epidemic periods and in jurisdictions with smaller population sizes. The performance of our forecasts as measured through CRPS was worse in these contexts (Fig. 4a–d). However, this is in large part due to the CRPS being calculated over log-transformed counts, effectively making it a measure of relative error. This would be expected to penalise forecasts produced in low count contexts, where small absolute changes can produce large relative differences19. Supplementary Fig. 7 provides further evidence for this, with some jurisdictions with smaller population sizes, such as Tasmania and the Northern Territory, performing particularly well when compared to a naive forecasting model. We also note that the performance of our occupancy forecasts across these low-count contexts may be of lesser importance to public health decision-makers, given they are typically (by definition) distant from capacity constraints.

Since the clinical forecasting model is informed by near-real-time estimates of key quantities such as probability of hospitalisation and length of stay, reasonable forecast performance could be expected in the absence of the approximate Bayesian fitting step. While this occasionally proved to be true in application (e.g. see Supplementary Methods, where the model output without fitting captures the reported ward occupancy counts for the Northern Territory), a few factors may have prevented this from being generally the case: firstly, we used patient length of stay distributions which were fit to data from the state of New South Wales and these distributions may not reflect the clinical practice or realised severity in other jurisdictions; secondly, the compartmental model we used may miss some components of hospital occupancy dynamics, such as outbreaks of COVID-19 within hospitals; thirdly, we assumed that the population which was reported as hospitalised in the case data was the same population as that reported in the hospital occupancy figures, which was not always the case due to differing upstream datasets (e.g. Victoria collected occupancy counts as a separate census of patients62); finally, our near-real-time estimates of ward and ICU admission probability were not adjusted for possible right-truncation due to reporting lags as the date of data entry was not available within the case dataset we had access to.

Our forecasting methodology did not (explicitly) include the effect of vaccination upon the clinical trajectory of a COVID-19 case, as linked case vaccination data were generally unavailable or incomplete during our study period. These data would be of substantial value, allowing for our key epidemiological quantities (i.e. the probability of hospitalisation, probability of ICU admission and length of stay) to be produced with stratification by vaccination status, and potentially enabling the production of more accurate forecasts. Data on infections were also limited during our study period, with no large-scale infection survey performed in Australia during our study period63 (although a number of sero-surveys were produced10,64,65,66). Such infection data would allow us to produce estimates of the infection hospitalisation risk, unbiased by changes in the case ascertainment rate.

The measure of hospital burden we chose to forecast—hospital occupancy—has an advantage over incidence measures such as daily hospital admissions since it directly relates to the capacity of the healthcare system. However, it has a few disadvantages of note. Because hospital occupancy is a prevalence measure, it is inherently slower to respond to changes in the epidemic situation than hospital admissions and is, therefore, less useful as an indicator of changes in epidemic activity. It may also be more difficult to measure at the hospital level, given that it requires either accurate accounting of admissions and discharges or recording of individual patient stays. Ideally, both admissions and occupancy would be monitored and reported; in such a context, our model could be easily extended to fit to and report admission counts, given that admission counts are already recorded within our simulations.

Throughout the period for which COVID-19 bed occupancy counts were collected and reported in Australia, no nationally consistent standard specified which COVID-19 cases should be included in the counts. As a result, distinct definitions were created and applied across jurisdictions. For example, during our study period, the state of New South Wales counted any patient in hospital who had been diagnosed with COVID-19 either during their hospital stay or within the 14 days prior to their admission to hospital67. This broad definition had the beneficial effect of reducing false negatives in the counting process but resulted in the inclusion of a large number of individuals who had since recovered from infection and/or whose stay was unrelated to the disease (with this effect then being captured in the estimates of length of stay used in our study). This was in contrast to Victoria, where COVID-19 cases were counted only until a negative test result was received62, reducing false positive inclusions but underestimating the total hospital burden of the disease, given COVID-19 cases may still require hospital care or be isolated for infection control reasons even when they no longer test positive. Although these differences would not be expected to substantially affect the forecast performance given our fitting methodology (which is able to adjust the probability of hospital admission and patient length of stay to account for such biases), the development of standard definitions that could be applied in future epidemics would allow for direct comparison of counts between jurisdictions and simplify modelling efforts.

The modelling framework we have described here is flexible and not inherently tied to COVID-19 hospital occupancy as the forecasting target. In general terms, our method stochastically simulates the convolution of a time series of case incidence into time series of subsequent outcomes. As such, the methodology could be applied to other viral respiratory pathogens that lead to substantial hospital burden, including respiratory syncytial virus (RSV) or the influenza viruses, both of which are currently the focus of international forecasting efforts68,69. Further, our framework could be used to model other infectious diseases outcomes, such as absenteeism from the workforce or long-term sequelae. The efficient simulation and inference methodology we present allows for forecasts to be produced within a short turnaround time, with forecasting across the eight states and territories of Australia taking less than one hour on an eight core virtual machine (AMD EPYC 7702), where approximately one quarter of this time was dedicated to the pre- and post-processing of data and results. Our approach is highly amenable to parallelisation (across both individual simulations and the regions we choose to forecast) and as such would be expected to be suitable in applications where there is a greater number of target regions or outcomes.

We have presented a robust approach for forecasting COVID-19 hospital ward and ICU bed occupancy and have examined the performance of this methodology as applied in the Australian context between March and September 2022. Our forecasting model takes as input an independently produced forecast of daily case incidence. This incidence is then transformed into ward and ICU occupancy counts through a stochastic compartmental model, with the probabilities of hospitalisation and of ICU admission informed by near-real-time data. Our use of independently produced forecasts of case incidence has allowed us to both develop our model independently of the input case forecasting models and take advantage of the performance benefits provided by ensemble case forecasts. Our computationally efficient inference method allowed us to generate forecasts for multiple Australian jurisdictions in near-real-time, enabling the rapid provision of evidence to public health decision-makers.