Introduction

The world is now facing a series of environmental degradations, from water and air pollution to the depletion of ecological resources and many of them are confirmed to be caused by human activities. According to the Global Footprint Network (GFN), the ecological pressure from human activities has exceeded the Earth’s carrying capacity by 75% (Network 2019). The significant impact of humans on the environment, in turn, affects human development, including economic activities, health conditions, and energy availability. Consequently, both developed and developing countries worldwide have taken various measures, such as conserving natural resources, limiting carbon emissions, and accelerating energy transitions, to mitigate the increasingly urgent climate and environmental issues. For instance, nearly all countries have signed the Paris Climate Change Agreement (PCCA) and committed to reducing their carbon emission levels. Additionally, many countries have announced their energy transition strategies, promoting a shift from fossil fuel dependence to renewable energy reliance to balance energy demand and reduce environmental impacts (Dong et al. 2022a). Therefore, besides economic growth, protecting ecological resources, reducing carbon emissions, and increasing the utilization of renewable energy have become important development goals for governments worldwide in recent years.

The advent of artificial intelligence (AI) has brought multiple impacts on people’s lives and production methods, with its applications increasingly extending into manufacturing, energy, healthcare, logistics, finance, and other fields (Zavyalova et al. 2023). According to a recent study published by Forbes, the global AI market is projected to reach a staggering $71 billion by 2024. As a game-changing technology, AI’s rapid development presents unprecedented opportunities and challenges for global environmental protection efforts (Ahmad et al. 2022). On one hand, AI’s powerful computing capabilities are believed to help increase productivity and achieve economies of scale, thereby conserving resources and energy for the whole society (Wang et al. 2023c). On the other hand, an increasing number of practitioners and scholars point out that the explosive growth in AI capabilities is accompanied by an exponential increase in the energy consumption required for AI training. For example, research indicates that training a single model like ChatGPT consumes 1.287 gigawatt-hours of electricity, roughly equivalent to the annual electricity consumption of 120 American households (Probst 2023). In short, AI is impacting the current energy system in different directions through multiple channels.

In response to the opportunities and threats brought by the rapid development of AI, more and more countries are turning their attention to regulating, guiding, and utilizing AI to protect the environment, reduce carbon emissions, or promote energy transition, aiming to align AI development with sustainable development standards. Table 1 summarizes some national strategies that emphasize harnessing AI’s potential for sustainability. However, the actual impact of AI on environmental actions remains unclear. Therefore, this study raises the question: What effects does AI development have on the environmental indicators, especially the ecological environment, carbon emissions, and energy transition? How do external conditions such as industrial structure and trade openness influence these effects? Answering these questions is crucial to ensuring AI stays on a sustainable development track and further optimizing AI policies.

Table 1 Summaries of national strategies of AI emphasizing the potential of AI for environment, carbon emissions reduction or energy transition.
Full size table

From the existing literature, the factors influencing environmental degradation and energy transition have been extensively studied, providing a solid theoretical foundation for subsequent research. However, the emerging variable of AI has rarely been integrated into traditional research frameworks. Additionally, some studies have explored the potential opportunities and threats of AI concerning the ecological environment, carbon emissions, and energy transition from various perspectives but lack systematic and quantitative evaluation. To fill in this gap, this paper aims to quantitatively assess the impact of AI on the ecological environment, carbon emissions, and energy transition and explore the possible heterogeneity and nonlinearity of these impacts. First, based on panel data from 67 countries between 1993 and 2019, a set of SYS-GMM models is employed to investigate the effects of AI on ecological footprint, carbon emissions, and energy transition. Second, the potential differences in AI’s impact across developed and middle-income countries are discussed by grouping countries according to their development stages. Finally, a series of threshold models are constructed using industrial structure, trade openness, AI development level, and energy transition level as threshold variables to clarify the nonlinear characteristics of these impacts. This article aims to clarify the multifaceted environmental impacts of AI and explore its potential heterogeneity and nonlinearity, providing a scientific foundation for global policymakers. Amid the current complex and controversial relationship between AI and the environment, this research helps policymakers develop and manage AI sustainably.

The remainder of the paper is organized as follows. Section 2 reviews the literature. Section 3 briefly introduces the methodology and data. Section 4 discusses the empirical results. Conclusions and policy implications are presented in Section 5.

Literature review

Although the core variables of this paper include carbon emissions, ecological footprint, energy transition, and AI, they come from a classic and broad topic, namely the technology-environment nexus. Therefore, we first review previous discussions on the impact of technological factors on important environmental indicators. Subsequently, we focus on the qualitative discussion and empirical research on the specific environmental impact of AI. Finally, we discussed the gap in existing literature.

Literature on the nexus between technological factors and environmental indicators

Ecological footprint, carbon emissions, and energy transition are three variables that have been widely used to assess sustainability in previous research: Ecological footprint refers to the biologically productive areas that can provide the resources needed for human survival or consume the waste discharged by human beings,.and can be used to measure the pressure of human activities on the ecological environment; reducing carbon emissions is the most direct way to slow down climate change; energy transition is the key path to achieve environmental protection and climate mitigation, marking the recognition of human beings on renewable energy, a clean resource. Examining the determinants of each of these sustainability indicators is a hot topic in the empirical literature on energy economics (Dong et al. 2022b; Ehigiamusoe and Dogan 2022; Wang et al. 2024b. Among the various factors that may affect the above environmental indicators, technological factors are considered to be crucial. Technology has a profound impact on many aspects of residents’ social life and economic production, and these impacts will ultimately change a country’s energy use and interaction with nature (Wang et al. 2024a). In other words, technological factors may have a positive or negative impact on carbon emissions, ecological footprint, and energy transition.

For example, in terms of the nexus of technology and carbon emissions, Cheng et al. (2018) used the DEA-Malmquist method to measure the total factor productivity of 30 provinces in China from 1998 to 2014 as an indicator of technological progress. The findings show that technological advances reduce carbon intensity by increasing production efficiency. Gu et al. (2019) used the number of energy technology patents to represent technological progress, and found an inverted U-shaped relationship between energy technology progress and carbon emissions. Technologies that affect carbon emissions include not only technological progress or innovation in a broad sense but also specific technologies such as digital technology and ICT. Moyer and Hughes (2012) used the International Futures (IFs) comprehensive assessment system to study the relationship between ICT and global carbon emissions, and believed that ICT has brought about a decline in carbon emissions in the past 50 years. Yi et al. (2022) used the spatial panel Durbin model to study the impact of the digital economy on carbon emission reduction in 30 provinces in China. They emphasized that the development of the digital economy not only has a direct emission reduction effect but also has a significant spatial spillover effect. The ecological footprint was first brought into the field of empirical research by (Wackernagel and Rees 1998) as another indicator of environmental sustainability, which is considered to be a more comprehensive measure of environmental degradation than carbon emissions. Therefore, many scholars use the ecological footprint to replace carbon emissions, and re-examine the already tested nexus between carbon emissions and technology. Huang et al. (2022) compiled the ICT index through principal component analysis, and found that the development of ICT significantly increased the ecological footprint of E-7 countries, but decreased that of G-7 countries.

Regarding the impact of technology on energy transition, Zheng et al. (2021) based on China’s provincial data from 2005 to 2017, examine the impact of renewable energy technology innovation represented by patent stock on renewable energy power generation. The results show that an average increase of 1% in the level of renewable energy technology innovation directly brings about a 0.411% increase in renewable energy power generation in the province and a 3.264% increase in renewable energy power generation in neighboring provinces through technology diffusion. Tzeremes et al. (2023) and Shahbaz et al. (2022) respectively confirm the role of ICT and digital techniques in promoting energy transition. In summary, based on the above review, the use of carbon emissions, ecological footprint, and energy transition variables can characterize the different impacts of technological factors. In addition, different technologies may have different impacts on the same indicator. Therefore, in order to fully understand the environmental impact of the current new technology of AI, it is necessary to select sufficiently detailed and accurate methods to distinguish AI from previous digital technologies and examine the impact of AI on each different environmental indicator.

The environmental impact of artificial intelligence

The debate over the environmental impact of artificial intelligence (AI) can be traced back to a classic theory related to technological progress—the rebound effect. The rebound effect refers to the phenomenon where improvements in efficiency do not always reduce demand; instead, they can lead to an increase in demand. For example, when a company improves efficiency and achieves raw material savings per unit of product, it may further expand production. This expansion in production resulting from efficiency improvements can completely offset the raw material savings brought about by technological upgrades, or even lead to a dramatic increase in the company’s raw material demand. This rebound effect suggests that although technology may enhance efficiency and save resources per unit product, the ultimate resource and energy consumption, as well as its environmental impact, are uncertain.

In this context, Hilty and Hercheui (2010) proposed the three-order effect theory to summarize the multiple aspects of the environmental impact that smart technologies may have. The first-order effects of smart technologies refer to the direct environmental impacts of specific products throughout their lifecycle, including production, usage, and disposal. This encompasses the environmental footprint of acquiring raw materials for production, the electricity consumption during usage, and the environmental pollution associated with disposal. Second-order effects represent the direct environmental benefits brought about by efficiency improvements and process optimizations enabled by smart technologies. For example, the use of electronic products directly replaces some paper materials, reducing deforestation. Third-order effects represent the negative environmental impacts arising from the rebound effect based on the second-order effects. For instance, the prevalence of electronic products might lead to long-term dependence or addiction to these devices, resulting in electricity consumption (primarily produced by fossil fuels) that far exceeds the environmental impact of paper-based materials like newspapers and books.

Understanding these effects is crucial for comprehensively grasping the multifaceted debate on the environmental impact of AI. On one hand, the second-order effects of AI are widely acknowledged. In other words, AI has enormous potential to improve production efficiency, enhance production processes, or support environmental protection and energy transition initiatives, thereby promoting environmental improvement (Lei et al. 2023; Lyu and Liu 2021). On the other hand, the energy consumption throughout its lifecycle (first-order effect) and the productivity rebound (third-order effect) may exacerbate environmental issues (Taddeo et al. 2021; Wu et al. 2022).

Although it is currently challenging to quantify each specific impact of AI, utilizing detailed macroeconomic statistical data for holistic assessment is a critical research direction. Many scholars leverage global or national-level time series or panel data, selecting environmental indicators such as carbon emissions, ecological footprints, and energy consumption to evaluate the overall environmental impact of AI and understand current trends in AI development. On the one hand, using a global panel and dynamic estimation approach, Ding et al. (2023) claim that AI reduces carbon emissions significantly. On the other hand, Luan et al. (2022) found that AI contributed to air pollution through a study of 74 countries and insisted that AI has exacerbated climate warming. There is a little article that studies ecological footprint (Chen et al., 2022b) which confirms the positive effect of AI on ecological footprint. And only (Wang et al. 2024c) discussed the impact of AI on energy transition and claimed a positive effect. Other related research about the environmental impact of AI is summarized in Table 2.

Table 2 Summary of empirical research related to AI environmental effects.
Full size table

Research gaps and contributions

In summary, the aforementioned studies proxy environmental sustainability carbon emissions, ecological footprint, and energy transition to explore and verify the environmental impact of broad-range factors of economics, energy, and technology. However, few studies are focusing on the important AI-environment sustainability nexus. Specifically, three detailed research gaps are identified. (1) From a research perspective, existing studies discussing the environmental sustainability of AI often focus on the perspective of carbon emissions. The impact of AI on ecological footprint and energy transition has rarely been studied, and there are almost no studies combining multiple indicators. (2) Regarding the research object, China has been the most fully studied, while research on other countries or global levels has received inadequate attention. (3) In terms of research ideas and methods, most studies presuppose linear relationships between AI and corresponding environment indicators and adopt linear research methods, thus ignoring the potential nonlinearity and heterogeneity relationships.

This paper fills the above research gaps by using a global panel to evaluate and compare the impact of AI on carbon emissions, ecological footprint, and energy transition. Moreover, dynamic threshold models are developed to explore the potential nonlinear impact under different conditions or stages of industrial structure, trade openness, AI development, and energy transition. Against the backdrop of the current complex and controversial relationship between AI and the environment, this article helps to clarify the multifaceted environmental impacts of AI and explore its potential heterogeneity and nonlinearity, providing a scientific basis for global policymakers to develop and manage AI.

Methods, variables, and data

Model setting

This study aims to evaluate the linear and nonlinear impact of AI on ecological footprint, carbon emissions, and energy transition respectively. For better modeling of these explained variables, dynamics can not be ignored. This is because in many cases, how much environmental impact a country will have or what kind of energy structure it adopts will be determined partially by its past behavior. For example, once a certain industrial production mode is determined, a lot of equipment and professionals need to be invested, and it is difficult for enterprises to switch to another production mode in a short time. Therefore, there may be inertia in carbon emissions, ecological footprint, and energy transition. Based on the above discussion, we first construct three dynamic linear models as the benchmark regression models in this paper to measure the effects of AI on ecological footprint, carbon emissions, and energy transition:

$${{Model}\,{L1}:{EF}}_{{it}}={\alpha }_{0}+{{\beta }_{0}{EF}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}+{u}_{i}+{\varepsilon }_{{it}}$$
$${{Model}\,{L2}:{CE}}_{{it}}={\alpha }_{0}+{{\beta }_{0}{CE}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{it}}+{u}_{i}+{\varepsilon }_{{it}}$$
$${{Model}\,{L3}:{ETR}}_{{it}}={\alpha }_{0}+{{\beta }_{0}{ETR}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{it}}+{u}_{i}+{\varepsilon }_{{it}}$$

where i represents individual and t represents time. EF, CE, and ETR are the explained variables, representing ecological footprint, carbon emission, and energy transition respectively. AI is the explanatory variable, representing the level of artificial intelligence development. C represents the control variables vector, which is kept the same in the three models. \({u}_{i}\) is the individual fixed effect, and \({\varepsilon }_{{it}}\) is the disturbance term.

Based on Model L1-L3, we need to further construct a series of nonlinear models to study the influence of external variables. In the literature that uses traditional methods to discuss nonlinearity, some add quadratic terms of independent variables to the equation, and some choose to divide the research objects into different samples according to certain standards (such as income, GDP, etc.). These methods can partially solve the problem of nonlinearity, but the rationality and effectiveness of artificially setting models and dividing samples have been questioned. To address the above issues, in this paper, we adopt the dynamic panel threshold models to model the nonlinearity. In a threshold model, the division of the sample interval is endogenously determined by the sample data, and the regression coefficient is allowed to be different across intervals, which overcomes the problem of artificial selection of the model. Therefore, the following dynamic threshold models are used in this paper:

$$\begin{array}{l}{Model}\,{N1}:{{EF}}_{{it}}={\alpha }_{0}+{{\alpha }_{1}{EF}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}\\\qquad\quad+\,{\delta }_{1}{{AI}}_{{it}}I({q}_{{it}}\ge \gamma )+{{\boldsymbol{\delta }}}_{{\boldsymbol{i}}}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}I({q}_{{it}}\ge \gamma )+{u}_{i}+{\varepsilon }_{{it}}\end{array}$$
$$\begin{array}{l}{Model}\,{N2}:{{CE}}_{{it}}={\alpha }_{0}+{{\alpha }_{1}{CE}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}\\\qquad+\,{\delta }_{1}{{AI}}_{{it}}I({q}_{{it}}\ge \gamma )+{{\boldsymbol{\delta }}}_{{\boldsymbol{i}}}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}I({q}_{{it}}\ge \gamma )+{u}_{i}+{\varepsilon }_{{it}}\end{array}$$
$$\begin{array}{l}{Model}\,{N3}:{{ETR}}_{{it}}={\alpha }_{0}+{{\alpha }_{1}{ETR}}_{{it}-1}+{\beta }_{1}{{AI}}_{{it}}+{\boldsymbol{\beta }}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}\\\qquad\qquad+\,{\delta }_{1}{{AI}}_{{it}}I({q}_{{it}}\ge \gamma )+{{\boldsymbol{\delta }}}_{{\boldsymbol{i}}}{{\boldsymbol{C}}}_{{\boldsymbol{it}}}I({q}_{{it}}\ge \gamma )+{u}_{i}+{\varepsilon }_{{it}}\end{array}$$

where \({{\boldsymbol{C}}}_{{\boldsymbol{it}}}\) is a vector of control variables consistent with Model L1-L3. \({q}_{{it}}\) is the threshold variable and \(\gamma\) is the corresponding threshold value. I(·) is an indicator function that takes 1 when the condition is satisfied and 0 otherwise. We specially focus on \({\delta }_{1}\) because it collects the change in the influence coefficient of AI when the threshold variable is in a higher interval.

Estimation strategy

System generalized moment estimation

The System Generalized Method of Moments (SYS-GMM) proposed by Blundell and Bond (1998) is adopted to estimate coefficients in Model L1-L3. This method uses GMM instead of the traditional OLS estimation method to solve the problem of downward bias (Nickell bias) of the estimator caused by the introduction of the dependent variable lag term in the traditional fixed effect model (Pesaran 2020). In addition, SYS-GMM makes full use of the residual information in the level equation and the difference equation to construct moment conditions, which improves the efficiency of parameter estimation. In order to explain the estimation strategy of SYS-GMM, we express Model L1-L3 in vector form as follows:

$${Y_{{it}}}={\alpha }_{0}+{\beta }_{0}{Y_{{it}-1}}+{\boldsymbol{\beta }}{{\boldsymbol{X}}}_{{\boldsymbol{it}}}+{u}_{i}+{\varepsilon }_{{it}}\,i=1,...,n{{;}}\,t=1,...,T$$
(1)

where \({Y_{it}}\) and \({Y_{{it}-1}}\) are the explained variable and its first-order lag, respectively. \({\boldsymbol{X}}\) is a vector of explanatory variables. ∆represents the first difference. εi and \({\boldsymbol{\Delta }}{{\boldsymbol{\varepsilon }}}_{{\boldsymbol{i}}}\) denote the residual series of the level and difference equations, respectively.

In order to estimate the parameters, we need to obtain all sample moment conditions for the level and difference equations. First, for the above level equation (original equation), we have the moment condition related to the level equation:

$$E\left({{\boldsymbol{Z}}}_{{\boldsymbol{li}}}^{{\prime} }{{\boldsymbol{\varepsilon }}}_{{\boldsymbol{i}}}\right)={\boldsymbol{0}}$$
(2)

Secondly, for the first-order difference equation of the level equation:

$${\triangle Y}_{{it}}={\beta }_{0}{\triangle Y}_{{it}-1}+{\boldsymbol{\beta }}{\boldsymbol{\triangle }}{{\boldsymbol{X}}}_{{\boldsymbol{it}}}+\triangle {\varepsilon }_{{it}}$$
(3)

we also have the moment condition for the difference equation:

$$E\left({{\boldsymbol{Z}}}_{{\boldsymbol{di}}}^{{\prime} }{\boldsymbol{\Delta }}{{\boldsymbol{\varepsilon }}}_{{\boldsymbol{i}}}\right)={\bf{0}}$$
(4)

where \({{\boldsymbol{Z}}}_{{\boldsymbol{li}}}^{{\boldsymbol{{\prime} }}}\) and \({{\boldsymbol{Z}}}_{{\boldsymbol{di}}}^{{\boldsymbol{{\prime} }}}\) are the transposes of the level and difference instrumental variable matrix, and

$${{\boldsymbol{Z}}}_{{\boldsymbol{li}}}=\left[\begin{array}{cccccccccccccccc}{y}_{i1} & {{\boldsymbol{X}}}_{{\boldsymbol{i}}{\bf{1}}} & {\cdots } & {{\boldsymbol{X}}}_{{\boldsymbol{iT}}} & 0 & 0 & 0 & \cdots & 0 & \cdots & 0 & \cdots & 0 & 0 & \cdots & 0\\ & & & & & & & & & & & & & & & \\ 0 & 0 & \cdots & 0 & {y}_{i1} & {y}_{i2} & {{\boldsymbol{X}}}_{{\boldsymbol{i}}{\bf{1}}} & {\cdots } & {{\boldsymbol{X}}}_{{\boldsymbol{iT}}} & \cdots & 0 & \cdots & 0 & 0 & \cdots & 0\\ & & & & & & & & & & & & & & & \\ \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ & & & & & & & & & & & & & & & \\ 0 & 0 & \cdots & 0 & 0 & 0 & 0 & \cdots & 0 & \cdots & {y}_{i1} & \cdots & {y}_{{iT}-2} & {{\boldsymbol{X}}}_{{\boldsymbol{i}}{\bf{1}}} & \cdots & {{\boldsymbol{X}}}_{{\boldsymbol{iT}}}\end{array}\right]$$
(5)
$${{\boldsymbol{Z}}}_{{\boldsymbol{di}}}=\left[\begin{array}{ccccccc}\varDelta {y}_{i2} & {\boldsymbol{\Delta }}{{\boldsymbol{X}}}_{{\boldsymbol{i}}{\bf{3}}} & 0 & 0 & \cdots & 0 & 0\\ & & & & & & \\ 0 & 0 & \varDelta {y}_{i3} & {\boldsymbol{\Delta }}{{\boldsymbol{X}}}_{{\boldsymbol{i}}{\bf{4}}} & \cdots & 0 & 0\\ & & & & & & \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \\ & & & & & & \\ 0 & 0 & 0 & 0 & \cdots & \varDelta {y}_{{iT}-1} & {\boldsymbol{\Delta }}{{\boldsymbol{X}}}_{{\boldsymbol{iT}}}\end{array}\right].$$
(6)

Finally, estimates of the unknown parameters \({{\boldsymbol{\theta }}}_{{\boldsymbol{i}}}\) = (α, β0, β) will be produced by solving the above sample moment conditions.

To ensure the validity of instrumental variables, two tests should be employed before analyzing the estimation result. First, the Sargan test should be adopted to prevent over-identification. Because the number of instrumental variables is a quadratic function of T in the SYS-GMM model. As T increases, the number of instrumental variables may exceed the parameters to be estimated, which is called over-identified. Second, the Arellano-Bond (AR) test needs to be employed to prevent residual serial correlation. Because SYS-GMM employs the instrumental strategy of using lagged variables, which relies on the presupposes that the residual series are uncorrelated.

DPTM with endogenous threshold variables

The dynamic panel threshold model (DPTM) newly proposed by Seo et al. (2019) with an endogenous threshold variable is adopted to estimate the nonlinear models (Model N1-N3). The key difference between DPTM and the traditional static panel threshold model is that the equation includes the lagged term of the explained variable, and relaxes the assumption that the threshold variable is completely exogenous, allowing it to become endogenous. In order to explain how DPTM solves the problem of lagged terms of explained variables and endogenous threshold variables, we express the DPTM model in the following vector form:

$${{\boldsymbol{Y}}_{{\boldsymbol{it}}}}={\boldsymbol{\beta }}{{\boldsymbol{X}}}_{{\boldsymbol{it}}}+{\boldsymbol{\delta }}({1{\boldsymbol{,}}{\boldsymbol{X}}}_{{\boldsymbol{it}}})I({q}_{{it}}\ge \gamma )+{u}_{i}+{\varepsilon }_{{it}}\,i=1,...,n{{;}}\,t=1,...,T$$
(7)

where \({{\boldsymbol{X}}}_{{\boldsymbol{it}}}\) is the set of explanatory variables including \({{\boldsymbol{Y}}_{{\boldsymbol{it}}}{\boldsymbol{-}}{\boldsymbol{1}}}\), and \({\boldsymbol{(}}{1{\boldsymbol{,}}{\boldsymbol{X}}}_{{\boldsymbol{it}}}{\boldsymbol{)}}\) additionally includes a constant term. \({\boldsymbol{\delta }}{\boldsymbol{(}}{{\boldsymbol{1}}{\boldsymbol{,}}{\boldsymbol{X}}}_{{\boldsymbol{it}}}{\boldsymbol{)}}I({q}_{{it}}\ge \gamma )\) records the change in the coefficient of all the explanatory variables when the threshold variable changes from low to high cross-country threshold. According to Seo et al. (2019), the difference generalized method of moments (Diff-GMM) is used to eliminate \({u}_{i}\) and estimate unknown parameters θ = (β, δ, γ). The difference form of Eq. (7) is:

$${\Delta Y_{{it}}}={\boldsymbol{\beta}}{{\boldsymbol{\Delta}}{\boldsymbol{X}}}_{{\boldsymbol{it}}}+{\boldsymbol{\delta }}{{\boldsymbol{\Delta}}{\boldsymbol{X}}}_{{\boldsymbol{it}}}I({q}_{{it}}\ge \gamma )+{\Delta\varepsilon }_{{it}}$$
(8)

Consider the following sample moment conditions:

$${\bar{g}}_{n}({\boldsymbol{\theta }})=\frac{1}{n}\mathop{\sum}\limits_{i=1}^{n}{g}_{i}({\boldsymbol{\theta }})$$
(9)

were

$${g}_{i}\left({\boldsymbol{\theta }}\right)=\left[\begin{array}{c}{{\boldsymbol{z}}}_{{\boldsymbol{i}}{{\boldsymbol{t}}}_{{\bf{0}}}}\left({\Delta Y_{i{t}_{0}}}-{\boldsymbol{\beta }}{{{\Delta}}{\boldsymbol{X}}}_{{\boldsymbol{i}}{t}_{0}}-{\boldsymbol{\delta }}{{{\Delta}}{\boldsymbol{X}}}_{{\boldsymbol{i}}{t}_{0}}{I}_{i{t}_{0}}(\gamma )\right)\\ \vdots \\ {{\boldsymbol{z}}}_{{\boldsymbol{iT}}}\left(\left({\Delta Y_{{iT}}}-{\boldsymbol{\beta }}{{\boldsymbol{\Delta }}{\boldsymbol{X}}}_{{\boldsymbol{i}}T}-{\boldsymbol{\delta }}{{{\Delta }}{\boldsymbol{X}}}_{{\boldsymbol{i}}T}{I}_{{iT}}(\gamma )\right)\right)\end{array}\right]$$
(10)

\({{\boldsymbol{z}}}_{{\boldsymbol{it}}}\) is a set of instrumental variables consisting of lagged items, but excluding threshold variables.Footnote 1 Assume that \({\rm{E}}\left({g}_{i}\left({\boldsymbol{\theta }}\right)\right)=0\), if and only if \({\boldsymbol{\theta }}={{\boldsymbol{\theta }}}_{{\boldsymbol{0}}}\). Then further let \({g}_{i}={g}_{i}\left({{\boldsymbol{\theta }}}_{{\boldsymbol{0}}}\right)=\) \({\left({z}_{i{t}_{0}}^{{\prime} }\varDelta {\varepsilon }_{i{t}_{0}},\ldots ,{z}_{{iT}}^{{\prime} }\varDelta {\varepsilon }_{{iT}}\right)}^{{\prime} }\), and let \(\varOmega ={\rm{E}}\left({g}_{i}{g}_{i}^{{\prime} }\right)\). It can be seen that \(\varOmega\) is a positive-definite matrix. Assume \({W}_{n}\) is a positive definite weight matrix that satisfies \({W_{n}}\mathop{\rightarrow}\limits^{p}{\varOmega }^{-1}\). Let the criterion function \({\bar{J}}_{n}({\boldsymbol{\theta }})={\bar{g}}_{n}({\boldsymbol{\theta }})^{\prime} {W_{n}}{\bar{g}}_{n}({\boldsymbol{\theta }})\), The GMM estimator for unknown parameter \(\hat{{\boldsymbol{\theta }}}\) = \(\left(\hat{{\boldsymbol{\beta }}},\hat{{\boldsymbol{\delta }}},\hat{\gamma }\right)\) is given as follows:

$${\widehat{{\boldsymbol{\theta}}}}=\mathop{\mathrm{argmin}}\limits_{\theta}{\bar{{J}}}_{{n}}({\boldsymbol{\theta }})$$
(11)

The above minimization problem can be solved in two steps. First, let the weight matrix Wn be specified as an identity matrix I or other known form, and minimize \({\bar{J}}_{n}({\boldsymbol{\theta }})\) to collect residuals \({\widehat{\varDelta \varepsilon }}_{{it}}\). In the second step, the weight matrix is updated using the collected residuals \({W_{n}}={\left(\frac{1}{n}{\sum}_{i=1}^{n}{\hat{g}}_{i}{\hat{g}}_{i}^{{\prime} }-\frac{1}{{n}^{2}}\mathop{\sum }\nolimits_{i=1}^{n}{\hat{g}}_{i}{\sum}_{i=1}^{n}{\hat{g}}_{i}^{\prime}\right)}^{-1}\), where \({\hat{g}}_{i}={\left({\widehat{\varDelta \varepsilon}}_{i{t}_{0}}{z}_{i{t}_{0}}^{{\prime} },\ldots ,{\widehat{\varDelta \varepsilon }}_{{iT}}{z}_{{iT}}^{{\prime} }\right)}^{{\prime} }\), and minimize \({\bar{J}}_{n}({\boldsymbol{\theta }})\) again to solve \(\hat{{\boldsymbol{\theta }}}\). It has been proved that the parameters estimated by the above method \(\hat{{\boldsymbol{\theta }}}=(\hat{{\boldsymbol{\beta }}},\hat{{\boldsymbol{\delta }}},\hat{\gamma })\) asymptotically obey the normal distribution, so \(t\)-statistics can be used to test the significance of parameter estimates and construct confidence intervals.

In order to test the significance of the threshold effect to see the rationality of establishing a nonlinear model, the following null hypothesis is proposed \(H0:{\boldsymbol{\delta }}=0\), for any \(\gamma\). The corresponding alternative hypothesis is \(H1:{\boldsymbol{\delta }}\,\ne \,0\), for some \(\gamma\). This null hypothesis means that the threshold effect does not exist and the model is linear. The \(\sup {Wald}\) statistic is used to test the hypothesis. A significant \(\sup {Wald}\) statistic means that the null hypothesis is rejected, that is, the threshold effect is considered to exist. The probability distributions of \(\sup {Wald}\) statistic and the p-value for rejecting the null hypothesis can be obtained by the bootstrap method according to Seo et al. (2019).

Variable definition

Explained variables: EF, CE and ETR

  1. (1)

    Ecological Footprint Consumption (EF) and Carbon Emissions (CE): Ecological Footprint Consumption (EF) can reflect the pressure of human activities on the ecological environment (Li et al., 2023). A country’s EF figure is calculated from the per capita amount of built-up land, carbon, arable land, fishing grounds, forest products, and pasture combined. CE is measured by annual per capita greenhouse gas emissions.

  2. (2)

    Energy transition (ETR): As stressed by Markard (2018), the modern energy transition is characterized by the gradual reduction of fossil fuels and the continuous shift to low-carbon energy such as wind energy and solar energy (Li et al., 2022a). Thus it can be considered that the purpose of energy transition is to replace fossil energy with renewable energy in the final energy consumption structure. Following Tzeremes et al. (2023), we take the share of renewable energy in a country’s total final energy consumption Footnote 2to represent the energy transition result.

Core explanatory variable: artificial intelligence development level (AI)

Artificial intelligence technology has experienced rapid development and multiple updates in the past forty years. With the continuous iteration of technology, the connotation of the concept of AI has also changed. Drawing on He et al. (2019), this paper defines AI as a branch of applied computer science that uses computer algorithms, including machine learning, deep learning, and natural language recognition, to be trained to perform tasks usually associated with human intelligence.

According to this definition, AI includes a variety of technologies, and the application scenarios are also rich. Therefore, how to measure the development level of AI is a major challenge of this paper. Considering that AI devices, such as robots and smart cars, often integrate hardware, software, and programming, and may integrate multiple technologies (Howard 2019). It can be inferred that the more advanced a country’s AI technology is, the more functions and application scenarios AI devices have, and the more they may be used. This insight led us to consider assessing AI development from the perspective of the number of devices. Inspired by the work of Acemoglu and Restrepo (2020), in this paper, we select the well-defined and easy-to-count operational stock of industrial robots as a proxy variable for a country’s AI development level and select per capita stock of industrial robots as an alternative explanatory variable for robustness test.

According to IFR, the global inventory of industrial robots in 2019 was about 2.3 million. The top five countries account for more than 75% of the total, namely China (27.5%), Japan (15.3%), South Korea (12.7%), the United States (11.5%) and Germany (8.4%), suggesting that the above-mentioned countries should have an advantage in AI development. This is supported by many reports assessing the level of AI development. For example, the 2022 Global Artificial Intelligence Innovation Index provided by the Institute of Scientific and Technological Information of China shows that the United States and China are in the first echelon of global AI innovation, while Germany, Japan, and South Korea have also entered the second echelon (ISTIC 2023). Therefore, we believe that the operational stock of industrial robots can well represent AI development.

Threshold variable

  1. (1)

    Industrial structure (IS), measured by the proportion of industrial added value in GDP. Various pieces of research pointed out that there are long-term and stable differences in the relationship between carbon emissions and economic development in different industries and sectors (Dong et al. 2020; Li et al. 2024). We can infer that the development and application of AI in a country will be affected by the existing industrial structure.

  2. (2)

    Trade openness (OPEN): Measured by the proportion of total trade in GDP. Trade openness will promote the international division of labor and the exchange of goods and technologies, which should be conducive to the development of AI. Therefore, AI development conditions in countries with various degrees of openness may be different.

  3. (3)

    Artificial intelligence development (AI): Recent studies have shown that AI technology is changing even faster than Moore’s LawFootnote 3 describes Taddeo et al. (2021). Thus, it is necessary to use the key independent variable AI as a threshold variable to reveal the dynamic change rules of AI’s effect, in other words, the heterogeneous environmental impact at different development levels of AI.

  4. (4)

    Energy transition (ETR): Inspired by Shahbaz et al. (2022) who found that the impact of the digital economy on ETR varies in different quantiles of ETR, we therefore use a threshold model and take ETR as a threshold to explore how the environmental effects of AI change as countries progress in energy transition.

Control variables

Based on the work of Huang et al. (2022) for EF, Li and Wang (2022) for CE, and Shahbaz et al. (2022) for ETR, the following vectors of control variables are constructed and introduced into Model L1-L3 and Model N1-N3 to model EF, CE and ETR. (1) Economic development level (ED), measured by per capita GDP; (2) Energy use (EUSE), measured by per capita energy consumption; (3) Natural resource rent (NRR), measured by the share of total natural resource rent in Footnote 4GDP (4) Fossil fuel power generation (FFE): measured by the proportion of fossil fuels in power generation; (5) Government size (GOV): measured by the ratio of fiscal expenditure to GDP; (6) Urbanization (URB): Measured by the proportion of urban population.

Data description and preliminary test

This study covers 67 countries from 1993 to 2019. The names of countries in the research scope are shown in Appendix Table 1. The data of the variables were sourced from GFN (Network 2019), WDI (WDI 2021), and IFR (IFR 2023). The descriptive statistics and data sources of variables are shown in Table 3, and all variables are logarithmic to alleviate the problem of heteroscedasticity. The covariance matrix and the variance inflation factors of the explanatory variables are shown in Appendix Table 2. It can be found that the largest positive correlation coefficient comes from ED and CE (0.734), and the largest negative correlation coefficient comes from ED and NRR (−0.430). The largest VIF is 3.39 of ED, indicating no obvious multicollinearity in our research case.

Table 3 Descriptive statistics, definitions, and data sources for all variables.
Full size table

The results of cross-section correlation tests for the three benchmark models are reported in Appendix Table A3. The results showed that all three models rejected the null hypothesis of no cross-section correlation at the 5% significance level. This suggests that cross-sectional correlations exist in Model L1-L3. Based on the result, second-generation unit root testing techniques such as CIPS and CADF should be adopted to overcome the issue of cross-sectional correlation (Ansari 2022). Appendix Table A4 shows the test results of CIPS and CADF, and it can be seen that all variables are first-order series stationary. Finally, the cointegration test proposed by Westerlund (2005) was applied to the three benchmark models to avoid spurious regressions. The results of Table A5 in the Appendix show that all three models have significantly rejected the null hypothesis of “No cointegration for all panels” at the 5% level, indicating that there is a long-term stationary relationship between the variable sequences of each model. In conclusion, the above results show that the preliminary tests are passed and the regression result is reliable.

Empirical results

Benchmark result

In order to evaluate the impact of AI on sustainability from the three perspectives of ecological footprint, carbon emissions and energy transition, we estimate Model L1–L3 based on the SYS-GMM method of Eqs. (1–6). The specific results are shown in Table 4. First, we judge the reasonableness of the model based on the results of the Sargan test and the AR test in the last three lines. The p-values of the Sargan test are 0.9945, 0.9943 and 0.9977, which are all greater than 0.1. Therefore, the null hypothesis that there is no over-identification of instrumental variables cannot be rejected, indicating that the Sargan test is passed. The p-values of the AR(2) tests in the three models are also greater than 0.1, indicating that there is no serial correlation. The above test results show that the SYS-GMM model is well set. The first two rows of the table represent the estimated coefficients for the lagged term of the dependent variable. We found that the coefficients of the lagged terms of EF, CE, and ETR are 0.8904, 0.8084, and 0.9245, respectively, which are significant at the 1% level. This means that the changes in ecological footprint, carbon emissions and energy transition have inertia and are largely affected by the previous year, which confirms the rationality of the dynamic model setting.

Table 4 Benchmark regression result of SYS-GMM.
Full size table

As for the result of the key variable, the coefficient of lnAI on lnEF is −0.0018%, which is significant at the 1% level. This means that for the 67 sample countries from 1993 to 2019, every 1% increase in the development level of artificial intelligence corresponds to an average decrease of 0.0018% in ecological footprint. This result suggests that AI contributes to sustainable development by reducing the global ecological footprint. Similar to our point of view, Holzinger et al. (2023) believe that AI technology can improve the sustainability of agriculture, forestry, and animal husbandry, especially for the preservation of biological resources. Compared with other empirical literature, Ahmad et al. (2020) and Huang et al. (2022) found that technological progress and ICT have an ecological footprint reduction effect, respectively. On this basis, our empirical results further expand their conclusions and confirm that AI also has an ecological footprint reduction effect.

According to Model L2, AI also has a significant reduction effect on CE. For every 1% increase in a country’s artificial intelligence development level, the country’s carbon emissions will decrease by 0.0013%. This means that the development of AI can help the country reduce its overall carbon emissions, thereby promoting sustainable development, which is consistent with the empirical findings of Liu et al. (2022b). Note that this influence coefficient is smaller than that of AI on EF (0.0013 < 0.0016). This may be because the positive impact of AI on carbon emissions is partially offset by the negative impact of AI itself such as power consumption (Taddeo et al., 2021).

Model L3 shows that at the 1% significance level, AI shows a promoting effect on energy transition. Every 1% increase in the development level of artificial intelligence will boost the energy transition by 0.0025%. The coefficient is the largest among the three models (0.0025 > 0.0018 > 0.0013), indicating that AI is an important driving force for the global energy transition process, which is of great significance for sustainable development. Some existing empirical literature supports our findings. For example, Lee and He (2021) confirmed that AI can promote wind power technology innovation, and Lyu and Liu (2021) proved that AI is conducive to the development of digital energy technology. In fact, AI and energy transition are already closely integrated and AI methods such as back propagation neural networks (BPNN) have been widely used in the field of renewable energy (Jha et al. 2017).

Combined with the analysis of Model L1-L3 results, we conclude that AI has three positive contributions to sustainability, including ecological footprint reduction effects, carbon reduction effects, and energy transition promotion effects. Therefore, when the sustainable development of countries is hindered after the pandemic, the AI industry can become the focus of countries to accelerate economic development while improving environmental sustainability especially in promoting energy transition.

Heterogeneity analysis

Given that this study involves a large number of countries at different stages of development, it is necessary to conduct a grouped analysis. Based on the World Bank’s 2018 classification of national development levels, we divided the sample into high-income and middle-income groupsFootnote 5. The results of the grouped study are shown in Table 5, where columns 1–3 represent the results for the high-income group and columns 4–6 for the middle-income group.

Table 5 Heterogeneity analysis results according to developmental stage.
Full size table

The results, with the ecological footprint as the dependent variable, indicate that the impact coefficient of AI is −0.0016 in high-income countries and −0.0028 in middle-income countries. Both coefficients are significant at the 1% level. This demonstrates that the effect of AI on reducing the ecological footprint is more pronounced in middle-income countries compared to high-income countries. Similarly, the research results on carbon emissions show that AI also significantly reduces carbon emissions in middle-income countries. These results may be because middle-income countries have more room for improvement in clean production, so the widespread application of AI technology can achieve greater reductions in carbon emissions and other ecological footprints in these countries. This contrasts with high-income countries, which have already optimized their production and resource use efficiency to a higher level, resulting in relatively smaller marginal improvements from AI.

However, the results regarding energy transition indicate that the effect of AI on energy transition is mainly concentrated in high-income countries, with an impact coefficient of 0.0053, while it is not significant in middle-income countries. This may suggest that high-income countries have more advanced infrastructure, higher technical capabilities, and more comprehensive policy support, enabling them to utilize AI technology more effectively to promote energy transition. For instance, high-income countries may have already established smart grids, renewable energy management systems, and advanced energy storage technologies, which provide a solid foundation for the application of AI in energy transition. On the other hand, middle-income countries have relatively less investment and infrastructure development in these areas, resulting in AI having a less significant role in promoting energy transition compared to high-income countries.

In summary, the grouped study results indicate that the reduction effects of AI on ecological footprint and carbon emissions are more significant in middle-income countries, whereas the effects on energy transition are mainly observed in high-income countries. This difference suggests that the developmental stage of a country may influence the environmental effects of AI, highlighting the need for countries to formulate corresponding strategies and policies based on their own developmental realities to maximize the positive effects of AI technology.

Threshold effect tests and sample distributions

Based on the benchmark results, we further use the dynamic threshold model to conduct two-pronged research on the nonlinear laws of the three environmental sustainability effects of AI: (1) Use the external variables IND and OPEN as threshold variables to discuss the impact of external macro factors (2) Taking the explanatory variable AI and the explained variable ETR as threshold variables, the impact of different AI and ETR development stages is discussed. In summary, each nonlinear model in Models N1-N3 includes 4 threshold variables (IND, OPEN, AI, ETR) and a total of 12 sub-models need to be estimated.

Before analyzing the regression results of the nonlinear model, we need to test the threshold effect and the validity of the threshold value. The results are shown in Table 6. The result of Sup Wald test shows that all 12 sub-models reject the null hypothesis of linearity at the 1% level, indicating the existence of a threshold effect. From the result of threshold values, we can see that the threshold values of the other 11 sub-models are all significant, and all fall within the 95% confidence interval except for the sub-model in Model N3 with AI as the threshold variable. It means the threshold values in these models are accurately estimated and the estimation results of these models are reasonable. For the AI sub-model of Model N3, the insignificance of the threshold means that the division of samples may not be optimal. However, considering that the threshold effect does exist, the nonlinear regression results of Model N3 are also worth analyzing.

Table 6 The results of the threshold effect test.
Full size table

The sample was classified into the upper or lower regime based on whether the threshold variable was higher than the threshold value obtained. Using the threshold estimated result of Model N1 as an example, we plot the sample distributions of the four threshold variables from 1993 to 2019 in Fig. 1. First, the proportion of samples below the IND threshold rose from 10% in 1993 to 45% in 2019 indicating that the industrial structure in the sample countries is being gradually optimized. Second, the proportion of samples below the OPEN threshold dropped from 63% to 30% from 1993 to 2007 but rose again to 37% in 2019. This suggests a slowdown in the pace of global openness after 2007 and a resurgence of reverse globalization in recent years. Third, AI has experienced explosive growth during the sample period, with the number of countries with an AI below the threshold of 6.5853 plummeting from 88% to 40%. Finally, the proportion of countries below the threshold energy transition of 3.89% only fell by 12% in 26 years, indicating a possible bottleneck in global renewable energy development.

Fig. 1: The quantile of the threshold values of Model N1 in the sample period.
figure 1

Thresholds are 3.1903 for IND, 3.9291 for OPEN, 6.5853 for AI and 1.3581 for ETR.

Full size image

Regression results of dynamic panel threshold models

According to the estimation method of DPTM shown in Eqs. 7–11, we obtained the parameter estimation results of 12 nonlinear sub-models. The results of the nonlinear regressions with IND, OPEN, AI, and ETR as thresholds are shown sequentially in Tables 6–9. We can see that the estimation result of each sub-model includes two parts, namely “Lower estimation” and “Threshold effect”. The former is the estimated coefficient for the low regime, while the latter represents the difference between the estimated coefficients for the high and low regimes, which can be regarded as the threshold effect when the threshold variable crosses the threshold.

Table 7 DPTM estimated result with IND as threshold variables.
Full size table
Table 8 DPTM estimated result with OPEN as threshold variables.
Full size table
Table 9 DPTM estimated result with AI as threshold variables.
Full size table

Result with IND as a threshold

Table 7 shows the nonlinear regression results when industrial structure is used as the threshold variable and ecological footprint, carbon emissions and energy transition are used as dependent variables. It can be found that the “threshold effect” estimation result includes the lag term of the dependent variable, all independent variables, and constant terms, which is consistent with the DPTM model setting shown in Eq. (7), indicating that the estimated coefficients of all variables may change in the high regime. However, this paper mainly focuses on the results of the key variable AI.

In Model T1, the ecological footprint is the explained variable. The lower regime results show that the impact coefficient of AI on EF is −0.0090, significant at the 1% statistical level. This means 1% AI development reduces ecological footprint by 0.0090% when IND is lower than the threshold. However, the threshold effect estimator is significantly positive at the 1% level, which means that when IND is higher than the threshold, the impact coefficient of AI on EF will increase by 0.0089, from −0.0090 to −0.0001. This shows that in countries with a high proportion of secondary industry, the reducing effect of AI on EF is weakened. In other words, a high proportion of industry is not conducive for AI to reduce its ecological footprint.

The low regime results of Model T2 show that when IND is low, AI significantly reduces carbon emissions with a coefficient of −0.0065. However, the threshold effect estimation results show that when IND is higher, the impact coefficient of AI will significantly increase by 0.0089. Thus the influence coefficient of AI in high areas has changed from negative to positive to 0.0024, exhibiting a U-shaped nexus of AI-CE. This indicates that IND is also not conducive to AI reducing carbon emissions.

Model T3 shows that when IND is low, AI inhibits the energy transition with a coefficient of −0.0209. However, when IND is high, the coefficient increases significantly and reaches 0.0054, which means that the impact of AI on energy transition changes from negative to positive, showing a U-shaped relationship. That is to say, IND promotes the role of AI in energy transition.

In summary, the above results show that IND is not conducive to the ecological footprint reduction and carbon reduction effects of AI, but can promote the energy transition effect of AI. Judging from the magnitude of the threshold effect, IND influences the impact of AI on EF by 0.0089, CE by 0.0089, and ETR by 0.0263. This means IND has a weaker impact on the first two effects of AI, but a stronger impact on the energy transition effect. Regarding such a “double-edged sword effect” brought about by IND, we compared the existing literature and briefly summarized two aspects of possible explanations. First, an important use of AI in industrial countries is to help industrial production, but industrial production activities are not so clean compared to the primary and tertiary industries. Therefore, if AI is used in heavily polluted production scenarios, it is possible that the use of AI in countries with a high proportion of industry corresponds to a higher ecological footprint and carbon emissions, which is supported by Wang et al. (2019); Zhang and Liu (2015). Second, the industrial system can provide infrastructure and technology readiness for energy transition (Heffron et al. 2020) and it is therefore reasonable that IND promotion the effect of AI on energy transition.

Result with OPEN as a threshold

Table 8 includes all results with OPEN as the threshold. First, both the low regime estimator and the threshold effect estimator in Model T4 are not significant, indicating that the relationship between AI and EF under the influence of OPEN is unclear. The results of Model T5 show that when OPEN is below the threshold, 1% AI corresponds to a significant increase in CE of 0.0058%. However, when OPEN is above the threshold, this coefficient drops significantly to −0.0023, showing an inverted U-shaped relationship between AI and CE, meaning that OPEN promotes the role of AI in reducing carbon emissions. The results of Model T6 show that although the lower regime estimator of AI is not significant, the threshold effect estimator is significant. The latter is much larger than the former in magnitude, so we can say that when OPEN levels are high, AI can significantly contribute to the energy transition. From the magnitude of the threshold effect, after trade openness crosses the threshold, every 1% AI growth will reduce an additional 0.0081% carbon emission and an additional 0.0132% energy transition. We conclude that a higher degree of trade openness overall amplifies the carbon emissions reduction effect and energy promotion effect of AI to exert a more positive sustainability effect.

Compared with the research of other scholars, Demena and Afesorgbor (2020) found that openness has a positive effect on reducing carbon emissions, Jacqmin (2018); Urom et al. (2022) discussed and confirmed the significance of openness in promoting energy transition. Based on the above discussion, from the perspective of AI, our results support the pollution halo theory that trade openness enhances the environmental sustainability in host countries, which runs counter to the arguments of the trade protectionists. In this regard, the global trend of trade protectionism and anti-globalization after the 2008 financial crisis is not a wise choose. We, therefore, call for worldwide countries to strengthen international coordination and create an open environment for free trade and knowledge sharing so as to make better use of AI and accelerate the pace of sustainable development.

Result with AI as a threshold

In order to investigate the differences in the sustainability effects of AI in different stages and levels of AI development, we analyze the threshold effect of AI as a threshold variable based on Table 9. The threshold effect estimators in Models T7–T9 show that the three sustainable effects of AI are all significantly affected by the level of AI development. Higher AI will bring an additional 0.1401% reduction in ecological footprint, 0.0804% reduction in carbon emissions, and 0.0423% increase in energy transition progress for every 1% AI growth. Therefore, we conclude that AI has a scale effect. It is worth noting that the threshold effect estimate of AI is significantly higher in magnitude than that of OPEN, which reminds us that we should pay more attention to this scale effect. Specifically, according to Models T7 and T8, the effect of AI on EF and CE is not significant in the lower regime. This insignificant effect will change into a significant reduction effect as the AI level increases. The results of Model T9 show that AI always has a significant promotion effect on energy transition, and this effect is gradually amplified as AI exceeds the threshold.

Similar scale effects are often shown in other scholars’ research on technological factors (Lahouel et al. 2021; Xu and Chen 2021). For example, (Lahouel et al. 2021) non-linear research results show that different ICT levels correspond to different relationships between TFP and carbon emissions. The higher the ICT, the stronger the carbon emission reduction effect of TFP. A possible explanation for this is, that as the application and research of AI technology in a country’s AI industry becomes more and more in-depth, AI-related experience, skills and talents will gradually accumulate. In turn, the cost of using AI will decrease, and the functions will become stronger, so the sustainability effects gradually appear and increase. Considering that AI has experienced explosive growth during the sample period, the continuation of this trend is of great significance for giving full play to the positive effects of AI. Recently, Indonesia, Russia, Saudi Arabia and other countries have launched medium and long-term plans to provide funding for the AI industry and improve AI development goals. Our results emphasize the significance of the uncompromising implementation of these plans for a sustainable future.

Result with ETR as a threshold

According to the threshold effect estimation results in Table 10, only Model T10 and Model T12 provide significant results. This shows that when ETR exceeds the threshold, the effect of AI on ecological footprint and energy transition is significantly affected, but the effect of AI on carbon emissions is not significant. Specifically, the complete results of Model T10 and Model T12 demonstrate the inverted V relationship both between AI and EF and between AI and ETR. That is to say, when ETR is lower, AI increases ecological footprint but promotes energy transition; when ETR is high, AI reduces ecological footprint but inhibits energy transition. The above results show that the impact of energy transition on the sustainability of AI is also two-fold. A higher level of energy transition improves the role of AI in reducing ecological footprint but limits the promotion effect of AI on ETR.

Table 10 DPTM estimated result with ETR as threshold variables.
Full size table

There are mainly two comments on this finding. On the one hand, a higher level of energy transition means a larger proportion of clean energy in a country’s energy structure. Therefore, in countries with high energy transition, it is reasonable that the ecological footprint reduction effect of AI is better. This finding is consistent with some recent studies, which confirmed that energy transition can improve the environmental performance of agriculture (Sharma et al. 2021), ICT (Huang et al. 2022) and digital economy (Li et al. 2021). On the other hand, it is quite surprising that in countries with higher energy transition levels, the effect of AI on ETR would shift from a facilitator to a depressor. This result contradicts the findings of Dong et al. (2022a), who believe that renewable energy development has a self-reinforcing effect, which means that as the energy transition progresses, the development of renewable energy will automatically become faster and faster. However, our results imply a bottleneck effect during the development of the energy transition from the perspective of AI. If renewable energy production cannot keep pace with demand growth, it is possible that the energy consumption requirement of AI may translate into demand for fossil fuels and undermine energy transition outcomes. Therefore, based on our findings, while accelerating the energy transition to improve the environmental effects of AI, countries need to address bottlenecks and structural issues in the energy transition to prevent the potential negative impacts of AI on the energy transition.

Robustness test

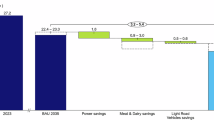
We test the robustness of the baseline regression results in two ways. First, we change the estimation method from system GMM to difference GMM(Diff-GMM). Second, we replace the core explanatory variable from the stock of industrial robots (AI) with the stock of industrial robots per capita (ai). The results are shown in Table 8 and key results are summarized in Fig. 2 accordingly. Figure 2 clearly shows that after changing the estimation method and replacing the core variables, the direction and relative size of AI’s influence coefficients on EF, CE, and ETR have not changed. In other words, AI reduces EF and CE and increases ETR; and AI has the largest impact coefficient on ETR, followed by EF, and finally CE. In addition, the Sargan test and AR (2) of the six robustness test models in Table 11 are both significantly greater than 0.1, indicating that the dynamic model used in the robustness test is effective. In summary, the linear research results are fully credible.

Fig. 2: Robustness check of linear results with the bar representing the coefficient of AI.
figure 2

According to Table 10, all coefficients are significant at the 1% level.

Full size image
Table 11 Robustness tests for baseline regression.
Full size table

Then we adopted the method of replacing the core explanatory variable with ai to improve the robustness of the nonlinear regression results (Model T1–T12), and the results are shown in Table 12. For all models, the Sup Wald p-value is less than 0.1, indicating that the non-linear relationship persists after replacing explanatory variables. Except for Model RT9, the estimates of other thresholds are all significant at the 5% level, and these results are in full agreement with the original model.

Table 12 Robustness tests for threshold model regression result.
Full size table

Subsequently, we are mainly concerned with the threshold effect estimation results of the core variable AI, which represents the impact of the threshold variable on the sustainability effect of AI after crossing the threshold. The comparison between the original results and the robustness check results is visualized in Fig. 3. First, IND is beneficial to ai to reduce EF and CE, and is not conducive to ai to increase ETR. Second, OPEN has no significant impact on the relationship between ai and EF, but it promotes the reduction effect of ai on CE and the improvement effect of ai on ETR. Third, when ai is at a high level, the reduction effect of ai on EF and CE is amplified, indicating that ai has a scale effect. Finally, a higher energy transition process can significantly help ai decrease EF and CE; however, it inhibited the promoting effect of ai on ETR. In conclusion, the results did not change significantly after replacing the core explanatory variables, suggesting the robustness of the non-linear results.

Fig. 3: Robustness test results of nonlinear models.
figure 3

Note: The bars represent the threshold effect estimator of AI under the influence of the corresponding threshold variable (IND, OPEN, AI or ETR). Results that are not significant at the 5% level are represented by 0. The original result coefficients collected from Tables 6–9, and the robustness coefficients collected from Table 11.

Full size image

Conclusions and policy implications

Conclusions

This article aims to comprehensively evaluate the linear and nonlinear impact of AI on environmental sustainability. First, this article uses panel data from 67 countries from 1993 to 2019 to construct a series of SYS-GMM models as benchmark models to evaluate the impact of AI on ecological footprint, carbon emissions and energy transition. On this basis, this paper further builds a series of DPTM models to explore how external variables, including industrial structure and trade openness, affect AI sustainability. Finally, we used the DPTM model to reveal the changing laws of AI’s environmental effects during the development process of AI and energy transition and obtained a series of robust research results. The fingdings are as follows.

From the real-world and multiple environmental impacts of AI, benchmark results show that AI contributes to environmental sustainability by reducing ecological footprints and carbon emissions, and promoting energy transition. Every 1% increase in the level of AI development corresponds to a 0.0025% increase in energy transition, a 0.0018% decrease in ecological footprint, and a 0.0013% decrease in carbon emissions. In other words, AI has the strongest effect in promoting energy transition, followed by the reduction effect on ecological footprint, and then the impact of AI on carbon emissions.

From the perspective of external conditions affecting AI, on the one hand, the nonlinear results of IND as a threshold variable indicate that the industrial share is a double-edged sword. More specifically, countries with a higher proportion of industries have a significantly stronger effect on AI’s promotion of energy transition, but the ecological footprint and carbon emissions corresponding to AI have also increased to a certain extent. In detail, for countries with a higher industrial share, every 1% AI growth corresponds to an additional 0.0263% energy transition, 0.0089% ecological footprint, and 0.0089% carbon emissions. On the other hand, the nonlinear results of OPEN as a threshold variable indicate that trade openness can overall promote the sustainability effect of AI. Specifically, when it is higher than the threshold of trade openness, for a 1% AI growth, carbon emissions are reduced by an additional 0.0081%, the energy transition effect is increased by an additional 0.0132%, and the ecological footprint does not change significantly.

From the nonlinear laws of AI’s effect as AI and energy transition process, there is a significant scale effect in the development process of AI. This effect is much stronger than the amplification effect brought about by trade openness. At a higher stage of AI development, every 1% of AI development will bring an additional 0.1401% ecological footprint reduction effect, 0.0804% carbon emission reduction effect, and 0.0423% energy transition promotion effect. However, there may be bottlenecks in the promotion effect of AI on energy transition. When the level of energy transition is high, the effect of AI on reducing the ecological footprint is increased but the promoting effect of AI on energy transition is suppressed. Specifically, as the energy transition process increases and exceeds the threshold, the ecological footprint corresponding to a 1% AI increase decreases by an additional 0.0319%, and the energy transition process also decreases by an additional 0.019%.

Policy implications

The findings discussed herein have significant policy implications:

  1. (1)

    Overall, the impact of AI on reducing ecological footprint, and carbon emissions and promoting energy transition shows that AI can help improve environmental sustainability. Countries should increase investment in AI R&D, propose AI development strategies and establish long-term development mechanisms. At the same time, policies should standardize the mode of the AI industry and guide AI to contribute to environmental protection actions or energy transition. At present, more than 30 countries have formulated AI development goals and action plans, aiming to encourage, fund and guide the investment and application of AI, such as China’s “The Next Generation Artificial Intelligence Development Plan” and the European Union’s “Artificial Intelligence Coordination Program”. The implementation of these goals is of great significance for promoting the development of the AI industry and moving toward sustainable development.

  2. (2)

    Countries with high industrial proportions should make full use of the advantages of their own industrial systems to develop renewable energy with the help of AI. At the same time, industrial countries cannot ignore the pollution problem in the industrial sector and should introduce policies as soon as possible to regulate the application scenarios of AI in industrial production to prevent AI from being used to accelerate pollution.

  3. (3)

    Trade openness plays an important role in exerting the positive effects of AI. The trends of anti-globalization and “trade protection” that have emerged in recent years are not conducive to the sustainable development of all countries. We call for strengthening international coordination and creating an open environment for free trade and knowledge sharing.

  4. (4)

    AI itself has scale effects, so setting binding long-term goals for AI development is of great significance to all countries, especially those countries that are lagging behind in AI. Recently, Indonesia proposed the Stranas KA plan to continue to provide funding for the AI industry and guide the country’s development of artificial intelligence from 2020 to 2045. Russia, Portugal, Saudi Arabia and other countries have also launched medium- and long-term plans to improve AI development goals. Our research supports these mid- to long-term strategies.

  5. (5)

    A higher level of energy transition can help AI better reduce its environmental footprint. However, governments need to focus on the structural problems and bottlenecks of energy transition such as rising marginal costs and difficulty in technological breakthroughs. For example, currently dozens of countries, including China, the United States, and Japan, have increased their renewable energy production targets in recent years, and have increased subsidies for renewable energy sources with high costs but huge potential, such as offshore wind power, to reduce their marginal costs and ensure supply.

Outlook and limitations

Although this study evaluated for the first time AI has linear and non-linear effects on EF, CE, and ETR, there are still some deficiencies. First, although this paper models the multiple impacts of AI, there are still some factors to be evaluated, such as the impact of AI on different types of energy or other pollutants. Future research can consider the impact of AI on sulfur dioxide, industrial wastewater, etc. Secondly, our research is based on the national level, and it is difficult to reveal specific rules at the sub-national level. In the future, this research can be expanded to a more granular level, such as the provincial or city level.