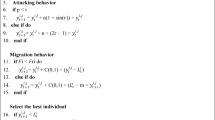Adaptive memory-based opposition and midpoint mutation in black winged kite algorithm for global optimization and engineering applications

Abstract

Metaheuristic algorithms play a vital role in addressing complex and nonlinear optimization problems. This study proposes an enhanced variant of the Black-winged Kite Algorithm (BKA), termed Adaptive Memory-based Opposition and Midpoint Mutation in BKA (AMOMM-BKA), developed to improve population diversity and convergence accuracy, particularly for complex optimization problems. The proposed framework integrates four complementary strategies to balance exploration and exploitation effectively. Blended Opposition-Based Learning (BOBL) combines classical opposition with population-mean guidance to adaptively expand the search space, while historical reflective opposition exploits individual memory to guide the search toward promising regions. Random opposition introduces controlled randomness to preserve population diversity and prevent premature convergence, and midpoint-based mutation directs individuals toward the midpoint between elite and peer solutions, enhancing focused exploration and convergence precision. AMOMM-BKA was evaluated using three CEC benchmark suites (CEC2005, CEC2019, and CEC2022), and its performance was compared with four categories of existing optimization algorithms:(i) widely cited classical optimizers, such as PSO and GWO; (ii) recently developed algorithms, including GJO, SO, SCSO, and AVOA; (iii) high-performance optimizers, such as CMAES and SHADE; and (iv) improved variants of BKA, including CBKA, IBKA, and QOBLBKA. Moreover, its successful application to four mechanical and structural engineering design problems further validates the algorithm’s effectiveness and practical relevance. The statistical analysis, including the Friedman rank test and Wilcoxon test, were conducted on the experimental results to verify the robustness and significance of the findings. AMOMM-BKA consistently demonstrated superior performance, achieving the top rank with an average score of 1.78 approximately 56.18% better than the second-best algorithm, SHADE (average rank: 4.56) highlighting its remarkable convergence rate, solution accuracy, and robustness across diverse optimization.

Introduction

Optimization problems are fundamental to advancing human well-being, as many real-world challenges can be modeled as optimization tasks aimed at identifying the most effective solutions¹. As science, technology, and industry continue to evolve, the scale and intricacy of optimization problems have grown substantially. These problems often encompass multiple variables, nonlinear relationships, and a mix of constrained and unconstrained objectives, resulting in vast and highly complex solution landscapes. Addressing such challenges requires sophisticated algorithms capable of navigating these spaces efficiently². To address such complexity, optimization algorithms have been developed to identify optimal of near-optimal solutions. These algorithms are broadly categorized into deterministic and stochastic approaches. Deterministic methods such as the simplex algorithm, Newton’s method, the conjugate gradient method, and Lagrangian techniques typically require prior knowledge of the problem domain and rely heavily on gradient information. While they perform well on smooth, convex functions, their gradient dependent iterative mechanisms often struggle with non-convex, non-differentiable, or constraint-sensitive problems, leading to local convergence or computational failure. Consequently, deterministic algorithms may fall short when applied to nonlinear or large-scale optimization tasks³. In response, stochastic algorithms have emerged as powerful alternatives. Free from the constraints of gradient dependency, these algorithms offer greater flexibility and resilience when tackling complex, nonlinear, and large-scale problems. Among them, Metaheuristic algorithms (MH) stand out for their global search capabilities, adaptability, and domain independent design⁴. Metaheuristics have demonstrated exceptional performance across a wide spectrum of applications, including engineering optimization⁵, image analysis⁶, mechanical design⁷, feature selection⁸, wireless sensor⁹, and UAV path planning¹⁰. Their growing success underscores the importance of continued research into advanced metaheuristic strategies, particularly as problem complexity and dimensionality continue to rise in modern scientific and industrial contexts.

MH has garnered substantial attention in recent years, especially within the realms of engineering optimization, due to the emergence of high-dimensional data generated from diverse sources such as digital platforms, and large-scale information systems. These algorithms are effective because they can avoid getting stuck in local optima by using simple strategies inspired by natural processes. As a result, they are widely used in many fields and offer flexible solutions to different types of problems. Currently, MH has demonstrated successful applications across a wide range of domains, including biomedical engineering, machine vision, intelligent manufacturing, and power system optimization. Their appeal lies in their structural simplicity and the foundational inspiration drawn from intuitive, nature inspired principles, which enable them to adapt effectively to diverse and complex problem environments.

MH can be broadly classified into four principal categories: Evolutionary-based algorithms (EAs), Swarm-based algorithms (SAs), Physics-based algorithms (PAs), and Human behavior-based algorithms (HAs) as shown in Fig. 1. EAs are represent the earliest class of metaheuristic techniques, drawing inspiration from biological principles such as natural selection, genetic inheritance, and evolutionary adaptation mechanisms. For instance, the Genetic Algorithm (GA)¹¹ emulate natural selection through operations like mutation and crossover to solve complex, nonlinear problems. Differential Evolution (DE)¹² enhances solutions via population-based strategies and is effective for continuous and multimodal optimization. Success-History based Adaptive Differential Evolution (SHADE)¹³ improves DE by adaptively tuning parameters based on historical success, while LSHADE¹⁴ further refines this approach by reducing population size over time, balancing exploration and exploitation for superior optimization performance. Covariance Matrix Adaption Evolution Strategy (CMAES)¹⁵ is a powerful evolutionary algorithm that adapts the covariance matrix of the search distribution, enabling efficient convergence with fewer generations. Its design reduces time complexity while enhancing robustness against noise, improving global search, and supporting parallel implementations. Conversely, SAs are among the most rapidly evolving branches of metaheuristics, rooted in the collective behaviors observed in biological populations including animals, plants, and microorganisms. Several foundational SAs have made significant contributions to the advancement of optimization methodologies. Over the past few decades, this class of algorithms has witnessed substantial diversification and advancement. Particle Swarm Optimization (PSO)¹⁶ exemplifies this paradigm by emulating the synchronized foraging dynamics of bird flocks and fish schools. The Artificial Bee Colony (ABC)¹⁷ algorithm replicates the decentralized decision-making and resource allocation strategies of honeybee swarms. Grey Wolf Optimization (GWO)¹⁸ draws inspiration from the hierarchical hunting tactics and social leadership exhibited by grey wolves. More recently, Golden Jackal Optimization (GJO)¹⁹ has emerged, modeling the cooperative predation and adaptive behavior of golden jackals in their natural habitat. Additional noteworthy swarm-based algorithms encompass the Snake Optimizer (SO)²⁰, Sand Cat Swarm Optimization (SCSO)²¹, African Vultures Optimization Algorithm (AVOA)²², Harris Hawks Optimizer (HHO)²³, Honey Badger Algorithm (HBA)²⁴, Artificial Rabbits Optimization (ARO)²⁵, Dung Beetle Optimizer (DBO)²⁶, Electric Eel Foraging Optimization (EEFO)²⁷, Greylag Goose Optimization (GGO)²⁸. Thirdly, PAs constitute a major category within metaheuristics, inspired by the dynamics and principles of physical systems. These algorithms are modeled on diverse physical laws and phenomena encompassing mechanics, thermodynamics, electromagnetism, optics, and atomic interactions. The Gravitational Search Algorithm (GSA)²⁹ emulates Newtonian mechanics, specifically the laws of motion and universal gravitation, to guide the optimization process through mass interactions. The Muti-verse Optimizer (MVO)³⁰ derives its conceptual framework from cosmological phenomena, notably the dynamics of white holes, black holes, and wormholes, to facilitate solution exchange across multiple universes. The gradient-Based Optimizer (GBO)³¹, influenced by Newton’s gradient descent methodology, integrates two principal mechanisms namely, the gradient search rule and the local escaping operator alongside a vector-based strategy to effectively navigate the solution space. Additional prominent PAs including the Energy Valley Optimizer (EVO)³², Arithmetic Optimizer Algorithm (AOA)³³, Kepler Optimization Algorithm (KOA)³⁴, and Special Relativity Search (SRS)³⁵. Finally, HAs, as a burgeoning class of metaheuristic techniques, are garnering significant scholarly interest due to their foundation in sociocognitive dynamics and behavioral patterns. These algorithms emulate various aspects of human interaction and decision-making. For instance, the Teaching Learning based Optimization (TLBO)³⁶ algorithm models pedagogical exchanges between instructors and learners to enhance solution refinement. Similarly, the Poor and Rich Optimization (PRO)³⁷ algorithm reflects socioeconomic motivation, simulating the aspirational drive of individuals across financial strata to elevate their status. Additional noteworthy HAs include the Political Optimizer (PO)³⁸, Student Psychology-Based Optimization (SPBO)³⁹, Sewing Training-Based Optimization (STBO)⁴⁰, Human Evolutionary Optimization Algorithm (HEOA)⁴¹.

The Black-winged Kite Algorithm (BKA)⁴² is a swarm-based optimization method inspired by the flight behavior of black-winged kites. It offers simple structure, fast convergence, and strong performance across benchmark functions. BKA has been successfully applied to multiple applications for feature selection and parameter optimization, demonstrating efficient and reliable results compared with related algorithms. Nevertheless, there remains scope for further improvement to enhance its overall optimization capability. However, the BKA operates through two main phases: attacking and migration. According to the No-Free-Lunch (NFL)⁴³ theorem, no single algorithm performs optimally across all optimization problems. Therefore, there is a continuous need to develop improved or modified algorithms to address complex optimization challenges. In certain cases, BKA exhibits slow convergence and may become trapped in local optima, particularly in high-dimensional or complex search spaces. To overcome these limitations and enhance its convergence performance, the AMOMM-BKA variant was proposed. Recent studies have focused on enhancing the BKA to overcome its inherent limitations. Some researchers have developed hybrid variants that combine BKA with other optimization algorithms to strengthen its exploitation ability and resistance to local optima, while others have proposed adaptive versions that dynamically adjust parameters to improve overall performance. In this study, we introduce four strategies that build on these ideas and offer new improvements. First, Blended Opposition-Based Learning (BOBL) combines classical opposition with the population mean to balance exploration and exploitation, helping the algorithm escape local optima and converge faster a limitation in earlier opposition-based methods. Second, Historical Reflective Opposition uses each individual’s best past solution to guide the search toward promising areas, strengthening learning in successful directions and complementing adaptive parameter strategies. Third, Random Opposition introduces controlled randomness to maintain diversity and prevent premature convergence, addressing the narrow search focus in some hybrid methods. Finally, Midpoint-Based Mutation directs individuals toward promising regions based on elite and peer knowledge, improving solution refinement and stability. Together, these strategies extend previous enhancements by providing a more balanced, diverse, and guided search, leading to better convergence and higher-quality solutions.

Fig. 1

Classification of Meta-heuristic algorithms (MH).

Related work

The Black-winged Kite Algorithm (BKA) is a recently proposed nature-inspired optimization method with promising results in solving diverse engineering problems. This section reviews the various BKA variants reported in the literature. Hanaa Mansouri et al⁴⁴. proposed the Modified Black-Winged Kite Optimizer (M-BWKO) to enhance convergence speed, robustness, and solution diversity of the original BWKO. The algorithm integrates six key strategies, including a top-k leader selection, adaptive chaos weighting, diversity-aware reactivation, chaotic index-based selection, adaptive Cauchy mutation, and a hybrid migration rule combining chaotic and directional updates. These mechanisms collectively balance exploration and exploitation while preventing stagnation. Sarada Mohapatra et al⁴⁵. introduced the Revamped Black-Winged Kite Algorithm (RBKA), which integrates logistic chaos-based initialization to enhance diversity and convergence speed. It employs chaotic perturbation and Brownian motion-based migration to balance exploration and exploitation, along with an opposition learning strategy to escape local optima and improve global search efficiency. Taybe Alabed et al⁴⁶. proposed the Chaotic Black-Winged Kite Algorithm (CBKA), which integrates logistic chaos mapping to enhance population diversity and prevent premature convergence. Junwen Liao et al⁴⁷. proposed the Hybrid Multi-Strategy Black-Winged Kite Algorithm (HBKA), which integrates Tent mapping in the predation stage to expand the search space, enhance global exploration, accelerate convergence, and help the algorithm escape local optima. Yancang Li et al⁴⁸. developed the Black-Winged Kite Algorithm by combining the Osprey Optimization Algorithm with Crossbar enhancement (DKCBKA) . It incorporates an adaptive index factor and probability distribution update to speed up convergence, a stochastic difference variant to prevent local trapping, and longitudinal–transversal crossover to enhance accuracy and maintain population diversity. Fu et al⁴⁹. introduced the Improved BKA (IBKA) by replacing the attack phase parameter with the Gompertz growth model, thereby achieving a more balanced exploration-exploitation trade-off and reducing step decay. Zhao et al⁵⁰. proposed a variant incorporating chaotic mapping and adversarial learning, which significantly boosted convergence speed and optimization accuracy. BKA has been successfully applied across divers optimal domains (⁵²-⁵³) and has undergone multiple refinements by researchers (⁵⁴-⁵⁵). Nonetheless, existing improvements do not fully resolve its inherent limitations, motivating the pursuit of a more comprehensive and efficient enhancement framework. This paper encapsulates its principal contributions and methodological novelties through the following highlights:

• Performance-based strategy selection: Each individual’s fitness change between iterations is used to compute a confidence score. Based on this score, the algorithm categorizes individuals as stagnated, improving, or uncertain.

• Blended opposition-based learning (BOBL): Applied to stagnated individuals showing negligible improvement. BOBL balances classical opposition with the population mean, enabling guided exploration.

• Historical reflective opposition (HRO): Used for significantly improving individuals. It reflects the current solution across the individual’s historical best, encouraging intensified exploitation in promising regions.

• Random opposition (RO): Applied to individuals with unclear progress. This maintains population diversity by generating stochastic opposite candidates.

• Memory integration: Each agent maintains its personal best (historical memory), updated upon improvement. This memory guides the reflective strategy and prevents over-reliance on the global best.

• Midpoint-based mutation (MM) strategy: After the attacking behavior, each solution is mutated toward the midpoint between the global best and a random peer, enhancing diversity while maintaining guided exploration.

• Extensive benchmarking: The AMOMM-BKA algorithm was rigorously evaluated across diverse benchmark suites, including CEC2005, CEC2019, and CEC2022. Comparative analysis against eleven cutting-edge algorithms, supported by statistical evidence, underscores its superior performance.

• Practical applicability: AMOMM-BKA was applied to four engineering optimization tasks, where comparative results and statistical analyses against other algorithms confirm its strong competitive advantage in real-world problem solving.

The structure of this paper is as follows: Section Black-winged Kite Algorithm (BKA) comprises a background on the Black-winged Kite Algorithm (BKA). Section Proposed framework introduces the proposed model and its components. Section  Experimental results and comprehensive analysis covers the implementation of numerical experiments and the detailed evaluation of the obtained results. Section Results and discussion of engineering applications presents the application of the proposed AMOMM-BKA to practical engineering problems. Section Conclusion and future work includes the concluding remarks and possible directions for future research

Black-winged Kite Algorithm (BKA)

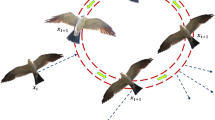
The Black-winged Kite Algorithm (BKA), introduced by Wang et al.⁴² in 2024, is a population-based optimization technique inspired by the hunting and migratory behavior of the black-winged kite, a small bird of prey known for its agility and precision. This species, identified by its blue-gray upper body and white underparts, typically preys on small animals such as birds, reptiles, mice, and beetles. Its remarkable hovering ability and sharp hunting skills serve as the core inspiration for BKA. The algorithm operates through two main phases attacking behavior, which models the bird’s hunting strategy, and migration behavior, which reflects its movement across regions. These two stages together form the basis of BKA’s search and optimization mechanism.

Mathematical model

This section presents the formulation of the BKA, a conceptually simple yet highly effective metaheuristic optimization approach inspired by the predatory and migratory behaviors of the black-winged kite.

Initialization phase

The BKA is a population-based metaheuristic framework in which each black-winged kite represents an individual agent. The position of each agent within the search space corresponds to a candidate solution for the optimization problem. Initially, these positions are generated randomly, as defined by Eq. 1

$$\begin{aligned} Z_i=lb+rand(ub-lb) \end{aligned}$$

(1)

Where $Z_i$ represents the $i^{th}$ individual, lb and ub represent the lower and upper limits for the $i^{th}$ black-winged kite in the $j^{th}$ dim, and rand is a randomly selected value between 0 and 1.

Attacking phase

Black-winged kites exhibit exceptional hunting proficiency, particularly in capturing small grassland animals and insects. During flight, they dynamically adjust their wing and tail angles in response to wind velocity, enabling them to hover silently while observing potential prey. Upon detection, they execute swift dives to secure their target. This adaptive hunting strategy reflects diverse attack patterns, which serve as a metaphor for global search and exploration within the optimization process. Figure 2 illustrates the kite’s calculated hunting sequence, reflecting the exploitation phase in optimization where precision is crucial. Figure 3 highlights its tactical prey assessment, mirroring the exploration phase of algorithms seeking promising solution areas. The following expression models the kite’s tactical attack behavior:

$$\begin{aligned} & z_{t+1}^{i,j}={\left\{ \begin{array}{ll} z_t^{i,j}+k(1+\sin (r))\times z_t^{i,j} & p<r\\ z_t^{i,j}+k(2r-1)\times z_t^{i,j} & else \end{array}\right. } \end{aligned}$$

(2)

$$\begin{aligned} & k=0.05\times e^{-2 \times (\frac{t}{T})^2} \end{aligned}$$

(3)

Here, $z_t^{i,j}$ and $z_{t+1}^{i,j}$ denote the position of the $i^{th}$ black-winged kite in the $j^{th}$ dimension during the $t^{th}$ and $(t+1)^{th}$ iteration, respectively. r is randomly generated value between 0 and 1, while p is a fixed constant set at 0.9. And T represents the total number of iteration, while t indicates the number of iterations completed up to the current point.

Migration phase

Bird migration is influenced by food availability and climate changes. To survive seasonal shifts, many birds move from north to south seeking better habitats. Leaders with strong navigation skills guide the group, helping maintain unity and success. Figure 4 shows how black-winged kites shift leadership during migration. The following formulation mathematically models the migration behavior exhibited by these birds:

$$\begin{aligned} & z_{t+1}^{i,j}={\left\{ \begin{array}{ll} z_t^{i,j}+C(0,1)\times (z_t^{i,j}-H_t^j) & f_i < f_{ri}\\ z_t^{i,j}+C(0,1)\times (H_t^j-l \times z_t^{i,j})& else \end{array}\right. } \end{aligned}$$

(4)

$$\begin{aligned} & l=2 \times \sin (r+\pi /2) \end{aligned}$$

(5)

Here, $H_t^j$ signifies the highest scorer among the black-winged kite’s in the $j^{th}$ dimension at the $t^{th}$ iteration, $z_t^{i,j}$ and $z_{t+1}^{i,j}$ denote the position of the $i^{th}$ black-winged kite in the $j^{th}$ dimension during the $t^{th}$ and $(t+1)^{th}$ iteration, respectively. Then $f_i$ refers to the fitness of a black-winged kite in the $j^{th}$ dimension at the $t^{th}$ iteration, while $f_{ri}$ represents the fitness value of a random position in the same dimension from any black-winged kite at the $t^{th}$ iteration. And C(0, 1) denotes the Cauchy mutation as outlined by Jiang et al.⁵⁶. Its definition is given below:

A one-dimensional Cauchy distribution is a continuous probability distribution characterized by two parameters. The equation below describes its probability density function:

$$\begin{aligned} f(y,\delta ,\mu )=\frac{1}{\pi } \frac{\delta }{\delta ^2+(y-\mu )^2},\qquad -\infty<y<\infty \end{aligned}$$

(6)

When $\delta =1$ and $\mu =0$, the probability density function assumes its standard form. The specific formula is as follows:

$$\begin{aligned} f(y,\delta ,\mu )=\frac{1}{\pi } \frac{1}{y^2+1}, \qquad -\infty<y<\infty \end{aligned}$$

(7)

Fig. 2

Sequential hunting behavior of the black-winged kite.

Fig. 3

The selective predation strategy embedded in black-winged kite.

Fig. 4

Dynamic reallocation of leadership roles in black-winged kite migration.

Proposed framework

As discussed in the earlier section, the BKA is a promising metaheuristic technique for solving a wide range of optimization problems due to its simplicity and flexibility. However, BKA still encounters certain limitations, particularly a tendency to converge prematurely to local optima. This drawback arises mainly from an imbalance between exploration and exploitation phases, limited diversity in the initial population, and insufficient use of historical or population-level knowledge during the search process. To overcome these challenges, this study introduces an enhanced variant named Adaptive Memory-based Opposition and Midpoint Mutation in Black-winged Kite Algorithm (AMOMM-BKA), which integrates four key strategies. First, a Blended Opposition-Based Learning (BOBL) approach balances exploration and exploitation by blending classical opposition with population mean, helping individuals escape local traps. Second, a historical reflective opposition strategy leverages each individual’s past best solution to intensify the search in successful directions. Third, random opposition introduces controlled stochasticity to handle uncertain cases and maintain diversity. Finally, a midpoint-based mutation is applied to guide individuals toward promising regions defined by both elite and peer knowledge. The combination of these strategies enables AMOMM-BKA to dynamically adapt its behavior based on individual performance, resulting in more robust and effective optimization. The details of each proposed strategy are explained in the following subsections.

Adaptive memory-based opposition (AMO)

The proposed Adaptive Memory-based Opposition (AMO) introduces an intelligent mechanism for generating and selecting opposition-based solutions in population-based optimization. Unlike static opposition strategies, AMO dynamically adjusts its behavior based on the performance of each solution throughout the search process. This section details the key components of AMO, the motivation behind their selection, and how they collectively address the limitations of existing OBL techniques.

Several variants of opposition-based learning (OBL) such as classical OBL⁵⁷, quasi OBL⁵⁸, random OBL⁵⁹, and their improved extensions have been explored in the literature. While these methods contribute to enhancing exploration in the early stages of optimization, they suffer from three major limitations:

• Lack of adaptiveness: Most techniques apply the same opposition logic to all individuals, regardless of their search behavior.

• Absence of learning memory: They do not consider historical success, thus losing valuable knowledge from previous high-quality solutions.

• Inflexible exploitation: Static opposition formulas can lead to over-exploration or premature convergence due to lack of feedback control.

To overcome these challenges, AMO incorporates a confidence-based switching mechanism that evaluates everyone’s improvement trend and applies a suitable opposition strategy accordingly.

Blended opposition-based learning (BOBL) for stagnated individuals

The Blended Opposition-Based Learning (BOBL) strategy is developed to enhance population diversity and prevent premature convergence. During the optimization process, stagnated individuals those exhibiting negligible improvement in fitness across successive iterations may become trapped in local optima. To effectively guide these individuals without compromising the overall stability of the population, BOBL integrates classical opposition with the population mean to generate new candidate solutions, thereby achieving a balanced trade-off between exploration and exploitation.

$$\begin{aligned} {z^{BOBL}_i}=r\left( lb_i+ub_i-z_i\right) +(1-r).\bar{z} \end{aligned}$$

(8)

Where $\bar{z}$ is the mean position of the population, $r \in [0,1]$ is a randomly chosen weight, $lb_i$ and $ub_i$ stands for the limit boundaries of the $i^{th}$ variable, $z_i$ is the current position of the $i^{th}$ variable of the individual z, and $z^{BOBL}_i$ is the new BOBL generated solution for the $i^{th}$ variable of individual z. This creates a balance between exploration and exploitation, providing a controlled push for individuals likely stuck in local traps.

Historical reflective opposition for improving individuals

The Historical Reflective Opposition (HRO) strategy is designed to enhance the progress of individuals exhibiting notable improvement during the search process. Such individuals are considered to follow promising search trajectories. In this approach, each individual utilizes its previously stored best solution as a reference to generate a new candidate, reinforcing successful exploration patterns and accelerating convergence. The new candidate is formulated as:

$$\begin{aligned} {z^{HR}_i}=z_{BH} + \beta (z_{BH}-z_i) \end{aligned}$$

(9)

Where $z_{BH}$ represents the best solution ever found by a specific individual, $z^{HR}_i$ is the new solution generated by historical reflective opposition for the $i^{th}$ variable of individual z, and $\beta \in [0.5,1.5]$ adjusts the reflection depth. This strategy intensifies the search in a successful direction and helps accelerate convergence in regions likely to contain the global optimum.

Random opposition for uncertain individuals

The Random Opposition (RO) strategy is introduced to handle individuals whose performance trends are uncertain, making it difficult to determine whether exploration or exploitation should be emphasized. To preserve population diversity and prevent premature convergence, AMO employs the RO mechanism, which generates new candidate solutions through random opposition as follows:

$$\begin{aligned} {z^{RO}_i}=lb_i+ub_i-r(z_i) \end{aligned}$$

(10)

where $z^{RO}_i$ denotes newly generated random opposition solution of $i^{th}$ variable of individual z, and r stands for uniform random number between 0 and 1. This introduces stochastic variation into the search space, allowing uncertain individuals to escape shallow basins and potentially discover better regions.

Mathematically, the AMO framework works as follows. For each solution $z_i$, the confidence score is computed as:

$$\begin{aligned} C_i=\frac{f(z_i^{t-1}-f(z_i))}{max(|f(z_i^{t-1})|,\epsilon )} \end{aligned}$$

(11)

Where, $z_i^{t-1}$ is the position of the same individual in the previous iteration, and $\epsilon$ is a small constant to avoid division by zero. This score reflects the quality of improvement, allowing the algorithm to adapt its opposition behavior. Based on the value of $C_i$, the algorithm selects one of the following strategies:

• If $C_i < t_1$, the BOBL strategy is applied

• If $C_i > t_2$, the algorithm generates a historical reflective opposition

• Otherwise, a random opposition is used

In this context, $t_1$ and $t_2$ are assigned the values 0.01 and 0.1, respectively.

Midpoint-based mutation strategy

In this section, we introduce the midpoint-based mutation mechanism. This strategy applies a randomized guidance mechanism that steers the current solution toward the midpoint between the global best and a randomly selected peer from the population. It helps maintain a balance between exploration and a soft focus on promising regions of the search space. For each individual $z_i$, a random peer $z^r$ is selected such that $z_i \ne z^r$, and $z^L$ be the global best (leader) solution. The midpoint between the best and random peer is computed as:

$$\begin{aligned} z^M=\frac{z^L+z^r}{2} \end{aligned}$$

(12)

A mutated solution is then generated by moving the current solution $z_i$ toward this midpoint using a scaling factor $r \in [0,1]$

$$\begin{aligned} z^{mut}_i=z_i+r(z^M-z_i) \end{aligned}$$

(13)

Here, r is a uniformly generated random number, controlling how far the mutated solution shifts toward the midpoint. This operator encourages the current solution to be influenced by both elite knowledge (via $z^L$ ) and the population diversity (via $z^r$), while maintaining the stochastic.

AMOMM-BKA algorithm frame work

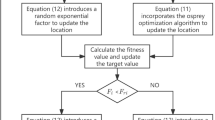
This study proposes an enhanced BKA by integrating four key mechanisms: BOBL, historical reflective opposition, random opposition, midpoint-based mutation strategy. The aim is to strengthen the algorithm’s ability to maintain diversity, escape local optima, and improve convergence behavior. The optimization process begins with a population initialization phase, where AMOMM-BKA generates refined opposite solutions using a blended approach that combines classical opposition and the population mean. Each individual also maintains a personal memory to store its historically best position, which supports learning during later stages. In each iteration, the AMOMM-BKA performs a sequence of operations: an attacking phase, followed by midpoint-based mutation, and then a migration step. The midpoint-based mutation, applied after attacking, adjusts individuals by moving them toward the midpoint between the global best and a randomly selected peer, encouraging exploratory moves in promising regions. To further enhance adaptability, AMOMM-BKA monitors the recent fitness trend of each individual and dynamically chooses the appropriate opposition strategy. If an individual’s performance is stagnating, a BOBL is applied to gently push it out of local optima. If the individual is showing significant improvement, a historical reflective opposition is used to intensify the search around successful directions. In cases where the performance trend is ambiguous, a random opposition is introduced to preserve diversity and prevent convergence stagnation. Together, these strategies allow the AMOMM-BKA to maintain a flexible balance between exploration and exploitation, leading to more reliable performance on complex and multi modal optimization tasks. To facilitate a clearer understanding of the proposed technique, the flowchart of AMOMM-BKA is illustrated in Fig. 5

Fig. 5

The flowchart of AMOMM-BKA.

Computational complexity analysis

This section presents the complexity analysis of the proposed AMOMM-BKA in terms of time and space complexity to assess the computational cost of the introduced enhancements. The theoretical complexities of the AMOMM-BKA are derived with reference to the procedural steps outlined in Algorithm 1

Time complexity of AMOMM-BKA

Time complexity is a key factor in assessing an algorithm’s overall performance. In optimization algorithms, it is primarily influenced by three operations: initialization, fitness evaluation, and position updates of the agents. In this subsection, we compare the time complexity of the original BKA with that of the proposed AMOMM-BKA. To systematically analyze the time complexity of AMOMM-BKA, we consider a population of N search agents, each with D dimensions, and denote the maximum number of function evaluations as Max FEs. The time complexity of the BKA algorithm can then be evaluated as follows:

• Initialization: The algorithm generates N solutions, each with D dimensions, once at the beginning of each run, leading to a time complexity of $O(N \times D)$

• Fitness Evaluation: The evaluation of all N solutions across D dimensions at each iteration requires a time complexity of $O(N \times D \times FEs)$

• Position Updates: Updating the positions of all agents during each iteration requires a time complexity of $O(N \times D \times FEs)$

Hence, the total time complexity of the original BKA is given by $O(N \times D)+O(N \times D \times FEs)+O(N \times D \times FEs) \approx O(N \times D \times FEs)$

For the proposed AMOMM-BKA, the computational complexity can be evaluated in a similar manner. Furthermore, AMOMM-BKA integrates additional procedures such as the Adaptive Memory-based Opposition and the Midpoint-based Mutation strategies, which contribute to an increased computational load. The step-by-step complexity analysis is outlined as follows:

• The initialization process, similar to that of the original BKA, involves generating N candidate solutions across D dimensions, resulting in a computational complexity of $O(N \times D)$

• The fitness assessment of the search agents at each iteration has a computational complexity of $O(N \times D \times FEs)$

• The computational complexity of updating the agents’ positions during both the exploration and exploitation phases remains $O(N \times D \times FEs)$

• The mutation strategy has a complexity of $O(N \times D \times FEs)$, as all individuals are dimension-wise mutated and evaluated.

• The AMO mechanism has a complexity of $O(N \times D \times FEs)$, as opposition solutions are generated and evaluated for all individuals.

Combining these factors,the over all time complexity of AMOMM-BKA is: $O(N \times D)+4\times O(N \times D \times FEs)\approx O(N \times D \times FEs)$

The space complexity of AMOMM-BKA

In computer science, space complexity refers to the memory required for an algorithm’s execution. In AMOMM-BKA, memory usage is primarily determined by the number of dimensions and the population size of black-winged kites, both set during initialization. Thus, the overall space complexity of AMOMM-BKA is $O(N \times D)$

Algorithm 1

Pseudo-code outlining the proposed AMOMM-BKA framework

Experimental results and comprehensive analysis

To ensure consistent and reliable experimentation, all simulations were carried out on a 64-bit Windows 11 platform using MATLAB 2023b. The computational environment comprised an intel R Core TM i3-1005G1 processor 1.20 GHz and 8 GB of RAM.

Benchmark functions

This section systematically investigates the efficacy of the proposed AMOMM-BKA through a series of comprehensive experimental studies. To ensure a robust evaluation, three well-established CEC benchmark suites are employed. Initially, the CEC2005⁶⁰ test suite comprising 23 widely recognized benchmark functions as outlined in Table 1 is utilized to analyze the balance between exploration and exploitation capabilities. Subsequently, the performance of AMOMM-BKA is further scrutinized on more intricate and compositional challenging landscapes using the CEC2019⁶¹ and CEC2022⁶² benchmark suites, presented in Tables 2 and 3, respectively. Additionally, the scalability and robustness of the proposed algorithm are examined on large-scale optimization problems using the high dimensional functions of CEC2005. To further validate the real-world applicability, AMOMM-BKA is applied to four diverse and complex engineering design problems, thereby demonstrating its competency in addressing practical global optimization scenarios.

Table 1 Overview of the standard CEC2005 test functions.

Table 2 Overview of the CEC2019 test functions.

Table 3 Overview of the CEC2022 test functions.

Parameter setting

This section outlines the parameter settings for both the proposed algorithm and its comparative counter parts. To evaluate the efficiency of the proposed algorithm on CEC2005, CEC2019, and CEC2022 benchmark functions, five distinct categories of optimization algorithms were considered: (1) widely cited classical optimizers, such as PSO¹⁶, and GWO¹⁸.(2) recently developed algorithms, including and GJO¹⁹, SO²⁰, SCSO²¹, and AVOA²². (3) high-performance optimizers, namely CMAES¹⁵, and SHADE¹³. (4) the classical and recent improvements of the BKA such as BKA⁴², CBKA⁴⁶, IBKA⁴⁹, QOBLBKA⁵¹. The parameter values for all competing algorithms were adopted from their respective original studies and are detailed in Table 4. To ensure a fair evaluation, each function was executed with a fixed population size of 30 agents and 15000 function evaluations FEs, across different dimensions. Furthermore, the sensitivity of the proposed algorithm to the control parameter ($\beta$) and the threshold values $t_1$ and $t_2$, as well as their impact on overall performance, is analyzed. To eliminate bias caused by randomness, each algorithm was independently tested against each benchmark function over 30 runs.

Table 4 Parameter configurations for the meta-heuristic algorithms.

CEC2005 result analysis and discussion

The experimental simulations employ twenty-three benchmark functions to comprehensively evaluate the proposed AMOMM-BKA against the original BKA and other competitive algorithms. Performance assessment is based on the statistical average (AVG) and standard deviation (STD) of the obtained fitness values. For the first thirteen non-fixed benchmark functions, a default dimension of 30 was used, while the remaining ten fixed-dimension functions were evaluated using their respective standard settings. The comparison algorithms selected are well-established and known for their strong performance on complex optimization problems. Table 5 presents the results of thirty independent runs for each algorithm. As shown, the proposed AMOMM-BKA consistently outperforms the original BKA and other competitors. Specifically, AMOMM-BKA achieved the best results in fifteen functions considering both AVG and STD values and reached optimal fitness values for functions Fun01, Fun03, Fun11, and Fun16–Fun23. In several cases such as Fun09, Fun11, Fun16–Fun19, and Fun21–Fun23 some algorithms demonstrated comparable performance with minimal differences in average fitness. For , Fun05, Fun06, Fun12, and Fun13, the AVOA algorithm exhibited superior performance in both average and standard deviation metrics, while Fun08 showed SO as the clear best performer. For Fun14, AMOMM-BKA and CBKA achieved nearly identical outcomes. In Fun20, the SO algorithm demonstrated slightly better standard deviation values, although AMOMM-BKA and SO produced similar average fitness results. For Fun21 - Fun23, AMOMM-BKA attained the smallest standard deviation values, indicating stable convergence. Overall, out of the twenty-three benchmark functions, AMOMM-BKA achieved the best performance in eight functions and delivered comparable results in nine others. These findings confirm that AMOMM-BKA exhibits robust and competitive optimization capability across diverse test scenarios. To ensure a more insightful comparative evaluation, the Friedman rank test⁶³ is employed to statistically assess the performance of the examined algorithms. Table 6 clearly highlights the Friedman mean ranks of all compared algorithms. Based on the Friedman rank test, AMOMM-BKA secures the first position, demonstrating superior performance over all competitors, while AVOA and IBKA achieve the second and third ranks, respectively. The subsequent analysis employed the Wilcoxon rank-sum test⁶⁴ to examine whether the performance differences between AMOMM-BKA and the comparative algorithms were statistically significant. Table 7 presents the Wilcoxon test outcomes (at a significance level of 0.05) for AMOMM-BKA against the competing algorithms on the CEC2005 benchmark functions, reported in terms of p-values. The results reveal that, for the majority of the tested functions, AMOMM-BKA exhibits statistically significant superiority, with p-values less than 0.05, indicating meaningful performance differences from the baseline algorithms. A few p-values are listed as NA, signifying that both algorithms achieved similar optimal results on simpler functions. In the results column, a $'+'$ symbol denotes a statistically significant improvement in favor of AMOMM-BKA, whereas a $'-'$ indicates no significant difference. The last row of Table 7, labeled (w/t/l), summarizes the counts of wins, ties, and losses, respectively, for AMOMM-BKA compared to its counterparts. The findings proved that the proposed AMOMM-BKA is superior and significantly different from other algorithms at most CEC2005 functions.

Convergence behavior analysis

The convergence curve provides a clear visual representation of how the optimal fitness values evolve throughout the function evaluations of the proposed and comparative algorithms. The convergence speed toward the global optimum is a critical indicator of an algorithm’s efficiency and overall performance. Figure 6 illustrates the convergence behavior for nine benchmark functions from the CEC2005 suite. For functions Fun01, Fun02, Fun03, and Fun04, AMOMM-BKA demonstrates the fastest convergence rate, reaching optimal values significantly earlier than the other algorithms. Particularly, for Fun01 and Fun03, the proposed algorithm attains optimal fitness in the early stages of evaluation. In the case of the multimodal function Fun10, AMOMM-BKA exhibits stable and consistent convergence toward the global optimum. Although AVOA and SHADE show slightly faster initial convergence for Fun12, AMOMM-BKA gradually achieves comparable fitness values as the evaluations progress. For Fun09 and Fun11, AMOMM-BKA again attains optimal values early, underscoring its rapid convergence capability. Regarding the fixed-dimension functions Fun14 and Fun15, AMOMM-BKA maintains excellent performance, outperforming others in both convergence speed and stability. While AMOMM-BKA, AVOA, and SHADE achieve similarly low fitness values, AMOMM-BKA converges more swiftly, reflecting its superior search efficiency.

Table 5 Experimental outcomes for various algorithms on CEC2005 test suite.

Table 6 Friedman test analysis on CEC2005 test suite.

Table 7 Results of the Wilcoxon rank-sum test at the 5% significance level on standard benchmark functions.

Fig. 6

Convergence of the AMOMM-BKA algorithm relative to other algorithms on the CEC2005 test functions.

Scalability analysis

A comprehensive performance assessment is indispensable for any newly introduced optimization algorithm, with scalability serving as a pivotal criterion in contemporary efficiency and solution quality as the dimensionality of the problem escalates. In this study, the scalability of both the baseline BKA and the enhanced AMOMM-BKA is rigorously examined using 13 benchmark functions evaluated at four dimensional settings 10, 30, 50, and 100. The experimental outcomes, presented in Table 8, report the AVG and STD values derive from 30 independent trials, each conducted with 500 iterations per function. The results indicate that AMOMM-BKA consistently attains the global optimum for several functions, including Fun01, Fun03, Fun09, and Fun11, across all tested dimensions. Although certain functions fall short of the global optimum, AMOMM-BKA exhibits markedly superior stability and search efficacy compared to the classical BKA. Additionally, the convergence profiles in Figs. 7, 8, 9 and 10 clearly demonstrate that AMOMM-BKA achieves faster convergence rates and heightened solution robustness across all dimensional settings. Collectively, these findings substantiate the improved scalability of AMOMM-BKA for tackling high-dimensional optimization challenges.

Table 8 Performance analysis of BKA and AMOMM-BKA across various dimensional settings (D=10, 30, 50, 100).

Fig. 7

Performance of function Fun03 across different dimensions.

Fig. 8

Performance of function Fun07 across different dimensions.

Fig. 9

Performance of function Fun10 across different dimensions.

Fig. 10

Performance of function Fun12 across different dimensions.

CEC2019 result analysis and discussion

This section presents the enhancement of the classical BKA through the integration of the proposed AMOMM strategy, leading to the development of the AMOMM-BKA variant. The effectiveness of this improved algorithm was assessed using ten complex benchmark functions from the CEC2019 suite, with detailed results summarized in Table 9. The analysis reveals that AMOMM-BKA outperforms competing algorithms in seven functions, demonstrating superior optimization ability. Although CBKA achieved the best fitness value for Fun24, the difference between CBKA and AMOMM-BKA is marginal, indicating that AMOMM-BKA performs comparably well on this function. For Fun25 and Fun26, while some algorithms achieved the best average fitness values, AMOMM-BKA exhibited greater stability, reflected in its consistent performance across runs. In contrast, for Fun27 and Fun28, SHADE showed slightly better results than AMOMM-BKA. For Fun29-Fun31 and Fun33, AMOMM-BKA achieved the better average fitness values and maintained the smallest standard deviations, highlighting its stability and reliability in convergence. Overall, across the ten benchmark functions, AMOMM-BKA achieved the best results in four cases and demonstrated comparable performance in three others, confirming its robustness and strong competitive capability in handling diverse and challenging optimization problems. To provide a comprehensive comparative analysis, the Friedman test is employed to evaluate the performance of the competing algorithms. As shown in Table 10, according to the Friedman rank test, AMOMM-BKA attains the best overall rank, showcasing its superior performance across all benchmark functions, while SHADE and CBKA follow in the second and third positions, respectively. Table 11. presents the Wilcoxon statistical test results for the CEC2019 benchmark suite. The test was performed between the proposed AMOMM-BKA and each comparative algorithm, with each experiment executed over 30 independent runs. The p-value was used to determine the statistical significance of the performance differences between algorithms. According to the results in Table 11, AMOMM-BKA consistently outperforms the competing algorithms in most cases, demonstrating statistically significant improvements. However, for function Fuc28, the significance level is lower due to the superior performance of certain competing algorithms on this particular function. Overall, the Wilcoxon test results confirm that AMOMM-BKA exhibits statistically significant superiority over the majority of compared algorithms across the CEC2019 benchmark functions, validating its strong optimization capability and robustness.

Convergence behavior analysis

To further demonstrate the efficacy of the proposed AMOMM-BKA algorithm, the convergence behaviors of AMOMM-BKA and 12 competing metaheuristics on the fixed dimensional CEC2019 benchmark functions are illustrated in Fig 11. The curves reveal that AMOMM-BKA exhibits a consistently faster and more stable convergence profile compared to its counterparts, indicating superior robustness and computational efficiency in approaching optimal solutions. Notably, AMOMM-BKA maintains a smooth and accelerated convergence trajectory across most test functions, suggesting enhanced search capability as iterations progress. For function Fun24, CBKA achieves better result values, but AMOMM-BKA exhibits superior convergence behavior. For function Fun29, AMOMM-BKA initially converges slower than PSO; however, as PSO becomes trapped in local optima, AMOMM-BKA maintains a steady and promising convergence. In function Fun33, AVOA shows faster initial convergence, but it eventually gets stuck in local optima, whereas AMOMM-BKA demonstrates superior exploration and ultimately identifies better solutions. The findings of this study reveal that AMOMM-BKA exhibits enhanced convergence speed and superior optimization accuracy compared to other algorithms, thereby substantiating the efficacy and competitiveness of the proposed approach

Table 9 Experimental outcomes for various algorithms on CEC2019 test suite.

Table 10 Friedman test analysis on CEC2019 test suite.

Table 11 Results of the Wilcoxon rank-sum test at the 5% significance level on CEC2019 benchmark functions.

Fig. 11

Convergence of the AMOMM-BKA algorithm relative to other algorithms on the CEC2019 test functions.

CEC2022 result analysis and discussion

In this section, the recent CEC2022 benchmark suite is employed to evaluate the capability of AMOMM-BKA in avoiding entrapment in local optima and to analyze its exploration-exploitation balance. The same parameter settings and experimental configurations used for the CEC2019 benchmarks are retained here, with the problem dimensionality set to D = 10. Table 12 presents the AVG and STD values used to assess the performance and stability of AMOMM-BKA in comparison with other algorithms across twelve complex test functions. To offer a comprehensive performance comparison, the Friedman test is employed across the evaluated algorithms. As presented in Table 13, AMOMM-BKA secures the first rank, demonstrating performance levels unmatched by any competitor. Its superiority in eight functions in terms of average fitness underscores its strong exploratory and exploitative capabilities and the effective balance between them. For Fun36 and Fun40, SHADE achieved slightly better results, showing marginal superiority over AMOMM-BKA. Similarly, for Fun43, SHADE attained the minimum fitness value, while IBKA exhibited a smaller standard deviation, indicating higher stability. Overall, AMOMM-BKA outperforms all competing algorithms across most CEC2022 functions, whereas SHADE ranks second, showing superiority in only three functions. These results confirm the robustness, adaptability, and balanced search behavior of AMOMM-BKA in addressing complex optimization problems. Table 14 presents the Wilcoxon statistical test results for the CEC2022 benchmark, comparing AMOMM-BKA with twelve competing algorithms at a significance level of 0.05. The results indicate that AMOMM-BKA shows statistically significant differences from most competitors, confirming its superior optimization performance.The summary metric (w/t/l) in the last row indicates the number of functions where AMOMM-BKA outperforms, ties, or underperforms against each competitor. Overall, the statistical analysis validates the robustness and high efficiency of AMOMM-BKA, establishing it as a promising algorithm for tackling complex optimization problems in the CEC2022 suite.

Convergence behavior analysis

To investigate the convergence properties of the algorithms in solving the test functions, Fig. 12 illustrates the convergence performance of the proposed AMOMM-BKA algorithm in comparison with its counterparts, evaluated across twelve benchmark functions selected from CEC2022. As observed, AMOMM-BKA consistently exhibits superior convergence behavior, achieving the lowest global fitness values in most cases. Notably, it demonstrates the fastest convergence across most test functions, except for Fun38, Fun40, and Fun43. In function Fun37, AMOMM-BKA initially converges slower than SO and CBKA. However, as the iterations progress, it accelerates and achieves a more promising convergence rate. For function Fun38, CMAES and SHADE attain faster convergence and superior fitness values, whereas AMOMM-BKA yields a slightly higher objective value. In the case of Fun40 and Fun43, SO shows accelerated convergence during the later stages of optimization. However, for function Fun44, AMOMM-BKA not only maintains an efficient convergence rate but also secures the best fitness value among all algorithms. Overall, AMOMM-BKA exhibits robust convergence efficiency and competitive global search capability, affirming its effectiveness across diverse optimization landscapes.

Table 12 Experimental outcomes for various algorithms on CEC2022 test suite.

Table 13 Friedman test analysis on CEC2022 test suite.

Table 14 Results of the Wilcoxon rank-sum test at the 5% significance level on CEC2022 benchmark functions.

Fig. 12

Convergence of the AMOMM-BKA algorithm relative to other algorithms on the CEC2022 test functions.

Ablation experiments

The AMOMM-BKA represents an enhanced version of the BKA, developed through a novel integration of Blended Opposition-Based Learning (BOBL), Historical Reflective Opposition (HRO), Random Opposition (RO), and a Midpoint-Based Mutation (MM) strategy. This combination substantially improves the algorithm’s convergence rate, robustness, and overall search efficiency. The study demonstrates that the synergy between the original BKA framework and these enhancement mechanisms enhances the adaptability of the proposed AMOMM-BKA when addressing diverse optimization problems. To comprehensively assess the contribution of each component, an ablation study was conducted using twelve benchmark functions from the CEC2022 test suite. Each algorithm was independently executed 30 times with 30 search agents, resulting in a total of 15,000 FEs. As summarized in Table 15, AMOMM-BKA achieved superior performance in terms of mean fitness values for most benchmark functions. Furthermore, the comparatively lower standard deviation values indicate that AMOMM-BKA exhibits greater stability than its counterpart variants. The convergence behavior presented in Figure 13 further highlights the efficiency of AMOMM-BKA compared to its simplified versions. The convergence curves reveal that AMOMM-BKA consistently achieves faster and more stable convergence, confirming that the incorporated strategies effectively balance exploration and exploitation across various problem landscapes. Overall, the ablation analysis validates the effectiveness of the proposed modifications and underscores the distinct contribution of each strategy, offering valuable insights for the design of future metaheuristic algorithms.

Table 15 Ablation experiments outcomes for AMOMM-BKA on CEC2022 test suite.

Fig. 13

Convergence of the AMOMM-BKA compared to other optimizer.

Balance and diversity analysis

Population diversity is vital for understanding the search behavior of evolutionary algorithms. These algorithms employ multiple agents to explore the search space and locate optimal solutions⁶⁵. As agents converge toward promising regions, their spacing decreases, enhancing exploitation, while greater spacing promotes exploration. To quantify these spatial dynamics, a diversity metric is utilized as defined in Eq. 15.

$$\begin{aligned}&Dive_j=\frac{1}{N} \sum _{i=1}^{N}|median(z^j)-z_i^j| \end{aligned}$$

(14)

$$\begin{aligned}&Dive=\frac{1}{dim} \sum _{j=1}^{dim} Dive_j \end{aligned}$$

(15)

Where Dive denotes the overall population diversity, while $Dive_j$ signifies the diversity within the data set corresponding to the jth dimension across all individuals. Here, dim represents the dimension of each search agent, and N indicates the total number of search agents. The term $median(z^j)$ refers to the median value of the jth dimension, while $x_i^j$ denotes the jth dimension component of the ith search agent. Moreover, the diversity metric, as defined in Eqs. 16 and 17, is utilized to quantify the proportion of exploration and exploitation at each iteration.

$$\begin{aligned}&zpl\%=\left( \frac{Dive}{Dive_{max}}\right) \times 100 \end{aligned}$$

(16)

$$\begin{aligned}&zpt\%=\left( \frac{|Dive_{max}-Dive|}{Dive_{max}}\right) \times 100 \end{aligned}$$

(17)

The maximum diversity is represented as $Dive_{max}$, while $zpl\%$ and $zpt\%$ and denote the exploration and exploitation rates at each iteration, respectively. The exploitation rate is obtained from the absolute difference between the maximum and current diversity. Achieving a proper balance between exploration and exploitation is crucial for enhancing algorithmic performance.

Figure 14 illustrates the diversity behavior of the standard BKA and the proposed AMOMMBKA across several benchmark functions. For analysis, three functions (Fun14, Fun15, and Fun20) were selected from CEC2005, and three (Fun25, Fun29, and Fun30) from CEC2019. In each case, BKA begins with high diversity that rapidly declines, indicating strong initial exploration followed by premature convergence. In contrast, AMOMMBKA sustains moderate and more stable diversity, reflecting a controlled balance between exploration and exploitation. Although its diversity decreases initially, it stabilizes over time, preventing rapid convergence and maintaining effective search dynamics.

Figure 15 further depicts the adaptive balance between exploration and exploitation in AMOMMBKA. The fluctuations of both curves across iterations demonstrate dynamic adjustment between global search and local refinement. Their close alignment signifies a well-maintained trade-off that enhances search efficiency and mitigates premature convergence across different test functions.

Fig. 14

The diversity analysis performed by AMOMM-BKA and BKA.

Fig. 15

The balance analysis performed by AMOMMBKA.

Sensitivity analysis

This subsection examines how different parameters influence the performance of the proposed AMOMM-BKA. As a population-based algorithm, AMOMM-BKA gradually converges to the best solution for a given optimization problem. Its performance mainly depends on the population size, the control parameter $\beta$ defined in Eq. 9. and threshold values ($t_1 \& t_2$) in the selection of confidence score . Therefore, a sensitivity analysis is conducted for these three parameters, population size (N), control parameter ($\beta$), and threshold values ($t_1 \& t_2$). Hence, prior experience and experimental insight play an important role in selecting suitable values.

Sensitivity of population size

To examine how the performance of the proposed AMOMM-BKA is influenced by population size, eight benchmark functions were selected from the CEC2005, CEC2019, and CEC2022 test suites, ensuring representation across various function categories to minimize bias. Each experiment was executed over 15000 FEs and repeated 30 times for population sizes of 10, 30, 50, 80, and 100 agents. The corresponding results, presented in Table 16, are analyzed using the AVG and STD of fitness values. The findings indicate that increasing the population size results in mean fitness values and reduced variance. This improvement is attributed to the enhanced exploration capability provided by a larger number of agents, which increases the likelihood of identifying optimal or near-optimal solutions.

Table 16 Sensitivity analysis of AMOMM-BKA for varying population sizes.

Sensitivity of control parameter $\beta$

The parameter $\beta$ in the Historical Reflective Opposition (HRO) phase controls the reflection depth toward an individual’s historical best position, influencing the balance between exploration and exploitation. To determine an appropriate value, $\beta$ was varied across ten settings (0.01to2.0) and tested on eight benchmark functions. For each value, the average and standard deviation of the best fitness were recorded. As shown in Table 17, $\beta$ = 0.5 achieved the lowest mean fitness with smaller deviations, indicating stable and efficient performance. Very small $\beta$ values resulted in overly cautious updates, while larger ones caused unstable reflections. Hence, $\beta$ = 0.5 is chosen as the optimal setting for the HRO phase.

Table 17 Sensitivity of AMOMM-BKA to the control parameter at different values.

Sensitivity of threshold values

The selection of suitable threshold values plays a crucial role in the AMOMM-BKA mechanism, as these thresholds determine when the algorithm should switch between exploration and exploitation strategies. In particular, the parameters $t_1$ and $t_2$ control the activation of different opposition strategies based on the confidence score $C_i$. Choosing inappropriate threshold values may lead to excessive exploration, premature convergence, or stagnation in local optima. Therefore, a sensitivity analysis was conducted to identify effective threshold settings for achieving stable and high-quality performance. In this experiment, four combinations of $t_1$ and $t_2$ were tested to evaluate their solution quality. The experiment was performed using a population size of 30 agents and a fixed number of function evolution, across eight representative benchmark functions. The four threshold combinations examined are summarized in Table 18, and the corresponding average and standard deviation of fitness values are reported in Table 19. The results show that Scenario 3 achieved the best performance across most functions. Hence, these values were selected as the default thresholds for AMOMM-BKA, as they provide a stable balance between exploration and exploitation.

Table 18 Summary of the four threshold combinations used for sensitivity analysis.

Table 19 Sensitivity analysis of AMOMM-BKA for the threshold parameter.

Results and discussion of engineering applications

To further validate the effectiveness of AMOMM-BKA in tackling real world engineering issues, this section presents a comprehensive analysis of its optimization performance across four engineering design problems. Table 20 provides a succinct summary of these problems, including their dimension (D), number of equality constraints ($\mathscr {H}$), inequality constraints ($\mathscr {Q}$), and the optimal cost. The evaluation was carried out using a population size of 30, a maximum of 15000 function evaluations (FEs), with each problem independently tested 30 times to ensure statistical reliability.

The proposed AMOMM-BKA is evaluated against various metaheuristic algorithms, including PSO¹⁶, GWO¹⁸, GJO¹⁹, SO²⁰, SCSO²¹, AVOA²², CMAES¹⁵, SHADE¹³, classical BKA⁴², CBKA⁴⁶, IBKA⁴⁹, and QOBLBKA⁵¹. For fairness, AMOMM-BKA and all compared algorithms maintain identical parameter settings when solving mathematical test functions.

Table 20 Description of the four real-world engineering optimization problem.

Multiple disk clutch brake design problem

The primary objective of this design is to minimize the mass of a multi disc clutch break system. The optimization problem is formulated using integer-valued decision variables, namely: the inner radius $(m_1)$, outer radius $(m_2)$, disc thickness $(m_3)$, actuator force $(m_4)$, and the number of frictional surfaces $(m_5)$. The formulation is subject to nine nonlinear constraints that govern the feasible design space⁶⁶. The geometric and functional configuration of these decision variables for the multi plate disc clutch break design problem is depicted in Fig. 16 . Formally, the problem can be expressed as follows:

Minimize:

$$\begin{aligned} \begin{aligned} f(\vec {m})&= \pi \left( m_2^2 - m_1^2 \right) m_3 \left( m_5 + 1 \right) \rho \end{aligned} \end{aligned}$$

subject to:

$$\begin{aligned} \begin{aligned} \mathscr {Q}_1(\vec {m})&= -p_{\max } + p_{rz} \le 0, \\ \mathscr {Q}_2(\vec {m})&= p_{rz} V_{sr} - V_{sr,\max } p_{\max } \le 0, \\ \mathscr {Q}_3(\vec {m})&= \Delta R + m_1 - m_2 \le 0, \\ \mathscr {Q}_4(\vec {m})&= -L_{\max } + (m_5 + 1)(m_3 + \delta ) \le 0, \\ \mathscr {Q}_5(\vec {m})&= s M_s - M_h \le 0, \\ \mathscr {Q}_6(\vec {m})&= T \ge 0, \\ \mathscr {Q}_7(\vec {m})&= -V_{sr,\max } + V_{sr} \le 0, \\ \mathscr {Q}_8(\vec {m})&= T - T_{\max } \le 0, \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} M_h&= \frac{2}{3} \mu m_4 m_5 \frac{m_2^3 - m_1^3}{m_2^2 - m_1^2} \ \text {N.mm}, \\ \omega&= \frac{\pi n}{30} \ \text {rad/s}, \\ A&= \pi (m_2^2 - m_1^2) \ \text {mm}^2, \\ p_{rz}&= \frac{m_4}{A} \ \text {N/mm}^2, \\ V_{sr}&= \frac{\pi R_{sr} n}{30} \ \text {mm/s}, \\ R_{sr}&= \frac{2}{3} \frac{m_2^3 - m_1^3}{m_2^2 m_1^2} \ \text {mm}, \\ T&= \frac{I_z \omega }{M_h + M_f}, \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned} \Delta R&= 20 \ \text {mm},&\quad L_{\max }&= 30 \ \text {mm},&\quad \mu&= 0.6, \\ V_{sr,\max }&= 10 \ \text {m/s},&\quad \delta&= 0.5 \ \text {mm},&\quad s&= 1.5, \\ T_{\max }&= 15 \ \text {s},&\quad n&= 250 \ \text {rpm},&\quad I_z&= 55 \ \text {Kg.m}^2, \\ M_s&= 40 \ \text {Nm},&\quad M_f&= 3 \ \text {Nm},&\quad p_{\max }&= 1. \end{aligned} \end{aligned}$$

with bounds:

$$\begin{aligned} \begin{aligned} 60&\le m_1 \le 80, \quad 90 \le m_2 \le 110, \quad 1 \le m_3 \le 3, \\ 0&\le m_4 \le 1000, \quad 2 \le m_5 \le 9. \end{aligned} \end{aligned}$$

Fig. 16

A schematic representation of the Multiple disk clutch brake design⁶⁶.

Table 21 A comparison of the Multiple disk clutch brake design using different algorithms.

The outcomes of applying AMOMM-BKA to the multiple disk clutch brake design problem are presented in Table 21. The findings indicate that both AMOMM-BKA and SHADE achieved the minimum cost for the problem while satisfying all constraints, whereas AVOA and PSO also produced competitive results. The superior performance of AMOMM-BKA can be attributed to the integration of AMOMM, which effectively balances exploration and exploitation, enhances solution diversity, and mitigates the risk of premature convergence. Collectively, these mechanisms enable AMOMM-BKA to efficiently navigate the solution space and improve solution quality, thereby underscoring its efficacy and robustness for the multiple disk clutch break design optimization task.

Step-cone pulley problem

The primary aim of this problem is to minimize the weight of a four-step cone pulley by optimizing five design variables. Among these, four variables $(s_1, s_2, s_3, s_4)$ correspond to the diameters of each pulley step, while the fifth variable (w) represents the pulley width. The problem is subject to eleven nonlinear constraints, ensuring that the transmitted power exceeds 0.75 hp⁶⁷. A schematic representation of the design is provided in Fig 17. The mathematical formulation of the optimization problem is expressed as follows:

Suppose   $\vec {x}=[x_1, x_2, x_3, x_4, x_5]= [s_1, s_2, s_3, s_4, w]$

Minimize:

$$\begin{aligned} \begin{aligned} f({\vec {x}}) =&\ \rho \omega \Bigg [ s_1^2 \left\{ 1 + \left( \frac{N_1}{N} \right) ^2 \right\} + s_2^2 \left\{ 1 + \left( \frac{N_2}{N} \right) ^2 \right\} \\&+ s_3^2 \left\{ 1 + \left( \frac{N_3}{N} \right) ^2 \right\} + s_4^2 \left\{ 1 + \left( \frac{N_4}{N} \right) ^2 \right\} \Bigg ] \end{aligned} \end{aligned}$$

subject to:

$$\begin{aligned} \begin{aligned} \mathscr {H}_1({\vec {x}})&= C_1 - C_2 = 0, \\ \mathscr {H}_2({\vec {x}})&= C_1 - C_3 = 0, \\ \mathscr {H}_3({\vec {x}})&= C_1 - C_4 = 0, \\ \mathscr {Q}_{i=1,2,3,4}({\vec {x}})&= -R_i \le 2, \\ \mathscr {Q}_{i=5,6,7,8}({\vec {x}})&= (0.75 \times 745.6998) - P_i \le 0, \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} \begin{aligned} C_i&= \frac{\pi s_i}{2} \left( 1 + \frac{N_i}{N} \right) + \frac{\left( \frac{N_i}{N} - 1 \right) ^2}{4a} + 2a,&i&= 1,2,3,4, \\ R_i&= \exp \left( \mu \left\{ \pi - 2 \sin ^{-1} \left\{ \left( \frac{N_i}{N} - 1 \right) \frac{s_i}{2a} \right\} \right\} \right) ,&i&= 1,2,3,4, \\ P_i&= u t \omega (1 - R_i) \frac{\pi s_i N_i}{60},&i&= 1,2,3,4, \end{aligned} \end{aligned}$$

with:

$$t = 8 \ \textrm{mm}, \quad u = 1.75 \ \textrm{MPa}, \quad \mu = 0.35, \quad \rho = 7200 \ \mathrm {kg/m^3}, \quad a = 3 \ \textrm{mm}.$$

Fig. 17

A schematic representation of the Step-cone pulley problem.

Table 22 A comparison of the Step-cone pulley problem using different algorithms.

Table 22 presents a comparative analysis of AMOMM-BKA against several established algorithms in addressing the Step-cone pulley optimization problem. The findings clearly indicate that AMOMM-BKA achieved the minimum design weight, effectively optimizing decision variables $x_1$ through $x_5$. Notably, high performance algorithms such as CMAES and SHADE under performed in this specific context. While other methods, including PSO, yielded competitive outcomes, AMOMM-BKA consistently outperformed them, affirming its superiority in solving this engineering design challenge.

Welded beam design

The welded beam design is a fundamental engineering optimization challenge aimed at minimizing manufacturing costs. The design process is constrained by four critical factors: shear stress $\tau$, bending stress $\sigma$ , buckling load $P_c$, and beam deflection $\delta$, all of which must be carefully considered to ensure structural integrity⁶⁸. A visual representation of the problem in both two and three dimensional perspectives is provided in Fig. 18. This optimization problem involves four key design variables namely the thickness of weld h, length of the clamping bar l, the height of the bar t, and thickness of the bar b. Additionally, the problem is governed by seven constraints, ensuring feasibility and performance. The complete mathematical formulation is presented as follows:

$$\begin{aligned} \begin{aligned}&\text {Suppose} \,\,\vec {b}=[b_1\, b_2\, b_3\, b_4]=[ hltb ]\\&\text {Minimize}\,\,f(\vec {b})=1.10471b_1^2b_2+0.04811b_3b_4(14.0+b_2)\\&\text {subject to}\quad \mathscr {Q}_1(\vec {b})=\tau (\vec {b})-\tau _{max}\le 0\\&\hspace{0.8in} \mathscr {Q}_2(\vec {b})=\sigma (\vec {b})-\sigma _{max}\le 0\\&\hspace{0.8in} \mathscr {Q}_3(\vec {b})=\delta (\vec {b})-\delta _{max}\le 0\\&\hspace{0.8in} \mathscr {Q}_4(\vec {b})=b_1-b_4\le 0\\&\hspace{0.8in} \mathscr {Q}_5(\vec {b})=P-P_c(\vec {b})\le 0\\&\hspace{0.8in} \mathscr {Q}_6(\vec {b})=0.125-b_1\le 0\\&\hspace{0.8in} \mathscr {Q}_7(\vec {b})=1.1047b_1^2+0.04811b_3b_4(14.0+b_2)-5.0\le 0\\&\text {variables range:}\\&\hspace{0.8in} 0.1\le b_1\le 2\\&\hspace{0.8in} 0.1\le b_2\le 10\\&\hspace{0.8in} 0.1\le b_3\le 10\\&\hspace{0.8in} 0.1\le b_4\le 2\\ \end{aligned} \end{aligned}$$

$$\begin{aligned} \begin{aligned}&\text {where} \quad \tau (\vec {b})=\sqrt{(\tau ^{\prime })^2+2\tau ^{\prime } \tau ^{\prime \prime }\frac{b_2}{2R}+(\tau ^{\prime \prime })^2}\\&\hspace{0.54in} \tau ^{\prime }=\frac{P}{\sqrt{2}b_1 b_2}, \, \tau ^{\prime \prime }=\frac{MR}{J}, \, M=P\left( L+\frac{b_2}{2}\right) \\&\hspace{0.54in} R=\sqrt{\frac{b_2^2}{4}+\left( \frac{b_1+b_3}{2}\right) ^2}, \, J=2\sqrt{2}b_1b_2[R]\\&\hspace{0.54in} \sigma (\vec {b})=\frac{6PL}{b_4b_3^2}, \, \delta (\vec {b})=\frac{6PL^3}{Eb_3^2b_4}\\&\hspace{0.54in} P_c(\vec {b})=\frac{4.013E\sqrt{\frac{b_3^2b_4^6}{36}}}{L^2}\left( 1-\frac{b_3}{2L}\sqrt{\frac{E}{4G}}\right) \\&\hspace{0.54in} P=6000lb,\,L=14in.,\,\sigma _{max}=0.25in.,\,E=30\times 1^6psi,\,G=12\times 10^6psi\\&\hspace{0.54in} \tau _{max}=13600psi,\,\sigma _{max}=30000psi,\,\delta _{max}=0.25in\\ \end{aligned} \end{aligned}$$

Fig. 18

A schematic representation of the Welded beam design.

Table 23 A comparison of the Welded beam design using different algorithms.

Table 23 presents a detailed comparison of the performance of the AMOMM-BKA on the welded beam design problem alongside other optimization algorithms. The results clearly show that AMOMM-BKA achieved the minimum cost while fully satisfying all design constraints, demonstrating its strong capability in addressing complex constrained engineering problems. This superior performance is likely due to the algorithm’s effective balance between exploration and exploitation, which allows it to search the solution space efficiently and refine potential solutions. However, both SCSO and SHADE yielded relatively higher cost values, suggesting that they may struggle to maintain optimal performance in such constrained design tasks.

Speed reducer design

The speed reducer is a crucial component is gearbox system, playing a vital role in mechanical performance. This optimization problem focuses on minimizing the total weight of the speed reducer while satisfying 11 constraints four of which are linear inequalities, and the remaining seven are nonlinear constraints⁶⁹. The linear constraints are bending stress of the gear teeth, transverse deflections of the shafts, surface stress, stresses in the shafts. This problem involves optimizing seven design variables namely, the face width $(c_1)$, the module of teeth $(c_2)$, the number of teeth in the pinon $(c_3)$, the length of the first shaft between bearings $(c_4)$, the length of the second shaft between bearings $(c_5)$, the diameter of the first shaft $(c_6)$, the diameter of the second shaft $(c_7)$. The 2D and 3D representation of the speed reducer design are illustrated in Fig. 19, and the complete mathematical formulation is provided below.

$$\begin{aligned} \begin{aligned}&\text {Suppose}\,\, \vec {c}=[c_1\,c_2\,c_3\,c_4\,c_5\,c_6\,c_7]\\&\text {Minimize}\,\, f(\vec {c})=0.7854c_1c_2^2(3.3333c_3^2+14.93334c_3-43.0934)\\&\hspace{1in} -1.508c_1(c_6^2+c_7^2)+7.4777(c_6^2+c_7^2)+0.7854(c_4c_6^2+c_5c_7^2)\\&\text {subject to} \quad \mathscr {Q}_1(\vec {c})=\frac{27}{c_1c_2^2c_3}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_2(\vec {c})=\frac{397.5}{c_1c_2^2c_3^2}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_3(\vec {c})=\frac{1.93c_4^3}{c_2c_6^4c_3}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_4(\vec {c})=\frac{1.93c_5^3}{c_2c_7^4c_3}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_5(\vec {c})=\frac{\sqrt{(745c_4/c_2c_3)^2+16.9\times 10^6}}{110c_6^3}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_6(\vec {c})=\frac{\sqrt{(745c_5/c_2c_3)^2+157.5\times 10^6}}{85c_7^3}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_7(\vec {c})=\frac{c_2c_3}{40}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_8(\vec {c})=\frac{5c_2}{c_1}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_9(\vec {c})=\frac{c_1}{12c_2}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_{10}(\vec {c})=\frac{1.5c_6+1.9}{c_4}-1\le 0\\&\hspace{0.8in}\mathscr {Q}_{11}(\vec {c})=\frac{1.1c_7+1.9}{c_5}-1\le 0\\&\text {variables range} \quad 2.6\le c_1\le 3.6\\&\hspace{1.15in} 0.7\le c_2\le 0.8\\&\hspace{1.15in} c_3\in \{17,18,19,\dots ,28\}\\&\hspace{1.15in} 7.3\le c_4\\&\hspace{1.15in} c_5\le 8.3\\&\hspace{1.15in} 2.9\le c_6\le 3.9\\&\hspace{1.15in} 5\le c_7\le 5.5 \end{aligned} \end{aligned}$$

Fig. 19

A schematic representation of the Speed reducer design.

Table 24 A comparison of the Speed reducer design using different algorithms.

Table 24 encapsulates the performance outcomes of the AMOMM-BKA algorithm applied to the reducer weight minimization problem. The algorithm demonstrated exceptional efficacy by attaining the minimal reducer weight while rigorously adhering to all constraint conditions, thereby showcasing its robust optimization proficiency. Furthermore, algorithms such as SO and SHADE also exhibited commendable performance, yielding competitive solutions. Collectively, these findings accentuate the operational efficiency of AMOMM-BKA, attributed to its well calibrated balance between exploration and exploitation, which enables effective navigation of constrained design landscapes and the identification of optimal solutions.

Table 25 presents the Friedman ranking of all algorithms applied to the engineering problem set. Remarkably, the AMOMM-BKA algorithm consistently secured the first position across all four evaluated engineering scenarios, underscoring its exceptional efficacy and robustness in addressing complex global optimization challenges. Overall, the empirical results demonstrate that AMOMM-BKA significantly surpasses competing methodologies, affirming its potential as a highly promising and effective solution for global optimization in engineering domains.

Table 25 Friedman-based performance rankings for the algorithms tested on four engineering challenges.

Conclusion and future work

To prevent the BKA from becoming trapped in local optima and to enhance its global optimization capability, this study introduces three innovative improvement strategies, collectively forming the proposed AMOMM-BKA framework. Firstly, BOBL is employed to guide stagnated individuals showing minimal fitness improvement toward more promising regions without destabilizing the population. Secondly historical reflective opposition leverages archived elite solutions to reinforce the trajectory of improving individuals. Thirdly, random opposition maintains diversity for uncertain individuals whose search behavior lacks clear direction. Finally, the midpoint-based mutation strategy employs a randomized convergence mechanism, guiding solutions toward the midpoint between the global best and a randomly selected peer, thereby maintaining a balance between exploration and exploitation. To comprehensively assess the effectiveness of AMOMM-BKA, an extensive comparative evaluation was conducted against twelve state-of-the-art metaheuristic algorithms on the CEC2005, CEC2019, and CEC2022 benchmark suites. Across a total of 45 numerical optimization problems, AMOMM-BKA consistently demonstrated superior performance, securing the first rank with an average score of 1.78, which is 56.18% superior to the second-best algorithm, SHADE (average rank: 4.56). The experimental and statistical analyses consistently highlight the algorithm’s superior convergence speed, solution accuracy, and robustness. Moreover, AMOMM-BKA is applied to solve four real-world engineering optimization problems, and the results and comparisons prove the algorithm’s effectiveness in solving practical problems, which is verified from the practical aspect. In conclusion, the proposed AMOMM-BKA algorithm exhibits superior convergence accuracy, speed, and optimization performance. Its effectiveness across both fixed and variable-dimensional functions confirms strong adaptability and robustness in solving diverse optimization problems. The current version of the AMOMM-BKA algorithm is restricted to single-objective optimization, limiting its applicability to broader real-world scenarios. Moreover, its structure requires further adaptation to effectively handle discrete optimization problems. Future work will focus on developing binary and multi-objective extensions of AMOMM-BKA to enhance its versatility. These advancements will enable AMOMM-BKA to address diverse optimization tasks, such as hyperparameter tuning in natural language processing, resource management in wireless sensor networks, and optimization modeling in digital twin systems.