Histology-informed microstructural diffusion simulations for MRI cancer characterisation—the Histo-μSim framework

Abstract

Diffusion Magnetic Resonance Imaging (dMRI) simulations in geometries mimicking the microscopic complexity of human tissues enable the development of innovative biomarkers with unprecedented fidelity to histology. Simulation-informed dMRI has traditionally focussed on brain imaging, and it has neglected other applications, as for example body cancer imaging, where new non-invasive biomarkers are still sought. This article fills this gap by introducing a Monte Carlo diffusion simulation framework informed by histology, for enhanced body dMR microstructural imaging: the Histo-μSim approach. We generate dictionaries of synthetic dMRI signals with coupled tissue properties from virtual cancer environments, reconstructed from hematoxylin-eosin stains of human liver biopsies. These enable the data-driven estimation of properties such as the intrinsic extra-cellular diffusivity, cell size or cell membrane permeability. We compare Histo-μSim to metrics from well-established analytical multi-compartment models in silico, on fixed mouse tissues scanned ex vivo (kidneys, spleens, and breast tumours) and in cancer patients in vivo. Results suggest that Histo-μSim is feasible in clinical settings, and that it delivers metrics that more accurately reflect histology as compared to analytical models. In conclusion, Histo-μSim offers histologically-meaningful tissue descriptors that may increase the specificity of dMRI towards cancer, and thus play a crucial role in precision oncology.

Introduction

The ultimate aim of diffusion MRI (dMRI) is the estimation of statistics of the cellular environment, referred to as tissue microstructure, from sets of diffusion-weighted (DW) signal measurements, by solving an inverse mathematical problem^1,2. Multi-compartment biophysical dMRI models have gained momentum as practical approaches capable of providing maps of biologically-meaningful properties, such as cell size (CS) indices. These have found applications in multiple organs, e.g., brain³, muscles⁴, breast⁵, liver⁶, prostate^7,8 and beyond. Non-invasive CS measurement may be particularly relevant for disease characterisation and treatment response assessment in oncology, given the variety of cell types that can coexist within tumours, each featuring unique, distinctive dimensions (e.g., normal vs malignant cells, immune cell infiltration, etc)^9,10,11,12.

However, current biophysical models are often based on idealised representations of tissue components, such as spheres of fixed radii to describe cells^6,7,11. This implies that they may neglect other, relevant features of intra-voxel microstructure, e.g., the existence of distributions of CSs, intra-cellular (IC) kurtosis^13,14, or extra-cellular (EC) diffusion time dependence^15,16. Neglecting such characteristics may bias parameter estimation, and may also cause clinically relevant information to be missed.

Recently, numerical methods based on more realistic tissue representations have enabled the development of accurate dMRI signal models^17,18, increasing the biological specificity of parameter estimation^{19,20,21,22,23}. In particular, Monte Carlo (MC) diffusion simulations within 3D meshes derived from histology have enabled the characterisation of fine, sub-cellular microstructural details, such as axonal beading/undulation^24,25, or neural process complexity^20,21. Nevertheless, to date histology-informed dMRI has focussed heavily on neural tissue, with only a few examples outside the central nervous system²⁶. More accurate biophysical models are urgently needed in a variety of other contexts beyond brain dMRI, as in oncological body imaging of solid tumours²⁷. New dMRI approaches could tackle several, unmet clinical needs, such as patient stratification for treatment selection, response assessment in immunotherapy²⁸, or the determination of the malignity of lesions that cannot be biopsied²⁹.

This article aims to fill this gap by introducing a histology-informed MC framework for microstructural diffusion simulations and parameter mapping, referred to as Histo-μSim. We present a rich database of virtual cellular environments reconstructed from hematoxylin and eosin (HE) stains of liver biopsies, and use these to synthesise signals for clinically feasible dMRI protocols. The database provides the community with reference values of key cellular properties in cancerous and non-cancerous tissues, information not easily accessible in the literature, yet essential to inform the development of the new dMRI techniques of tomorrow. The set of cellular-level characteristics and corresponding dMRI signals allowed us to devise a strategy for the numerical estimation of unexplored tissue properties with clinically feasible acquisitions. In particular, we tested the estimation of the intrinsic EC diffusivity (referred to as D_0∣ex) and of cell characteristics, as CS statistics and cell membrane permeability κ, which we showcase in pre-clinical scans of fixed mouse tissues and in cancer patients in vivo. Results from in silico, ex vivo, and in vivo data suggest that Histo-μSim enables the computation of microstructural metrics that more accurately reflect the underlying histology than standard analytical signal models, and that these can be obtained in clinically acceptable times. In summary, Histo-μSim is a promising new approach for the non-invasive characterisation of body cancers, and may play a crucial role in both clinical practice and research settings, enhancing precision oncology.

Results

The virtual tissue environments enable histologically-realistic diffusion simulations

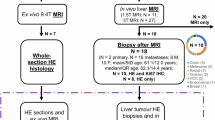
We reconstructed 18 virtual tissue environments from regions-of-interest (ROIs) of HE stains of liver tumour biopsies, which we will refer to as substrates. The environments enable the generation of synthetic dMRI signals through MC diffusion simulations, based entirely on open-source software (Fig. 1). The set of environment properties and paired signals can be used to inform cancer parameter estimation on a new patient’s dMRI scan. The substrates include tissue from non-cancerous liver parenchyma, as well as from primary and metastatic cancers of the liver, such as: primary hepatocellular carcinoma (HCC); metastatic colorectal cancer (CRC); melanoma; breast cancer. The cancer environments encompass a rich variety of cytoarchitectures, including areas of active tumour with high cell density; areas rich in desmoplastic stroma or fibrosis; areas of necrosis; a mix of all of those, as well as regions at the tumour-liver interface. High-resolutions images of the substrates are shown in Supplementary Figs. S2, S3, and S4. In practice, the virtual tissue environments are represented through triangular meshes derived from the outline of cellular structures identified on HE images. As a first demonstration, the environments effectively consist of 3D structures with cylindrical geometry, obtained by prolonging 2D segmentations along the third dimension. dMRI signals are obtained from a substrate through MC simulations, in which water molecules are seeded uniformly within each substrate in both intra-cellular (IC) and extra-cellular (EC) spaces. Afterwards, molecules experience Brownian random walks, simulating diffusion, during which they interact with the boundaries of the cellular structures through elastic reflection or permeation. We simulated 225 realisations of each substrate by varying the intrinsic IC and EC diffusivities (D_0∣in and D_0∣ex) and the cell membrane permeability κ, obtaining a total of 4050 microstructures.

Fig. 1: Illustration of our MC simulation framework generating synthetic dMRI signals from histological images.

The framework relies on the following open-source software packages: QuPath, Inkscape, Blender, MCDC. a Simulation of dMRI signals from histology, used to build numerical signal models. b Inference of cancer biological properties on a new patient’s scan based on such numerical models.

The virtual tissue environments characterise a variety of tissue microstructures

We characterised the reconstructed tissue environments through several metrics, related to the cell size (CS), cell density and to other IC and EC properties. The metrics were:

• the substrate area and cellularity (number of cells per mm²);

• the IC area fraction f_in;

• the fraction of the EC space occupied by luminal structures f_l;

• the diameters of the lumina d_lumen, when these are present;

• the mean of the cell size (CS) distribution mCS;

• the variance of the CS distribution varCS;

• the skewness of the CS distribution skewCS;

• two volume-weighted mean CS (vCS) indices, vCS_sph and vCS_cyl (for a system with spherical vs cylindrical geometry);

• shape and scale parameters of a gamma-distribution³⁰, which we fitted to the set of cell diameters {d_cell,1,  d_cell,2,  … } (see Supplementary Methods for details).

vCS_sph and vCS_cyl provide a characteristic CS for the substrate, similarly to mCS. However, as compared to mCS, they put more emphasis on larger cells, and are thus more direct counterparts of dMRI-derived cell size statistics compared to mCS^3,14 (note that in dMRI large cells contribute more to the measured signals than small cells, since they contain more water).

Table 1 reports value of the metrics for all substrates. The reconstructed cancer substrates encompass a rich variety of cytoarchitectures, showing large between-substrate contrasts in all histological metrics. For example, f_in values as high as 0.868 are seen in areas featuring densely packed cells, as in the non-cancerous liver parenchyma, while f_in as low as 0.130 in seen in CRC fibrosis, or as low as 0.024 in necrosis. The table also highlights contrasts in terms of CS. The largest cells are found in the non-cancerous liver (mCS around  ~ 16 μm), while all cancers feature the presence of smaller cells. Differences in CS are also seen within the same type of cancer, e.g., mCS of  ~13 μm and  ~6 μm in two different CRC substrates. Substrates also feature different skewnesses of the CS distribution, with positive skewCS in most cancers, and negative skewCS in the non-cancerous liver. Finally, in some substrates (e.g., CRC) the EC space features the presence of large lumina, with equivalent diameters as large as  ~ 90 μm. Substrates also include areas of partial volume between non-cancerous hepatocytes and cancer cells (substrates 10, 11, 12) with different proportions, a fact that is reflected in different values of skewCS.

Table 1 Properties of the substrates used for MC simulations, drawn on histological tissue coming from liver tumour biopsies from 10 cancer patients

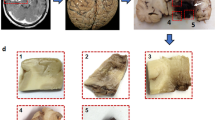
Figure 2 illustrates the different cellular structures that have been identified on HE histology to enable the substrate reconstruction. These are shown in four representative substrates, namely: non-cancerous liver, CRC, breast cancer, and melanoma. The figure highlights again the richness of microstructural characteristics included in our substrates. Tightly packed cells are seen in both non-cancerous liver and in melanoma, with the former showing much larger cells than the latter (mCS of almost 16 μm in non-cancerous liver, twice as large as the approximately 8 μm seen in melanoma). A wide range of IC fraction f_in is also seen, ranging from 0.076 in the breast cancer substrate (containing fibrotic areas and extensive necrosis) up to 0.846 for the non-cancerous liver. Finally, large luminal spaces in CRC substrates occupy a considerable portion of the EC space, with areas equivalent to the space taken by hundreds of cells.

Fig. 2: Visualisation of four illustrative substrates used for MC diffusion simulations.

a, d, g, j HE histological images. b, e, h, k SVG files reconstructed with the Blender software package, showing different substrate features (e.g., cells and debris in green, vessels in red, lumina in dark blue). c, f, i, l Histograms depicting the CS (i.e., cell diameter) distribution for each substrate, with summary statistics and with a Gamma distribution fit superimposed onto it (black solid line). From top to bottom: non-cancerous liver (substrate 4), colorectal cancer (substrate 8), breast cancer (substrate 17), melanoma (substrate 18).

The simulation of the diffusion random walks on the virtual cancer substrates corresponding to Table 1 is feasible on standard computational hardware. We timed the simulation time for a representative substrate (substrate 4) on a 64-core, 3.169 GHz AMD Ryzen Threadripper^TM PRO 5995WX CPU. The simulation of 110 ms of diffusion for 20,000 spins, for a temporal resolution of 46.4 μs, took 45 s on a single thread for a fixed value of IC/EC diffusivity and permeability κ. The simulation time can be approximately 10 times longer in some rare cases, when the IC fraction is very low (e.g., in necrotic substrates), due to internal memory handling in the MCDC simulator.

Histo-μSim parameter estimation outperforms analytical signal modelling

We used the set of paired examples made of synthetic dMRI signals from MC simulations and corresponding histological features to inform tissue parameter estimation on unseen dMRI signals. The approach was compared to the fitting of a well-established, multi-exponential analytical dMRI signal model, which accounts for restricted IC diffusion within impermeable cylindrical structures (given the cylindrical symmetry of our substrates), as well as hindered, EC diffusion^6,7 (see Methods, Eq. (4)). The experiment, performed on signals obtained for κ = 0 (impermeable cells, as assumed in the analytical signal model), unequivocally suggests that our proposed parameter estimation strategy outperforms more standard analytical model fitting, since the former provides tissue parameter estimates that correlate more strongly to ground truth values than the latter, and which show less variability. For this experiment, we built an MC-informed forward signal model (referred to as forward model 1) taking vCS_cyl, f_in, D_0∣in and D_0∣ex as input tissue parameters, being these the same tissue parameters of the analytical model. To build the signal model, we only used signals generated from impermeable cells (κ = 0), as the analytical model used for benchmarking does not account for water exchange. For the same reason, we also tested both Histo-μSim and the analytical model on signals corresponding to substrates made of impermeable cells.

Figure 3 shows scatter density plots of ground truth versus estimated tissue parameters in in silico experiments. The figure refers to the analysis of dMRI signals synthesised with a pulsed-gradient spin echo (PGSE) protocol matching that of available in vivo scans, and referred to as protocol PGSE-in (see Materials and Methods). The protocol includes multiple b-values (maximum b = 1500 s/mm²) and multiple diffusion times, and results refer to simulations of impermeable cells (κ = 0). It is apparent that f_in and D_0∣in are, respectively, the metrics that are the most/the least accurately predicted. Correlation coefficients between ground truth and predicted values are consistently higher for Histo-μSim than for the analytical model. While for both models a strong correlation between estimated and ground truth is seen for f_in, a moderate correlation is seen for vCS_cyl for MC-informed fitting (r = 0.63), and a low correlation for the analytical model (r = 0.14). For D_0∣in instead, the correlation is weak for both approaches, although considerably higher for Histo-μSim (r = 0.30 against 0.04). Interestingly, we also observe a moderate correlation between ground truth and predicted D_0∣ex for MC-informed fitting (r = 0.47). Note that the analytical model in Eq. (4) enables the estimation of the EC apparent diffusion coefficient (ADC) ADC_ex, and not of the intrinsic EC diffusivity D_0∣ex. The existence of “hot spots” (clustered points) in the scatter density plots in Fig. 3 is a consequence of the discrete nature of the distribution of the ground truth tissue properties, given that our data set consists of 18 unique values on IC fraction and volume-weighted CS (vCS), 5 values of D_0∣in and D_0∣ex, and 9 values of κ. For example, it is apparent that histological vCS tends to cluster around 10 μm and 18 μm, with fewer values around 14 μm. Clustering in the y-direction outside the diagonal instead indicates bias in the estimation, as seen clearly, for example, for D_0∣in inference through the analytical signal model.

Fig. 3: Scatter density plots between ground truth and estimated tissue parameters and Bland-Altman plots comparing the performances of MC-informed forward model 1 with a standard analytical signal model.

First row, (a–d): scatter density plots and correlation between ground truth and estimated parameters for forward model 1 (from left to right: f_in, vCS_cyl, D_0∣in, D_0∣ex). Second row, (e–g): scatter density plots and correlation between ground truth and estimated parameters for the analytical signal model (from left to right: f_in, vCS_cyl, D_0∣in). Third row, (h–k): Bland-Altman plots for forward model 1 (from left to right: f_in, vCS_cyl, D_0∣in, D_0∣ex). Fourth row, (l–n): Bland-Altman plots for the analytical signal model (from left to right: f_in, vCS_cyl, D_0∣in). Scatter density plots also include the identity line for reference, and the Pearson’s correlation coefficient between ground truth and estimated parameter values (n=4050 unique data points from 18 independently-simulated substrates per subplot). Bland-Altman plots relate the average values between estimated/ground truth parameters (x-axis) to their difference (y-axis), and include the bias and upper/lower limit-of-agreement (LOA). The figure refers to the estimation for protocol PGSE-in.

Histo-μSim enables the data-driven estimation of cell size and permeability

Motivated by the encouraging results on CS and density mapping obtained by comparing Histo-μSim to a standard analytical signal model, we also investigated whether our framework enables the data-driven, equation-free estimation of additional microstructural properties of cells. To this end, we investigated the joint estimation of a volume-weighted CS index (vCS_cyl) and of a characteristic cell membrane permeability metric κ, given their potential relevance as non-invasive biomarkers in cancer^31,32.

We tested MC-informed fitting of a second signal model, referred to as forward model 2, with tissue parameters vCS_cyl, f_in, D_0∣in, D_0∣ex and κ. Figure 4 shows parameter estimation results for the same PGSE-in protocol used previously in Fig. 3 as well as for two additional dMRI protocols, namely: a DW twice-refocussed spin echo (TRSE) acquisition, matching that of another set of available in vivo dMRI scans (maximum b-value: 1600 s/mm²); a second PGSE acquisition, matching a high-field acquisition performed on fixed ex vivo mouse tissue (maximum b-value: 4500 s/mm²). We will refer to the former as protocol TRSE, while to the latter as protocol PGSE-ex.

Fig. 4: Scatter density plots between ground truth and estimated tissue parameters for MC-informed parameter estimation (forward model 2) and for the three MRI protocols considered in this study.

Each plot corresponds to a metric and protocol. Top row (a–e): PGSE-in protocol; mid row (f–j): TRSE protocol; bottom row (k–o): PGSE-ex protocol. First column form left (a, f, k): IC fraction f_in; second column form left (b, g, l): CS index vCS_cyl; third column form left (c, h, m): intrinsic IC diffusivity D_0∣in; fourth column form left (d, i, n): intrinsic EC diffusivity D_0∣ex; fifth column form left (e, j, o): cell membrane permeability parameter κ. Pearson’s correlation coefficients between ground truth and estimated parameters are included in each plot (n = 4050 unique data points from 18 independently-simulated substrates per subplot).

Findings from all protocols converge towards the feasibility of estimating jointly vCS_cyl and κ through simulation-informed fitting, given that moderate-to-strong correlations are seen between ground truth and estimated parameter values for these metrics. Regarding vCS_cyl, we observed moderate and strong correlations between ground truth and estimated values (minimum r of 0.55 for protocol PGSE-in, maximum r of 0.81 for protocol PGSE-ex, featuring the shortest diffusion times). As far as κ is concerned instead, we observe a moderate correlation between ground truth and estimated parameters (maximum r of 0.45 for the TRSE protocol, featuring instead the longest diffusion times). Results for the estimation of f_in, D_0∣in and D_0∣ex are in line with what was seen for forward model 1, namely: good agreement for f_in in all cases, with highest correlation r = 0.89 for TRSE; moderate correlations for D_0∣ex, with highest correlation r = 0.43 for PGSE-in; weaker correlations for D_0∣in, with highest r = 0.38 for PGSE-ex.

Figure 5 reports Bland-Altman plots corresponding to the estimation of tissue parameters from forward model 2. The panels report plots for all metrics and protocols, and include bias and limit-of-agreement (LOA) figures. While no systematic biases in the estimation are seen for any metrics, the figure highlights that the estimates of D_0∣in, D_0∣ex, and, to a lesser extent, κ are considerably more variable than those of f_in and vCS_cyl. The plots clearly highlight the challenge of resolving jointly D_0∣in and a CS index from compact protocols that are feasible in the clinic. It also demonstrates that the protocols that include short diffusion times allow for higher precision in the inference of this metric (compare protocol PGSE-ex, featuring short diffusion times, against the clinical TRSE protocol, featuring much longer diffusion times).

Fig. 5: Bland-Altman plots relating ground truth and estimated parameters for all tested dMRI protocols.

The plots relate the average values between estimated/ground truth parameters (x-axis) to their difference (y-axis), and include the bias and upper/lower limit-of-agreement (LOA) (n = 4050 unique data points from 18 independently-simulated substrates per subplot). Top row (a–e): PGSE-in protocol; mid row (f–j): TRSE protocol; bottom row (k–o): PGSE-ex protocol. First column form left (a, f, k): IC fraction f_in; second column form left (b, g, l): CS index vCS_cyl; third column form left (c, h, m): intrinsic IC diffusivity D_0∣in; fourth column form left (d, i, n): intrinsic EC diffusivity D_0∣ex; fifth column form left (e, j, o): cell membrane permeability parameter κ.

Histo-μSim microstructural parameters correlate with their histological counterparts in fixed mouse tissue

We tested Histo-μSim fitting on pre-clinical PGSE scans, acquired at 9.4T on 8 formalin-fixed ex vivo mouse tissue specimens, for which HE sections were also available. These were: a non-cancerous breast and 3 breast tumours from the mouse mammary tumour virus (MMTV) polyomavirus middle T antigen (PyMT) transgenic mouse model^33,34, obtained at weeks 9, 11 and 14; a normal spleen and a spleen suffering from splenomegaly from the MMTV mice; two kidneys from C57BL/6 WT male mice (9 weeks old), one normal and one featuring folic acid-induced injury³⁵. Quantitative analyses also show that key Histo-μSim metrics correlate with their direct histological counterparts, as illustrated by the correlation matrix in Fig. 6. For example, we observe a statistically significant, positive, strong correlation between Histo-μSim f_in and vCS with histological f_in and vCS (r = 0.68 between f_in∣MC and f_in∣histo, p = 0.002; r = 0.74 between vCS_cyl∣MC and vCS_cyl∣histo, p = 0.001) These correlations are systematically stronger than those obtained for the analytical signal model, demonstrating the potential of Histo-μSim for increasing dMRI biological specificity (Fig. 6: r = 0.63, p = 0.005 between f_in∣AN and f_in∣histo; r = 0.37, p = 0.125 between vCS_AN and vCS_sph∣histo). Histo-μSim permeability κ also correlates moderately with the histological metrics. For example, positive correlations between κ and f_in∣histo and with all histological CS indices are seen (e.g., r = 0.56, p = 0.015 with f_in∣histo; r = 0.63, p = 0.006 with mCS_histo). Figure 6 also reports Bland-Altman plots relating MRI metrics to their histological counterparts. Both Histo-μSim and the analytical signal model underestimate the IC fraction and overestimate CS compared to histology, to a similar extent. However, Histo-μSim estimates show less variability than those from the analytical model, given the narrower range between the upper/lower LOA.

Fig. 6: Relationship between all MRI metrics and histological indices as obtained on fixed mouse tissue ex vivo.

Metrics from Histo-μSim are indicated by subscript MC, for “Monte Carlo simulation-informed''; metrics from the analytical signal models are indicated by subscript AN, for “analytical''; metrics from histology are indicated by subscript histo. MRI metrics are: IC fraction f_in; volume-weighted characteristic CS indices (vCS); intrinsic IC and EC diffusivities (D_0∣in and D_0∣ex); EC ADC (ADC_ex); cell membrane permeability κ. Panels to the left: results for Histo-μSim; panels to the right: results for the analytical two-compartment model. Top row: correlation matrices (a) for Histo-μSim; (b) for the analytical model. p < 0.05 is flagged by yellow squares (sample size n = 18 ROIs). Histological metrics were obtained through manual segmentation of cells on HE data. Middle row: Bland-Altman plots, with biases and upper/lower limit-of-agreement (LOA) comparing MRI and histological f_in ((c) for Histo-μSim; (d) for the analytical model). Bottom row: Bland-Altman plots, with biases and LOAs comparing MRI and histological vCS ((e): vCS_cyl for Histo-μSim; (f) vCS_sph for the analytical model). To aid the visual comparison of the results of each model, the same limits have been used for the axes related to f_in and related to vCS in both models. This leads to an abrupt cut-off of the contours, and to the presence of empty white space, since the two models provide f_in and vCS estimates in slightly different numerical ranges.

Tables 2 and 3 list dMRI and histological metrics within all ROIs. The values in the tables were used to generate Fig. 6. Contrasts in histological metrics agree with dMRI in several cases. For example, histological mCS and vCS, as well as permeability κ are lower in necrotic compared to non-necrotic areas in the week 14 breast tumour (ROI 2 vs 1), or in the normal spleen compared to the normal kidney (ROI 17 compared to ROI 16). Histological f_in is higher in the week 9 breast tumour than in the non-cancerous breast (ROI 1 vs 5), and very low in necrosis (ROI 2). κ is lower in the non-cancerous breast, compared to the breast tumours. In some cases, differences between dMRI and corresponding histology metrics are also seen, e.g., the low dMRI f_in seen in the healthy kidney underestimates considerably the corresponding f_in values from histology (ROI 16).

Table 2 Mean values of metrics from Histo-μSim forward model 2 and from histology within different ROIs drawn on the breast, kidney and spleen tissue scanned ex vivo on a pre-clinical 9.4T MRI system

Table 3 Mean values of metrics from the analytical signal model and from histology within different ROIs drawn on the breast, kidney, and spleen tissue scanned ex vivo on a pre-clinical 9.4T MRI system

Figure 7 shows examples of dMRI and co-localised HE images in the four breast specimens. These contain a variety of cytoarchitectural environments, with higher inter-sample and intra-sample heterogeneity. For example, the non-cancerous breast features areas rich in stroma. Conversely, higher cell densities are observed in the three MMTV-PyM tumours. At late stages (week 14 tumour), widespread necrosis is also seen. Figure 7 also shows parametric maps from forward model 2 in the same breast specimens, namely: f_in, D_0∣in, vCS_cyl, D_0∣ex and κ.

Fig. 7: Images from the breast tissue samples that were scanned ex vivo at 9.4T, and Histo-μSim parametric maps.

Panel (a) on top: b = 0 image and HE sections. Moving clock-wise: week 9 MMTV-PyM breast tumour (top left), non-cancerous breast (top right), week 11 MMTV-PyM breast tumour (bottom right), week 14 MMTV-PyM breast tumour (bottom left). Second row (b–d): IC fraction f_in (b); volume-weighted cell size index vCS_cyl∣MC (c); intrinsic IC diffusivity D_0∣in (d). Third row (e, f): intrinsic EC diffusivity D_0∣ex (e); cell membrane permeability κ (f). For each metric, we show results on the four breast specimens. Examples of histological tiles in different ROIs are also included, alongside with corresponding quantitative histological indices and mean MRI metrics for each ROIs. The coefficient of determination R² between measured dMRI signals and signals predicted through Histo-μSim model fitting is reported for the shown ROIs, alongside Histo-μSim and histological metrics. Areas with high concentration of fat (resulting in very low b = 0 signal due to fat suppression) were not included in the parametric map computation.

The variability of cellular microarchitectures seen in Fig. 7 is reflected in the parametric maps. Reduced f_in is seen in areas compatible with necrosis within the week 14 tumour (ROI 2, Fig. 7). Additionally, higher f_in is seen in the week 11 tumour, compared to the non-cancerous breast. On histology, this contrast corresponds to presence of areas featuring high cellularity (Fig. 7, ROI 4), compared to stroma in the non-cancerous breast (Fig. 7, ROI 5). Changes in CS with respect to the non-cancerous breast are also seen, e.g., reduced vCS in areas compatible with the presence of cell debris in necrosis (ROI 2, Fig. 7). Local variations of IC and EC diffusivities D_0∣in and D_0∣ex are also seen. For instance, D_0∣in is lower in areas with high f_in (e.g., in ROI 4 in the week 14 tumour), and D_0∣ex is the highest at the interface between specimens and the agarose. Within- and between-sample variations in cell membrane permeability κ are observed, such as lower κ in the week 9 tumour, compared to week 14.

Supplementary Fig. S5 reports maps of microstructural parameters from analytical signal model fitting in the mouse breast specimens. Map contrasts generally match those from Histo-μSim fitting, and highlight similar microstructural characteristics (e.g., necrosis in the week 14 MMTV breast tumour). Overall, the presence of luminal spaces in breast tissue appears underestimated in the f_in map from both the analytical signal model and from Histo-μSim. We speculate that this may result, at least in part, from partial volume effects with highly cellular areas, which is likely more intense in MRI (slice thickness: 570 μm) than on histology (section thickness: 3 μm).

Supplementary Figs. S6 and S7 show Histo-μSim maps and HE data in a normal spleen and in splenomegaly secondary to late-stage MMTV tumour growth. The spleens exhibit a patchy structure in most dMRI metrics. The same pattern is seen on HE histology, where an alternation of white and red pulps is seen (white pulps are known to contain higher T-cell density than red pulps, which are instead rich in blood and iron). Supplementary Figs. S6 and S8 show results from the two kidney samples: one normal, and one following folic acid-induced injury. On histology, the former shows normal representation of all kidney structures, while the injured case shows proximal tubule alteration and extensive inflammation. In terms of dMRI metrics, the injured kidney shows increased f_in and reduced D_0∣in and D_0∣ex as compared to the normal case. Higher f_in is also seen in the injured kidney cortex as compared to its medulla, a finding that corresponds to higher cell density on visual inspection of histology stains. Higher permeability κ is observed in the injured kidney, compared to the control organ.

Supplementary Table S8 reports the coefficient of determination (R²) for Histo-μSim as obtained in all mouse tissue ROIs. Histo-μSim explains most of the signal variability in almost all ROIs, with R² as high as 0.99 in various breast and kidney ROIs. However, between-ROI differences in R² values exist, with lower R² seen, for example, in necrotic ROIs (R² of around 0.68) or, even more, in the ROI drawn in the enlarged spleen (splenomegaly; R² of around 0.05). The lower R² values in these ROIs likely result from noise effects, since (i) the DW signal decay is stronger in necrosis than in highly cellular areas, (ii) the enlarged spleen has a short T2 (see b = 0 image in Supplementary Fig. S6). The average R² across all ROIs is just below 0.88. This finding demonstrates that Histo-μSim captures the salient characteristics of the dMRI signal, and is therefore a valid representation to explain its variability across b-values and diffusion times.

Histo-μSim is feasible in cancer patients in vivo and reveals meaningful inter- and intra-tumoural contrasts

Lastly, we tested Histo-μSim for tumour characterisation in cancer patients in vivo. In this demonstration, we included scans from 27 patients suffering from advanced solid tumours, primary or metastatic. These were scanned at abdominal or pelvic level, on either a clinical 1.5T or 3T MRI scanner, with a 15-minute dMRI protocol, maximum b-value of 1600 s/mm² on the 1.5T system (mean signal-to-noise ratio (SNR) of 36.4 at b = 0 and minimum TE), and of 1500 s/mm² on the 3T system (mean SNR of 77.3 at b = 0 and minimum TE; per-patient SNR statistics reported in Supplementary Table S2). Moreover, we also included HE-stained histological material from a biopsy, which was collected from one of the patient’s tumours, approximately one week after MRI. The analysis of the dMRI scans shows that Histo-μSim is feasible in vivo within clinically acceptable scan times, and that it provides metrics whose intra-tumour and inter-tumour contrasts are compatible with the cellular environments seen on the biopsies. Furthermore, despite the inherent challenge of comparing dMRI maps obtained over large tumoural areas with histological metrics obtained from a tiny sliver of biopsied tissue, MRI-histology correlations show that Histo-μSim IC fraction f_in∣MC and vCS_cyl∣MC are positively correlated with their histological counterparts from the HE images, albeit weakly (Fig. 8: r = 0.32 and p = 0.102 between f_in∣MC and f_in∣histo; r = 0.29 and p = 0.148 between vCS_cyl∣MC and vCS_cyl∣MC). These correlations are stronger than those of a standard analytical signal model (r = 0.25, p = 0.203 between f_in∣AN and f_in∣histo; r = 0.014, p = 0.943 between vCS_AN and vCS_sph∣histo). Notably, cell membrane permeability κ shows negative correlations with all histological indices. However, the correlation strength is much weaker than what was observed in mice (e.g., r = −0.136, p = 0.500 with f_in∣histo; r = −0.248, p = 0.213 with mCS_histo). While these correlations are not significant, they feature opposite sign compared to the same correlations seen between MRI/histology in mouse tissue scanned ex vivo. We speculate that this difference may arise, at least partially, from the fact that mouse specimens were fixed. As a consequence, cells do not exhibit active functions, a fact that may alter water exchange considerably compared to a living organism. All in all, these findings show that Histo-μSim has clinical potential, as it may serve as a useful tool for enhanced non-invasive tumour biology characterisation through dMRI in real-world clinical settings.

Fig. 8: Relationship between all MRI metrics and histological indices obtained in cancer patients scanned in vivo.

Metrics from Histo-μSim are indicated by subscript MC, for “Monte Carlo simulation-informed''; metrics from the analytical signal models are indicated by subscript AN, for “analytical''; metrics from histology are indicated by subscript histo. MRI metrics are: IC fraction f_in; volume-weighted characteristic CS indices (vCS); intrinsic IC and EC diffusivities (D_0∣in and D_0∣ex); EC ADC (ADC_ex); cell membrane permeability κ. Panels to the left: results for Histo-μSim; panels to the right: results for the analytical two-compartment model. Top row: correlation matrices ((a) for Histo-μSim; (b) for the analytical model). p < 0.05 is flagged by yellow squares (sample size n = 26 biopsies). Histological metrics were obtained by automatic image processing in QuPath. Middle row: Bland-Altman plots, with biases and upper/lower limit-of-agreement (LOA) comparing MRI and histological f_in ((c) for Histo-μSim; (d) for the analytical model). Bottom row: Bland-Altman plots, with biases and LOAs comparing MRI and histological vCS ((e): vCS_cyl for Histo-μSim; (f) vCS_sph for the analytical model). To aid the visual comparison of the results of each model, the same limits have been used for the axes related to f_in and related to vCS in both models. This leads to an abrupt cut-off of the contours, and to the presence of empty white space, since the two models provide f_in and vCS estimates in slightly different numerical ranges.

Figure 8 also visualises the agreement in IC fraction and CS estimation of Histo−μSim and of the analytical signal model with respect to histology, through Bland-Altman plots. Similarly to what was observed for the mouse data, both Histo−μSim and the analytical signal model underestimate f_in compared to histology, to similar extents. Conversely, in this case both MRI approaches underestimate CS compared to histology. This result does not match what was observed in the mouse data, where MRI CS was systematically higher than histological CS. This discrepancy likely results from the fact that biopsies may have shrunk less than the whole-tumour HE sections obtained in mice. Other effects may also have played a role, e.g., mechanical compression of the cells in situ due to mass effects, which affected the in vivo dMRI acquisition, but that was not present once tissue was extracted from the body.

Tables 4 and 5 summarises dMRI and histological metrics within all biopsied tumours. Both dMRI and histology reveal inter-tumour heterogeneity. dMRI-derived values of IC fraction f_in are consistently lower than reference histological f_in∣histo, and so is MRI vCS_cyl∣MC, compared to both vCS_cyl∣histo and vCS_sph∣histo. Between-tumour contrast in terms of diffusion metrics is also seen, as for the permeability κ. For example, the lowest κ values are observed in two melanoma cases.

Table 4 dMRI and histology metrics in cancer patients, with salient patients’ demographic and clinical information

Table 5 dMRI and histology metrics in cancer patients, with salient patients’ demographic and clinical information

Supplementary Table S7 investigates differences across the two most frequent primary tumour types in our in vivo MRI cohort, namely CRC and melanoma. This experiment is motivated by the fact that distinguishing cellular phenotypes non-invasively through imaging has potential application for differential diagnosis or for patient stratification in the clinic. These two cancers are characterised by distinct cellular phenotypes, with the former exhibiting the presence of large luminal spaces unlike the latter, and hence lower cell density (Table 1). As expected, CRC exhibits lower f_in∣histo than melanoma (mean/standard deviation: 0.498/0.139 in CRC and 0.685/0.073 in melanoma, with t-test p = 0.0173), a finding compatible with the presence of luminal spaces in the former type of cancer. Such a between-cancer cytoarchitectural difference seen on histology is replicated in MRI. Comparing CRC against melanoma, we observe a trend towards lower f_in∣MC in the former compared to the latter for Histo-μSim (mean/standard deviation of f_in∣MC: 0.219/0.0486 in CRC, while to 0.277/0.0556 in melanoma, t-test p = 0.0789), and lower f_in∣AN for the analytical signal model (mean/standard deviation of f_in∣AN: 0.193/0.035 in CRC, while to 0.273/0.060 in melanoma, t-test p = 0.0132). No differences between these two types of cancer are seen on cell size indices for any of histology, Histo-μSim and the analytical model.

Examples of parametric maps from Histo-μSim forward model 2 obtained in vivo are shown in Fig. 9 in two patients (ovarian cancer liver metastases, scanned at 1.5T; endometrial cancer, scanned at 3T), alongside clinical ADC. Maps show intra-tumour variability. For example, in the ovarian cancer case, the largest liver metastasis features reduced f_in and mCS and increased D_0∣ex in the necrotic core compared to the tumour outer ring, a fact that corresponds to hyperintense clinical ADC. Conversely, no within-tumour contrast is seen for other diffusion metrics, as for example D_0∣in and cell membrane permeability κ. For the endometrial cancer case, maps reveal different microstructural environments within the tumour, i.e., areas with higher/lower f_in, matching areas with lower/higher vCS. Inspection of histological images confirms the existence of heterogeneous cellular characteristics in both cases (Fig. 9), i.e., presence of active cancer and necrosis in the ovarian cancer case, and presence of necrotic areas with abundance of cell debris adjacent to areas with high cellularity in the endometrial tumour. Fitting of a standard analytical model provides metrics that show similar trends, highlighting again, for example, the necrotic core in the ovarian cancer metastasis (Supplementary Figs. S9 and S10).

Fig. 9: Parametric maps from Histo-μSim forward model 2 as obtained on two representative patients in vivo, scanned on two different MRI scanners.

Top: maps on ovarian cancer liver metastases (3T system); bottom: endometrial cancer (1.5T MRI system). From left to right, each panel reports a b = 0 image with the tumour outline ((a) and (l)) and then metrics f_in ((b) and (m)), vCS_cyl ((c) and (n)), D_0∣in ((d) and (o)), D_0∣ex ((e) and (p)) and κ ((f) and (q)). Below the metrics, details from a biopsy taken from one of the imaged tumours are also included (HE-stained biopsy in (h) and (s); necrosis in (i) and (t); active tumour in (j) and (u)). Below the b = 0 image, the standard Apparent Diffusion Coefficient (ADC) map is also shown ((g) and (r)).

Histo-μSim fits dMRI signal measurements in mouse tissue and in humans in vivo

Lastly, we studied the quality of Histo-μSim signal fitting against that of other popular dMRI signal models, which are being increasingly used in cancer applications. In more detail, we compared the fitting mean squared error (MSE) and the Bayesian Information Criterion (BIC)^36,37 of Histo-μSim against that of the other models. Lower values of both MSE and BIC are indicative of better fitting performances. While MSE provides a measure of the overall discrepancy between measured dMRI signals and model predictions, BIC also accounts for model complexity, penalising models with more parameters, compared to those with fewer. For this experiment, we compared Histo-μSim forward model 2 (the model accounting for water exchange) against the two-compartment analytical model described above. Additionally, we also compared it to popular Diffusion Kurtosis Imaging (DKI)³⁸ and to Restriction Spectrum Imaging (RSI)³⁹. Tables S3 and S5 report MSE rankings performed on the mouse and in vivo human data, while Tables S4 and S6 report BIC figures. When looking at MSE, Histo-μSim is the signal model that provides the best quality of fit in the highest number of mouse specimens (3 out of 8), as well as in the highest number of human scans in vivo (15 out of 27). However, when considering the BIC index, the performances of Histo-μSim drop, since the model contains more parameters than compact techniques such as as RSI and DKI (5 against 2 of RSI and DKI). In this case, RSI surpasses Histo-μSim in model rankings obtained on both mouse and human data. However, despite the better performances in terms on fitting quality, RSI only captures salient characteristics of the dMRI signal (i.e., the IC signal fraction), and fails to provide estimates of specific characteristics of the cellular compartment (CS and cell membrane permeability), which could become per se biologically-specific biomarkers in cancer.

Discussion

Summary and key findings

This article presents Histo-μSim, a new dMRI approach for microstructural parameter estimation informed by MC diffusion simulations within cellular environments reconstructed from histology. Our article has three main contributions. Firstly, it describes a practical step-by-step procedure, based entirely on freely available software, to reconstruct meshed cellular environments from histological images. These can be used to generate large dictionaries of realistic dMRI signals, coupled with histological properties. Secondly, it provides the scientific community with unique reference values of histology-derived cell size and density in non-cancerous and cancerous human liver tissues, information not easily found in the literature, yet essential to design the next-generation of cancer imaging techniques in radiology. Lastly, our paper showcases a numerical approach for dMRI parameter estimation informed directly by the simulated MC diffusion signals. The approach, feasible in cancer patients in vivo, is shown to outperform classical fitting of analytical signal models. As compared to the latter, Histo-μSim enhances parameter estimation on in silico data, and delivers metrics that correlate more strongly with co-localised histology.

Simulation framework

Our simulation framework combines freely available software tools (i.e., QuPath⁴⁰, Inkscape and Blender) to reconstruct meshed cellular environments from 2D histological images. These are stored as sets of ASCII PLY files, a common file format for meshed geometrical models, being accepted by popular open-source MC diffusion simulators such as MCDC⁴¹ or Camino⁴². The procedure to convert histological data into PLY files has been described in detail in this article, and practical examples as well as tutorials for would-be users are provided in our freely accessible online repository, at the permanent address https://github.com/radiomicsgroup/dMRIMC. Our detailed guidelines equip the community with a practical tool to increase the realism of dMRI simulations, narrowing the gap between radiology and histology in cancer applications.

Substrates

To demonstrate our framework, we segmented 18 cellular environments from HE-stained liver tumour biopsies, referred to as substrates. These included tissues of different kinds, e.g., non-cancerous liver parenchyma as well as primary cancers of the liver and liver metastases, which were characterised in terms of cell density, IC area fraction, presence and morphology of EC luminal spaces, and CS distribution characteristics. We compiled a table reporting this information in a systematic manner, providing the community with reference histological values for cancer applications. To our knowledge, histology-derived cell morphometry literature has traditionally focussed on the study of neuroanatomy^43,44, and limited quantitative data are available in body tissues or cancer, especially in relation to CS. Information on the expected CS and cell density of a tissue is essential to optimise dMRI acquisition protocols, e.g., to design b-values or diffusion times. Therefore, delivering such a data base is a major contribution of our work, as it may be used to devise innovative dMRI acquisition protocols tailored for body imaging.

Simulation-informed parameter inference in silico

We investigated whether synthetic dMRI signals generated through our histology-informed framework can be used to devise new strategies for microstructure parameter mapping, urgently sought in applications such as cell population profiling in oncology^10,11. To this end, we interpolated the discrete dictionary of paired examples of tissue parameters and synthetic dMRI signals using Radial Basis Function (RBF) regressors. This provided numerical forward models that do not rely on approximated analytical functional forms for the IC/EC signal, e.g., restricted diffusion within cells of regular shape and equal size^6,7, or Gaussian EC diffusion. Our new numerical forward models can be easily embedded into routine non-linear least squares (NNLS) fitting, based on likelihood maximisation⁴⁵.

We compared the performance of our approach in predicting a single CS (effective cell diameter) statistic³ against standard analytical approaches based on restricted diffusion within cylinders, in a scenario in which cell membrane permeability is negligible. Results not only point towards the superiority of our approach in CS estimation, but also show benefit in the estimation of other diffusion properties, such as the intrinsic cytosolic diffusivity or the IC fraction. We also studied the feasibility of estimating the intrinsic EC diffusion coefficient and a volume-weighted CS (vCS) statistics, jointly with the cell membrane permeability κ, without imposing any analytical functional form to the signal (forward model 2). Results in scatter density and Bland-Altman plots show that Histo-μSim enables the successful estimation of these metrics. We observe an accurate estimation of IC fraction and of the vCS, for a variety of acquisition protocols, with estimates that are moderately to strongly correlated to the ground truth. Satisfactory performances (i.e., moderate correlations with ground truth values) are also seen for the estimation of the intrinsic EC diffusivity D_0∣ex and the cell membrane permeability κ. These are microstructural properties that are still unexplored in cancer, and the satisfactory estimation in silico observed here motivates their investigation on actual preclinical and clinical MRI scans. These new indices may play a role in characterising the tumour microenvironment non-invasively, i.e., to describe properties of the stromal compartment, or the aggressiveness of tumours. Lastly, our in silico results confirm that the estimation of the intrinsic IC diffusivity D_0∣in is an extremely complex task^46,47,48 on clinically feasible protocols as those considered here. As a note, we point out that owing to the discrete nature of the input parameter space of the simulations, both density and Bland-Altman plots show a preference for areas corresponding to the input values inputs, a fact that is most apparent for metrics D_0∣in, D_0∣ex and κ.

Simulation-informed parameter inference in fixed ex vivo mouse tissue

After demonstrating CS and permeability mapping in silico, we tested its feasibility on actual MRI scans. For this experiment, we analysed both pre-clinical ex vivo data from 8 mouse tissue samples, as well as in vivo scans acquired on cancer patients with two clinical MRI systems. Notably, the tissue scanned on the pre-clinical system was considerably different from that used to build the numerical signal models (e.g., mouse breast tumours, kidneys, and spleens, versus human liver parenchyma and liver tumours), and thus served as a useful out-of-distribution test bed for generalisation. On these ex vivo mouse data, Histo-μSim captures most of the variability exhibited by the measured dMRI signal across diffusion times and b-values, with an average R² or around 0.88. Additionally, its parametric maps show a number of interesting and potentially relevant inter-sample and intra-sample contrasts, which are in most cases confirmed by histology both qualitatively and quantitatively. The co-localised MRI and histology data acquired in mice enabled a detailed MRI-correlation analysis, which essentially confirms findings from in silico experiments. Specifically, we observed moderate-to-strong correlations between dMRI and histological f_in and vCS. The MRI-histology correlation analysis also reveals that despite the good correlation between MRI and histological values of f_in and vCS, some differences between MRI and histological estimates of IC fraction f_in and CS exist. This is apparent, for example, in the Bland-Altman plots in Fig. 6, where an ellipsoidal clustering of the points is seen, pointing towards the fact that similar values of histological f_in (or vCS) can be mapped to different values of f_in (or vCS) in MRI. On the one hand, this can be a result of the known degeneracy of parameter estimation in dMRI^46,47,48. On the other hand, inaccuracies in histological metric computation may also have contributed, since histology is not free from artifacts (see detailed methodological discussion in section 3.8 below on this point).

However, all in all, the MRI-histology correlation study demonstrates the potential of Histo-μSim to boost the biological specificity of dMRI towards cancer, and are encouraging, given i) the relatively small size of our sample; ii) the inherent difficulty of ensuring accurate co-localisation between dMRI and histology; iii) the differences between the substrates used to build the models and the tissue imaged ex vivo; iv) the fact that these MRI-histology correlations were stronger than those from standard analytical signal model. Globally, the ex vivo experiments suggest that Histo-μSim, beyond being a useful representation that captures most of the observed signal variability, may also provide new biomarkers of tissue microstructure to shed new light onto the presence of different cell populations in a voxel, through CS morphology and permeability mapping.

Simulation-informed parameter inference in cancer patients in vivo

Following extensive comparison to histology on preclinical MRI data, we also demonstrated Histo-μSim in a pilot cohort of patients in vivo, and compared Histo-μSim metrics to histological indices from HE biopsies collected from one of the imaged tumours. This demonstration shows that Histo-μSim maps can be obtained with dMRI scans that are feasible in the clinic, i.e., not exceeding 15 minutes, with moderate maximum b-values (around 1500 s/mm²), and based on vendor-provided sequences. The inspection of parametric maps reveals key inter-tumour and intra-tumour contrasts, which are plausible given the high microstructural heterogenity seen in the HE-stained biopsied tissue. For example, areas lying within tumour necrotic cores show reduced f_in and vCS, compatible with necrosis and presence of cell debris. Histologically-meaningful contrasts in MRI metrics are also seen, for example, when comparing tumour types, as CRC and melanoma malignancies. These are the two most common cancers in our pilot cohort, and are known to feature notably different architectures at the cellular level. We observed lower IC fraction in CRC than melanoma tumours in histology, a finding compatible with the presence of large, fluid-filled luminal structures in the former. This contrast was replicated in MRI metrics obtained from both Histo-μSim and, even more clearly, for the analytical signal model, highlighting the utility of dMRI signal models in enhancing the biological specificity of imaging towards cancer.

The collection of biopsy data enabled a second MRI-histology correlation study. Despite the inherent challenge of relating a small sliver of biopsied tissue to MRI metrics evaluated over large tumours, the new biopsy-MRI comparison confirms that Histo-μSim provides metrics that correlate more strongly to their histological counterparts than standard analytical signal models. This result suggests, again, that Histo-μSim may contribute to increasing the biological specificity of dMRI, compared to current state-of-the-art multi-exponential approaches. Nevertheless, we acknowledge that in this case correlations between dMRI and histology are weaker. The observed correlation levels are not surprising given that we could not locate the exact tumour location where the needle was inserted. Because of this, we included all MRI voxels within the tumour to obtain per-tumour MRI metrics in our MRI-histology comparison, a fact that has reduced the accuracy of the co-localisation between the two modalities. Nevertheless, we also acknowledge that other factors may have contributed to explaining the difference in correlation seen on in vivo human data, compared to ex vivo mouse tissue. A possible explanation could be, for example, that tumours in mice are more homogeneous than in humans, given that human data was acquired in advanced, heavily pre-treated patients. This might have caused histological sampling bias to be less problematic in mice than in patients, leading to higher MRI-histology correlations. Other aspects potentially contributing to the discrepancy between histological and MRI estimates of IC fraction f_in and CS are similar to those discussed for the ex vivo data above, namely: degeneracy in MRI parameter estimation^46,47,48; inaccuracies in histological metric computation.

All in all, our pilot in vivo demonstration in cancer patients demonstrates the potential of microstructural imaging to provide phenotypical characterisations of tumours at the cellular level, and thus complement gross information on tumour size provided by standard-of-care radiology.

Histo-μSim fitting quality in mouse and human scans

Lastly, we studied the quality of Histo-μSim model fitting, comparing its fitting performances to those of other popular diffusion techniques, as for example DKI³⁸ and RSI³⁹, by means of the fitting MSE and the BIC³⁶ indices. Lower values of both metrics point towards better fitting performances, with BIC essentially correcting MSE to penalise model complexity. Results on both fixed mouse tissue and in cancer patients in vivo show that Histo-μSim provides the best performances in terms of MSE, being the top-ranking model in most mouse and human scans. This finding demonstrates the excellent capabilities of Histo-μSim to describe dMRI contrasts across a variety of b-value ranges, diffusion times, and acquisition schemes. However, detailed analyses of BIC show that simpler models, containing fewer parameters than Histo-μSim, surpass the performances of the proposed approach when model complexity is penalised. This is the case, for example, for RSI, a model which, in our custom implementation, features only 2 free parameters, against 5 of Histo-μSim. Despite the drop in performances, Histo-μSim still ranks either first or second in BIC in the majority of in vivo cases, i.e., even after being penalised for model complexity.

Overall, these results suggest that the good fitting performances of Histo-μSim, jointly with its histology-informed design, make it a promising new tool to characterise dMRI contrasts with biologically meaningful metrics. Nonetheless, the results also highlight that simple approaches may still suffice to deliver compact representations of the dMRI signal, especially in those applications where biomarker sensitivity, rather than biological specificity, is of interest. This is the case, for example, also for well-established clinical ADC measurement. We point out that Histo-μSim aims to tell apart the different biological sources underlying contrasts in simple metrics such as ADC, e.g., by distinguishing between areas featuring different cell sizes, for a fixed cell density. In other words, with Histo-μSim we aim to provide complementary information to standard diffusion imaging, boosting the biological specificity of standard-of-care radiology. Nevertheless, it should be remembered that in contexts where only an ADC map is sufficient to solve a clinical task, there would be no need to acquire longer scans for Histo-μSim computation, as short protocols (e.g., featuring as few as two-b-value) and simple processing pipelines could suffice.

Methodological considerations and limitations

We acknowledge some potential limitations of our approach. The first one relates to the manual reconstruction of virtual tissue environments from histology. Despite some remaining inaccuracies, the manual outlining has enabled the segmentation of cell boundaries, difficult to achieve with high accuracy and high precision through automatic cell segmentation software such as QuPath⁴⁰ (Supplementary Table S1). Nevertheless, we acknowledge that the approach is inherently slow and difficult to scale up to create larger dictionaries of synthetic signals and histological properties, essential to support more advanced parameter estimation techniques (e.g., through deep learning). In future, we plan to expand our tissue environment data bases through automatic histological image processing, and explore more sophisticated parameter estimation methods as those used in the first demonstration of Histo-μSim.

Secondly, we built virtual tissue environments effectively characterised by cylindrical geometries, and then focussed on the analysis of 2D diffusion. This was due to the availability of a large data set of HE-stained sections in human and mouse tissue (inherently 2D). From the 2D segmentations, we essentially had two options to build 3D meshes for Monte Carlo simulation, namely: (i) inferring somehow the 3D shape of the cells from the 2D outlines, or (ii) focussing on diffusion random walks in the cut plane, disregarding completely the third dimension. We preferred the latter option, as the former would have required strong assumptions on the 3D shape of the cells, a fact that could have equally led to biases. In future, we plan to perform simulations that capture the full 3D complexity of the tissue substrates, reconstructing these, for example, from 3D micrographs²⁴ or from 3D confocal microscopy⁴⁹ data.

To give an intuition of the effect of our 2D modelling strategy on the diffusion signal decay, we compared the diffusion signal from a cell cylindroid derived from a 2D cell segmentation against that of a 3D spheroid derived from the same outline (effective cell radius: 7.5 μm). The spheroid was derived by shrinking the 2D outline of the cell isotropically, along the through-plane direction, on both sides of the 2D cut plane. The comparison, reported in Supplementary Fig. S11, shows the instantaneous, radial IC diffusion coefficient D_in(t) as a function of the diffusion time t, as well as the signal ${e}^{-b{D}_{in}(t)}$ for various b-values (D_0∣in = 2 μm²/ms). The figure shows that D_in(t) from the cylindroid is always higher than that of the spheroid, leading to stronger signal decay for any t. This difference is more apparent at shorter t, and at higher b. In practice, this implies that if actual dMRI signal measurements arise from roughly spherical cells, the proposed cylindroid model likely underestimates histological cell size, compared to a spheroid model. This is due to the fact that for a fixed diffusion time and intrinsic IC diffusivity, the cylindroid model always provides higher IC ADC than the spheroid model. Hence, the CS that best explains any measured IC ADC is going to be smaller for the cylindroid model, compared to the spheroid one. This potential source of bias should be accounted for when interpreting results from Histo-μSim.

Another consequence of relating 2D histological information to 3D MRI data is that the co-localisation between the two is only approximate. The two modalities feature not only different in-plane resolutions (0.45 μm histology, 200 μm dMRI), but also different thicknesses (3 μm in histology, 570 μm in MRI). To minimise effects coming from the first resolution discrepancy, we extracted histological ROIs over large patches of size comparable to that of a dMRI voxel (i.e., between approximately 50 to 100 μm; Supplementary Fig. S13). However, the wild difference in terms of thickness implies that tissue that contributed to the dMRI signal was not captured in the histological assessment. We speculate that this may have impoverished the correlation between MRI and histology indices, and we acknowledge that this is a severe limitation of any MRI-histology correlation study that does not rely on full, 3D histology. Aware of this intrinsic shortcoming of our approach, we obtained different HE sections for each mouse specimen, at different microtome depths, across the whole organ. On visual inspection, the best match between MRI and histology was obtained when both MRI and histology images were derived roughly in the middle of the specimen. However, we remark once more that the correspondence between MR and HE images in our mouse data set is only approximate, and that full 3D histology (e.g., through confocal microscopy) would be required to enhance MRI-histology co-localisation.

Regarding the set-up of a dictionary of virtual cancer environments to inform dMRI model fitting, we stress that in this first demonstration of Histo-μSim we only used 18 histology-derived tissue reconstructions. While we effectively created a rich dictionary of signals and coupled tissue parameters by varying the IC/EC diffusivities and the cell membrane permeability, we point out that such a limited set-up does not suffice to deliver a comprehensive dictionary that can be deployed in all applications. For example, our virtual tissue dictionary did not include examples of large areas featuring tightly packed lymphocytes, which are seen, for examples, in lymphomas, where malignant lymphocytes can invade the liver parenchyma. This implies that care is needed when interpreting current Histo-μSim maps in contexts such as lymphoma imaging, or for immune cell infiltration detection, as in immunotherapy. In future work we aim to expand the data base of virtual cancer environments considerably by virtue of automated histological image processing, and thus broaden the range of applicability of the proposed technique.

Related to the tissue parameters used to build tissue-signal dictionaries, we would like to remark that one of the key parameters studied in this article, cell membrane permeability κ, is difficult to determine accurately, given the challenge in independently measuring it from other parameters (Eq. (1) and Eq. (2)). Future experiments in vitro are warranted to further validate Histo-μSim cell permeability estimates. These could include cell pellets or suspensions with controlled permeability levels⁵⁰, and comparisons of Histo-μSim κ values to those from other MR contrasts, e.g., T1 mapping from inversion recovery imaging⁵¹.

Moreover, in this study we illustrated the benefits of relaxing some of the constraints and hypotheses underlying standard analytical diffusion models through numerical simulations. However, we point out that this first demonstration is not free from assumptions, since Histo-μSim tissue parameter estimates inherit the hypotheses made to conduct the MC simulations themselves. It is possible that some of the discrepancies observed between dMRI and histology may have been exacerbated by important microstructural properties that were not accounted for in our simulated random walks, as for example: variability in intrinsic diffusivity or permeability among cells or between lumina and EC space; differences in intra-compartament relaxation properties^8,12,52; additional sources of diffusion hindrance or restrictions, like intra-cellular organelles, the presence of a dense nucleus, or extra-cellular collagen depositions. Related to this point, we remind the readers that our signal models do not account for contributions coming from intra-voxel incoherent flow within capillaries⁵³, which we did not simulate. For this reason, we took care to exclude b  < 100 s/mm² measurements in vivo, where vascular signals are not negligible⁵⁴. In future, we aim to increase the realism of our simulations by including a third compartment of capillary perfusion, alongside IC and EC diffusion.

Importantly, in this first demonstration of Histo-μSim we deployed numerical signal models developed from human cancers of the liver on a variety of conditions, including even, for example, fixed mouse tumours of the breast. Such an “out-of-distribution” deployment test gives confidence on the generalisability of the approach. However, this also implies that better performances could have been obtained had a more representative set of virtual tissue substrates been used to build signal models tailored for these cases (e.g., meshed mouse breast tumours for the 9.4T ex vivo mouse data). Also, we point out that care would be needed to deploy Histo-μSim in cancers that were not included in the generation of the virtual tissue models, as for example lymphomas. These are characterised by the infiltration of small, malignant lymphocytes in an organ parenchyma - a type of microstructural environment that was not included in our cancer substrates. Adding examples of lymphocyte infiltration in our meshed tissue models is one of our priorities for the next developments of Histo-μSim.

Additionally, when analysing histological images for MRI-histology validation, we segmented cellular structures manually for the ex vivo mouse data, while we used the automated cell segmentation for the analysis of patients’ biopsies. We did not carry out manual cell segmentation for the patients’ data because it was not possible to identify the exact, within-tumour location on dMR images from which the biopsy was taken. Due to this, metrics from all tumour tissue found on the HE had to be compared to a whole tumour seen on dMRI, making manual cell segmentation on HE images unfeasible. Comparisons between manual and automatic QuPath⁴⁰ cell segmentation show that while QuPath-derived varCS and skewCS differ considerably from varCS and skewCS from manual segmentations (high bias for the former, poor correlation for the latter), QuPath-derived vCS and mCS are acceptable surrogates of their manually-derived counterparts (Supplementary Table S1).

Another important aspect revealed by our MRI-histology correlation analysis is that each Histo-μSim metric exhibits correlations with several histological indices at the same time, beyond its direct histological counterpart. This is apparent, for example, for f_in∣MC, which correlates also with vCS_histo, and not only with f_in∣histo. These can be, at least in part, spurious correlations arising from the complex landscape of our non-linear fitting objective function⁴⁶, which may limit the biological specificity of the proposed technique. However, it is also possible that these correlations capture biologically meaningful associations between histological indices, since these are not fully independent among each other (Supplementary Fig. S12). For example, we observe a positive correlation between density and size of cells (i.e., between f_in∣histo and vCS_histo), which may indicate that the size of a cell influences how it interacts with the environment, and hence how a cell ensemble organises spatially, influencing the local cell density. Future work is warranted to characterise relationships among histological indices in more detail, and thus guide dMRI-based cell property characterisation.

Regarding the MRI-histology correlation study, we also point out that its main aim was to test whether salient contrasts seen in histological metrics across samples/patients are picked up non-invasively by MRI. It should be noted that an analysis of this type, while informative, does not allow for the detailed characterisation of more complex characteristics of tumours, as for example intra-tumour heterogeneity⁵⁵, defined as the existence of different clonal populations within a tumour’s cell microenvironment, and a hallmark of treatment resistance. Cancer cell heterogeneity, while commonly assessed from a genetic point of view⁵⁶, has also been shown to lead to multiple radiological phenotypes within a tumour⁵⁷, opening up its non-invasive assessment with MRI. Techniques such as Histo−μSim may equip oncologists with new tools for intra-tumour heterogeneity assessment. Ultimately, quantitative imaging approaches of this kind may play a key role for patient stratification in treatment planning, or in response assessment. However, we stress that a more sophisticated histological validation would be required compared to what has been done here, in order to deploy new intra-tumour heterogeneity assessment tools in the radiology clinic. For example, accurate co-registration between in vivo MRI and whole-tumour excisions would be required, beyond simple biopsies and ROI comparisons. Future work is warranted to elucidate these aspects.

Another aspect worth emphasising is that histopathological properties were obtained from formalin-fixed tissue. Formalin fixation can cause considerable shrinkage of tissues⁵⁸, implying that quantitative properties assessed on formalin-fixed tissue are biased, distorted versions of the true histopathological characteristics. To minimise variability caused by differing distortions from various histopathological techniques, we processed all histological material using the same pipeline and laboratory instrumentation. Nonetheless, we acknowledge that the histological properties reported in our study likely differ from the true characteristics exhibited by tissues in vivo, before excision and fixation. More accurate histological quantification could have been potentially obtained by taking the actual specimen’s shrinkage into account, and by collecting calibration data in which specimens from the same tumour undergo distinct histological procedures. Ultimately, improvements on the histological pipeline of this kind would lead to benefits on any downstream histology-informed MRI technique. In future work, we aim to explore complementary histological pipelines to enhance the performances of our proposed Histo-μSim framework even further.

Furthermore, in this work we did not study advanced diffusion encodings such as oscillating gradients⁶, double diffusion⁵⁹ or b-tensor⁶⁰ encoding, since we focussed on off-the-shelf, widespread clinical protocols. Some of these advanced encodings may improve parameter estimation compared to what has been shown here. For example, including ultra-short diffusion times through oscillating gradients may improve the estimation of D_0∣in, as this is a challenging parameter to be estimated independently of CS^46,47,48. Its inference is known to benefit from acquisitions that include short diffusion times, a fact that is confirmed in our study, being in line with the better estimation seen for protocol PGSE-ex compared, for example, to TRSE. In the future we aim to simulate more advanced dMRI acquisitions, beyond routine PGSE. These may give access to more detailed information on cancer microstructure than standard diffusion encoding, and potentially improve the estimation of CS and cell membrane permeability, with important applications in non-invasive cell profiling in cancer¹¹. Moreover, future work is warranted to assess the influence of the acquisition protocol design on Histo-μSim metrics, and to deliver compact, optimised acquisitions that maximise Histo-μSim metric quality and that are feasible under time pressure in radiology settings.

Another biological feature that was not included in our modelling framework is diffusion anisotropy. In this first demonstration of Histo-μSim, we studied diffusion protocols that include only 3 mutually orthogonal directions, and thus do not allow for accurate anisotropy quantification. In future, we plan to extend Histo-μSim to account for features related to microscopic and macroscopic diffusion anisotropy, and thus enable the modelling of signals acquired with protocols with higher angular resolution.

Lastly, we acknowledge that this work provides only a first proof-of-concept of Histo-μSim. Demonstrating adequate repeatability and reproducibility of the technique is essential before it can be adopted widely in the clinic. This will be addressed in future scan-rescan analyses, involving larger cohorts of travelling volunteers scanned across multiple sites and machines with different dMRI protocols, or patients scanned multiple times at the same site. Similarly, future optimisations will also focus on reducing the scan time required to obtain images of sufficient quality for Histo-μSim analysis. These could guide the design of acquisition strategies that bring down the scan time required from 15 to 5 minutes or less, and thus enhance the clinical applicability of the proposed method.

Conclusions

Histo-μSim, a new dMRI parameter estimation approach informed by MC simulations within tissue environments reconstructed from histology, provides histologically-meaningful indices in solid tumours within clinically-acceptable scan times. The method outperforms standard multi-compartment analytic models on in silico data, as well as in dMRI scans acquired on fixed mouse tissue ex vivo and on cancer patients in vivo. Histo-μSim may therefore play a key role in the development of new assays for the non-invasive characterisation of solid tumors in the body, and thus contribute to bringing precision oncology one step closer to the clinic.

Materials and Methods

Simulation framework

In our framework, illustrated in Fig. 1, we create 3D meshes of histological structures, such as cells, from segmentations drawn on histological images. These meshes can be used to generate random walks in MC simulations and, finally, dMRI signals, for any dMRI protocol of interest. We proceed as follows.

First, a histological image is opened with QuPath⁴⁰ and a ROI is selected and cropped, taking care to include in the image the scale of magnification. The image is then opened in Inkscape, where cells and other geometric features are manually segmented and separated into layers. We segmented cells and cell debris, luminal spaces, and vessels. Here we demonstrate the framework with careful, manual segmentation, but automatic segmentations would also be possible. Two types of files are then exported: a 3D object with all the features included included in a single SVG file, as well as an individual SVG file for each feature. The SVG format is used as it allows for further manipulation with Blender. In Blender, SVG files are then transformed into 3D ASCII PLY triangular meshes. We reconstructed 2D cellular environments from standard HE biopsies and obtained 3D meshes by simply replicating 2D contours along the trough-plane direction, thus generating cylinders with irregular sections. Nonetheless, 3D segmentations could also be used (e.g., from 3D confocal microscopy).

Meshes are fed to the MCDC Simulator, an open-source MC engine⁴¹, in order to synthesise water molecules Brownian random walks within the substrate. We used a beta-version simulating water exchange (Triangles_dev branch). Spins were seeded uniformly within the substrates, and cells where modelled as permeable³². We indicate with D_0∣in and D_0∣ex the intrinsic IC and EC diffusivities, while with κ the cell membrane permeability, with IC/EC water exchange increasing as κ increases. The water exchange implementation in MCDC follows¹⁸ and³². In this implementation, the probabilities of a spin crossing a cell membrane from the IC to the EC space or, vice versa, from the EC to the IC spaces, are

$${p}_{in\to ex}=\frac{\frac{2\,\kappa \,{l}_{in}}{3\,{D}_{0| in}}}{1+\frac{1}{2}\left(\frac{2\,\kappa \,{l}_{in}}{3\,{D}_{0| in}}+\frac{2\,\kappa \,{l}_{ex}}{3\,{D}_{0| ex}}\right)}$$

(1)

and

$${p}_{ex\to in}=\frac{\frac{2\,\kappa \,{l}_{ex}}{3\,{D}_{0| ex}}}{1+\frac{1}{2}\left(\frac{2\,\kappa \,{l}_{in}}{3\,{D}_{0| in}}+\frac{2\,\kappa \,{l}_{ex}}{3\,{D}_{0| ex}}\right)},$$

(2)

Above, ${l}_{in}=\sqrt{6\,\Delta t\,{D}_{0| in}}$ and ${l}_{ex}=\sqrt{6\,\Delta t\,{D}_{0| ex}}$ are the elementary diffusion displacements during a simulation iteration of duration Δt in the IC and EC spaces⁶¹, and κ is the effective cell membrane permeability³².

We used 5 linearly-spaced values in the range [0.8, 3] μm²/ms for both IC and EC intrinsic diffusivities (referred to as D_0∣in and D_0∣ex), and 9 values of cell membrane permeability κ in the range [0; 40] μm/s (a similar range of κ values as those used in Gardier et al.³²), covering all possible combinations of the three (225 unique (D_0∣in, D_0∣ex, κ) triplets for each substrate). Each simulation was conducted over a duration of T = 110 ms and with a step number of N_step = 2370 (temporal resolution of 46.4 μs). The simulation was performed using 20 000 walkers per substrate. As mentioned, vessel structures were included in the segmentation as they influence the patterns of diffusion, but they were not seeded with walkers. Cell debris found in necrotic areas were seeded with diffusing spins, and thus contribute to restricted diffusion. Simulations were timed for a representative substrate (substrate 4) on a 64-core, 3.169 GHz AMD Ryzen Threadripper PRO 5995WX CPU.

Regarding the range of variation of the intrinsic diffusivities D_0∣in and D_0∣ex, we chose the upper bound to match the intrinsic self-diffusivity of water at 37°C (or room temperature for ex vivo imaging). The lower bound is instead even lower than the intrinsic diffusivity of water at 0 °C (≈ 1.26 μm²/ms). This value was chosen to account for potential short-time interactions between water and nanometric structures of the IC/EC space on the microsecond scale as, for example, nuclear macromolecules, organelles or collagen fibres.

Lastly, custom-written python code was used to synthesise dMRI signals from the random walks for a given acquisition protocol of interest. The magnitude dMRI signal S is obtained as in⁵², i.e.,

$$S\,\,=\,\,\left| \frac{1}{W}{\sum}_{w=1}^{W}{e}^{-j\gamma \Delta t{\sum }_{t = 0}^{TE}{{{{\bf{g}}}}}{(t)}^{{{{{\rm{T}}}}}}{{{{{\bf{r}}}}}}_{w}(t)}\right| .$$

(3)

Above, r_w(t) is the w-th walker trajectory; Δt = T/N_step is the temporal resolution; T is the simulation duration; and g(t) is the diffusion-encoding gradient. Note that IC and EC signal fractions f_in and f_ex = 1 − f_in are T₂-weighted in principle, given that the IC/EC spaces may feature different T₂ constants^8,12. Nonetheless, in this first demonstration of our MC framework, we do not account for intra-compartment relaxation properties, in order to reduce the number of tissue parameters required to characterise the signal. A repository with step-by-step guidelines on how to implement the framework is released at https://github.com/radiomicsgroup/dMRIMC.

Reconstruction of virtual tissue environments

We reconstructed 18 cellular environments, referred to as substrates. These were derived from biopsies of malignant solid tumours of the liver (primary cancer and metastatic) of 10 different patients (1 to 3 substrates drawn per patient, see Table 1), acquired as part of ongoing imaging studies at the Vall d’Hebron Institute of Oncology (Barcelona, Spain). The substrates spanned a rich set of different cytoarchitectures, from non-cancerous liver parenchyma to cancer areas, such as dense cancer cell packings, fibrosis, necrosis, and a mix of all the above.

We characterised each substrate with the following microstructural parameters:

• ROI area and cellularity (number of cells per mm² of biopsied tissue);

• IC area fraction f_in;

• lumen fraction of EC area f_l;

• lumen diameters ${d}_{lumen}=2\sqrt{{A}_{lumen}/\pi }$, with A_lumen being the segmented lumen area;

• mean CS index mCS =  〈d_cell〉, where ${d}_{cell}=2\sqrt{{A}_{cell}/\pi }$ is the individual cell diameter calculated from its area A_cell, and 〈… 〉 is the average over the distribution in a substrate;

• CS variance index ${{{{\rm{varCS}}}}}=\langle {({d}_{cell}-{{{{\rm{mCS}}}}})}^{2}\rangle$;

• CS skewness index

  $${{{{\rm{skewCS}}}}}=\langle {({d}_{cell}-{{{{\rm{mCS}}}}})}^{3}\rangle /{{{{{\rm{varCS}}}}}}^{3/2};$$

• volume-weighted CS (vCS) index for a system with spherical geometry^1,14 (vCS_sph), defined as

  $${{{{{\rm{vCS}}}}}}_{sph}={\left(\frac{\langle {d}_{cell}^{7}\rangle }{\langle {d}_{cell}^{3}\rangle }\right)}^{1/4};$$

• vCS index for a system with cylindrical geometry^3,15 (vCS_cyl), defined as

  $${{{{{\rm{vCS}}}}}}_{cyl}={\left(\frac{\langle {d}_{cell}^{6}\rangle }{\langle {d}_{cell}^{2}\rangle }\right)}^{1/4};$$

• shape h (dimensionless) and scale c (units: μm) parameters of a gamma-distribution³⁰

  $$p({d}_{cell};h,c)\,\,=\,\,\frac{1}{\,\,\Gamma (h)\,{c}^{h}\,\,}\,{d}_{cell}^{h-1}\,{e}^{-{d}_{cell}/c},$$

  fitted to the set of cell diameters {d_cell,1,  d_cell,2,  … }. Above, $\int_{0}^{\infty }p({d}_{cell};h,c)\,d{d}_{cell}\,=\,1$, d_cell is the generic cell diameter (units: μm), and Γ(z) is the Gamma function

  $$\Gamma (z)=\int_{0}^{\infty }{t}^{z-1}{e}^{-t}\,dt,\quad \Re (z) > 0.$$

Development of simulation-informed parameter inference

We investigated the potential utility of our synthetic signals to inform microstructural parameter estimation. We synthesised DW signals according to three dMRI protocols, matching those implemented for the acquisition of ex vivo and in vivo MRI data (see sections below). We simulated 225 signals per substrate (5 values of D_0∣in × 5 values of D_0∣ex × 9 values of κ), for a total of 4050 signals. For all protocols, we obtained the final measurement set by averaging signals generated for two orthogonal directions, perpendicular to the substrate longitudinal axis, emulating trace imaging on a clinical scanner. Note that our meshes are essentially made by cylindroids with axes aligned along the z axis, implying that random walks produce free diffusion in the z direction. Because of this, we emulated trace imaging by averaging two mutually orthogonal gradient directions spanning the (x, y) plane, such that their z component was 0 (namely, g = [1 0 0]^T and g = [0 1 0]^T). However, our signal synthesis code allows for the simulation of signals for any desired gradient direction.

The simulated protocols were:

• PGSE-in: a PGSE protocol, matching that implemented on a 3T clinical system in vivo. It consisted of 3 b = 0 and 18 DW measurements, namely: b = {50, 100, 400, 900, 1200, 1500, 50, 100, 400, 900, 1200, 1500, 50, 100, 400, 900, 1200, 1500} s/mm², δ = {3.9, 5.2, 9.2, 15.0, 18.2, 21.0, 3.9, 5.2, 9.2, 13.0, 15.8, 18.5, 3.9, 5.2, 9.2, 13.0, 15.8, 18.5} ms, Δ = {27.8, 29.0, 33.0, 28.7, 31.8, 34.7, 7.8, 29.0, 33.0, 37.0, 39.6, 42.3, 7.8, 29.0, 33.0, 37.0, 39.6, 42.3} ms.

• TRSE: a DW twice-refocussed spin echo (TRSE) protocol, matching that implemented on a 1.5T clinical system in vivo. It consisted of 3 b = 0 and 18 DW measurements, namely: b = {0, 50, 100, 400, 900, 1200, 1600} s/mm², repeated for 3 different diffusion times. The duration/separation of the gradient lobes (Supplementary Fig. S1) for the 3 diffusion times were: δ₁= {8.9, 13.2, 18.9} ms, δ₂= {17.6, 19.3, 21.0} ms, δ₃ = {20.4, 24.8, 30.5} ms, δ₄ = {6.0, 7.7, 9.5} ms, Δ_1,2 = {17.4, 21.7, 27.5} ms, Δ_1,4 = {63.9, 74.2, 87.5} ms.

• PGSE-ex: a second PGSE protocol, matching that implemented on a pre-clinical 9.4T system for ex vivo imaging. It consisted of 2 b = 0 and 6 DW measurements, namely: b = {0, 500, 2000, 4500} s/mm² acquired for each of Δ = {16.5, 37.0} ms, with δ = 12 ms.

We then interpolated the set of paired examples of tissue parameters p and dMRI signals s(p) with a RBF regressor, which implements the forward model p ↦ s(p). This was finally embedded into routine NNLS fitting, based on maximum-likelihood estimation⁴⁵. To test the feasibility of using simulation-informed forward models for parameter estimation, we performed a leave-one-out experiment. Briefly, for all substrates in turn, we learnt p ↦ s(p) on noise-free signals from 17/18 substrates, and then plugged the learnt model in NNLS fitting of the noisy signals from the 18^th substrate (Rician noise; b = 0 SNR of 50). This ensured that the performance of the simulation-informed forward models was not tested on signals used to build the model itself.

We performed fitting twice, considering two different forward models p ↦ s(p):

• in forward model 1,

  $${{{{\bf{p}}}}}=\left\{{f}_{in},{D}_{0| in},{{{{{\rm{vCS}}}}}}_{cyl},{D}_{0| ex}\right\},$$

  estimating a single CS statistic (vCS_cyl) per voxel. We chose to estimate vCS_cyl, rather than mCS, to enable the comparison of model 1 to fitting a well-established multi-compartment analytical signal model (see below);

• in forward model 2 instead,

  $${{{{\bf{p}}}}}=\left\{{f}_{in},{D}_{0| in},{{{{{\rm{vCS}}}}}}_{cyl},\kappa ,{D}_{0| ex}\right\},$$

  estimating a CS statistic and the cell membrane permeability.

The quality of parameter estimation was assessed by scatter density plots and Pearson’s correlation coefficients between estimated and ground truth parameter values. Bland-Altmann plots with biases and LOA figures were also evaluated. Moreover, fitting of forward model 1 was compared to a widely-used analytical model, describing the dMRI signal as the sum of IC/EC contributions. The comparison was performed on synthetic signals from impermeable cells (κ = 0). The analytical signal model to which forward model 1 was compared against is

$$S\,\,=\,\,{f}_{in}\,{e}^{-b{{{{{\rm{ADC}}}}}}_{in}({D}_{0| in},R,\delta ,\Delta )}\,\,+\,\,(1-{f}_{in})\,{e}^{-b{{{{{\rm{ADC}}}}}}_{ex}},$$

(4)

where ADC_in characterises signal decay due to restriction within cells. This approach is used, for example, in popular techniques such as VERDICT and IMPULSED^6,7. However, while VERDICT and IMPULSED ADC_in is based on a model of spherical cells, here we used the expression for diffusion within cylinders, given the cylindrical symmetry of our substrates. We used an effective radius $R=\frac{1}{2}{{{{{\rm{vCS}}}}}}_{cyl}$. We used vCS_cyl rather than mCS since the former accounts for the fact that larger cells contain more water, and hence contribute more to the DW signal, than smaller cells³. Nonetheless, we point out that vCS_cyl is a metric prone to mesoscopic fluctuations, being highly sensitive to the tails of the cell size distribution within a voxel, with increasing sensitivity the smaller the voxel gets¹. In practice, ADC_in in Eq. (4) is written as

$${{{{{\rm{ADC}}}}}}_{in}=\frac{2\,{R}^{4}}{{D}_{0| in}\,\delta \,(\Delta -\delta /3)}{\sum}_{m=1}^{\infty }\frac{2\,{a}_{m}^{2}\,+\frac{{R}^{2}}{{D}_{0| in}\,\delta }\,({u}_{m}-2)}{{a}_{m}^{6}({a}_{m}^{2}-1)},$$

(5)

where

$${u}_{m}=2\,{e}^{-\frac{{D}_{0| in}}{{R}^{2}}\delta {a}_{m}^{2}}+2\,{e}^{-\frac{{D}_{0| in}}{{R}^{2}}\Delta {a}_{m}^{2}}-{e}^{-\frac{{D}_{0| in}}{{R}^{2}}(\Delta -\delta ){a}_{m}^{2}}-{e}^{-\frac{{D}_{0| in}}{{R}^{2}}(\Delta +\delta ){a}_{m}^{2}}.$$

(6)

Above, D_0∣in is the intra-cylinder diffusivity, a_m is the m-th root of ${J}_{1}^{{\prime} }(x)=0$, with J₁(x) being the Bessel function of the first kind, order 1, and ${J}_{1}^{{\prime} }(x)=\frac{d}{dx}{J}_{1}(x)$⁶². Note that the analytical model in Eq. (5), while common in dMRI literature, lacks higher-order terms in each compartment. It is therefore only a crude approximation of the signal from realistic biological structures at a given b, δ and Δ, since variety in cell shape and morphology exists. This fact is indeed what motivates our efforts to build numerical dMRI signal models informed directly by simulations, which do not rely on approximated analytical signal expressions.

Histological validation of Histo-μSim MRI on ex vivo mouse tissue

We tested simulation-informed fitting on pre-clinical dMRI data, which were acquired on 8 formalin-fixed ex vivo mouse tissue specimens, namely: a non-cancerous breast sample; 3 breast tumours from the MMTV PyMT model^33,34, obtained at weeks 9, 11 and 14; a normal spleen and a spleen suffering from splenomegaly, secondary to advanced breast cancer in one MMTV mouse; two kidneys from C57BL/6 WT male mice (9 weeks old), one normal and one with folic acid-induced injury³⁵. Mice were housed at the Specific Pathogen-Free barrier area of the Vall d’Hebron Institute of Oncology (VHIO). We have complied with all relevant ethical regulations for animal use. All animal procedures were approved by the Animal Care unit and the Ethics Committee for Animal Experimentation (CEEA) of the Vall d’Hebron Research Institute (VHIR) and the Generalitat de Catalunya, and were performed according to the European legal framework for research animal use and bioethics. Animals were monitored daily and euthanised upon signs of humane endpoints. Two mouse models were used, generating breast, spleen and kidney samples. These were processed for further histological analyses, as part of ongoing studies at VHIO. A dMRI scan of the tissue was performed at room temperature before inclusion in paraffin for histology.

MMTV-PyMT transgenic mouse model

The MMTV-PyMT FVB/NJ mouse strain³³ is commonly employed to mimic human breast cancer progression³⁴. The model relies on the MMTV long terminal repeat promoter, which drives the expression of the antigen of PyMT, a potent oncogene. These transgenic mice are viable despite loss of lactational ability, which is coincident with the transgene expression. Breast tumours arise in virgin and breeder females as well as in males starting from 9 weeks of age. Splenomegaly is also observed at the latter stages of the tumour growth. For this study, we used 4 MMTV-PyMT FVB/NJ female mice, which were euthanised by CO₂ asphyxiation at different time points to collect the following samples: non-cancerous breast and non-pathological spleen (2 weeks); a breast tumour at weeks 9, 11 and 14; an enlarged spleen (splenomegaly) at late stage cancer (14 weeks).

Folic acid-induced kidney injury

The folic acid-induced kidney injury mouse model is based on the fact that high doses of folic acid are toxic, despite being the same substance beneficial at low doses³⁵. For this study, we used two male mice (C57BL/6 WT, approximately 9 weeks old), which were intra-peritoneally injected with a single dose of vehicle (300 mM NaHCO₃) or with folic acid (250 mg/kg). 30 days after the injection, mice were euthanised by CO₂ asphyxiation and the kidneys were collected for downstream processing.

dMRI acquisition

Briefly, collected tissues were fixed for 24 hours in buffered 4% formaldehyde, transferred to phosphate-buffered saline (PBS) solution and embedded in 1% agarose gel dissolved in PBS, within a histological cassette. Embedded samples were kept in PBS solution, and scanned at room temperature on a 9.4T Bruker Avance system, with 200 mT/m gradient insert and a RX/TX birdcage coil. The protocol included a high resolution anatomical T2-weighted RARE scan, and dMRI (DW spin echo), with the protocol matching the PGSE-ex protocol described above (see Materials and Methods; same nominal b-values, and same gradient timings). Other salient dMRI scan parameters were: fat suppression with a frequency-selective 90 degree gauss512 pulse (bandwidth: 1400.1  Hz); resolution 0.2 × 0.2 × 0.57 mm³, TE = 55.1 ms, TR = 2250 ms, 3 mutually-orthogonal direction for each gradient timing and b-value. The maximum gradient strength was of 189.5 mT/m. The total duration of the dMRI protocol was of 210 minutes.

Histology acquisition

After MRI, samples were transferred to 70% ethanol for 24 hours and then embedded in paraffin. 3 μm-thick sections were obtained on a manual microtome and stained with HE, using a robust carousel tissue stainer (Slee Medical) according to common methods. Digital images of the HE-stained sections were acquired on a Hamamatsu C9600-12 scanner (resolution: 0.45 μm). To maximise the co-localisation between MRI and histology in our mouse data, we took several HE sections of each mouse specimen, at different depths, spanning the whole tissue sample.

dMR image processing

dMRI scans were denoised⁶³ and Gibbs ringing was mitigated⁶⁴. Maps from forward model 2 were computed voxel-by-voxel, via NNLS regularised maximum-likelihood fitting. Metrics were: f_in, D_0∣in, vCS_cyl, κ, D_0∣ex. When learning the forward signal model via RBF regression, we pooled together all 4050 signals from all substrates. For comparison, we also fitted an analytical signal model voxel-by-voxel. The model accounted again for restricted IC diffusion and hindered EC diffusion, and is thus equivalent to that of Eq. (4). However, in this case we used the expression of IC ADC derived for diffusion within spheres, rather than for cylinders⁶⁵. For all model fitting (MC-informed and analytical), L2 regularisation of the fitting objective function was used. The freely-available bodymritools python tools were used (https://github.com/fragrussu/bodymritools; scripts mri2micro_dictml.py and pgse2sphereinex.py).

We computed the mean values of the IC fraction, volume weighted CS and cell membrane permeability in 18 ROIs, drawn in homogenous areas, far from edges and from the location of sharp contrasts on the b = 0 dMRI image, and in areas with negligible fat content as seen on histology (ROIs illustrated in Supplementary Fig. S13). We indicated the metrics as follows: f_in∣MC, vCS_cyl∣MC and κ for Histo-μSim MC-informed fitting; f_in∣AN, vCS_sph∣AN for analytical model fitting.

Histological image processing

In parallel, we also processed the HE images to obtain histological counterparts of MRI metrics. We manually segmented cells in histological ROIs, and computed f_in∣histo, vCS_sph∣histo, vCS_cyl∣histo and mCS_histo, given the set of segmented cells, as illustrated for the tissue environment generation above. Note that we did not co-register HE and MR images in this study; practically, this means that each ROI had to be drawn twice, once on the b = 0 dMR image, and once on the HE, in the same approximate location. Segmentation was not performed in areas rich of fat as seen on HE images, given that dMRI acquisitions are fat-suppressed. For reference, we also obtained cell segmentations automatically, using QuPath⁴⁰, and compared manually-derived and QuPath-derived histological metrics. For this, we calculated Pearson’s correlations between manually-derived and QuPath-derived histological metrics. Additionally, we also evaluated a Bias Index (BI), defined as BI = median(E), where $E=100\,\frac{({m}_{QuPath}-{m}_{manual})}{{m}_{manual}}$. m_QuPath/m_manual represents the generic metric obtained from QuPath/manual segmentations, and IQR is the inter-quartile range. BI quantifies the bias of QuPath-derived histological indices compared to reference values obtained through manual cell segmentation. Note that when processing histological ROIs for MRI-histological comparison, we did not create 3D meshes, since the 2D cell outlines drawn on the HE images sufficed for histological property estimation (e.g., estimation of f_in, vCS, etc).

MRI-histology correlation analysis and ROI characterisation

We computed Pearson’s correlation coefficients among all possible ROI-wise mean values of Histo-μSim and histological metrics, namely: f_in∣histo, vCS_sph∣histo, vCS_cyl∣histo, mCS_histo (manually-derived histological metrics); f_in∣MC, vCS_cyl∣MC, κ, D_0∣in∣MC and D_0∣ex∣MC (Histo-μSim MC-informed fitting). To characterise the performance of Histo-μSim in each ROI, we also computed a summary coefficient of determination (R²) between the dMRI signal measurements and the signal predictions from model fitting. R² quantifies the fraction of the signal measurement variability that is explained by the model, and is is directly comparable across ROIs. In practice, R² was computed as

$${{{{{\rm{R}}}}}}^{2}=1-\frac{S{S}_{res}}{S{S}_{tot}},$$

(7)

pooling together DW measurements from all voxels within an ROI. Above, $S{S}_{res}={\sum }_{voxels}{\sum }_{m = 1}^{M}{\left({a}_{m}-\sqrt{{s}_{m}^{2}+{\eta }^{2}}\right)}^{2}$ is the residual sum of squares, while $S{S}_{tot}={\sum }_{voxels}\mathop{\sum }_{m = 1}^{M}{({a}_{m}-\bar{a})}^{2}$ is the total sum of squares, having indicated with M the number of dMRI measurements; with a_m and s_m the m-th dMRI measurement and the m-th signal prediction from Histo-μSim; with η the estimated noise floor; and with $\bar{a}$ the quantity $\bar{a}=\frac{1}{M}\mathop{\sum }_{m = 1}^{M}{a}_{m}$.

The correlations between Histo-μSim and histological metrics were benchmarked against those of the corresponding metrics from the standard two-compartment analytical signal model, namely: f_in∣AN, vCS_sph∣AN, D_0∣in∣AN and ADC_ex∣AN.

In vivo demonstration of Histo-μSim in cancer patients

Lastly, we also tested the feasibility of Histo-μSim in actual in vivo dMRI scans of cancer patients, which were acquired as part of ongoing imaging studies at the Vall d’Hebron Institute of Oncology. All ethical regulations relevant to human research participants were followed. All participants provided informed written consent, and were scanned in imaging sessions approved by the Clinical Research Ethics Committee (CEIm) of the Barcelona Vall d’Hebron University Hospital (VHUH) (code: PR(AG)29/2020). We studied scans from 27 patients suffering from advanced solid tumours, candidate for phase I clinical trials at the VHUH, and referred to as Cases 0 to 26, with the case ID being randomly generated for this article. Scans were acquired at either abdominal or pelvic level, using a 1.5T Siemens Avanto system (10 cases) and a 3T GE SIGNA Pioneer system were used (17 cases). Additionally, an ultrasound-guided biopsy was collected from one of the tumours approximately one week after MRI.

dMRI acquisition

For the 1.5T system, the protocol included anatomical T2-weighted fast spin echo imaging and dMRI. dMRI was based on a DW TRSE Echo Planar Imaging (EPI) sequence, with the diffusion encoding protocol matching exactly the TRSE protocol used in simulations (see above for details). Other salient parameters were: resolution 1.9  × 1.9  × 6 mm³, TE = {93, 105, 120} ms, TR = 7900 ms, trace DW imaging, NEX = 2, GRAPPA = 2, 6/8 Partial Fourier imaging, BW = 1430 Hz/pixel, acquisition of a b = 0 image with reversed phase encoding. The maximum gradient strength was of 40.8 mT/m. For the 3T scanner instead, the protocol also included anatomical T2-weighted fast spin echo imaging and dMRI, acquired with PGSE EPI according to the “PGSE-in” protocol described in simulations above. Other salient parameters were: resolution 2.4  × 2.4  × 6 mm³, TE = {75, 90, 105} ms, TR  ≈ 3000 ms (respiratory gated), trace DW imaging, NEX = 2, ASSET = 2, BW = 1953 Hz/pixel. The maximum gradient strength was of 48.5 mT/m. The dMRI protocol took approximately 15 minutes in both machines. A schematic of the PGSE and TRSE DW sequences is included in Supplementary Fig. S1.

Histology acquisition

We obtained ultrasound-guided biopsies from one of the imaged tumours, obtained approximately one week after dMRI. The histological material underwent standard processing, form which we obtained HE-stained sections, which we digitised a Hamamatsu C9600-12 slide scanner (resolution: 0.45 μm).

dMR image processing

Scans were denoised⁶³, corrected for Gibbs ringing⁶⁴ and motion, and EPI distortions mitigated (1.5T system only)⁶⁶. A characteristic SNR was computed for each subject by dividing the signal at b = 0 and at the minimum TE after denoising, by the estimated noise standard deviation σ. Afterwards, each DW image was normalised to the b = 0 acquired at the corresponding TE⁷, and forward model 2 was fitted voxel-by-voxel (regularised maximum-likelihood NNLS fitting; images for b ≤ 100 s/mm² were excluded to minimising vascular contributions) within tumours, whose outline was drawn manually on the dMRI scan by an experienced radiologist (R.P.L.). For comparison, we also fitted the same multi-exponential analytical model deployed on the ex vivo mouse scans, accounting for restricted IC diffusion within spherical cells and hindered extra-cellular diffusion. Note that to our knowledge, no analytical signal expression exists for restricted IC diffusion within spherical cells for the TRSE acquisition. For this reason, we replaced the IC analytical signal expression with a continuous RBF interpolation of signals generated through MC simulations⁴¹ within meshed spheres.

For all model fitting (MC-informed and analytical), L2 regularisation of the fitting objective function was used. Finally, mean values of all dMRI metrics within the tumours were extracted and reported just like in the ex vivo demonstration.

Histology image processing

Histological material underwent standard histological processing (dehydration; paraffin-embedding; cutting on a microtome of 3 μm-thick sections; HE staining). An experienced pathologist (S.S.) inspected HE-stained biopsies and outlined the tumour tissue, on which we segmented cells automatically using QuPath⁴⁰. Segmented cells were collected and per-biopsy histological metrics were computed. As mentioned for the mouse data above, we did not create 3D meshes from the 2D cell segmentations obtained on the HE biopsies, since these 2D outlines sufficed for histological property estimation.

MRI-histology correlation analysis

Similarly to what was performed with mouse dMRI data, we evaluated Pearson’s correlation coefficients between histological and dMRI metrics. To this end, we obtained per-patient representative dMRI indices by averaging parametric maps across tumoural voxels. In summary, we focussed on the following metrics. For histology: IC fraction f_in∣histo, volume-weighted CS and mean CS (vCS_cyl∣histo, vCS_sph∣histo and mCS_histo). For Histo-μSim: IC fraction f_in∣MC vCS_cyl∣MC and κ. For the analytical signal model: IC fraction f_in∣MC and vCS_sph∣AN.

Comparison across primary cancer types

We compared MRI and histological metrics through t-tests across the two most frequent primary cancer types in our in vivo cohort, namely CRC and melanoma. These tests investigated whether MRI can non-invasively detect different cancer phenotypes at the cellular level, given that CRC is known to be characterised by the presence of large luminal spaces, with reduced cell density, unlike melanoma.

Analysis of Histo-μSim model fitting quality

Models and parameters

Lastly, we compared the quality of Histo-μSim fitting to other popular models and representation of the dMRI signal. This analysis was performed on dMRI measurements from both mouse tissue scanned ex vivo, as well as on human scans acquired in vivo. In more detail, we compared Histo-μSim forward model 2 to the two-compartment analytical model described above. Additionally, we also compared it to popular DKI³⁸ and to RSI³⁹.

In DKI, the dMRI signal is parametrised as

$$s\,\,\,=\,\,\,{s}_{0}\,\,{e}^{-b\,{{{{\rm{ADC}}}}}+\,\frac{K}{6}\,{(b\,{{{{\rm{ADC}}}}})}^{2}},$$

(8)

as a function of the b-value, where ADC and K are respectively the apparent diffusion and kurtosis coefficients.

In RSI instead, the dMRI signal is expressed as a linear combination of exponential functions, describing signal contribution from different water compartments. In this work, we used a 3-compartment RSI model, where the dMRI signal is written as

$$s\,\,\,=\,\,\,{s}_{0}\,\,\mathop{\sum }_{n=1}^{3}{c}_{n}\,{e}^{-b{D}_{n}}.$$

(9)

In Eq. (9) above, the 3 exponential functions describe signal from restricted, hindered and free water. Their diffusion coefficients are fixed to D₁ = 0.1 μm²/ms (restricted water), D₂ = 1.8 μm²/ms (hindered water) and D₃ = 3.6 μm²/ms (free water) in vivo⁶⁷, while to D₁ = 0.1 μm²/ms, D₂ = 1.3 μm²/ms and D₃ = 2.5  μm²/ms ex vivo. The lower diffusivity values ex vivo account for the lower temperature (room temperature vs body temperature), as well as for reduced water mobility caused by formalin fixation⁶⁸.

In summary, the following parameters were estimated for each dMRI technique (excluding the b = 0 signal):

• 5 parameters for Histo-μSim: {f_in, D_0∣in, vCS_cyl, D_0∣ex, κ};

• 4 parameters for the two-compartment analytical model: {f_in, D_0∣in, vCS_sph, ADC_ex};

• 2 parameters for RSI: {f₁, f₂}, such that c₁ = f₁, c₂ = (1 − f₁)f₂ and c₃ = (1 − f₁)(1 − f₂) in Eq. (9) above;

• 2 parameters for DKI: {ADC, K}.

Quality of fit comparison

For all dMRI approaches (Histo-μSim, two-compartment analytical model, DKI, and RSI), fitting was performed by minimising the MSE over the dMRI measurement set for an offset Gaussian noise model⁴⁵, defined as

$$MSE\,\,\,=\,\,\,\frac{1}{M}\mathop{\sum }_{m=1}^{M}{\left({a}_{m}-\sqrt{{s}_{m}^{2}+{\eta }^{2}}\right)}^{2}.$$

(10)

In the expression above, a_m is the m-th out of M measurements, s_m is the corresponding model prediction, and η accounts for the noise floor. MSE measures the model fitting quality, with lower MSE pointing towards better fits. From the MSE, the BIC³⁶ can be computed as

$$BIC\,\,\,=\,\,\,P\,ln(M)\,\,-\,\,2\,ln({{{{\mathscr{L}}}}}),$$

(11)

where

$$ln\,({{{{\mathscr{L}}}}})\,\,\,=\,\,\,-\,\frac{M}{\,2{\sigma }^{2}\,}MSE\,\,-\,\,\frac{M}{2}\,ln\left(\sqrt{2\pi {\sigma }^{2}}\right)$$

(12)

is the log-likelihood function, σ the noise standard deviation, P the number of free model parameters, and M the number of dMRI signal measurements. Lower BIC values point towards better model performances. However, as compared to MSE, BIC includes a penality term that penalises model complexity (∝ P).

We computed MSE and BIC for all models voxel-by-voxel on both mouse and human scans. Afterwards, we ranked models for each mouse/human scans according to both MSE and BIC. The top-ranking model was the one providing the lowest MSE/BIC in the largest proportion of voxels.

Statistics and reproducibility

All statistical analysis was performed with custom Python scripts using standard scientific libraries when possible. Comparisons between ground truth and estimated tissue parameters in silico, and between histological and MRI metrics in the mouse and human data set were performed by computing the Pearson’s correlation coefficient. Our analysis code relied on SciPy⁶⁹ (v.1.12.0) and NumPy⁷⁰ (v.1.26.4). A p-value < 0.05 was considered statistically significant. The sample size (n) varied across in silico, mouse, and human data. The exact value of n has been reported in the caption of each relevant figure.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.